磁学_6
电磁学练习题

电磁学练习题2第六章 静电场1一、选择题1、下列几个叙述中哪一个是正确的? [ ](A )电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向。
(B )在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同。
(C )场强方向可由E =F/q 定出,其中q 为试验电荷的电量,q 可正、可负,F为试验电荷所受的电场力。
(D )以上说法都不正确。
2、一均匀带电球面,电荷面密度为σ,球面内电场强度处处为零,球面上面元dS 带有dS σ的电荷,该电荷在球面内各点产生的电场强度为 [ ] (A) 处处为零; (B) 不一定都为零; (C) 处处不为零; (D) 无法判断。
3、如图所示,任一闭合曲面SO为S面上任一点,若将q由闭合曲面内的P点移到T点,且OP=OT,那么[ ](A) 穿过S面的电通量改变,O点的场强大小不变;(B) 穿过S面的电通量改变,O点的场强大小改变;(C) 穿过S面的电通量不变,O点的场强大小改变;(D) 穿过S面的电通量不变,O点的场强大小不变。
4、关于高斯定理的理解有下面几种说法,其中正确的是[ ](A) 如果高斯面内无电荷,则高斯面上E 处处为零;(B) 如果高斯面上E 处处不为零,则该面内必无电荷;(C) 如果高斯面内有净电荷,则通过该面的电通量必不为零;34(D) 如果高斯面上E处处为零,则该面内必无电荷。
5、 两个均匀带电的同心球面,半径分别为R 1、R 2(R 1<R 2),小球带电Q ,大球带电-Q ,下列各图中哪一个正确表示了电场的分布 [ ](A) (B) (C) (D) 二、填空题1、 如图所示,边长分别为a 和b的矩形,其A 、B 、C 三个顶点上分别放置三个电量均为q的点电荷,则中心O 点的场强为 方向 。
2、在场强为E的均匀电场中,有一半径ABC60b aOO 1R 2R ErO 1R 2R E rO 1R 2R E rO 2R E1R r5为R 长为L 的圆柱面,其轴线与E的方向垂直,在通过轴线并垂直E方向将此柱面切去一半,如图所示,则穿过剩下的半圆柱面的电场强度通量等于 。
电磁学-自测题6

第六章 磁场中的磁介质一、判断题(正确划“√”错误码划“×” )1.顺磁性物质也具有抗磁性。
( )2.只有当M =恒量时,介质内部才没有磁化电流。
( )3.只要介质是均匀的,在介质中除了有体分布的传导电流的地方,介质内部无体分布的磁化电流。
( )4.磁化电流具有闭合性。
( )5.H 仅由传导电流决定而与磁化电流无关。
( )6.均匀磁化永久磁棒内H 与B 方向相反,棒外H 与B 方向相同。
( )7.永磁铁磁场的H 线有头有尾不能闭合。
( )8.由磁场的高斯定理0S d ⋅=⎰B S ,可以得出0S d ⋅=⎰H S 的结论。
( )9. 当各向同性而均匀的线性磁介质磁化后,磁化电流密度与传导电流密度的关系为()r 01j j μ'=-.( )10. 任何长度的沿轴向磁化的磁棒中垂面上侧表面内外两点1、2(见图)的磁场强度H 相等;磁感应强度不B 相等. ( )11.磁感线在两种不同磁介质的分界面上一般都会发生“折射”,设界面两侧介质的相对磁导率分别为21r r μμ和,界面两侧磁感线与界面法线的夹角分别为212121r r tg tg μμ=θθθθ,则有和。
( )12.如果均匀磁介质未充满磁场存在的整个空间,但介质在磁场中的分布具有适合应用安培环路定理的对称性时,介质中的磁感强度为传导电流单独产生的磁感强度的r μ倍。
( )13.对细长磁棒,磁棒内任意点的磁感强度都相等,即0B M μ=。
( ) 14.B H r μμ01=,只适用于各向同性线性非铁磁介质。
( ) 15.有人说,因为磁感线是连续的、闭合的。
既然在细长均匀永久磁化棒内M B 0μ=,那么在磁棒两端,不论在棒内还是在棒外,M B 0μ=都成立。
( )16.在铁磁质中,B 和H 的关系不是线性的,比例系数r μ也不是常数。
( )17.铁磁性物质的磁化强度比顺磁性物质要达得多,其磁性起源于电子的自旋。
( )18.在磁介质中,H 一定与B 同方向的. ( )19.实用上可用铁壳作磁屏蔽,当把一个薄铁壳放在磁场中时,其包围空间的磁场就绝对为零. ( )20. 在均匀磁化的无限大磁介质中挖去一个半径为r ,高为h 的圆柱形空腔,而不扰乱其余部分的磁化,此空腔的轴平行于磁化强度M 。
高考物理电磁学知识点之磁场知识点总复习附答案(6)
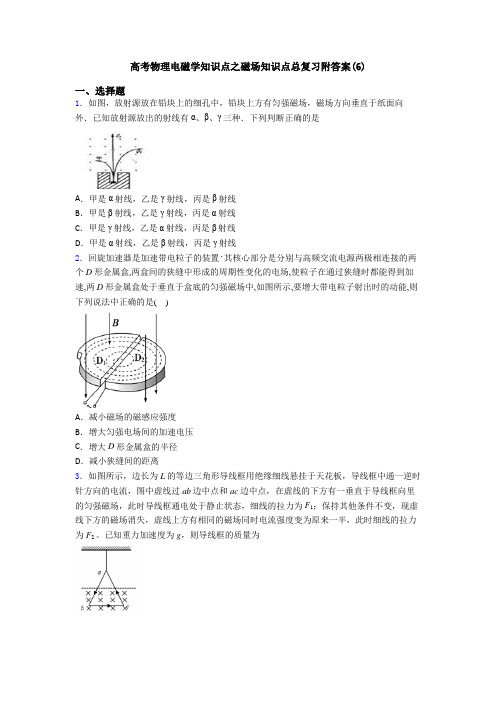
高考物理电磁学知识点之磁场知识点总复习附答案(6)一、选择题1.如图,放射源放在铅块上的细孔中,铅块上方有匀强磁场,磁场方向垂直于纸面向外.已知放射源放出的射线有α、β、γ三种.下列判断正确的是A.甲是α射线,乙是γ射线,丙是β射线B.甲是β射线,乙是γ射线,丙是α射线C.甲是γ射线,乙是α射线,丙是β射线D.甲是α射线,乙是β射线,丙是γ射线.其核心部分是分别与高频交流电源两极相连接的两2.回旋加速器是加速带电粒子的装置个D形金属盒,两盒间的狭缝中形成的周期性变化的电场,使粒子在通过狭缝时都能得到加速,两D形金属盒处于垂直于盒底的匀强磁场中,如图所示,要增大带电粒子射出时的动能,则下列说法中正确的是( )A.减小磁场的磁感应强度B.增大匀强电场间的加速电压C.增大D形金属盒的半径D.减小狭缝间的距离3.如图所示,边长为L的等边三角形导线框用绝缘细线悬挂于天花板,导线框中通一逆时针方向的电流,图中虚线过ab边中点和ac边中点,在虚线的下方有一垂直于导线框向里的匀强磁场,此时导线框通电处于静止状态,细线的拉力为F1;保持其他条件不变,现虚线下方的磁场消失,虚线上方有相同的磁场同时电流强度变为原来一半,此时细线的拉力为F2 。
已知重力加速度为g,则导线框的质量为A .2123F F g +B .212 3F F g -C .21F F g -D .21 F F g+ 4.如图甲是磁电式电流表的结构图,蹄形磁铁和铁芯间的磁场均匀辐向分布。
线圈中a 、b 两条导线长度均为l ,未通电流时,a 、b 处于图乙所示位置,两条导线所在处的磁感应强度大小均为B 。
通电后,a 导线中电流方向垂直纸面向外,大小为I ,则( )A .该磁场是匀强磁场B .线圈平面总与磁场方向垂直C .线圈将逆时针转动D .a 导线受到的安培力大小始终为BI l5.对磁感应强度的理解,下列说法错误的是( )A .磁感应强度与磁场力F 成正比,与检验电流元IL 成反比B .磁感应强度的方向也就是该处磁感线的切线方向C .磁场中各点磁感应强度的大小和方向是一定的,与检验电流I 无关D .磁感线越密,磁感应强度越大6.如图,一带电粒子在正交的匀强电场和匀强磁场中做匀速圆周运动。
电磁学[赵凯华]答案及解析[第6章麦克斯韦电磁理论]
![电磁学[赵凯华]答案及解析[第6章麦克斯韦电磁理论]](https://img.taocdn.com/s3/m/a3274606453610661ed9f42b.png)
1 一平行板电容器的两极板都是半径为的圆导体片,在充电时,其中电场强度的变化率为:。
试求:(1)两极板间的位移电流;(2)极板边缘的磁感应强度。
解: (1)如图所示,根据电容器极板带电情况,可知电场强度的方向水平向右(电位移矢量的方向与的方向相同)。
因电容器中为真空,故。
忽略边缘效应,电场只分布在两板之间的空间内,且为匀强电场。
已知圆板的面积,故穿过该面积的的通量为由位移电流的定义式,得电容器两板间位移电流为因,所以的方向与的方向相同,即位移电流的方向与的方向相同。
(2)由于忽略边缘效应,则可认为两极板间的电场变化率是相同的,则极板间的位移电流是轴对称分布的,因此由它所产生的磁场对于两板中心线也具有轴对称性。
在平行板电容器中沿极板边缘作以半径为的圆,其上的大小相等,选积分方向与方向一致,则由安培环路定理可得(全电流)因在电容器内传导电流,位移电流为,则全电流为所以极板边缘的磁感应强度为根据右手螺旋定则,可知电容器边缘处的磁感应强度的方向,如图所示。
2 一平行板电容器的两极板为圆形金属板,面积均为,接于一交流电源时,板上的电荷随时间变化,即。
试求:(1)电容器中的位移电流密度的大小;(2)设为由圆板中心到该点的距离,两板之间的磁感应强度分布。
解: (1)由题意可知,,对于平行板电容器电位移矢量的大小为所以,位移电流密度的大小为(2)由于电容器内无传导电流,故。
又由于位移电流具有轴对称性,故可用安培环路求解磁感应强度。
设为圆板中心到场点的距离,并以为半径做圆周路径。
根据全电流安培环路定理可知通过所围面积的位移电流为所以. 最后可得3. 如图(a)所示,用二面积为的大圆盘组成一间距为的平行板电容器,用两根长导线垂直地接在二圆盘的中心。
今用可调电源使此电容器以恒定的电流充电,试求:(1)此电容器中位移电流密度;(2)如图(b)所示,电容器中点的磁感应强度;(3)证明在此电容器中从半径为﹑厚度为的圆柱体表面流进的电磁能与圆柱体内增加的电磁能相等。
第六章 材料的磁学性能

5、亚铁磁体 • μr>>1,χ>0。 • 它是反铁磁体的一个变种,其内部的原子磁 矩之间存在着反铁磁相互作用,只是两种相 反平行排列的磁矩大小不同,导致了一定的 自发磁化。所以在外加磁场中的表现与铁磁 体相似。 • 亚铁磁体多为金属氧化物。Χ比铁磁体小。 • 例如:铁氧体(磁铁矿,Fe3O4)、V、Cr、 Mn、Fe、Co等与O、S、Te、P、As、Sb 等的化合物,钕铁硼磁体,稀土与金属间的
2012-10-25 24
三、正离子的顺磁性 • 正原子的顺磁性来源于原子的固有磁矩。 • 原子的固有磁矩就是电子轨道磁矩和电子自旋磁矩的 矢量和,又称本征磁矩,Pm。 • 如果原子中所有电子壳层都是填满的,由于形成一个 球形对称的集体,则电子轨道磁矩和自旋磁矩各自相 抵消,Pm=0,不产生顺磁性。 • 因此,产生顺磁性的条件就是: Pm≠0。在如下情况下, Pm≠0: 1. 具有奇数个电子的原子或点阵缺陷; 2. 内壳层未被填满的原子或离子。如过渡族金属(d壳层 没有填满电子)和稀土金属(f壳层未填满电子)。
2012-10-25 25
• 在B0=0时,由于原子的热运动,各原子的磁矩倾 向于混乱分布,此时原子的动能Ek∝kT。对外表 现出宏观磁特性H’=0。 • 当加上外加磁场时,外磁场要使原子磁矩Pm与 B0的夹角θ 减小。使原子磁矩转向外加磁场方向。 • 当外磁场逐渐增加到使能量U=-PmB0cosθ 的减 少能补偿热运动能量时,原子磁矩就一致排列了。 此时有kT=PmB0。
2
rj
22
2012-10-25
则可得:
2
抗
Ne 0
2
6m
j1
z
rj
磁学基础知识

磁学基础知识一、磁性材料1.磁性:物体吸引铁、镍、钴等物质的性质。
2.磁体:具有磁性的物体。
3.磁极:磁体上磁性最强的部分,分为南极和北极。
4.磁性材料:具有磁性的物质,如铁、镍、钴及其合金。
5.硬磁材料:一经磁化,磁性不易消失的材料,如铁磁性材料。
6.软磁材料:磁化后,磁性容易消失的材料,如软铁、硅钢等。
7.磁场:磁体周围存在的一种特殊的物质,它影响着磁体和铁磁性物质。
8.磁场线:用来描述磁场分布的假想线条,从磁南极指向磁北极。
9.磁感线:用来表示磁场强度和方向的线条,从磁南极出发,回到磁北极。
10.磁通量:磁场穿过某一面积的总量,用Φ表示,单位为韦伯(Wb)。
11.磁通密度:单位面积上磁通量的大小,用B表示,单位为特斯拉(T)。
三、磁场强度1.磁场强度:磁场对单位长度导线所产生的力,用H表示,单位为安培/米(A/m)。
2.磁感应强度:磁场对放入其中的导线所产生的磁力,用B表示,单位为特斯拉(T)。
3.磁化强度:磁性材料内部磁畴的磁化程度,用M表示,单位为安培/米(A/m)。
4.磁化:磁性材料在外磁场作用下,内部磁畴的排列发生变化,产生磁性的过程。
5.顺磁性:磁化后,磁畴的排列与外磁场方向相同的现象。
6.抗磁性:磁化后,磁畴的排列与外磁场方向相反的现象。
7.铁磁性:磁化后,磁畴的排列在外磁场作用下,相互一致的现象。
8.磁路:磁场从磁体出发,经过空气或其他磁性材料,到达另一磁体的路径。
9.磁阻:磁场在传播过程中遇到的阻力,类似于电学中的电阻。
10.磁导率:材料对磁场的导磁能力,用μ表示,单位为亨利/米(H/m)。
11.磁芯:具有高磁导率的材料,用于集中和引导磁场。
六、磁现象的应用1.电动机:利用电流在磁场中受力的原理,将电能转化为机械能。
2.发电机:利用磁场的变化在导体中产生电流的原理,将机械能转化为电能。
3.变压器:利用电磁感应原理,改变交流电压。
4.磁记录:利用磁性材料记录和存储信息,如硬盘、磁带等。
第6章 恒定磁场

第6章 恒定磁场一、目的与要求1.掌握磁感应强度的概念和毕奥—萨伐尔定律,能用毕奥—萨伐尔定律和磁场叠加原理熟练求解简单情况下电流的磁场分布。
2.掌握磁通量的概念,磁场的高斯定理及安培环路定理,会计算给定面的磁通量,并能利用安培环路定理求解具有对称性的电流的磁场分布。
3.掌握磁场对载流导线的作用和对平面载流线圈的作用力矩,会计算磁力的功;能分析和计算电荷在正交的均匀电磁场中的受力和运动情况;了解霍尔效应。
4.理解磁介质的磁化机理,掌握有磁介质时的安培环路定理及其应用。
二、内容提要1.描述磁场的物理量——磁感应强度 (1)磁感应强度的概念 磁感应强度B 的大小:lI F B d d max=磁感应强度B 的方向:电流元l d I 受力为零时l d I 的所在方向,且满足关系B l F ⨯=d d I(2)毕奥——萨伐尔定律 30d π4d r I rl B ⨯=μ(3)运动电荷的磁场30π4r q r B ⨯=v μ2.磁通量⎰⋅=ΦSm S B d3.描述磁场性质的两个定理 (1)磁场的高斯定理: 0d =⋅⎰SS B(2)安培环路定理: ∑⎰=⋅)(0d 内i L I μl B 4.磁场对电流的作用 (1)磁场对载流导线的作用力B l F ⎰⨯=LI d(2)均匀磁场对刚性平面载流线圈的作用线圈所受的合力∑=0F线圈所受的力矩B P M ⨯=m 其中n P IS m =,为载流线圈的磁矩。
5.磁力的功若载流导线或线圈中有恒定电流I 时,均匀磁场对载流导线或载流线圈所作的功均可表示为m I A ∆Φ=其中m ∆Φ通过载流线圈的磁通量的增量。
6.磁场对运动电荷的作用力B f ⨯=v q7.霍尔效应:在磁场中载流导线上出现横向电势差的现象。
横向电势差为dd IBk nq IB u ab ==8.物质的磁化(1)磁介质的分类:顺磁质,抗磁质,铁磁质。
(2)磁介质中的安培环路定理:∑⎰=⋅ii LI)(d 0内l H(3)铁磁质有磁滞现象。
电磁学 (6)

15。一个载流线圈的磁距m定义为m=SI其中为线圈面积。 试证明,对于习题11_4中各种形状的线圈,到中心的距离 r0远大于线圈的线度使,轴线上磁感强度都具有如下形式 B=µ0m/2π r03 证明:(1)圆电流中心轴线上 B = 它可写为
3( B cos α ) = 3 3µ 0 Ia 2π a 2 + 3r0
a I a I a a I
I
2 × 4π × 10 −7 × 20 −5 (2) B = = 8 . 0 × 10 (T ) −2 π × 20 × 10
10.如附图所示,两条无限长直载流导线垂直而不相交,其 间最近距离为d=2.0厘米,电流分别为I=4.0安和I=6.0安.点 到两直线距离都是d,求点的磁感强度B. 解:依题意可求得
[
µ 0 I 1 R1
2
2 2 3/ 2
]
+
2 R2 + (b − x)
[
µ 0 I 2 R2
2
2 2 3/ 2
]
18. 电流均匀地穿过宽为2a的无穷长平面薄板,电流强度为I, 通过板的中线并与板面垂直的平面上有一点P,P到板的垂直 距离为x,设板厚可略去不极,求P点的磁感应强度B. 解:依题意,做如图所示.y~y+dy细长电流 dI = jdx = Idy / 2a µ dI µ Idy / 2a dB = 0 = 0 2πr 2π x 2 + y 2
B1 = µ 0 I 1 / 2πd
B2 = µ 0 I 2 / 2πd
d d d P
I2
但
B1 ⊥B 2 故
I1
−7 µ 4 10 × π 2 2 2 2 0 4.0 2 + 6.0 2 = 7.2 × 10 −5 (T ) B = B1 + B2 = I1 + I 2 = 2πd 2π × 0.02
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§6.5 与变化的电场相联系的磁场 L 安培环路定理遇到的问题: • 安培环路定理遇到的问题: S1 在稳恒条件下 ∂I = 0 ∂t I 安路环路定理成立
S2
考虑电容器充放电时的 ∂I 在非稳恒条件下 ∂I ≠ 0 磁感应强度沿任何闭合 ∂t 回路L的线积分 的线积分: 回路 的线积分: L 若按S 面计算穿过L的电流 的电流, 若按 1面计算穿过 的电流, S2 S1 等于I。 面计算, 等于 。但如果按 S2 面计算, 没有通过L回路的环流 回路的环流。 没有通过 回路的环流。说 I 明上述安培环路定理不适用 于非稳恒的情况。 于非稳恒的情况。
Id
ε 0ε r Φ e ≡
∫∫ D ⋅ d S
S
位移电流密度矢量 全电流
dΦ e ∂E ≡ ε 0ε r = ε 0 ε r ∫∫ ⋅ dS dt ∂t S
全电流是连续的。 I = ∫∫ j0 + jd ) ⋅ dS 全电流是连续的。 (
S
∂D jd = ∂t
缩小至导线的截面积,因导体内E~0不仅高频 将S1缩小至导线的截面积,因导体内 不仅高频
∴
dt
=
ε o S dt
=
εoS
I
在平行板间取一半径为r 的圆为回路 穿过该回路的电通量随时间的变化率
πr I dΦ e 2 dE = πr = dt dt εoS
2
充电电流
极板面积
所取回路半径
r≤R
d ∵ ∫ B ⋅ dl = µ o ( I + ε o ∫∫SE ⋅ d S ) L dt dΦ e dE πr 2I B ∵ = πr 2 = dt dt εoS 2 πr I ∴ 2 π rB = µ o S πr 2I B = µo , r ≤ R 2π r ⋅ S
d
+++++++++
λ2
V2
这两根带电长直导线单位长度线段相互作用磁力: 这两根带电长直导线单位长度线段相互作用磁力:
µ o I 2 I1 µ o λ 2V 2 λ 1V 1 Fm = = 2π d 2π d λ1 清华p32 清华 λ 1带电线上的运动电荷 E1 = 2 πε 0 d 在λ 2带电线处的电场强度 ∵γ ∼ 1
结果表明: 结果表明:虽然电场强度的时间变化率已经相当大 但它所激发的磁场仍然是很弱,在实验上不易测到。 但它所激发的磁场仍然是很弱,在实验上不易测到。
µoε o
例题二 2:一板面半径为 :一板面半径为R=0.2m的圆形平板电容器, 的圆形平板电容器, 正以I=10A的电流充电。求在板间距轴线r1=0.1m处 正以 的电流充电。 处 处的磁场。 和r2=0.3m 处的磁场。 1 q 解: ∵ E = εo S r S dE 1 dq 1
∫∫
S
dq j0 ⋅ d S = − dt
S
S2
高斯定理: 高斯定理:
∫∫ D ⋅ dS = q
I
∫∫
S
∂D ∫∫ D ⋅ d S = ∫∫ ∂ t ⋅ d S S S ∂D ∂D ( ⋅ j0 ⋅ dS = − ∫∫ ⋅ dS ∫∫ j0 + ∂t )dS = 0 ∂t S S dq d = dt dt
得位移电流的瞬时值
Id = ε 0ε r ρω I0
一般良导体
ρ ≈ 10 Ω⋅ m, εr = 1
−8
一般良导体 ρ ≈ 10
−8
Ω⋅ m, ε r = 1
Id << 1 I0
Id −12 −8 ∴ = 9.0 ×10 ×10 × 2πf I0 18 只要电流变化频率 f << 10 Hz
结论
虽然,只要有电位移通量的变化就有位移电流存在, 虽然,只要有电位移通量的变化就有位移电流存在, 但实际上当电场变化的频率不是非常高时, 但实际上当电场变化的频率不是非常高时,在导体 内位移电流与传导电流相比是微不足道的。 内位移电流与传导电流相比是微不足道的。如,当 −17 导体内该比值为: 频率 f=50Hz 时,导体内该比值为: d / I 0 ≈ 10 I 另外,位移电流的相位超前传导电流 另外, 所以, 所以, 2 位移电流不消耗功率,不产生焦耳热。 位移电流不消耗功率,不产生焦耳热。
2 πε 0 d
Fe
=
c
2
≈ 10
磁力比电力小很多! 磁力比电力小很多!
实验上总是观察到磁力而没发现电力的原因 是导线上的正、负电荷的电场彼此抵消了。 是导线上的正、负电荷的电场彼此抵消了。 在原子内部电荷间的相互作用主要是电力, 在原子内部电荷间的相互作用主要是电力,而 磁力不过是一种小到“二级” 的效应。 磁力不过是一种小到“二级”(V2/c2 )的效应。 的效应
i
∫ B ⋅ dl
L
= µo ∑ Ii
变化的电场和磁场的联系: • 变化的电场和磁场的联系: 1861年麦克斯韦注意到充电时, 年麦克斯韦注意到充电时, 年麦克斯韦注意到充电时 极板间电场是变化的,穿过S 极板间电场是变化的,穿过 1 面的电流在极板上积累, 面的电流在极板上积累,根据 L 电流连续性原理(适于非稳恒) 适于非稳恒) 适于非稳恒 S1 MAG_3
∂D 虽然导体表面E≠ 但可证明 ∴ j ⋅ dS = 虽然导体表面 ≠0但可证明* ∫∫ 0 ∫∫ ∂t ⋅ dS 其位移电流远小于传导电流。 其位移电流远小于传导电流。 S S2 1
电流有趋肤效应, 电流有趋肤效应,就是真电流在低频时也趋肤*。
∫ B ⋅ dl
L
= µ o ∫∫ j 0 ⋅ d S = µ o ∫∫
R
r
r1 I B = µo = 5 × 10 − 6 T r1=0.1m 2π R 2 r2=0.3m>R I πR 2 I −6 B = µo = µo = 6.67 ×10 T 2πr2 ⋅ S 2πr2
6.6平行电流间的相互作用力 平行电流间的相互作用力 的两平行长直载流导线, 相距为 d 的两平行长直载流导线,求每单位长度 线段受另一电流磁场的作用力。 线段受另一电流磁场的作用力。 处所产生的磁场为: 电流 I1在电流 I2处所产生的磁场为: µ o I1 B1 = B2 2π d µ o I1I 2 导线2单位 导线 单位 F2 = B1 I 2 = 长度受力 2π d 处所产生的磁场为: 电流 I2在电流 I1 处所产生的磁场为:
∵ ∫ B ⋅ dl = µ oε o
L
∫∫ E ⋅ d S dt
S
dE ∴ 2π rB = µ o ε oπ r dt
2
两极板间磁感应强度的分布
∴B =
µ oε o
2
dE r ∝ r dt
极板边缘处的磁感应强度。 极板边缘处的磁感应强度。
dE −6 ∴ B(R) = R = 5.6 ×10 T 2 dt
λ 2带电长直导线单位长度 F e = λ 2 λ 1
线段上的电荷受的电力
Fm V 2V 1 = ε 0 µ 0V 2V 1 = 所以磁力与电力的比值为 Fe c2
设有两根载流分别为I 的静止铜导线, 设有两根载流分别为 1 和I 2的静止铜导线,正电荷 几乎不动,而自由电子作定向漂移的速度约为10 几乎不动,而自由电子作定向漂移的速度约为 -4 m/s c = 3×108 m/ s 3× Fm V 2V 1 − 25
d q dq = µ oε o ( S) = µo dt S ε o dt
∂D ∴ ∫∫ j0 ⋅ dS = ∫∫ ⋅ dS ∂t S1 S2
• 普遍的安培环路定理
d ∫LB ⋅ dl = µ o ( I 0 + ε dt ∫∫SE ⋅ dS )
∫ B ⋅ dl
L
= µo ( I 0 + I d )
目录 §6.5 与变化的电场相联系的磁场 • 安培环路定理遇到的问题
• 变化的电场和磁场的联系 • 普遍的安培环路定理
例题一: 例题一:导体中传导电流与位移电流的比值 例题二: 例题二:充电平行板电容器间的磁场 §6.6平行电流间的相互作用力 平行电流间的相互作用力 例题三: 例题三:两长直带电线沿长度方向 运动时, 运动时,其间的作用力
dΦ e ∂E 解: Id ≡ ε0 = ε 0 ∫∫ ⋅ dS r S dt ∂t S dE Id = ε0 π R 2 = 1 .4 A dt 根据对称性,取以轴点为圆心, 根据对称性,取以轴点为圆心, 的圆为回路,其上磁场沿切向、大小相等。 半径为r 的圆为回路,其上磁场沿切向、大小相等。 与电流成右手螺旋。 与电流成右手螺旋。 d
π
例题二 1:一板面半径为 :一板面半径为R=5.0cm的圆形平板电容器, 的圆形平板电容器, 设充电后电荷在极板上均匀分布, 设充电后电荷在极板上均匀分布,两极板间电场强度 的变化率为dE/dt=2.0×1013V/ms.求 两极板间的位移 的变化率为 × 求 电流。 电流。 两极板间磁感应强度的分布和极板边缘处 的磁感应强度。 的磁感应强度。
dΦ e dE di ρ S = ε 0ε r id = ε 0ε r = ε 0ε r S dt dt dt S π id = ε 0ε r ρωI 0 cos(ωt + ) 2
于是,导体中位移电流和传导电流的振幅比: 于是,导体中位移电流和传导电流的振幅比:
i i E= = =ρ σ σS S
j
运动电荷“产生”了电场和磁场。 变化的电场“产生”磁场。实质上 实质上 是电场和磁场的相对论联系的表现。 是电场和磁场的相对论联系的表现。
另一种证明:通过以 为边介的面 和面S 另一种证明 通过以L为边介的面 1和面 2的 通过以 为边介的面S 电流相等的方法: 电流相等的方法: 极板上电量
