卧式储罐不同液位下地容积(高质量)计算
卧式椭园封头储罐内液体质量与液位高度的对应关系计算

卧式椭园封头储罐内液体质量与液位高度的换算方法
利用电子表格可以计算更复杂的问题,而使计算
变得十分容易,下面是就公司内一个卧式储罐内
储存甲醛成品数量的计算方法。
卧式罐如右图所示:筒体部分长:12.65m ,
内部直径3.0m ,标准椭园封头a/b=2 直边:0cm ;
首先,把整体罐的容积分成两部分计算:即封
头部分的容积V2和筒体部分所对应的容积V1,
再测出液体常温状态下的密度(ρ)然后再代
入液体质量公式:M =ρ×(V1+V2) (1)
(一)筒体部分(如右图所示):
令过圆心的铅直线为x 轴,过圆底边水平切线为y 轴,
罐内液位高度为h ,则圆的方程为:y
2+(x-1.5)2=1.52
图中阴影部分的面积为: ()()()()()⎥⎦⎤⎢⎣⎡+⎪⎭⎫ ⎝⎛-+---=∙=+⎪⎭
⎫ ⎝⎛-+---=--=⎰ππ125.15.15.125.25.15.15.1125.15.15.125.25.15.15.15.15.1222122022h arcSin x h L S
L V h arcSin x h dx
x S h
(二)封头部分:
椭圆水平截面积为:
再将V1与V2代入(1)式,然后用电子表Excel 计算出液位高度每升高1cm 所对应的液体质量,过程十分简便。
愚公2013-4-20 ()[]()π
πππ5625.0125.15.165.125.223202-+-=--=⎰h h dh h V h ()[]2
5.125.22h ab S --==ππ。
卧式储罐体积容积计算

卧式储罐体积容积计算卧式储罐是一种常见的储存液体或气体的设备,其体积容积计算涉及到储罐的几何形状和尺寸参数。
下面将介绍卧式储罐体积容积的计算公式及计算步骤。
卧式储罐的体积容积计算公式主要基于储罐的几何形状,包括圆柱部分和两个盖子(圆形或椭圆形)的形状。
首先,我们需要了解以下几个参数:1.储罐的总长度L(包括两个盖子);2.储罐的圆柱直径D;3.储罐的圆柱高度H;4.储罐的盖子高度h。
根据以上参数,卧式储罐的体积容积计算公式如下:V=Vc+Vg其中,Vc为圆柱部分的容积,Vg为两个盖子的容积。
圆柱部分的容积(Vc)计算公式如下:Vc=π*(D/2)^2*H两个盖子的容积(Vg)计算公式如下:Vg=Vg1+Vg2Vg1为前盖子的容积,Vg2为后盖子的容积。
当盖子为圆形时:Vg1=Vg2=(π*(D/2)^2*h)/2当盖子为椭圆形时:Vg1=Vg2=(π/4)*D*(D-2h)*h将以上公式代入主公式,即可得到卧式储罐的体积容积。
下面以一个具体的例子来进一步说明卧式储罐体积容积的计算。
假设储罐的总长度L为10m,圆柱直径D为3m,圆柱高度H为6m,盖子高度h为1m。
根据上述参数,我们可以逐步计算出储罐的各个部分的容积。
首先计算圆柱部分的容积Vc:Vc=π*(D/2)^2*H=3.14*(3/2)^2*6≈21.21m³然后计算两个盖子的容积Vg:Vg1=Vg2=(π*(D/2)^2*h)/2=(3.14*(3/2)^2*1)/2≈2.36m³将圆柱部分和盖子的容积加起来可以得到总体积容积V:V=Vc+Vg=21.21+2.36+2.36≈25.93m³所以,该卧式储罐的体积容积约为25.93m³。
以上是卧式储罐体积容积的计算公式和步骤。
需要注意的是,在实际应用中,储罐的尺寸和形状可能会有所变化,因此计算时需根据具体情况进行调整。
卧式油罐容积计算

卧式油罐容积计算卧式油罐容积计算是工程中的一个重要问题,它涉及到油罐的设计、选型和使用。
由于油罐的形状是卧式的,因此容积的计算相对复杂一些。
本文将介绍卧式油罐容积计算的原理和方法,并通过一个实例来说明具体的计算步骤。
首先,我们需要了解卧式油罐的几何形状。
卧式油罐有一个圆筒部分和两个半球形的罐盖,它们组成了一个完整的油罐。
在计算容积时,我们可以将卧式油罐分解为三个部分:圆筒形部分、一个半球形罐盖和一个球形的底部。
通过计算这三个部分的体积,然后相加得到整个油罐的容积。
首先,我们计算圆筒形部分的体积。
圆筒部分的体积可以通过圆的面积乘以高度来计算。
假设卧式油罐的半径为R,高度为H,那么圆筒的体积为V1=π*R^2*H。
接下来,我们计算半球形罐盖的体积。
半球形罐盖的体积可以通过球的体积公式计算。
假设卧式油罐的半径为R,那么半球形罐盖的体积为V2=(4/3)*π*R^3/2最后,我们计算球形底部的体积。
球形底部的体积也是通过球的体积公式计算。
假设卧式油罐的半径为R,那么球形底部的体积为V3=(4/3)*π*R^3最后,将圆筒的体积、半球形罐盖的体积和球形底部的体积相加,即可得到整个油罐的容积V=V1+V2+V3下面我们通过一个实例来进行具体的计算。
假设卧式油罐的半径R=5m,高度H=10m。
首先计算圆筒的体积V1=π*5^2*10=250πm^3、接下来计算半球形罐盖的体积V2=(4/3)*π*5^3/2=250π/3m^3、最后计算球形底部的体积V3=(4/3)*π*5^3=500π/3m^3、将这三个体积相加,整个油罐的容积V=250π+250π/3+500π/3=1000πm^3在实际工程中,容积计算是设计和选型卧式油罐时的重要参数。
根据设计要求,我们需要根据油罐的尺寸来计算其容积。
这样可以确保油罐容纳的油品数量符合工程需求,同时也能在油罐选型阶段给出参考和建议。
除了以上介绍的计算方法,还可以使用计算软件进行卧式油罐容积的计算。
卧式罐剩余容积计算公式

卧式罐剩余容积计算公式引言。
在工业生产和化工领域,储罐是一种常见的储存设备,用于储存液体或气体。
在储罐的设计和运行过程中,剩余容积的计算是非常重要的。
特别是对于卧式储罐来说,剩余容积的计算涉及到罐体的形状和尺寸等因素。
本文将介绍卧式罐剩余容积计算的公式和相关知识。
卧式罐剩余容积计算公式。
卧式罐剩余容积的计算公式可以通过以下步骤进行推导:1. 首先,我们需要了解卧式罐的基本形状。
卧式罐通常是一个长方形的容器,底部为平底,两侧为直立。
我们可以将卧式罐的形状简化为一个长方形底部和两个直立的侧面。
2. 接下来,我们需要确定卧式罐的尺寸。
具体来说,我们需要知道卧式罐的长度、宽度和高度。
3. 然后,我们可以使用以下公式来计算卧式罐的剩余容积:V = L W H (L 2x) (W 2x) H。
其中,V表示卧式罐的剩余容积,L表示卧式罐的长度,W表示卧式罐的宽度,H表示卧式罐的高度,x表示卧式罐的壁厚。
4. 最后,我们可以根据具体的尺寸和壁厚数据,代入公式进行计算,得到卧式罐的剩余容积。
卧式罐剩余容积计算公式的应用。
卧式罐剩余容积的计算公式可以应用于工业生产和化工领域的多个方面。
首先,它可以用于设计防溢流系统。
通过计算卧式罐的剩余容积,我们可以确定在罐体达到一定液位时需要启动防溢流系统,从而避免液体溢出造成安全事故。
其次,它可以用于优化储罐的储存效率。
通过计算卧式罐的剩余容积,我们可以确定最佳的填充液位,从而最大限度地利用储罐的容量,提高储存效率。
此外,它还可以用于计算液体的消耗量。
通过监测卧式罐的剩余容积变化,我们可以计算出液体的消耗量,从而进行生产计划和成本控制。
总之,卧式罐剩余容积计算公式在工业生产和化工领域具有重要的应用价值,可以帮助我们进行安全设计、提高效率和控制成本。
卧式罐剩余容积计算的注意事项。
在使用卧式罐剩余容积计算公式时,我们需要注意以下几个方面:首先,我们需要准确测量卧式罐的尺寸和壁厚。
尺寸和壁厚的不准确数据会导致计算结果的误差。
卧式储罐体积计算公式

卧式储罐体积计算公式卧式储罐是一种广泛应用于石油、化工、医药等行业的容器,用于储存液体或气体物质。
其体积计算是设计、制造和使用储罐的基础。
卧式储罐的体积计算公式可以根据罐体形状和尺寸的不同而有所不同,下面将介绍几种常见的体积计算公式。
矩形卧式储罐一般由长方形和两个半圆柱体组成。
其体积可以通过以下公式计算:V=L*W*H+π*r²*L其中,V表示储罐的体积,L表示储罐的长,W表示储罐的宽,H表示储罐的高,r表示半圆柱体的半径。
圆柱型卧式储罐由一个长圆柱体和两个半圆锥体构成。
其体积可通过以下公式计算:V=π*r²*L+2/3*π*r³其中,L表示储罐的长度,r表示储罐的半径。
椭圆型卧式储罐由一个长椭球和两个半长椭球构成。
其体积可以通过以下公式计算:V=4/3*π*a*b*c其中,a、b、c分别表示椭圆长半轴、短半轴和半长轴。
需要注意的是,以上公式仅为简化计算公式,可能无法完全准确地计算出储罐的实际体积,因为储罐的形状、尺寸以及内部结构等因素都会对体积产生影响。
在实际工程设计中,还需要考虑到其他因素,如罐壁的厚度、罐底的形状等。
此外,卧式储罐的容积计算还需要考虑到液位的变化。
大多数卧式储罐会设置液位计来监测储罐内的液位,并通过液位计的信息计算出实际液位的体积。
通过根据液位的变化来计算储罐内的液体体积,可以更加准确地掌握储罐的储存能力。
综上所述,卧式储罐的体积计算需要结合储罐的形状和尺寸来确定合适的计算公式。
在实际应用中,设计和使用人员需要仔细考虑各种因素,并结合实际情况进行合理计算和判断。
卧式储罐体积容积计算(带公式)
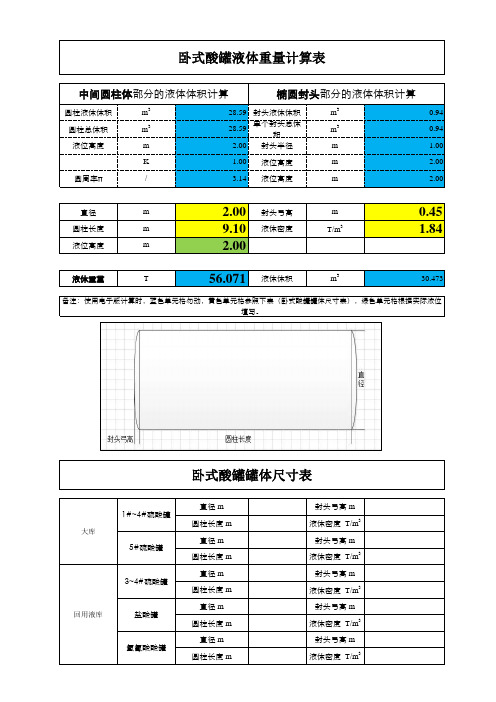
圆柱液体体积m 328.59封头液体体积
m 30.94圆柱总体积m
3
28.59
单个封头总体
积
m
3
0.94液位高度
m 2.00封头半径m 1.00K
1.00液位高度m
2.00圆周率π/
3.14
液位高度
m
2.00
直径m 2.00封头弓高m 0.45圆柱长度m 9.10液体密度
T/m
3
1.84
液位高度
m
2.00液体重量T 56.071
液体体积m
3
30.473
直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3
直径 m 封头弓高 m 圆柱长度 m 液体密度 T/m 3直径 m 封头弓高 m 圆柱长度 m
液体密度 T/m 3
大库
回用液库
1#~4#硫酸罐
5#硫酸罐
3~4#硫酸罐
盐酸罐
氢氟酸酸罐
卧式酸罐液体重量计算表
中间圆柱体部分的液体体积计算
椭圆封头部分的液体体积计算
备注:使用电子版计算时,蓝色单元格勿动,黄色单元格参照下表(卧式酸罐罐体尺寸表),绿色单元格根据实际液位
填写。
卧式酸罐罐体尺寸表。
卧式储罐不同液位下的容积简化计算公式

卧式储罐不同液位下的容积简化计算公式
赵文兵
【期刊名称】《安装》
【年(卷),期】1996(000)006
【总页数】2页(P27-28)
【作者】赵文兵
【作者单位】中国石化第十建设公司
【正文语种】中文
【中图分类】TE972
【相关文献】
1.卧式贮罐液位高度下装载容积的计算 [J], 胡树武;刘湘秋
2.卧式容器任意液位高度下液体容积的计算 [J], 胡国清;赵宝伟
3.卧式容器容积与液位的关系式 [J], 刘奇央
4.水平地震激励下卧式储罐考虑储液晃动的简化力学模型 [J], 吕远;孙建刚;孙宗光;崔利富;王振
5.基于MATLAB的卧式储罐不同液位下的容积修正计算 [J], 冯超
因版权原因,仅展示原文概要,查看原文内容请购买。
卧式容器液位体积计算

卧式容器液位体积计算
液位的测量方式有很多种,常用的液位传感器包括浮子式液位计、压力式液位计、雷达液位计、超声波液位计等。
这些液位传感器可以精确地测量液位并将其转换为相应的电信号。
液位体积计算的原理是根据容器的几何形状和液位的高度来计算液体的体积。
在卧式容器中,通常采用水平切面积乘以液位高度的方法进行计算。
卧式圆柱形容器的液位体积计算可以使用以下公式:
V=π*R^2*H
如果容器的底部是平的,液体的高度可以通过测量液体表面到容器底部的垂直距离来确定。
对于容器的底部是圆锥形的情况,液位体积计算的公式略有不同。
在这种情况下,可以使用以下公式进行计算:
V=(1/3)*π*(R1^2+R2^2+R1*R2)*H
其中,V表示液体的体积,π表示圆周率,R1表示底部较小半径(圆锥顶部半径),R2表示底部较大半径(圆锥底部半径),H表示液位的高度。
卧式容器的液位体积计算涉及到容器的几何形状和液体的液位测量,因此在进行计算时需要准确地测量液位和容器的尺寸。
此外,还需要注意单位的一致性,在计算中使用相同的单位。
液位体积计算在工业生产中非常重要,可以帮助企业准确掌握液体的储存量、流量和消耗情况,从而进行生产计划和资源调配。
此外,液位体
积计算还可以用于监测液体储罐的安全性能,确保液位不超过容器的额定容积,避免溢出和泄露。
总之,卧式容器液位体积计算是一项重要的工程计算,涉及到液位测量和容器几何形状分析。
通过准确地测量液位和应用相应的公式,可以计算出容器中液体的体积,为工业生产提供准确的数据支持。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
卧式储罐不同液位容积(质量)计算椭圆形封头卧式储罐图
参数:
l:椭圆封头曲面高度(m);
l i:椭圆封头直边长度(m);
L:卧罐圆柱体部分长度(m);
r:卧式储罐半径(d/2,m);
d:卧式储罐径,(m)
h:储液液位高度(m);
V:卧式储罐总体积(m3);
ρ:储液密度(kg/m3)
V h:对应h高度卧罐储液体积(m3);
m h:对应h高度卧罐储液重量(kg);
椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
简化模型图如下。
以储罐底部为起点的液高
卧式储罐储液总体积计算公式:
()()()⎥
⎦⎤⎢⎣⎡⎪⎭⎫ ⎝
⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212
222πr h r r r h r r h Lr L r V h
若密度为ρ,则卧式储罐储液总重量为:
h
h V m ρ=
表1 卧式储罐不同液位下容积(重量)
该计算公式推导过程如下
卧式储罐不同液位下的容积简化计算公
椭圆形封头卧式储罐由直段筒体及两侧封头组焊而成,去掉直段筒体,两侧封头可组成椭圆球体。
以储罐中心为起点的液高
(1)椭圆球体部分
该椭圆球体符合椭圆球体公式:
2222221x y z a b c ++= 其中a=b=r ,则有222
221x y z a c
++= 垂直于y 轴分成无限小微元,任一微元面积为:
22()yi c
S a y a
π=
-
当液面高度为h 时,椭圆球体液氨容积为 V1=h
yi a S dy -⎰ 2
2
()h
a
c
a y dy a
π-=-⎰33
2
2()33c
h a a h a π=-+ (2)直段筒体部分:
筒体的纵断面方程为222x y a +=
任一微元的面积为yj S = 则筒体部分容积为:
2h
yj a V S -=
⎰h
a L -=
⎰2
(arcsin )2
h La a π
=+
(arcsin
)2
2
h a π
π-
≤≤ (3)卧式储罐储液总体积
总容积为V=V1+V2,
V=232
42()33c
h a a h a π-
+
+2
(arcsin )2
h La a π+ 此公式中液位高度h 是以储罐径中心为原点,其中a=b=r 化简后卧式储罐储液总体积为:
⎥
⎦⎤⎢⎣⎡⎪⎭⎫ ⎝
⎛++⎪⎭⎫ ⎝⎛+=2-arcsin 3212
222πh r r h r h Lr L r V h
若液位高度h 以卧罐底部为起点,如下图
则卧式储罐储液总体积计算公式:
()()()⎥
⎦⎤⎢⎣⎡⎪⎭⎫ ⎝
⎛++⎪⎭⎫ ⎝⎛+=2----arcsin 3212
222πr h r r r h r r h Lr L r V h
若密度为ρ,则卧式储罐储液总重量为:
h
h V m ρ=
其它方法如下:
第一种方法
卧式储罐不同液位下的容积简化计算公
卧式储罐储液总体积计算公式:
)]arcsin(2)[(]3)(1)[(222
23
2r
r h r h hr r h L r r h r h l V V h -+--+---+=π若密度为ρ,则卧式储罐储液总重量为:
h
h V m ρ=
此方式用到参数较多ρ、V 、r 、l 、L 、h 。
当液高为0时理论上液体体积应为0,此公式结果为负值,不合逻辑。
第二种方法
卧式储罐储液总体积计算公式:
()()())
434(123
h d h h
h d h h L h d dh V h -+-+-=π
若密度为ρ,则卧式储罐储液总重量为:
h
h V m ρ=
此公式是由体积公式推算的,相对误差较大,如储罐中储液在一般高度时,体积间误差偏大。
此外,由于公式中存在分数,液高为0和最大公式不适用。
三种方法对比详见excel 表格。
