相似三角形一线三等角型
相似三角形之一线三等角型
相似三角形之一线三等角型一、知识梳理：（图1） （图2）（1）如图1：已知三角形ABC 中，AB=AC,∠ADE=∠B,那么一定存在的相似三角形有___（2）如图2：已知三角形ABC 中，AB=AC,∠DEF=∠B,那么一定存在的相似三角形有___二、习题精选1.如图，已知在△ABC 中， AB =AC =6，BC =5，D 是AB 上一点，BD =2，E 是BC 上一动点，联结DE ，并作DEF B ∠=∠，射线EF 交线段AC 于F ． （1）求证：△DBE ∽△ECF ；（2）当F 是线段AC 中点时，求线段BE 的长；（3）联结DF ，如果△DEF 与△DBE 相似，求FC 的长.2.如图，在△ABC 中，AB =AC =5，BC =6，P 是BC 上一点，且BP =2，将一个大小与∠B 相等的角的顶点放在P 点，然后将这个角绕P 点转动，使角的两边始终分别与AB 、AC 相交，交点为D 、E 。
（1）求证△BPD ∽△CEP （2）是否存在这样的位置，△PDE 为直角三角形？若存在，求出BD 的长；若不存在，说明理由。
3.等腰△ABC ，AB =AC =８，∠BAC =120°，P 为BC 的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P ，三角板绕P 点旋转．（1）如图a ，当三角板的两边分别交AB 、AC 于点E 、F 时．求证：△BPE ～△CFP ；（2）操作：将三角板绕点P 旋转到图b 情形时，三角板的两边分别交BA 的延长线、边AC 于点E 、F ．CP EA D①探究１：△BPE与△CFP还相似吗？②探究２：连结EF，△BPE与△PFE是否相似？请说明理由；③设EF=m，△EPF的面积为S，试用m的代数式表示S．B CPBP。
中考数学相似三角形重要模型一线三等角模型
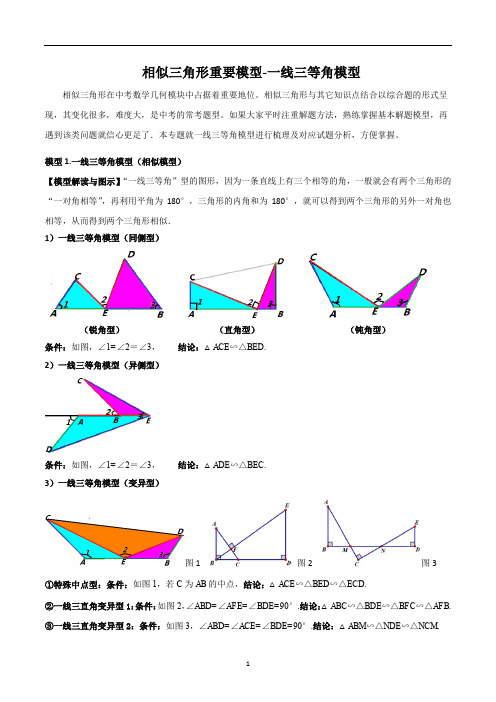
相似三角形重要模型-一线三等角模型相似三角形在中考数学几何模块中占据着重要地位。
相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。
如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了．本专题就一线三等角模型进行梳理及对应试题分析，方便掌握。
模型1.一线三等角模型（相似模型）【模型解读与图示】“一线三等角”型的图形，因为一条直线上有三个相等的角，一般就会有两个三角形的“一对角相等”，再利用平角为180°，三角形的内角和为180°，就可以得到两个三角形的另外一对角也相等，从而得到两个三角形相似．1）一线三等角模型（同侧型）（锐角型）（直角型）（钝角型）条件：如图，∠1=∠2＝∠3，结论：△ACE∽△BED.2）一线三等角模型（异侧型）条件：如图，∠1=∠2＝∠3，结论：△ADE∽△BEC.3）一线三等角模型（变异型）图1 图2 图3①特殊中点型：条件：如图1，若C为AB的中点，结论：△ACE∽△BED∽△ECD.②一线三直角变异型1：条件：如图2，∠ABD=∠AFE=∠BDE=90°.结论：△ABC∽△BDE∽△BFC∽△AFB.③一线三直角变异型2：条件：如图3，∠ABD=∠ACE=∠BDE=90°.结论：△ABM∽△NDE∽△NCM.例1．（2023·山东东营·统考中考真题）如图，A B C为等边三角形，点D，E分别在边B C，A B上，60A D E∠=︒，若4B D D C=， 2.4D E=，则A D的长为（）A．1.8B．2.4C．3D．3.2例2．（2023·湖南·统考中考真题）如图，,C A ADE D A D⊥⊥，点B是线段A D上的一点，且C B B E⊥．已知8,6,4A B A C D E===．(1)证明：A B C D E B∽△△．(2)求线段B D的长．例3．（2022·河南新乡·九年级期中）某学习小组在探究三角形相似时，发现了下面这种典型的基本图形．（1）如图1，在ABC中，∠BAC＝90°，A BA C＝k，直线l经过点A，BD⊥直线I，CE上直线l，垂足分别为D、E．求证：B DA E＝k．（2）组员小刘想，如果三个角都不是直角，那么结论是否仍然成立呢？如图2，将（1）中的条件做以下修改：在ABC中，A BA C＝k，D、A、E三点都在直线l上，并且有∠BDA＝∠AEC＝∠BAC＝α，其中α为任意锐角或钝角．请问（1）中的结论还成立吗？若成立，请你给出证明；若不成立，请说明理由．（3）数学老师赞赏了他们的探索精神，并鼓励他们运用这个知识来解决问题：如图3，在ABC中，沿ABC的边AB、AC向外作矩形ABDE和矩形ACFG，A BA E ＝A CA G＝12，AH是BC边上的高，延长HA交EG于点I．①求证：I是EG的中点．②直接写出线段BC与AI之间的数量关系：．例4．（2022·四川·一模）某学习小组在探究三角形全等时，发现了下面这种典型的基本图形：（1）如图1，已知：在△ABC 中，A B A C=，D 、A 、E 三点都在直线m 上，并且有B D AA E CB AC α∠=∠=∠=．试猜想DE 、BD 、CE 有怎样的数量关系，请证明你的结论；（2）老师鼓励学习小组继续探索相似的情形．于是，学习小组又研究以下问题：如图2，△ABC 中，(060)B C αα∠=∠=<<︒．将一把三角尺中30°角顶点P 放在BC 边上，当P 在BC 边上移动时，三角尺中30°角的一条边始终过点A ，另一条边交AC 边于点Q ，P 、Q 不与三角形顶点重合．设C P Qβ∠=．当β在许可范围内变化时，α取何值总有△ABP ∽△PCQ ？当α在许可范围内变化时，β取何值总有△ABP ∽△QCP ？（3）试探索有无可能使△ABP 、△QPC 、△ABC 两两相似？若可能，写出所有α、β的值（不写过程）；若不可能，请说明理由．例5．（2022·山西晋中·一模）阅读材料：我们知道：一条直线经过等腰直角三角形的直角顶点，过另外两个顶点分别向该直线作垂线，即可得三垂直模型”如图①，在A B C中，90A C B ∠=︒，A C B C=，分别过A 、B 向经过点C 直线作垂线，垂足分别为D 、E ，我们很容易发现结论：A D C C E B△≌△．（1）探究问题：如果A CB C≠，其他条件不变，如图②，可得到结论；A D CC E B△∽△．请你说明理由．（2）学以致用：如图③，在平面直角坐标系中，直线12y x=与直线C D 交于点()2,1M ，且两直线夹角为α，且3ta n 2α=，请你求出直线C D 的解析式．（3）拓展应用：如图④，在矩形A B C D 中，3A B=，5B C=，点E为B C 边上—个动点，连接A E ，将线段A E 绕点E 顺时针旋转90︒，点A 落在点P 处，当点P 在矩形A B C D外部时，连接P C ，P D ．若D P C △为直角三角形时，请你探究并直接写出B E 的长．Rt ABD中，上一动点，连接折叠得H E F，延长②B E M H E M≅；③当M2B，则正确的有（九年级校考阶段练习）已知A B C是等边三角形，E F和B D F∠，将B C E沿B则A F=P C D△；九年级校考阶段练习）如图，在A B C中，12．（2022·山东济宁·二模）情境观察:将含45°角的三角板的直角顶点R放在直线l上，分别过两锐角的顶点M，N作l的垂线，垂足分别为P，Q，（1）如图1.观察图1可知：与NQ相等的线段是______________，与N R Q∠相等的角是_____(2)问题探究直角A B C中，90B∠=︒，在AB边上任取一点D，连接CD，分别以AC，DC为边作正方形ACEF 和正方形CDGH，如图2，过E，H分别作BC所在直线的垂线，垂足分别为K，L.试探究EK与HL之间的数量关系，并证明你的结论.(3)拓展延伸：直角A B C中，90B∠=︒，在AB边上任取一点D，连接CD，分别以AC，DC为边作矩形ACEF和矩形CDGH，连接EH交BC所在的直线于点T，如图3.如果A C kC E=，试探究TE与TH=，C D kC H之间的数量关系，并证明你的结论.将．A B P沿着这样的点P，使得点问题解决（3）15．（2023春·四川广安·九年级校考阶段练习）如图1和图2，在平面直角坐标系中，点C的坐标为（0，4），A是x轴上的一个动点，M是线段AC的中点．把线段AM以A为旋转中心、按顺时针方向旋转90°得到AB．过B作x轴的垂线、过点C作y轴的垂线，两直线交于点D，直线DB交x轴于点E．设A点的横坐标为m．（1）求证：△AOC∽△BEA；（2）若m=3，则点B的坐标为；若m=﹣3，则点B的坐标为；（3）若m＞0，△BCD的面积为S，则m为何值时，S=6？（4）是否存在m，使得以B、C、D为顶点的三角形与△AOC相似？若存在，求此时m的值；若不存在，请说明理由．16．（2020·四川雅安·中考真题）如图，已知边长为10的正方形A B C D E、不重，是B C边上一动点（与B C 合），连结A E G，是B C延长线上的点，过点E作A E的垂线交D C G∠的角平分线于点F，若F G B G⊥．（1）求证：A B E E G FE C=，求C E F△△；（2）若2∽△的△的面积；（3）请直接写出E C为何值时，C E F面积最大．的何位置时有B E H B A E∽？B C。
(挑战压轴)专项27.4 相似三角形-一线三等角综合应用(解析版)
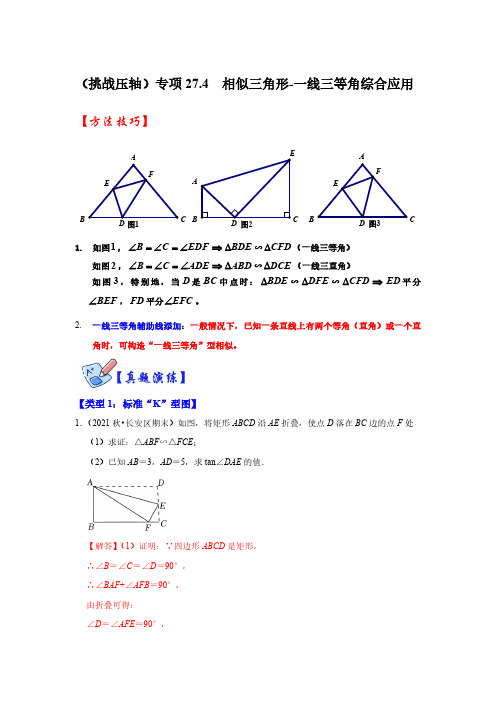
（挑战压轴）专项27.4 相似三角形-一线三等角综合应用【方法技巧】1.如图1，BDE EDF C B ∆⇒∠=∠=∠∽CFD ∆（一线三等角）如图2，ABD ADE C B ∆⇒∠=∠=∠∽DCE ∆（一线三直角）如图3，特别地，当D 是BC 中点时：BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠，FD 平分EFC ∠。
2.一线三等角辅助线添加：一般情况下，已知一条直线上有两个等角（直角）或一个直角时，可构造“一线三等角”型相似。
【类型1：标准“K ”型图】1．（2021秋•长安区期末）如图，将矩形ABCD 沿AE 折叠，使点D 落在BC 边的点F 处（1）求证：△ABF ∽△FCE ；（2）已知AB ＝3，AD ＝5，求tan ∠DAE 的值．【解答】（1）证明：∵四边形ABCD 是矩形，∴∠B ＝∠C ＝∠D ＝90°，∴∠BAF +∠AFB ＝90°，由折叠可得：∠D ＝∠AFE ＝90°，CB BC A A∴∠AFB+∠EFC＝180°﹣∠AFE＝90°，∴∠BAF＝∠EFC，∴△ABF∽△FCE；（2）解：∵四边形ABCD是矩形，∴AB＝CD＝3，AD＝BC＝5，由折叠可得：AD＝AF＝5，∴BF＝＝＝4，∴CF＝BC﹣BF＝1，∵△ABF∽△FCE，∴＝，∴＝，∴CE＝，∴DE＝CD﹣CE＝3﹣＝，∴tan∠DAE＝＝＝，∴tan∠DAE的值为．2.如图，在正方形ABCD中，M为BC上一点，ME⊥AM，ME交CD于F，交AD的延长线于点E．（1）求证：△ABM∽△MCF；（2）若AB＝4，BM＝2，求△DEF的面积．【解答】（1）证明：∵四边形ABCD是正方形，∴AB＝BC＝CD，∠B＝∠C＝90°，BC∥AD，∴∠BAM+∠AMB＝90°，∵ME⊥AM，∴∠AME＝90°，∴∠AMB+∠FMC＝90°，∴∠BAM＝∠FMC，∴△ABM∽△MCF；（2）解：∵AB＝4，∴AB＝BC＝CD＝4，∵BM＝2，∴MC＝BC﹣BM＝4﹣2＝2，由（1）得：△ABM∽△MCF，∴＝，∴＝，∴CF＝1，∴DF＝CD﹣CF＝4﹣1＝3，∵BC∥AD，∴∠EDF＝∠MCF，∠E＝∠EMC，∴△DEF∽△CMF，∴＝，∴＝，∴DE＝6，∴△DEF的面积＝DE•DF＝×6×3＝9，答：△DEF的面积为9．3.已知矩形ABCD的一条边AD＝8，将矩形ABCD折叠，使得顶点B落在CD边上的P点处．如图，已知折痕与边BC交于点O，连接AP、OP、OA．（1）求证：＝；（2）若OP与PA的比为1：2，求边AB的长．【解答】（1）证明：由折叠的性质可知，∠APO＝∠B＝90°，∴∠APD+∠OPC＝90°，∵四边形ABCD为矩形，∴∠D＝∠C＝90°，∴∠POC+∠OPC＝90°，∴∠APD＝∠POC，∴△OCP∽△PDA，∴＝；（2）解：∵△OCP∽△PDA，∴，∵OP与PA的比为1：2，AD＝8，∴，∴PC＝4，设AB＝x，则DC＝x，AP＝x，DP＝x﹣4，在Rt△APD中，AP2＝AD2+PD2，∴x2＝82+（x﹣4）2，解得：x＝10，∴AB＝10．4.（2020•香洲区校级一模）如图，四边形ABDC为矩形，AB＝4，AC＝3，点M为边AB上一点（点M不与点A、B重合），连接CM，过点M作MN⊥MC，MN与边BD交于点N．（1）当点M为边AB的中点时，求线段BN的长；（2）直接写出：当DN最小时△MNB的面积为 ．【解答】解：（1）∵AB＝4，∴当点M为边AB的中点时，AM＝BM＝2，∵四边形ABDC为矩形，∴∠A＝∠B＝90°，∵MN⊥MC，∴∠CMN＝90°，∵∠ACM+∠AMC＝90°，∠BMN+∠AMC＝180°﹣∠CMN＝90°，∴∠ACM＝∠BMN，又∵∠A＝∠B，∴△ACM∽△BMN，∴，∵AC＝3，AM＝BM＝2，∴＝，∴BN＝；（2）设BM＝x，DN＝y，∵四边形ABDC为矩形，AB＝4，AC＝3，∴AM＝AB﹣BM＝4﹣x，BN＝BD﹣DN＝3﹣y，由（1）知，，∴＝，∴（4﹣x）x＝3（3﹣y），∴﹣x2+4x＝9﹣3y，∴y＝x2﹣x+3＝（x﹣2）2+，∴当x＝2时，y取得最小值，即DN最小，此时DN＝y＝，∴BM＝2，BN＝3﹣＝，∴△MNB的面积为：×2×＝．故答案为：．5．（2019•玉州区二模）已知：如图，正方形ABCD中，E是边AB上一点，AM⊥DE于点M，CN⊥DE于点N．（1）求证：MN＝DM﹣AM；（2）连接AN，如果＝，求证：MN＝ME．【解答】证明：（1）∵四边形ABCD是正方形，∴AD＝DC，∠ADC＝90°，∴∠ADM+∠CDN＝90°，∵AM⊥DE，CN⊥DE，∴∠AMD＝∠CND＝90°，∴∠CDN+∠DCN＝90°，∴∠ADM＝∠DCN，∴△ADM≌△DCN（AAS），∴DN＝AM，∵MN＝DM﹣DN，∴MN＝DM﹣AM；（2）如图：∵四边形ABCD是正方形，∴AD＝DC，∠DAE＝90°，∵∠DAE＝∠DNC＝90°，∠ADM＝∠DCN，∴△CDN∽△DEA，∴＝，∴＝，∵＝，∴＝，∴AE＝AN，∵AM⊥DE，∴MN＝ME．6．（2022•郴州）如图1，在矩形ABCD中，AB＝4，BC＝6．点E是线段AD上的动点（点E不与点A，D重合），连接CE，过点E作EF⊥CE，交AB于点F．（1）求证：△AEF∽△DCE；（2）如图2，连接CF，过点B作BG⊥CF，垂足为G，连接AG．点M是线段BC的中点，连接GM．①求AG+GM的最小值；②当AG+GM取最小值时，求线段DE的长．【解答】（1）证明：∵四边形ABCD是矩形，∴∠A＝∠D＝90°，∴∠CED+∠DCE＝90°，∵EF⊥CE，∴∠CED+∠AEF＝90°，∴∠DCE＝∠AEF，∴△AEF∽△DCE；（2）解：①连接AM，如图2，∵BG⊥CF，∴△BGC是直角三角形，∵点M是BC的中点，∴MB＝CM＝GM＝，∴点G在以点M为圆心，3为半径的圆上，当A，G，M三点不共线时，由三角形两边之和大于第三边得：AG+GM＞AM，当A，G，M三点共线时，AG+GM＝AM，此时，AG+GM取得最小值，在Rt△ABM中，AM＝＝＝5，∴AG+GM的最小值为5．②方法一：如图3，过点M作MN∥AB交FC于点N，∴△CMN∽△CBF，∴，设AF＝x，则BF＝4﹣x，∴MN＝BF＝（4﹣x），∵MN∥AB，∴△AFG∽△MNG，∴，由（2）可知AG+GM的最小值为5，即AM＝5，又∵GM＝3，∴AG＝2，∴，解得x＝1，即AF＝1，由（1）得，设DE＝y，则AE＝6﹣y，∴，解得：y＝3+或y＝3﹣，∵0＜6，0＜3﹣＜6，∴DE＝3+或DE＝3﹣．方法二：如图4，过点G作GH∥AB交BC于点H，∴△MHG∽△MBA，∴，由（2）可知AG+MG的最小值为5，即AM＝5，又∵GM＝3，∴，∴GH＝，MH＝，由GH∥AB得△CHG∽△CBF，∴，即，解得FB＝3，∴AF＝AB﹣FB＝1．由（1）得，设DE＝y，则AE＝6﹣y，∴，解得：y＝3+或y＝3﹣，∵0＜6，0＜3﹣＜6，∴DE＝3+或DE＝3﹣．、【类型2：做辅助线构造“K”型图】7．（2022春•定海区校级月考）【基础巩固】（1）如图1，在△ABC中，∠ACB＝90°，直线l过点C，分别过A、B两点作AE⊥l，BD⊥l，垂足分别为E、D．求证：△BDC∽△CEA．【尝试应用】（2）如图2，在△ABC中，∠ACB＝90°，D是BC上一点，过D作AD的垂线交AB 于点E．若BE＝DE，，AC＝20，求BD的长．【拓展提高】（3）如图3，在平行四边形ABCD中，在BC上取点E，使得∠AED＝90°，若AE＝AB，，CD＝，求平行四边形ABCD的面积．【解答】（1）证明：∵∠ACB＝90°，∴∠BCD+∠ACE＝90°，∵AE⊥CE，∴∠AEC＝90°，∴ACE+∠CAE＝90°．∴∠BCD＝∠CAE．∵BD⊥DE，∴∠BDC＝90°，∴∠BDC＝∠AEC．∴△BDC∽△CEA．（2）解：过点E作EF⊥BC于点F．由（1）得△EDF∽△DAC．∴．∵AD⊥DE，，AC＝20，∴，∴DF＝16．∵BE＝DE，∴BF＝DF．∴BD＝2DF＝32．（3）解：过点A作AM⊥BC于点M，过点D作DN⊥BC的延长线于点N．∴∠AMB＝∠DNC＝90°．∵四边形ABCD是平行四边形，∴AB∥CD，AB＝CD．∴∠B＝∠DCN．∴△ABM≌△DCN（AAS）．∴BM＝CN，AM＝DN．∵AB＝AE，AM⊥BC，∴BM＝ME，∵，设AM＝b，BE＝4a，EC＝3a．∴BM＝ME＝CN＝2a，EN＝5a．∵∠AED＝90°，由（1）得△AEM∽△EDN．∴，∴，∴，∵，∴（2a）2+b2＝14，∴a＝1，．∴平行四边形ABCD的面积＝【类型2：特殊“K”型图】8．（2022秋•二道区月考）如图，在△ABC中，AB＝AC＝9，BC＝12，D，E分别是BC，AB上的动点（点D与B，C不重合），且2∠ADE+∠BAC＝180°，若BE＝4，则CD的长为 ．【解答】解：∵AB＝AC，∴∠C＝∠B，∴∠C+∠B+∠BAC＝2∠C+∠BAC＝180°，又∵2∠ADE+∠BAC＝180°，∴∠C＝∠ADE，又∵∠BDE+∠ADC＝180°﹣∠ADE，∠CAD+∠ADC＝180°﹣∠C，∴∠BDE＝∠CAD，∴△BDE∽△CAD，∴＝，即＝，解得CD＝6．故答案为：6．9．（2020秋•南京期末）如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD＝60°，2BP＝3CD，BP＝1．（1）求证△ABP∽△PCD；（2）求△ABC的边长．【解答】（1）证明：∵△ABC是等边三角形，∴AB＝BC＝AC，∠B＝∠C＝60°，∵∠BPA+∠APD+∠DPC＝180°，且∠APD＝60°，∴∠BPA+∠DPC＝120°，∵∠DPC+∠C+∠PDC＝180°，∴∠DPC+∠PDC＝120°，∴∠BPA＝∠PDC，∴△ABP∽△PCD；（2）解：∵2BP＝3CD，且BP＝1，∴CD＝，∵△ABP∽△PCD，∴＝，设AB＝x，则PC＝x﹣1，∴，∴x＝3．即AB＝3．∴△ABC的边长为3．10.如图，AB＝9，AC＝8，P为AB上一点，∠A＝∠CPD＝∠B，连接CD．（1）若AP＝3，求BD的长；（2）若CP平分∠ACD，求证：PD2＝CD•BD．【解答】（1）解：∵AB＝9，AC＝3，∴BP＝AB﹣AP＝9﹣3＝6，∵∠A＝∠CPD，∠ACP+∠APC＝180°﹣∠A，∠APC+∠BPD＝180°﹣∠CPD，∴∠ACP＝∠BPD，∵∠A＝∠B，∴△ACP∽△BPD，∴＝，∴＝，∴BD＝，∴BD的长为；（2）证明：∵CP平分∠ACD，∴∠PCD＝∠ACP，∵∠ACP＝∠DPB，∴∠PCD＝∠DPB，∵∠CPD＝∠B，∴△CPD∽△PBD，∴＝，∴PD2＝CD•BD．。
初三相似三角形几何模型-一线三等角
相似三角形几何模型——一线三等角【模型讲解】模型一：一线三直角图一 图二90;B ACE D ABC CDE ∠=∠=∠=∆∆如图一、二，已知：结论：（1）∽（2）AB DE=BC CD模型二：一线三等角图三 图四 ;B ACE D ABC CDE ABC CDE ACEα∠=∠=∠=∆∆∆∆∆如图三、四，已知：结论：（1）∽（2）AB DE=BC CD（3）当C 为BD 中点时，∽∽【典型例题】1.△ABC 和△DEF 是两个全等的等腰直角三角形，∠BAC =∠EDF =90°，△EDF 的顶点E 与△ABC 的斜边BC 的中点重合，将△DEF 绕点E 旋转，旋转过程中，线段DE 与线段AB 相交于点P ，线段EF 与射线CA 相交于点Q ．（1）如图①，当点Q 在线段AC 上，且AP=AQ 时，求证：△BPE≌△CQE；（2）如图②，当点Q 在线段CA 的延长线上时，求证：△BPE∽△CEQ；（3）在（2）的条件下，BP=2，CQ=9，则BC 的长为_______．2．如图，已知AB BD ⊥，CD BD ⊥.（1）若9AB =，4CD =，10BD =，请问在BD 上是否存在点P ，使以P ，A ，B 三点为顶点的三角形与以P ，C ，D 三点为顶点的三角形相似？若存在，求BP 的长；若不存在，请说明理由；（2）若9AB =，4CD =，12BD =，请问在BD 上存在几个点使以三点为顶点的三角形与以P ，C ，D 三点为顶点的三角形相似？并求BP 的长.3．如图，点P是正方形ABCD边AB上一点（点P不与点A，B重合），连接PD，将线段PD 绕点P顺时针方向旋转90°得到线段PE，PE交边BC于点F，连接BE，DF.（1）求∠PBE的度数；（2）若△PFD∽△BFP，求APAB的值.4．感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，可知△ABP∽△PCD．（不要求证明）探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，求证：△ABP∽△PCD．拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，CE=4，则DE的长为______．5.如图，点B 在线段AC 上，点D 、E 在AC 同侧，90A C ∠=∠=︒，BD BE ⊥，AD BC =．若3AD =，5CE =，点P 为线段AB 上的动点，连结DP ，作PQ DP ⊥，交直线BE 于点Q ．（1）当点P 与A ，B 两点不重合时，求DP PQ的值； （2）当点P 从A 点运动到AC 的中点时，求线段DQ 的中点所经过的路径（线段）长．（直接写出结果，不必写出解答过程）6．如图，在ABC △中，点D E 、分别在边BC AC 、上，连接AD DE 、，且B ADE C ∠=∠=∠．（1）证明：BDA CED △∽△；（2）若45,2B BC ∠=︒=，当点D 在BC 上运动时（点D 不与B C 、重合），且ADE △是等腰三角形，求此时BD 的长．。
相似三角形模型讲一线三等角问题讲义解答
、相似三角形判定的基本模型认识（一） A 字型、反A 字型（斜A 字型）（二） 8字型、反8字型（平行） （三）母子型（四）一线三等角型:三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（平行） （不平行）（蝴蝶型）（不平行）A BB（五）一线三直角型:（六）双垂型:相似三角形判定的变化模型实用文案DA, ' ' /B c C■一线三直角的1 .如图，梯形ABCD中，AD //BC,对角线AC、BD交于点0 , BE//CD交CA延长线于E.求证：OC2=OA2 .如图，在△ ABC 中，AB=AC=10 ，BC=16，点D 是边BC 上（不与B，C 重合）一动点，/ ADE= ZB= a, DE交AC于点E.下列结论：① AD 2=AE ?AB :② 3.6 W AE V 10 ;③当AD=2 Ji」.时，△ABD ^/DCE ;④ADCE为直角三角形时，BD为8或12.5 .其中正确的结论是________________ .（把你认为正确结论的序号都填上）3 .已知：如图，△ ABC中，点E在中线AD上，/DEB= /ABC . 求证：(1 ) DB2=DE ?DA ;(2)/ DCE= ZDAC .4 .已知：如图，等腰△ ABC中，AB=AC , AD丄BC于D , CG//AB , BG分别交AD、AC于E、F.求证:5 .如图，已知AD为△ABC的角平分线，EF为AD的垂直平分线.求证：FD2=FB 7FC.6 .已知：如图，在 Rt △ABC 中，/ C=90 °,BC=2 , AC=4 , P 是斜边AB 上的一个动点， PD 丄AB ,交边 AC 于点D (点D 与点A 、C 都不重合)，E 是射线DC 上一点，且/ EPD= Z A .设A 、P 两点的距离为 x , △BEP 的面积为y .(1 )求证：AE=2PE ;(2 )求y 关于x 的函数解析式, ,BD 、CE 分别是 AC 与AB 边上的高，求证： BC=2DE .8 .如图，已知△ ABC 是等边三角形，点 D 、B 、C 、E 在同一条直线上，且/ DAE=120并写出它的定义域;求厶BEP 的面积.7 .如图，在△ ABC 中，/ A=60(1 )图中有哪几对三角形相似？请证明其中的一对三角形相似；9 .（已知：如图，在Rt△ABC 中，AB=AC，/DAE=45 ° .求证:10 .如图，在等边厶ABC中，边长为6, D是BC边上的动点，/ EDF=60（1 ）求证：△ BDEs/CFD ;求BE的长.11 . （1 ）在A ABC中，AB=AC=5 , BC=8，点P、Q分别在射线CB、AC上（点P不与点C、点B重合），且保持/ APQ= Z ABC .①若点P在线段CB上（如图），且BP=6，求线段CQ的长；②若BP=x , CQ=y ,求y与x之间的函数关系式，并写出函数的定义域；（2）正方形ABCD的边长为5 （如图），点P、Q分别在直线CB、DC上（点P不与点C、点B重合），且保持/APQ=90度.当CQ=1时，写出线段BP的长（不需要计算过程，请直接写出结果）13 .已知梯形ABCD 中，AD //BC,且AD V BC, AD=5 , AB=DC=2 .(1 )如图，P为AD上的一点，满足/ BPC= Z A，求AP的长；(2)如果点P在AD边上移动(点P与点A、D不重合)，且满足/ BPE= ZA , PE交直线BC于点E,同时交直线DC于点Q .①当点Q在线段DC的延长线上时，设AP=x , CQ=y，求y关于x的函数关系式，并写出自变量x的取值范围；②当CE=1时，写出AP的长.(不必写解答过程)14 .如图，在梯形ABCD中，AD //BC, AB=CD=BC=6 , AD=3 .点M 为边BC的中点，以M 为顶点作Z EMF= ZB，射线ME交腰AB于点E,射线MF交腰CD于点F，连接EF.(1 )求证：△ MEF s/BEM ;(2 )若厶BEM是以BM为腰的等腰三角形，求EF的长；(3 )若EF丄CD , 求BE的长.15 .已知在梯形 ABCD 中，AD //BC , AD V BC ,且 BC=6 , AB=DC=4 ，点 E 是 AB 的中点.(1 )如图，P 为BC 上的一点，且 BP=2 .求证：△ BEPs/CPD ;(2)如果点P 在BC 边上移动(点P 与点B 、C 不重合)，且满足/ EPF= ZC , PF 交直线CD 于点F ，同时 交直线AD 于点M ，那么①当点F 在线段CD 的延长线上时，设 BP=x , DF=y ，求y 关于x 的函数解析式，并写出函数的定义域；16 .如图所示，已知边长为 3的等边△ ABC ，点F 在边BC 上，CF=1，点E 是射线BA 上一动点，以线段 EF 为边向右侧作等边△ EFG ，直线EG , FG 交直线AC 于点M , N ,(1 )写出图中与△ BEF 相似的三角形; (2) 证明其中一对三角形相似；(3) 设BE=x , MN=y ，求y 与x 之间的函数关系式，并写出自变量17 .如图所示，已知矩形 ABCD 中，CD=2 , AD=3，点P 是AD 上的一个动点(与 A 、D 不重合)，过点P作PE 丄CP 交直线AB 于点E ,设PD=x , AE=y ,(1) 写出y 与x 的函数解析式，并指出自变量的取值范围； (2) 如果△ PCD 的面积是厶AEP 面积的4倍，求CE 的长；(3) 是否存在点 卩，使厶APE 沿PE 翻折后，点A 落在BC 上？证明你的结论.x 的取值范围;的面积.18 .如图，在 Rt △KBC 中，/ C=90 °,AB=5，-丁讦二上，点D 是BC 的中点，点 E 是AB 边上的动点,4丄DE 交射线AC 于点F . (1 )求AC 和BC 的长； (2)当EF//BC 时，求BE 的长；19 .如图，在 Rt △KBC 中，/ C=90 °,AC=BC , D 是AB 边上一点，E 是在AC 边上的一个动点(与点 C 不重合)，DF 丄DE , DF 与射线BC 相交于点F .(1 )如图2，如果点D 是边AB 的中点，求证：DE=DF ; (2) 如果 AD : DB=m ，求 DE : DF 的值；(3) 如果 AC=BC=6 , AD : DB=1 : 2，设 AE=x , BF=y , ① 求y 关于x 的函数关系式，并写出定义域；② 以CE 为直径的圆与直线 AB 是否可相切？若可能，求出此时x 的值；若不可能，请说明理由.DF(3)连接EF ,当厶DEF 和△ABC 相似时，求 BE 的长.20 .如图，在△ ABC中，/ C=90 °,AC=6 , X^b-~，D是BC边的中点，E为AB边上的一个动点，作/4DEF=90 °,EF交射线BC于点F.设BE=x , ABED的面积为y(1 )求y关于x的函数关系式，并写出自变量x的取值范围；(2)如果以线段BC为直径的圆与以线段AE为直径的圆相切，求线段BE的长；(3)如果以B、E、F为顶点的三角形与△ BED相似，求△ BED的面积.421 .如图，在梯形ABCD 中，AB //CD, AB=2 , AD=4 , tanC=「，/ADC= ZDAB=90 °,P 是腰BC 上一个动点(不含点B、C),作PQ丄AP交CD于点Q.(图1)(1 )求BC的长与梯形ABCD的面积；(2 )当PQ=DQ 时，求BP的长；(图2)•••ZCDE=90 °■//B= a且,•• Z AD=90a=AB=10 ,/-cosB=AB 4LJ." '■,25—.故④正确.••AE=AC - CE=10 - x ,「36 <AE v 10 .故②正确.③作AG丄BC于G,4••AB=AC=10 , Z ADE= Z B= a, COS a=—,5••BC=16 ,「.AG=6 ,••AD=2 | J... H,ADG=2 ,「.CD=8 ,：AB=CD , •△ABD 与△DCE 全等；故③正确;④当Z AED=90。
相似三角形的基本模型一线三等角
模型中的相似三角形（2）【基本模型】1. 如图1，BDE EDF CB ∆⇒∠=∠=∠∽CFD ∆（一线三等角） 如图2，ABD ADEC B ∆⇒∠=∠=∠∽DCE ∆（一线三直角）如图3，特别地，当D 是BC 中点时：BDE ∆∽DFE ∆∽CFD ∆⇒ED 平分BEF ∠，FD 平分EFC ∠。
2. 一线三等角辅助线添加：一般情况下，已知一条直线上有两个等角（直角）或一个直角时，可构造“一线三等角”型相似。
【巩固提高】1. 已知ABC ∆中,120,6︒=∠==BAC AC AB ，D 是BC 的中点，AB 边上有一点AC E ,延长线上有一点F ，使.C EDF ∠=∠ 已知4=BE ，则=CF 427 提示：,120,6︒=∠==B A C AC AB ，D 是BC 的中点 ∴33==CD BD由B D E ∆∽CFD ∆ ∴CF DB DC BE =, 427=CF 2. 如图，等边ABC ∆中，D 是边BC 上的一点，且3:1:=DC BD ，把ABC ∆折叠，使点A 落在BC 边上的点D 处．那么ANAM 的值为 75 ． 提示：由翻折可得：A MDN DN AN DM AM ∠=∠==,,设：,3,1==DC BD 则4,4=+=+DN CN DM BM∵BDM ∆∽CND ∆， ∴753414=++===∆∆CND BDM C C DN DM AN AM 3. 在矩形ABCD 中，6=AB ，8=AD ，把矩形ABCD 沿直线MN 翻折，点B 落在边AD 上的E 点处，若AM AE 2=，那么EN 的长等于 提示：作AD NF ⊥于F ，则6==AB FN∵MAE ∆∽EFN ∆,∴EFAM FN AE = ∵AM AE 2=∴53,321===EN FN EF 4. 在矩形ABCD 中，15=AD ，点E 在边DC 上，联结AE ，△ADE 沿直线AE 翻折后点D 落到点F ，过点F 作AD FG ⊥，垂足为点G ,如果3:1:=AD DG ，那么=DE提示：作过点F 作MN ∥BC ，分别交AB 、CD 于M 、N 。
一线三等角问题培训资料
ABCDE相似三角形模型之“一线三等角型”一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景引例：如图，等边△ABC 中，D是BC 上一点，F 为AC 边上一点，且∠A DF =60°，BD=3，CF=2.求△ABC 边长。
例1、如图，在△ABC 中，8==AC AB ，10=BC ，D 是BC 边上的一个动点，点E 在AC 边上，且C ADE ∠=∠．(1) 求证：△ABD ∽△DCE ；(2) 如果x BD =，y AE =，求y 与x 的函数解析式例2、如图，已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AP ＝1，AB ＝DC ＝2．P 为AD 上的一点，满足∠BPC ＝∠A ．求AD 的长． C DB FACCBECDCADBEF例3、正方形ABCD 的边长为4（如下图），点P 、Q 分别在线段CB 、DC 上（点P 不与点C 、点B 重合），且保持︒=∠90APQ .当1=CQ 时，求出线段BP 的长。
相关练习：1、如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF=60° （1）求证：△BDE ∽△CFD （2）当BD=1，FC=3时，求BE2、如图，已知在△ABC 中， AB =AC =6，BC =5，D 是AB 上一点，BD =2，E是BC 上一动点，联结DE ，并作DEF B ∠=∠，射线EF 交线段AC 于F ． （1）求证：△DBE ∽△ECF ； （2）当F 是线段AC 中点时，求线段BE 的长3、在ABC ∆中，5==AC AB ，8=BC ，点P 、Q 分别在线段CB 、AC 上（点P 不与点C 、点B 重合），且保持ABC APQ ∠=∠.若点P 在线段CB 上（如图），且6=BP ，求线段CQ 的长BCABCDABCQ4、已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且BC =6，AB =DC =4，点E 是AB 的中点． （1）如图，P 为BC 上的一点，且BP =2．求证：△BEP ∽△CPD ； （2）如果点P 在BC 边上移动（点P 与点B 、C 不重合），且满足∠EPF =∠C ，PF 交CD 于点F ，那么当点F 在线段CD 的延长线上时，设BP =x ，DF =y ，求y 关于x 的函数解析式。
相似三角形模型讲解-一线三等角问题
第一部分 相似三角形模型分析一、相似三角形判定的基本模型认识（一）A 字型、反A 字型（斜A 字型）ABCDE（平行）CBA DE（不平行）（二）8字型、反8字型J OADBCAB CD（蝴蝶型）（平行） （不平行）（三）母子型ABCDCAD（四）一线三等角型：三等角型相似三角形是以等腰三角形（等腰梯形）或者等边三角形为背景（五）一线三直角型：（六）双垂型：CAD二、相似三角形判定的变化模型旋转型：由A 字型旋转得到。
8字型拓展CB EDA共享性GABCEF一线三等角的变形一线三直角的变形第二部分 相似三角形典型例题讲解母子型相似三角形例1：如图，梯形ABCD 中，AD ∥BC ，对角线AC 、BD 交于点O ，BE ∥CD 交CA 延长线于E ． 求证：OE OA OC ⋅=2．例2：已知：如图，△ABC 中，点E 在中线AD 上, ABC DEB ∠=∠．求证：（1）DA DE DB ⋅=2； （2）DAC DCE ∠=∠．例3：已知：如图，等腰△ABC 中，AB ＝AC ，AD ⊥BC 于D ，CG ∥AB ，BG 分别交AD 、AC 于E 、F ．求证：EG EF BE ⋅=2．相关练习：1、如图，已知AD 为△ABC 的角平分线，EF 为AD 的垂直平分线．求证：FC FB FD ⋅=2．AC D E B2、已知：AD 是Rt △ABC 中∠A 的平分线，∠C=90°，EF 是AD 的垂直平分线交AD 于M ，EF 、BC 的延长线交于一点N 。
求证：(1)△AME ∽△NMD; (2)ND 2=NC ·NB3、已知：如图，在△ABC 中，∠ACB=90°，CD ⊥AB 于D ，E 是AC 上一点，CF ⊥BE 于F 。
求证：EB ·DF=AE ·DB4.在∆ABC 中，AB=AC ，高AD 与BE 交于H ，EF BC ⊥，垂足为F ，延长AD 到G ，使DG=EF ，M 是AH 的中点。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
相似三角形（3）“一线三等角型”
教学目标：
1、掌握相似三角形的判定和性质，并能熟练运用其解决重要类型“一线三等角”的类型题.
2、经历运用相似三角形的基础知识解决问题的过程，再次体验图形运动、分类讨论、方程
与函数等数学思想.
3、通过问题的解决，体验探究问题成功的乐趣，积极探索，提高学习几何的兴趣.
重点：
相似三角形的判定性质及其应用.
难点：
与相似、函数有关的综合性问题的解决技巧和方法.
教学方法：
启发式教学方法，尝试指导教学法.
一、知识梳理：
（图1） （图2）
（1）如图1：已知三角形ABC 中，AB=AC,∠ADE=∠B,那么一定存在的相似三角形有___
（2）如图2：已知三角形ABC 中，AB=AC,∠DEF=∠B,那么一定存在的相似三角形有___
二、【例题解析】
【例1】如图，在边长为2的等边三角形ABC 中，D 是BC 边上任意一点，AB 边上有一点E ，
AC 边上有一点F ，使∠EDF=∠ABC. 已知BD=1，BE=3
1,求CF 的长
【练】1、已知△ABC 中AB=AC=6、BC=8，∠BAC=120度，D 是BC 边上任意一点，AB 边上有
一点E ，AC 边上有一点F ，使∠EDF=∠C. 已知BD=6、BE=4，求:CF 的长
2、如图，等边△ABC 中，边长为6，D 是BC 上动点，∠EDF =60°
（1）求证：△BDE ∽△CFD
（2）当BD =23，FC =1时，求BE
【例2】在ABC ∆中，O BC AC C ,3,4,90===∠o 是AB 上的一点，且5
2=AB AO ，点P 是AC 上的一个动点，OP PQ ⊥交线段BC 于点Q ，（不与点B,C 重合），已知AP=2，求CQ
【练】在直角三角形ABC 中，D BC AB C ,,90==∠o 是AB 边上的一点，E 是在AC 边
上的一个动点，（与A,C 不重合），DF DE DF ,⊥与射线BC 相交于点F.
(1)、当点D 是边AB 的中点时，求证：DF DE =
(2)、当m DB
AD =，求DF DE 的值
【例3】已知在等腰三角形ABC 中，AB=AC,D 是BC 的中点，∠EDF=∠B,
求证：△BDE ∽△DFE.
【练】在边长为4的等边ABC ∆中，D 是BC 的中点，点E 、F 分别在AB 、AC 上（点D 不与点C 、点B 重合），且保持ABC EDF ∠=∠,连接EF .
(1)已知BE=1,DF=2.求DE 的值
(2)求∠BED=∠DEF
【例4】 如图，已知边长为3的等边ABC ∆，点F 在边BC 上，1CF =，点E 是射线BA 上一动点，以线段EF 为边向右侧作等边EFG ∆，直线,EG FG 交直线AC 于点,M N ，
（1）写出图中与BEF ∆相似的三角形；
（2）证明其中一对三角形相似；
（3）设,BE x MN y ==，求y 与x 之间的函数关系式，并写出自变量x 的取值范围；
【练】 如图，在△ABC 中，8==AC AB ，10=BC ，D 是BC 边上的一个动点，点E 在
AC 边上，且C ADE ∠=∠．
(1) 求证：△ABD ∽△DCE ；
(2) 如果x BD =，y AE =，求y 与x 的函数解析式，并写出自变量x 的定义域；
(3) 当点D 是BC 的中点时，试说明△ADE 是什么三角形，并说明理由．
【例5】已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且AD ＝5，AB ＝DC ＝2．
（1）如图8，P 为AD 上的一点，满足过点D 作DG ⊥EF 于点G ，∠BPC ＝∠A ． ①求证；△ABP ∽△DPC
②求AP 的长．
【练】如图，在梯形ABCD 中，AD ∥BC ，6AB CD BC ===，3AD =．点M 为边BC 的中点，以M 为顶点作EMF B ∠=∠，射线ME 交腰AB 于点E ，射线MF 交腰CD 于点F ，联结EF ．
（1）求证：△MEF ∽△BEM ；
（2）若△BEM 是以BM 为腰的等腰三角形，求EF 的长；
（3）若EF CD ⊥，求BE 的长．
【家庭作业】 1、如图，在ABC ∆中，90C ∠=︒，6AC =，4
3=BC AC ，D 是BC 边的中点，E 为AB 边
上的一个动点，作90DEF ∠=︒，EF 交射线BC 于点F ．设BE x =，BED ∆的面积为y ．
（1）求y 关于x 的函数关系式，并写出自变量x 的取值范围；
（2）如果以B 、E 、F 为顶点的三角形与BED ∆相似，求BED ∆的面积.
2、如图，已知在△ABC 中， AB =AC =6，BC =5，D 是AB 上一点，BD =2，E 是BC 上一动
点，联结DE ，并作DEF B ∠=∠，射线EF 交线段AC 于F ．
（1）求证：△DBE ∽△ECF ；
（2）当F 是线段AC 中点时，求线段BE 的长；
（3）联结DF ，如果△DEF 与△DBE 相似，求FC 的长．
3、已知在梯形ABCD 中，AD ∥BC ，AD ＜BC ，且BC =6，AB =DC =4，点E 是AB 的中点．
（1）如图，P 为BC 上的一点，且BP =2．求证：△BEP ∽△CPD ；
（2）如果点P 在BC 边上移动（点P 与点B 、C 不重合），且满足∠EPF =∠C ，PF 交直
线CD 于点F ，同时交直线AD 于点M ，那么
①当点F 在线段CD 的延长线上时，设BP =x ，DF =y ，求y 关于x 的函数解析式，
并写出函数的定义域；
②当BEP DMF S S ∆∆=4
9时，求BP 的长。