坐标平面内图形的轴对称和平移(1)
坐标平面内图形的轴对称和平移-完整版课件

(8、-5)第四象限
思考题: • 将例题各个“顶点”中横坐标加2,“鱼”发生了什么变化,纵坐标 加2呢? • 将例题各个“顶点”中横坐标乘2,“鱼”发生了什么变化,纵坐标 乘2呢? • 将例题各个“顶点”中横、纵坐标都乘2,“鱼”发生了什么变化? • 自己总结一下“鱼的变化”的规律
二、方法小结 1、作图 2、学习方法
小测验:
1、点B(-2,1)关于y轴对称的点的坐标是 ____, 关于原点对 称点的坐标是_____.
2、(点2(、m1,)-1)和点(2,n)关于x轴对称,则mn等于(( 2、)-1)
A.- 2 B.2 C.1
D.- 1
3、若点A(1-a,5),B(3 ,b)关于y轴对称,求(2a,-b)的坐 标,指出它在第几象限?
(-x , y)
猜一猜,做一做
y
5 与原图形关于x轴对称
4
3 2 1 0 12345678 –1 –2
将所得图案的各个 顶点的横坐标保持 不变,纵坐标分别 乘-1,依次连接这 些点,你会得到怎 样的图案?观察坐 标系中的两条鱼的 位置关系?
关于x轴对称的图 x 形:各点的横坐
标保持不变,纵 坐标互为相反数
(x , y)
(-x , -y)
应用:
如图所示:
1、你能做出ABCD关于x轴对称
的图形吗?关于原点对称的图
呢?
2、图中那些图关于x轴对称,
关于y轴对称,和原点对称的
D3
D2
呢?
B3
C3
C2
B2
A3
A2
巩固提升:
1、已知点P(2a-3,4),点A(-1,2b+2),
(1)如果点P与点A关于x轴对称,那么a+b=_-_2 _
坐标平面内图形的轴对称和平移(基础) 知识讲解

坐标平面内图形的轴对称和平移(基础)【学习目标】1.能在同一直角坐标系中,感受图形经轴对称后点的坐标的变化.2.掌握左右、上下平移点的坐标规律.【要点梳理】要点一、关于坐标轴对称点的坐标特征1.关于坐标轴对称的点的坐标特征P(a,b)关于x轴对称的点的坐标为 (a,-b);P(a,b)关于y轴对称的点的坐标为 (-a,b);P(a,b)关于原点对称的点的坐标为 (-a,-b).2.象限的角平分线上点坐标的特征第一、三象限角平分线上点的横、纵坐标相等,可表示为(a,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a,-a).3.平行于坐标轴的直线上的点平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同.要点二、用坐标表示平移1.点的平移:在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).要点诠释:(1)在坐标系内,左右平移的点的坐标规律:右加左减;(2)在坐标系内,上下平移的点的坐标规律:上加下减;(3)在坐标系内,平移的点的坐标规律:沿x轴平移纵坐标不变,沿y轴平移横坐标不变.2.图形的平移:在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.要点诠释:(1)平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决.(2)平移只改变图形的位置,图形的大小和形状不发生变化.【典型例题】类型一、用坐标表示轴对称1.已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则b a的值为_______. 【思路点拨】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得a+b=-3,1-b=-1,再解方程可得a、b的值,进而算出b a的值.【答案】25【解析】解:∵点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),∴a+b=-3,1-b=-1,解得:b=2,a=-5,ba=25,【总结升华】此题主要考查了关于y轴对称点的坐标特点,关键是掌握点的坐标的变化规律.举一反三:【变式】点(3,2)关于x轴的对称点为()A.(3,-2)B.(-3,2)C.(-3,-2)D.(2,-3)【答案】A.2.已知点A(-3,2)与点B(x,y)在同一条平行于y轴的直线上,且点B到x轴的距离等于3,求点B的坐标.【思路点拨】由“点A(-3,2)与点B(x,y)在同一条平行于y轴的直线上”可得点B的横坐标;由“点B到x轴的距离等于3”可得B的纵坐标为3或﹣3,即可确定B的坐标.【答案与解析】解:如图,∵点B与点A在同一条平行于y轴的直线上,∴点B与点A的横坐标相同,∴ x=-3.∵点B到x轴的距离为3,∴ y=3或y=-3.∴点B的坐标是(-3,3)或(-3,-3).【总结升华】在点B的横坐标为-3的条件下,点B到x轴的距离等于3,则点B可能在第二象限,也可能在第三象限,所以要分类讨论,防止漏解.举一反三:【变式1】若x轴上的点P到y轴的距离为3,则点P的坐标为().A.(3,0) B.(3,0)或(–3,0)C.(0,3) D.(0,3)或(0,–3)【答案】B.【变式2】若点P (a ,b)在第二象限,则:(1)点P1(a ,-b)在第象限;(2)点P2(-a ,b)在第象限;(3)点P3(-a ,-b)在第象限;(4)点P4( b ,a )在第象限.【答案】(1)三;(2)一;(3)四;(4)四.类型二、用坐标表示平移3.(2015•海安县校级二模)在平面直角坐标系中,将点A(﹣2,3)向右平移2个单位长度,再向下平移6个单位长度得点B,则点B的坐标是.【思路点拨】根据向右平移横坐标加,向下平移纵坐标减列式计算即可得解.【答案】(0,﹣3).【解析】解:∵将点A(﹣2,3)向右平移2个单位长度,再向下平移6个单位长度得点B,∴点B的坐标是(﹣2+2,3﹣6),即(0,﹣3).故答案为:(0,﹣3).【总结升华】本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.举一反三:【变式1】已知:两点A(-4,2)、B(-2,-6),(1)线段AB的中点C坐标是;(2)若将线段AB沿x轴向右平移5个单位,得到线段A1B1,则A1点的坐标是 ,B1点的坐标是.(3)若将线段AB沿y轴向下平移3个单位,得到线段A2B2,则A2点的坐标是 ,B2点的坐标是.【答案】(1)(-3, -2); (2)(1,2),(3,-6); (3)(-4,-1),(-2,-9).【变式2】点P(-2,5)向右平移个单位长度,向下平移个单位长度,变为P′(0,1).【答案】2、4.4.(2016春•江西期末)如图中,A、B两点的坐标分别为(2,3)、(4,1),(1)求△ABO的面积.(2)把△ABO向下平移3个单位后得到一个新三角形△O′A′B′,求△O′A′B′的3个顶点的坐标.【思路点拨】(1)把△ABO放在一个矩形里面,用矩形COED的面积﹣△ACO的面积﹣△ABD的面积﹣△BEO的面积即可算出△ABO的面积;(2)根据点的坐标平移的规律,用A、B、O的坐标的纵坐标分别减去3即可.【答案与解析】解:(1)如图所示:S△ABO=3×4﹣×3×2﹣×4×1﹣×2×2=5;(2)A′(2,0),B′(4,﹣2),O′(0,﹣3).【总结升华】此题主要考查了点的平移,以及求三角形的面积,当计算一个三角形的面积时,可以把它放在一个矩形里,然后用矩形的面积减去周围三角形的面积.举一反三:【变式】(2014秋•宣汉县期末)如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标.【答案】解:A1(﹣3,5),B1(0,6),C1(﹣1,4).。
坐标平面内图形的轴对称和平移(1)教案浙教版数学八年级上册
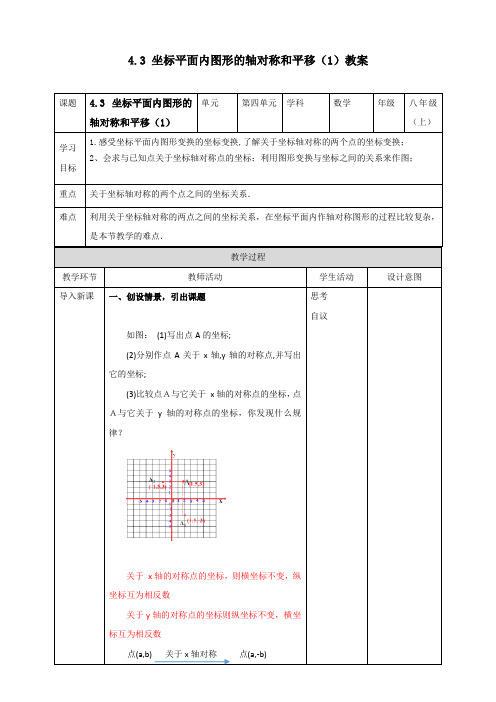
4.3 坐标平面内图形的轴对称和平移(1)教案课题 4.3 坐标平面内图形的轴对称和平移(1)单元第四单元学科数学年级八年级(上)学习目标1.感受坐标平面内图形变换的坐标变换,了解关于坐标轴对称的两个点的坐标变换;2、会求与已知点关于坐标轴对称点的坐标;利用图形变换与坐标之间的关系来作图;重点关于坐标轴对称的两个点之间的坐标关系.难点利用关于坐标轴对称的两点之间的坐标关系,在坐标平面内作轴对称图形的过程比较复杂,是本节教学的难点.教学过程教学环节教师活动学生活动设计意图导入新课一、创设情景,引出课题如图:(1)写出点A的坐标;(2)分别作点A关于x轴,y轴的对称点,并写出它的坐标;(3)比较点A与它关于x轴的对称点的坐标,点A与它关于y轴的对称点的坐标,你发现什么规律?关于x轴的对称点的坐标,则横坐标不变,纵坐标互为相反数关于y轴的对称点的坐标则纵坐标不变,横坐标互为相反数点(a,b) 关于x轴对称点(a,-b)思考自议点(a,b) 关于y轴对称点(-a,b)简单的说:关于什么轴对称,就什么坐标不变。
讲授新课二、提炼概念三、典例精讲例 1 (1)求出图形轮廓线上各转折点A,O,B,C,D,E,F的坐标以及它们关于y轴的对称点A′,O′,B′,C′,D′,E′,F′的坐标。
(2)在同一坐标系中,描点A′,O′,B′,C′,D′,E′,F′,并用线段依次将它们连接起来。
解:(1)图形轮廓线上各转折点的坐标依次是:A(0,-2) O(0,0)B(3,2) C(2,2) D(2,3) E(1,3) F(0,5)A'(0,-2) O'(0,0) B'(-3,2) C'(-2,2) D'(-2,3) E'(-1,3)F'(0,5)(2)点A′,O′,B′,C′,D′,E′,F′及其连线如图。
(1)关于x轴对称的两个点,横坐标相等,纵坐标互为相反数;(2)关于y轴对称的两个点,纵坐标相等,横坐标互为相反数.在直角坐标系中,P点的坐标为(a,b),P点关于x轴对称的对称点为P1(a,-b),关于y轴对称的对称点为P2(-a,b).一个零件的横截面如图,请完成以下任务:1.按你自己所认为合适的比例,建立直角坐标系。
坐标平面内图形的轴对称和平移(提高) 知识讲解

坐标平面内图形的轴对称和平移(提高)【学习目标】1.能在同一直角坐标系中,感受图形经轴对称后点的坐标的变化.2.掌握左右、上下平移点的坐标规律.【要点梳理】要点一、关于坐标轴对称点的坐标特征1.关于坐标轴对称的点的坐标特征P(a,b)关于x轴对称的点的坐标为 (a,-b);P(a,b)关于y轴对称的点的坐标为 (-a,b);P(a,b)关于原点对称的点的坐标为 (-a,-b).2.象限的角平分线上点坐标的特征第一、三象限角平分线上点的横、纵坐标相等,可表示为(a,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a,-a).3.平行于坐标轴的直线上的点平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同.要点二、用坐标表示平移1.点的平移:在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).要点诠释:(1)在坐标系内,左右平移的点的坐标规律:右加左减;(2)在坐标系内,上下平移的点的坐标规律:上加下减;(3)在坐标系内,平移的点的坐标规律:沿x轴平移纵坐标不变,沿y轴平移横坐标不变.2.图形的平移:在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a ,相应的新图形就是把原图形向上(或向下)平移a 个单位长度. 要点诠释:(1)平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决.(2)平移只改变图形的位置,图形的大小和形状不发生变化. 【典型例题】类型一、用坐标表示轴对称1.在直角坐标系中,已知点A (a +b ,2-a )与点B (a -5,b -2a )关于y 轴对称, (1)试确定点A 、B 的坐标;(2)如果点B 关于x 轴的对称的点是C ,求△ABC 的面积.【思路点拨】(1)根据在平面直角坐标系中,关于y 轴对称时,横坐标为相反数,纵坐标不变,得出方程组求出a ,b 即可解答本题;(2)根据点B 关于x 轴的对称的点是C ,得出C 点坐标,进而利用三角形面积公式求出即可.【答案与解析】解:(1)∵点A (a +b ,2-a )与点B (a -5,b -2a )关于y 轴对称,∴2250a b aa b a -=-⎧⎨++-=⎩,解得:13a b =⎧⎨=⎩, ∴点A 、B 的坐标分别为:(4,1),(-4,1);(2)∵点B关于x轴的对称的点是C,∴C点坐标为:(-4,-1),∴△ABC的面积为:12×BC×AB=12×2×8=8.【总结升华】本题主要考查了平面直角坐标系中,各象限内点的坐标的符号的确定方法以及三角形面积求法,熟练记忆各象限内点的坐标符号是解题关键.举一反三:【变式】小华看到了坐标系中点B关于X轴的对称点为C(-3,2),点A关于Y轴对称点为D(-3,4),若将A、B、C、D顺次连接,此图形的面积是多少?【答案】解:∵B关于x轴的对称点为C(-3,2),∴B(-3,-2),∵点A关于y轴对称点为D(-3,4),∴A(3,4),∴△ABD的面积为:12×AD×DB=12×6×6=18.2.已知点A(a,3)、B(-4,b),试根据下列条件求出a、b的值.(1)A、B两点关于y轴对称;(2)A、B两点关于x轴对称;(3)AB∥x轴;(4)A、B两点在第二、四象限两坐标轴夹角的平分线上.【思路点拨】(1)关于y轴对称,y不变,x变为相反数.(2)关于x轴对称,x不变,y变为相反数.(3)AB∥x轴,即两点的纵坐标不变即可.(4)在二、四象限两坐标轴夹角的平分线上的点的横纵坐标互为相反数,即分别令点A,点B的横纵坐标之和为0,列出方程并解之,即可得出a,b.【答案与解析】解:(1)A、B两点关于y轴对称,故有b=3,a=4;(2)A、B两点关于x轴对称;所以有a=-4,b=-3;(3)AB∥x轴,即b=3,a为≠-4的任意实数.(4)如图,根据题意,a+3=0;b-4=0;所以a=-3,b=4.【总结升华】本题主要考查学生对点在坐标系中的对称问题的掌握;在一、三象限角平分线上的点的横纵坐标相等,在二、四象限角平分线上的点的横纵坐标互为相反数.类型二、用坐标表示平移3.如图,△A′B′C′是由△ABC平移后得到的,已知△ABC中一点P(x0,y0)经平移后对应点为P′(x0+5,y0﹣2).(1)已知A(﹣1,2),B(﹣4,5),C(﹣3,0),请写出A′、B′、C′的坐标;(2)试说明△A′B′C′是如何由△ABC平移得到的;(3)请直接写出△A′B′C′的面积为.【思路点拨】(1)根据点P(x0,y0)经平移后对应点为P′(x0+5,y0﹣2)可得A、B、C三点的坐标变化规律,进而可得答案;(2)根据点的坐标的变化规律可得△ABC先向右平移5个单位,再向下平移2个单位;(3)把△A′B′C′放在一个矩形内,利用矩形的面积减去周围多余三角形的面积即可.【答案与解析】解:(1)A′为(4,0)、B′为(1,3)C′为(2,﹣2);(2)△ABC先向右平移5个单位,再向下平移2个单位(或先向下平移2个单位,再向右平移5个单位);(3)△A′B′C′的面积为6.【总结升华】此题主要考查了坐标与图形的变化,在平面直角坐标系内,把一个图形各个点的横坐标都加上(或减去)一个整数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加(或减去)一个整数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.(即:横坐标,右移加,左移减;纵坐标,上移加,下移减.)举一反三:【变式】(大庆校级模拟)如图所示,△COB是由△AOB经过某种变换后得到的图形,观察点A与点C的坐标之间的关系,解答下列问题:(1)若点M的坐标为(x、y),则它的对应点N的坐标为.(2)若点P(a,2)与点Q(﹣3,b)关于x轴对称,求代数式…的值.【答案】解:(1)由图象知点M和点N关于x轴对称,∵点M的坐标为(x、y),∴点N的坐标为(x,﹣y);(2)∵点P(a,2)与点Q(﹣3,b)关于x轴对称,∴a=﹣3,b=﹣2,∴…=+++…+,=﹣+﹣+…+,=﹣,=.类型三、综合应用4. 如图是某台阶的一部分,如果建立适当的坐标系,使A点的坐标为(0,0),B点的坐标为(1,1)(1)直接写出C,D,E,F的坐标;(2)如果台阶有10级,你能求得该台阶的长度和高度吗?【思路点拨】(1)根据平面直角坐标系的定义建立,然后写出各点的坐标即可;(2)利用平移的性质求出横向与纵向的长度,然后求解即可.【答案与解析】解:(1)∵点P(a﹣2,2a+8),在x轴上,∴2a+8=0,解得:a=﹣4,故a﹣2=﹣4﹣2=﹣6,则P(﹣6,0);(2))∵点P(a﹣2,2a+8),在y轴上,∴a﹣2=0,解得:a=2,故2a+8=2×2+8=12,则P(0,12);(3)∵点Q的坐标为(1,5),直线PQ∥y轴;,∴a﹣2=1,解得:a=3,故2a+8=14,则P(1,14);(4)∵点P到x轴、y轴的距离相等,∴a﹣2=2a+8或a﹣2+2a+8=0,解得:a1=﹣10,a2=﹣2,故当a=﹣10则:a﹣2=﹣12,2a+8=﹣12,则P(﹣12,﹣12);故当a=﹣2则:a﹣2=﹣4,2a+8=4,则P(﹣4,4).综上所述:P(﹣12,﹣12),(﹣4,4).【总结升华】此题主要考查了点的坐标性质,用到的知识点为:点到坐标轴的距离相等,那么点的横纵坐标相等或互为相反数以及在坐标轴上的点的性质.。
4.3坐标平面内的图形的轴对称和平移(1)课件(共25张ppt)
F' F
求出航线上各转折点 A,O,B,C,D,E,F的坐标。
A(0,-2) O(0,0) B(3,2) C(2,3) D(2,3) E(1,3) F(0,5)
A'(0,-2) O'(0,0) B'(-3,2) C'(-2,2) D'(-2,3) E'(-1,3) F'(0,5)
E' 3
E
D' 2
y
A
A’
4
3
C’
-4
-3
-2
2 1 -1 0 -1
C
1
2
3
4
x
-2
- ————
B’
-23.5
B
-4
A (-4,4)
y
4 3
你有什么
A’
(4,4)
发现吗?.
2
C’(-3,0)
1
(3,0) C
-4 -3 -2 -1 0 1 2 3 4
-1
(-2,-2.5) B’
-2 -3
— — —(2,-2.5B)
A' A
2、画出一侧的关键点,并求坐标
3、利用坐标关系,求另一侧关键点坐标
4、描点、连线
讨论:点P(2,-3)到x轴、y轴和坐标原点的距
离分别多少?
点M(-3,4)到x轴、 y轴和坐标原点的距离分 别多少?
y
M(-3,4) H
1
A
N -2 O 1
x
B
P(2,-3)
纵坐标的绝对值
y
P(a,b)
N
4 3 D’
(0,2.5)
2
1
-1 0 1 2 -1
图形的变化与对称

图形的变化与对称一、图形的变换1.平移:在平面内,将一个图形整体按照某个直线方向移动一定的距离,这种移动叫做图形的平移。
2.旋转:在平面内,将一个图形绕一点按某个方向转动一个角度,这种移动叫做图形的旋转。
3.轴对称:在平面内,如果一个图形沿一条直线对折,对折后的两部分都能完全重合,这样的图形叫做轴对称图形,这条直线叫做对称轴。
二、图形的对称性1.对称轴:一个图形沿一条直线对折,对折后的两部分都能完全重合,这条直线就叫做这个图形的对称轴。
2.对称点:一个图形沿一条直线对折,对折后的两部分都能完全重合,这个图形的每个点都有一个对应的对称点。
3.中心对称:在平面内,如果把一个图形绕某一点旋转180°,旋转后的图形能和原图形完全重合,那么这个图形就叫做中心对称图形,这个点叫做对称中心。
三、图形的对称性质1.对称图形的性质:对称图形的大小、形状和位置都不变,只是位置发生了变化。
2.轴对称图形的性质:轴对称图形沿对称轴对折,对折后的两部分完全重合。
3.中心对称图形的性质:中心对称图形绕对称中心旋转180°,旋转后的图形和原图形完全重合。
四、图形的变换与对称的应用1.利用图形的变换与对称解决实际问题,如设计图案、解决几何题等。
2.了解图形的变换与对称在生活中的应用,如建筑设计、艺术创作等。
1.判断题:(1)平移是将图形沿着一个方向移动一定的距离。
()(2)旋转是将图形绕一个点转动一个角度。
()(3)如果一个图形沿一条直线对折,对折后的两部分完全重合,这个图形就是轴对称图形。
()(4)对称轴是将图形分成两个完全相同部分的一条直线。
()2.选择题:(1)以下哪个选项不是图形的变换?()A.平移B.旋转C.翻转D.缩放(2)一个图形沿一条直线对折,对折后的两部分完全重合,这个图形沿该直线叫做什么?( )A.对称轴B.对称点C.对称线D.对称面3.解答题:(1)请描述轴对称图形的特点。
(2)请描述中心对称图形的特点。
坐标平面内图形的轴对称和平移(基础) 知识讲解

坐标平面内图形的轴对称和平移(基础)责编:杜少波【学习目标】1.能在同一直角坐标系中,感受图形经轴对称后点的坐标的变化.2.掌握左右、上下平移点的坐标规律.【要点梳理】要点一、关于坐标轴对称点的坐标特征1.关于坐标轴对称的点的坐标特征P(a,b)关于x轴对称的点的坐标为 (a,-b);P(a,b)关于y轴对称的点的坐标为 (-a,b);P(a,b)关于原点对称的点的坐标为 (-a,-b).2.象限的角平分线上点坐标的特征第一、三象限角平分线上点的横、纵坐标相等,可表示为(a,a);第二、四象限角平分线上点的横、纵坐标互为相反数,可表示为(a,-a).3.平行于坐标轴的直线上的点平行于x轴的直线上的点的纵坐标相同;平行于y轴的直线上的点的横坐标相同.要点二、用坐标表示平移1.点的平移:在平面直角坐标系中,将点(x,y)向右或向左平移a个单位长度,可以得到对应点(x+a,y)或(x-a,y);将点(x,y)向上或向下平移b个单位长度,可以得到对应点(x,y+b)或(x,y-b).要点诠释:(1)在坐标系内,左右平移的点的坐标规律:右加左减;(2)在坐标系内,上下平移的点的坐标规律:上加下减;(3)在坐标系内,平移的点的坐标规律:沿x轴平移纵坐标不变,沿y轴平移横坐标不变.2.图形的平移:在平面直角坐标系内,如果把一个图形各个点的横坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向右(或向左)平移a个单位长度;如果把它各个点的纵坐标都加上(或减去)一个正数a,相应的新图形就是把原图形向上(或向下)平移a个单位长度.要点诠释:(1)平移是图形的整体位置的移动,图形上各点都发生相同性质的变化,因此图形的平移问题可以转化为点的平移问题来解决.(2)平移只改变图形的位置,图形的大小和形状不发生变化.【典型例题】类型一、用坐标表示轴对称1.已知点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),则b a的值为_______. 【思路点拨】根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得a+b=-3,1-b=-1,再解方程可得a、b的值,进而算出b a的值.【答案】25【解析】解:∵点P(3,-1)关于y轴的对称点Q的坐标是(a+b,1-b),∴a+b=-3,1-b=-1,解得:b=2,a=-5,ba=25,【总结升华】此题主要考查了关于y轴对称点的坐标特点,关键是掌握点的坐标的变化规律.举一反三:【变式】点(3,2)关于x轴的对称点为()A.(3,-2)B.(-3,2)C.(-3,-2)D.(2,-3)【答案】A.2.已知点A(-3,2)与点B(x,y)在同一条平行于y轴的直线上,且点B到x轴的距离等于3,求点B的坐标.【思路点拨】由“点A(-3,2)与点B(x,y)在同一条平行于y轴的直线上”可得点B的横坐标;由“点B到x轴的距离等于3”可得B的纵坐标为3或﹣3,即可确定B的坐标.【答案与解析】解:如图,∵点B与点A在同一条平行于y轴的直线上,∴点B与点A的横坐标相同,∴ x=-3.∵点B到x轴的距离为3,∴ y=3或y=-3.∴点B的坐标是(-3,3)或(-3,-3).【总结升华】在点B的横坐标为-3的条件下,点B到x轴的距离等于3,则点B可能在第二象限,也可能在第三象限,所以要分类讨论,防止漏解.举一反三:【变式1】若x轴上的点P到y轴的距离为3,则点P的坐标为().A.(3,0) B.(3,0)或(–3,0)C.(0,3) D.(0,3)或(0,–3)【答案】B.【变式2】若点P (a ,b)在第二象限,则:(1)点P1(a ,-b)在第象限;(2)点P2(-a ,b)在第象限;(3)点P3(-a ,-b)在第象限;(4)点P4( b ,a )在第象限.【答案】(1)三;(2)一;(3)四;(4)四.类型二、用坐标表示平移3.(2015•海安县校级二模)在平面直角坐标系中,将点A(﹣2,3)向右平移2个单位长度,再向下平移6个单位长度得点B,则点B的坐标是.【思路点拨】根据向右平移横坐标加,向下平移纵坐标减列式计算即可得解.【答案】(0,﹣3).【解析】解:∵将点A(﹣2,3)向右平移2个单位长度,再向下平移6个单位长度得点B,∴点B的坐标是(﹣2+2,3﹣6),即(0,﹣3).故答案为:(0,﹣3).【总结升华】本题考查了坐标与图形变化﹣平移,平移中点的变化规律是:横坐标右移加,左移减;纵坐标上移加,下移减.举一反三:【高清课堂:第二讲平面直角坐标系2 369935 练习4 】【变式1】已知:两点A(-4,2)、B(-2,-6),(1)线段AB的中点C坐标是;(2)若将线段AB沿x轴向右平移5个单位,得到线段A1B1,则A1点的坐标是 ,B1点的坐标是.(3)若将线段AB沿y轴向下平移3个单位,得到线段A2B2,则A2点的坐标是 ,B2点的坐标是.【答案】(1)(-3, -2); (2)(1,2),(3,-6); (3)(-4,-1),(-2,-9).【变式2】点P(-2,5)向右平移个单位长度,向下平移个单位长度,变为P′(0,1).【答案】2、4.4. 如图所示的直角坐标系中,△ABC的顶点坐标分别是A(0,0),B(6,0),C(5,5).(1)求△ABC的面积;(2)如果将△ABC向上平移1个单位长度,得△A1B1C1,再向右平移2个单位长度,得到△A2B2C2,试求A2、B2、C2的坐标;(3)△A2B2C2与△ABC的大小、形状有什么关系.【思路点拨】 (1)已知AB=6,故只要求得C到x轴距离即可.(2)在平面直角坐标系中,将图形向右(或左)平移a个单位长度,那么图形的点(x,y)向右(或向左)平移a个单位长度,可得对应点(x+a,y)或(x-a,y),将图形向上(或向下)平移b个单位长度,可得到对应点(x,y+b)或(x,y-b).(3)可根据平移的性质进行分析和判断.【答案与解析】解:(1)点C到x轴的距离为5,所以11651522ABCS AB h==⨯⨯=△;(2)根据题意求出三角形A2B2C2各顶点的坐标为A2(2,1),B2(8,1),C2(7,6);(3)连接A2B2C2三点可以看出△A2B2C2与△ABC的大小、形状相等或相同.【总结升华】平移只改变图形的位置,不改变图形的形状和大小.举一反三:【变式】(2014秋•宣汉县期末)如图所示,△ABC三个顶点A,B,C的坐标分别为A(1,2),B(4,3),C(3,1).把△A1B1C1向右平移4个单位长度,再向下平移3个单位长度,恰好得到△ABC,试写出△A1B1C1三个顶点的坐标.【答案】解:A1(﹣3,5),B1(0,6),C1(﹣1,4).。
4.3 坐标平面内的图形的轴对称和平移(答案版)

坐标平面内的图形的轴对称和平移知识提要1.关于坐标轴对称的两个点的坐标关系在直角坐标系中,若点A与点A1关于x轴对称,则横坐标不变,纵坐标互为相反数;若点A与点A2关于y轴对称,则纵坐标不变,横坐标互为相反数.即点(a,b)关于x轴的对称点的坐标为(a,-b),关于y轴的对称点的坐标为(-a,b).2.坐标平面内图形的轴对称坐标平面内图形的轴对称是借助平面直角坐标系进行的一种图形的基本变换.(1)如果两个图形关于x轴对称,那么这两个图形的对应点的横坐标不变,纵坐标互为相反数.(2)如果两个图形关于y轴对称,那么这两个图形的对应点的纵坐标不变,横坐标互为相反数.(3)如果两个图形关于原点对称,那么这两个图形的对应点的横、纵坐标分别互为相反数.3.坐标平面内图形平移时对应点之间的坐标关系(1)原图形上的点(a,b)向左平移n(n>0)个单位,平移后对应点的坐标为(a-n,b);(2)原图形上的点(a,b)向右平移n(n>0)个单位,平移后对应点的坐标为(a+n,b);(3)原图形上的点(a,b)向上平移n(n>0)个单位,平移后对应的点坐标为(a,b+n);(4)原图形上的点(a,b)向下平移n(n>0)个单位,平移后对应点的坐标为(a,b-n).(5)点的坐标平移口诀:右加左减,上加下减.练习一、选择题1.在平面直角坐标系中,点A(-1,2)关于x轴的对称点B的坐标为( D )A. (-1,2)B. (1,2)C. (1,-2)D. (-1,-2)2.点A(-4,0)与点B(4,0)的位置关系是( B )A. 关于x轴对称B. 关于y轴对称C. 关于原点对称D. 不能确定3.(福州中考)如图,在3×3的正方形网格中有四个格点A, B, C, D,以其中一点为原点,网格线所在直线为坐标轴,建立平面直角坐标系,使其余三个点中存在两个点关于一条坐标轴对称,则原点是( B )A.点AB. 点BC. 点CD. 点D4.(贵港中考)在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( A )A. 第一象限B. 第二象限C. 第三象限D. 第四象限【解】由题意,得m=2,m-n=-3,∴n=5.∴点M(m,n)在第一象限.5.将下列图形画在平面直角坐标系中:①圆心在原点的圆;②与y轴垂直的一条直线;③与y轴平行的一条直线;④一个等边三角形的一个顶点与原点重合,且一条边在x轴的正半轴上.若图形上各点的横坐标均乘-1,纵坐标不变,则图形不发生变化的是( C )A.①④B.②④C.①②D.②③【解】图形上各点的横坐标乘-1,纵坐标不变,即将图形作一次关于y轴的轴对称变换,不发生变化的只有①②.6.已知点P(1,2)与点Q(x,y)在同一条平行于x轴的直线上,且点Q到y轴的距离等于2,则点Q的坐标是( C )A. (2,2)B. (-2,2)C. (-2,2)或(2,2)D. (-2,-2)或(2,-2)7.在平面直角坐标系中,已知线段AB的两个端点分别是A(-4,-1),B(1,1),将线段AB平移后得到线段A′B′.若点A′的坐标为(-2,2),则点B′的坐标为( B)A. (4,3)B. (3,4)C. (-1,-2)D. (-2,-1)【解】由点A(-4,-1)平移到点A′(-2,2),可知点A向右平移了2个单位,向上平移了3个单位.∴点B (1,1)也按此规律平移,平移后的点B ′的坐标为(3,4).8.已知点M(1-2m ,m -1)关于x 轴的对称点在第一象限,则m 的取值范围在数轴上表示正确的是( A )【解】∵点M (1-2m ,m -1)关于x 轴的对称点(1-2m ,1-m )在第一象限,∴⎩⎨⎧1-2m >0,1-m >0,解得⎩⎪⎨⎪⎧m <12,m <1.故选A. 9. 点P ⎝ ⎛⎭⎪⎫ac2,b a 在第二象限,点Q(a ,b)关于y 轴对称的点在( D ) A .第一象限B .第二象限C .第三象限D .第四象限【解析】D 第二象限点的横坐标为负,纵坐标为正,即ac2<0且b a >0,∴a<0,b<0,∴Q(a ,b)在第三象限,∴点Q 关于y 轴的对称点在第四象限.二、填空题1. 在平面直角坐标系中,把点P (a ,b )先向左平移1个单位,再向上平移2个单位,再把所得的点以x 轴为对称轴作轴对称变换,最后所得的像的坐标为(-4,6),则a =__-3__,b =__-8__.【解】用逆推法先求出(-4,6)关于x 轴的对称点是(-4,-6),再把(-4,-6)向右平移1个单位,向下平移2个单位得点(-3,-8), 即点P (a ,b ).2.已知点P(a +1,2a -1)关于x 轴的对称点在第一象限,则|a +2|-|1-a|=2a +1.3.把以(-3,6)和(-3,-2)为端点的线段向左平移4个单位,所得的像上任意一点的坐标可表示为(-7,y ),其中-2≤y ≤6.【解】 原线段向左平移4个单位后的端点分别为(-7,6),(-7,-2),此线段与y 轴平行,横坐标都为-7,纵坐标y 的取值范围是-2≤y ≤6.4.如图,在平面直角坐标系中,右边的图案是左边的图案经过平移得到的,左边的图案中,左、右两只眼睛的坐标分别是(-4,2),(-2,2),右边的图案中左眼的坐标是(3,4),则右边的图案中右眼的坐标是(5,4).5.已知平面直角坐标系中一点P (2x -y ,3x +2y ),先将它关于x 轴作一次轴对称变换,再关于y 轴作一次轴对称变换,最终得到点(-3,-8),则点Q (x ,y )的坐标为 .【解】 由题意,得⎩⎨⎧2x -y =3,3x +2y =8,解得⎩⎨⎧x =2,y =1.∴点Q 的坐标为(2,1).6. 如图,把∴ABC 经过一定的变换得到∴A′B′C′,如果∴ABC 上点P 的坐标为(a ,b),那么这个点在∴A′B′C′中的对应点P′的坐标为________.【解析】由题意可知,图形是向右平移3个单位,向上平移2个单位, 从而可知点P′的坐标为(a +3,b +2).答案:(a +3,b +2)7.如图,弹性小球从点P(0,3)出发,沿箭头方向运动,每当小球碰到矩形OABC 的边时反弹,反弹时反射角等于入射角,当小球第1次碰到矩形的边时的点为P1,第2次碰到矩形的边时的点为P2,…第n次碰到矩形的边时的点为Pn,则点P3的坐标是_(8,3)________,点P2 020的坐标是(5,0)_________.【解析】如答图,当点P第6次碰到矩形的边时,点P回到出发点(0,3),当点P第3次碰到矩形的边时,点P3的坐标是(8,3).∴2 020÷6=336……4,∴当点P第2 020次碰到矩形的边时为第337个循环组的第4次反弹,∴点P2 020的坐标是(5,0).三、解答题1.已知点A(-4,3),它与点B(a,b)在同一条平行于y轴的直线上,且AB=6,求点B的坐标.【解】∵点A(-4,3),AB∥y轴,∴点B的横坐标为-4.当点B在点A的上边时,点B的纵坐标为3+6=9;当点B在点A的下边时,点B的纵坐标为3-6=-3,∴点B的坐标为(-4,9)或(-4,-3).2.在平面直角坐标系中,点P的坐标为(a+1,3a-1).将点P向下平移2个单位,再向左平移1个单位后得到点Q,若点Q在第一象限,求a的取值范围.【解】∵将点P(a +1,3a -1)向下平移2个单位,再向左平移1个单位后得到点Q ,∴点Q 的坐标为(a ,3a -3).∵点Q 在第一象限,∴⎩⎨⎧a >0,3a -3>0,解得a >1.3.如图点P 的坐标为(4,3),把点P 绕坐标原点O 逆时针旋转90°后得到点Q .(1)点Q 的坐标为(-3,4).(2)若把点Q 向右平移m 个单位,向下平移2m 个单位后,得到的点Q ′恰好在第三象限,求m 的取值范围.【解】 (2)把点Q(-3,4)向右平移m 个单位,向下平移2m 个单位后, 得到的点Q′的坐标为(-3+m ,4-2m).∵点Q′在第三象限,∴⎩⎨⎧-3+m<0,4-2m<0,解得2<m<3.4.△ABO如图所示.(1)写出△ABO各顶点的坐标,以及它们关于y轴的对称点的坐标,描出这些对称点并将它们连结起来.(2)写出△ABO各顶点关于x轴的对称点的坐标,描出这些对称点并将它们连结起来.并说明这三个三角形之间的关系.【解】(1)点A(2,3),B(3,1),O(0,0);它们关于y轴的对称点的坐标分别是A′(-2,3),B′(-3,1),O′(0,0),如图所示.(2)点A,B,O关于x轴的对称点的坐标分别是A″(2,-3),B″(3,-1),O″(0,0),如图所示.关系:△ABO≌△A′B′O′≌△A″B″O″,△A′O′B′与△AOB关于y轴对称,△A″O″B″与△AOB关于x轴对称,△A′O′B′与△A″O″B″关于原点对称.5.如图,某公路(可视为x轴)的同一侧有A,B,C三个村庄,要在公路边建一货仓D,向A,B,C三个村庄送农用物资,路线是D→A→B→C→D.(1)试问:在公路边是否存在一点D,使送货路程最短?(2)求出点D的坐标.【解】 (1)存在.(2)∵路程为DA +AB +BC +CD ,AB +BC 的长度固定,∴要使路程最短,只需DA +CD 最短即可.作点A 关于x 轴的对称点A ′(0,-2),连结A ′C ,则A ′C 与x 轴的交点即为所求的点D ,过点C 作CE ⊥x 轴于点E ,则点E (5,0),易得△OA ′D ≌△ECD ,得OD =ED ,∴点D ⎝ ⎛⎭⎪⎫52,0.6.如图,已知点P(3,4),MN 是第一、三象限夹角平分线,求点P 关于直线MN 的对称点P 1的坐标.【解】 如解图,过点P 作PE ⊥MN 于点E ,延长PE 至点P 1 ,使PE =P 1E ,则点P 1就是点P 关于直线MN 的对称点.连结OP ,OP 1,则有OP =OP 1,∠POE =∠P 1OE.过点P 作PD ⊥y 轴于点D ,过点P 1作P 1H ⊥x 轴于点H.∵MN 是第一、三象限夹角平分线,∴∠DOE =∠HOE =45°,∴∠1=∠2.在Rt △PDO 和Rt △P 1HO 中,∵⎩⎨⎧∠1=∠2,∠PDO =∠P 1HO ,OP =OP 1,∴Rt △PDO ≌Rt △P 1HO(AAS),∴PD =P 1H =3,OD =OH =4,∴点P 1的坐标为(4,3).7.如图①,在6×6的方格纸中,给出如下三种变换:P 变换,Q 变换,R 变换.将图形F 沿x 轴向右平移1格得到图形F 1,称为作1次P 变换;将图形F 沿y 轴翻折得到图形F 2,称为作1次Q 变换;将图形F 绕坐标原点顺时针旋转90°得到图形F 3,称为作1次R 变换.规定:PQ 变换表示先作1次Q 变换,再作1次P 变换;QP 变换表示先作1次P 变换,再作1次Q 变换;R n 变换表示作n 次R 变换,解答下列问题:(1)作R 4变换相当于至少作__2__次Q 变换.(2)请在图②中画出图形F 作R 2017变换后得到的图形F 4.(3)PQ 变换与QP 变换是否是相同的变换?请在图③中画出PQ 变换后得到的图形F 5,在图④中画出QP 变换后得到的图形F 6.【解】(1)根据操作,观察发现:每作4次R变换便与图形F重合.因此R4变换相当于作2n次Q变换(n为正整数).(2)由于2017=4×504+1,故R2017变换即为R1变换,其图象如解图①.(3)PQ变换与QP变换不是相同的变换.正确画出图形F5,F6,如解图②③.。
