东北大学最优化第一章例题
最优化方法复习题66882.docx

《最优化方法》复习题第一章概述(包括凸规划)一、判断与填空题ar§ max /W =玄生min【―/(兀)】・71xeR n xeR n2max |/(x): x e D o }= - min [f(x): x e D Q R H\ x3设f : D u RJ R・若T wR”,对于一切xeR n恒有/(Z)</(x),则称T为最优化问题m in fM的全局最优解.xxeD4设f •・D U RJ R.若Z eD ,存在F的某邻域Ng,使得对一切恒有/U*)</(兀),则称T为最优化问题min /(兀)的严格局部最xeD优解.X5给定一个最优化问题,那么它的最优值是一个定值.V6非空集合D匸/?"为凸集当且仅当D屮任意两点连线段上任一点属于D. V 7非空集合D o 7?"为凸集当J1仅当D中任意有限个点的凸组合仍属于D. V 8任意两个凸集的并集为凸集.x9 函数f : D匸R” T R为凸集£>上的凸函数当且仅当—/为D上的凹函数.V1()设f : D u R” T R为凸集D上的可微凸函数,Z G Z).则对V XG D,有/(x)-/(x*)<V/(x*/(x-x*). x11若c(兀)是凹函数,则D = {xeR n\ c(x) > 0}是凸集。
V12设{*}为由求解min的算法A产生的迭代序列,假设算法A为下降算法,XG D则对\^^{0,1,2,・・・},恒有____ /(x A.+1)< f(x k) ____________ :13算法迭代时的终止准则(写出三种): ____________________________ o 14凸规划的全体极小点组成的集合是凸集。
V15函数f : D u R“ T R在点('沿着迭代方向d* eR n \ {()}进行精确一维线搜索的步长匕.,则其搜索公式为_____________________________ .16函数f •. D匚R“ T R在点*•沿着迭代方向d k e/?z, \{0}进行梢确一•维线搜索的步长匕,则V/(x A+a k d k Yd k = ___________ 0 .17设d k eR n\{0}为点/ w D匸R“处关于区域D的一个下降方向,则对于Va >0, 3«G(0,a)使得x二、简述题1写出Wolfe-Powell非精确一维线性搜索的公式。
最优化方法教案 东北大学

第一章最优化问题与数学预备知识最优化分支:线性规划,整数规划,几何规划,非线性规划,动态规划。
又称规划论。
应用最优化方法解决问题时一般有以下几个特点:1. 实用性强2. 采用定量分析的科学手段3. 计算量大,必须借助于计算机4. 理论涉及面广应用领域:工业,农业,交通运输,能源开发,经济计划,企业管理,军事作战……。
§1.1 最优化问题实例最优化问题:追求最优目标的数学问题。
经典最优化理论:(1) 无约束极值问题:),,,(opt 21n x x x f(),,,(min 21n x x x f 或),,,(max 21n x x x f )其中,),,,(21n x x x f 是定义在n 维空间上的可微函数。
解法(求极值点):求驻点,即满足⎪⎪⎩⎪⎪⎨⎧='='='0),,(0),,(0),,(11121n x n x n x x x f x x f x x f n并验证这些驻点是否极值点。
(2) 约束极值问题:),,,(opt 21n x x x fs.t. )(,,2,1,0),,,(21n l l j x x x h n j <==解法:采用Lagrange 乘子法,即将问题转化为求Lagrange 函数),,(),,,(),,;,,,(1121121n j j lj n l n x x h x x x f x x x L λλλ∑=+=的无约束极值问题。
近代最优化理论的实例:例1 (生产计划问题) 设某工厂有3种资源B 1,B 2,B 3,数量各为b 1,b 2,b 3,要生产10种产品A 1,…,A 10 。
每生产一个单位的A j 需要消耗B i 的量为a ij ,根据合同规定,产品A j 的量不少于d j ,再设A j 的单价为c j 。
问如何安排生产计划,才能既完成合同,又使总收入最多?(线性规划问题)数学模型:设A j 的计划产量为 j x ,z 为总收入。
最优化方法部分课后习题解答(1-7)

最优化方法部分课后习题解答习题一1.一直优化问题的数学模型为:22121122123142min ()(3)(4)5()02()50..()0()0f x x xg x x x g x x x s t g x x g x x =−+−⎧=−−≥⎪⎪⎪=−−+≥⎨⎪=≥⎪=≥⎪⎩试用图解法求出:(1)无约束最优点,并求出最优值。
(2)约束最优点,并求出其最优值。
(3)如果加一个等式约束,其约束最优解是什么?12()0h x x x =−=解:(1)在无约束条件下,的可行域在整个平面上,不难看出,当=(3,4)()f x 120x x *x 时,取最小值,即,最优点为=(3,4):且最优值为:=0()f x *x *()f x (2)在约束条件下,的可行域为图中阴影部分所示,此时,求该问题的最优点就是()f x 在约束集合即可行域中找一点,使其落在半径最小的同心圆上,显然,从图示中可12(,)x x 以看出,当时,所在的圆的半径最小。
*155(,)44x =()f x 其中:点为和的交点,令求解得到:1()g x 2()g x 1122125()02()50g x x x g x x x ⎧=−−=⎪⎨⎪=−−+=⎩1215454x x ⎧=⎪⎪⎨⎪=⎪⎩即最优点为:最优值为:=*155(,)44x =*()f x 658(3).若增加一个等式约束,则由图可知,可行域为空集,即此时最优解不存在。
2.一个矩形无盖油箱的外部总面积限定为S,怎样设计可使油箱的容量最大?试列出这个优化问题的数学模型,并回答这属于几维的优化问题.解:列出这个优化问题的数学模型为:该优化问题属于三维的优化问题。
123122313123max ()220..00f x x x x x x x x x x S x s t x x =++≤⎧⎪>⎪⎨>⎪⎪>⎩32123sx y z v⎛⎞=====⎜⎟⎝⎠习题二3.计算一般二次函数的梯度。
应用数学第1-11章作业

. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
. . . .
22 7 最 优控制法[习 题1、 2] 7.1 习题1: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 22 7.2 习题2: . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
−
反之,必要性:严格凸函数=》Hesse矩阵G正定.
类似,当对任意x ̸= y ,及任意实数λ ∈ (0, 1)都有f (λx + (1 − λ)y ) < λf (x) + (1 − λ)f (y ).
1 T T λf (x) + (1 − λ)f (y ) − f (λx + (1 − λ)y )=λ( 1 2 x Gx)+(1 − λ)( 2 y Gy ) 1 1 1 1 T T T [ 2 (λx) G(λx) + 2 (1 − λ)y G(1 − λ)y + 2 λx G(1 − λ)y + 2 (1 − λ)y T Gλx] 1 1 1 T T T T =1 2 λx G(1 − λ)x + 2 (1 − λ)y Gλy − 2 λx G(1 − λ)y − 2 (1 − λ)y Gλx 1 1 T T = 2 λx G(1 − λ)(x − y ) + 2 (1 − λ)y Gλ(y − x) 1 =2 λ(1 − λ)(x − y )T G(x − y ) > 0
最优化试题及答案

mi 1 m *m j * g j (x*) 0最优化理论、方法及应用试题一、(30 分)1、针对二次函数f(x) 1x T Qx b T x c,其中Q是正定矩阵,试写出最速下降算法的详细步骤,并简要说明其优缺点?答:求解目标函数的梯度为g(x) Qx b,g k g(x k) Qx k b,搜索方向:从X k出发,沿g k作直线搜索以确定x k 1。
Stepl:选定X。
,计算f o,g oStep2:做一维搜索,f k i min f X k tg k , x k 1 X k tg k.Step3 :判别,若满足精度要求,则停止;否则,置 k=k+1,转步2优缺点:最速下降法在初始点收敛快,收敛速度慢。
算法简单,在最优点附近有锯齿现象,2、有约束优化问题min f (x)g i(x) 0,i 1,2,L ,ms.th j (x) 0,j 1,2,L ,l最优解的必要条件是什么?答:假设x*是极小值点。
必要条件是f,g,h函数连续可微,而且极小值点的所有起作用约束的梯度h(x*)(i 1,2丄,1)和g j(x*)( j 1,2,L ,m)线性无关,则* * * *存在1 , 2丄,I, 1, 2丄,m,使得lf(x*) i* h i(x*)i 1j*g j(x*) 0,j 1,2,L* * * * *1 ,2 ,L , l , 1 , 2 ,L ,*0, j 03、什么是起作用约束?什么是可行方向?什么是下降方向?什么是可行下降方向?针对上述有约束优化问题,如果应用可行方向法,其可行的下降方向怎样确定?答:起作用约束:若g j(x0) 0,这时点x0处于该约束条件形成的可行域边界上,它对x0的摄动起到某种限制作用可行方向:x0是可行点,某方向 p,若存在实数0 0,使得它对任意2、应用共轭梯度方法求解无约束优化问题 min X 28X |,初始点为X 0 1 1 丁 。
答:假设误差范围是0.001。
最优化方法习题答案
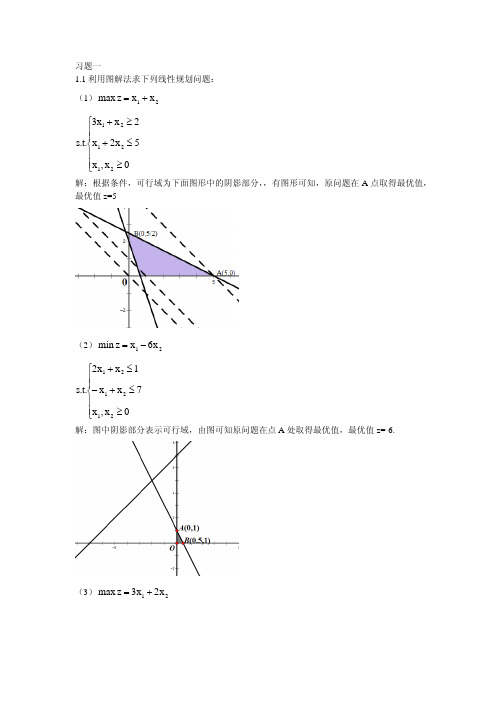
习题一1.1利用图解法求下列线性规划问题: (1)21x x z max +=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 5x 2x 2x x 3.t .s 212121 解:根据条件,可行域为下面图形中的阴影部分,,有图形可知,原问题在A 点取得最优值,最优值z=5(2)21x 6x z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+-≤+0x ,x 7x x 1x x 2.t .s 212121 解:图中阴影部分表示可行域,由图可知原问题在点A 处取得最优值,最优值z=-6.(3)21x 2x 3z max +=⎪⎪⎩⎪⎪⎨⎧≥-≥-≤+-0x ,x 4x 2x 1x x .t .s 212121 解:如图所示,可行域为图中阴影部分,易得原线性规划问题为无界解。
(4)21x 5x 2z min -=⎪⎪⎩⎪⎪⎨⎧≥≤+≥+0x ,x 2x x 6x 2x .t .s 212121 解:由图可知该线性规划可行域为空,则原问题无可行解。
1.2 对下列线性规划问题,找出所有的基解,基可行解,并求出最优解和最优值。
(1)4321x 6x 3x 2x 5z min -+-=⎪⎪⎩⎪⎪⎨⎧≥=+++=+++0x ,x ,x ,x 3x 2x x x 27x 4x 3x 2x .t .s 432143214321 解:易知1x 的系数列向量⎪⎪⎭⎫ ⎝⎛=21p 1,2x 的系数列向量⎪⎪⎭⎫ ⎝⎛=12p 2,3x 的系数列向量⎪⎪⎭⎫⎝⎛=13p 3,4x 的系数列向量⎪⎪⎭⎫⎝⎛=24p 4。
①因为21p ,p 线性无关,故有⎪⎩⎪⎨⎧--=+--=+43214321x 2x 3x x 2x 4x 37x 2x ,令非基变量为0x x 43==,得⎪⎪⎩⎪⎪⎨⎧=-=311x 31x 21,所以得到一个基解)0,0,311,31(x )1(-=是非基可行解; ②因为31p ,p 线性无关,可得基解)0,511,0,52(x)2(=,543z 2=;③因为41p ,p 线性无关,可得基解611,0,0,31(x )3(-=,是非基可行解;④因为32p ,p 线性无关,可得基解)0,1,2,0(x )4(=,1z 4-=;⑤因为42p ,p 线性相关,42x ,x 不能构成基变量; ⑥因为43p ,p 线性无关,可得基解)1,1,0,0(x )6(=,3z 6-=;所以)6()4()2(x ,x ,x是原问题的基可行解,)6(x 是最优解,最优值是3z -=。
最优化考试例题.doc

优化方法与最优控制例题1 • Find the curve x (t) that minimizes the functionalAnd passes through the points ^(0) = 1 and x(l) = 3.4" g(x,x,t) = y x 2(0 + 5x(t)x(t) + x 1 ⑺ + 5x(0,可求得gv =5i⑺+ 2%⑺+ 5 ^ = x(r) + 5x(z) ^ = ^(z) + 5i(z) dt若J 在x(z)处取极值,则有= 即 atX ⑺一2x ⑺一5 = 0解微分方程沿7) - 2x(z) = 0 ,可得通解%(z) = c x e~<21 + c 2Z 2/。
设对)-2冰)-5 = 0的通解为%(0 = <^,得力)=」。
故原微分方程的解为 2x(r) = c 1e'^ + c 2e^+|又已知x(0) = l, x ⑴=3,带入上式可得所以x ⑺=c,e'r2t + c 2^+-o 2Such that: f 7 e[x,x,t]dt = CWhere we will assume that t f is free but x(t f ) is fixed.2 One important calculus of variations problem that we did not discuss in class has the same basic form, but with constraints that are given by an integral - called isoperimetric constraints:min J = [ g[x, x,t\lt山0e^+32(^2-1)e^+3C ,2 =2(e 3 45-l)e[x,x,t]dt = CWhere g a = g v T e •(b) Use the results of part (a) to clearly state the differential equations and corresponding boundary conditions that must be solved to find the curve y(x) of a specified length L with endpoints on the x-axis (i.e.,at x = 0 and x = x f ) that encloses the maximum area, so that7 = £7ydx and £+ y 2dx = LWhere t, free.(a)引入拉格朗口矢量因子V ,另'g[x,x 9t]dt + v T ^f e(x ,i ,t)dt-C求变分有SJ a = 7 (§'—& + g^Sx)dt + g{t f )dt f + v T ^J^ {e x Sx + e {Sc)dt + e(t f )dt f + 1edt (g x - ::^-)Sxdt + + +〔{ edt-C Sv +v*l | 7 {e x -+ e..(t f) 4- e(t f )dt f有&, =&(◊) + 々(,,)々,,并令么=g + v T 《,带入上式,整理可得因为z f 自由,对rp 固定,所以要使<5/=0,则需满足条件:dSa _ d (d Sa dxdt \ dx=0Tclds, \T a = £[U.r + )—(音 + ^)]&cdt + 7 edt - Cj <5v +[A(,,)+ vTG(〜)]&,+(U(z ,) +’冲,)]-[心(z ,) + vT ¥(r)]地,))々,k dx dtSxdt +〔edt-C I 4--(r z )&c f +g a (t f )-^-dxdxdSa _d ( ^S a dx dt\ dxe[x,x,t]dt = C(b)令 = >’ ++ y 2,则有自由。
最优化方法及其matlab程序设计习题答案

证明:根据严格凸函数定义证明。
定义:对任意x ̸= y,及任意实数λ ∈ (0, 1)都有f (λx + (1 − λ)y) ≤ λf (x) + (1 − λ)f (y).
充分条件:∀x, y ∈ ℜn, 有f (x + y) ≤ f (x) + f (y)
对任意x ̸= y,及任意实数λ ∈ (0, 1)都有f (λx+(1−λ)y) ≤ f (λx)+f ((1−λ)y)
8
k= 2 (2)阻尼牛顿法 function He=Hesstwo(x) n=length(x); He=zeros(n,n); He=[8, 0; 0, 2]; ≫ x0=[0,1]’;[x val k]=dampnm(’funtwo1’,’gfuntwo1’,’Hesstwo’,x0) x= 1 2 val = -8 k= 1 第3题. function f=fun(x) f = (x(1) − 2)4 + (x(1) − 2 ∗ x(2))2; function gf=gfun(x) gf = [4 ∗ (x(1) − 2)3 + 2 ∗ (x(1) − 2 ∗ x(2)), −4 ∗ (x(1) − 2 ∗ x(2))]′; ≫clear all; ≫x0=[0 3]’;[v,val,k]=grad(’fun’,’gfun’,x0)
(1
−
λ)y)=
1 2
(λx
+
(1
−
λ)y)T
G(λx
+
(1
−
λ)y)
+
bT
(λx
+
(1
−
λ)y)
λf
(x)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
=
x (2) 1
-
x (1) 1
+
(2x
(1) 2
-
5)(x
(2 2
)
-
x (1) 2
)
[ ] r
-s1(x2 ) -
r -s1 (x1 )
{ } -
Ñ[
-
s1
(
r x1
)]
Tr r (x2 - x1 )
=
x (2) 1
-
x (1) 1
+ [x2(2) ]2
- [x2(1) ]2
-
5 éë x 2( 2)
-s1(x1) =
1, 2x2
-
5
T
,
r x1
=
é ê ë
x (1) 1
x (1) 2
ù ú, û
r x2
x (1) 1
+
[
x (1) 2
]2
-
5 x2(1)
,
=
é ê ë
x (2) 1
x (2) 2
ù ú, û
r -s2 (x2 )
=
x (2 ) 1
+
[ x2( 2)
]2
-
5 x2( 2)
,
r -s1(x2
s.t
x1
+
x
2 2
- 5x2
=
0,
x1 + x2 - 5 ³ 0,
x1 ³ 0,
x2 ³
解:①画出目标函数
0.
r f (x)
=
(x1
-
7 )2 4
+
(x2
-
5 )2 2
的等值线;
②画出等式约束 x1 + x22 - 5x2 = 0
的图形,它是一条抛物线;
③画出不等式约束所代表的区域。
x2
o
x1
容许集为抛物线的一段,最优解为目标函数的等 值线与容许集的切点,即最优点满足方程
)
=
é0 êë0
0ù 2 úû
各阶主子式非负,
-s1(x1, x2 )
=
x1
+
x
2 2
- 5x2
为凸函数。
s1(x1, x2 ) = -x1 - x2 2 + 5x2 ³ 0 为凸集。
即容许集为凸集。
用一阶导数判别
-s1(x1, x2 )
=
x1
+
x
2 2
- 5x2
的凸性。
[ ] [ ] Ñ
-s1(x1, x2 ) = r
f (4,1) = 117 > 5.
16
交点 (4,1),
例3:用图解法求解
min
s.t
(
x1x1-+141x)222+-(
x2 +
5x2
3 )2 2
= 0,
x1 + 2x2 -10 ³ 0,
x1 ³ 0,
x2 ³ 0.
解:①画出目标函数
min
(
x1
-
11)2 4
+ ( x2
+
3 )2 2
的等值线;
2 2
-
或
x2
=
9. 2
20x2
+9
=
0,
得切点
æ çè
9 4
,
1 2
ö ÷ø
,æçè
9 4
,
9 2
ö÷ø.
æ çè
9 4
,
1 2
ö ÷ø
不在容许集上,最优点为
æ çè
9 4
,
9 2
ö÷ø.
最优值点
f
æ çè
9 4
,
9 2
ö ÷ø
=
5.
ì í
x1
+
x
2 2
- 5x2
= 0,
î x1 + x2 - 5 ³ 0.
ê ë
3
ú û
.
Ñf
(
xr
)
=
é ê ë
2x1 + x2 x1 + 2x2
+ -
4ù 1úû
,
r é3ù Ñf (z) = êë3úû.
Ñf
( zr)T
r p
=
[3
3]
é-1ù
ê ë
1
ú û
=
0.
例5:判别最优化问题是否为凸规划
min
(x1 -
7 )2 4
+
( x2
-
5 )2 2
s.t -x1 - x22 + 5x2 ³ 0,
=
0,
8x23 - 60 x22 +126 x2 - 49 = 0,
1 9 7 21
(2x2 -
切点 f ( 21
7)2(2 x2 -1) = 0, x2
(9 , 1 ), (21, 7). 42 4 2
点
, 7 ) = 125 > 101.
= 2 , x1 = (9 ,1) 42
最优解
4 ;x2 = 2 , x1 = 4
=
-2 x1,
¶2 f (xr) ¶x22
= 1.
Ñf
r (x)
=
éê2 x1 (x12 ë
- x2) + 2(x1 x2 - x12
- 1)ù ú û
,Ñ2
f
r (x)
=
é6 ê
x12
ë
- 2x2 -2x1
+2
-2x1 1
ù ú û
.
例2:用图解法求解
min
(x1 -
7 )2 4
+
( x2
-
5 )2 2
ì ï ïí ï
x1 x2
-
7
4 5
2
=
-
1 2x2 -
, 5
ï î
x1 + x22 - 5x2 = 0.
⑴
x2
=
5, 2
公切线平行 x2 轴,切点为
æ çè
25 4
,
5 2
ö÷ø .
⑵
x2
¹
5 2
,
x1
-
7 4
=
1, 2
9
x1
=
, 4
代入得
9 4
+
x22
解得 x2
- 5x2
= 1, 2
=
0,
4
x
x1 + x2 - 5 ³ 0,
x1 ³ 0,
x2 ³ 0.
并用图解法求出最优点。
解:f
(
r x1
r ,x2
)
=
( x1
-
7 )2 4
+
( x2
-
5)2 ,Ñ2 2
f
rr (x1,x2 )
=
é2 êë0
0ù
2
ú. û
Ñ2
f
(
rr x1,x2
)
=
é2 êë0
0ù 2 úû
正定
x2
o
x1
从图上可判别出容许集为淡绿色区域,此 区域为凸集,故此最优化问题为凸规划。
例1:已知
r Ñf (x),
f (x)
Ñ2 f
=1
r2
(
x2
( x ).
-
x12
)2
+
(1 -
x1 ) 2
求
解:
¶f (xr) ¶x1r
=
2x1 (x12
-
x2 )
+
2(x1
- 1),
¶
¶f (x
2
f
(
xr
¶x2
)
=
¶x12
)
6
= x2 -
x12 - 2
x1 2
x2
.
+
2,
¶2 f (xr) ¶x1¶x2
)
-
[
-s1
r (x1
)]
=
x (2) 1
-
x (1) 1
+ [x2(2) ]2
- [x2(1) ]2
-
5 éë x 2( 2)
-
x (1) 2
ùû
{ [ ]} [ ] r
Ñ -s1(x1)
T
rr (x2 - x1) =
1,2x2
-5
é ê ë
x1( x2(
2) 2)
-
x (1) 1
x (1) 2
ù ú û
即容许集为凸集。
由图解法可求得局部极小点,它一定是此 最优化问题的全局最优点。
最优点满足条件
ì ï ïí ï
x1 x2
-
7
4 5
2
=
-1,
ï î
x1 + x2 = 5.
ì ï í ïî
x1
x1
7 4 +
= x2 x2 =
-5 2
5.
,
Þ
ì4 í î
x1 - 4 x2 x1 + x2
= -3, = 5.
解得
x1
=
17 8 , x2
=
23 .
8
xr*
=
é17 êë 8
,
23
T
ù
8 úû
.
为全局最优点。
-
x (1) 2
