高等代数与解析几何第七章
高等数学第七章向量代数与空间解析几何习题
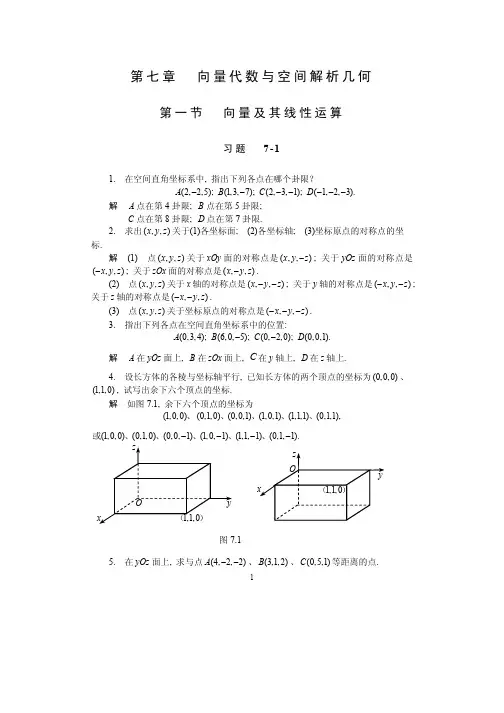
解 ∵ a + b = AC = 2MC = −2MA ,
D
C
b
M
b − a = BD = 2MD = −2MB ,
∴
MA
=
−
1 2
(a
+
b),
MB
=
−
1 2
(b
−
A a ),
a
B
图 7.2
MC
=
1 2
(a
+
b),
MD
=
1 2
(b
−
a ).
10. 用向量的方法证明: 连接三角形两边中点的线段(中位线)平行且等于第三
而
a⋅b =
a
⋅
b
⋅
cos(a,
b)
=
10
×
cos
π 3
=5,
所以
r 2 = 100 − 60 + 36 = 76 ,
故 r = 76 .
3. 已知 a + b + c = 0 , 求证 a × b = b × c = c × a
证 法1
∵a + b + c = 0 ,
所以
c = −(a + b) ,
解 因 a = m − 2n + 3 p = (8i + 5 j + 8k) − 2(2i − 4 j + 7k) + 3(i + j − k) = 7i + 16 j − 9k ,
故沿 x 轴方向的分向量为 axi = 7i ; 沿 y 轴方向的分向量为 ay j = 16 j .
16. 若线段 AB 被点 C(2, 0, 2)和D(5, −2, 0) 三等分, 试求向量 AB 、点 A 及点 B 的
高等代数课件(北大版)第七章-线性变换§7.7

若 V W1 W2 Ws,则
11, ,1n1 , 21, , 2一组基,且在这组基下 的矩阵为准对角阵
A1
A2
.
As
2023/8/17§7.7 不变子空间 数学与计算科学学院
(1)
反之,若 在基 11, ,1n1 , 21, , 2n2 , , s1, , sns 下的矩阵为准对角矩阵(1), 则由 i1, i2 , , ini 生成 的子空间 Wi 为 的不变子空间,且V具有直和分解:
其次,任取 Vi , 设
( i E )ri Wi 0.
1 2 s , i Wi . 即 1 2 (i ) s 0 令 j j , ( j i); i i .
2023/8/17§7.7 不变子空间 数学与计算科学学院
由(2), 有 ( i E)ri (i ) 0, i 1,2, , s. 又 ( i E)ri (i ) ( i E)ri (i )
Wi fi ( )V , 则Wi 是 fi ( ) 的值域, Wi是 的不变子空间.
又 ( i E)ri Wi ( i E)ri fi ( )V
( i E)ri fi ( ) V f V
( i E)ri Wi 0.
(2)
2023/8/17§7.7 不变子空间 数学与计算科学学院
下证 V V1 V2 Vs . 分三步:
1 . 证明 V W1 W2 Ws .
2 . 证明f1(V1),fV2(2), fVs (s是)直和1 .
3∴. 证存明在多Vi 项 W式i
, i
u1 (
1, 2,
), u2(
, s. ),
, us ( ),
使
u1( ) f ( )1 u2( ) f2( ) us ( ) fs ( ) 1
高代第7章习题参考答案

第七章 线性变换1. 判别下面所定义的变换那些是线性的,那些不是:1) 在线性空间V 中,A αξξ+=,其中∈αV 是一固定的向量; 2) 在线性空间V 中,A αξ=其中∈αV 是一固定的向量;3) 在P 3中,A),,(),,(233221321x x x x x x x +=; 4) 在P 3中,A ),,2(),,(13221321x x x x x x x x +-=;5) 在P[x ]中,A )1()(+=x f x f ;6) 在P[x ]中,A ),()(0x f x f =其中0x ∈P 是一固定的数; 7) 把复数域上看作复数域上的线性空间, A ξξ=。
8) 在P nn ⨯中,A X=BXC 其中B,C ∈P nn ⨯是两个固定的矩阵. 解 1)当0=α时,是;当0≠α时,不是。
2)当0=α时,是;当0≠α时,不是。
3)不是.例如当)0,0,1(=α,2=k 时,k A )0,0,2()(=α, A )0,0,4()(=αk , A ≠)(αk k A()α。
4)是.因取),,(),,,(321321y y y x x x ==βα,有 A )(βα+= A ),,(332211y x y x y x +++=),,22(1133222211y x y x y x y x y x ++++--+ =),,2(),,2(1322113221y y y y y x x x x x +-++- = A α+ A β, A =)(αk A ),,(321kx kx kx),,2(),,2(1322113221kx kx kx kx kx kx kx kx kx kx +-=+-== k A )(α,故A 是P 3上的线性变换。
5) 是.因任取][)(],[)(x P x g x P x f ∈∈,并令)()()(x g x f x u +=则A ))()((x g x f += A )(x u =)1(+x u =)1()1(+++x g x f =A )(x f + A ))((x g , 再令)()(x kf x v =则A =))((x kf A k x kf x v x v =+=+=)1()1())((A ))((x f , 故A 为][x P 上的线性变换。
高等代数 讲义 第七章

(στ ) δ
= σ (τδ )
D( f ( x )) = f ′( x )
J ( f ( x ) ) = ∫ f ( t )dt
x
(2) Eσ = σ E = σ ,E为单位变换 (3)交换律一般不成立,即一般地,
( DJ ) ( f ( x ) ) = D ∫0 f ( t ) dt
x
στ ≠ τσ .
2.线性变换保持线性组合及关系式不变,即
若 β = k1α1 + k2α 2 + L + krα r , 则 σ ( β ) = k1σ (α1 ) + k2σ (α 2 ) + L + krσ (α r ).
例4. 闭区间 [a , b]上的全体连续函数构成的线性空间
C ( a , b ) 上的变换
σ ( X ) = AX , τ ( X ) = XB ,
∀X ∈ P n×n
则 σ ,τ 皆为 P n×n 的线性变换,且对 ∀X ∈ P n×n , 有
(στ )( X ) = σ (τ ( X )) = σ ( XB ) = A( XB ) = AXB , (τσ )( X ) = τ (σ ( X )) = τ ( AX ) = ( AX ) B = AXB .
= σ (τ (α )) + σ (τ ( β )) = (στ )(α ) + (στ )( β ), (στ )( kα ) = σ (τ ( kα )) = σ ( kτ (α )) = kσ (τ (α )) = k (στ )(α )
§7.1 线性变换的定义
2.基本性质
(1)满足结合律:
例1. 线性空间 R[ x ]中,线性变换
高等数学第七章空间解析几何与向量代数课件.ppt

D
b a BD
2 MB
b M
MA
1 2
(
a
b
)
MB
1 2
(
b
a
)
A
a
MC
1 2
(
a
b
)
MD
1 2
(
b
a
)
首页
上页
返回
下页
结束
C B
第9页,共33页。
三、空间直角坐标系
1. 空间直角坐标系的基本概念
过空间一定点 o ,由三条互相垂直的数轴按右手规则
组成一个空间直角坐标系.
• 坐标原点
Ⅲ
z z 轴(竖轴)
和
计算向量
的模 、方向余弦和方向角 .
解: M1M 2 ( 1 2, 3 2 , 0 2 ) (1, 1, 2 )
(1)2 12 ( 2)2 2
cos 1 , cos 2
2
2
2 ,
,
3
3
3
4
首页
上页
返回
下页
结束
第21页,共33页。
3. 向量在轴上的投影与投影定理
z
r
在三个坐标轴上的分向量:
cos
x r
x x2 y2 z2
z
r
o
y
x
首页
上页
返回
下页
结束
第19页,共33页。
cos x
r
cos y
r
cos rz
x x2 y2 z2
y x2 y2 z2
z x2 y2 z2
方向余弦的性质:
z
r
o
y
高等代数与解析几何第七章知识题7答案解析

习题7.4习题7.4.1设A 是一个n 阶下三角矩阵。
证明:(1)如果A 的对角线元素jj ii a a ≠),,2,1,(n j i Λ=,则A 必可对角化; (2)如果A 的对角线元素nn a a a ===Λ2211,且A 不是对角阵,则A 不可对角化。
证明:(1)因为A 是一个n 阶下三角矩阵,所以A 的特征多项式为)())((||2211nn a a a A E ---=-λλλλΛ,又因jj ii a a ≠),,2,1,(n j i Λ=,所以A 有n 个不同的特征值,即A 有n 个线性无关的特征向量,以这n 个线性无关的特征向量为列构成一个可逆阵P ,则有AP P 1-为对角阵,故A 必可对角化。
(2)假设A 可对角化,即存在对角阵⎪⎪⎪⎪⎪⎭⎫⎝⎛=n B λλλO21,使得A 与B 相似,进而A 与B 有相同的特征值n λλλ,,,21Λ。
又因为矩阵A 的特征多项式为n a A E )(||11-=-λλ,所以1121a n ====λλλΛ,从而E a a a a B nn 112211=⎪⎪⎪⎪⎪⎭⎫⎝⎛=O,于是对于任意非退化矩阵X ,都有B E a EX a X BX X ===--111111,而A 不是对角阵,必有A B BX X ≠=-1,与假设矛盾,所以A 不可对角化。
习题7.4.2设n 维线性空间V 的线性变换σ有s 个不同的特征值s λλλ,,,21Λ,i V 是i λ的特征子空间),,2,1(s i Λ=。
证明:(1)s V V V +++Λ21是直和;(2)σ可对角化的充要条件是s V V V V ⊕⊕⊕=Λ21。
证明:(1)取s V V V +++Λ21的零向量0,写成分解式有021=+++s αααΛ,其中i i V ∈α,s i ,,2,1Λ=。
现用12,,,-s σσσΛ分别作用分解式两边,可得⎪⎪⎩⎪⎪⎨⎧=+++=+++=+++---0001212111221121s s s s s ss s αλαλαλαλαλαλαααΛΛΛΛΛΛΛΛΛ。
高等代数和解析几何第七章(1~3习题集)线性变换和相似矩阵答案解析
第七章线性变换与相似矩阵习题7.1习题7.1.1判别下列变换是否线性变换?(1)设是线性空间中的一个固定向量,(Ⅰ),,解:当时,显然是的线性变换;当时,有,,则,即此时不是的线性变换。
(Ⅱ),;解:当时,显然是的线性变换;当时,有,,则,即此时不是的线性变换。
(2)在中,(Ⅰ),解:不是的线性变换。
因对于,有,,所以。
(Ⅱ);解:是的线性变换。
设,其中,,则有,。
(3)在中,(Ⅰ),解:是的线性变换:设,则,,。
(Ⅱ),其中是中的固定数;解:是的线性变换:设,则,,。
(4)把复数域看作复数域上的线性空间,,其中是的共轭复数;解:不是线性变换。
因为取,时,有,,即。
(5)在中,设与是其中的两个固定的矩阵,,。
解:是的线性变换。
对,,有,。
习题7.1.2在中,取直角坐标系,以表示空间绕轴由轴向方向旋转900的变换,以表示空间绕轴由轴向方向旋转900的变换,以表示空间绕轴由轴向方向旋转900的变换。
证明(表示恒等变换),,;并说明是否成立。
证明:在中任取一个向量,则根据,及的定义可知:,,;,,;,,,即,故。
因为,,所以。
因为,,所以。
因为,,所以。
习题7.1.3在中,,,证明。
证明:在中任取一多项式,有。
所以。
习题7.1.4设,是上的线性变换。
若,证明。
证明:用数学归纳法证明。
当时,有命题成立。
假设等式对成立,即。
下面证明等式对也成立。
因有,即等式对也成立,从而对任意自然数都成立。
习题7.1.5证明(1)若是上的可逆线性变换,则的逆变换唯一;(2)若,是上的可逆线性变换,则也是可逆线性变换,且。
证明:(1)设都是的逆变换,则有,。
进而。
即的逆变换唯一。
(2)因,都是上的可逆线性变换,则有,同理有由定义知是可逆线性变换,为逆变换,有唯一性得。
习题7.1.6设是上的线性变换,向量,且,,,都不是零向量,但。
证明,,,线性无关。
证明:设,依次用可得,得,而,故;同理有:,得,即得;依次类推可得,即得,进而得。
高等代数与解析几何第七章习题7答案
习题7.4习题7.4.1设A是一个n阶下三角矩阵。
证明:(1)如果A的对角线元素aii a(i,j1,2,,n),则A必可对角化;jj(2)如果A的对角线元素a1122,且A不是对角阵,则aannA不可对角化。
证明:(1)因为A是一个n阶下三角矩阵,所以A的特征多项式为|E|()()(),又因a ii a jj(i,j1,2,,n),所以A有Aa11aa nn22n个不同的特征值,即A有n个线性无关的特征向量,以这n个线性无1为对角阵,故A必关的特征向量为列构成一个可逆阵P,则有PAP可对角化。
1(2)假设A可对角化,即存在对角阵2,使得ABn与B相似,进而A与B有相同的特征值1,2,,。
又因为矩阵A的特n征多项式为n|EA|(a11),所以12na11,从而a 11Ba22 aE11,于是对于任意非退化矩阵X,都有ann1,而A不是对角阵,必有X1BXBA,与1XBXXa11EXa11EB假设矛盾,所以A不可对角化。
习题7.4.2设n维线性空间V的线性变换有s个不同的特征值1,V i是i的特征子空间(i1,2,,s)。
证明:s,2,,(1)V1VV是直和;2s(2)可对角化的充要条件是 V 12。
VVVs证明:(1)取VV1V 的零向量0,写成分解式有2s1s0,其中iV i ,i1,2,,s 。
现用2, 2,,s1分别作用分解式两边,可得012s 01122ss。
s 1 1 1s 2 1 2s s 1 s 0写成矩阵形式为 11 s 1 1( , 1 , 2,s11 22s )。
(0,0,,0)1ss s11 1s 11 由于1,2,,是互不相同的,所以矩阵ss1122B 的行列式不1 ss s1 为零,即矩阵B 是可逆的,进而有 (11 1s BBB ,(1,2,,s )(0,0,,0)。
,,,)(0,0,,0)(0,0,,0) 2这说明V 1V 2V s 的零向量0的分解式是唯一的,故由定义可得 V 12是直和。
高等代数.第七章.线性变换.课堂笔记
第七章 线性变换§7.1 线性变换的定义与判别一、线性变换的定义:定义1 设V 为数域P 上线性空间,A 为V 的一个变换(即V ⟶V 的映射),若A 保持加法和数乘运算,即A (α+β)=A (α)+ A (β),∀α,β∈V ,A (kα)=k A (α),∀k ∈P ,则称A 为V 的一个线性变换.注记: 以后我们用花体拉丁字母A,B,C,...表示V 的线性变换,除了特别说明外,本章节中V 均指数域P 上有限维线性空间.例1.说明下列变换均为线性变换: (1)把V 中任一向量都映射为0(称为零变换,记作0); (2)把V 中任一向量α映射为本身(恒等变换,记作E ); (3)取定k ∈P ,把V 中的每一个向量α映射为kα(数乘变换,记作k ).例2.判定下列规则σ是否为指定线性空间的线性变换: (1)ℝ,x -:σ(f (x ))=f′(x );(2)C ,a,b -: σ(f (x ))=∫f (t )dt x0;(3)P n×n : σ(A )=A +A ′,σ2(A )=SAT ,S,T 为固定二个n ×n 矩阵. (4)ℝ,x -n : σ1(f (x ))=xf (x ),σ2(f (x ))=f (x )+1. 解:可验证(1)-(3)均为线性变换,下面证明(1): ∀ f (x )∈ℝ,x -,其导函数唯一确定,且f (x )∈ℝ,x -,因而σ为V ⟶V 的变换,即V 的一个变换,σ(f (x )+g (x ))=(f (x )+g (x ))′=f ′(x )+g ′(x )= σ(f (x ))+ σ(g (x )), ∀k ∈ℝ,σ(kf (x ))=(kf (x ))′=kf ′(x )=kσ(f (x )).(4): σ1与σ2均不是线性变换,取f (x )=x n−1+1=ℝ,x -n ,但σ1(f (x ))=xf (x )=x n +x ∉ℝ,x -n , 因而σ1不是ℝ,x -n 的一个变换, σ2是ℝ,x -n 的一个变换,但运算不保持,因而不是线性变换.习题:P320、1例3.设α为通常几何空间ℝ3中固定的向量,把空间中每个向量η映射为η在α上的内映射(正投影),即Πα: η⟶(α∙η)(α∙α)α是ℝ3的线性变换,这里(α∙η),(α∙α)表示通常向量的内积.证:如图,Πα(η)=OD ⃗⃗⃗⃗⃗ =ηcos (η∙α)α|α|=(α∙η)(α∙α)α,唯一确定, 从而Πα为ℝ3的一个变换,如图,AC ⊥W(垂足为C),OCD LA Wα1α2η因此L 与W 为ℝ3的子空间且ℝ3=W ⊕L ,令 η=α1+α2,α1=OD⃗⃗⃗⃗⃗ =Πα(η),α2∈W , δ=β1+β2,β1=Πα(δ)∈L,β2∈W ,则η+δ=(α1+β1)+(α2+β2),α1+β1∈L,α2+β2∈W , 从而Πα(η+δ)=α1+β1=Πα(η)+Πα(δ), 同理,Πα(kη)=kΠα(η).二、线性变换的性质: 设A 为V 的线性变换,则: (1) A (0)=0, A (−α)=−A (α),∀α∈V ; (2) A (k 1α1+k 2α2+⋯+k t αt )=k 1A (α1)+k 2A (α2)+⋯+k t A (αt ); (3) A 把线性相关的向量组映射为线性相关的向量组(反之不真).2011-04-02A : V ⟶V 线性变换性质: (3) A 为V 中线性相关的向量组,映为V 中线性相关的向量组,即α1,α2,…,αs 相关⟹A (α1), A (α2),…, A (αs )相关;但A (α1), A (α2),…, A (αs )线性相关⇒α1,α2,…,αs 相关. 如A =0,∀ α∈V,α≠0, A (α)=0.(4)设α1,α2,…,αn 为V 的一个基,∀ α∈V,α=x 1α1+x 2α2+⋯+x n αn ⟹A (α)=A (x 1α1+x 2α2+⋯+x n αn ) 线性变换A 由V 中一个基中的像唯一确定;(5)设α1,α2,…,αn 为V 的一个基,则对V 中任一向量组β1,β2,…,βn 必存在一个线性变换 A : V ⟶V ,使得:A (αi )=βi ,1≤i ≤n ;证:作V ⟶V 映射:A (α)= x 1β1+x 2β2+⋯+x n βn ,其中:α=x 1β1+x 2β2+⋯+x n βn ,则A (αi )=βi ,1≤i ≤n ; 下证:A 为V 的线性变换:∀ α=x 1α1+x 2α2+⋯+x n αn ∈V,β=y 1α1+y 2α2+⋯+y n αn ∈V,A (α+β)= A .(x 1+y 1)α1+(x 2+y 2)α2+⋯+(x n +y n )αn /=(x 1+y 1)β1+(x 2+y 2)β2+⋯+(x n +y n )βn=(x 1β1+x 2β2+⋯+x n βn )+(y 1β1+y 2β2+⋯+y n βn ) = A (x 1α1+x 2α2+⋯+x n αn )+ A (y 1α1+y 2α2+⋯+y n αn )= A (α)+A (β)同理,∀k ∈P ,A (kα)=k A (α).§7.2 线性变换的运算为方便,引入记号:Hom (V,V ),它表示数域P 上线性空间V 的所有线性变换的集合。
高等代数课件 第七章
二、坐标变换
设V是F上一个n 维向量空间, {1, 2 ,,n}
是它的一个基, ξ关于这个基的坐标是 (x1, x2,, x而n ),
σ(ξ)的坐标是
( y1, y2,,问yn:).
( y1, y2,和, yn )
(x1, x2,, xn ), 之间有什么关系?
设
x11 x22 xnn
(5)
k( ) k k ,
(6)
(k l) k l ,
(7)
(kl) k(l ),
(8)
1 ,
这里k,l是F中任意数,σ,τ是V的任意线性变换.
定理7.2.1 L(V)对于加法和数乘来说作成数 域F上一个向量空间.
二、线性变换的积
设 , L(V ),容易证明合成映射 也是V上的 线性变换,即 L(V ). 我们也把合成映射 叫
坐标. 3.已知线性变换关于某个基的矩阵,熟练地求出σ关于
另一个基的矩阵。 三、重点难点:
线性变换和矩阵之间的相互转换, 坐标变换, 相似矩阵。
一、线性变换的矩阵
设V是数域F上一个n维向量空间,令σ是V的一 个线性变换,取定V的一个基 1,2,,令n,
(1) a111 a212 an1n (2 ) a121 a222 an2n
二、教学目的:
掌握线性映射的加法、数乘和积定义,会做运算. 掌握线性变换的多项式, 能够求出给定线性变换的多 项式.
三、重点难点:
会做运算.
一、线性变换的加法和数乘
令V是数域F上一个向量空间,V到自身的一个线 性映射叫做V 的一个线性变换.
我们用L(V)表示向量空间和一切线性变换所成的 集合,设 , L(v), k F, 定义
所以 是V的一个线性变换
