哈工大_结构力学(王焕定第二版)影响线一章答案
结构力学 第二版 (王焕定 著) 高等教育出版社 课后答案
kh
FN5 = −1.956 6FP
由这两杆内力取隔离体图(c)列投影方程 FN6 cos β − FN5 sin α + FN4 cos θ = 0 可得
(2)用截面从杆 1、3、4 处截开,取下边左图为隔离体 K FN4 FN3 FN1 2.5Fp
FN3 =
w.
2-3 答: (1)取整体为对象,求A(左)与B(右)支座的支座反力。列 ∑ M B = 0, ∑ F y = 0 可得 FAy = FBy = 2.5FP
da
FN2 = −0.5FP
课
求得这两杆内力后,由隔离体图(b)列投影方程 FN 4 cos θ + FN2 cos α − FN1 sin β = 0 FN 4 = −2.5 FP FN3 + FN4 sin θ − FN2 sin α − FN1 cos β = 0 FN3 = 0.5 FP
后
ww
取 1、3、4 杆件相交的结点作隔离体图(c)所示,往FN1方向投影,列方程得:
2-6 (c) 将荷载与支座反力分解成对称和反对称情况。对称情况 1、2、3 杆轴力为零。 反对称情况 4 杆轴力为零。 30 kN 4 30 kN 30 kN 2 3 30 kN
w.
1 30 kN
kh
4×2m
∑F
课
FN2 +FP × cos 45D = 0
2
w.
13 FN6 = 1.352 1FP
案 网
sin α =
1
cos α =
2
sin β =
2
cos β =
3
FN6 sin β + FN5 cos α − FN4 sin θ = 0
结构力学课后习题答案
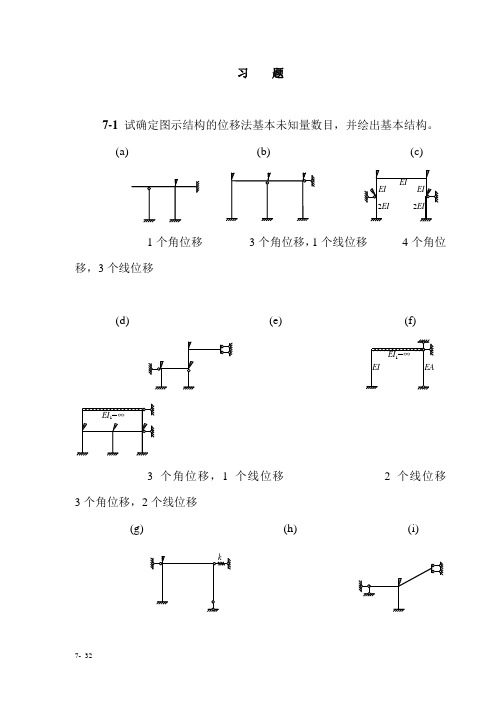
习题7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)1个角位移3个角位移,1个线位移4个角位移,3个线位移(d) (e) (f)3个角位移,1个线位移2个线位移3个角位移,2个线位移(g) (h)(i)7- 327- 33一个角位移,一个线位移 一个角位移,一个线位移 三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
lll7- 34Z 1M 图(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==(4)画M 图M 图(b)4m4m 4m7- 35解:(1)确定基本未知量1个角位移未知量,各弯矩图如下1Z =1M 图32EIp M 图(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 1115,352p r EI R ==- 153502EIZ -=114Z EI=(4)画M 图()KNm M ⋅图(c)6m6m9m7- 36解:(1)确定基本未知量一个线位移未知量,各种M 图如下1M 图243EI 243EI 1243EI p M 图F R(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 1114,243p pr EI R F ==- 140243p EIZ F -=12434Z EI=(4)画M 图7- 3794M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下11Z1111r 252/25EA a 简化a2a a2aa F P7- 38图1pR pp M(2)位移法典型方程11110pr Z R +=(3)确定系数并解方程 11126/,55p pr EA a R F ==-126055p EA Z F a -=13a Z EA=(4)画M 图图M(e)l7- 39解:(1)确定基本未知量两个线位移未知量,各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M p(2)位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++=(3)确定系数并解方程7- 4011122122121,1,0p p p EA r r r l EA r l R F R ⎛=== ⎝⎭⎛=+ ⎝⎭=-=代入,解得12p p lZ F EAlZ F EA=⋅=⋅(4)画M 图图M p7-6 试用位移法计算图示结构,并绘出M 图。
哈尔滨工业大学结构力学答案一

结构力学 答案(开卷,时间:120 分钟)
(所有答案必须写在答题纸上) 一、 是非题(每题 4 分共 20 分,正确的标〇,错误的标) 1. 所谓静定结构就是没有多余约束的几何不变体系( 〇 ) 2. 影响线表示的是结构在移动荷载作用下内力图( ) 3. 用图乘法可以求等刚度直杆体系的位移( 〇 ) 4. 力矩分配法的转动刚度表示杆端抵抗转动的能力( 〇 ) 5. 位移影响系数指的就是在外力作用下的位移( ) 二、 选择题(每题 4 分共 20 分,将正确的答案的字母填在空内) 1. 静定结构产生支座移动时将( A ) A. 无内力无变形; B. 无内力有变形; C. 有内力有变形; D. 有内力无变形。 2. 均匀分布竖向荷载作用下,三铰拱的合理拱轴线为( B ) A. 圆弧线; B. 抛物线; C. 正弦曲线; D. 三角形。 3. 力法基本方程的物理意义是( A ) A. 几何条件; B. 物理条件; C. 外力条件; D. 平衡条件。 4. 单自由度体系固有频率表示( D ) A. 反应约束的参数; B. 振动一次所用时间; C. 反应结构尺寸的参数; D. 单位时间内振动次数。 5. 在荷载作用下超静定结构内力与各杆件刚度的关系是(A) A. 与各杆的相对刚度有关; B. 与各杆的绝对刚度无关; C. 与各杆的绝对刚度有关; D. 与各杆的相对刚度无关。 三、 填空题(每题 2 分共 10 分,将正确的叙述填在空内) 1. 刚架结构的受力特点是( 以受弯为主,结点传递弯矩 ) 2. 柔度系数δij 的物理意义是(当第 j 个多余力等于 1 时引起的第 i 个 多余力方向的位移大小 ) 3. 力矩分配法中某分配单元的分配系数之和等于( 1 ) 4. 静定结构对称要求满足(几何对称、约束对称 ) 5. 能量法求得的自振频率总是比体系精确解( 大 )
结构力学王焕定答案

结构力学王焕定答案引言结构力学是工程学中一门重要的学科,它研究各种结构的力学性能和稳定性。
在结构设计和分析中,结构力学的基本原理和方法是必不可少的工具。
在结构力学领域,王焕定教授被公认为权威人物,他的研究和贡献对于该领域的发展起到了重要的推动作用。
本文将以王焕定教授的研究成果为基础,回答一些常见的结构力学问题。
1. 王焕定教授简介王焕定教授是中国工程院院士,同济大学结构工程系的教授。
他的研究领域主要是结构力学和抗震工程。
他在结构优化设计、结构动力学和结构抗震性能等方面做出了杰出的贡献。
他的研究成果不仅在国内具有广泛的应用,也对同行在国际上产生了积极的影响。
2. 结构力学基本原理结构力学的基本原理是力学的基础。
在结构设计和分析中,掌握这些基本原理是非常重要的。
以下是一些结构力学的基本原理:2.1. 受力分析结构受力分析是结构力学的起点。
它通过力的平衡原理和受力分解的方法,确定结构在不同载荷下的受力状态。
在受力分析中,常常使用静力学和力矩平衡原理来解决受力问题。
2.2. 应变和应力应变和应力是结构物力学性能的重要指标。
应变表示物体在外力作用下相对变形程度的大小,而应力表示单位面积上的力的大小。
结构力学中常常关注材料的线弹性行为,通过应力应变关系分析材料的变形和破坏情况。
2.3. 刚度和变形刚度是结构物抵抗变形的能力。
结构在受到外力作用时,常常会发生变形。
刚度常常用杨氏模量和截面惯性矩等指标来表征,它是结构力学分析中十分重要的参数。
刚度与自由度的数量相关联,它可以对结构的强度和稳定性进行评估。
2.4. 稳定性和挠度稳定性和挠度是结构力学的重要概念。
结构在不同载荷作用下,可能会发生不稳定破坏现象。
稳定性分析能够判断结构在外力作用下的抗承载能力,而挠度分析能够评估结构的变形程度。
结构的稳定性和挠度分析是结构设计和评估的重要内容。
3. 结构力学问题的解答王焕定教授通过多年的研究和实践,积累了丰富的经验和知识。
结构力学王焕定答案

结构力学王焕定答案引言结构力学是一门研究物体变形和受力行为的学科,是工程学中的重要基础学科。
结构力学的研究可以帮助我们了解结构物在受力时的行为,为工程设计和分析提供理论依据。
本文将介绍结构力学领域权威专家王焕定的相关问题答案。
问题1:简单支座和铰支座的区别是什么?答案:简单支座和铰支座是结构中常见的两种支座形式。
简单支座是指支座在所有方向上均能提供垂直支撑的一种支座形式,通常由一个平面或球面来提供支撑,可以阻止结构在任何方向上的平移和旋转。
铰支座则是指结构中的连接点允许在某些方向上发生旋转的一种支座形式,它只提供垂直支撑,不能阻止结构在平面内的移动。
简单支座所提供的支撑主要是通过摩擦力来实现的,而铰支座是通过连接点的旋转来实现的。
由于简单支座可以阻止结构在水平方向上的移动,因此它通常用于需要限制水平位移的结构中,如桥梁的支座。
而铰支座则适用于允许结构发生旋转或位移的情况,如房屋的支撑结构。
两种支座形式在结构分析和设计中起着不同的作用。
问题2:如何计算弹性变形?答案:弹性变形是指物体在受力作用下所发生的可逆形变。
它可以通过应力和材料的弹性模量来计算。
弹性模量是描述材料抵抗弹性变形的特征参数,记作E。
弹性变形可以用胡克定律来描述,即应变与应力成正比。
弹性变形的计算公式为:ε = σ / E其中,ε表示应变,σ表示应力,E表示材料的弹性模量。
在实际工程中,经常需要计算结构体的弹性变形。
例如,在计算梁的弯曲变形时,可以根据梁的几何形状、受力情况和材料的弹性模量来计算弯曲应变和弯曲角度。
这对于工程设计和结构分析来说非常重要。
问题3:什么是结构物的静力平衡?描述其应用领域。
答案:结构物的静力平衡是指结构物在受到外力作用时,所有受力部分的合力和合力矩均为零的一种平衡状态。
在结构力学中,静力平衡是分析和设计结构物的基本要求之一。
结构物的静力平衡可以应用于各种工程领域。
例如,在建筑结构设计中,静力平衡可以用来确定各个构件的受力情况,以确保结构的安全性和稳定性。
结构力学影响线习题及答案复习进程

结构力学影响线习题及答案收集于网络,如有侵权请联系管理员删除影响线及其应用一、判断题:1、图示结构M C 影响线已作出如图(a )所示,其中竖标E y 表示P = 1在E 时,C 截面的弯矩值。
M C 影 响 线y E(a )12mAB6m60kNC(b )2、图(b )所示梁在给定移动荷载作用下,支座B 反力最大值为110 kN 。
二、作图、计算题:3、作图示梁中R A 、M E 的影响线。
2aa a ABCDEa4、单位荷载在梁DE 上移动,作梁AB 中R B 、M C 的影响线。
aa2a收集于网络,如有侵权请联系管理员删除5、作图示结构R B 、Q B 右影响线。
4m4m2m2m6、作图示梁的M K 、Q E 影响线。
aaaa aaaaKEF 27、单位荷载在刚架的横梁上移动,作M A 的影响线(右侧受拉为正)。
8、图示结构P = 1在DG 上移动,作M C 和Q C 右的影响线。
4m9、作图示结构的M B 影响线。
4m 2m10、作图示结构:(1)当P = 1在AB上移动时,M A影响线;(2)当P = 1在BD上移动时,MA影响线。
ll11、作图示结构的M C、Q F影响线。
设M C以左侧受拉为正。
l/2l/2l/2l/212、单位荷载在桁架上弦移动,求N a的影响线。
d d d13、单位荷载在桁架上弦移动,求N a的影响线。
d d d收集于网络,如有侵权请联系管理员删除收集于网络,如有侵权请联系管理员删除14、作图示桁架的V 3影响线。
a aaa15、单位荷载在DE 上移动,求主梁R A 、M C 、Q C 的影响线。
16、作图示结构Q C 右的影响线。
lllllll17、作出图示梁M A 的影响线,并利用影响线求出给定荷载下的M A 值。
2m2m1m18、P = 1沿AB 及CD 移动。
作图示结构M A 的影响线,并利用影响线求给定荷载作用下M A 的值。
收集于网络,如有侵权请联系管理员删除2m2m4m40kN/mA19、作图示梁的Q C 的影响线,并利用影响线求给定荷载作用下Q C 的值。
结构力学课后习题答案
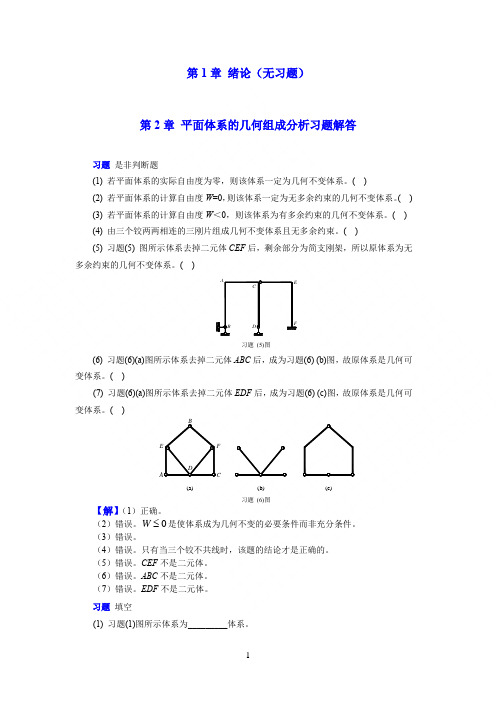
第1章 绪论(无习题)第2章 平面体系的几何组成分析习题解答习题 是非判断题(1) 若平面体系的实际自由度为零,则该体系一定为几何不变体系。
( )(2) 若平面体系的计算自由度W =0,则该体系一定为无多余约束的几何不变体系。
( ) (3) 若平面体系的计算自由度W <0,则该体系为有多余约束的几何不变体系。
( ) (4) 由三个铰两两相连的三刚片组成几何不变体系且无多余约束。
( )(5) 习题(5) 图所示体系去掉二元体CEF 后,剩余部分为简支刚架,所以原体系为无多余约束的几何不变体系。
( )习题 (5)图(6) 习题(6)(a)图所示体系去掉二元体ABC 后,成为习题(6) (b)图,故原体系是几何可变体系。
( )(7) 习题(6)(a)图所示体系去掉二元体EDF 后,成为习题(6) (c)图,故原体系是几何可变体系。
( )习题 (6)图【解】(1)正确。
(2)错误。
0W 是使体系成为几何不变的必要条件而非充分条件。
(3)错误。
(4)错误。
只有当三个铰不共线时,该题的结论才是正确的。
(5)错误。
CEF 不是二元体。
(6)错误。
ABC 不是二元体。
(7)错误。
EDF 不是二元体。
习题 填空(1) 习题(1)图所示体系为_________体系。
B DACEF(a)(b)(c)D习题(1)图(2) 习题(2)图所示体系为__________体系。
习题2-2(2)图(3) 习题(3)图所示4个体系的多余约束数目分别为_______、________、__________、__________。
习题(3)图(4) 习题(4)图所示体系的多余约束个数为___________。
习题(4)图(5) 习题(5)图所示体系的多余约束个数为___________。
习题(5)图(6) 习题(6)图所示体系为_________体系,有_________个多余约束。
习题(6)图(7) 习题(7)图所示体系为_________体系,有_________个多余约束。
结构力学课后习题答案[1]
![结构力学课后习题答案[1]](https://img.taocdn.com/s3/m/8c0493dc80eb6294dd886c23.png)
)e( 移位线个 1�移位角个 3 移位角个 1
)d(
)c(
。构结本基出绘并�目数量知未本基法移位的构结示图定确试 1-7
)b(
) a(
题
习
33 -7
下如图矩弯各�量知未移位角个 1 m4 m4
量知未本基定确�1� �解 C IE
m4
D Nk01
IE
B
IE2 m/Nk5.2
A )b(
图M
42 lq 2 5
图矩弯终最画�4� 得解�入代
61.53
IE
3
0 � p 2 R , 0 3 � p 1R 6 � 2 2r IE � 1 2r � 2 1r , I E 2 � 1 1r
程方解并数系定确�3�
p2
11
1
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
N K 0 3 � � p 2 R , N K 0 3 � p 1R 4 � � 2 2r 0 � 1 2r � 2 1r , i1 1 � 1 1r
p2
得解�入代
i3
程方解并数系定确�3�
0�
R � 2 Z 2 2r � 1 Z 1 2r R � 2 Z 2 1r � 1 Z 11r
程方型典法移位�2�
程方型典法移位�2�
0�
p1
图p M
03 � p 1R � 0 � p 1R
03
04 -7
m2
m2 数常=IE F
B E
m2
m2
D
A
m2
Nk03
C )c(
90.92 55.43
图M
81.8 19.02 54.57 02
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-1 用静力法作图示梁的支杆反力F N1、F N2、F N3及内力M K 、F Q K 、F N K 的影响线。
解:取隔离体如图(a)所示∑M A =0F N3 = 52l (x−32l)∑F x =0F N1 =F N2∑F y = 0F N1 = 52 (4−x l )x<3l 时取隔离体如图(e)所示M K = F N3lF Q K =−F N3F N K =0x >3l 时取隔离体如图(f)所示M K = F N3l −1×(x−3l) =−x+l8 2F Q K =1−F N3 = − x5 5lF N K =0由求出的影响系数方程可作出影响线如图所示。
5-2 用静力法作图示梁的F By 、M A 、M K 和F Q K 的影响线。
解:取隔离体如图(a)所示∑F y =0F By =1∑M B =0M A =x x<l/2时, 取隔离体如图(f)所示M K =l/2F Q K =−1x >l/2时, 取隔离体如图(e)所示M K =l −xF Q K =0由影响系数方程可作出影响线如图所示。
5-3 用静力法作图示斜梁的F Ay、F Ax、F By 、M C 、F Q C 和F N C 的影响线。
(1)解:∑M A =0F By = x/l∑F y =0F Ay =1−x/l∑F x =0F Ax =0x<a,取右侧∑M c=0 M C = bx/l∑F r =0 F Q C =−x l cosα∑Fβ=0 F N C = x l sinαx>a,取左侧∑M c =0 M C = a(1−x/l)∑F r =0 F Q C = (1−x l )cosαx ∑Fβ=0 F N C =−(1−l )sinα由影响系数方程可作出影响线如图所示。
5-3(2)解:∑M A =0F By = x l tanαx∑F y = 0F Ay =− l tanα∑F x =0 F Ax =−1x<a,取右侧∑M c =0 M C = bl x tanα∑F r =0 F Q C =−x l sinα∑Fβ= 0 F N C = x l sinα⋅tanαx>a,取左侧∑M c =0 M C = tanα⋅a(1−x/l)∑F r =0 F Q C = sinα−x l sinα∑Fβ= 0 F N C = cosα+ x l tanα⋅sinα由影响系数方程可作出影响线如图所示。
5-4 用静力法作图示刚架F Q1、M2(以左侧受拉为正)、F N2、M3、和F Q3的影响线。
F P =1在BC 上移动。
解:取1 点左侧作隔离体,如图(g) 所l ∑F y = 0 F Q1 = 0x <l∑F y = 0 F Q1 =−1取2 点上侧做隔离体,如图(h)所示∑M2 = 0 M2 = x−2l∑F y =0F N2 =−1取3 点上侧做隔离体,如图(i)所示∑M3 = 0 M3 = x−3l∑F=0F Q3 =−1由影响系数方程可作出影响线如图所示。
5-5 用静力法作图示刚架F Ax、F Ay、F Q R E 和F Q L E 的影响线。
F P =1在DF上移动。
解:x <l时∑M C=0FBy =FBx∑M A =02lF By = 2l F Bx +1⋅x联立求解,得F By = F Bx = 2x/3lF Ax = F Bx = 2x/3lF Q R E = 0,F Q L E =−2x/3lx >l∑M C =02F Ay =F Ax∑M B =0 F Ax 2l +2lF Ay =1×(2l −x)联立求解,得F Ax1F Ay = (2l −x)3l1 xF By =1−F Ay = +3 3ll < x <2l FQ LE=−FBy=−(1+ x )3 3lF Q R E = 0x >2l F Q LE =1− F By =1−(1 + x ),F Q RE =1 3 3l由影响系数方程可作出影响线如图所示。
5-6 用静力法作图示刚架M J 、F N J 、M K 和F Q K 的影响线。
F P =1在CE 上移动。
解:首先做出F By 的影响线x <4mF By = 0xx >4m F By = −22作M K 、F Q K 的影响线x <2m M K =0,F Q K = 0 4m >x >2m M K =2−x ,F Q K =1 x >4m取隔离体如图(f )所示M K =−(F By −1)×2 = 6−x ,F Q K =1−F By =3−x /2作M J 、F N J 影响线 取隔离体如图(g )、(h)所示 x <4mM J = x ,F N J =−1 x >4mM J = (1−F By )×4 =12− x ,F Q K = F By −1= x /2−3由影响系数方程可作出影响线如图所示。
5-7 作三铰拱 D 截面M D 、F Q D 、F N D 影响线。
4 f拱轴方程 y = l 2 x (l − x )解::1)做M D 影响线M D =M D 0 −F H y DF H = M C 0 / f做出M D 0 、M C 0 和F H 影响线如图(b)、(c)、(d)所示。
y D =×3×(9−3) = 2 通过叠加可得M D 影响线如图(e)所示。
2) 作F Q D 、F N D 影响线 F Q D = F Q 0D cos ϕD −F H sin ϕDF N D =−F Q 0D sin ϕD − F H cos ϕD 做出F Q 0D 影响线如图(f)所示,4 f y ′(3) = 0.3337 y ′(x ) = 2 (l − 2x )lϕD =18.432D cos ϕD = 0.9487,sin ϕD = 0.3162通过叠加可得F Q D和F N D 影响线如图(f)、(g)所示。
5-8 作静定多跨梁F By 、M K 、F Q R K 和F Q L K 影响线。
解:(1)作出荷载在主梁上移动时的影响线,如图(a)、(b)、(d)所示;(2) 作出荷载在次梁上移动时的影响线,如图(e)、(f)、(g)、(h)所示(红线为间接荷载影响线,黑线为直接荷载影响线)。
5-9 分别就F P=1 在上弦颌下弦移动作图示桁架指定杆件的内力影响线。
解:(1)荷载上行时做出支座反力影响线如图(a)、(b)所示。
F N1: x=0时,F N1 =0;x>d时,取Ⅰ-Ⅰ截面右侧为隔离体∑M C = 0F N1 =−2F AyF N2 : x> 2d 时,取Ⅱ-Ⅱ截面左侧为隔离体∑M C = 0F N2 =−2F Ay ;x<d时,取Ⅱ-Ⅱ截面右侧为隔离体∑M C =0F N2 =−F ByF N3 : x>d 时,取Ⅰ-Ⅰ截面左侧为隔离体∑F y =0 F N2 = 5F Ay ; x =0 时,F N2 =0F N 4: x >2d 或x =0时,F N4 =0; x = d 时,用结点法得F N4 =− 2F N 5: x <d 或x >d 时,F N5 =0 ; x =2d 时,用结点法得F N5 =−1(2)荷载下行时 FN 1 、F N 2 、F N 3、F N 4的影响线与荷载上行时相同。
FN 5 : 用结点法得 F N5 =0;做出的各条影响线如图所示。
5-10 用静力法作图示组合结构的指定量值的影响线。
解:取整体为隔离体∑MA= 0 F Bx = x /2F N BC = F Bx = x /2∑MA= 0 F By =1− x / 4 取 BD 杆段作为隔离体如图(b)所示,x > 2m 时 M D = F By × 2 = 2 − x / 2F Q D = F By =1−x/ 4x < 2m时M D =F By × 2 −1×(2 −x) = x/ 2F Q D = F By −1 = −x/ 4做出的各条影响线如图所示。
5-11 作图示结构F By 、M C 、F Q R C 和F Q L C 影响线。
(a) 解:取隔离体如图(f)所示∑M D = 0 F N CD = x/2l取隔离体如图(g)所示∑M A = 0 F By = F N CD /2 = x/4l由截面法可得M C = F By ⋅4l = x/ 4F Q R C =−F By=−x/4lF Q L C = F N CD −F By = x/4l做出的影响线如图所示。
5-11(b) 解:x < 2l 时,与题5-11(a)相同;x > 2l 时,与简支梁相同。
利用题5-11(a)的结果和简支梁的影响线可作出影响线如图所示。
5-12 图示简支梁上有单位力偶移动荷载m =1,试作F Ay 、F By 、F Q C 、M C 影响线。
解:∑MA = 0 F By =1/l ∑F y = 0 F Ay = −F By = −1/l x <a M C =F By ⋅b = b /l x >a M C = F Ay ⋅a = a /lF Q C = −1/l作出影响线如图所示。
5-13 试用机动法重作习题 5-2 的各项影响线。
5-15 试用机动法作图示多跨静定梁M F 和F Q G 的影响线。
解:解:5-14试用机动法重作习题 5-8 的各项影响线。
5-16试求图示吊车梁在两台吊车移动过程中,跨中央截面的最大弯矩。
F P1 = F P2 = F P3 = F P4 = 324.5kN 。
解:做出跨中央截面弯矩M K 的影响线如图b 所示,由影响线可判断出M K 的最不利荷载位置为图c。
M K max = F P1 ×0.1+ F P2 × 2.5 + F P3 ×1.775= 324.5× (0.1+ 2.5 +1.775) = 1419.69kN.m5-17两台吊车的轮压和轮距如图(a)所示,试求B柱的最大压力。
F P1 = F P2 = 478.5kN,F P3 = F P4 = 324.5kN 。
解:做出F By 影响线如图b 所示,图c 为使F By 取得最大值的荷载位置。
F By = F P 1 ×0.2 + F P 2 ×1+ F P 3 × 0.758= 478.5×0.2 + 478.5×1+ 324.5×0.758 = 820.17kN解:做出F N a 影响线F By = x /5dx < 4d 取结点B 为隔离体,如图所示,∑F y = 0 F N a = − 5F Byx = 5d F N a = 05-18 试求在图示移动荷载作用下,桁架杆件 a 的内力最小值。
