剪切扭转的内力与强度计算 习题
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
扭转强度计算

工程背景
工程背景
工程背景
6.3 扭转强度计算 ——思路
6.3 扭转强度计算 ——内容
建立圆轴扭转时横截面上的应力公式 理解公式,分析应力分布规律 建立强度条件(类比轴向拉压变形) 应用解决强度计算问题
建立圆轴扭转时 横截面上的应力公式
两个假设 平面假设 横截面间距不变假设 三种关系 变形几何关系 物理关系 静力学关系
MD0.96kNm,已知材料的许用切应力 80MPa
试校核该轴的强度。
解:用截面法求得BA、AC、CD段的扭矩,并
绘出扭矩图如图所示。
因为传动轴为等截面,所以最大切应力发生在 AC段内各截面周边上各点。
m axT W m a p x 1 .7 6 ( 0 1 .0 0 5 3N m ) 3 m 7 1 .7 1 0 6P a7 1 .7 M P a
横截面上任一点切应力的计算公式
τρ
Tρ Ip
T(或Mn)——横截面上的扭矩
ρ——待求点到圆心的距离
Ip——截面对其形心的极惯性矩
IP 2dA A
分析应力分布规律
横截面上任一点切应力大小同ρ呈正比
m ax
Tr Ip
Wp
Ip r
——抗扭截面系数
max
T
Wp
思考及练习
思考: 实心圆轴纯扭转时,如何破坏? 从外向内,逐层破坏
练习: 例题6-2
建立强度条件
横截面最大切应力不超过材料的许用切应力
τmax τ
τ max
Tmax Wp
塑性材料: 0 .5 0 .6
脆性材料: 0 .8 1 .0
强度计算理论
强度校核 截面设计 许用荷载计算
max
剪切实用计算例题

(2)铆钉的挤压计算
jy
Fb F /n [ jy ] A jy t1d
F n 3.72 t1d [ jy ]
材料力学
剪切实用计算
因此取 n=4. I F/n F/n
(3)主板拉断的校核。 危险截面为I-I截面。 F 主板的强度条件为(忽略
x l时,FN ,max Al
(2)应力
m
x
m
x
o
FN ( x) ( x) A
FN ( x) FN max FN
x
max xl l
由强度条件:
max [ ]
l
[ ]
拉伸与压缩/轴向拉(压)时的变形
FN ( x) dFN
dx m x dx
拉应力:
P [ ] 2 d 4 材料力学
(1) 得: (2) (1) d [ ] 4 2.4 h [ ] (2) 挤压应力: P bs 2 (D d 2 ) 4
P
剪切实用计算
例题3-4 两矩形截面木杆,用两块钢板连接如图示。已知拉杆的 截面宽度 b=25cm,沿顺纹方向承受拉力F=50kN,木材的顺纹许 用切应力为 [ j ] 1MPa , 顺纹许用挤压应力为 [ jy ] 10 MPa 。试求 接头处所需的尺寸L和 。
别为 [ j ] 100MPa, [ jy ] 280MPa 。若F=250kN,试求 (1)每边所需的铆钉个数n;
(2)若铆钉按图(b)排列,所需板宽b为多少?
F F
材料力学
剪切实用计算
F
F
图(a) F
F
图(b)
扭转典型习题解析

扭转典型习题解析1 一内径d =100mm 的空心圆轴如图示,已知圆轴受扭矩m kN 5⋅=T ,许用切应力][τ=80MPa ,试确定空心圆轴的壁厚。
解题分析:因为不知道壁厚,所以不能确定是不是薄壁圆管。
分别按薄壁圆管和空心圆轴设计。
解: 1、按薄壁圆管设计薄壁圆管扭转时,假设切应力沿壁厚均匀分布,设壁厚为δ,平均半径为2/0)(δ+=d R ,则扭转切应力为 δτ20π2R T=强度条件为][ττ≤,于是得][π22τδδTd =+)( ][π22223τδδδTd d =++ ()Pa1080πm N 1052m 10100m 1010026323233××⋅××=×+××+−−δδδ解得 mm 70.3m 1070.33=×=−δ 2、按空心圆轴设计强度条件为 ][pmax ττ≤=W T将δ216π44p +=−=d D d D DW );(代入得][π16][π][π164444=−−≤−τττd TD D d D DT,)(0Pa)108(m 1.0πm N 10516Pa 1080π64346=××−×⋅××−×××)(D D解得mm 107.7m 10107.73=×=−Dmm 85.32mm100mm 7.1072=−=−=d D δ 比较可知,两种设计的结果非常接近。
讨论: 当10/0R ≤δ时,即认为是薄壁圆管,可以直接使用薄壁管扭转公式。
2 图示受扭圆杆,沿平面ABCD 截取下半部分为研究对象,如图b 所示。
试问截面ABCD 上的切向内力所形成的力偶矩将由哪个力偶矩来平衡?解题分析:由切应力互等定理可知截面ABCD 上的切向内力分布及其大小。
该截面上切向内力形成一个垂直向上的力偶矩。
在图b 中,左右两个横截面上的水平切向内力分量形成垂直于截面ABCD 的竖直向下的力偶矩,正好与截面ABCD 上切向内力的合力偶矩平衡。
材料力学扭转练习题

材料力学扭转练习题基本概念题一、选择题1. 图示传动轴,主动轮A的输入功率为PA =0 kW,从动轮B,C,D,E的输出功率分别为PB =0 kW,PC = kW,PD = 10 kW,PE = 1kW。
则轴上最大扭矩T。
A.BA段 B.AC段 C.CD段 D.DE段max出现在题1图2. 图示单元体的应力状态中属正确的纯剪切状态的是。
题2图3. 上题图示单元体的应力状态中属正确的是。
4. 下列关于剪应力互等定理的论述中正确的是。
A.剪应力互等定理是由平衡B.剪应力互等定理仅适用于纯剪切的情况C.剪应力互等定理适用于各种受力杆件D.剪应力互等定理仅适用于弹性范围E.剪应力互等定理与材料的性能无关5. 图示受扭圆轴,其横截面上的剪应力分布图正确的是。
-12-题5图6. 实心圆轴,两端受扭转外力偶作用。
直径为D时,设轴内的最大剪应力为?,若轴的直径改为D2,其它条件不变,则轴内的最大剪应力变为。
A.8? B.?C.16? D.?7. 受扭空心圆轴,在横截面积相等的条件下,下列承载能力最大的轴是。
A.??0 B.??0.5C.??0. D.??0.88. 扭转应力公式T?的适用范围是。
IpA.各种等截面直杆 B.实心或空心圆截面直杆C.矩形截面直杆 D.弹性变形 E.弹性非弹性范围 9. 直径为D的实心圆轴,最大的容许扭矩为T,若将轴的横截面积增加一倍,则其最大容许扭矩为。
A.2TB.2T C.22TD.4T10. 材料相同的两根圆轴,一根为实心,直径为D1;另一根为空心,内径为d2,外径为D2d2D??。
若两轴横截面上的扭矩T,和最大剪应力?max均相同,则两轴外径之比1 D2D2为。
A.1??B.1?? C.343D.411. 阶梯圆轴及其受力如图所示,其中AB段的最大剪应力?max1与BC段的最大剪应力?max2的关系是。
A.?max1??max2B.?max1?313?max2C.?max1??max2D.?ma x1??max248-13-题12图题13图12. 在图示的圆轴中,AB段的相对扭转角?1和BC段的相对扭转角?2的关系是。
理论力学扭转例题

,
题解:
由于B端固定,φB¹ 则有: =0
B
T1 a GI P T2 (a b) GI P TB (a b c) GI P
2
0
T1 2
式中设TB与T1同向,代入 T 其中: a c 得 T 5T1 B
8
4
b
2
(与假设方向相反)
画出图如图所示。
12tl
2
题13:图示一实心钢轴插入一铜管中,设彼此之间无摩 擦力,A端用一销钉连接,此时B端轴与管的销钉相差φ 角,施加外力偶使轴与管相对转动,插入另一销钉,已 知:轴长为l,实心钢轴的抗扭刚度为GIp,铜管的抗扭刚 度为轴的2倍,求移去外力偶后轴与管的内力。
题解:
设轴和管的扭矩分别为T1 和T2
39、题解:
M x 0
有
T 0
Dt
D 2
2T
D t
2
'
由剪应力互等定律,纵截面上的 纵向截面上的总剪力
'
,
Q l t l t
n Q A 2T
由铆钉的剪切强度条件,有
D A
2
一、剪应力流的方向与扭矩的方向一致。
x
4
1 32T l 1 1 d d d d 3 d 3 0 GI x 3G b p a a b Tdx
题7:若圆截面轴AB,其左端固定,承受 均布力矩 t 作用,试导出该轴B端的扭转 角。 题解:
二、开口薄壁截面杆在自由扭转时的剪应力分布如图(a),厚 度中点处,应力为零。
当h/b>10时,截面为狭长矩形: =1/3
(仅供参考)第十九章-扭转的强度与刚度计算
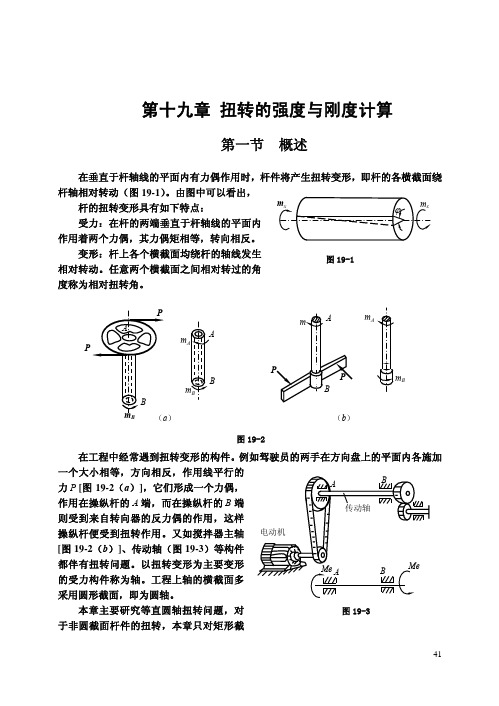
一、外力偶矩的计算
前面已经指出 ,使轴产生扭转变形的是外力偶矩。但是作用于轴上的外力偶矩往
往不是直接给出的,而是给定轴所传递的功率和轴的转速。以图 19-3 所示的传动轴为例,
由电动机的转速和功率可以求出传动轴 AB 的转速及通过皮带轮输入的功率。功率由皮
带轮传到轴 AB 上,再经右端的齿轮输出。设通过皮带轮给 AB 轴输入的功率为 N(kW),
因为 1kW=1000N·m/s 因此每秒钟输入功应为 : W = N ×1000(N ⋅ m)
(a)
电动机是通过皮带轮以力偶矩 Me 作用于 AB 轴上的,若 AB 轴的转速为每分钟 n 转,
则力偶矩 Me 在每秒内完成的功应为 :
W = 2π × n × Me(N ⋅ m)
(b)
60
因为 Me 所完成的功也就是皮带轮给 AB 轴输入的功,故(a)、(b)两式应相等,这
据微元的平衡要求,不仅左右一对面上有大小相等,方向相反的剪应力 τ ,在上下一对
面也必须有剪应力τ ′ ,而且由力矩平衡条件 ∑ mz = 0 有:
(τtdy)dx = (τ ′tdx)dy
由此得到:
τ =τ′
(19-2)
这表明,在相互垂直的两个微面上,剪应力总是成对出现的,它们数值相等,而方
向均垂直于两微面的交线,或指向或背离这一交线。这就是剪应力互等定理。
利用第三节中的(b)式和(c)式,上式可以写成:
φ
φ
图 19-9
u = 1 τγ 2
再由剪切胡克定律(式 19-3)得:
u = 1 τγ = τ 2 2 2G
46
第四节 圆轴扭转时的应力与变形
一、横截面上剪应力计算公式
圆轴扭转时,在已知横截面上的扭矩后,还应进一步研究横截面上的应力分布规律,
材料力学复习例题

t
P
d
t
P/4
1
2
3
工程力学教程电子教案
20
1
2
3 P
3板(杆)拉伸强度计算 板 杆 拉伸强度计算
σ max =
FN P = (b 2 d )t Amin
3
1 110 × 10 = = 200 MPa ≥ [σ ] 4 (8 . 5 1 .6 × 2 ) × 1 × 10
P/4
一拉伸压缩 1,轴力图 2,强度条件应用:校核,设计,计算 3,低碳钢拉伸实验,应力-应变曲线 4,连接件强度:剪切,挤压实用计算
例题
30 kN A B 3 30 kN A 2
3
B 2
作轴力图. 要作ABCD杆的 作轴力图. 解:要作 杆的 20 kN 20 kN 轴力图, 轴力图,则需分别将 C D AB,BC,CD杆的轴 杆的轴 20 kN 1 20kN 力求出来.分别作截 力求出来. x 1 面1-1,2-2,3-3,如 , , , D C 20kN 左图所示. 左图所示. F
Me B
(a)
(b)
图示为一受集中荷载F作用的简支 图示为一受集中荷载 作用的简支 试作其剪力图和弯矩图. 梁.试作其剪力图和弯矩图. a F b 根据整体平衡, 解:根据整体平衡,求 A B 得支座约束力 C FA FB x FA=Fb/l, FB=Fa/l
例
梁上的集中荷载将 梁分为AC和 两段 两段, 梁分为 和CB两段, 根据每段内任意横截面 左侧分离体的受力图容 易看出, 易看出,两段的内力方 程不会相同. 程不会相同.
σ x1 σ x2
σ x3
FNx1 400 × 10 3 = = 160 × 10 6 Pa = 160MPa = 6 A1 2500 × 10 FNx 2 -100 × 10 3 = = -40 × 10 6 Pa = -40MPa = A2 2500 × 10 6
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
剪切扭转的内力与强度计算
一、填空题
图示铆接钢板用两个铆钉连接,钢板所受的力F = 10KN,则每个铆钉横截面上的剪力Q =_____ 。
图 1
二、判断题
1.图示两块钢块用四个铆钉对接,铆钉直径d相同,铆钉剪切面上剪应力大小为。
()
图 2
2.穿过水平放置的平板上的圆孔,在其下端受有一拉力F,该插销的剪切
面积和挤压面积分别等于πdh,。
()
3.图示木接头,左右两部分形状完全一样,当F作用时,接头的剪切面积等于ab,挤压面积等于cb。
()
图3 图4
4.图示连接件,插销剪切面上的剪应力为τ=。
()
图 5
5.剪应力的计算公式τ= 适用于任何受扭构件。
()
6.圆轴的最大扭转剪应力τmax必发生在扭矩最大截面上。
()
7.相对扭转角的计算公式φ= 适用于任何受扭构件。
()
8.空心圆轴的内.外径分别为d和D,则其抗扭截面y数为。
()
9.若实心圆轴的直径增大一倍,则最大扭转剪应力将下降为原来的1/16。
()
10.一实心圆轴直径为d,受力如图所示,轴内最大剪应力为τmax=。
( )
图 6
11.轴扭转时,同一截面上各点的剪应力大小全相同。
()
12.轴扭转时,横截面上同一圆周上各点的剪应力大小全相同。
()
13.实心轴和空心轴的外径和长度相同时,抗扭截面模量大的是实心轴。
()
三、选择题
1.剪切强度的实用计算的强度条件为()
A.σ= N/A≤[σ]
B. τ=Q/A≤[τ]
C.σ= Pc/Ac≤[σc]
D. τmax=Mx/Wp≤[τ]
2.螺栓连接两块钢板,当其它条件不变时,螺栓的直径增加一倍,挤压应力将减少()倍。
A.1 B.1/2 C.1/4 D.3/4
3.图示扭转轴1——1截面上的扭矩Mx为()
A. Mx =–2KN·m
B.Mx = 5 KN·m
C.Mx = 1 KN·m
D.Mx = 4 KN·m
图 7
4.圆轴扭转时,横截面上同一圆周上各点的剪应力大小应是()
A.全不同 B.全相同 C.部分相同 D.无法比较
四、分析题
1.在校核受扭圆轴的刚度时,发现原设计是扭转角超过了许用扭转角。
现有两种修改方案:①改用优质材料;②加大圆轴直径。
你选择方案,为什么?因为。
2.单位扭转角的计算公式是什么?
3.直径相同,材料不同的两根等长的实心圆轴,在相同的扭矩作用下,其
是否相同。
4.在校核受扭圆轴的刚度时,发现原设计是扭转角超过了许用扭转角。
现
有两种修改方案:①改用优质材料;②加大圆轴直径。
你选择方案,为什么?因为。
5.单位扭转角的计算公式是什么?
6.直径相同,材料不同的两根等长的实心圆轴,在相同的扭矩作用下,其
是否相同。
五、计算题
1.实心圆轴受力如图示,已知直径d=20mm,试绘扭矩图,并求轴内最大剪应力.
图 8
2.图9所示圆轴直径d=60mm,长L=1m,转矩M=5KN·m,材料的剪切弹性模量Mpa试求:
〈1〉截面上a,b,c三点的剪应力值,并在图上画出其方向;〈2〉最大剪应力及单位扭转角。
图 9
3.圆轴尺寸及载荷如图10所示。
已知:材料简切弹性摸量
试校核该轴强度和刚度。
图10
4.一传动轴受力情况如图所示。
已知材料的许用剪应力[τ]=40MPa,许用扭转角,材料的剪切弹性模量。
(a) 试设计轴的直径。
(b) 已知轴的直径为60mm,试校核轴的强度和刚度。
图 11
5.一空心圆轴外径D=100mm,内径d=50mm,两端受外力偶矩Mx=1000N·m ,求截面上的最大剪应力,最小剪应力,并绘出截面剪应力分布图。
