基本统计分析`频数分布表
频数分布表及图形描述
数据量大、杂乱无章！如何从这些数据中得
到有价值的信息？这就是统计分析所研究的
课题，而SPSS正是解决这样问题的工具及手
段。
2) SPSS的发展过程
20世纪60年代末，美国斯坦福大学的3位 研究生研制开发了统计分析软件： 社会科学 统计软件包(Statistical Package for Social Science) 1975年成立了SPSS软件公司，专门进行 统计分析软件的研发。由于市场前景广阔， 多家从事统计分析软件开发的公司相继出现， 但SPSS公司始终处于市场领先的位置。
顾 客 性 别
男
女
Total
Count % within 顾 客 性 别 % within 饮 料 类 型 % of Total Count % within 顾 客 性 别 % within 饮 料 类 型 % of Total Count % within 顾 客 性 别 % within 饮 料 类 型 % of Total
统计的应用实例
【例1-3】挑战者号航天飞机失事预测 在此次失事前，该航天飞机 24 次发射成功。将航天飞机 送入太空的两个固体燃料推进器由 6只O型项圈密封。在几次 飞行中，曾发生过O型项圈被腐蚀或气体泄漏事故。这样的事 故是及其危险的。前24 次发射中有一次发动机遭到了永久性 破坏。根据23次飞行中发生腐蚀或泄漏事故的次数(因变量)及 火箭连接处的温度(自变量)数据，进行线性回归得到的回归方 程为
统计的应用实例
【例1-2】用简单的描述统计量得到一个重要发现 费舍 (R ． A ． Fisher) 在 1952 的一篇文章中举了一个例 子，说明如何由基本的描述统计量的知识引出一个重要 的发现。 20 世纪早期，哥本哈根卡尔堡实验室的施密特 (J.Schmidt) 发现不同地区所捕获的同种鱼类的脊椎骨和 鳃线的数量有很大不同；甚至在同一海湾内不同地点所 捕获的同种鱼类，也发现这样的倾向 然而，鳗鱼的脊椎骨的数量变化不大。施密特从欧洲 各地、冰岛、亚速尔群岛以及尼罗河等几乎分离的海域 里所捕获的鳗鱼的样本中，计算发现了几乎一样的均值 和标准偏差值。由此，施密特推断所有各个不同海域内 的鳗鱼是由海洋中某公共场所繁殖的。后来名为“戴纳 (Dana)”的科学考察船在一次远征中发现了这个场所
频数及其分布四种统计图
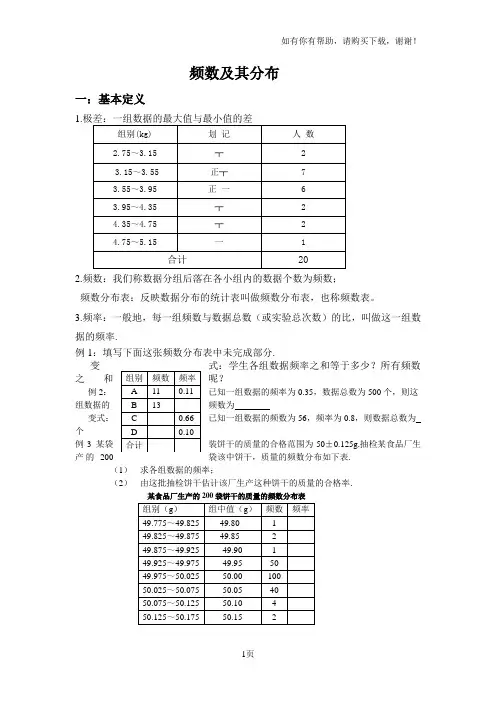
频数及其分布一：基本定义1.2.频数：我们称数据分组后落在各小组内的数据个数为频数；频数分布表：反映数据分布的统计表叫做频数分布表，也称频数表。
3.频率：一般地，每一组频数与数据总数（或实验总次数）的比，叫做这一组数据的频率.例1：填写下面这张频数分布表中未完成部分.变式：学生各组数据频率之和等于多少？所有频数Array之和呢？例2：已知一组数据的频率为0.35，数据总数为500个，则这组数据的频数为变式：已知一组数据的频数为56，频率为0.8，则数据总数为个例3 某袋装饼干的质量的合格范围为50±0.125g.抽检某食品厂生产的200袋该中饼干，质量的频数分布如下表.（1）求各组数据的频率；（2）由这批抽检饼干估计该厂生产这种饼干的质量的合格率.某食品厂生产的200袋饼干的质量的频数分布表二：频数分布直方图一：用来表示频数分布的基本统计图叫做频数分布直方图，简称直方图(Mstogram)．在统计数据时，按照频数分布表，在平面直角坐标系中，横轴标出每个组的端点，纵轴表示频数，每个矩形的高代表对应的频数，我们称这样的统计图为频数分布直方图，如图12-5所示，直方图中各矩形之间没有空隙.【说明】在画频数分布直方图时，首先要列出频数分布表.在分组时要注意：（1）组数适当；（2）组距相等.同时，分组要遵循三个原则：（1）不空，即该组必须有数据；（2）不重，即一个数据只能在一个组中；（3）不漏，即不能漏掉某一个数据.思考：频数分布直方图与条形统计图的区别？（1）条形统计图中，横轴上的数据是孤立的，是一个具体的数据。
而直方图中，横轴上的数据是连续的，是一个范围。
（2）条形统计图中，各个数据之间是相对独立的，各个条形之间是有空隙的。
而在直方图中，各长方形对应的是一个范围，由于每两个相邻范围之间不重叠、不遗漏，因此在直方图中，长方形之间没有空隙。
例．请观察图，并回答下面的问题：(1)被检测的矿泉水总数有多少种?(2)被检测矿泉水的最低pH为多少?(3)组界为6.9~7.3这一组的频数、频率分别是多少(每一组包括前一个边界值，不包括后一个边界值)?(4)根据我国2001年公布的生活饮用水卫生规范，饮用水的pH应在6.5—8.5的范围内．被检测的矿泉水不符合这一标准的有多少种?占总数的百分之几?思考：图中的频数分布直方图的每一组的边界值为多少？A．10.5 B．14.5 C．12.5 D．8.5三：拆线统计图及其特点折线统计图是用一个单位长度表示一定的数量，根据数量的多少描出各点，然后用线段顺次把各点连接起来.它既可以表示出项目的具体数量，又能清楚地反映事物变化的情况.折线统计图的特点：易于显示数据的变化趋势，如图12-4所示.例．超速行驶是交通事故频发的主要原因之一．交警部门统计某日7：00～9：00经过高速公路某测速点的汽车的速度，得到如下频数分布折线图（1）这一天7：00～9：00经过该观察点的车辆总数是多少（2）数据分组的组距是多少（3）若该路段汽车限速为110km/h，请问超速行驶的汽车有多少辆？占总数的百分之几（4）简单描述折线的波动情况，并说明它所表示的实际意义四：扇形统计图用圆代表总体，圆中的各个扇形分别代表总体中的不同部分，扇形的大小反映部分占总体的百分比的大小，这样的统计图叫做扇形统计图.扇形统计图主要是反映具体问题中的部分与整体的数量关系.扇形统计图的各部分占总体的百分比之和为100%或1，如图12-2所示.例1 如图12-6所示的是扇形统计图，求扇形B占总体的百分比.例每人捐书的册数/册 5 10 15 20相应的捐书人数/人17 22 4 2（1）该班的学生共多少名？（2）全班一共捐了多少册书？（3）若该班所捐图书按图12-7所示的比例分，则送给山区学校的书比送给本市兄弟学校的书多多少册？总结：条形统计图显示每组中的具体数据；扇形图显示部分在总体中占的百分比；频数直方图显示数据的分布情况；折线图显示数据的变化趋势综合练习：1 为了了解小学生的体能情况，抽取了某小学同年级学生进行跳绳测试，将所得数据整理后，画出如图12-11所示的频率分布直方图，已知图中从左到右前三个小组的频率分别是0.1，0.3，0.4，第一小组的频数为5，则第四小组的频率是，参加这次测试的学生有人.2某班同学参加环保知识竞赛，将学生的成绩（得分取整数）进行整理后分成五组，绘制成频率分布直方图，如图12-12所示，图中从左到右各小组的长方形的高的比是1∶3∶6∶4∶2，最右边一组的频数是6，结合直方图提供的信息，解答下列问题.。
频数分布表和频数分布直方图(课件)
课堂练习
1.为了绘制一组数据的频数直方图，首先要算出这组 数据的变化范围，数据的变化范围是指数据的( C ) A．最大值 B．最小值 C．最大值与最小值的差 D．个数
课堂练习
2.一组数据的最小数是12，最大数是38，如果分组的组
距相等，且组距为3，那么分组后的第一组为( B )
A．11.5～13.5
为了参加全校各年级之间的广播操比赛,七年级准备从63名同学中挑出身
高相差不多的40名同学参加比赛为此收集到这63名同学的身高(单位：cm)
如下：
158 158 160 168 159 159 151 158 159 168 158 154 158 154 169 158 158 158 159 167 170 153 160 160 159 159 160 149 163 163 162 172 161 153 156 162 162 163 157 162 162 161 157 157 164 155 156 165 166 156 154 166 164 165 156 157 153 165 159 157 155 164 156
典型例题
例题1 已知一组数据，最大值为93，最小值为22，
现要把它分成6组，则下列组距合适的是( B )
A．9
B．12
C．15
D．18
典型例题Βιβλιοθήκη 例题2 在绘制频数直方图时，计算出最大值与最小值
的差为25 cm，若取组距为4 cm，则组数为( D )
A．4组
B．5组
C．6组
D．7组
典型例题
例题3 某中学部分同学参加全国初中数学竞赛，并取得了优异的成 绩，指导老师统计了所有参赛同学的成绩(成绩都是整数，试 题满分120分)，并且绘制了如图的频数直方图(每组中含最低分 数，但不含最高分数)，请回答： (1)该中学参加本次数学竞赛的共有多少人？ (2)如果成绩在90分以上(含90分)的同学获奖， 那么该中学参赛同学的获奖率是多少？ (3)图中还提供了其他信息，例如该中学没有 获得满分的同学等，请再写出两条信息．
频数分布表的构成_解释说明以及概述
频数分布表的构成解释说明以及概述1. 引言1.1 概述在数据分析和统计学中，频数分布表是一种常见的数据展示方法，它可以用于对数据进行整理、总结和描述。
频数分布表能够将大量的数据按照具体数值或者数量范围进行分类，并统计每个类别中的观测次数或占比情况。
通过频数分布表，我们可以直观地了解数据的集中趋势、离散程度以及异常值等重要特征，帮助我们更好地理解和分析数据。
1.2 文章结构本文将围绕频数分布表展开讨论，首先在引言部分介绍概述、文章结构和目的。
接下来，在第二部分中，我们将详细探究频数分布表的构成，包括定义和目的、表格格式和布局以及组距和组数选择等方面。
在第三部分中，我们将详细说明如何解释和说明频数分布表，包括总体描述性统计量、数据分布特征分析以及异常值检测与处理等内容。
第四部分将提供频数分布表的概述与应用场景讨论，包括常见应用场景介绍、数据可视化方法与工具使用以及实际案例的分析与讨论。
最后，在结论部分对文章进行总结。
1.3 目的本文的目的是帮助读者全面理解和掌握频数分布表的构成、解释说明以及概述，以及其在数据分析中的应用。
通过阅读本文，读者将能够了解频数分布表的基本概念和构成要素，学会如何解读和分析频数分布表，并了解其在实际问题中的应用场景。
同时，本文还将介绍一些常见的数据可视化方法和工具，帮助读者更好地展示和传达数据统计结果。
2. 频数分布表的构成：2.1 定义和目的频数分布表是一种用于展示数据分布情况的统计工具。
它将一组数据按照不同数值范围进行划分，然后记录每个范围内的数据数量，以及对应的频数（即出现次数）。
其目的是为了更好地理解数据的特征和统计性质，并通过直观的方式呈现给读者。
2.2 表格格式和布局频数分布表通常以表格形式进行呈现，其中包含若干列和行。
首先，第一列通常标识出各个区间（也可以称为组距）或类别，并且这些区间应该是互不重叠、完全覆盖整个数据集。
第二列则表示每个区间内数据出现的频数。
此外，还可以包含其他列来显示累积频率、相对频率等统计指标。
统计学制作频数分布表
统计学制作频数分布表统计学是一门研究随机现象变化的规律和定量关系的学科，通过对数据的收集、整理和分析，可以得到一系列的统计指标，辅助决策和问题解决。
频数分布表是统计学中最基础的工具之一，它可以直观的展现数据的分布情况，是进一步进行数据分析和研究的基础。
在本文中，我将介绍如何制作频数分布表以及其中涉及的一些概念和注意事项。
一、频数分布表的定义与意义频数分布表是将一个数据集中的数据按照不同分组范围分组，并统计各组的频数和频率的表格。
其中，频数指某一区间内的数据个数，频率指该区间内的数据个数与总数据个数之比。
使用频数分布表可以清晰地了解数据的分布情况，比如哪些数值出现的频率较高，哪些数值较为稀少等。
此外，频数分布表还可以用来寻找趋势和规律，进行数据的比较和分析，以及辅助进一步的数据处理和统计推断，是统计学研究的重要工具。
二、制作频数分布表的步骤与注意事项1.确定数据的分组方式。
由于数据多样性和数量的不同，需要根据实际情况选择合适的分组方式。
常见的分组方式有等距分组法、等频分组法等。
例如，设定每个组跨度为10，数据集的最小值为65，最大值为99，则可以分组为65~74，75~84，85~94，95~99各一组。
2.确定各分组的频数和频率。
对于每个分组，统计其中的数据量，即为该分组的频数；计算该分组的频率，即该分组的频数除以总数据量。
例如，分组为65~74的频数为15，分组为75~84的频数为20，则分组为65~74的频率为15/50=0.3，分组为75~84的频率为20/50=0.4。
3.根据数据的性质确定累积频数和累积频率。
累积频数是指在某个区间之前所有的频数之和，累积频率是指在某个区间之前的所有频率之和。
例如，累积频数为65~74的区间为15，累积频率为0.3，累积频数为65~84的区间为35，累积频率为0.7。
4.添加表头和表尾。
在频数分布表的开头添加数据集合的名称和计量单位，在表尾添加总频数和总频率。
频数及其分布四种统计图
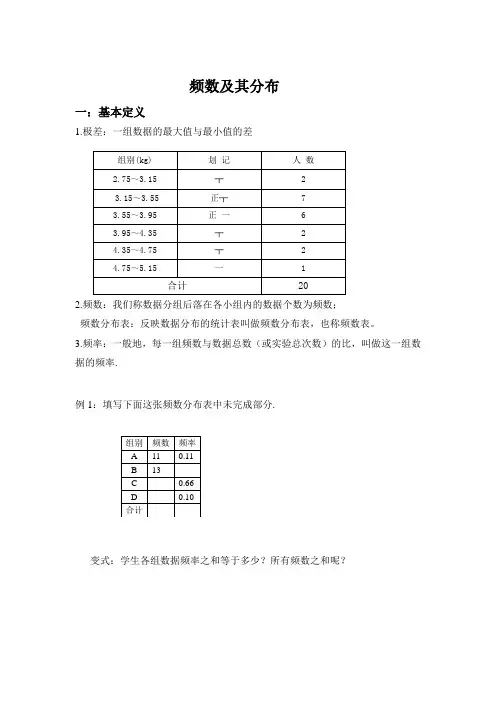
频数及其分布一：基本定义1.极差：一组数据的最大值与最小值的差组别(kg) 2.75～3.15 3.15～3.55 3.55～3.95 3.95～4.35 4.35～4.75 4.75～5.15 划 记 ┬ 正┬ 正 一 ┬ ┬ 一 人 数 2 7 6 2 2 1合计202.频数：我们称数据分组后落在各小组内的数据个数为频数； 频数分布表：反映数据分布的统计表叫做频数分布表，也称频数表。
3.频率：一般地，每一组频数与数据总数（或实验总次数）的比，叫做这一组数 据的频率.例 1：填写下面这张频数分布表中未完成部分.组别 A B C D 合计频数 11 13频率 0.11 0.66 0.10变式：学生各组数据频率之和等于多少？所有频数之和呢？例 2：已知一组数据的频率为 0.35，数据总数为 500 个，则这组数据的频数为 变式：已知一组数据的频数为 56，频率为 0.8，则数据总数为 个例 3 某袋装饼干的质量的合格范围为 50±0.125g.抽检某食品厂生产的 200 袋该中饼干，质 量的频数分布如下表. （1） 求各组数据的频率； （2） 由这批抽检饼干估计该厂生产这种饼干的质量的合格率.某食品厂生产的 200 袋饼干的质量的频数分布表组别（g） 49.775～49.825 49.825～49.875 49.875～49.925 49.925～49.975 49.975～50.025 50.025～50.075 50.075～50.125 50.125～50.175组中值（g） 49.80 49.85 49.90 49.95 50.00 50.05 50.10 50.15频数 1 2 1 50 100 40 4 2频率二：频数分布直方图一：用来表示频数分布的基本统计图叫做频数分布直方图，简称直方图(Mstogram)． 在统计数据时，按照频数分布表，在平面直角坐标系中，横轴标出每个组的端点，纵轴 表示频数，每个矩形的高代表对应的频数，我们称这样的统计图为频数分布直方图，如图 12-5 所示，直方图中各矩形之间没有空隙.【说明】 在画频数分布直方图时，首先要列出频数分布表.在分组时要注意： （1）组 数适当； （2）组距相等. 同时，分组要遵循三个原则： （1）不空，即该组必须有数据； （2）不重，即一个数据只 能在一个组中； （3）不漏，即不能漏掉某一个数据.思考：频数分布直方图与条形统计图的区别？（1）条形统计图中，横轴上的数据是孤立的，是一个具体的数据。
第一节基本统计分析一`频数分布表
第一节基本统计分析一`频数分布表
第一节基本统计分析一`频数分布表
二、数据描述分析过程 适用条件：对于定距以上变量，可以进行
集中趋势和离中趋势的统计 命 令：Analyze—— Descriptive
Statistics ——Descriptives 变量要求：可多选 可 选 项：Mean、Std.deviation、
第一节基本统计分析一`频数分布表
n 统计分析软件的一般特点 n 功能全面，系统地集成了多种成熟的统计
分析方法； n 有完善的数据定义、操作和管理功能； n 方便地生成各种统计图形和统计表格； n 使用方式简单，有完备的联机帮助功能； n 软件开放性好，能方便地和其他软件进行
数据交换。
第一节基本统计分析一`频数分布表
第一节基本统计分析一`频数分布表
三、独立样本T检验 要求被比较的两个样本彼此独立，没有配
对关系。要求两个样本均来自正态总体。 例：检验男女雇员现工资是否有显著性差
异。09-03 Analyze—Compare Means—
Independent Samples T Test
第一节基本统计分析一`频数分布表
n 软件发展
n 1960 年代：美国斯坦福大学三位研究生研制 n 1970 年代：SPSS 总部成立于芝加哥，推出 SPSS 中小
型机版 SPSSX— n 1980 年代：微机版（ V1~3 SPSS/PC+ 3） n 1990 年代：Windows 版（ v5~17） n 2009年4月：被IBM公司收购，改名为PASW。
第一节基本统计分析一`频数分布表
分析：起始工资、现工资与雇员受教育水 平、工作经验、职务等级之间是否存在 线性关系。
第一节基本统计分析一`频数分布表
统计学中的频数分布与频率分布
统计学中的频数分布与频率分布统计学是一门研究数据收集、分析和解释的学科，而频数分布与频率分布是统计学中常用的数据展示方法。
它们能够帮助我们更好地理解数据的特征和分布规律。
一、频数分布频数分布是将数据按照不同数值进行分类，并统计每个数值出现的次数，从而得到一个数据表。
以下是一个关于某班级学生考试成绩的频数分布表：成绩范围频数60-69 570-79 880-89 1290-100 10通过这个表格，我们可以直观地看到学生在各个成绩范围内的分布情况。
例如，在80-89分数段内，有12个学生获得了这个分数范围内的成绩。
频数分布表不仅可以展示数据的分布情况，还能帮助我们计算各个分数段内学生人数的百分比。
二、频率分布频率分布是通过统计每个数值出现的次数，然后将次数转化为频率（占总数的比例），得到一个数据表。
以下是使用相同数据的频率分布表：成绩范围频率60-69 0.2570-79 0.480-89 0.690-100 0.5与频数分布表相比，频率分布表更加直观地展示了各个成绩范围内学生所占的比例。
例如，在80-89分数段内的学生占总人数的0.6，即60%。
频数分布和频率分布都能够帮助我们更好地理解数据的特征和分布规律。
它们的选择取决于我们想要表达的信息。
如果我们更关注每个数值出现的次数，那么使用频数分布表更为合适；如果我们更关注各个数值所占的比例，那么使用频率分布表更为合适。
总结起来，频数分布和频率分布是统计学中常用的数据展示方法。
通过这些分布表，我们可以更加直观地了解数据的特征和分布规律，从而做出更准确的统计和分析。
在实际应用中，我们可以根据具体情况选择合适的分布表来展示数据。
【资料】频数分布表课件汇编
2 (X= )2 N
(2)样本方差:
(XX)2
S2
n1
▪ 方差性质:方差越大说明数据的变异越大 ▪ 自由度(degree of freedom,简记为DF)
(1)定义:随机变量能自由取值的个数 (2)计算公式:υ=n-限制条件个数
▪ 例:有一四个(n=4)数据样本,受到 的条件限制,在自由确定4,2,5三个数据 后,第四个数只能是9, 因而 υ=n-1=3 。
三、中位数（median) 中位数是将一组观察值按大小顺序排列后， 位次居中的观察值。 （一）计算方法
1.直接法：适用于样本量较小的计量资料。 当 为奇数时
当 为偶数时
2.频数表法（百分位数法）：适用于样本量 较大的计量资料，如频数表资料。
（二）中位数的应用注意事项 1.中位数可用于各种分布的资料。 2.中位数不受极端值的影响，因此，实际 工作中主要用于： （1）偏态分布资料 （2）端点无确切值的资料 （3）分布不明确的资料
常用的平均数——算术平均数、几何均 数、中位数
一、算术均数
算术均数简称均数（mean)，描述一组同质 资料的平均水平。
总体均数：
样本均数：
（一）计算方法 1.直接法：适用于样本量较小的计量资料。
2.加权法：适用于样本量较大的计量资料。
（二）均数的特性 1.各观察值与均数之差（离均差）的总 和等于零，即
频数分布表课件
第一节 频数分布表和频数分布图
频数表适用于: 观察例数较多的计量资料。 一、频数分布表:
频数（frequency):不同组别内的观察
值个数称为频数，表示观察值在各组内出 现的频繁程度。
频数表：将分组标志和相应的频数列表，
即为频数分布表，简称频数表。
统计学制作频数分布表
统计学制作频数分布表
统计学是一门研究数据收集、分类、统计、分析和解释的学科。
在统计学中，制作频数分布表是一项基本技能。
频数分布表显示了数据集中每个数据值出现的次数。
以下是制作频数分布表的步骤：
1. 确定数据集的范围和数据值的类型。
例如，您可能有一个包含100个学生分数的数据集，分数范围在0到100之间。
2. 确定类别或区间。
根据数据集的范围和分布，将数据值分成类别或区间。
例如，您可能将学生成绩分为10个等级，每个等级之间的大小为10分。
3. 计算每个类别或区间的频数。
对于每个类别或区间，计算数据集中出现的次数。
例如，如果您的第一个区间是0-9分，而有10个学生得到这个分数，那么这个区间的频数为10。
4. 列出每个类别或区间的频数。
将每个类别或区间的频数列在表格中，可以使用Excel或其他统计软件进行制表。
5. 可以在频数分布表中添加其他的信息，例如相对频率、累积频数和累积相对频率等。
制作频数分布表对于数据的分析和解释非常有用，可以帮助我们更好地了解数据集的分布情况。
- 1 -。
频数分布表的步骤
频数分布表的步骤
1.数据收集
在进行频数分布表的分析之前，首先要进行数据收集。
收集数据时需要明确收集的对象和范围，并采用适当的方法进行数据采集。
常用的数据采集方法包括调查法、实验法和观察法等。
2.数据筛选
数据筛选是频数分布表制作的必要步骤之一，目的是为了剔除异常值或错误数据。
筛选时可以根据数据的性质和实际情况，采用不同的筛选方法，如逻辑筛选、经验筛选等。
3.数据分组
数据分组是将原始数据按照一定的规则进行分类，以便于进行频数统计和分布分析。
分组时应根据研究目的和数据的性质，选择合适的分组方式，如等距分组、不等距分组等。
4.统计频数
统计频数是频数分布表中的关键步骤之一，需要按照分组的组距统计每组内的数据个数。
在统计频数时，可以采用手工计数或使用统计软件进行自动计数。
5.制作频数分布表
制作频数分布表是将统计好的频数按照一定的格式进行整理和排列。
在制作时，需要选择合适的表格形式，如简单表格、透视表等，并根据需要添加必要的统计指标，如平均数、标准差等。
6.分析频数分布
分析频数分布是频数分布表的重要应用之一，通过对频数分布的分析，可以了解数据的分布特征和规律。
在分析时，可以采用定性和定量分析方法，如描述性分析、方差分析等。
7.绘制频数分布图
绘制频数分布图是将频数分布表中的数据以图形的方式呈现出来，以便更直观地了解数据的分布情况。
在绘制时，可以选择合适的图表类型，如柱形图、饼图等，并根据需要添加图例、坐标轴等元素。
频数分布表与频数分布图(一)
交流意识优秀率、极差、标准差[新课学习]一、数据的分组整理将一组数据分成若干个数段，每个分数段是一个“组区间”，分数段两端的数值是“组限”，在一组两端数值中最大的数值为上限，最小的数值为下限，分数段的最大值与最小值的差为“组距”，分数段的个数是“组数”。
小结：分组整理的方法——⑴确定分组的方法并分组①计算极差；②确定组距和组数，，组数取大于商的最小整数；③决定组限并分组。
注意：各分数段中的分数，通常包括分数段的最低分，不包括最高分。
二、频数、频率与频数分布表频数：落在各个小组内的数据的个数是这一小组的频数。
（每个分数写P153表格通过引导学生动手实践完成数据的整理，使学生掌握一定统计知识和方法通过对数据分段的分数的个数）频率：每个小组的频数与数据总数的比值叫做这一小组的频率。
计算公式：完成频数分布表思考回答问题分组讨论回答问题学生练习：书P155小结所学黑板布的整理使学生学会用统计知识分析解决实际问题，体会统计在社会生活和科学领域中的作用和价值想一想：根据上表，回答以下问题⑴组数是多少？举例说明组区间是什么？⑵在“80~90”这一组中，组限各是什么？哪个是下限，哪个是上限？组距是多少？频数是多少？频率有多大？⑶假设在“70~80”这一组中，如果频数已知，频率漏掉，怎样补上？如果频数漏掉，怎样补上？如果频数、频率都漏掉，又怎样补上？小结规律：①各小组的频数之和等于数据总数；②各小组的频率之和等于1。
观察频数分布表，从以下几方面对数据分布信息进行分析：⑴数据在哪个组分布最多最集中（称该组为众数组），在哪个组分布最少，各占总数的比值（或百分比）是多少。
⑵各组数据分布的数量变化趋势是什么。
⑶测算中位数在哪个组（该组称为中位数组），获得数据分布状态的信息。
⑷测算平均数=各组组中值×该组频率的积之和（组中值=），从中体会频数分布的作用。
[课堂小结]：分组整理的方法⑴确定分组的方法并分组⑵累计各组的数据个数（频数），有时要计算频率[作业]：白皮练习册18.3内容板书设计§ 18.3 频数分布表与频数分布图（一）一、数据的分组整理二、频数、频率与频数分布表1. （略）2.教学后记学科数学课题§18.3 频数分布表与频数分布图（二）授课人张莉班级二（5，6）时间月日课型新课教学目标知识与技能：1.会画频数分布直方图和频数分布折线图；2.能从频数分布图中观察数据分布的特征；3.能解决一些实际问题；过程与方法：教师讲解引导，学生动手实践，观察思考探究情感态度与价值观：通过实例了解统计应用的广泛性和统计工作的基本步骤，能根据统计结果作出合理的判断和预测，并进行交流，初步学会用统计知识解决一些简单的实际问题，体会统计在社会生活和科学领域中的作用和价值。
频数分布表与频数分布直方图
大数据整合与共享
未来将有更多的数据整合和共享平台出现，频数分布表与频数分布直方图将作为重要的数据分析工具， 为全球范围内的数据共享和分析提供支持。
谢谢
THANKS
频数分布直方图的优点
可以直观地看出数据的分布趋势和异常值，便于进行定性分析；通过颜色的深浅、柱子的高低可以快 速判断数据的集中和离散程度。缺点：无法详细记录每个数据值的频数，定量分析时需要结合其他工 具或方法。
04 频数分布表与频数分布直方图的应用
CHAPTER
在统计学中的应用
描述数据分布特征
频数分布表和直方图可以清晰地展示数据的 分布情况，帮助我们了解数据集中和离散的 程度。
数据探索和可视化
通过频数分布直方图，我们可以直观地了解数据 的分布情况，进一步探索数据之间的关系和规律。
3
对比不同数据集
通过比较不同数据集的频数分布表和直方图，我 们可以发现它们之间的差异和相似之处，进而进 行数据分析和解释。
在实际生活中的应用
人口普查数据统计
在人口普查中，频数分布表和直 方图被广泛应用于展示不同地区、
03 频数分布表与频数分布直方图的比较
CHAPTER
特点比较
频数分布表
以表格形式展示数据的频数分布情况 ，可以清晰地看出数据的数量和分布 特征。
频数分布直方图
以图形方式展示数据的频数分布情况 ，可以直观地看出数据的分布趋势和 异常值。
应用场景比较
频数分布表
适用于需要详细了解数据分布情况，进行定量分析的场景。例如，在市场调研中，可以使用频数分布表来分析不 同年龄段、性别等人群的数量分布情况。
基本统计分析一`频数分布表
与回归分析的比较
回归分析主要用于研究自变量和因变量之间的因果关系和预测模型，而频数分布表则更侧重于数据的 分类和计数。
回归分析通过建立数学模型来描述自变量和因变量之间的关系，并预测因变量的取值，而频数分布表则 通过频率和频数来反映数据在不同类别或区间内的分布情况。
在实际应用中，频数分布表被广 泛应用于各个领域，如社会学、 经济学、医学等，以帮助研究者 了解数据的特征和规律。
频数分布表的定义和重要性
频数分布表
通过将数据按照一定的分类标准进行 分组，并统计每个组内的数据个数， 形成频数分布表。
1. 了解数据分布特征
通过频数分布表，可以直观地了解数 据的分布情况，如集中趋势、离散程 度等。
易于理解
频数分布表的结构简单，易于理 解，方便非统计学背景的人也能 快速掌握。
便于比较
通过频数分布表，我们可以方便 地比较不同数据集的分布特征， 从而进行数据间的比较分析。
缺点
数据量大时处理困难
当数据量较大时，频数分布表的数据整理和制作过程会比较繁琐，容易出错。
无法揭示数据内在关系
频数分布表仅能展示数据的分布情况，无法揭示数据之间的内在关系和变化规律。
回归分析通常用于处理连续型数据和预测未来趋势，而频数分布表则适用于处理分类数据，对数据进行 分类和计数。
07
频数分布表的实际应用 案例
人口普查数据频数分布分析
人口普查数据通常涉及大量的人口样 本，通过频数分布表可以直观地展示 不同人口特征的分布情况，例如年龄 、性别、教育程度等。
分析人口普查数据频数分布有助于了 解人口结构、变化趋势和分布特点， 为政府制定人口政策、社会发展规划 提供科学依据。
stata频数分布表的命令
stata频数分布表的命令Stata频数分布表是数据分析中常用的工具之一。
在Stata软件中，可以利用命令生成频数分布表。
以下是具体操作步骤和命令语句。
1. 打开Stata软件，并打开要分析的数据集。
2. 点击菜单栏中的“统计分析（Statistics）”选项，选择“描述统计（Descriptive Statistics）”。
3. 在出现的对话框中，选择要分析的变量并将其拖入“变量（Variables）”一栏中。
4. 点击“选项（Options）”按钮，在弹出的对话框中，选择“频数表（Frequency Tables）”选项。
5. 在“频数表”选项中，可以选择输出的内容，包括总计（Total）、频数（Frequency）、比例（Percentages）等。
选择完后，点击“确定（OK）”按钮。
6. 在主窗口中，可以看到生成的频数分布表。
除了通过菜单栏生成频数分布表外，也可以直接在Stata命令行中输入命令生成频数分布表。
以下是两个常用的命令。
- tabstat命令：该命令可以生成变量的基本统计特征，包括频数、均值、标准差、最小值、最大值等。
命令语句为：```tabstat varname, by(byvarname)```其中，“varname”表示要分析的变量名称，“byvarname”表示按照哪个变量分类计算。
例如：```tabstat income, by(gender)```表示生成“income”变量在“gender”变量下的频数分布表。
- tabulate命令：该命令可以生成单个变量的频数分布表。
命令语句为：```tabulate varname```其中，“varname”表示要分析的变量名称。
例如：```tabulate gender```表示生成“gender”变量的频数分布表。
总之，在Stata软件中，生成频数分布表是十分简单且常用的操作。
通过使用菜单栏或输入命令，可以方便地分析和掌握数据的分布情况，为后续的数据分析提供有力的支持。
基本统计分析`频数分布表共52页文档
46、法律有权打破平静。——马·格林 47、在一千磅法律里，没有一盎司仁 爱。— —英国
48、法律一多，公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿；只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
6、最大的骄傲于最大的自卑都表示心灵的最软弱无力。——斯宾诺莎 7、自知之明是最难得的知识。——西班牙 8、勇气通往天堂，怯懦通往地狱。——塞内加 9、有时候读书是一种巧妙地避开思考的方法。——赫尔普斯 10、阅读一切好书如同和过去最杰出的人谈话。——笛卡儿
Than
频数分布表课件
表 5 130 名 健 康 成 年 男 子 脉 搏 （ 次 /分 ） 的 频 数 分 布
脉搏
人数
56～
2
59～
5
62～
12
65～
15
68～
25
71～
26
74～
19
77～
15
80～
10
83～ 85
1
合计
130
第二节 计量资料集中趋势的描述
平均数（average):是一类描述计量资料
集中位置或平均水平的统计指标。
2.观察值中若有0或负值，则不宜直接使 用几何均数。
3.观察值一般不能同时有正值和负值。若 全是负值，计算时可先将负号去掉，得出 结果后再加上负号。
三、中位数（median) 中位数是将一组观察值按大小顺序排列后， 位次居中的观察值。 （一）计算方法
1.直接法：适用于样本量较小的计量资料。
当n为奇数时
对称分布:集中位置在中间。左右两侧频 数基本对称。
偏态分布 正偏态分布：集中位置偏向数 值较小的一侧。
负偏态分布：集中位置偏向数 值较大的一侧。
（3）便于发现资料中的可疑值
（4）当 n足够大时,以f P的估 计值，便于进一步计算统计指标 和进行统计分析。
二、频数分布图
直方图：适合描述连续型资料的 频数分布。
2.连续型资料（continuity data): 是指变量取值不能一一列举（即变 量取值为一定范围内的任意值）的 资料。例如，人体的身高（cm)、体 重（kg) 等。
第一节 频数分布表和频数分布图
频数表适用于: 观察例数较多的计量资料。 一、频数分布表:
频数（frequency):不同组别内的观察
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Gen eral Happi ness Frequency Valid Very Happy 467 Pretty Happy 872 Not Too Happy 165 Total 1504 Missing NA 13 Total 1517 Percent Valid Percent 30.8 31.1 57.5 58.0 10.9 11.0 99.1 100.0 .9 100.0 Cumulative Percent 31.1 89.0 100.0
数据的收集 数据的整理 数据的分析
统计学为数据分析过程提供一套完整的科学 的方法论。统计软件为数据分析提供了实 现手段。
统计分析软件的一般特点 功能全面，系统地集成了多种成熟的统计分 析方法； 有完善的数据定义、操作和管理功能； 方便地生成各种统计图形和统计表格； 使用方式简单，有完备的联机帮助功能； 软件开放性好，能方便地和其他软件进行数 据交换。
Valid
Missing Total
0 1 2 3 4 5 6 7 Eight tistics: Dispersion(离差栏）: Std.Deviation 标准差 Variance 方差 Range 全距 Minimum 最小值 Maximum 最大值 S.E.mean 均值的标准误 Central Tendency (集中趋势栏） Mean 均值 Median 中位数 Mode 众数 Sum 总和 Skewness 偏度（0，1.5，0.5，-0.5） Kurtosis 峰度（0，正，负） 例：09-01
Number of Children Frequency 419 255 375 215 127 54 24 23 17 1509 8 1517 Percent 27.6 16.8 24.7 14.2 8.4 3.6 1.6 1.5 1.1 99.5 .5 100.0 Valid Percent 27.8 16.9 24.9 14.2 8.4 3.6 1.6 1.5 1.1 100.0 Cumulative Percent 27.8 44.7 69.5 83.8 92.2 95.8 97.3 98.9 100.0
第一节 描述性统计
频数分布（Frequencies） 数据描述（Descriptives） 数据探索（Explore） 交互列联表（Crosstab）
一、频数分布 在SPSS中可以很容易地得出频数分布表，平均数， 标准差等。 频数分布：可以概略地看到资料的分布情况，可做 初步整理之用，从中还可检查数据输入情况。 命令选择：Analyze —— Descriptive Statistics —— Frequencies 备 注：可选入多个变量
N Mean Std. Error of Mean Median Mode Std. Deviation Variance Skewness Std. Error of Skewness Kurtosis Std. Error of Kurtosis Range Minimum Maximum Sum
软件发展
1960 年代：美国斯坦福大学三位研究生研制 1970 年代：SPSS 总部成立于芝加哥，推出 SPSS 中小型 机版 SPSSX— 1980 年代：微机版（ V1~3 SPSS/PC+ 3） 1990 年代：Windows 版（ v5~17） 2009年4月：被IBM公司收购，改名为PASW。
Sta tisti cs Number of Children 1509 8 1.90 .045 2.00 0 1.765 3.114 1.034 .063 1.060 .126 8 0 8 2869 Highest Year of School Completed 1510 7 12.88 .077 12.00 12 2.984 8.904 -.168 .063 .710 .126 20 0 20 19455
还可直接作出图形（Charts）： Bar charts:条形图 Pie Charts:圆图、饼图 Histograms:直方图，只适用于连续的 数值型变量。
Valid Missing
Num ber o f Chi ldren Frequency Valid 0 419 1 255 2 375 3 215 4 127 5 54 6 24 7 23 Eight or More 17 Total 1509 Missing NA 8 Total 1517 Percent Valid Percent 27.6 27.8 16.8 16.9 24.7 24.9 14.2 14.2 8.4 8.4 3.6 3.6 1.6 1.6 1.5 1.5 1.1 1.1 99.5 100.0 .5 100.0 Cumulative Percent 27.8 44.7 69.5 83.8 92.2 95.8 97.3 98.9 100.0
常用统计软件简介
SAS：真正的巨无霸。被誉为国际上的标准统计软 件和最权威的组合式优秀统计软件。 SPSS：统计软件中的贵族 S-Plus：S语言（AT&T贝尔实验室）的后续发展 Stata：软件小巧、功能强大 以下，我们介绍的主要是SPSS。
SPSS（PASW）基础
软件名称
Statistical Package for Social Science （1975-2000年） Statistical Product and Service Solutions(2000年-2009年4月) Predictive Analytics Software（2009年4月起）
SPSS在社会统计中的应用
社会统计中的统计软件 SPSS基础 SPSS在社会统计学中的应用 描述性统计（ Descriptive Statistics） 相关分析（Correlate） 回归分析（Regression） 均值比较与检验（Compare Means）
社会统计中的统计软件
统计分析软件是数据分析的主要工具 完整的数据分析过程包括：