等差等比数列的证明

合集下载

等差数列与等比数列的通项公式求法总结

等比数列的通项公式
定义：等比数列中任意一项与它的前一项的比值是常数
公
式
：
an=a1*q^(n-
1)，其中a1是首
项，q是公比
推导：由等比数列的定义和性质，通过累乘法或迭代法得到通项公式
应用：用于求解等比数列中的任意一项，以及解决与等比数列相关的数学问题
公式推导过程
设等比数列的首项为a1，公比为q，则第n项为a1*q^(n-1) 利用等比数列的性质，可以推导出等比数列的通项公式为a1*q^(n-1) 公式推导过程中需要注意公比的取值范围，当公比为1时，等比数列变为等差数列公式推导过程中还需要注意等比数列的性质，即每一项与前一项的比值都相等
式
：
an=a1*q^(n-1)
推导过程：利用等差数列和等比数列的定义，通过数学归纳法或极限法推导出变式公式
运用：在解决实际问题时，根据已知条件选择合适的变式公式进行计算，提高解题效率
等差数列的实际应用案例
银行存款：计算利息股票投资：计算股票价格保险费用：计算保险费工资计算：计算工资总额
公式形式上的异同
等比数列通项公式： an=a1*q^(n-1)
相同点：都包含首项a1和公差或公比
等差数列通项公式： an=a1+(n-1)d
不同点：等差数列通项公式包含项数n，等比数列通项
公式包含幂指数(n-1)
应用场景的异同
等差数列：常用于描述连续变化的量，如温度、人口增长等
等比数列：常用于描述连续增长的量，如复利、人口增长等
WPS,a click to unlimited possibilities
汇报人：WPS

28 高中数学等差等比数列证明专题训练

专题28高中数学等差等比数列证明专题训练【方法总结】1．等差数列的四个判定方法(1)定义法：a n ＋1－a n ＝d (常数)(n ∈N *)⇔{a n }是等差数列．(2)等差中项法：2a n ＋1＝a n ＋a n ＋2(n ∈N *)⇔{a n }是等差数列．(3)通项公式法：a n ＝pn ＋q (p ，q 为常数，n ∈N *)⇔{a n }是等差数列．(4)前n 项和公式法：S n ＝An 2＋Bn (A ，B 为常数，n ∈N *)⇔{a n }是等差数列．提醒：(1)定义法和等差中项法主要适合在解答题中使用，通项公式法和前n 项和公式法主要适合在选择题或填空题中使用．(2)若要判定一个数列不是等差数列，则只需判定存在连续三项不成等差数列即可．2．等比数列的四个判定方法(1)定义法：a n ＋1a n＝q (q 是不为0的常数，n ∈N *)⇔{a n }是等比数列． (2)等比中项法：a 2n ＋1＝a n ·a n ＋2(a n ·a n ＋1·a n ＋2≠0，n ∈N *)⇔{a n }是等比数列．(3)通项公式法：a n ＝cq n (c ，q 均是不为0的常数，n ∈N *)⇔{a n }是等比数列．(4)前n 项和公式法：S n ＝k ·q n －k (k 为常数且k ≠0，q ≠0，1)，则{a n }是等比数列．提醒：(1)定义法和等比中项法主要适合在解答题中使用，通项公式法和前n 项和公式法主要适合在选择题或填空题中使用．(2)若要判定一个数列不是等比数列，则只需判定存在连续三项不成等比数列即可．【高考真题】1．(2022·全国甲理文) 记S n 为数列{a n }的前n 项和．已知2S n n＋n ＝2a n ＋1． (1)证明：{a n }是等差数列；(2)若a 4，a 7，a 9成等比数列，求S n 的最小值．【题型突破】1．已知等差数列{a n }的前n 项和为S n ，且a 3＝7，a 5＋a 7＝26．(1)求a n 及S n ；(2)令b n ＝S n n(n ∈N *)，求证：数列{b n }为等差数列． 2．已知数列{a n }中，a 1＝35，a n ＝2－1a n －1(n ≥2，n ∈N *)，数列{b n }满足b n ＝1a n －1(n ∈N *)． (1)求证：数列{b n }是等差数列；(2)求数列{a n }中的最大项和最小项，并说明理由．3．在数列{a n }中，a 1＝4，na n ＋1－(n ＋1)a n ＝2n 2＋2n ．(1)求证：数列⎩⎨⎧⎭⎬⎫a n n 是等差数列；(2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和S n ． 4．数列{a n }满足a 1＝1，na n ＋1＝(n ＋1)a n ＋n (n ＋1)，n ∈N *．(1)求证：数列⎩⎨⎧⎭⎬⎫a n n 是等差数列； (2)设b n ＝3n ·a n ，求数列{b n }的前n 项和S n ．5．若数列{a n }的前n 项和为S n ，且满足a n ＋2S n S n －1＝0(n ≥2)，a 1＝12． (1)求证：⎩⎨⎧⎭⎬⎫1S n 成等差数列； (2)求数列{a n }的通项公式．6．已知数列{a n }的前n 项和为S n ，且2S n ＝3a n －3n ＋1＋3(n ∈N *)．(1)设b n ＝a n 3n ，求证：数列{b n }为等差数列，并求出数列{a n }的通项公式； (2)设c n ＝a n n －a n 3n ，T n ＝c 1＋c 2＋c 3＋…＋c n ，求T n ． 7．(2021·全国乙)设S n 为数列{a n }的前n 项和，b n 为数列{S n }的前n 项积，已知2S n ＋1b n＝2． (1)证明：数列{b n }是等差数列；(2)求{a n }的通项公式．8．(2014·全国Ⅰ)已知数列{a n }的前n 项和为S n ，a 1＝1，a n ≠0，a n a n ＋1＝λS n －1，其中λ为常数．(1)证明：a n ＋2－a n ＝λ；(2)是否存在λ，使得{a n }为等差数列？并说明理由．9．设数列{a n }的前n 项和为S n ，且满足a n －12S n －1＝0(n ∈N *)． (1)求数列{a n }的通项公式；(2)是否存在实数λ，使得数列{S n ＋(n ＋2n )λ}为等差数列？若存在，求出λ的值；若不存在，请说明理由．10．若数列{b n }对于任意的n ∈N *，都有b n ＋2－b n ＝d (常数)，则称数列{b n }是公差为d 的准等差数列．如数列c n ，若c n ＝⎩⎪⎨⎪⎧4n －1，n 为奇数，4n ＋9，n 为偶数，则数列{c n }是公差为8的准等差数列．设数列{a n }满足a 1＝a ，对于n ∈N *，都有a n ＋a n ＋1＝2n ．(1)求证：{a n }是准等差数列；(2)求{a n }的通项公式及前20项和S 20．11．已知数列{a n }的首项a 1>0，a n ＋1＝3a n 2a n ＋1(n ∈N *)，且a 1＝23． (1)求证：⎩⎨⎧⎭⎬⎫1a n －1是等比数列，并求出{a n }的通项公式； (2)求数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和T n ．12．已知数列{a n }的前n 项和为S n ，n ∈N *，a 1＝1，a 2＝32，a 3＝54，且当n ≥2时，4S n ＋2＋5S n ＝8S n ＋1＋S n － 1．(1)求a 4的值；(2)证明：⎩⎨⎧⎭⎬⎫a n ＋1－12a n 为等比数列． 13．已知数列{a n }的前n 项和S n 满足S n ＝2a n ＋(－1)n (n ∈N *)．(1)求数列{a n }的前三项a 1，a 2，a 3；(2)求证：数列⎩⎨⎧⎭⎬⎫a n ＋23(－1)n 为等比数列，并求出{a n }的通项公式． 14．已知在正项数列{a n }中，a 1＝2，点A n (a n ，a n ＋1)在双曲线y 2－x 2＝1上，数列{b n }中，点(b n ，T n )在直线y ＝－12x ＋1上，其中T n 是数列{b n }的前n 项和． (1)求数列{a n }的通项公式；(2)求证：数列{b n }是等比数列．15．已知数列{a n }满足：a 1＝1，a n ＋1＝⎩⎪⎨⎪⎧a n ＋1，n 为奇数，2a n ，n 为偶数(n ∈N *)，设b n ＝a 2n －1． (1)求b 2，b 3，并证明b n ＋1＝2b n ＋2；(2)①证明：数列{b n ＋2}为等比数列；②若a 2k ，a 2k ＋1,9＋a 2k ＋2成等比数列，求正整数k 的值．16．(2019·全国Ⅱ)已知数列{a n }和{b n }满足a 1＝1，b 1＝0，4a n ＋1＝3a n －b n ＋4，4b n ＋1＝3b n －a n －4．(1)证明：{a n ＋b n }是等比数列，{a n －b n }是等差数列；(2)求{a n }和{b n }的通项公式．17．(2018·全国Ⅰ)已知数列{a n }满足a 1＝1，na n ＋1＝2(n ＋1)a n ，设b n ＝a n n． (1)求b 1，b 2，b 3；(2)判断数列{b n }是否为等比数列，并说明理由；(3)求{a n }的通项公式．18．已知数列{a n }的前n 项和为S n ，a 1＝1，a n >0，S 2n ＝a 2n ＋1－λS n ＋1，其中λ为常数．(1)证明：S n ＋1＝2S n ＋λ；(2)是否存在实数λ，使得数列{a n }为等比数列，若存在，求出λ；若不存在，说明理由．19．设等差数列{a n }的前n 项和为S n ，a ＝(a 1，1)，b ＝(1，a 10)，若a·b ＝24，且S 11＝143，数列{b n }的前n项和为T n ，且满足12n a -＝λT n －(a 1－1)(n ∈N *)．(1)求数列{a n }的通项公式及数列⎩⎨⎧⎭⎬⎫1a n a n ＋1的前n 项和M n ； (2)是否存在非零实数λ，使得数列{b n }为等比数列？并说明理由．20．已知数列{a n }满足a 1＝1，a n ＋1＝2a n ＋λ(λ为常数)．(1)试探究数列{a n＋λ}是不是等比数列，并求a n；(2)当λ＝1时，求数列{n(a n＋λ)}的前n项和T n．。

SXC039高考数学必修_等差等比数列下标和的性质运用

等差、等比数列“下标和”性质的运用定理：等差数列{a n }中，m+n=i+j ，则a m +a n =a i +a j ，等比数列{a n }中，m+n=i+j ，则a m ·a n =a i ·a j （m 、n 、i 、j ∈+N ）。

证明：若{a n }是等差数列，a m +a n =2a 1+(m+n -2)d, a i +a j =2a 1+(i+j -2)d ,∵m+n=i+j ,∴(m+n -2)d=(i+j -2)d,即a m +a n = a i +a j (其中d 为公差)若{a n }是等比数列，a m ·a n =a 12q m+n-2, a i ·a j = a 12q i+j-2, ∵ m+n=i+j ∴q m+n-2= q m+n-2 即a m ·a n =a i ·a j (其中q 为公比)。

这一性质可表述为：等差数列的下标和相等则相应的项的和相等，等比数列的下标和相等则相应的项的积相等；但必须注意：两项和（积）只能等于两项和（积），三项和只能等于三项和……。

等差（等比）数列中简化运算的技巧多源于这条性质。

例1．在等差数列{}n a 中，972a a a ++为常数，则其前（）项和也为常数（A ）6 （B ）7 （C ）11 （D ）12解析：等差数列{}n a 的前k 项和为常数即k a a +1为常数，而972a a a ++=36a 为常数， ∴26a =111a a + 为常数，即前11项和为常数，选C 。

注意：千万不要以为972a a a ++= 18a =171a a +，那就大错特错了！等差数列中“n 项和”与“两项和（转化为a 1+a n ）”有关，某一项或某几项和均需转化为“两项和”才能与“n 项和”联系起来。

例2．等比数列{n a }中，a 4+a 6=3，则a 5（a 3+2a 5+a 7）=解析：a 5（a 3+2a 5+a 7）=a 5a 3+2a 52+a 5a 7=a 42+2a 4a 6+a 62=(a 4+a 6)2=9例3．在正项的等差数列{n a }和正项的等比数列{n b }中，有11b a =，1212--=k k b a ，试比较k a 与k b 的大小。

等差、等比数列常用公式对照表

是等差数列
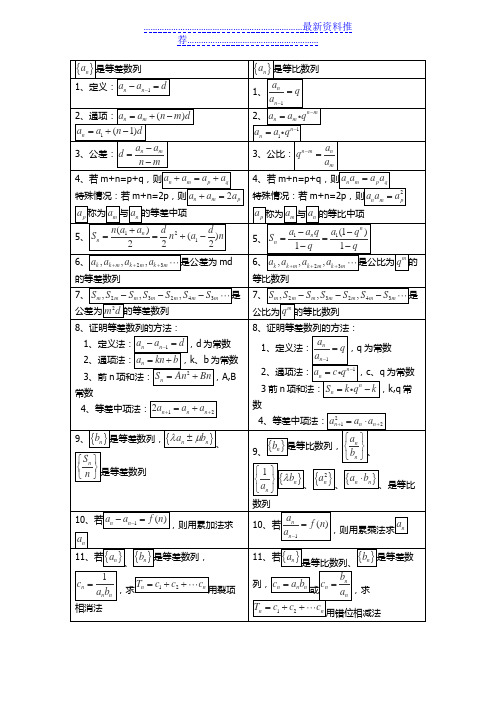
是等比数列
1、定义：
1、
2、通项：
2、
3、公差：
3、公比：
4、若m+n=p+q，则
特殊情况：若m+n=2p，则பைடு நூலகம்
称为与的等差中项
4、若m+n=p+q，则
特殊情况：若m+n=2p，则
称为与的等比中项
5、
5、
6、是公差为md的等差数列
6、是公比为的等比数列
7、是公差为的等差数列
7、是公比为的等比数列
8、证明等差数列的方法：
1、定义法：，d为常数
2、通项法：，k、b为常数
3、前n项和法：，A,B常数
4、等差中项法：
8、证明等差数列的方法：
1、定义法：，q为常数
2、通项法：，c、q为常数
3前n项和法：，k,q常数
4、等差中项法：
9、是等差数列，、是等差数列
9、是等比数列，、、、、是等比数列
10、若，则用累加法求
10、若，则用累乘法求
11、若、是等差数列，，求用裂项相消法
11、若是等比数列、是等差数列，或，求用错位相减法
一、求的方法：1、公式法；2、观察归纳法；3、累加法、累乘法；4、特征方程法
二、求的方法：1、裂项相消法；2、错位相减法；3、倒序相加法；4、分组求和法

(完整版)等差等比数列知识点总结

1.等差数列：一般地，如果一个数列从第2项起，每一项与它的前一项的差等于同一个常数d ，那么这个数列就叫做等差数列，这个常数d 叫做等差数列的公差，即d a a n n =--1（d 为常数）（2≥n ）；.2.等差中项：（1）如果a ，A ，b 成等差数列，那么A 叫做a 与b 的等差中项．即：2ba A +=或b a A +=2 （2）等差中项：数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a3.等差数列的通项公式：一般地，如果等差数列{}n a 的首项是1a ，公差是d ，可以得到等差数列的通项公式为：()d n a a n 11-+=推广： d m n a a m n )(-+=．从而mn a a d mn --=； 4．等差数列的前n 项和公式：1()2n n n a a S +=1(1)2n n na d -=+211()22d n a d n =+-2An Bn =+ （其中A 、B 是常数，所以当d ≠0时，S n 是关于n 的二次式且常数项为0） 5．等差数列的判定方法（1）定义法：若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列．（2）等差中项：数列{}n a 是等差数列)2(211-≥+=⇔+n a a a n n n 212+++=⇔n n n a a a ．（3）数列{}n a 是等差数列⇔b kn a n +=（其中b k ,是常数）。

（4）数列{}n a 是等差数列⇔2n S An Bn =+,（其中A 、B 是常数）。

6．等差数列的证明方法定义法：若d a a n n =--1或d a a n n =-+1(常数*∈N n )⇔ {}n a 是等差数列．（1）当m n p q +=+时,则有q p n m a a a a +=+，特别地，当2m n p +=时，则有2m n p a a a +=.(2) 若{n a }是等差数列，则232,,n n n n n S S S S S -- ，…也成等差数列（3）设数列{}n a 是等差数列，d 为公差，奇S 是奇数项的和，偶S 是偶数项项的和，n S 是前n 项的和 1.当项数为偶数n 2时，()121135212n n n n a a S a a a a na --+=+++⋅⋅⋅+==奇 ()22246212n n n n a a S a a a a na ++=+++⋅⋅⋅+==偶 ()11=n n n n S S na na n a a nd ++-=-=-偶奇 11n n n n S na a S na a ++==奇偶2、当项数为奇数12+n 时，则21(21)(1)1n S S S n a S n a S n S S a S na S n +⎧=+=+=+⎧+⎪⎪⇒⇒=⎨⎨-==⎪⎪⎩⎩n+1n+1奇偶奇奇n+1n+1奇偶偶偶（其中a n+1是项数为2n+1的等差数列的中间项）． 1、等比数列的定义：()()*12,nn a q q n n N a -=≠≥∈0且，q 称为公比 2、通项公式：()11110,0n nn n a a a q q A B a q A B q-===⋅⋅≠⋅≠，首项：1a ；公比：q推广：n m n m n n n m m a a a q q q a --=⇔=⇔=3、等比中项：（1）如果,,a A b 成等比数列，那么A 叫做a 与b 的等差中项，即：2A ab =或A = 注意：同号的两个数才有等比中项，并且它们的等比中项有两个（两个等比中项互为相反数）（2）数列{}n a 是等比数列211n n n a a a -+⇔=⋅ 4、等比数列的前n 项和n S 公式：（1）当1q =时，1n S na = （2）当1q ≠时，()11111n n n a q a a qS qq--==-- 11''11n n n a aq A A B A B A q q=-=-⋅=---（,,','A B A B 为常数）5、等比数列的判定方法：（1）用定义：对任意的n ，都有11(0){}n n n n n na a qa q q a a a ++==≠⇔或为常数，为等比数列（2）等比中项：21111(0){}n n n n n n a a a a a a +-+-=≠⇔为等比数列（3）通项公式：()0{}n n n a A B A B a =⋅⋅≠⇔为等比数列 6、等比数列的证明方法：依据定义：若()()*12,nn a q q n n N a -=≠≥∈0且或1{}n n n a qa a +=⇔为等比数列 7、等比数列的性质：（1）若*(,,,)m n s t m n s t N +=+∈，则n m s t a a a a ⋅=⋅。

等差等比数列的证明ppt课件

等差、等比数列的证明
1、定义法 an+1 - an=d 或 an-an-1=d
2、中项法 2an=an-1+an+1 (n>1)
3、通项公式法 an=pn+q(关于n的一次函数)
4、前n项和法 Sn=An2+Bn
1
等差、等比数列的证明一、等差数列的证明
例1 已知数列an的前n项和为Sn=3n2 -2n，证明数列an 成等差数列，并求其首项、
11
12
13
14
（2）
证明
an 2n
为等差数列，并求an
5
第七课时B组
8.已知数列an 的前n项和为Sn，Sn
=
1 3
(an
1)
（1）求a1、a2 .
（2）求证：数列an 是等比数列
6
等差、等比的计算问题的常用方法
方法1、利用等差、等比的性质方法2、利用基本量（解方程组）
项(an)的性质： an=am+(n-m)d 任两项的关系式
am+an=ap+aq(m+n=p+q)角标和性质
和(Sn)的性质： Sm ,S2m -Sm ,S3m -S2m ,L 成等差
Sn与项an的关系：
7
重点回顾
数列
等差数列
等比
定义通项公式
an+1-an=d 或 an-an-1=d
an= a1+(n-1)d
前n项和
性质和Sn与项an 的关系
aanm=+ama+n(=n-amp)+d aq(m+n=p+q)
公差、通项公式
2
第四课时拓展延伸（2015新课标全国卷）

证明或判断等差(等比)数列的四种方法

证明或判断等差(等比)数列的四种方法
判断等差数列的四种方法：
公差相等法：如果一个数列中任意两项之间的差值相等，则该数列为等差数列。

通项公式法：如果一个数列的通项公式是an=a1+(n-1)d，则该数列为等差数列。

前后项差值法：如果一个数列中任意两项之间的差值相等，则该数列为等差数列。

证明法：对于一个数列，如果它满足an+1 - an = d，则可以通过归纳法证明该数列是等差数列。

判断等比数列的四种方法：
公比相等法：如果一个数列中任意两项之间的比值相等，则该数列为等比数列。

通项公式法：如果一个数列的通项公式是an=a1*r^(n-1)，则该数列为等比数列。

前后项比值法：如果一个数列中任意两项之间的比值相等，则该数列为等比数列。

证明法：对于一个数列，如果它满足an+1 / an = r，则可以通过归纳法证明该数列是等比数列。

以上是判断等差数列和等比数列的四种常见方法，它们都比较简单易行，可以帮助我们快速判断一个数列是否为等差数列或等比数列。

同时，在具体应用中，我们还可以根据题目要求选择合适的方法，从而更好地解决问题。

等差数列与等比数列的证明方法

等差数列与等比数列的证明方法等差数列和等比数列是数学中常见的数列形式，它们在数学和实际问题中都有重要的应用。

下面我们来介绍等差数列和等比数列的证明方法。

等差数列是指数列中每两个相邻的数之间的差值都相等的数列。

等差数列的通项公式为An=a1+(n-1)d，其中a1是首项，d是公差，n是项数。

1. 通过公式法证明等差数列：假设有数列{an}，首项为a1，公差为d，我们可以使用数列的通项公式An = a1 + (n-1)d。

通过将通项公式代入证明，我们可以得到每一项与前一项之间的差值都为d，从而证明这是一个等差数列。

2. 通过递推法证明等差数列：假设有数列{an}，如果我们知道数列的首项a1和公差d，我们可以通过递推关系式an = an-1 + d来证明这是一个等差数列。

我们可以通过验证递推关系式对于所有项都成立，从而证明这是一个等差数列。

3.通过数列的性质证明等差数列：等差数列有很多重要的性质，例如，等差数列的中项等于首项与末项的平均数，等差数列的前n项和等于n倍首项与末项和的平均数。

如果我们通过对这些性质进行验证，可以得出结论这是一个等差数列。

等比数列是指数列中每两个相邻的数之间的比值都相等的数列。

等比数列的通项公式为An=a1*r^(n-1)，其中a1是首项，r是公比，n是项数。

1. 通过公式法证明等比数列：假设有数列{an}，首项为a1，公比为r，我们可以使用数列的通项公式An = a1 * r^(n-1)。

通过将通项公式代入证明，我们可以得到每一项与前一项之间的比值都为r，从而证明这是一个等比数列。

2. 通过递推法证明等比数列：假设有数列{an}，如果我们知道数列的首项a1和公比r，我们可以通过递推关系式an = an-1 * r来证明这是一个等比数列。

我们可以通过验证递推关系式对于所有项都成立，从而证明这是一个等比数列。

3.通过数列的性质证明等比数列：等比数列有很多重要的性质，例如，等比数列的任意两项的比值都相等，等比数列的前n项和等于首项与末项和的乘积与公比的差的商。

数学中证明等差数列的常用方法

数学中证明等差数列的常用方法数学中证明等差数列的常用方法等差数列是数学的现象，这类的现象该怎么证明呢?证明的`公式是的呢?下面就是店铺给大家整理的如何证明等差数列内容，希望大家喜欢。

等差数列证明一设等差数列 an=a1+(n-1)d最大数加最小数除以二即[a1+a1+(n-1)d]/2=a1+(n-1)d/2{an}的平均数为Sn/n=[na1+n(n-1)d/2]/n=a1+(n-1)d/2得证1 三个数abc成等差数列，则c-b=b-ac^2(a+b)-b^2(c+a)=(c-b)(ac+bc+ab)b^2(c+a)-a^2(b+c)=(b-a)(ac+bc+ab)因c-b=b-a，则(c-b)(ac+bc+ab)=(b-a)(ac+bc+ab)即c^2(a+b)-b^2(c+a)=b^2(c+a)-a^2(b+c)所以a^2(b+c), b^2(c+a), c^2(a+b) 成等差数列等差：an-(an-1)=常数(n≥2)等比：an/(an-1=常数(n≥2)等差：an-(an-1)=d或2an=(an- 1)+(an+1),(n≥2)等比：an/(an-1)=q或an平方=(an-1)*(an+1)(n≥2).等差数列二我们推测数列{an}的通项公式为an=5n-4下面用数学规纳法来证明：1)容易验证a1=5*1-4=4，a2=5*2-4=6，a3=5*3-4=11，推测均成立2)假设当n≤k时，推测是成立的，即有aj=5(j-1)-4，(j≤k)则Sk=a1+a2+…ak=5*(1+2+…+k)-4k=5k(k+1)/2-4k=k(5k-3)/2于是S(k+1)=a(k+1)+Sk而由题意知：(5k-8)S(k+1)-(5k+2)Sk=-20k-8即：(5k-8)*[a(k+1)+Sk]-(5k+2)Sk=-20k-8所以(5k-8)a(k+1)-10Sk=-20k-8即：(5k-8)a(k+1)=5k(5k-3)-20k-8=25k^2-35k-8=(5k-8)(5k+1) 所以a(k+1)=5k+1=5(k+1)-4即知n=k+1时，推测仍成立。

高考数学：证明等差等比数列的解法

高考数学：证明等差等比数列的解法
我们在数列部分常碰到这样的问题：证明某个复杂数列为等差或者等比数列。

比如下面这道题：
从求证出发，我们回顾等比数列的定义：从第2项开始，数列的后一项除以前一项等于同一个不为零的常数，则这个数列为等比数列。

这就是我们证明等比数列的主要办法，也称定义法.即只需证明后项/前项为常数即可。

使用定义法的技巧，就是在化简过程中，保持前项不变，然后后项用题中给定的关系式代入。

道理也是显然的，要使得计算结果为常数，必须要出现消项、约分，所以把后项朝前项去靠近，才能最终通过消项、约分得到常数。

根据条件中给定的关系式，代入上式。

结果还真是一个常数，神奇吗？
其实一点也不神奇，只要方法正确，常数是命题者设计好了的，你不用担心。

下面，增加一点难度，看这一道分段形式给出的数列递推式。

请自觉做题3分钟.不要往下看。

分析：首先来理解数列递推式传递的信息.我们用具体的例子来理解它。

通过这种方式，我们对数列有了一些感性的认识。

不管怎样，还是采用定义法来证明。

还是采用前面介绍的技巧：保持前项不变，把后项用题中给定的关系式代入。

注意看，分子项和分母项的脚标相差2，我们根据题目所给递推式，可以分两步来。

咦！结果又是一个常数。

废话，要不是常数，那就是题目出错了。

总结：定义法来真好用，证明等比显奇功。

初中数学中的等差数列与等比数列

初中数学中的等差数列与等比数列在初中数学中，等差数列和等比数列是两个重要的概念。

它们在数列及其应用中具有重要的地位和作用。

本文将介绍等差数列和等比数列的定义、性质以及它们在数学问题中的应用。

一、等差数列等差数列是指数列中任意两个相邻数之差相等的数列。

数列中的这个常数差称为等差数列的公差。

1. 定义设数列 {an} 是一个等差数列，若存在常数 d，对于任意的正整数 n （n≥2），都有 an - an-1 = d 成立，则称数列 {an} 是一个等差数列，公差为 d。

2. 性质等差数列的常用性质如下：（1）通项公式：设等差数列的首项为 a1，公差为 d，则第 n 项的通项公式为 an = a1 + (n - 1)d。

（2）前 n 项和公式：设等差数列的首项为 a1，公差为 d，则前 n 项和的公式为 Sn = (a1 + an) * n / 2，其中 an 为第 n 项。

3. 应用等差数列在代数运算中有广泛的应用，比如计算数列的和、寻找数列的规律等。

在解决实际问题时，等差数列也常常发挥着重要的作用。

比如在等间隔的时间内，某物体的位置、速度等等问题都可以用等差数列来表示和求解。

二、等比数列等比数列是指数列中任意两个相邻数的比相等的数列。

数列中的这个常数比称为等比数列的公比。

1. 定义设数列 {an} 是一个等比数列，若存在常数 q（q ≠ 0），对于任意的正整数 n（n≥2），都有 an / an-1 = q 成立，则称数列 {an} 是一个等比数列，公比为 q。

2. 性质等比数列的常用性质如下：（1）通项公式：设等比数列的首项为 a1，公比为 q，则第 n 项的通项公式为 an = a1 * q^(n - 1)。

（2）前 n 项和公式：设等比数列的首项为 a1，公比为 q，则前 n项和的公式为 Sn = a1 * (q^n - 1) / (q - 1)。

3. 应用等比数列在数学和实际问题中都有许多应用。

证明或判断等差等比数列的常用方法

证明或判断等差（等比）数列的常用方法湖北省王卫华玉芳翻看近几年的高考题，有关证明、判断数列是等差（等比）数列的题型比比皆是，如何处理这些题目呢？且听笔者一一道来.一、利用等差（等比）数列的定义等差（等比）数更最主要的方法•如:记 bn""1"1,2,….1 1 所以｛b n ｝是首项为a ，公比为一的等比数列. 42评析：此题并不知道数列｛b n ｝的通项，先写出几项然后猜测出结论，再用定义证明, 这是常规做法。

1猜想：｛b n ｝是公比为一的等比数列.21 1 证明如下：因为b n^a 2n^V-a 2n 2n 42bn,(nN )在数列{a n }中，若a na n-1（d 为常数）或a na n-1q （ q 为常数），则数列｛a n｝为等差（等比）数列.这是证明数列｛耳｝为例1 • （2005北京卷）设数列｛a n ｝的首项a1 =:a =丄，且a41-an 2 1|a 」 an 4n 为偶数n 为奇数所以b 1 （n ）判断数列｛b n ｝是否为等比数列，并证明你的结论.)a ? = a 1 ■—4 =a ；，a 3a ?=-2 : * 1 13 1 a4 = a 3 = a，所以 a5 = 4 2 82 1 1 b 2 = 1 1 =a 1a - 4 *3 一 a 1 4 3 4 2 . J a 」， 4 .4(i)求 a ?, 83 ；解：（i 1a 1 ；2 81 3a 4 一 4a16， 1 4」例2 •（ 2005山东卷）已知数列｛a n｝的首项a i =5 ,前n项和为S n ,且Sn 1 =2S n n •5（T N）（i）证明数列｛a n 1｝是等比数列；（n）略.解：由已知S n .1 =2S n • n • 5(n • N*)可得n _ 2时，& -n • 4两式相减得：S n 1 -S n = 2(S n -S ni) 1，即a n 1 = 2a n • 1，从而a n 1 T = 2(a n 1), 当n =1 时，s2=20 1 5，所以a2 a^2a1 6,又q =5，所以a2=11，从而a2 1 ^2(a1 1).a +1故总有a n「仁2(a n 1), n • N ”，又=5, a1 ^0，从而亠2 .a n +1所以数列｛a n 1｝是等比数列.评析：这是常见题型，由依照含S n的式子再类似写出含S n」的式子，得到a n pa n q 的形式，再利用构造的方法得到所要证明的结论.本题若是先求出通项a n的表达式，则较繁.注意事项：用定义法时常采用的两个式子a n—a n」=d和a n 4 -a n = d有差别，前者必a须加上“ n > 2 ”否则n=1时a0无意义，等比中一样有：n > 2时，有亠才|| = q (常a n」数式0 )；②n w N州时，有(常数=0).二•运用等差或等比中项性质a n■ a n2 - 2a n1 ：= ｛a n｝是等差数列，a n a n2 - a n1(a n0) ：= ｛a n｝是等比数列，这是证明数列｛坯｝为等差(等比)数列的另一种主要方法.例3. (2005江苏卷)设数列｛a n｝的前项为S n，已知a1 =1, a2 = 6, a3 = 11，且(5n -8)S n 1 -(5n 2)S n=An B, n =1,2,3,|,其中A, B 为常数.(1 )求A与B的值；(2)证明数列｛a n｝为等差数列；(3)略.解：(1 )由印=1, a2 =6, a3 =11，得S =1, S2 = 7, S3 = 18 .― A B 二-28, 把n =1,2 分别代入(5n-8)S1-(5n 2)S=An B，得2A• B =-48L解得，A = -20 , B = -8 .(n )由(I )知，5n(S n 1—S n) -8S n 1 —2£ = -20n -8，即又 5(n l)a n 2 -8S 2 -2S n i = -20(n 1) —8 . ②②-①得，5(n 1)a n 2 -5na n彳-8a n 2 -2a n* - -20 ,即(5n -3间2 -(5n 2)a. 1 = -20 . ③又(5n 2)a n 3 -(5n 7)% 2 - -20 . ④④-③得，(5n 2)(a n 3 — 2a. .2 a. .J =0 ,二兔3 — 2a. .2 a. 1 =0 ,…a n 3・一a n 2 = 2・一1 | = a3 —玄2 =5，又玄2 —玄1 =5 ,因此，数列是首项为1,公差为5的等差数列.评析：此题对考生要求较高，通过挖掘S n的意义导出递推关系式，灵活巧妙地构造得到中项性质，这种处理大大简化了计算.例4.(高考题改编)正数数列｛a n｝和｛b n｝满足：对任意自然数n, a n, b n, a n..成等差数列，b n, a n i, b n.成等比数列.证明：数列｛Jb n｝为等差数列.证明：依题意，a n 0, b n 0,2b n =a n •a n 1，且a n d ='••、b n b n 1 ,a n =b n」b n(n > 2).2b n 二.b n」b n b n b n 1 .由此可得2 m=.昭「b n?.即._昭-m - bn -兀(门> 2).数列｛.,0｝为等差数列.5na n i . —8S n i. -2S h = _20n -8 , ①评析：本题依据条件得到an与bn的递推关系，通过消元代换构造了关于 f. bj的等差数列，使问题得以解决.三.运算数学归纳法这种方法关键在于猜想要正确，用数学归纳法证明的步骤要熟练，从“n = k时命题成立”到“ n = k • 1时命题成立”要会过渡.例5 . (2004全国高考题)数列的前n项和记为& ,已知a^1 ,n 亠2 i S Ia* 1 = S n(n =1,2」1().证明：数列-n是等比数列.n L n J证明：由a1 -1, a n 1 =Sn (n - 1,2j H)，知a? ― S = 3a1, —1 = 2 ,1 2 2勺=1，猜测 S n 是首项为1,公比为2的等比数列.1 nS下面用数学归纳法证明：令 b^S n .n（1）当 n =2时，b 2 =2b\，成立.⑵当 n = 3时，S 3 = a 1 a 2 a 3 =13 2(1 3) = 12,0 = 4 = 2b 2，成立. 假设n =k 时命题成立，即b k =2b k 」.c k 2S S + ----------------------- 2那么当 n =k 1 时，b k j =汪1 二 S k ' a k 1 Jk+1 k+1k+1综上知 §n 是首项为1，公比为2的等比数列.I n J例6. （2005浙江卷）设点代（人,0, P n （X n ,2n 」）和抛物线2 * 1G ： y =x - a n X b n （n ・N ）,其中a . = -2 -4n - ^nJ , X n 由以下方法得到：花=1,点P （x 2,2）在抛物线G 注仝 a 1x b 上，点A （x 1,0）到p 的距离是 A 到G 上点的最短距离，…，点P n 1（X n 1,2"）在抛物线C n ： y = X 2 * a n X * b n 上，点A （绻0）到P n 1的距离是A到C n 上点的最短距离.(1 )求X 2及C 1的方程.(2)证明 {X n } 是等差数列. 解：(I)由题意得：A(1,0), G : y =x 2-7x • d .设点 P(x, y)是 C 1 上任意一点，贝U |AP|「(x-1)2 y 2「(x-1)2 (x 2-7x bj 2 令 f (x) =(x -1) (x -7x bi),则f (x) =2(x -1)2(x -7x bi)(2x _7).由题意：f ，(x 2) =0,即 2( x 2 -1) 2(X 22 -7X 2 bj(2x 2 _7) =0.又 F 2(x 2,2)在 C 1 上，2=x 22-7x 2 d,解得：x 2 =3,3 =14.，故 C 1 方程为 y =x 2 -7x • 14.2& = 2b k ,命题成立.(II)设点P(x, y)是C n上任意一点，则I A n PF ・.(X-X n)2• (X2• a n X • b n)2令g(x) =(x -X n)2(X2a n X b n)2,则g'(x) =2(x -X n) 2(X2a n X b n)(2x a n).由题意得 g '(X n 』=O ，即 2(X n 卑—X n )+2(X nf +a n X n 申 +b n )(2X n 出 +a n )=O 又；"2n =Xn] +anXn 卑 +g ,■ (X n 1 -X n ) 2n (2X nia." 0(n 一 1).即(1 2「1)X ni-X n 2匕=0(* )F 面用数学归纳法证明 x n =2n -1①当n 二1时，X-] =1,等式成立.即当n =k T 时，等式成立.由①②知，等式对 n N 成立..｛x n ｝是等差数列.评析：例5是常规的猜想证明题，考查学生掌握猜想证明题的基本技能、掌握数列前n 项和这个概念、用数学归纳法证明等差数列的方法；例6是个综合性比较强的题目，通过求二次函数的最值得到递推关系式，再直接猜想然后用归纳法证明，解法显得简洁明了，如果直接利用递推关系式找通项，反而不好作.四.反证法解决数学问题的思维过程，一般总是从正面入手，即从已知条件出发，理和运算，最后得到所要求的结论，但有时会遇到从正面不易入手的情况，考虑.如：例7.（2000年全国高考（理））设｛a .｝，b n ｝是公比不相等的两等比数列, 明数列｛C n ｝不是等比数列.证明：设｛a n ｝｛ b n ｝的公比分别为p , q , p = q , c^ a n b n ，为证｛q ｝不是等比数列只需证 c ；工 G L C 3 .事实上， c 2 =（a i p bq ）2 二a ： p 2 b 2q 2 2aib pq二佝 bOG b ?） = （a 「b ）（4 p 2 dq 2） =aip 2 b ^2q 2 a 1b 1（p 2 q 2）Tp^q, p 2+q 2 >2pq ，又a , b 不为零，二c f ^^Lc 3，故｛cj 不是等比数列.评析：本题主要考查等比数列的概念和基本性质、推理和运算能力，对逻辑思维能力有较高要求.要证｛c n ｝不是等比数列，只要由特殊项（如c f =6“）就可否定.一般地讲,否定性的命题常用反证法证明，其思路充分说明特殊化的思想方法与正难则反的思维策略的②假设当n =k 时，等式成立, 即 x k =2k-1,则当n 二k T 时，由（* ）知 k 山1k(1 2 风 - X • 2 % 兰1又 a k = -2 -4k -2 肓X k 1kX k _ 2 a ^- 厂占=2k 1 .经过一系列的推这时可从反面去五•看通项与前n项和法若数列通项a能表示成a n= a n・b ( a, b为常数)的形式，则数列是等差数列；右通项a n能表示成a n - cq (c, q均为不为0的常数，n・N ) 的形式，则数列^n? 是等比数列.若数列：a n f的前n项和Sn能表示成& = an2• bn(a,b为常数)的形式，则数列：a n f 等差数列；若S n能表示成S n =Aq n-A(A, q 均为不等于0的常数且1)的形式，则数列是公比不为1的等比数列•这些结论用在选择填空题上可大大节约时间.例8 (2001年全国题)若S n是数列牯」的前n项和，S n = n2,则｛a j是( ).A.等比数列，但不是等差数列 B .等差数列，但不是等比数列C.等差数列，而且也是等比数列D.既非等比数列又非等差数列解析：用到上述方法，一下子就知道答案为B,大大节约了时间，同时大大提高了命中率.六•熟记一些常规结论，有助于解题若数列｛a n｝是公比为q的等比数列，则(1)数列｛a n｝｛ a n｝( ■为不等于零的常数)仍是公比为q的等比数列；(2)若｛b n｝是公比为q ■的等比数列，则数列｛a n Lb n｝是公比为qq ■的等比数列；‘1〕 1(3)数列」丄〉是公比为1的等比数列；冃J q(4)｛a n｝是公比为q的等比数列；(5)在数列｛a n｝中，每隔k(k・N )项取出一项，按原来顺序排列，所得新数列仍为等比数列且公比为q k 1；(6) {a n a n 1}{ a n —an 1}{ a2n4}{ a2n}, g a2 a3, a4 a5 a6, a? p等都是等比数列；(7)若m , n , p(m n, p N )成等差数列时，a m, a. , a p成等比数列；(8)S n , S2n _S n , S3^ _ S2n均不为零时，则S , Sn〜, §3^ S2n成等比数列;(9)若｛log b a n｝是一个等差数列，则正项数列｛a n｝是一个等比数列.若数列｛a n｝是公差为d等差数列，则(1) ｛ka n b｝成等差数列，公差为kd (其中k = 0, k, b是实常数)；(2)｛S(n i)k -S kn｝, ( k • N , k为常数)，仍成等差数列，其公差为k2d ；(3) 若｛a n｝｛ b n｝都是等差数列，公差分别为d i, d2，则｛a n二b n｝是等差数列，公差为d^d2;(4)当数列｛a n｝是各项均为正数的等比数列时，数列｛lg a n｝是公差为lgq的等差数列；(5)m, n, p(m, n, p N )成等差数列时，a m，a n，a p成等差数列.例9.(96年全国高考题)等差数列｛a n｝的前n项和为30,前2n项和为100则它的前3n 项和为( ) A. 130 B. 170 C. 210 D. 260解：由上面的性质得：S n, S zn-S, S3n-S2n成等比数列，故2(S2n - S n) =S n (S3n - S2n),.2(100-30) =3O(S3n -100),S3n =210 .故选c.评析：此题若用其它方法，解决起来要花比较多的时间，对于选择题来说得不断尝试. 记住上面这些结论，在做选择填空题时可大大节约时间，并且能提高命中率.。

等差与等比数列的判定(第三讲)

当n 5时，Tn Sn 9n n2
当n 6时，
Tn a1 a2 a5 a6 an a1 a2 a5 a6 a7 an
Tn
9n n2 n2 9n 40
Sn 2S5
n2 9n 2 (20)
n2 9n 40
(n 5) (n 6)
③通项公式法：
a2 n1
an
an2
(an 0) an 为等比数列；
③通项公式法：
an kn b (k,b为常数) an 是等差数列
④前n 项和公式法：
an k q n (k, q为常数） an 为等比数列；
④前n 项和法：
Sn An 2 Bn ( A, B为常数) an 是等差数列 Sn k(1 qn ) （k, q为常数） an 为等比数列。
是以
S1
1 为首项，2 为公差的等差数列。
bn
Sn 2n 1
1 (2n 1)(2n 1)
1( 1 1 ) 2 2n 1 2n 1
Tn 3
(1 3
1) 5
(1 2n 1
1 2n
1)
1 (1 1 ) n 2 2n 1 2n 1
变式、数列 an 的前 n 项和 S n =2 an －1，数列 bn 满足：b1 3，bn1 an bn （n N ）
⑵： ①证明：当 n 2 时，
Sn2
an (Sn
1) 2
(Sn
Sn1 )(Sn
1) 2
所以 S n
S n1
1 2
(S n1
Sn )
即 1 1 2 S n S n1
②：由 ①得
1 1 (n 1) d 1 (n 1) 2 Sn S1 2n 1
所以

等差数列及等比数列的性质总结

【说明】）d -a （dn d ）1-n （a a 1m n +=+=，nS =d 2）1-n （n na 1´+【说明】d a -a a ac c c c 1-n n 1-n n ==7、偶奇n 偶奇n S S S 表示偶数项的和，则S 表示奇数项的和，S 项和，n 是前S += 当n 为偶数时，d 2n S -S 奇偶´=当n 为奇数时，n a S中n´=，中偶奇a S -S =，1-n 1n S S 偶奇+=【说明】当n 为偶数时，d 2n ）a -a （）a -a （）a -a （S -S 123-n 2-n 1-n n 奇偶´=+¼¼++= 当n 为奇数时，中11-n n 231偶奇a d 21-n a ）a -a （）a -a （a S -S =+=+¼¼++=，，1-n 1n 21-n ）a a （2121n ）a a （21S S 1-n 2n 1偶奇+=´++´+=n a S S -S S S 中n 偶奇偶奇==+ 8、设1-2n 1-n 2n n n n n n T Sb a项和，则n 的前}{b 、}{a 分别表示等差数列T 和S = 【说明】nn 中中1-2n 1-n 2b ab ）1-n 2（a ）1-n 2（T S == 【例】等差数列1515n n n n n n b a，求1-n 31n 5T S ，若T 和S 项和分别为n 的前}{b 、}{a +=9、1-d ，0a），则q p （p a ，q a qp qp==¹==+q--p a），则q p （p S ，q S qp qp=¹==+a），则q p （S S qp qp=¹=+= n ）2d-a （n ）2d （12´+´ 6、若、若数列数列}{a n是等差数列，则}{c n a 为等比数列，c>0+ïîí，q -1q a -a q -1）q -1（a n 11【说明】m 2k m k a a a a ++【说明】n 22n 1n n n 2a a a a a a S S -S +¼¼++++++【说明】q log a a log a log -a log c 1-n nc1-n c n c == 7、偶奇n 偶奇n S S S 表示偶数项的和，则S 表示奇数项的和，S 项和，n 是前S +=；若n 为偶数时，q a a 奇偶=；当n 为奇数时，q S a -S 偶1奇=；【说明】当n 为偶数时，q a a a a a a a a 1-n 41n 42奇偶=+¼¼+++¼¼++=；当n 为奇数时，q a a a a a a S a -S 1-n 42n 53偶1奇=+¼¼+++¼¼++=； 8、设偶奇n 偶奇n T T T 表示偶数项的积，则T 表示奇数项的积，T 项积，n 是前T ×=当n 为偶数时，n 中奇中偶奇2n 奇偶a T ，a T T 为奇数时，n ；当q T T ===；【说明】当n 为偶数时，2n 1-n 42n42奇偶q a a a a a a T T =×¼¼×××¼¼××=；当n 为奇数时，中1-n 42n421偶奇a a a a a a a a T T =×¼¼×××¼¼××=；n中1-n 2n 1n 21奇a a a a a a a a T =¼¼××=×¼¼××=。

第2讲数列篇(教师版)

第2讲数列[考点分析]数列问题是高考的必考内容，主要考查：1．等差等比数列的证明．2．数列求通项．3．数列求和．4．个别时候考查数列不等式问题．在新高考中很多题目开始以开放性题型命题．[特训典例]题型一等差等比数列的证明例1 （2019全国2卷理19）已知数列{a n }和{b n }满足a 1=1，b 1=0，，. （1）证明：{a n +b n }是等比数列，{a n –b n }是等差数列；（2）求{a n }和{b n }的通项公式.[特训跟踪]1、（2021全国卷）已知数列{}n a 满足11a =，11,,2,.n n na n a a n ++⎧=⎨+⎩为奇数为偶数（1）记2n n b a =，写出1b ，2b ，并求数列{}n b 的通项公式；1434n n n a a b +-=+1434n n n b b a +-=-（2）求{}n a 的前20项和.【答案】（1）122,5b b ==；（2）300. 【解析】【分析】（1）根据题设中的递推关系可得13n n b b +=+，从而可求{}n b 的通项. （2）根据题设中的递推关系可得{}n a 的前20项和为20S 可化为()2012910210S b b b b =++++-，利用（1）的结果可求20S .【详解】（1）由题设可得121243212,1215b a a b a a a ==+===+=++= 又22211k k a a ++=+，2122k k a a +=+，故2223k k a a +=+即13n n b b +=+即13n n b b +-= 所以{}n b 为等差数列，故()21331n b n n =+-⨯=-. （2）设{}n a 的前20项和为20S ，则2012320S a a a a =++++，因为123419201,1,,1a a a a a a =-=-=-，所以()20241820210S a a a a =++++-()1291091021021023103002b b b b ⨯⎛⎫=++++-=⨯⨯+⨯-= ⎪⎝⎭.2.在数列{a n }中，a 1＝2，a n 是1与a n a n ＋1的等差中项．(1)求证：数列⎩⎨⎧⎭⎬⎫1a n －1是等差数列，并求{}a n 的通项公式；(2)求数列⎩⎨⎧⎭⎬⎫1n 2a n 的前n 项和S n .解 (1)∵a n 是1与a n a n ＋1的等差中项， ∴2a n ＝1＋a n a n ＋1，∴a n ＋1＝2a n －1a n， ∴a n ＋1－1＝2a n －1a n －1＝a n －1a n ，∴1a n ＋1－1＝a n a n －1＝1＋1a n －1，∵1a 1－1＝1，∴数列⎩⎨⎧⎭⎬⎫1a n －1是首项为1，公差为1的等差数列，∴1a n －1＝1＋(n －1)＝n ，∴a n ＝n ＋1n .(2)由(1)得1n 2a n ＝1n (n ＋1)＝1n －1n ＋1，∴S n ＝⎝⎛⎭⎫1－12＋⎝⎛⎭⎫12－13＋⎝⎛⎭⎫13－14＋…＋⎝⎛⎭⎫1n －1n ＋1＝1－1n ＋1＝n n ＋1. 3.已知数列{a n }的前n 项和为S n ，且满足a 1＝12，a n ＝－2S n S n －1(n ≥2)．(1)求证：数列⎩⎨⎧⎭⎬⎫1S n 是等差数列；(2)求S n 和a n .[听前试做] (1)证明：当n ≥2时， a n ＝S n －S n －1＝－2S n S n －1，① ∵S 1＝a 1≠0，由递推关系知S n ≠0(n ∈N *)，由①式得1S n －1S n －1＝2(n ≥2)．∴⎩⎨⎧⎭⎬⎫1S n 是等差数列，其中首项为1S 1＝1a 1＝2，公差为2.(2)由(1)知1S n ＝2＋2(n －1)＝2n ，∴S n ＝12n .当n ≥2时，a n ＝S n －S n －1＝－12n (n －1)，当n ＝1时，a 1＝S 1＝12不适合上式，∴a n＝⎩⎨⎧12，n ＝1，－12n (n －1)，n ≥2.题型二数列求通项和求和例2 (2015·新课标全国卷Ⅰ)S n 为数列{a n }的前n 项和．已知a n >0，a 2n ＋2a n ＝4S n ＋3. (1)求{a n }的通项公式；(2)设b n ＝1a n a n ＋1，求数列{b n }的前n 项和．[听前试做] (1)由a 2n ＋2a n ＝4S n ＋3，①可知a 2n ＋1＋2a n ＋1＝4S n ＋1＋3.②②－①，得a 2n ＋1－a 2n ＋2(a n ＋1－a n )＝4a n ＋1，即2(a n ＋1＋a n )＝a 2n ＋1－a 2n ＝(a n ＋1＋a n )(a n ＋1－a n )．由a n >0，得a n ＋1－a n ＝2.又a 21＋2a 1＝4a 1＋3，解得a 1＝－1(舍去)或a 1＝3. 所以{a n }是首项为3，公差为2的等差数列，通项公式为a n ＝2n ＋1，n ∈N *.(2)由a n ＝2n ＋1可知b n ＝1a n a n ＋1＝1(2n ＋1)(2n ＋3)＝12⎝⎛⎭⎫12n ＋1－12n ＋3.设数列{b n }的前n 项和为T n ，则T n ＝b 1＋b 2＋…＋b n ＝12⎣⎡⎦⎤⎝⎛⎭⎫13－15＋⎝⎛⎭⎫15－17＋…＋⎝⎛⎭⎫12n ＋1－12n ＋3＝n3(2n ＋3). 例3 (2020衡水2调）已知数列{}n a 满足：211231333()3n n n a a a a n N -*+++++=∈. （1）求数列{}n a 的通项公式；（2）设111,3(1)(1)n n n n b a a ++=--数列{}nb 的前n 项和为n S ，试比较n S 与716的大小. 解：（1）数列{}n a 满足211231333()3n n n a a a a n N -*+++++=∈，所以2n ≥时，212133,3n n n a a a --+++=相减可得113,3n n a -=所以1.3n n a =n=1时,12.3a =综上可得2,1,31, 2.3n nn a n ⎧=⎪⎪=⎨⎪≥⎪⎩（5分）(2)因为111,3(1)(1)n n n n b a a ++=--所以12213.2183(1)(1)33b ==⨯-⨯-2n ≥时，1111111.11231313(1)(1)33n n n n n n b +++⎛⎫==- ⎪--⎝⎭-- 所233413111111182313131313131n n n S +⎡⎤⎛⎫⎛⎫⎛⎫=+-+-++- ⎪ ⎪ ⎪⎢⎥------⎝⎭⎝⎭⎝⎭⎣⎦131117.8283116n +⎛⎫=+-< ⎪-⎝⎭ 例4 (2019衡水2调）已知{}n a 是各项都为正数的数列，其前n 项和为n S ，且n S 为n a 与1na 的等差中项. （1）求数列{}n a 的通项公式；（2）设()1,nnnb a -=求{}n b 的前n 项和n T .解：（1）由题意知，12n n nS a a =+，即221,n n n S a a -=① 当n=1时，由①式可得11;S =当2n ≥时,有1,n n n a S S -=-带入①式，得2112()()1,n n n n n S S S S S -----=整理得221 1.n n S S --= 所以{}2nS 是首项为1，公差为1的等差数列，211.nSn n =+-=因为{}n a各项都为正数，所以n S =所以12),n n n a S S n -=-=≥ 又111,a S ==所以n a =（6分）（2）()(1)1,n n nn n b a -===-当n 为奇数时，(11)1n T n=-+-++--=当n 为偶数时，(11)1n T n =-+-+--+=所以{}n b 的前n 项和()1nn T =-（12分）例5 （潍坊市高三下学期第一次模拟）已知数列{}n a 是等差数列，其前n 项和为n S 。

等差数列、等比数列知识点梳理

等差数列、等比数列知识点梳理等差数列和等比数列知识点梳理第一节:等差数列的公式和相关性质1、等差数列的定义:对于一个数列，如果它的后一项减去前一项的差为一*n,2个定值，则称这个数列为等差数列，记:(d为公差)(，) nN,a,a,dnn,1 d2、等差数列通项公式: ，为首项，为公差 aaand,，,(1)1n1推导过程:叠加法推广公式: aanmd,，,()nma,anmd, 变形推广: n,m3、等差中项a，bbbA,(1)如果，，成等差数列，那么叫做与的等差中项(即:aaAA22A,a，b 或(2)等差中项:,,a数列是等差数列,2a,a，a(n,2),2a,a，a nnn-1n，1n，1nn，24、等差数列的前n项和公式:naa()，nn(1),1nS,,，nad 1n22d122,，,nadn(),，AnBn 122mnpq，,，a，a,a，a前N相和的推导:当时,则有，特别地，当mnp，,2mnpq aaa，,2aaaaaa，,，,，,,,,时，则有。

(注:，)当然扩充到3项、mnp12132nnn,,4项……都是可以的，但要保证等号两边项数相同，下标系数之和相等。

5、等差数列的判定方法,(1) 定义法:若或(常数) 是等差数列( n,N,,aa,a,da,a,d,nn,1n，1nn(2)等差中项:数列是等差数列 ,,an,2a,a，a(n,2),2a,a，an，1nn，2nn-1n，1(3)数列是等差数列(其中是常数)。

,,aa,kn，bk,b,nn2(4)数列是等差数列,(其中A、B是常数)。

,,aSAnBn,，,nn6、等差数列的证明方法定义法或者等差中项发是等差数列( ,,a,n7、等差数列相关技巧:d(1)等差数列的通项公式及前和公式中，涉及到5个元素:、、、ann1da及S，其中a、称作为基本元素。

只要已知这5个元素中的任意3个，便nn1可求出其余2个，即知3求2。

等差与等比数列性质中的15个充要条件

性质５｛ｎ）为等差数列的充要条件是＝
ｎ（ａｌ＋ａ）
—
—
一
’
性质６｛ｎ｝是公比为口的等比数列的充要条件是
ｔ：｛＋）＝｛筹）
也是等比数列．性质ｌ５公差ｄ≠０的等差数列｛ｏ）中包含一个无穷
等比子数列的充要条件是－５－∈Ｑ．证明设ａ＝ｂ＋ｄｎ（ｄ ≠ ０），则６１＝ｂ＋ｄ，故
等∈Ｑ甘＝＋ ∈Ｑ甘ｂ∈Ｑ．
必要性：设等差数列ｆ６＋｝中包含一个等比子数列：
ｂ＋ｄｎｌ，ｂ＋ｄｎ２，ｂ＋ｄｎａ，… （７２１＜ｎ２＜？２３＜… ）
４－１ａｌ＋ｑＳ．．
由前三项成等比数列可以推得：＝
∈Ｑ
２４
中学数学研究
２０１８年第４期（上）
例２设ｙ（ｘ）＝Ｘ。＋ｌｏｇ２＋而），则对任意实数０，ｂ，０＋ｂ≥０是，（ａ）＋ｆ（ｂ）≥０的（）
本文给出等差与等比数列性质中的ｌ５个充要条件，供大家
性质８ｆ口｝为等差数列的充要条件是数列
参考．
｛１１＋置２＋曼３暑＋ …＋ｎ｝Ｊ也一为 …等…差数～列．
本文中，一律表示数列｛０）的前ｎ项和．
性质９（２０１０安徽卷理科第２Ｏ题）＜０｝为非零等差数
ａ＝２Ａｎ＋Ｂ —Ａ（佗 ∈Ｎ’），贝０ａｎ＋ｌ～ａ＝２Ａ，从而｛ｎ）是等差数列．
必要性：若｛０｝是等差数列，则ａｌ＝２＋ —Ａ：Ａ＋Ｂ＝Ａ＋Ｂ＋，故＝０．
注若＝Ａｎ＋Ｂｎ＋Ｃ（Ｃ≠０），则数列｛ａ）从第二项起组成等差数列．