理论力学08第六章 点的合成运动(1)
合集下载
理论力学：第6章 点的合成运动
2 2 r
，
aeτ 0 ，解出 aa＝142r。所以小环 M 的加速度为 142r。
6-23 已知 O1 A O2 B l 1.5 m，且 O1A 平行于 O2 B ，题 6－23 图所示位置，
滑道 OC 的角速度=2 rad/s，角加速度 =1 rad/s2，OM = b =1 m。试求图示位置
第 6 章 点的合成运动
6-7 题 6－7 图所示曲柄滑道机构中，杆 BC 为水平，而杆 DE 保持铅直。 曲柄长 OA=10 cm，以匀角速度 = 20 rad/s 绕 O 轴转动，通过滑块 A 使杆 BC 作 往复运动。求当曲柄与水平线的交角为 = 0、30、90时，杆 BC 的速度。
·8·
由图得 vr＝ve＝b＝2 m/s， va O1 l 。
得到 O1
l
b cos 45
21
1.5
2 2
1.89 rad/s 。
（2）求加速度。动点，动坐标系的选择不变，则动点 M 的加速度图如图（c）
所示。由加速度合成定理
aa ae ar aC
即 aan aaτ aeτ aen ar aC
时 O1A 的角速度和角加速度。
M
45 45
vr
ve
va
x
ae
ane
ana
45
ar
aC
aa
（a）
（b）
（c）
题 6-23 图
解：（1）求速度。
选取 M 为动点，动坐标系固连于滑道 OC 上，则动点 M 的速度图如图（b）
所示。由速度合成定理
va＝ve＋vr
沿 OC 轴的垂直方向投影得
理论力学习题册答案
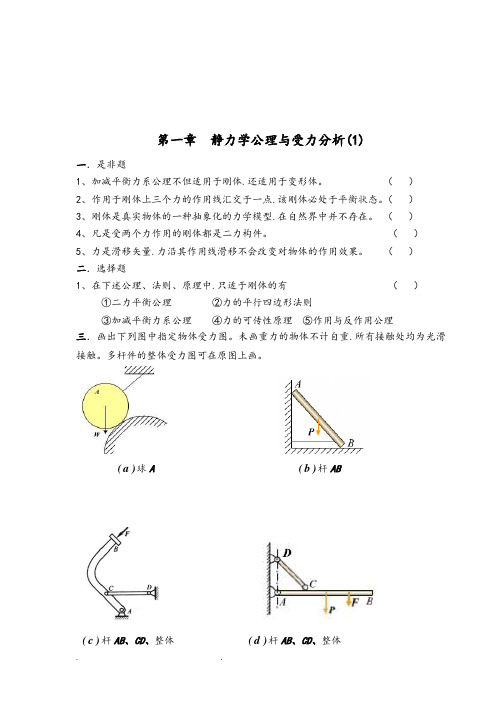
第一章静力学公理与受力分析(1)一．是非题1、加减平衡力系公理不但适用于刚体.还适用于变形体。
（）2、作用于刚体上三个力的作用线汇交于一点.该刚体必处于平衡状态。
（）3、刚体是真实物体的一种抽象化的力学模型.在自然界中并不存在。
（）4、凡是受两个力作用的刚体都是二力构件。
（）5、力是滑移矢量.力沿其作用线滑移不会改变对物体的作用效果。
（）二．选择题1、在下述公理、法则、原理中.只适于刚体的有（）①二力平衡公理②力的平行四边形法则③加减平衡力系公理④力的可传性原理⑤作用与反作用公理三．画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
b(杆ABa(球A ))d(杆AB、CD、整体)c(杆AB、CD、整体))e(杆AC、CB、整体)f(杆AC、CD、整体四．画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
)a(球A、球B、整体)b(杆BC、杆AC、整体第一章 静力学公理与受力分析（2）一．画出下列图中指定物体受力图。
未画重力的物体不计自重.所有接触处均为光滑接触。
多杆件的整体受力图可在原图上画。
WADB CE Original FigureAD B CEWWFAxF AyF BFBD of the entire frame)a (杆AB 、BC 、整体)b (杆AB 、BC 、轮E 、整体)c (杆AB 、CD 、整体 )d (杆BC 带铰、杆AC 、整体)e(杆CE、AH、整体)f(杆AD、杆DB、整体)g(杆AB带轮及较A、整体)h(杆AB、AC、AD、整体第二章平面汇交和力偶系一．是非题1、因为构成力偶的两个力满足F= - F’.所以力偶的合力等于零。
（）2、用解析法求平面汇交力系的合力时.若选用不同的直角坐标系.则所求得的合力不同。
（）3、力偶矩就是力偶。
（）二．电动机重P=500N.放在水平梁AC的中央.如图所示。
理论力学 第6章 点的合成运动
求：杆OA的角速度。 分析：相接触的两个物体的接触点位置都随时间而变化，
因此两物体的接触点都不宜选为动点，否则相对运动的分析 就会很困难。这种情况下，需选择满足上述两条原则的非接 触点为动点。
18
解: 取凸轮上C点为动点, 动系固结于OA杆上, 静系固结于基座。
绝对运动: 直线运动, 绝对速度: va v, 方向
们的方向不变，是常矢量，所以
di ' dt
0,
dy' dt
0,
dz' dt
0
）
又
dvO' dt
aO' ae ,
ar
d2 dt
x'i'
2
d2 dt
y'
2
j' d 2z'k' dt 2
aa ae ar —牵连运动为平动时点的加速度合成定理 即当牵连运动为平动时，动点的绝对加速度等于牵连加速度 与相对加速度的矢量和。
2r 2r 3 6r
（）
19
§6-3 牵连运动为平动时点的加速度合成定理
设有一动点M按一定规律沿着固连于动系O'x'y'z' 的曲线AB
运动, 而曲线AB同时又随同动系O'x'y'z' 相对静系Oxyz平动。
由于牵连运动为平动，故
ve vO' , ae aO'
由速度合成定理 va ve vr
相对运动中,动点的速度和加速度称为相对速度 vr 与相对加速度ar
牵连运动中,牵连点的速度和加速度称为牵连速度 ve与牵连加速度 ae
牵连点：在任意瞬时，动坐标系中与动点相重合的点，也就是 设想将该动点固结在动坐标系上，而随着动坐标系一起运动时 该点叫牵连点。
因此两物体的接触点都不宜选为动点，否则相对运动的分析 就会很困难。这种情况下，需选择满足上述两条原则的非接 触点为动点。
18
解: 取凸轮上C点为动点, 动系固结于OA杆上, 静系固结于基座。
绝对运动: 直线运动, 绝对速度: va v, 方向
们的方向不变，是常矢量，所以
di ' dt
0,
dy' dt
0,
dz' dt
0
）
又
dvO' dt
aO' ae ,
ar
d2 dt
x'i'
2
d2 dt
y'
2
j' d 2z'k' dt 2
aa ae ar —牵连运动为平动时点的加速度合成定理 即当牵连运动为平动时，动点的绝对加速度等于牵连加速度 与相对加速度的矢量和。
2r 2r 3 6r
（）
19
§6-3 牵连运动为平动时点的加速度合成定理
设有一动点M按一定规律沿着固连于动系O'x'y'z' 的曲线AB
运动, 而曲线AB同时又随同动系O'x'y'z' 相对静系Oxyz平动。
由于牵连运动为平动，故
ve vO' , ae aO'
由速度合成定理 va ve vr
相对运动中,动点的速度和加速度称为相对速度 vr 与相对加速度ar
牵连运动中,牵连点的速度和加速度称为牵连速度 ve与牵连加速度 ae
牵连点：在任意瞬时，动坐标系中与动点相重合的点，也就是 设想将该动点固结在动坐标系上，而随着动坐标系一起运动时 该点叫牵连点。
理论力学基础点的合成运动
1
平动和转动的区别
2
它们之间的关系对于理解合成运动具有
重要意义；
3
运动学基本公式
4
位置、速度、加速度等运动学基本公式 是研究合成运动的基础知识。
牛顿第二定律
合力产生加速度，加速度与力成正比。 一切合成运动都符合牛顿第二定律；
匀速圆周运动的分解
它是所有曲线合成运动的基础，掌握分 解方法可以为其他曲线合成运动的研究 提供启示；
结论和总结
合成运动是力学基础点之一，但不同于其他运动，它是由多个运动步骤组 成的复杂过程，因此有其独特的研究方法和工具。对合成运动理论及其实 际应用的深度理解和掌握，具有重要意义。 ——陈晓明，中国科技大学教授
机器人动作设计
机器人动作设计中需要进行多种复杂的合成运动分析与控制。合成运动理论可以指导机器人 的运动规划、轨迹跟踪和动作执行。
运动传感设计
合成运动分解是一种重要的运动测量技术。在车辆安全、物流配送、航空监控等领域，合成 运动传感器为复杂运动测量提供了有效手段。
合成运动的实验方法和技术
1
高速相机
观测高速运动的一种重要方法。运用指定的曝光时间和快门速度，拍摄合成运动 过程中的关键帧。
2
追踪仪器
用于测量运动物体的位置、速度和加速度等多种参数，对于合成运动的分析和控 制有着重要作用。
3
动力学仿真软件
自动地计算合成运动的轨迹、速度、加速度等参数。可以模拟物体的运动过程， 为结构设计和工艺分析提供有力支持。
合成运动的分类和特点
线性合成运动
由两个或两个以上直线运动叠 加而成；
圆周合成运动
由两个或两个以上曲线运动叠 加而成；
复合合成运动
由不同类型直线运动或曲线运 动叠加而成。
点的合成运动
种位移之间的关系为
MM'' =MM' + M' M''
目录
刚体的运动\点的合成运动
将上式两边分别除以Δt ,并取Δt→0 时的极限，得
y Ox
lim lim lim MM
MM
M M
t0 t
t0 t
t0 t
式在中绝：对lit运m0动M中Mt 的 表速示度动，点称在为瞬动时点t的、
y
vr
va
系相固结的物体的运动，因而是指一个刚体的运动，它可以是平移、
转动或其他复杂的运动。
目录
刚体的运动\点的合成运动
1.2 点的速度合成定理
以图示桥式起重机为例，研究
y Ox
绝对运动、相对运动和牵连运动三
者速度之间的关系。设在瞬时t，动 点在位置M。假如动点不作相对运
y
M''
动，则经Δt时间后，动点随动系运
理论力学
刚体的运动\点的合成运动
点的合成运动
在研究刚体的平面运动之前，先介绍点的合成运动的有关概念 及点的速度合成定理，这既是研究点的运动的又一种方法，又是研 究刚体复杂运动的基础。
1.1 点的合成运动的概念
在不同的物体上观察同一物体的运动时，会得出不同的结果。 例如，当火车行驶时，在车厢上观察车轮上一点的运动是圆周运动， 在地面上观察则是复杂的曲线运动，若在车轮上观察则是静止的。 因此，在研究一个物体的运动时，必须指明是相对于哪个物体而言， 即必须选定参考体或参考系。在工程上如果没有特别的说明，都是 以地面作为参考系。
目录
刚体的运动\点的合成运动 【例6.5】 凸轮机构（如图）中，导
杆AB可在铅垂管D内上下滑动，其下端 与凸轮保持接触。凸轮以匀角速度ω绕O 轴逆时针转动，在图示瞬时OA=a ，凸轮
理论力学第六章 点的合成运动 [同济大学]
![理论力学第六章 点的合成运动 [同济大学]](https://img.taocdn.com/s3/m/63fd0a4dbe1e650e53ea9909.png)
解： 从例6-2已知得： 1 =
vr r 3 , 2
ω 4
O
解： 从上例已知得： 1 =
r
M
ω 4
va
A
aaτ =0 ，
3 , 4
aan=2r aen=
ωr 8
x’
2
ac 21vr 2 r
va
30°
3 1 1/ s2 8
2
动点取A，
va v A
ar
dvr d 2 x ' ' d 2 y ' ' d 2 z ' ' 2 r 2 j 2 k dt dt dt dt
dx ' di ' dy ' dj' dz ' dk ' dt dt dt dt dt dt
ar ω vr
a a ae a r ac； ac= 2vr
ve
a n a ae a rn a rτ
矢量
1.瞬时状态； 2.可解两个未知量 (大小，方向)。
例6-5 曲柄滑道机构，OA=01A=r=10cm, =30°,=4, 求: 转到30°时直杆的加速度a。 va vr 动点取A； 绝对:圆周； ve 解：相对:圆周；牵连:直线。 [速度] =
a a ae a r ac； aa a an ae aen ar arn ac；
例6-8 曲柄绕O转动，並通过滑块M带动滑槽绕O′摆动， ’ y 求摆动到30°时的角加速度1。
例6-9 将例6-8滑槽改变为图示牛头刨床机构，MA=2r, 求:刨床刨刀的速度，加速度。
vr
dv e dω dr r ω dt dt dt α r ω v e ω v r ae ω v r
理论力学点的合成运动
例 8-4 曲柄OA以匀角速度 w绕O轴转动，其上
套有小环 M，而小环 M又在固定的大圆环上运动，大 圆环的半径为 R。
试求当曲柄与水平线成的角 j ωt 时，小环 M
的绝对速度和相对曲柄 OA 的相对速度。
A
M w
R
O
j
C
解：（1）选择动点及 动系： 小环M为动点，动系固连在 OA上。
（2）分析三种运动：绝 对运动为圆周运动，相对运 动为沿OA的直线运动，牵连 运动为定轴转动。
y
OA杆转动的角速度为
O
wOA
ve OC
ve 2r
3u 6r
y
wOA B
j va vr
A
r ve C
x
u x
8.3 牵连运动是平动时点的加速度合成定理
在图8-9中，设 Oxyz为定系，Oxyz为动系且作平
动，M为动点。动点M在动系中的坐标为 x、y 、z， 动系单位矢量为 i、 j、k。动系平动，i、j、k 的
Oxyz 作某种运动，在瞬时t，动系连同相对轨迹AB在
定系中的I位置，动点则在曲线 AB
上的 M 点。经过时间间 隔 t ，动系运动到定系 中的II位置，动点运动到
点 M。 如果在动系上观
察点M 的运动，则它沿 曲线 AB 运动到点 M2。
z B
M2
vr
z
M O
A
O I
x
va
M B
ve M1
z
O x A
例 8-1 汽车以速度 v1 沿直线的道路行驶，雨滴 以速度 v2 铅直下落，试求雨滴相对于汽车的速度。
v1
解： 因为雨滴相对运动的汽车有运动，所以本题 为点的合成运动问题，可应用点的速度合成定理求解。
理论力学(第6章)
t 已知：O1A=O2B=18cm，AB=O1O2=2R，R=18cm ， 18 t2 求： va , aa s BM
π
加速度合成定理的矢量形式向 直角坐标轴x、y上投影，得：
π aax a a cos 6.67cm / s 2 6 π n n aay ar ae sin 20cm / s 2 6
绝对：大圆周（半径R）
相对：沿OA的直线运动 牵连：定轴转动（绕o轴）
2.速度分析 v a ve 大小 ? 方向 √
ve va 2Rω cos
vr
OM√?√ Nhomakorabeavr ve tan 2 R ω sin ω t
6.3 牵连运动为平移时点的加速度合成定理
点的加速度合成定理：
解：（1） 动点：取顶杆AB的A点 动系：固连在凸轮上。 绝对运动：沿AB竖直方向 的平移。 相对运动：A点沿凸轮边 缘的圆周运动。 牵连运动：动系凸轮沿水 平面向右平移。
已知:
v0
30
2.速度分析
va ve vr
由几何关系可以得到：
3 vB vA v tan 30 v 3
例6-5 平面机构中直杆O1A、O2B平行且等长，分别 绕O1、O2轴转动，直杆的A、B连接半圆形平板，动 点M沿半圆形平板ABD边缘运动，起点为点B。已知 π t， O1A=O2B=18cm，AB=O1O2=2R，R=18cm ， 18 t2 。 s BM
求：当 t 3s 时， 动点M的绝对速度 和绝对加速度。
方向竖直向上
例6-2 刨床的急回机构如图所示。曲柄OA的一端 A与滑块用铰链连接。当曲柄OA以匀角速度ω绕固 定轴O转动时，滑块在摇杆O1B上滑动，并带动杆 O1B绕定轴O1摆动。设曲柄长为OA=r，两轴间距 离OO1=l。 B 求： O ① 曲柄在水平位 A 置时摇杆的角 速度 1 。 ② 滑块A对于摇 杆 的相对角 O1 速度
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
Theoretical Mechanics
ve
ae
第六章 点的合成运动
刘习军
动点的选择原则： 一般选择主动件与从动件的连接点，它是 对两个坐标系都有运动的点。 动坐标系的选择原则： 动点对动坐标系有相对运动，且相对运 动的轨迹是已知的，或者能直接看出的。
Theoretical Mechanics
第六章 点的合成运动
§ 6-2 点的速度合成定理
刘习军
板K上开槽，动点M 沿槽相对于板运动， 同时板也运动。设t瞬 时点M与板上点M重 合，经过△t瞬时后， K板运动到K‘处，M ︵ 沿 MM1 运动M1'到， ︵ MM 板M上点沿 运动 到M1。
1
t
t t
Theoretical Mechanics
第六章 点的合成运动
刘习军
3．牵连运动、牵连速度和牵连加速度 动坐标系相对于静坐标系的运动称为牵连运动。 （1）牵连点的概念 定义：在任一瞬时，动坐标系上与动点相重合的那一点即为 动点的牵连点。
（2）牵连速度 定义：某瞬时牵连点 的速度称为动点的牵连 速度。用ve表示。 （3）牵连加速度 定义：某瞬时牵连点 的加速度称为动点的牵 连加速度，ae用表示。
Theoretical Mechanics
第六章 点的合成运动
其中
si n OA O1 A r l r l
2 2
刘习军
, ,
va cos 0 vr va sin ve 0
rl l2 r2
1
OO1 cos O1 A
l2 r2
a r
得 因为
z
z
O
y
Oanics
第六章 点的合成运动
动点
刘习军
动点是指相对于静坐标系和动坐标系均有运 动的点。本章就是研究动点相对于静坐标系和动坐 标系的运动。如图中任选车轮上的一点作为动点。
z
z
O
y
O x
y
x
Theoretical Mechanics
第六章 点的合成运动
Theoretical Mechanics
第六章 点的合成运动
刘习军
1．动点的绝对运动· 绝对速度和绝对加速度 （1）绝对运动：动点相对于静坐标系的运动。 （2）绝对速度：动点绝对运动的速度，用va表示。 （3）绝对加速度：动点绝对运动的加速度，用aa表示。
va
aa
Theoretical Mechanics
刘习军
︵ 则：MM1 为动点M的绝
对轨迹，MM1 为绝对位 移。 ︵ M M 为动点 M 的相对 轨迹， M M 为相对位移 。 ︵ MM 1 为 牵 连 点 的 轨 迹 ， MM1 为牵连位移。
1 1
1 1
t
t t
Theoretical Mechanics
第六章 点的合成运动
于是有：
第六章 点的合成运动
刘习军
第六章 点的合成运动
§6–1 点的合成运动的概念 §6–2 点的速度合成定理 §6–3 点的加速度合成定理
Theoretical Mechanics
第六章 点的合成运动
刘习军
研究方法 首先将复杂运动分解为两个简单的运动，然后分 别进行研究，并得到各自的运动，再求合成运动。 解题思路：先分解、再合成。
1
Theoretical Mechanics
第六章 点的合成运动
解：取曲柄OA端点A为动 点，动坐标系与摇杆固连 ，由点的速度合成定理。
刘习军
va ve vr
? √ ? √
va
vr
大小 √ 方向 √
ve
画速度矢量图，如图 所示。将矢量方程分别向 x' 、y'轴上投影，得
1
va cos 0 vr va sin ve 0
第六章 点的合成运动
刘习军
2．动点的相对运动· 相对速度和相对加速度 （1）相对运动：动点相对于动坐标系的运动。 （2）相对速度：动点相对运动的速度，用vr表示。 （3）相对加速度：动点相对运动的加速度，用ar表示。
vr
a r arn
Theoretical Mechanics
第六章 点的合成运动
Theoretical Mechanics
va v e v r
第六章 点的合成运动
刘习军
例:刨床的急回机构如图所 示。曲柄OA的一端与滑块 A用铰链连接。当曲柄OA 以匀角速度绕固定轴O转 动时，滑块在摇杆O1B上 滑动，并带动摇杆O1B绕 固定轴O1摆动。OA= r， OO1=l。求当曲柄在水平位 置时摇杆的角速度 1。
MM1 M1M1 MM1
刘习军
则 当 t 0 时，取极限
MM1 MM1 M1 M1 lim lim lim t 0 t t 0 t t 0 t
t t
MM1 M1 M1 MM1 t t t
t 即 定理：某瞬时动点的绝对速度等于该瞬时动点的相 对速度和牵连速度之矢量和。
三种运动 绝对运动：动点相对于静坐标系的运动。 相对运动：动点相对于动坐标系的运动。
刘习军
牵连运动：动坐标系相对于静坐标系的运动。
Theoretical Mechanics
第六章 点的合成运动
几 点 说 明
刘习军
动点的绝对运动和相对运动都是点的运动，它可 能是直线运动，也可能是曲线运动。 牵连运动则是动坐标系的运动，属于刚体的运动， 有平移、定轴转动和其它形式的运动。 动坐标系作何种运动取决于与之固连的刚体的运 动形式。
Theoretical Mechanics
第六章 点的合成运动
刘习军
§6-1相对运动· 牵连运动· 绝对运动 研究点的合成运动问题，总要涉及到两个参考 坐标系。建立在运动的物体上的坐标系称为动坐标 系，以Oxyz表示。一般固结在地球表面的坐标系 称为静坐标系，或定坐标系，以Oxyz表示，如图所 示。
e
r 2 l r
2 2
,
r
e O1 A 1 l 2 r 2 1
所以，摇杆在此瞬时的角速度为
Theoretical Mechanics
r 1 2 2 l r
2
第六章 点的合成运动
刘习军
例: 如图所示，半径为R、偏心距为e的凸轮，以匀 角速度 绕轴转动，杆AB能在滑槽中上下平移，杆的 端点 A 始终与凸轮接触，且 OAB 成一直线。求在图示 位置时，杆AB的速度。
ve
ae
第六章 点的合成运动
刘习军
动点的选择原则： 一般选择主动件与从动件的连接点，它是 对两个坐标系都有运动的点。 动坐标系的选择原则： 动点对动坐标系有相对运动，且相对运 动的轨迹是已知的，或者能直接看出的。
Theoretical Mechanics
第六章 点的合成运动
§ 6-2 点的速度合成定理
刘习军
板K上开槽，动点M 沿槽相对于板运动， 同时板也运动。设t瞬 时点M与板上点M重 合，经过△t瞬时后， K板运动到K‘处，M ︵ 沿 MM1 运动M1'到， ︵ MM 板M上点沿 运动 到M1。
1
t
t t
Theoretical Mechanics
第六章 点的合成运动
刘习军
3．牵连运动、牵连速度和牵连加速度 动坐标系相对于静坐标系的运动称为牵连运动。 （1）牵连点的概念 定义：在任一瞬时，动坐标系上与动点相重合的那一点即为 动点的牵连点。
（2）牵连速度 定义：某瞬时牵连点 的速度称为动点的牵连 速度。用ve表示。 （3）牵连加速度 定义：某瞬时牵连点 的加速度称为动点的牵 连加速度，ae用表示。
Theoretical Mechanics
第六章 点的合成运动
其中
si n OA O1 A r l r l
2 2
刘习军
, ,
va cos 0 vr va sin ve 0
rl l2 r2
1
OO1 cos O1 A
l2 r2
a r
得 因为
z
z
O
y
Oanics
第六章 点的合成运动
动点
刘习军
动点是指相对于静坐标系和动坐标系均有运 动的点。本章就是研究动点相对于静坐标系和动坐 标系的运动。如图中任选车轮上的一点作为动点。
z
z
O
y
O x
y
x
Theoretical Mechanics
第六章 点的合成运动
Theoretical Mechanics
第六章 点的合成运动
刘习军
1．动点的绝对运动· 绝对速度和绝对加速度 （1）绝对运动：动点相对于静坐标系的运动。 （2）绝对速度：动点绝对运动的速度，用va表示。 （3）绝对加速度：动点绝对运动的加速度，用aa表示。
va
aa
Theoretical Mechanics
刘习军
︵ 则：MM1 为动点M的绝
对轨迹，MM1 为绝对位 移。 ︵ M M 为动点 M 的相对 轨迹， M M 为相对位移 。 ︵ MM 1 为 牵 连 点 的 轨 迹 ， MM1 为牵连位移。
1 1
1 1
t
t t
Theoretical Mechanics
第六章 点的合成运动
于是有：
第六章 点的合成运动
刘习军
第六章 点的合成运动
§6–1 点的合成运动的概念 §6–2 点的速度合成定理 §6–3 点的加速度合成定理
Theoretical Mechanics
第六章 点的合成运动
刘习军
研究方法 首先将复杂运动分解为两个简单的运动，然后分 别进行研究，并得到各自的运动，再求合成运动。 解题思路：先分解、再合成。
1
Theoretical Mechanics
第六章 点的合成运动
解：取曲柄OA端点A为动 点，动坐标系与摇杆固连 ，由点的速度合成定理。
刘习军
va ve vr
? √ ? √
va
vr
大小 √ 方向 √
ve
画速度矢量图，如图 所示。将矢量方程分别向 x' 、y'轴上投影，得
1
va cos 0 vr va sin ve 0
第六章 点的合成运动
刘习军
2．动点的相对运动· 相对速度和相对加速度 （1）相对运动：动点相对于动坐标系的运动。 （2）相对速度：动点相对运动的速度，用vr表示。 （3）相对加速度：动点相对运动的加速度，用ar表示。
vr
a r arn
Theoretical Mechanics
第六章 点的合成运动
Theoretical Mechanics
va v e v r
第六章 点的合成运动
刘习军
例:刨床的急回机构如图所 示。曲柄OA的一端与滑块 A用铰链连接。当曲柄OA 以匀角速度绕固定轴O转 动时，滑块在摇杆O1B上 滑动，并带动摇杆O1B绕 固定轴O1摆动。OA= r， OO1=l。求当曲柄在水平位 置时摇杆的角速度 1。
MM1 M1M1 MM1
刘习军
则 当 t 0 时，取极限
MM1 MM1 M1 M1 lim lim lim t 0 t t 0 t t 0 t
t t
MM1 M1 M1 MM1 t t t
t 即 定理：某瞬时动点的绝对速度等于该瞬时动点的相 对速度和牵连速度之矢量和。
三种运动 绝对运动：动点相对于静坐标系的运动。 相对运动：动点相对于动坐标系的运动。
刘习军
牵连运动：动坐标系相对于静坐标系的运动。
Theoretical Mechanics
第六章 点的合成运动
几 点 说 明
刘习军
动点的绝对运动和相对运动都是点的运动，它可 能是直线运动，也可能是曲线运动。 牵连运动则是动坐标系的运动，属于刚体的运动， 有平移、定轴转动和其它形式的运动。 动坐标系作何种运动取决于与之固连的刚体的运 动形式。
Theoretical Mechanics
第六章 点的合成运动
刘习军
§6-1相对运动· 牵连运动· 绝对运动 研究点的合成运动问题，总要涉及到两个参考 坐标系。建立在运动的物体上的坐标系称为动坐标 系，以Oxyz表示。一般固结在地球表面的坐标系 称为静坐标系，或定坐标系，以Oxyz表示，如图所 示。
e
r 2 l r
2 2
,
r
e O1 A 1 l 2 r 2 1
所以，摇杆在此瞬时的角速度为
Theoretical Mechanics
r 1 2 2 l r
2
第六章 点的合成运动
刘习军
例: 如图所示，半径为R、偏心距为e的凸轮，以匀 角速度 绕轴转动，杆AB能在滑槽中上下平移，杆的 端点 A 始终与凸轮接触，且 OAB 成一直线。求在图示 位置时，杆AB的速度。