自相关性检验
实验四--自相关性的检验及修正

实验四 -- 自相关性的检验及修正实验四自相关性的检验及修正一、实验目的掌握自相关性的检验与处理方法。
二、实验学时: 2三、实验内容及操作步骤建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
1.回归模型的筛选2.自相关的检验3.自相关的调整四、实验要求利用表 5-1 资料,试建立我国城乡居民储蓄存款模型,并检验模型的自相关性。
我国城乡居民储蓄存款与GDP统计资料( 1978 年= 100)存款GDP 年份存款余额Y GDP指数X年份余额指数Y X19919241.6 199211759.4 199315203.5 199421518.8 199529662.3 199638520.8 199746279.8 199853407.5 199959621.8 200064332.4308.2200286910.6888.5 351.52003103617.7981.6 399.62004119555.41084.5 452.020051410511201.7 494.22006161587.31361.2 544.520071725341560.5 596.920082178851717.8 640.620092607721861.1 691.520103033022050.0 750.62011343635.92228.9 811.12410.3200173762.43995512012【实验步骤】(一)回归模型的筛选⒈相关图分析SCAT X Y相关图表明, GDP指数与居民储蓄存款二者的曲线相关关系较为明显。
现将函数初步设定为线性、双对数、对数、指数、二次多项式等不同形式,进而加以比较分析。
⒉估计模型,利用LS命令分别建立以下模型⑴线性模型: LS Y C Xy?62251.79175.4516 xt (-9.5629) (33.3308)R2= 0.9823 F=1110.940S.E=15601.32⑵双对数模型: GENR LNY=LOG(Y)GENR LNX=LOG(X)LS LNY C LNX?0.59996 1.7452 ln xln yt(-1.6069) (31.8572)R2= 0.9807 F= 1014.878 S.E=0.1567⑶对数模型: LS YCLNX?y1035947170915.4 ln xt(-10.2355)(11.5094)R2=0.8688 F =132.4672 S.E =42490.60⑷指数模型: LS LNY C Xln y? 9.5657 0.001581xt (55.0657) (11.2557)2R = 0.8637 F=126.6908 S.E=0.4163LS Y CXX2?16271.5477.8476x0.0378x2yt(-2.4325)(6.1317) (7.8569)R2= 0.9958F=2274.040 S.E= 7765.275⒊选择模型比较以上模型,可见各模型回归系数的符号及数值较为合理。
自相关性检验
国民生产 总值
596.7 637.7 691.1 756.0
…
物价 指数 0.7167 0.7277 0.7436 0.7676
…
年份 序号
11 12 13 14
…
投资额
229.8 228.7 206.1 257.9
…
国民生 产总值
1326.4 1434.2 1549.2 1718.0
…
物价 指数 1.0575 1.1508 1.2579 1.3234
DW t 2 n
et2
t2
样本容量n=20,回归
变量数目k=3,=0.05
DWold < dL
原模型有 正自相关
查表
临界值dL=1.10, dU=1.54
ˆ 1 DW / 2 0.5623
作变换
yt* yt 0.5623 yt1
xi*t xit 0.5623xi,t1, i 1,2
0 dL dU 2 4-dU 4-dL 4 DW 正 不无 不负 自 能自 能自 相 确相 确相 关 定关 定关
模型优点 R2=0.9908,拟合度高
s=12.7164
模型缺点 没有考虑时间序列数据的滞后性影响 可能忽视了随机误差存在自相关;如果
存在自相关性,用此模型会有不良后果
自相关性的定性诊断
模型残差 et yt yˆt
et为随机误差t 的估计值
残差诊断法
et 20
10
0
在MATLAB工作区中输出 作残差 et~et-1 散点图
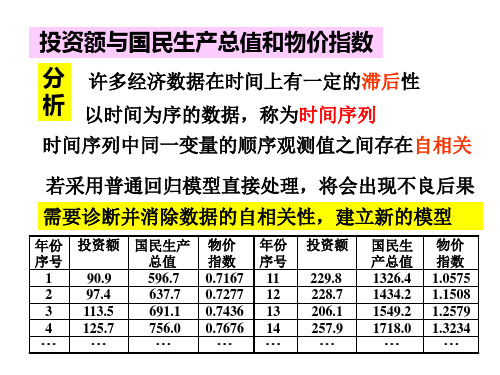
投资额与国民生产总值和物价指数
分 许多经济数据在时间上有一定的滞后性 析 以时间为序的数据,称为时间序列
时间序列中同一变量的顺序观测值之间存在自相关
《应用回归分析》自相关性的诊断及处理实验报告

《应用回归分析》自相关性的诊断及处理实验报告
二、实验步骤:(只需关键步骤)
1、分析→回归→线性→保存→残差
2、转换→计算变量;分析→回归→线性。
3、转换→计算变量;分析→回归→线性
三、实验结果分析:(提供关键结果截图和分析)
1.用普通最小二乘法建立y与x1和x2的回归方程,用残差图和DW检验诊断序列的自相关性;
由图可知y与x1和x2的回归方程为:
Y=574062+191.098x1+2.045x2
从输出结果中可以看到DW=0.283,查DW表,n=23,k=2,显著性水平由DW<1.26,也说明残差序列存在正的自相关。
自相关系数,也说明误差存在高度的自相关。
分析:从输出结果中可以看到DW=0.745,查DW表,n=52,k=3,显著性水平 =0.05,dL=1.47,dU=1.64.由DW<1.47,也说明残差序列存在正的自相关。
α
625.0745.02
1121-1ˆ=⨯-=≈DW ρ 也说明误差项存在较高度的自相关。
2.用迭代法处理序列相关,并建立回归方程;
回归方程为:y=-178.775+211.110x1+1.436x2
从结果中看到新回归残差的DW=1.716,
查DW 表,n=52,k=3,显著性水平0.5 由此可知DW 落入无自相关性区
域,说明残差序列无自相关
3.用一阶差分法处理序列相关,并建立回归方程;
从结果中看到回归残差的DW=2.042,根据P 104表4-4的DW 的取值范围来诊断 ,误差项。
实验四--自相关性的检验及修正

实验四--自相关性的检验及修正
自相关性的检验是研究经济数据中自身序列的行为特征,它可用于识别趋势、判断虚
假反应、探究影响力以及衡量规律的发展变化,以及有助于指导未来政策的制定。
因此,自相关性检验是一项重要的经济学技术,它可以为序列分析获取相关信息,让研究者对特
定事件影响有更深刻的认识。
自相关性检验大概分为两个步骤:也就是统计学检验和模型修正。
统计学检验流程大
致包括参数估计、假设检验和结论。
其中,假设检验可以让研究者判断序列是否有自相关性,而参数估计则可以得到自相关性的大小和方向。
从模型修正的角度来说,研究的目的
是建立一个能够自相关数据的特性并形式化处理的模型,这个模型必须注意记录自相关数
据的自身行为特征。
研究者也可以尝试采用其他方法进行模型修正,比如添加外生变量、增加时间序列滞后期、建立自回归模型和分析突变点等。
自相关性检验和模型修正在实践中都带有一定的挑战,例如原始数据的质量,可能存
在噪声;外生变量的准确性和凝聚力;记录的常数和参数的可靠性;动态变化趋势的准确
性等。
因此,研究者在进行自相关性检验和模型修正时要注意仔细进行检测和修正,以确
保研究结果的可靠性和有效性。
空间自相关检验 被解释变量-概述说明以及解释

空间自相关检验被解释变量-概述说明以及解释1.引言1.1 概述概述部分将为读者提供文章的一个整体背景,并简要介绍空间自相关检验的概念和相关背景。
空间自相关是一个重要的统计分析工具,用于探索和研究地理现象之间的空间关联性。
在地理学、环境科学、城市规划、经济学等领域,空间自相关检验被广泛应用于分析和解释各种地理现象和社会经济现象。
随着科技的飞速发展和数据获取的进一步完善,我们可以轻松获得各种地理和社会经济数据,这些数据往往具有空间属性,即它们在地理空间中具有一定的位置关联性。
空间自相关检验通过统计方法,可以帮助我们判断这些数据是否存在空间相关性,并进一步揭示地理现象背后的潜在机制和规律。
在本文中,我们将探讨空间自相关检验的原理和方法。
首先,我们将介绍空间自相关的概念和背景,包括相关的理论基础和研究背景。
其次,我们将详细说明空间自相关检验的原理,包括相关统计量的计算公式和假设检验的步骤。
最后,我们将讨论空间自相关检验的方法和应用,并举例说明如何在实际问题中进行空间自相关检验。
通过本文的学习,读者将能够深入了解空间自相关检验的概念、原理和应用方法,从而为他们在地理分析和研究中应用空间自相关检验提供一定的参考和指导。
此外,本文还将对空间自相关检验的意义和应用进行讨论,探讨该方法在解释地理现象和预测未来趋势方面的潜力和局限性。
2. 正文部分将详细阐述空间自相关的概念和背景,以及空间自相关检验的原理、方法和应用。
请继续阅读下一部分“2.1 空间自相关的概念和背景”。
1.2文章结构文章结构部分的内容可以写成如下形式:1.2 文章结构本文分为三个主要部分:引言、正文和结论。
在引言部分,我们先概述了空间自相关检验的背景和概念,介绍了本文的目的。
通过对空间自相关检验的原理、方法和应用进行综合分析和比较,我们旨在探讨空间自相关的特性和其在实际问题中的应用。
在正文部分,首先我们将详细介绍空间自相关的概念和背景,包括其在地理学、经济学和环境科学等领域的重要性和应用。
stata组内自相关检验命令

stata组内自相关检验命令摘要:1.介绍stata 组内自相关检验2.解释组内自相关检验的原因3.说明组内自相关检验的步骤4.列举stata 中进行组内自相关检验的命令5.总结组内自相关检验的重要性正文:一、介绍stata 组内自相关检验组内自相关检验,又称为内部自相关性检验,是一种用于检验数据中同一组内各个观测值之间是否存在相关性的统计方法。
在实证研究中,组内自相关检验可以帮助研究者识别潜在的数据问题,如数据重复、测量误差等,从而提高研究的可靠性和准确性。
stata 作为一款广泛应用于社会科学领域的统计软件,提供了丰富的组内自相关检验命令供研究者使用。
二、解释组内自相关检验的原因组内自相关检验的原因主要来自两个方面:一是数据收集过程中可能存在的数据重复或测量误差,导致同一组内的观测值之间存在相关性;二是模型设定错误,如遗漏变量、错误模型等,导致模型估计出的参数与真实参数之间存在偏误,从而影响研究结果的有效性。
因此,进行组内自相关检验有助于提高研究的可靠性和准确性。
三、说明组内自相关检验的步骤组内自相关检验的步骤主要包括以下两步:1.计算组内自相关系数:根据数据中同一组内各个观测值的信息,计算组内自相关系数。
常用的组内自相关系数包括皮尔逊相关系数、斯皮尔曼相关系数等。
2.检验组内自相关系数:根据计算出的组内自相关系数,选取合适的检验方法进行检验。
常用的检验方法包括t 检验、卡方检验等。
若检验结果表明组内自相关系数显著不为零,则说明数据存在内部自相关性问题。
四、列举stata 中进行组内自相关检验的命令stata 中进行组内自相关检验的命令主要包括以下两个:1.cor:计算组内自相关系数。
使用方法为`cor [options] [var1][var2]...`,其中[options] 为可选项,[var1]、[var2] 等为需要计算自相关系数的变量名。
2.test:进行组内自相关检验。
使用方法为`test [options] [testname] [var1] [var2]...`,其中[options] 为可选项,[testname] 为检验方法(如ttest、chisquare 等),[var1]、[var2] 等为需要进行检验的变量名。
自相关检验 r语言

自相关检验 r语言自相关检验是统计学中常用的方法之一,用于检验时间序列数据的相关性。
在R语言中,我们可以使用多种方法进行自相关检验。
首先,我们可以使用acf()函数来绘制自相关函数图像。
自相关函数(Autocorrelation Function, ACF)是衡量时间序列数据与其滞后版本之间相关性的指标。
通过观察ACF图像,我们可以了解数据是否存在自相关性,并确定相关性的程度。
其次,我们可以使用pacf()函数来绘制偏自相关函数图像。
偏自相关函数(Partial Autocorrelation Function, PACF)衡量了去除其他滞后版本影响后两个时间点之间的相关性。
PACF图像可以帮助我们确定时间序列数据的AR模型阶数。
另外,我们还可以使用Box.test()函数进行自相关检验。
Box-Ljung检验是一种常用的自相关检验方法,用于检验时间序列数据是否存在自相关性。
该方法基于一组滞后版本的自相关系数进行计算,并对其进行假设检验。
在进行自相关检验时,我们通常需要注意以下几点:1. 选择合适的滞后阶数。
在绘制ACF和PACF图像时,可以根据图像的衰减程度和显著性截尾来选择合适的滞后阶数。
一般来说,ACF 在滞后阶数为0后逐渐衰减至零,PACF在滞后阶数为0后截尾于零。
2. 进行假设检验。
在使用Box-Ljung检验时,我们需要设置显著性水平,并对检验结果进行判断。
如果检验结果的p值小于显著性水平,我们可以拒绝原假设,认定数据存在自相关性。
3. 注意时间序列数据的特点。
自相关检验通常适用于平稳时间序列或差分后的平稳时间序列。
对于非平稳时间序列,我们可以首先进行平稳性检验,并在需要时进行差分处理。
总之,R语言提供了多种方法进行自相关检验,我们可以根据具体情况选择合适的方法进行分析。
熟练掌握这些方法,可以帮助我们更好地理解和分析时间序列数据的相关性。
6.3自相关的检验

三、LM检验(BG检验) LM检验既可以检验一阶自相关,也可以检 验高阶自相关。 对于k元线性回归模型
Y X X X t 01 1 t 2 2 t k k tu t
设自相关形式为: u u u v t 1 t 1 p tp t 原假设为:
图 示 法 有 两 种 绘 制 方 式 , 一 种 是 绘 制 ee 与 的 t t 1 散 点 图 。
et
e t1
图 6 . 1e 与 e 的 关 系 t t 1
如果大部分点落在第Ⅰ、Ⅲ象限,表明随机误差 项ut存在着正自相关。
et et
e t1 e t1
图 6 . 2e 与 e 的 关 系 t t 1
然后,通过分析这些“近似估计量”之间的相 关性,以判断随机误差项是否具有自相关性。
一、图示法
由 于 残 差是 e 随 机 误 差 项的 u 计 , 因 此 , 如 t t 估 果存 u 在 自 相 关 性 , 必 然 会 由 残 差 项反 e 映 出 来 。 t t 因 此 , 可 以 利 用 残 差的 e 化 来 判 断 随 机 误 差 项 t 变 的 自 相 关 性 。
L
不 能 确 定
d
U
无 自 相 关
2
4 dU
不 能 确 定
4 dL
负 自 相 关
4
DW
DW检验的缺点和局限性 • DW检验有两个不能确的区域,一旦DW值落在这 两个区域,就无法判断。这时,只有增大样本容 量或选取其他方法
• DW统计量的上、下界表要求 n>15 ,这是因为 样本如果再小,利用残差就很难对自相关的存在 性做出比较正确的诊断 • DW检验不适应随机误差项具有高阶序列相关的检验
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于x y的散点图
由散点图可以判断出才可能存在异方差。
运用怀特检验判断是否有异方差
White Heteroskedasticity Test:
F-statistic 5.71174
5 Probability
0.00831
1
Obs*R-squared 8.98267
0 Probability
0.01120
6
由此可见,1%的显著水平上存在异方差。
运用加权最小二乘法消除异方差:
Dependent Variable: Y
Method: Least Squares
Date: 10/29/14 Time: 14:46 Sample: 1 31
Included observations: 31
Weighting series: 1/ABS(RESID)
Variable Coeffici
ent Std. Error t-Statistic Prob.
C -2171.3
76 418.8113 -5.184616 0.0000
X 0.97610
4 0.022593 43.20372 0.0000 Weighted Statistics
R-squared 0.99927
0 Mean dependent var
16676.9
9
Adjusted R-squared 0.99924
5 S.D. dependent var
18232.7
8
S.E. of regression 501.062
0 Akaike info criterion
15.3336
8
Sum squared resid 728082
9. Schwarz criterion
15.4261
9
Log likelihood -235.67
20 F-statistic
1866.56
1
Durbin-Watson stat 1.37353
7 Prob(F-statistic)
0.00000
0 Unweighted Statistics
R-squared 0.92681
6 Mean dependent var
17975.6
8
Adjusted R-squared 0.92429
2 S.D. dependent var
5667.54
2
S.E. of regression 1559.42
4 Sum squared resid
705223
38
Durbin-Watson stat 1.57587
5
由上表,f检验的伴随概率为0.000000,说明在1%的显著水平上,拒绝原假设,t检验的伴随概率为0.0000,说明在1%的显著水平上,拒绝原假设y x 之间存在显著的线性关系,该模型很好的反映了实际情况,所以消除了异方差。
自相关模型的检验和处理:
用Eviews5.0 做出国民生产总值(gdp)和出口(m)的散点图:
运用拉格朗日成数进行检验。
Breusch-Godfrey Serial Correlation LM Test:
F-statistic 4.59799
0 Probability
0.05004
6
Obs*R-squared 4.20291
8 Probability
0.04035
4
可以判断出存在一阶线性相关。
