卵形曲线辅助点计算(即完整缓和曲线起点的支距)解算步骤.
卵形曲线中间缓和曲线的放样计算

卵形曲线的相邻两圆曲线为包含关系 ,但 非同心圆 ,半径也不相等 ,其间的回旋线为不完 整回旋线 ( R1 > R2 或 R2 > R1 ) ,因而其放样计 量比基本型曲线中的完整回旋线较为复杂 。文 献〔1〕中介绍的方法为圆弧支距法 ,是以圆曲线 为基础来测设中间缓和曲线 ,该法精度较差 ,而 且与常用的测设方法不相适应 。本文采用完整
1999 年第 1 期
卵形曲线中间缓和曲线的放样计算
张 王月 杨根义 武文清
(内蒙古包头市公路总段 , 014040)
【摘 要】 从完整回旋线的计算方法出发 ,通过坐标转换 ,说明了卵形曲线中间缓和曲线 (不完整 回旋线) 的逐桩放样数据的计算方法 ,使其能按基本平曲线的放样方法进行放样 。 【关键词】 卵形曲线 中间缓和曲线 放样
2. 1 R1 > R2 的情况 (图 1)
在 X0 - Y 0 坐标系中 , Y H1 的坐标为 : x 0 = x (φ) , y0 = y (φ)
在 X1 - Y1 坐标系中 , 将中间缓和曲线延
伸后 ,设 Y H1 至起点的曲线长为 L 1 , 则 L 1 =
A
2 f
/
R1 , Y H1 处的缓和曲线角 β1
半径分别为 R1 、R2 , 则中间缓和曲线的曲率半
径为 : Rf = R1 ·R2/ | R1 - R2 | ;其回旋线参数
为
:
A
2 f
=
L f ·Rf 。
卵形曲线计算方法
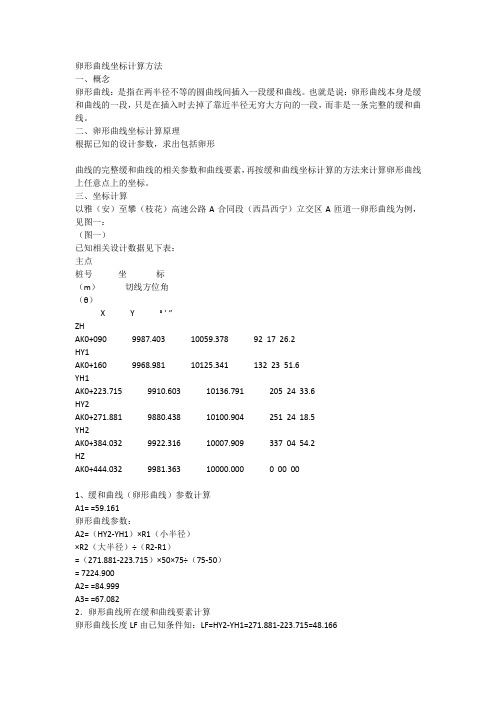
卵形曲线坐标计算方法一、概念卵形曲线:是指在两半径不等的圆曲线间插入一段缓和曲线。
也就是说:卵形曲线本身是缓和曲线的一段,只是在插入时去掉了靠近半径无穷大方向的一段,而非是一条完整的缓和曲线。
二、卵形曲线坐标计算原理根据已知的设计参数,求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素,再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。
三、坐标计算以雅(安)至攀(枝花)高速公路A合同段(西昌西宁)立交区A匝道一卵形曲线为例,见图一:(图一)已知相关设计数据见下表:主点桩号坐标(m)切线方位角(θ)X Y ° ’ ”ZHAK0+090 9987.403 10059.378 92 17 26.2HY1AK0+160 9968.981 10125.341 132 23 51.6YH1AK0+223.715 9910.603 10136.791 205 24 33.6HY2AK0+271.881 9880.438 10100.904 251 24 18.5YH2AK0+384.032 9922.316 10007.909 337 04 54.2HZAK0+444.032 9981.363 10000.000 0 00 001、缓和曲线(卵形曲线)参数计算A1= =59.161卵形曲线参数:A2=(HY2-YH1)×R1(小半径)×R2(大半径)÷(R2-R1)=(271.881-223.715)×50×75÷(75-50)= 7224.900A2= =84.999A3= =67.0822.卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知:LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段,因此先求出整条缓和曲线的长度LS,由此找出HZ'点的桩号及坐标(实际上不存在,只是作为卵形曲线辅助计算用)LM=LS(YH1至HZ'的弧长)=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166(校核)HY2=HZ'-LE=368.213-96.332=271.881(校核)由上说明计算正确3.HZ'点坐标计算(见图二)(图二)①用缓和曲线切线支距公式计算,缓和曲线切线支距公式通式:Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义:n —项数序号(1、2、3、……n)!—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算(有关书籍中一般为2-3项,不能满足小半径的缓和曲线计算精度要求,如本例中AK0+090~AK0+160段缓和曲线,如AK0+160中桩坐标带2项算误差达8cm),公式如下:X=L-L5÷[40(RLS)2]+L9÷[3456(RLS)4]–L13÷[599040(RLS)6]+L17÷[175472640(RLS)8]- L21÷[7.80337152×1010(RLS)10] (公式1)Y=L3÷[6(RLS)] - L7÷[336(RLS)3]+L11÷[42240(RLS)5] - L15÷[9676800(RLS)7]+L19÷[3530096640(RLS)9] - L23÷[1.8802409472×1012(RLS)11] (公式2)公式中L为计算点至ZH'或HZ'的弧长HZ':AK0+368.213的坐标从YH1:AK0+223.715推算,L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式(1)、(2)得:X=117.1072 Y=59.8839L对应弦长C=√(X2+Y2)=131.5301偏角a1=arctg(Y÷X)=27°05’00.2”* 偏角计算用反正切公式,不要用其它公式。
高等级公路卵形曲线的计算公式

高等级公路卵形曲线的计算方法摘要在高等级公路施工过程中,常遇到卵形曲线,而设计单位的出发点不同,中线的解算方法也大相径庭。
本文着重从卵形中线几种计算方法入手,在此基础之上阐述了卵形曲线的测设。
关键词卵形曲线复曲线匝道桥高等级公路卵形曲线是高等级公路、立交桥匝道常见的曲线形式,它由基本的三部分构成:第一圆曲线段、缓和曲线段和第二圆曲线段。
中间段缓和曲线用来连接两个不同半径的圆曲线。
其中线坐标解算方法有如下几种:1 补全缓和曲线我国公路上采用的缓和曲线为辐射螺旋线,夹在两圆曲线中间的缓和曲线为整个缓和曲线的一部分,缓和曲线上任一点半径与该点至该缓和曲线起点的距离乘积为一定值:R×L = A ,假设 R1> R2,可由两圆半径及两圆间的缓和段长 ls,求缓和曲线的总长 L 。
Δl = L - ls(1)Δl 就是夹在两圆曲线间缓和段省去的部分,由 YH 点补长Δl 至 o 点,以 o 点为该缓和曲线起点,起点的切线方向为 x 轴,与之垂直的曲线内侧方向为 y 轴方向建立坐标系(图 1 )。
缓和曲线公式(推导过程略)如下:(2)(3)图 1利用 x 、 y 值可以求得 o—YH 弦与 x 轴的夹角:β =3δ 。
α1为YH 点的切线方位角,则 ox 的方位:α =α1±β 。
o 点的坐标可由几何关系求得为( x0, y)。
缓和段上任一点统一坐标可求得:(4)y=yo+xsinα±ycosα (5) 2 曲率推算缓和曲线段曲率半径由第一段圆曲线半径 R1变为第二段曲率半径 R2(假设 R1> R2),则缓和曲线曲率半径变化为:(6)其中 ls为中间段缓和曲线长,为求缓和曲线方程,现建立以缓和曲线起点为坐标原点,起点的切线方向为 x 轴,与之垂直的曲线内侧方向为 y 轴的坐标系(图2 ),设 P 点为缓和曲线上任一点,距原点的曲线长为 l ,该点附近的微分弧长为 dl ,缓和曲线偏角为β ,则有dx=dlcosβ (7)dy=dlsinβ (8)图 2由于将其代入上式并进行积分可得缓和曲线方程:(9)(10)中间缓和段统一坐标计算为:(11)Y = yYHxsinα±ycosα (12)α 为曲线 YH 点切线方位。
公路工程测量放线圆曲线、缓和曲线(完整缓和曲线、非完整缓和曲线)计算解析
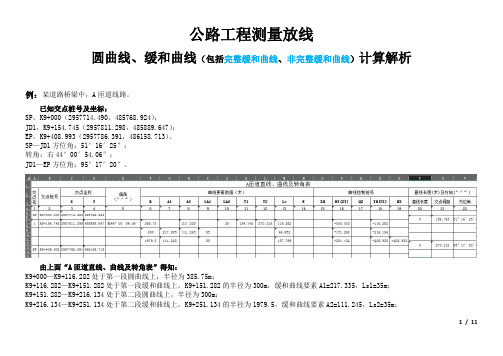
公路工程测量放线圆曲线、缓和曲线(包括完整缓和曲线、非完整缓和曲线)计算解析例:某道路桥梁中,A匝道线路。
已知交点桩号及坐标:SP,K9+000(2957714.490,485768.924);JD1,K9+154.745(2957811.298,485889.647);EP,K9+408.993(2957786.391,486158.713)。
SP—JD1方位角:51°16′25″;转角:右44°00′54.06″;JD1—EP方位角:95°17′20″。
由上面“A匝道直线、曲线及转角表”得知:K9+000—K9+116.282处于第一段圆曲线上,半径为385.75m;K9+116.282—K9+151.282处于第一段缓和曲线上,K9+151.282的半径为300m,缓和曲线要素A1=217.335,Ls1=35m;K9+151.282—K9+216.134处于第二段圆曲线上,半径为300m;K9+216.134—K9+251.134处于第二段缓和曲线上,K9+251.134的半径为1979.5,缓和曲线要素A2=111.245,Ls2=35m;1 / 11K9+251.134—K9+408.933处于第三段圆曲线上,半径为1979.5m。
求:K9+130、K9+200、K9+230、K9+300的中桩坐标,切线方位角,左5米边桩的坐标,右10米边桩的坐标。
解:首先,我们知道要求一个未知点的坐标,必须知道起算点坐标,起算点至未知点的方位角,起算点至未知点的直线距离,然后利用坐标正算的计算公式,就可以直接求出未知点的坐标。
那么,关于圆曲线和缓和曲线(包括完整缓和曲线和非完整缓和曲线)的计算,我们需要知道如何求出起算点至圆曲线或缓和曲线上某点的方位角和直线距离。
下面,先列出关于圆曲线和缓和曲线中角度和距离计算的相关公式。
2 / 113 / 11y 轴。
过圆曲线上任意点P 的切线与ZY —JD 相交,夹角(切线角)为β,ZY —P 与ZY —JD 的夹角(弦切角)为α,ZY —P 的弧长为L ,ZY —P 的直线距离为d ,圆曲线的半径为R 。
卵形曲线辅助点计算(即完整缓和曲线起点的支距)解算步骤.

5800卵形曲线坐标计算歪哥收集整理50卵形曲线辅助点计算(即完整缓和曲线起点的支距)解算步骤卵形曲线:是指在两半径不等的圆曲线间插入一段缓和曲线。
也就是说:卵形曲线本身是缓和曲线的一段,只是在插入时去掉了靠近半径无穷大方向的一段,而非是一条完整的缓和曲线,计算前只需要把不完整的缓和曲线(也就是卵型曲线)补充完整即可。
在计算小半径的缓和曲线或卵形曲线坐标时,由于切线支距公式取项少而造成计算精度低,现有书中一般介绍也就只有2~4项,为提高计算精度就需要将支距公式多展开几项。
以下计算卵型曲线的完整缓和曲线长支距模型:重在学习掌握解算流程,现在空间里有更好的计算程序。
曲线参数A2=LS×R1×R2÷(R2-R1)=卵形曲线长×小半径×大半径÷(大半径-小半径)在同一段回旋线内,它的参数永远是不变的。
LS=卵型曲线长. (已知)完整缓和曲线长L= A2÷R1=曲线参数÷小半径当L=LS时:代入完整缓和曲线切线支距公式:(式中R均为小半径R1)E=L-L5÷[40(RLS)2]+L9÷[3456(RLS)4]–L13÷[599040(RLS)6]+L17÷[175472640(RLS)8]- L21÷[7.80337152×1010(RLS)10]F=L3÷[6(RLS)] - L7÷[336(RLS)3]+L11÷[42240(RLS)5] - L15÷[9676800(RLS)7]+L19÷[3530096640(RLS)9] - L23÷[1.8802409472×1012(RLS)11] 完整缓和曲线切线角(即两切线交角)L所对应玄长C=√(E2+F2)大半径处偏角P1=tan- 1(F2÷E2)小半径处偏角P3=180- P1-(180- p2)O=小半径处切线方位角(已知)小半径处至完整缓和曲线起点方位角Q=O±P3 (右向取+号;左向取-号)完整缓和曲线(起点)坐标:X=A+CcosQY=B=CsihQ完整缓和曲线(起点)处切线方位角:O=Q+180±p2 (右向取+号;左向取-号)以起点为基点用回旋线编程计算卵型曲线上任意桩号的中边桩点位坐标。
匝道中卵形曲线坐标的计算

匝道中卵形曲线坐标的计算happy【摘要】在高速公路立交平面线型中,现在越来越多采用卵形曲线这一线型形式,而卵形曲线坐标的计算在现有的书籍中很少提到,这就给施工中坐标的计算和放样增加了难度。
在***施工中**互通式立交的匝道上就有卵形曲线的形式,我通过实践和对缓和曲线坐标计算的分析研究,总结出了卵形曲线的计算方法和技巧。
【关键词】卵形曲线缓和曲线坐标计算一、卵形曲线的概念卵形曲线是指在两个半径不等的同向圆曲线间插入一段缓和曲线(目前高速公路多采用以回旋线形式的缓和曲线,本文所说的缓和曲线均是回旋线的形式)。
也就是说:卵形曲线本身是缓和曲线的一段,只是在插入时去掉了靠近半径无穷大方向的一段,而非是一条完整的缓和曲线。
二、卵形曲线坐标的计算原理根据图纸上提供的已知的设计参数,求出包括卵形曲线的完整的缓和曲线的相关参数和曲线要素,然后再按照缓和曲线坐标计算的方法来计算卵形曲线上任意一点的坐标。
972D(图一)三、坐标计算的实例以我所在沧黄高速六合同段黄骅互通式立交B匝道上的卵形曲线为例。
见图一所示,已由图一和上表可知:YH1→HY2、YH2→HY3段均是卵曲线,半径变化为R=50→R=200、R=200→R=50。
下面就以YH1—HY2段卵曲线为例进行计算。
1. 卵曲线参数计算A2=(HY2-YH1)×R1(小半径)×R2(大半径)÷(R2-R1)=(196.873-159.373)×50×200÷(200-50)=2500 ∴A=502. 卵形曲线所在的缓和曲线要素计算卵形曲线的长度L F由已知条件知:L F=HY2-YH1=196.873-159.373=37.5卵形曲线作为缓和曲线的一段,因此先求出整条缓和曲线的长度L S,由此找出HZ点的桩号及坐标(实际上HZ点不存在,只是作为卵形曲线的辅助计算用)。
L S=(YH1至HZ的弧长)= A2÷R1=2500÷50=50∴HZ桩号=YH1+ L S=159.373+50=209.373L E=HY2至HZ的弧长= A2÷R2=2500÷200=12.5或L E= L S- L F=50-37.5=12.5卵形曲线长度L F= L S- L E=50-12.5=37.5(校核)HY2=HZ- L E=209.373-12.5=196.873(校核)由以上说明计算正确。
浅谈道路线形设计中卵型平曲线的计算方法

107科技创新导报 Science and Technology Innovation Herald 工 程 技 术道路线形设计在道路整体设计中占有重要地位,设计合理的线形可以提高道路行车安全保障,同时对道路连续性和美观都起到重要作用。
道路线形设计中一般包括6种线形,即:基本型、S型、卵型、凸型、复合型和C型。
其中,基本型是现代道路线形设计中最基本、最常用、计算最简单的线形之一,但在设计中往往由于地形或其它因素的影响不能采用基本型设计,而采用其他5种线形中的一种,其中卵型是计算最为复杂的线形。
卵型平曲线是指用一个回旋线连接两个同向圆曲线的组合形式。
卵型组合的前提条件:(1)大圆必须把小圆完全包含在内,但不是同心圆。
(2)延长两相邻圆曲线的圆弧不能相互交叉。
(3)连接的回旋线不是由回旋线的原点开始,而是曲率为121/1/R R 的部分。
下面我将结合自己的实践经验对道路线形设计中的卵型平曲线进行案例分析。
本案例中, 5JD 和 6JD 构成卵形平曲线,并且两交点的坐标分别为(76816.62,45314.107),(76615.557,45541.151),两交点的偏角分别为30°30'07″和23°21'06″,初拟 5JD 的半径R 1=400 m ,缓和曲线1165s L m 。
本案例采用切线长度控制曲线半径法(直线型定线)进行计算,按两同向曲线(未设缓和曲线时)在公切点处直接相接在的思想进行设计(公切线即为两交点的连线)两曲线应满足:12()tan ()tan 112222R p R p L(交点间距)221111652.8362424400s L p mRm1111()tan109.8332T R p mm303.274T m m21193.441T T T m m22222222()tan 2cot936.0792T R p R p T m1111()214.454180R p L mm2211936.079 2.324402.836R p R p由于>2.0,故两边设缓和曲线 3s L ,中间加一个缓和曲线,构成卵形平曲线。
卵曲线计算

卵曲线计算如图1所示,卵曲线的两个圆曲线的半径分别为R1、R2,两端所加的缓和曲线长分别为Ls1、Ls2,中间缓和曲线长为Lf ,线路转向角为α1+α2、交点为C ,曲线主点:直缓1点:ZH1、缓1圆1点:H1Y1、圆1缓2点:Y1H2、缓2圆2点:H2Y2、圆2缓3点:Y2H3、缓3直点:H3Z 。
图1计算缓和曲线参数: 圆曲线内移量: P1= Ls1224∗R1 P2=Ls2224∗R2切垂距: m1=Ls12- Ls13240∗R12m1=Ls22- Ls23240∗R22缓和曲线切线角:β1=Ls12∗R1∗ρ β1=Ls22∗R2∗ρ 其中: ρ=180゜π βs1=Ls12∗R1∗ρ βs1=Ls22∗R2∗ρ其中: ρ=180゜π计算曲线要素:t1=t2=(R1+P1)*tan α12t3=t4=(R2+P2)*tanα22AB=t2+t3 AC=AB∗sin α2sin (α1+α2)BC=AB∗sin α1sin (α1+α2)切线长:T1=t1+AC+m1 T2=t4+BC+m2 曲线长:L=Ls1+Ls2+Lf+α1−β1−βs1ρR1+α2−β2−βs2ρR2图2如图2在缓和曲线 ZH'-E-F 中:l=cRLf=lF-lE lE=cR1lF=cR2其中c 为缓和曲线半径变更率所以: c=Lf∗R1∗R2R1−R2lE=Lf∗R2R1−R2lF=Lf∗R1R1−R2在坐标系X4-ZH'-Y4中 X4E= lE −lE 540∗R22∗lF 2Y4E=lE 36∗R2∗lF−lE 7336∗lF ∗R2 α4=lE 26∗cX4i= li −li 540∗R22∗lF 2Y4i=li 36∗R2∗lF−li 7336∗lF ∗R2其中li=Ki-KE+lE , Ki>KE 。
Ki 、KE 分别为i 点和E 点的里程 将坐标系X4-ZH'-Y4中的X4i 、Y4i 转换到坐标系X3-E-Y3中 [X3i Y3i ]=[cos (−α4 ) −sin (−α4)sin (−α4) cos (−α4)]∗[X4i Y4i ]+[X4EY4E ] X3i 、Y3i 近似值算法: li0=Ki-KE δ=(3∗lE+li0)∗li06∗cX3i ≈li0*cos δ Y3i ≈li0*sin δ将坐标系X3-E-Y3中的X3i 、Y3i 转换到坐标系X1-ZH1-Y1中 X1E=m1+R1*sin(β1+LE−Ls1R1∗ρ)Y1E=P1+R1*(1-cos (β1+LE−Ls1R1∗ρ))其中 LE=KE-KZH1,KE 、KZH1分别为E点和ZH1点的里程 α3=α1-βs1[X1i Y1i ]=[cos (α3 ) −sin (α3)sin (α3) cos (α3)]∗[X3i Y3i ]+[X1E Y1E ] 将坐标系X2-H3Z-Y2中的X2i 、Y2i 转换到坐标系X1-ZH1-Y1中 X H3Z=T1+T2*cos (α1+α2) Y H3Z= T2*sin (α1+α2) 坐标系X1-ZH1-Y1中个点的计算: X2i=-( li −li 540∗R22∗Ls22) Y2i=li 36∗R2∗Ls2−li 7336∗Ls2∗R2其中 li=KH3Z-Ki,Ki、KH3Z分别为缓和曲线Ls2上i点和H3Z点的里程X2i=-(m2+R2*sin(β2+Li−Ls2R2∗ρ) )Y2i=P2+R2*(1-cos(β2+Li−Ls2R2∗ρ))其中 Li= KH3Z-Ki,Ki、KH3Z分别为圆2曲线上i点和ZH1点的里程[X1i Y1i ]=[cos(α1+α2 )−sin(α1+α2 )sin(α1+α2 ) cos(α1+α2 )]∗[X2iY2i]+[X H3ZY H3Z]坐标系X1-ZH1-Y1中个点的计算:X1i= li−li 540∗R1∗Ls1Y1i=li 36∗R1∗Ls1−li7336∗Ls13∗R13其中 li=Ki-KZH1,Ki、KZH1分别为缓和曲线Ls1上i点和ZH1点的里程X1i=m1+R1*sin(β1+Li−Ls1R1∗ρ)Y1i=P1+R1*(1-cos(β1+Li−Ls1R1∗ρ))其中 Li=Ki-KZH1,Ki、KZH1分别为圆1曲线上i点和ZH1点的里程将坐标系X1-ZH1-Y1中的坐标转换到系统坐标中[Xi Yi ]=[cos(α0 )−sin(α0 )sin(α0 ) cos(α0 )]∗[X1iY1i]+[XZH1YZH1]其中 XZH1、YZH1为ZH1点在系统坐标系中的坐标α0为ZH1-C的方位角自编曲线计算软件代码:using System;using System.Collections.Generic; using ponentModel;using System.Data;using System.Drawing;using System.Linq;using System.Text;using System.Windows.Forms;namespace 曲线计算{public partial class Form1 : Form {public Form1(){InitializeComponent();}public class xy{public double y;public xy(){x = 0.0;y = 0.0;}}public double PI = 3.14159265358;public double Ls1 = 0.0,Ls2=0.0,Lf=0.0, R1 = 0.0,R2=0.0, a1 =0.0,a2=0.0,Kzh=0.0,Ki=0.0;public string fx;public double c = 0.0;public double la = 0.0;public double lb = 0.0;// public double li = 0.0;public double B1 = 0.0;public double Ly1 = 0.0;public double Ly2 = 0.0;public double P1 = 0.0;public double P2 = 0.0;public double m1 = 0.0;public double m2 = 0.0;public double L = 0.0;public double T01 = 0.0;public double T02 = 0.0;public double Khy1 = 0.0, Kyh1 = 0.0, Khy2 = 0.0, Kyh2 = 0.0, Khz = 0.0; public xy JD1 = new xy();public xy JD2 = new xy();public xy JD3 = new xy();public double xa = 0.0;public double ya = 0.0;private void Form1_Load(object sender, EventArgs e){comboBox方向.Text = comboBox方向.Items[0].ToString();}/*角度弧度转换*/public double dms_rad(double a){//提取角度double sign=(a<0.0)?-1.0:1.0;a=Math.Abs(a);int d=(int)((a+0.00001)/10000.0);a=a-d*10000.0;{d=d-1;a=a+10000;}int m=(int)((a+0.00001)/100.0);a=a-m*100;if (a<0.0){m=m-1;a=a+100.0;}a=sign*(d*3600.0+m*60.0+a)/206264.806247096363;return a;}public double rad_dms(double a){a=a*206264.806247096363;double sign=(a<0.0)?-1.0:1.0;a=Math.Abs(a);int d=(int)(a/3600.0+0.0000001);a=a-d*3600.0;if(a<0.0){d=d-1;a=a+3600.0;}int m=(int)(a/60.0+0.0001);a=a-m*60.0;if(a<0.0){m=m-1;a=a+60.0;}a=d*10000.0+m*100.0+a;return a*sign;}//计算曲线要素及主点里程public void jisu(object sender, EventArgs e){//计算常数及要素B1 = Ls1 / (2 * R1 + 0.00000000000001);double B2 = Ls2 / (2 * R2 + 0.00000000000001); double B3 = Lf / (2 * R1 + 0.00000000000001);double B4 = Lf / (2 * R2 + 0.00000000000001);double c = Lf / (R2 - R1);P1 = Ls1 * Ls1 / (24 * R1 + 0.00000000000001);P2 = Ls2 * Ls2 / (24 * R2 + 0.00000000000001);m1 = Ls1 / 2 - Ls1 * Ls1 * Ls1 / (240 * R1 * R1 + 0.00000000000001); m2 = Ls2 / 2 - Ls2 * Ls2 * Ls2 / (240 * R2 * R2 + 0.00000000000001); double E = 0.0;if (a2 == 0.0){if (Ls1 == Ls2){T01 = m1 + (R1 + P1) * Math.Tan(a1 / 2);T02 = T01;}else{T01 = m1 + (R1 + P1) * Math.Tan(a1 / 2) - (P1 - P2) / Math.Sin(a1);T02 = m2 + (R2 + P2) * Math.Tan(a1 / 2) + (P1 - P2) / Math.Sin(a1);}Ly1 = R1 * (a1 - B1 * 2);Ly2 = 0.0;E = (R1 + P1) / Math.Cos(a1 / 2) - R1;}else{double t1 = (R1 + P1) * Math.Tan(a1 / 2);double t2 = (R2 + P2) * Math.Tan(a2 / 2);T01 = m1 + t1 + (t1 + t2) * Math.Sin(a2) / Math.Sin(a1 + a2); T02 = m2 + t2 + (t1 + t2) * Math.Sin(a1) / Math.Sin(a1 + a2); /* int temp = 0;if (a2 == 0.0){a1 = a1 / 2;a2 = a1;temp = 1;}*/c = Lf * R1 * R2 / (R1 - R2);la = Lf * R2 / (R1 - R2);lb = Lf * R1 / (R1 - R2);Ly1 = R1 * (a1 - B1 - B3);Ly2 = R2 * (a2 - B2 - B4);}L = Ls1 + Ls2 + Lf + Ly1 + Ly2;double q = T01 + T02 - L;//计算里程Khy1 = Kzh + Ls1;double Kqz1 = Khy1 + Ly1 / 2;Kyh1 = Khy1 + Ly1;Khy2 = Kyh1 + Lf;double Kqz2 = Khy2 + Ly2 / 2;Kyh2 = Khy2 + Ly2;Khz = Kyh2 + Ls2;double KHZ = Kzh + T01 + T02 - q;/* if (temp == 1){a1 = a1 + a2;a2 = 0.0;Ly1 = R1 * (a1 - B1 - B3);Ly2 = R2 * (a2 - B2 - B4);L = Ls1 + Ls2 + Lf + Ly1 + Ly2;}*/if (Khz != KHZ){listBox1.Items.Add("---里程计算错误---");}else{// listBox1.Items.Clear();listBox1.Items.Add("---曲线常数及要素---");listBox1.Items.Add("缓和曲线切线角B1:" +Convert.ToString(B1));listBox1.Items.Add("内移距P:" + Convert.ToString(P1)); listBox1.Items.Add("切垂距m:" + Convert.ToString(m1)); listBox1.Items.Add("内移距P:" + Convert.ToString(P2)); listBox1.Items.Add("切垂距m:" + Convert.ToString(m2)); listBox1.Items.Add("切线长T1:" + Convert.ToString(T01)); listBox1.Items.Add("切线长T2:" + Convert.ToString(T02)); listBox1.Items.Add("曲线长L:" + Convert.ToString(L));listBox1.Items.Add("外矢距E:" + Convert.ToString(E));listBox1.Items.Add("切曲差q:" + Convert.ToString(q));listBox1.Items.Add("------主点里程-------");listBox1.Items.Add("缓圆点里程Khy1:" +Convert.ToString(Khy1));listBox1.Items.Add("曲中点里程Kqz1:" +Convert.ToString(Kqz1));listBox1.Items.Add("圆缓点里程Kyh1:" +Convert.ToString(Kyh1));listBox1.Items.Add("缓圆点里程Khy2:" +Convert.ToString(Khy2));listBox1.Items.Add("曲中点里程Kqz2:" +Convert.ToString(Kqz2));listBox1.Items.Add("圆缓点里程Kyh2:" +Convert.ToString(Kyh2));listBox1.Items.Add("缓直点里程Khz:" +Convert.ToString(Khz));listBox1.Items.Add("检校缓直点里程KHZ:" +Convert.ToString(KHZ));}listBox1.SelectedIndex = listBox1.Items.Count - 1;}public void turn_left(object sender, EventArgs e){double a = a1 + a2;double li = Ki - Kzh;double xi=0.0;double yi = 0.0;int flg = 0;if (li <= Ls1){xi = li - li * li * li * li * li / (240 * R1 * R1 * Ls1*Ls1); yi = -(li * li * li / (6 * R1 *Ls1)-li*li*li*li*li*li*li/(336*R1*R1*R1*Ls1*Ls1*Ls1));flg = 1;}else if (li<=(Ls1+Ly1)&&li>Ls1){xi = m1 + R1 * Math.Sin((li-0.5*Ls1)/R1);yi = -(P1 + R1 * (1 - Math.Cos((li - 0.5 * Ls1) / R1)));if (Ki == Kyh1){xa = xi;ya = yi;}flg = 1;}else if (li > (Ls1 + Ly1) && li < (Ls1 + Lf + Ly1)){if ((xa == 0.0) && (ya == 0.0)){Ki = Kyh1;if (comboBox方向.Text == "左转弯"){turn_left(sender, e);}else if (comboBox方向.Text == "右转弯"){turn_right(sender, e);}else{listBox1.Items.Add("---转弯方向输入错误!---");}}double l=Ki-Kyh1;double ax=(3*la+l)*l/(6*c);double ay = B1 + Ly1 / R1;xi = l * Math.Cos(ax);yi = -l * Math.Sin(ax);double temp1 = xi * Math.Cos(ay) + yi * Math.Sin(ay) + xa; double temp2 = yi * Math.Cos(ay) - xi * Math.Sin(ay) + ya; xi = temp1;yi = temp2;flg = 1;}else if (li >= (Ls1 + Lf + Ly1) && li <= (L-Ls2)){li = Khz - Ki;xi = -(m2 + R2 * Math.Sin((li - 0.5 * Ls2) / R2));yi = -(P2 + R2 * (1 - Math.Cos((li - 0.5 * Ls2) / R2)));if (JD3.x == 0 && JD3.y == 0){double temp1 = xi * Math.Cos(a) + yi * Math.Sin(a) + T01 + T02 * Math.Cos(a);double temp2 = yi * Math.Cos(a) - xi * Math.Sin(a) - T02 * Math.Sin(a);xi = temp1;yi = temp2;flg = 1;}else{flg = 2;}}else if (li > (L-Ls2) && li <= L){li = Khz - Ki;xi = -li + li * li * li * li * li / (240 * R2 * R2 * Ls2 * Ls2); yi = -(li * li * li / (6 * R2 * Ls2) - li * li * li * li * li * li * li / (336 * R2 * R2 * R2 * Ls2 * Ls2 * Ls2));if (JD3.x == 0 && JD3.y == 0){double temp1 = xi * Math.Cos(a) + yi * Math.Sin(a) + T01 + T02 * Math.Cos(a);double temp2 = yi * Math.Cos(a) - xi * Math.Sin(a) - T02 * Math.Sin(a);xi = temp1;yi = temp2;flg = 1;}else{flg = 2;}}else{listBox1.Items.Add("---次点不在曲线上---");}double x0 = 0.0, y0 = 0.0;double xi0 = 0.0,yi0=0.0 ;double ai = 0.0;if (flg == 1){ai = Math.Atan((JD2.y - JD1.y) / (JD2.x - JD1.x));x0 = JD2.x + T01 * Math.Cos(ai + PI);y0 = JD2.y + T01 * Math.Sin(ai + PI);xi0 = x0 + xi * Math.Cos(ai) - yi * Math.Sin(ai);yi0 = y0 + yi * Math.Cos(ai) + xi * Math.Sin(ai);listBox1.Items.Add("里程为K"+Convert.ToString(Ki)+"点的坐标为x="+Convert.ToString(xi0)+",y="+Convert.ToString(yi0));}else if (flg == 2){ai = Math.Atan((JD3.y - JD2.y) / (JD3.x - JD2.x));x0 = JD2.x + T02 * Math.Cos(ai );y0 = JD2.y + T02 * Math.Sin(ai );xi0 = x0 + xi * Math.Cos(ai) - yi * Math.Sin(ai);yi0 = y0 + yi * Math.Cos(ai) + xi * Math.Sin(ai);listBox1.Items.Add("里程为K"+Convert.ToString(Ki) + "点的系统坐标为x=" + Convert.ToString(xi0) + ",y=" + Convert.ToString(yi0));}else{listBox1.Items.Add("---次点不在曲线上---");}listBox1.SelectedIndex = listBox1.Items.Count - 1;}public void turn_right(object sender, EventArgs e){double a = a1 + a2;double li = Ki - Kzh;double xi = 0.0;double yi = 0.0;int flg = 0;if (li <= Ls1){xi = li - li * li * li * li * li / (240 * R1 * R1 * Ls1 * Ls1); yi = (li * li * li / (6 * R1 * Ls1) - li * li * li * li * li * li * li / (336 * R1 * R1 * R1 * Ls1 * Ls1 * Ls1));flg = 1;}else if (li <= (Ls1 + Ly1) && li > Ls1){xi = m1 + R1 * Math.Sin((li - 0.5 * Ls1) / R1);yi = (P1 + R1 * (1 - Math.Cos((li - 0.5 * Ls1) / R1)));if (Ki == Kyh1){xa = xi;ya = yi;}flg = 1;}else if (li > (Ls1 + Ly1) && li < (Ls1 + Lf + Ly1)){if ((xa == 0.0) && (ya == 0.0)){Ki = Kyh1;if (comboBox方向.Text == "左转弯"){turn_left(sender, e);}else if (comboBox方向.Text == "右转弯"){turn_right(sender, e);}else{listBox1.Items.Add("---转弯方向输入错误!---");}}double l = Ki - Kyh1;double ax = (3 * la + l) * l / (6 * c);double ay = B1 + Ly1 / R1;xi = l * Math.Cos(ax);yi = l * Math.Sin(ax);double temp1 = xi * Math.Cos(ay) - yi * Math.Sin(ay) + xa; double temp2 = yi * Math.Cos(ay) + xi * Math.Sin(ay) + ya; xi = temp1;yi = temp2;flg = 1;}else if (li >= (Ls1 + Lf + Ly1) && li <= (L-Ls2)){li = Khz - Ki;xi = -(m2 + R2 * Math.Sin((li - 0.5 * Ls2) / R2));yi = (P2 + R2 * (1 - Math.Cos((li - 0.5 * Ls2) / R2)));if (JD3.x == 0 && JD3.y == 0){double temp1 = xi * Math.Cos(a) - yi * Math.Sin(a) + T01 + T02 * Math.Cos(a);double temp2 = yi * Math.Cos(a) + xi * Math.Sin(a) + T02 * Math.Sin(a);xi = temp1;yi = temp2;flg = 1;}else{flg = 2;}}else if (li > (L-Ls2) && li <= L){li = Khz - Ki;xi = -li + li * li * li * li * li / (240 * R2 * R2 * Ls2 * Ls2);yi = (li * li * li / (6 * R2 * Ls2) - li * li * li * li * li * li * li / (336 * R2 * R2 * R2 * Ls2 * Ls2 * Ls2));if (JD3.x == 0 && JD3.y == 0){double temp1 = xi * Math.Cos(a) - yi * Math.Sin(a) + T01 + T02 * Math.Cos(a);double temp2 = yi * Math.Cos(a) + xi * Math.Sin(a) + T02 * Math.Sin(a);xi = temp1;yi = temp2;flg = 1;}else{flg = 2;}}else{listBox1.Items.Add("---次点不在曲线上---");}double x0 = 0.0, y0 = 0.0;double xi0 = 0.0, yi0 = 0.0;double ai = 0.0;if (flg == 1){ai = Math.Atan((JD2.y - JD1.y) / (JD2.x - JD1.x));x0 = JD2.x + T01 * Math.Cos(ai + PI);y0 = JD2.y + T01 * Math.Sin(ai + PI);xi0 = x0 + xi * Math.Cos(ai) - yi * Math.Sin(ai);yi0 = y0 + yi * Math.Cos(ai) + xi * Math.Sin(ai);listBox1.Items.Add("里程为K" + Convert.ToString(Ki) + "点的坐标为x=" + Convert.ToString(xi0) + ",y=" + Convert.ToString(yi0));}else if (flg == 2){ai = Math.Atan((JD3.y - JD2.y) / (JD3.x - JD2.x));x0 = JD2.x + T02 * Math.Cos(ai );y0 = JD2.y + T02 * Math.Sin(ai );xi0 = x0 + xi * Math.Cos(ai) - yi * Math.Sin(ai);yi0 = y0 + yi * Math.Cos(ai) + xi * Math.Sin(ai);listBox1.Items.Add("里程为K" + Convert.ToString(Ki) + "点的系统坐标为x=" + Convert.ToString(xi0) + ",y=" + Convert.ToString(yi0));}else{listBox1.Items.Add("---次点不在曲线上---");}listBox1.SelectedIndex = listBox1.Items.Count - 1;}private void comboBox方向_SelectedIndexChanged(object sender, EventArgs e){fx = comboBox方向.Text;}private void text缓和曲线长_TextChanged(object sender, EventArgs e) {string l = "0";if (l != "0"){text缓和曲线长.Text = "0";}l = l + text缓和曲线长.Text;Ls1 = Convert.ToDouble(l);}private void textBox曲线长Ls2_TextChanged(object sender, EventArgs e) {string l = "0";if (l != "0"){textBox曲线长Ls2.Text = "0";}l = l + textBox曲线长Ls2.Text;Ls2 = Convert.ToDouble(l);}private void textBox曲线长Lf_TextChanged(object sender, EventArgs e) {string l = "0";if (l != "0"){textBox曲线长Lf.Text = "0";}l = l + textBox曲线长Lf.Text;Lf = Convert.ToDouble(l);}private void textBox半径R1_TextChanged(object sender, EventArgs e) {string r = "0";if (r.Length == 0){textBox半径R1.Text = "0";}r = r + textBox半径R1.Text;R1 = Convert.ToDouble(r);}private void text转弯半径R2_TextChanged(object sender, EventArgs e) {string r = "0";if (r.Length == 0){text转弯半径R2.Text = "0";}r = r + text转弯半径R2.Text;R2 = Convert.ToDouble(r);}private void textBox转角a1_TextChanged(object sender, EventArgs e) {string a0 = "0";if (a0.Length == 0){textBox转角a1.Text = "0";}a0 = a0 + textBox转角a1.Text;double a4 = Convert.ToDouble(a0);a1 = dms_rad(a4);}private void textBox转角a2_TextChanged(object sender, EventArgs e) {string a0 = "0";if (a0.Length == 0){textBox转角a2.Text = "0";}a0 = a0 + textBox转角a2.Text;double a4 = Convert.ToDouble(a0);a2 = dms_rad(a4);}private void textBox里程_TextChanged(object sender, EventArgs e){string k = "0";if (k.Length == 0){textBox里程.Text = "0";}k = k + textBox里程.Text;Kzh = Convert.ToDouble(k);}private void button退出_Click(object sender, EventArgs e){Close();}private void button计算里程_Click_1(object sender, EventArgs e) {jisu(sender,e);}private void textBoxJD1X_TextChanged(object sender, EventArgs e) {string jd = "0";if (jd.Length == 0){textBoxJD1X.Text = "0";}jd = jd + textBoxJD1X.Text;JD1.x = Convert.ToDouble(jd);}private void textBoxJD1Y_TextChanged(object sender, EventArgs e) {string jd = "0";if (jd.Length == 0){textBoxJD1Y.Text = "0";}jd = jd + textBoxJD1Y.Text;JD1.y = Convert.ToDouble(jd);}private void textBoxJD2X_TextChanged(object sender, EventArgs e) {string jd = "0";if (jd.Length == 0){textBoxJD2X.Text = "0";}jd = jd + textBoxJD2X.Text;JD2.x = Convert.ToDouble(jd);}private void textBoxJD2Y_TextChanged(object sender, EventArgs e){string jd = "0";if (jd.Length == 0){textBoxJD2Y.Text = "0";}jd = jd + textBoxJD2Y.Text;JD2.y = Convert.ToDouble(jd);}private void textBoxJD3X_TextChanged(object sender, EventArgs e) {string jd = "0";if (jd.Length == 0){textBoxJD3X.Text = "0";}jd = jd + textBoxJD3X.Text;JD3.x = Convert.ToDouble(jd);}private void textBoxJD3Y_TextChanged(object sender, EventArgs e) {string jd = "0";if (jd.Length == 0){textBoxJD3Y.Text = "0";}jd = jd + textBoxJD3Y.Text;JD3.y = Convert.ToDouble(jd);}private void button坐标_Click(object sender, EventArgs e){if (comboBox方向.Text == "左转弯"){turn_left(sender, e);}else if (comboBox方向.Text == "右转弯"){turn_right(sender, e);}else{listBox1.Items.Add("---转弯方向输入错误!---");}}private void textBoxli_TextChanged(object sender, EventArgs e) {string ki = "0";if (ki.Length == 0){textBoxli.Text = "0";}ki = ki + textBoxli.Text;Ki = Convert.ToDouble(ki);}}}。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5800卵形曲线坐标计算歪哥收集整理
50卵形曲线辅助点计算(即完整缓和曲线起点的支距)解算步骤
卵形曲线:是指在两半径不等的圆曲线间插入一段缓和曲线。
也就是说:卵形曲线本身是缓和曲线的一段,只是在插入时去掉了靠近半径无穷大方向的一段,而非是一条完整的缓和曲线,计算前只需要把不完整的缓和曲线(也就是卵型曲线)补充完整即可。
在计算小半径的缓和曲线或卵形曲线坐标时,由于切线支距公式取项少而造成计算精度低,现有书中一般介绍也就只有2~4项,为提高计算精度就需要将支距公式多展开几项。
以下计算卵型曲线的完整缓和曲线长支距模型:重在学习掌握解算流程,现在空间里有更好的计算程序。
曲线参数A2=LS×R1×R2÷(R2-R1)=卵形曲线长×小半径×大半径÷(大半径-小半径)在同一段回旋线内,它的参数永远是不变的。
LS=卵型曲线长. (已知)
完整缓和曲线长L= A2÷R1=曲线参数÷小半径
当L=LS时:代入完整缓和曲线切线支距公式:(式中R均为小半径R1)
E=L-L5÷[40(RLS)2]+L9÷[3456(RLS)4]–L13÷[599040(RLS)
6]+L17÷[175472640(RLS)8]- L21÷[7.80337152×1010(RLS)10]
F=L3÷[6(RLS)] - L7÷[336(RLS)3]+L11÷[42240(RLS)5] - L15÷[9676800(RLS)7]+L19÷[3530096640(RLS)9] - L23÷[1.8802409472×1012(RLS)11] 完整缓和曲线切线角(即两切线交角)
L所对应玄长C=√(E2+F2)
大半径处偏角P1=tan- 1(F2÷E2)
小半径处偏角P3=180- P1-(180- p2)
O=小半径处切线方位角(已知)
小半径处至完整缓和曲线起点方位角Q=O±P3 (右向取+号;左向取-号)
完整缓和曲线(起点)坐标:
X=A+CcosQ
Y=B=CsihQ
完整缓和曲线(起点)处切线方位角:
O=Q+180±p2 (右向取+号;左向取-号)
以起点为基点用回旋线编程计算卵型曲线上任意桩号的中边桩点位坐标。
5800卵形曲线坐标计算歪哥收集整理
51 LXQX 卵形曲线辅助计算点(即完整缓和曲线起点的支距)坐标及切线方位角编程Lbl 1: ?A : ?B : ?O : ?W :“R1”?I : “R2”?J :
I×J÷(J-I) →R : WR→U : U÷I→L ↙
“E=”: L-L5÷[40(I L)2]+L9÷[3456(I L)4]–L13÷[599040(I L)
6]+L17÷[175472640(I L)8]- L21÷[7.80337152×1010(I L)10] →E◢
“F=”: Abs(L3÷[6(I L)] - L7÷[336(I L)3]+L11÷[42240(I L)5] - L15÷[9676800(I L)7]+L19÷[3530096640(I L)9] - L23÷[1.8802409472×1012(I L)11] →F◢Abs(90 L2 ÷()) →V : tan- 1(F÷E)→P : √(E2+F2)→C :
O±(180-P-(180-V)) →Q (右向取+号;左向取-号)
“X=”:A+CcosQ→X◢
“Y=”:B+CsihQ→Y◢
“FWJ=”: Q+180±P→O ◢O►DMS◢ (右向取+号;左向取-号)
Prog“ ZDHUX ”:
G0t0 1
说明:A B为小半径处坐标,O为切线方位角。
W为卵型曲线长,L为完整缓和曲线长。
U为缓和曲线参数(A2) , C为L所对应弦长
XY为完整缓和曲线起点坐标
“FWJ=” →O为完整缓和曲线(起点)处切线方位角
按示例2:完整缓和曲线起点K0+100 处X=9890.293Y=1006.838 FWJ=108°12′02″接下来可按完整回旋线计算卵型曲线上任意桩号的中边桩点位坐标。
52 ZDHUX(匝道回旋线)Fx-5800p中边桩计算
20→DimZ ↙扩充20个数据库变量
“QD(X)=”?X:“QD(Y)=”Y:“QDLC=”?C:“ZDLC=”?E:“U(→Y-1,R1)=”?U:“QDR(1÷R)=”?P:“ZDR(1÷R)=”?Q:“FWJ=”?O ↙
Lbl 0:“KP=”?D:( D-C)÷5→H:(D-C)÷10→G ↙
P+(Q+P)×G÷(E-C)→Z[1] ↙
P+(Q+P)×(H+G)÷(E-C)→Z[3] ↙
P+(Q+P)×(2H+G)÷(E-C)→Z[5] ↙
P+(Q+P)×(3H+G)÷(E-C)→Z[7] ↙
P+(Q+P)×(4H+G)÷(E-C)→Z[9] ↙
P+(Q+P)×H÷(E-C)→Z[2] ↙
P+(Q+P)×2H÷(E-C)→Z[4] ↙
P+(Q+P)×3H÷(E-C)→Z[6] ↙
P+(Q+P)×4H÷(E-C)→Z[8] ↙
O+U×90×(Z[1]+P)×G÷Π→Z[11] ↙
O+U×90×(Z[3]+P)×(H+G)÷Π→Z[13] ↙
5800卵形曲线坐标计算歪哥收集整理
O+U×90×(Z[5]+P)×(2H+G)÷Π→Z[15] ↙ O+U×90×(Z[7]+P)×(3H+G)÷Π→Z[17] ↙ O+U×90×(Z[9]+P)×(4H+G)÷Π→Z[19] ↙ O+U×90×(Z[2]+P)×H÷Π→Z[12]↙ O+U×90×(Z[4]+P)×2H÷Π→Z[14] ↙ O+U×90×(Z[6]+P)
×3H÷Π→Z[16] ↙ O+U×90×(Z[8]+P)×4H÷Π→Z[18] ↙ “M=”:P+(Q-P)×(D-C)÷(E-C)→M ◢ “F=”:O+U×90×(M+P)×(D-C)÷Π→F ◢ “A=”:
X+Abs(H)÷6×(cos(O)+4(cos(Z[11])+cos(Z[13])+ cos (Z[15])+ cos(Z[17])+ cos(Z[19]))+2(cos(Z[12])+ cos(Z[14])+ cos(Z[16])+ cos(Z[18]))+ cos (F))→A◢ “B=”:Y+Abs(H)÷6×(sin(O)+4(sin(Z[11])
+sin(Z[13])+sin(Z[15])+ sin(Z[17])+ sin(Z[19]))+2(sin(Z[12])+ sin(Z[14])+ sin(Z[16])+ sin (Z[18]))+ sin(F))→B◢ “S”?S ↙
“N1=”:Rec(S , (F±90))+A ◢ (左负右正) “E=”:J+B◢右侧边桩坐标“N1=”:Rec(S , (F±90+180))+A ◢(左负右正) “E=”:J+B◢左侧边桩坐标 G0t0 0
说明:本程序可用于高速公路匝道,立交桥匝道曲线放样。
避免了传统切线支距法在小半径情况下误差大的缺点,主要解决卵型曲线计算。
(两个程序也可独立运行)“QD(X)=”起点X坐标;“QD(Y)=”起点Y坐标;“FWJ=”?O线元起点方位角;此前三项为前程序算出值,按确认键EXE过即可。
“QDLC=”线元起点里程;“ZDLC=”线元终点里程;“U(→Y-1,R1)=”线元转向(逆向计算时
Y1,R-1);“QDR(1÷R)=”线元起点曲率;“ZDR(1÷R)=” 线元终点曲率;“KP=”计算点里程。
卵形曲线计算图示2
左向卵形曲线计算图示: JD1 X=9858.265 Y=10034.988 R=75 卵形曲线长
Ls=48.166 JD2 X=9949.871 Y=10155.449 R=50
QD K0+084.182 X=9922.319 Y=10007.905 (QX)FWJ=157 04 52
YH K0+196.332 X=9880.441 Y=10100.900 (QX)FWJ=71 24 17.4 HY K0+244.498
X=9910.602 Y=10136.790 (QX)FWJ=25 24 34.8 ZD K0+316.067 X=9973.800
Y=10119.149 (QX)FWJ=303 23 51.5
计算结果: X Y 切线
5800卵形曲线坐标计算歪哥收集整理卵形曲线示图。
