立方根优秀教案

合集下载

立方根教学教案5篇

立方根教学教案5篇Cube root teaching plan立方根教学教案5篇前言：本文档根据题材书写内容要求展开，具有实践指导意义，适用于组织或个人。

便于学习和使用，本文档下载后内容可按需编辑修改及打印。

本文简要目录如下：【下载该文档后使用Word打开，按住键盘Ctrl键且鼠标单击目录内容即可跳转到对应篇章】1、篇章1：61立方根范文实用版2、篇章2：6．3去括号范文3、篇章3：63去括号范文4、篇章4：§11具有相反意义量范文(最新版)5、篇章5：题：52图形变化样本篇章1:61立方根范文实用版课型：新授学习目标：1.了解立方根的概念，会用根号表示一个数的立方根.2.能用立方运算求某些数的立方根，了解开立方与立方互为逆运算。

3.了解立方根的性质，区分立方根与平方根的不同。

4.体会类比，化归思想学习重点：立方根的概念.，求某些数的立方根。

学习难点；了解立方根的性质，区分立方根与平方根的不同。

学习过程：一、学习准备1、上节课我们学习了平方根的定义，若x2=a，则x叫a的平方根。

若x3=a，则x叫a的什么呢？完成下面填空。

33 = （）（）3 = 27（－3）3= （）（）3 = －27（）3= （）（）3 =（）3 =（）（）3 =03 =（）（）3 = 02、左边算式已知底数、指数求幂，右边算式已知幂、指数求底数一般地,如果一个数的立方等于a,那么这个数叫做a的立方根，也叫做a的三次方根。

即如果X3=a,那么叫做的立方根。

请按照第7页的举例你再举两个例子说明：叫做开立方，立方与互为逆运算4、观察上面两组算式，归纳一个数的立方根的性质是：正数有一个立方根，零有一个立方根；负数立方根。

交流：（1）的立方根是什么？（2）0.001的立方根是什么？（3）0的立方根是什么？（4）-729的立方根是什么？5、立方根的表示方法一个正数a有一个立方根,.正数a的立方根,记作“ ”负数a的立方根,记作“ ”吗？如果X3=a，那么X= ，其中符号“ ”读作三次根号，a 叫做被开方数这里的a表示什么样的数？ a是任意数二、合作探究1、阅读课本第7页例题4，按例题格式求其立方根。

立方根教案人教版

立方根教案人教版第一章：立方根的概念引入教学目标：1. 让学生理解立方根的概念。

2. 让学生学会使用立方根的性质进行简单的计算。

教学内容：1. 引入立方根的概念，通过实际例子让学生感受立方根的意义。

2. 讲解立方根的性质，如正数的立方根是正数，负数的立方根是负数等。

教学步骤：1. 引入立方根的概念，让学生举例说明。

2. 讲解立方根的性质，让学生进行实际计算。

教学练习：1. 让学生进行一些简单的立方根计算练习。

第二章：立方根的计算方法教学目标：1. 让学生掌握立方根的计算方法。

2. 让学生能够熟练运用立方根的计算方法解决实际问题。

教学内容：1. 讲解立方根的计算方法，如用立方公式进行计算。

2. 讲解如何运用立方根的计算方法解决实际问题。

教学步骤：1. 讲解立方根的计算方法，让学生进行实际计算。

2. 讲解如何运用立方根的计算方法解决实际问题，让学生举例说明。

教学练习：1. 让学生进行一些立方根的计算练习。

2. 让学生运用立方根的计算方法解决一些实际问题。

第三章：立方根的应用教学目标：1. 让学生理解立方根在日常生活中的应用。

2. 让学生能够运用立方根解决实际问题。

教学内容：1. 讲解立方根在日常生活中的应用，如计算物体的体积等。

2. 讲解如何运用立方根解决实际问题。

教学步骤：1. 讲解立方根在日常生活中的应用，让学生举例说明。

2. 讲解如何运用立方根解决实际问题，让学生进行实际操作。

教学练习：1. 让学生运用立方根解决一些实际问题。

2. 让学生进行一些与立方根相关的应用题练习。

第四章：立方根的综合练习教学目标：1. 让学生巩固立方根的知识。

2. 让学生能够灵活运用立方根解决实际问题。

教学内容：1. 进行立方根的综合练习，包括计算题和应用题。

教学步骤：1. 给学生发放练习题，让学生独立完成。

2. 对学生的练习进行讲解和指导。

教学练习：1. 让学生完成一些立方根的综合练习题。

第五章：立方根的拓展知识教学目标：1. 让学生了解立方根的拓展知识。

《立方根》优质教案#(精选.)

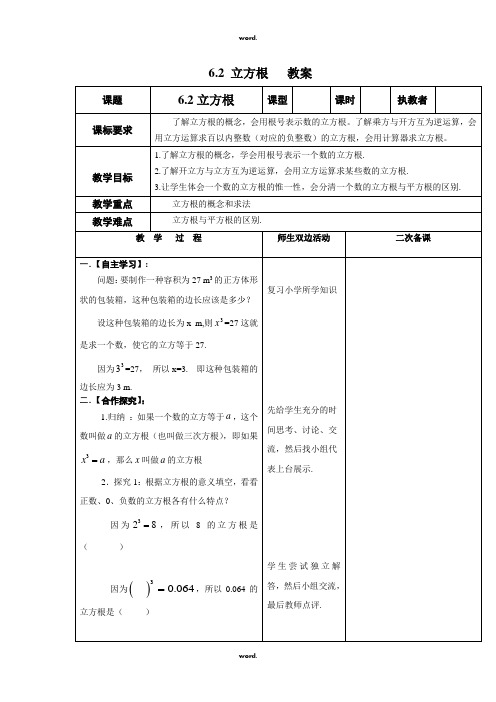
6.2 立方根教案一个正数有一个正的立方根 0有一个立方根，是它本身一个负数有一个负的立方根任何数都有唯一的立方根因为()30=，所以8的立方根是（）因为()38=-，所以-8的立方根是（）因为3827⎛⎫=- ⎪⎝⎭，所以827-的立方根是（）归纳：一个数a 的立方根，记作3a ，读作：“三次根号a ”，其中a 叫被开方数，3叫根指数，不能省略，若省略表示平方。

例如：327表示27的立方根，3273=；327-表示27-的立方根，3273-=-.3．探究2：因为338____,8____,-=-=所以38- = 38- ；因为3327____,27____-=-=，所以327- = 327-。

学生独立完成学生归纳总结，教师补充.学生阅读让学生观察归纳，得出结论.三．【巩固运用】：例.求下列各式的值：(1)364= （2） 318-= (3)32764-=你会用计算器计算(精确到0.001):3333...,0.000216,0.216,216,216000,...你发现了什么规律? 利用以上规律探究下列问题:已知3100≈ 4.6417…, 求3330.1,0.0001,100000的近似值(精确到0.001) 四．【反思总结】： 1、这节课我最大的收获是：2、我还需解决的问题有：五．【达标测试】：同步学习：达标测试探究规律让学生板演，纠错.类比平方根进行研究.学生独立完成在同步学习中.教师关注学生的完成情况并适时指导.最新文件仅供参考已改成word文本。

方便更改。

3.3立方根教学设计5篇范文

3.3立方根教学设计5篇范文第一篇：3.3立方根教学设计[教学设计]3.3 立方根乐清市白象镇中屠勤秧● 教材与学生的认知起点分析“立方根”是浙教版七年级上册第三章“实数”中的第三小节，它是在学生知道了无理数、算术平方根、平方根、开平方运算的概念基础上学习的。

教材从实际问题引入立方根的概念，说明学习数的立方根的意义。

通过具体数的计算，让学生体会，一个数的立方根的唯一性。

虽然这一节在实数一节之后，但仍起着加深对实数的认识的作用。

在实数范围内进行开立方的运算，无论从认知的角度，还是从表述的角度，都较为方便。

● 教学目标知识与技能：了解立方根的概念，会用根号表示一个数的立方根，并能用立方根运算求某些数的立方根教学思考：创设问题情境，学生进一步发展对数学知识的抽象概括力。

解决问题：通过学生的积极参与培养学生独立思考的能力，提高数学表达和运算能力。

情感态度与价值观：在参与数学学习活动中，不断培养合作交流的良好习惯。

● 教学重点本节重点是立方根的意义、性质。

● 教学难点本节难点是立方根的求法，立方根与平方根的联系及区别。

● 教学过程一、创设情境电脑显示一个魔方师：你们喜欢玩魔方吗？这是由8个同样大小的单位立方体组成的魔方，这8个小立方体可以重新排列，组成魔方表面的各种不同的美丽图案。

现在要做一个体积为8cm3的立方体魔方，它的棱要取多少长？你是怎么知道的？生：思考后回答。

设计意图：从熟悉的事物引入立方根概念，说明学习立方根的意义。

师：体积为27 cm3和体积为1000 cm3的立方体的棱又是要取多少长呢？生：思考、讨论后回答。

电脑演示：()3=8 ()3=27 ()3=1000 设计意图：为概念引入作准备并渗透从个别到一般的规律。

二、讲授新课师：让学生在平方根基础上试述立方根概念。

设计意图：渗透学生的类比思想和语言表达能力。

师（总结）：一般地，一个数x的立方等于a，即x3=a，那么这个数x就叫做a的立方根（也叫做a的三次方根），记做3a。

《立方根》优质教案

《立方根》优质教案教案内容：一、教学内容本节课的教学内容选自人教版初中数学八年级上册第6章第3节《立方根》。

本节课主要内容包括：立方根的定义，立方根的性质，立方根的运算方法，以及立方根在实际问题中的应用。

二、教学目标1. 理解立方根的概念，掌握立方根的性质和运算方法。

2. 能够运用立方根解决实际问题。

3. 培养学生的逻辑思维能力和创新精神。

三、教学难点与重点1. 立方根的概念和性质。

2. 立方根的运算方法。

3. 立方根在实际问题中的应用。

四、教具与学具准备1. 教具：黑板、粉笔、多媒体教学设备。

2. 学具：笔记本、尺子、圆规、三角板、计算器。

五、教学过程1. 实践情景引入：教师展示一个正方体模型，引导学生观察正方体的特征，并提出问题：“正方体的体积是多少？”学生通过观察和思考，可以得出正方体的体积是边长的三次方。

2. 立方根的定义：教师引导学生思考：“如果我们知道一个数的立方是另一个数，那么我们如何求出这个数呢？”学生通过讨论和思考，可以得出这个数就是原数的立方根。

教师给出立方根的定义，并解释立方根的性质。

3. 立方根的运算方法：4. 立方根在实际问题中的应用：教师提出一个实际问题：“一个正方体的体积是27立方米，求这个正方体的边长。

”学生运用立方根的知识，解决问题并得出答案。

六、板书设计1. 立方根的定义。

2. 立方根的性质。

3. 立方根的运算方法。

4. 立方根在实际问题中的应用。

七、作业设计1. 题目：已知一个数的立方是27，求这个数。

答案：3。

2. 题目：已知一个正方体的体积是64立方米，求这个正方体的边长。

答案：4米。

八、课后反思及拓展延伸1. 课后反思：教师反思本节课的教学效果，是否达成了教学目标，学生是否掌握了立方根的知识，哪些学生需要进一步辅导。

2. 拓展延伸：教师提出一个拓展问题：“立方根在实际生活中有哪些应用？”引导学生思考和讨论，进一步巩固立方根的知识。

重点和难点解析一、立方根的概念和性质1. 立方根的定义：教师在讲解立方根的定义时，应强调“立方根”就是一个数乘以自身两次后得到的结果。

2024年《立方根》优质教案

2024年《立方根》优质教案一、教学内容本节课选自2024年教材《数学》七年级下册第十章第一节“立方根”。

具体内容包括：1. 立方根的定义及性质；2. 立方根的计算方法；3. 立方根在实际问题中的应用。

二、教学目标1. 知识与技能：理解立方根的定义，掌握立方根的计算方法，能解决实际问题；2. 过程与方法：通过实例分析，培养学生运用立方根解决实际问题的能力；3. 情感、态度与价值观：培养学生对数学的兴趣，提高数学素养。

三、教学难点与重点教学难点：立方根的计算方法，特别是非整数的立方根；教学重点：立方根的定义，计算方法及其应用。

四、教具与学具准备教具：立方体模型，多媒体教学设备；学具：计算器，草稿纸，笔。

五、教学过程1. 实践情景引入（1）展示立方体模型，引导学生观察其特征，提出问题：如何计算立方体的体积？（2）通过计算立方体的体积，引出立方根的概念。

2. 例题讲解（1）讲解立方根的定义及性质；（2）举例讲解立方根的计算方法，如：2的立方根，8的立方根等；（3）讲解立方根在实际问题中的应用。

3. 随堂练习（2）解决实际问题，如：一个立方体的体积是64立方厘米，求它的棱长。

4. 知识拓展（1）介绍立方根在科学、生活中的应用；（2）探讨立方根与平方根的关系。

六、板书设计1. 立方根的定义及性质；2. 立方根的计算方法；3. 立方根在实际问题中的应用；4. 立方根与平方根的关系。

七、作业设计1. 作业题目：（2）一个立方体的体积是216立方厘米，求它的棱长；（3）比较两个数的大小：2的立方根与3的立方根。

2. 答案：（1）3，2，5；（2）6厘米；（3）2的立方根小于3的立方根。

八、课后反思及拓展延伸1. 反思：本节课学生对立方根的概念及计算方法掌握情况，对实际问题的解决能力；2. 拓展延伸：探讨立方根的估算方法，如：牛顿迭代法等。

重点和难点解析1. 教学难点：立方根的计算方法，特别是非整数的立方根；2. 例题讲解：立方根在实际问题中的应用；3. 知识拓展：立方根与平方根的关系；4. 作业设计：比较两个数的大小，如2的立方根与3的立方根。

《立方根》教学设计优秀4篇

《立方根》教学设计优秀4篇作为一名专为他人授业解惑的人民教师，总不可避免地需要编写教学设计，教学设计是对学业业绩问题的解决措施进行策划的过程。

那么教学设计应该怎么写才合适呢？下面是勤劳的编辑帮家人们找到的《立方根》教学设计优秀4篇，欢迎参考阅读，希望大家能够喜欢。

《立方根》教学设计篇一一、教材分析《立方根》是义务教育课程标准实验教科书北师大版八年级（上）第二章《实数》第三节、本节内容安排了1个学时完成、主要是通过对立方根与平方根的比较与归类，探索立方根的概念、计算和简单性质、因此，除了具体的知识技能（如知道一个数的立方根的意义，会用根号表示一个数的立方根，掌握立方根运算，掌握求一个数的立方根的方法和技巧）外，还需要昂学生感受类比的思想方法，为今后的学习打下基础、二、学情分析在学习了平方根概念的基础上学习立方根的概念，学生比较容易接受，因此教学重点放在立方根具有先进性（实数范围内）的讨论上、在学生对数的立方根概念及个数的先进性有了一定理解的基础上，再提出数的立方根与数的平方根有什么区别，学生就容易解决问题、三、目标分析教学目标知识与技能目标1、了解立方根的概念，会用根号表示一个数的立方根、2、会用立方运算求一个数的立方根，了解开立方与立方互为逆运算、3、了解立方根的性质、4、区分立方根与平方根的不同、过程与方法目标1、经历对立方根的探究过程，在探究中学会解决立方根的一些基本方法和策略、2、在学习了平方根的基础上，学生经历用类比的方法学习立方根的有关知识，领会类比思想、3、通过对立方根性质的探究，在探究中培养学生的逆向思维能力和分类讨论的意识、情感与态度目标：1、在立方根概念、符号、运算及性质的探究过程中，培养学生联系实际、善于观察、勇于探索和勤于思考的精神、2、学生通过对实际问题的解决，体会数学的实用价值、教学重点立方根的概念及计算、教学难点立方根的求法，立方根与平方根的联系及区别、四、教法学法1、教学方法：类比法、2、课前准备：教具：教材，软件Microsoft PowerPoint 2002，电脑、学具：教材，练习本、五、教学过程本节课设计了七个教学环节：一环节：创设问题情境；第二环节：复习引入、类比学习；第三环节：初步探究；第四环节：尝试反馈，巩固练习；第五环节：深入探究；第六环节：课时小结；探究与思考；第七环节：作业布置及课外探究、一环节：创设问题情境：内容：某化工厂使用一种球形储气罐储藏气体，现在要造一个新的球形储气罐，如果它的体积是原来的8倍，那么它的半径是原储气罐的多少倍？如果储气罐的体积是原来的4倍呢？（球的体积公式为v＝R，R为球的半径）提问：怎样求出半径R？学完本节知识后，相信你会有一个满意的答案、有关体积的。

七年级数学上册《立方根》教案、教学设计

2.基本概念：讲解立方根的定义，让学生理解立方根的含义，并通过实例加深理解。
3.性质探究：引导学生观察、发现立方根的性质，如正数的立方根是正数，负数的立方根是负数，0的立方根是0等。
4.运算方法：讲解计算立方根的方法，包括手算和计算器计算，让学生熟练掌握运算技巧。
5.应用举例：结合实际问题，让学生运用立方根知识解决问题，巩固所学。
三、教学重难点和教学设想
（一）教学重难点
1.理解并掌握立方根的定义及其性质，能够准确地计算立方根。
2.将立方根应用于解决实际问题，培养学生的数学建模和问题解决能力。
3.消除平方根与立方根之间的混淆，提高学生的运算准确性和速度。
（二）教学设想
1.利用生活实例和数学故事导入新课，激发学生的学习兴趣和探究欲望。例如，通过讲述“阿基米德和国王下棋”的故事，让学生了解立方根在古代数学中的应用，从而引出立方根的概念。
七年级数学上册《立方根》教案、教学设计
一、教学目标
（一）知识与技能
1.理解立方根的概念，掌握立方根的定义和性质，能够准确找出一个数的立方根。
2.学会使用计算器计算立方根，提高运算速度和准确性。
3.能够解决实际问题中涉及立方根的问题，如体积、密度等，培养将数学知识应用于实际生活中的能力。
（二）过程与方法
二、学情分析
七年级学生正处于青春期，思维活跃，好奇心强，具备一定的数学基础和逻辑思维能力。在学习《立方根》这一章节之前，他们已经掌握了实数的概念、平方根的性质等基础知识，为本章节的学习奠定了基础。然而，由于立方根的概念较为抽象，学生可能会在理解上存在困难，需要通过具体实例和形象化的教学手段帮助他们构建概念。
-教学策略：情境教学法，激发学生的好奇心和求知欲。

第9讲-立方根(教案)

3.发展数学建模素养：将立方根应用于实际问题，培养学生建立数学模型，运用数学知识解决现实问题的能力。
4.增强数学运算能力：通过立方根的计算练习，提高学生对数学运算的熟练度和准确性，培养严谨的数学计算习惯。
5.激发数学探究精神：鼓励学生在学习过程中积极思考、探索立方根的奥秘，发展学生的创新意识和探究精神。
（三）实践活动（用时10分钟）
1.分组讨论：学生们将分成若干小组，每组讨论一个与立方根相关的实际问题。
2.实验操作：为了加深理解，我们将进行一个简单的实验操作，如用立方根计算不同边长立方体的体积。
3.成果展示：每个小组将向全班展示他们的讨论成果和实验操作的结果。
（四）学生小组讨论（用时10分钟）
1.讨论主题：学生将围绕“立方根在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法，并与其他小组成员进行交流。
-举例：一个立方体的体积是64立方厘米，求其边长。
2.教学难点
估算，这是学生容易感到困难的地方。
-举例：估算15的立方根，在2和3之间，学生需要掌握估算的方法和技巧。
-立方根与平方根的区别和联系：学生容易混淆平方根和立方根的概念，需要明确它们的区别和联系。
在教学过程中，教师应针对以上重点和难点内容，采用直观演示、实例讲解、互动提问、小组讨论等多种教学方法，帮助学生透彻理解立方根的概念、性质和计算方法，并能将其应用于实际问题中，从而有效突破教学难点。
四、教学流程
（一）导入新课（用时5分钟）
同学们，今天我们将要学习的是《立方根》这一章节。在开始之前，我想先问大家一个问题：“你们在日常生活中是否遇到过需要求解一个数的立方根的情况？”（如：计算一个立方体的体积）这个问题与我们将要学习的内容密切相关。通过这个问题，我希望能够引起大家的兴趣和好奇心，让我们一同探索立方根的奥秘。

《立方根》参考教案

2.3 立方根教学目标：(一)教学知识点1.了解立方根的概念，会用根号表示一个数的立方根.2.能用立方运算求某些数的立方根，了解开立方与立方互为逆运算.3.了解立方根的性质.4.区分立方根与平方根的不同.(二)能力训练要求1.在学了平方根的基础上，要求学生能用类比的方法学习立方根的有关知识，领会类比思想.2.发展学生的求同求异思维，使他们能在复杂环境中明辨是非.(三)情感与价值观要求当今社会是科学飞速发展、信息千变万化的时代，每一个人都不可能把一生中要接触的知识全部学会，因此让他们会学知识比学会知识更重要，这就要从小培养良好的学习习惯，能自己解决的问题就自己解决，其中类比的学习方法就是一种重要的学习方法，本节课重点训练学生的类比思想的养成.教学重点：立方根的概念.教学难点：1.正确理解立方根的概念.2.会求一个数的立方根.3.区分立方根与平方根的不同之处.教学方法：类比学习法.教学过程：Ⅰ.新课导入上节课我们学习了平方根的定义，若x2=a，则x叫a的平方根，即x=±a.若正方体的棱长为a，体积为8，根据正方体体积的公式得a3=8，那a叫8的什么呢？本节课请大家根据上节课的内容自己来类推出结论，若x3=a，则x叫a的什么呢？Ⅱ.新课讲解1.请大家先回忆平方根的定义.下面大家能不能再根据平方根的写法来类推立方根的记法呢？.若x的平方等于a，则x叫a的平方根，记作x=±2a，读作x等于正、负二次根号a，简称为x等于正，负根号a.若x的立方等于a，则x叫a的立方根，记作x=±3a，读作x等于正、负三次根号a，简称x等于正、负根号a.［师］请大家对这位同学的回答展开讨论，小组总结后选代表发言.［生甲］我认为这位同学回答得不对.如果x2=a，则x=±a，x3=a时，x=±a也成立的话，那如何区分平方根与立方根呢？［生乙］因为乘方与开方是互为逆运算，求立方根可通过逆运算立方来求，如x3=8，因为23=8，所以x=2，只有一个根而不是±2，所以立方根的个数不正确.［师］大家的分析非常有道理，请认真看书第44页可知，若一个数x的立方等于a，即x3=a，那么这个数x就叫做a的立方根(cube root；也叫三次方根)如2是8的立方根，记为x=3a，读作x等于三次根号a.开立方的定义［师］大家先回忆开平方的定义，再类推开立方的定义.［生］求一个数a的平方根的运算，叫做开平方，则求一个数a的立方根的运算，叫做开立方，其中a叫做被开方数.(2)立方根的性质［师］2的立方等于多少？是否有其他的数，它的立方也是8？［生］2的立方等于8，(－2)3=－8，所以没有其他的数的立方等于8.［师］－3的立方等于多少？是否有其他的数，它的立方也是－27？［生］－3的立方等于－27，33=27，所以没有其他的数的立方等于－27.［师］0的立方等于多少？0有几个立方根？［生］0的立方等于0，0有1个立方根是0.［师］从刚才的讨论中，大家总结一下正数有几个立方根？0有几个立方根？负数有几个立方根？［生］正数有一个立方根，0有一个立方根是0，负数有一个立方根.［师］对.正数有一个正的立方根、负数有一个负的立方根，0的立方根有一个，是0.(3)平方根与立方根的区别与联系.［师］我们已经学习了平方根与立方根的定义，并会求某些数的平方根和立方根，下面请大家说说它们的联系与区别.［生］从定义来看，若一个数x 的平方等于a ，即x 2=a ，则x 叫a 的平方根；若一个数x 的立方等于a ，即x 3=a ，则x 叫a 的立方根，都是一个数x 的乘方等于a ，但一个是平方，另一个是立方.［生］一个正数的平方根有两个，一个负数没有平方根，零的平方根有一个是零；一个正数的立方根有一个，并且是正数，一个负数有一个负的立方根，零的立方根有一个是零.［生］它们的表示方法和读法不同，一个正数a 的平方根表示为±a ，立方根表示为3a .下面我再系统地总结一下：［例1］求下列各数的立方根：(1)－27；(2)1258；(3)0.216；(4)－5. ［师］请大家思考下列问题.3a 表示a 的立方根，则(3a )3等于什么？33a 等于什么？大家可以先举例后找规律.： (3a )3=a .又∵a 3是a 的立方,所以a 3的立方根就是a ，所以33a =a .下面就这两个式子进行练习.［例2］求下列各式的值： (1)38-；(2)3064.0；(3)－31258；(4)(39)3 Ⅲ.课堂练习(一)随堂练习1.求下列各式的值：333333)16(;5;64;125.0-.2.一个正方体，它的体积是棱长为3cm 的正方体体积的8倍，这个正方体的棱长是多少？解：设正方体的棱长是x cm ，得x 3=8×33，解得x =6.即改正方体的棱长是6cm.(二)补充练习1.求下列各数的立方根：0，1，－8127，6，－1000125，0.001 2.求下列各式的值：3233333333)278(;)2(;)2(;16463;1251;1;027.0------ 3.下列说法对不对？－4没有立方根；1的立方根是±1；361的立方根是61；－5的立方根是－35；64的算术平方根是±8.Ⅳ.议一议1.某化工厂使用一种球形储气罐储藏气体.现在要造一个新的球形储气罐，如果它的体积是原来的8倍，那么它的半径是原储气罐半径的多少倍？2.一个正方体的体积变为原来的n 倍，它的棱长变为原来的多少倍？解：设原正方体的棱长为a ，后来的正方体的棱长为b ，得na 3=b 3∴3333n a b =33 .∴b=ana3n即后来的棱长变为原来的3n倍.Ⅴ.课时小结1.立方根的定义.2.立方根的性质.3.开立方的定义.4.平方根与立方根的区别与联系.5.会求一个数的立方根.Ⅵ.课后作业习题2.5.Ⅶ.活动与探究1.求下列各式中的x.(1)8x3+27=0；(2)(x－1)3－0.343=0；(3)81(x+1)4=16；(4)32x5－1=0.板书设计：学生用类推的方法得出立方根的相关结论。

立方根教案(3)

立方根教案(3)
一、教学目标
1. 理解立方根的定义和性质；
2. 能够计算一个数的立方根；
3. 能够在实际问题中应用立方根。

二、教学内容
1. 立方根的概念和基本性质；
2. 立方根的求解方法；
3. 立方根的应用场景。

三、教学准备
1. 教学课件和教辅资料；
2. 计算器；
3. 练题。

四、教学步骤
步骤一：导入
1. 引导学生回顾二次方根的概念和求解方法；
2. 引入立方根的定义和概念，与二次方根进行对比。

步骤二：理解立方根的概念和性质
1. 介绍立方根的定义：一个数的立方根是指它的立方等于该数的数；
2. 解释立方根的性质：每个正数都有唯一的一个正的立方根。

步骤三：求解立方根的方法
1. 介绍近似法：通过试探和调整的方法逼近准确的立方根；
2. 介绍二分法和牛顿迭代法两种常用的求解立方根的方法；
3. 演示使用计算器进行立方根计算的步骤。

步骤四：练与应用
1. 分发练题，进行小组讨论和解答；
2. 引导学生在实际问题中应用立方根，如体积、边长相关的计算等。

五、教学评估
1. 教师观察学生的参与度和掌握程度；
2. 批改练题，检查学生的求解立方根的能力；
3. 提出针对性的问题，检验学生对立方根的应用能力。

六、教学延伸
1. 引导学生深入研究其他根的求解方法；
2. 探究立方根的运算规律和特殊性质。

以上就是本次立方根教案的内容，希望能够帮助学生提高对立方根的理解和运用能力。

《立方根》教案

《立方根》教案教案：《立方根》(一)一、教学目标：1.理解什么是立方根。

2.能够找出给定数的立方根。

3.掌握立方根的计算方法。

二、教学重点：1.立方根的定义和性质。

2.理解立方根的求解方法。

三、教学难点：1.立方根的计算方法。

2.难题解析与策略。

四、教学准备：1.教师准备：教学课件、教具、课堂练习题。

2.学生准备：课本、笔记。

五、教学过程：Step 1. 导入新知1.以一个实际问题引入：“小明有一块长为8米、宽为8米、高为8米的立方体，求立方体的体积。

”2.引导学生思考立方体和立方根之间的关系。

3.提出问题：“如果已知一个数的体积，如何求这个数的边长呢？”Step 2. 讲解立方根的定义和性质1.定义：立方根是指一个数的立方等于给定数的运算。

2.性质：a)任何正整数的立方根都是正整数。

b)任何负整数的立方根既可以是正整数也可以是负整数。

Step 3. 计算立方根1.先引导学生通过实验法求解立方根。

2.介绍立方根的计算方法：a)开方法：将一个数的立方根写成开平方的形式，然后用平方根的计算方法求解。

b)近似法：通过近似计算得到一个数的近似立方根。

3.示范计算方法，并进行练习。

Step 4. 难题解析与讨论1.给出一些难题，引导学生进行思考和讨论。

2.解析难题的解题思路和策略。

Step 5. 课堂练习1.出示练习题，让学生独立完成。

2.班级合作，互相讨论和解答。

六、教学反思：本节课主要是讲解立方根的定义和性质，以及立方根的计算方法。

通过实例引入，学生能够理解立方根的概念，并学会通过开方法和近似法求解立方根。

在教学过程中，我注意通过引导让学生主动思考问题，培养他们的数学思维能力。

同时，通过讨论解析难题，学生能够深入理解问题的本质和解题的策略。

在课堂练习环节，我采用了合作学习的方式，让学生在小组内共同解答问题，提高了课堂练习的效果。

总体来说，本节课教学效果较好，学生对立方根的理解和计算能力都有了一定的提高。

七年级数学下册《立方根》教案、教学设计

3.分层教学，关注个体差异：
-针对不同学生的学习需求，设计不同难度的练习题，使每个学生都能在原有基础上得到提高。
4.自主探究，合作交流：
-引导学生通过自主探究、小组讨论等形式，发现立方根的性质和计算方法，培养学生合作交流和解决问题的能力。
5.渗透数学思想方法：
-在教学中，引导学生运用数形结合、分类讨论等数学思想方法，提高解决问题的策略和技巧。
（二）过程与方法
在本章节的学习过程中，学生将通过以下过程与方法来提高数学素养：
1.通过观察、猜想、验证等活动，培养学生发现问题和提出问题的能力。
2.通过自主探究、合作交流等形式，培养学生的逻辑思维能力和团队合作意识。
3.运用数形结合、分类讨论等数学方法，提高学生解决问题的策略和技巧。
4.通过解决实际问题，培养学生将数学知识应用于生活的意识和能力。
2.对于选做题和拓展题，学生可根据自己的兴趣和实际水平选择完成。
3.教师将根据学生的作业完成情况，给予评价和反馈，帮助学生查漏补缺，提高数学素养。
4.鼓励学生主动思考、积极探索，将所学知识应用于生活实践。
6.梯度练习，巩固提高：
-设计具有梯度性的练习题，让学生在练习中逐步提高计算速度和准确性，巩固所学知识。
7.课堂小结，总结规律：
-在课堂小结环节，引导学生总结立方根的定义、性质和计算方法，形成系统化、结构化的知识体系。
8.融入情感教育，培养价值观：
-在教学过程中，注重培养学生的数学情感，让学生认识到数学在生活中的重要性，形成正确的价值观。
5.关注学生在学习过程ห้องสมุดไป่ตู้可能出现的困难和误区，及时进行指导和纠正，帮助学生建立正确的数学概念。
三、教学重难点和教学设想
（一）教学重点

(浙教版)七年级数学上册第3章第3节《立方根》优秀教学案例

五、案例亮点
1.生活情境的创设：本节课通过生活中的立方根实例导入新课，使学生能够感受到数学与生活的紧密联系，提高了学生的学习兴趣和积极性。
2.问题导向的教学策略：教师在教学过程中提出了多个问题，引导学生进行思考和探究，激发了学生的数学思维，培养了学生的问题解决能力。
3.小组合作的学习方式：教师将学生分成小组，进行合作讨论，使学生能够在团队中发挥各自的优势，互相学习和交流，提高了学生的团队合作精神和沟通能证，提高运用现代技术手段解决数学问题的能力。
（三）情感态度与价值观
1.学生体验数学学习的乐趣，培养对数学的兴趣和好奇心。
2.学生在学习立方根的过程中，培养克服困难的意志，增强自信心。
3.学生认识到立方根在实际生活中的重要性，培养运用数学知识解决实际问题的意识。
在实际教学中，本节课的内容与学生的生活实际紧密相连，教师可以充分利用学生的经验，通过生活实例引入立方根的概念，激发学生的学习兴趣。同时，本节课的教学内容也是对学生已有知识的一次拓展和深化，教师需要引导学生从具体的事物中抽象出立方根的概念，帮助学生建立良好的知识体系。
二、教学目标
（一）知识与技能
1.学生能够理解立方根的概念，掌握求一个数的立方根的方法，能够运用立方根解决一些实际问题。
4.学生学会与他人合作、交流，培养团队协作精神和良好的学习习惯。
5.学生树立正确的数学价值观，认识数学对于个人和社会发展的意义。
本节课的教学目标旨在全面提高学生的知识与技能、过程与方法、情感态度与价值观，使学生在学习立方根的过程中，既掌握了数学知识，又培养了数学思维，更体验到了数学学习的乐趣，从而提高学生的整体数学素养。
本节课的案例亮点体现了以学生为主体的教学理念，注重培养学生的数学思维能力、团队合作精神、自我评价和自我改进能力，使学生在实际应用中提高数学素养，为今后的数学学习打下坚实的基础。

立方根(教案).doc

3.3立方根（教案）一、教学目标：（一）知识目标：1.理解立方根的概念，会用根号表示一个数的立方根。

2.能用开立方运算求数的立方根，体会立方与开立方运算的互逆性。

（二）能力目标：培养学生的理解能力和运算能力．（三）情感目标：体会立方根与平方根的区别与联系．二、教学重点：本节重点是立方根的意义、性质。

三、教学难点：本节难点是立方根的求法，立方根与平方根的联系及区别。

四、教学过程：（一）复习1.口答：(1) 平方根的概念?如何用符号表示数a(≥0)的平方根?(2) 正数有几个平方根?它们之间的关系是什么?负数有没有平方根?0平方根是什么?2.计算：（二）合作学习：给出一个3×3×3魔方，并提问这是这是由几个大小相同的单位立方体组成的魔方?（三）想一想：1、要做一个体积为27立方厘米的立方体模型,它的棱要多少长？你是怎么知道的？2、什么数的立方等于-27？归纳：1.立方根的概念：一般地，如果一个数的立方等于a ，这个数就叫做a 的立方根(也叫做三次方根)。

即X 3=a ,把X 叫做a 的立方根。

如53=125 则把5叫做125的立方根。

（-5）3=-125 则把-5叫做-125的立方根。

数a 的立方根用符号“表示，读作“三次根号a ” .2.开立方：求一个数的立方根的运算，叫做开立方。

开立方与立方也是互为逆运算，因此求一个数的立方根可以通过立方运算来求。

（四）例题讲解例1、求下列各数的立方根：（1）-8 （2） 8（3）（4）0.216 （5）0 引导学生根据平方根的性质得出立方根的性质：1、正数有一个正的立方根。

2、负数有一个负的立方根。

3、0的立方根还是0。

让学生说出平方根，算术平方根以及立方根是本身的数分别是多少？。

(1) 412 (2) ±22)7(81)5(- (3)+-827-练一练：1.判断下列说法是否正确,并说明理由。

（1）827的立方根是±23(2) 25的平方根是5 (3) -64没有立方根(4) -4的平方根是±2 （5）0的平方根和立方根都是0 例2求下例各式的值：（教师讲解，可以提问学生）（五）当堂检测（检查学生掌握情况）计算：（六）归纳小结：学生概括：1、通过本节课的学习你获得了那些知识？2、你能总结出平方根和立方根的异同点吗？教师概括：相同点: （1）0的平方根、立方根都有一个是0（2）平方根、立方根都是开方的结果。

立方根(第一课时) 教学设计

立方根（第一课时）教学设计一、教学目标•理解立方根的概念和计算方法。

•能够应用立方根计算相关问题。

•培养学生的逻辑思维能力和解决问题的能力。

二、教学重点•立方根的概念和计算方法。

•立方根的应用。

三、教学内容1. 理论知识讲解•介绍立方根的概念和符号表示。

•讲解立方根的计算方法，包括开立方公式和计算器的使用方法。

2. 计算实例演示•通过示例演示如何计算一个数的立方根。

•引导学生理解立方根计算的步骤和思路。

3. 练习和巩固•提供一些简单的立方根计算题目，让学生进行练习。

•组织学生进行小组讨论，共同解决一些立方根相关的问题。

四、教学过程1. 导入新知识引入立方根的概念和应用，激发学生的学习兴趣。

2. 理论知识讲解通过课件或黑板等教学工具，讲解立方根的概念和计算方法。

重点解释开立方公式的原理和计算器的使用方法。

3. 示例演示以一个具体的例子，演示如何计算一个数的立方根。

详细解释计算的步骤和思路，帮助学生理解立方根的计算过程。

4. 练习和巩固让学生进行立方根的练习题，通过大量的实践来帮助学生掌握计算方法和提升计算速度。

同时，组织小组讨论，鼓励同学们分享解题思路和方法。

5. 总结和延伸对本节课的重点内容进行总结，并提供一些拓展问题，引导学生进一步思考和探索。

五、教学评估通过课堂练习和小组讨论，检查学生对立方根概念和计算方法的理解程度。

可以布置一些作业题目，作为课后巩固和评估的依据。

六、教学反思通过本节课的教学设计和实施，我发现学生对立方根的概念和计算方法有了较好的理解。

示例演示的方式让学生更加直观地了解了立方根的计算过程。

小组讨论也激发了学生的思维，培养了合作解决问题的能力。

然而，在教学过程中，有些学生的计算速度较慢，需要提供更多的练习机会来提升他们的计算能力。

下一节课我将考虑设置更多的练习环节，帮助学生巩固所学内容。

《立方根》优质教案

《立方根》优质教案一、教学内容本节课选自人教版八年级下册数学教材，第十七章《数的开方》第二节《立方根》。

具体内容包括：1. 立方根的定义及其性质；2. 立方根的计算方法；3. 立方根在实际问题中的应用。

二、教学目标1. 知识目标：让学生理解并掌握立方根的概念，熟练运用立方根的性质进行计算；2. 能力目标：培养学生运用数学知识解决实际问题的能力，提高学生的逻辑思维和运算能力；3. 情感目标：激发学生学习数学的兴趣，培养学生的合作意识和探究精神。

三、教学难点与重点教学重点：立方根的定义、性质及计算方法。

教学难点：立方根性质的灵活运用，解决实际问题。

四、教具与学具准备1. 教具：多媒体课件、黑板、粉笔；2. 学具：立方体模型、计算器、练习本。

五、教学过程1. 情景引入通过展示立方体模型，引导学生思考如何计算立方体的体积，从而引入立方根的概念。

2. 知识讲解（1）立方根的定义：讲解立方根的概念，举例说明；（2）立方根的性质：引导学生观察立方根的性质，如正数的立方根为正数，负数的立方根为负数，0的立方根为0；（3）立方根的计算方法：介绍立方根的计算方法，如分解质因数法、估算法等。

3. 例题讲解讲解教材中的例题，分析解题思路，示范解题过程。

4. 随堂练习布置教材中的练习题，让学生独立完成，并及时给予反馈。

5. 课堂小结六、板书设计1. 《立方根》2. 内容：（1）立方根的定义；（2）立方根的性质；（3）立方根的计算方法；（4）例题及解题过程；（5）课堂练习。

七、作业设计1. 作业题目：（1）求下列数的立方根：8、27、64、1；（2）已知一个数的立方根是3，求这个数；（3）一个立方体的体积是343cm³，求它的棱长。

2. 答案：八、课后反思及拓展延伸1. 反思：本节课学生对立方根的概念和性质掌握情况较好，但在计算立方根时，部分学生对方法掌握不够熟练，需要加强练习；2. 拓展延伸：引导学生思考立方根在其他领域的应用，如科学计算、工程设计等，激发学生学习兴趣。

立方根教案人教版

立方根教案人教版【篇一：立方根教案】人教版义务教育教科书◎数学七年级下册6.2 立方根教学目标1.了解立方根的概念，会用根号表示数的立方根.2.了解开方与乘方互为逆运算，会用立方运算求某些数的立方根，会用计算器求立方根.3. 能用有理数估计一个无理数（立方根）的大致范围.教学重点立方根的概念与性质及求法.教学难点立方根的概念与性质及求法.课时安排2课时.第1课时教学内容立方根的概念和求法.一、复习导入复习上节内容，导入新课的教学.二、新课教学1. 问题要制作一种容积为27 m3的正方体形状的包装箱，这种包装箱的棱长应该是多少？设这种包装箱的边长为x m，则x3＝27.这就是求一个数，使它的立方等于27.因为33＝27，所以x＝3.因此这种包装箱的棱长应为3 m.归纳：一般地，如果一个数的立方等于a，这个数叫做a的立方根或三次方根，这就是说，如果x3＝a，那么x叫做a的立方根.2. 探究根据立方根的意义填空，你能发现正数、0、负数的立方根各有什么特点吗？教师备课系统──多媒体教案因为23＝8，所以8的立方根是（）；因为()3＝0.064，所以0.064的立方根是（）；因为()3＝0，所以0的立方根是（）；因为()3＝－8，所以－8的立方根是（）；因为()3＝－88，所以－的立方根是（）. 2727归纳：正数的立方根是正数，负数的立方根是负数，0的立方根是0，任何数都有唯一的立方根.类似与平方根，一个数a的立方根，用符号“3a”表示，读作“三次根号a”，其中a叫被开方数，3叫根指数，不能省略，若省略表示平方.3. 探究因为＝，－＝；因为27＝，－27＝27.利用开立方和立方互为逆运算关系，求一个数的立方根，就可以利用这种互逆关系，检验其正确性，求负数的立方根，可以先求出这个负数的绝对值的立方根，再取其相反数，一般地，3 a＝－a.三、课堂小结1. 立方根和开立方的定义．2. 正数、0、负数的立方根的特征．3. 立方根与平方根的异同．四、布置作业教材p51、p52习题6.2第1、2、3、5题.第2课时教学内容用有理数估计一个无理的大致范围.一、复习引入复习上节内容，导入新课的教学.二、新课教学1.问题：350有多大呢？人教版义务教育教科书◎数学七年级下册因为33＝27，43＝64，所以3＜＜4；因为3.63＝46.656，3.73＝50.653，所以3.6＜＜3.7；因为3.683＝49.836 032，3.693＝50.24 349，所以3.68＜＜3.69；?? 如此循环下去，可以得到更精确的3的近似值，它是一个无限不循环小数，50＝－3.684 031 49??事实上，很多有理数的立方根都是无限不循环小数．我们用有理数近似地表示它们．2. 利用计算器来求一个数的立方根用计算器求数的立方根的步骤及方法：用计算器求立方根和求平方根的步骤相同，只是根指数不同. 步骤：输入→ 被开方数→ ＝→根据显示写出立方根. 例：用计算器求-5（保留三个有效数字），可以按照下面步骤进行：→ 被开方数→ ＝→ 1.709975947. 所以，-5≈－1.71.三、练习教材p51练习2.四、小结1.立方根的概念和性质.2.用计算器来求一个数的立方根.五、作业教材p52习题6.2第4、8题.【篇二：(新)人教版七年级数学下册6.2《立方根》教学设计】课题：6.2 立方根教学目标：了解立方根和开立方的概念；掌握立方根的性质；会求一个数的立方根．重点：立方根的运算难点：立方根的概念及其运算教学流程：一、知识回顾问题1：什么叫做平方根？如果一个数的平方等于a，那么这个数叫做a的平方根（也叫二次方根）. 即：x2＝a，那么x叫做a的平方根a的平方根记作：_______9的平方根记作：_______144的平方根记作：_______答案：，追问：怎么求一个数的平方根？填空：（1）2的平方根是________;（2）0的平方根是________;（3）－16的平方根是____________.答案：0，没有平方根问题2：平方根具有什么性质呢？正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．二、探究1问题：要制作一种容积为27m3的正方体形状的包装箱，这种包装箱的棱长应该是多？追问1：你还记得正方体的体积与棱长有什么关系吗？答案：v＝a3追问2：谁的立方等于27呢？解：设这种包装箱的棱长为xm，则x3＝27∵ 33＝27∴ x＝3定义：如果一个数的立方等于a，那么这个数叫做a的立方根（也叫三次方根）.即：x3＝a，那么x叫做a的立方根∵ 33＝27∴____是27的立方根答案：3练习1：求下列各数的立方根：解：（1）∵(－3)3＝－27∴－27的立方根是－3（2）∵(333)＝3 2833的立方根是 82 ∴ 3（3）∵(－4)3＝－64∴－64的立方根是－4填空：答案：1，－8，27，－27，1，－2，3，－3定义：求一个数的立方根的运算，叫做开立方.追问：左右两图中的运算有什么关系？想一想：到现在我们学了哪些运算?答案：加、减、乘、除、乘方、开方.三、探究2根据立方根的意义填空.∵（2 ）3 ＝8，∴ 8的立方根是（）；∵（）3 ＝0.064 , ∴ 0.064的立方根是（）；∵（）3 ＝ 0，∴ 0的立方根是（）；∵（）3 ＝－8 ，∴－8的立方根是（）；∵（）3 ＝-88 ，∴-的立方根是（）． 272722，- 33答案：2，0.4，0.4，0，0，－2，－2，-追问：你能发现正数、0和负数的立方根各有什么特点吗？立方根的性质：（1）正数的立方根是正数；（2）负数的立方根是负数；（3）0的立方根是0. 一个数a读作：“三次根号a”，被开方数：a；根指数：3；根指数3，不能省略！8的立方根，表示为：__________的立方根8的根指数是2，根指数2，可以省略！思考：你能归纳出平方根和立方根的异同点吗?(2) 25的平方根是5 （）(3)－64没有立方根（）(5) 0的平方根和立方根都是0 （）追问1：立方根是它本身的数有那些?追问2：算术平方根是它本身的数有那些?答案：0，1四、探究3填空，你能发现其中的规律吗？______，______ ，＝______，______ ，______答案：－2，－2，＝，－3，－3，＝=.例：求下列各式的值：1（2）；（3.13-；（3- 24解：（2）14；练习3：求下列各式的值：1（2）；（3）3.3=-；（3）3=-9 5解：（2）-12；五、探究4问题1：用计算器求下列各式的值：(1(20.001）．解：(1)8 、＝，显示：2．=2．(2)1845、＝，显示：12.264 940 81．≈12.265．强调：有些计算器要用到第二功能键来求一个数的立方根.答案：如第（1）问中，按键顺序为：2nd f、8 、＝问题2：利用计算器计算，并将计算结果填在表中，你发现了什么规律？规律：被开方数的小数点向右（或向左）移动3位，其算术平方根的小数点向右（或向左）移动1位.问题3：0.001）吗？并利用刚才的得到规律说出≈4.624≈0.4624≈46.24 想一想：答：不能六、应用提高1. 你能比较3，4解：∵33＝27，∴ 3=∵ 43＝64 ，∴4=∴3 4强调：被开方数越大，对应的立方根也越大.2. 求下列各式中的 x：（1）9x3＋72＝0；（2）2(x－1)3＝54.解： (1) 9x3＋72＝09x3＝－72【篇三：新人教版数学七年级下册立方根教学设计】数学课时教学计划。

《立方根》优质教案

《立方根》优质教案一、教学目标1.知识与技能a.了解立方根的概念及求解方法；b.掌握求解立方根的基本步骤；c.能够运用立方根求解实际问题。

2.过程与方法培养学生主动思考、合作学习的意识和能力，通过引导与实践，提高学生的学习兴趣和主动参与的积极性。

二、教学重点掌握求解立方根的基本步骤。

三、教学难点能够运用立方根求解实际问题。

四、教学准备多媒体课件、教学资源等。

五、教学过程1.引入新知通过一个生活实例引入立方根的概念。

教师：同学们，你们在生活中是否遇到过需要求立方根的问题呢？学生：暂无回答。

教师：比如，你们在购买物品时，想知道它的体积或边长，就需要求解其立方根。

那么，立方根到底是什么呢？我们来研究一下。

2.概念解释教师出示相关图片或图示，引导学生思考，学生回答问题并进行合作讨论。

教师：根据你们对生活实例的观察和思考，立方根的概念是什么呢？学生：立方根是一个数，它与平方根类似，是指一个数的立方等于给定数字的根。

教师：很好，立方根就是一些数字的立方等于给定数字的根。

那么，我们怎样求解一个数的立方根呢？3.求解立方根的方法教师向学生介绍求解立方根的方法，并进行示范。

教师：求解一个数的立方根，可以通过近似法和进位法两种方法。

我们先来看看近似法。

(1)近似法教师：比如，我们要求解27的立方根，首先，我们要估算它的范围，27大致在什么范围内呢？学生：27大约在3和4之间。

教师：对的。

那么，我们先猜测一个数，比如3，将3的立方计算出来，看看它与原数27的差距有多大。

学生：3的立方是27，恰好等于原数27教师：很好。

我们再尝试另一个数，比如4，将4的立方计算出来，比较它与原数27的大小。

学生：4的立方是64，比原数27要大。

教师：所以，27的立方根应该在3和4之间，可以估算为3.5、我们再计算一下3.5的立方。

学生：3.5的立方是42.875教师：很好。

通过近似法，我们大致求出27的立方根是3.5(2)进位法教师：除了近似法，我们还可以使用进位法来求解立方根。

立方根教案人教版

立方根教案人教版第一章：立方根的概念与性质教学目标：1. 理解立方根的概念；2. 掌握立方根的性质；3. 学会求一个数的立方根。

教学重点：立方根的概念与性质。

教学难点：求一个数的立方根。

教学准备：教师准备PPT或者黑板，用于展示立方根的图像和例子。

教学过程：1. 引入：教师通过展示一个正方体，引导学生思考正方体的体积是由什么决定的。

引导学生认识到正方体的体积是由边长的立方决定的。

2. 讲解：教师讲解立方根的概念，解释立方根的定义和性质。

通过PPT或者黑板展示立方根的图像和例子，帮助学生理解立方根的概念和性质。

3. 练习：教师给出一些例子，让学生求出这些数的立方根。

学生独立完成练习，教师进行讲解和解答。

4. 巩固：教师给出一些练习题，让学生练习求一个数的立方根。

学生独立完成练习，教师进行讲解和解答。

教学反思：通过本节课的学习，学生应该能够理解立方根的概念和性质，并能够求一个数的立方根。

在教学过程中，要注意引导学生通过观察和思考来理解立方根的概念，并通过练习来巩固所学知识。

第二章：立方根的运算教学目标：1. 掌握立方根的运算规则；2. 学会进行立方根的运算。

教学重点：立方根的运算规则。

教学难点：进行立方根的运算。

教学准备：教师准备PPT或者黑板，用于展示立方根的运算规则和例子。

教学过程：1. 引入：教师通过展示一个正方体，引导学生思考正方体的体积是由什么决定的。

引导学生认识到正方体的体积是由边长的立方决定的。

2. 讲解：教师讲解立方根的运算规则，通过PPT或者黑板展示立方根的运算规则和例子，帮助学生理解立方根的运算规则。

3. 练习：教师给出一些例子，让学生进行立方根的运算。

学生独立完成练习，教师进行讲解和解答。

4. 巩固：教师给出一些练习题，让学生进行立方根的运算。

学生独立完成练习，教师进行讲解和解答。

教学反思：通过本节课的学习，学生应该能够掌握立方根的运算规则，并能够进行立方根的运算。

在教学过程中，要注意引导学生通过观察和思考来理解立方根的运算规则，并通过练习来巩固所学知识。