二次函数与字母系数间的关系
二次函数的图象与各项字母系数之间的关系

的关系
学习目标
1、能由a,b,c,∆的符号确定抛物线的位置;由 抛物线的位置确定a,b,c,∆等式子的符号;
2、经历探究问题的过程,加强推理技能训练, 体验类比、转化、符号表示及数形结合的思 想方法.
1.二次函数图象开口方向、大小和二次项系数a的关系
y
y
的图像如图,则下列a、b、
c间的关系判断正确的是( D )
A.ab < 0
B.bc < 0
C.a+b+c > 0 D.a-b+c < 0
8.(绵阳)二次函数y=ax2+bx+c的
图像如图,则不等式bx+a>0的
解为 A.x > a/b
(D)
B.x > -a/b
C.x < a/b D.x < -a/b
谈收获
1.(天津)已知二次函数y=ax2+bx+c,
且a<0,a-b+c>0,则一定有( A )
A.b2-4ac>0
B. b2-4ac=0
C.b2-4ac<0
D. b2-4ac≤0
2.(重庆)二次函数y=ax2+bx+c的图
像如图所示,则点M(b,c/a)在( D )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
图像如图所示,下列结论:
① a+b+c<0,②a-b+c>0;
③ abc>0;④b=2a
中正确个数为
( A)
A.4个
B.3个
C.2个
D.1个
6、无论m为任何实数,二次函数y=x2-(2-m)x+m
二次函数y=ax2+bx+c的图象与字母系数的关系PPT教学课件
12.(阿凡题:)如图,直线y=x+m和抛物线y=x2+bx+c都经过点A(1, 0),B(3,2).
(1)求m的值和抛物线的解析式; (2)求不等式x2+bx+c>x+m的解集;(直接写出答案) (3)若M(a,y1),N(a+1,y2)两点都在抛物线y=x2+bx+c上,试比较y1 与y2的大小.
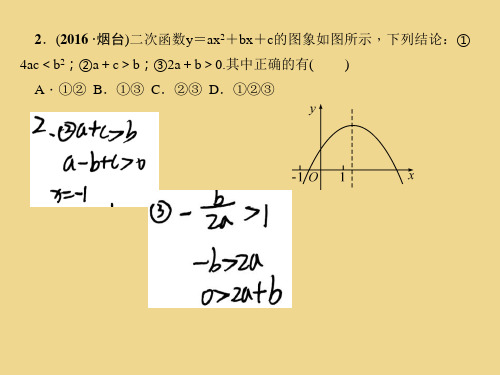
2.(2016·烟台)二次函数y=ax2+bx+c的图象如图所示,下列结论:① 4ac<b2;②a+c>b;③2a+b>0.其中正确的有( )
A.①② B.①③ C.②③ D.①②③
3.二次函数 y=ax2+bx+c(a≠0)的图象如图所示,下列结论正 确的是( )
A.a<0 B.b2-4ac<0 C.当-1<x<3 时,y>0 D.-2ba=1
A.1 ·广安)已知二次函数y=ax2+bx+c(a≠0)的图象如图
所示,并且关于x的一元二次方程ax2+bx+c-m=0有两个不相等的实数根,
下列结论:①b2-4ac<0;②abc>0;③a-b+c<0;④m>-2.其中,正
确的个数有(
)
A.1 B.2 C.3 D.4
解:(1)x=-5或x=1 (2)-5<x<1 (3)y≤9
7.如图,一次函数y1=x与二次函数y2=ax2+bx+c图象相交于P,Q两点,
则函数y=ax2+(b-1)x+c的图象可能是(
)
A
8.(阿凡题:1070544)(2016·巴中)如图是二次函数 y=ax2+bx+c 图 象的一部分,图象过点 A(-3,0),对称轴为直线 x=-1,给出四个结论: ①c>0;②若点 B(-23,y1),C(-25,y2)为函数图象上的两点,则 y1<y2; ③2a-b=0;④4ac4-a b2<0.其中,正确结论的个数是( )
专题05_二次函数与各系数之间的关系(知识点串讲)(解析版)

专题05 二次函数与各系数之间的关系重点突破抛物线中,与函数图像的关系(灵活掌握)⏹二次项系数二次函数中,作为二次项系数,显然.⑴当时,抛物线开口向上,越大,开口越小,反之的值越小,开口越大;⑵当时,抛物线开口向下,越小,开口越小,反之的值越大,开口越大.【总结起来】决定了抛物线开口的大小和方向,的正负决定开口方向,的大小决定开口的大小.⏹一次项系数在二次项系数确定的前提下,决定了抛物线的对称轴.⑴在的前提下,当时,,即抛物线的对称轴在轴左侧(a、b同号);当时,,即抛物线的对称轴就是轴;当时,,即抛物线对称轴在轴的右侧(a、b异号).⑵在的前提下,结论刚好与上述相反,即当时,,即抛物线的对称轴在轴右侧(a、b异号);当时,,即抛物线的对称轴就是轴;当时,,即抛物线对称轴在轴的左侧(a、b同号).【总结起来】在确定的前提下,决定了抛物线对称轴的位置.⏹常数项⑴当时,抛物线与轴的交点在轴上方,即抛物线与轴交点的纵坐标为正;⑵当时,抛物线与轴的交点为坐标原点,即抛物线与轴交点的纵坐标为;⑶当时,抛物线与轴的交点在轴下方,即抛物线与轴交点的纵坐标为负.【总结起来】决定了抛物线与轴交点的位置.总之,只要都确定,那么这条抛物线就是唯一确定的.考查题型考查题型一 根据二次函数的图像判断各系数、各式子符号典例1(2019·莆田市期中)已知二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,下列结论:①abc >0;②2a+b >0;③b 2﹣4ac >0;④a ﹣b+c >0,其中正确的个数是( )A .1B .2C .3D .4【答案】D【详解】①∵抛物线对称轴是y 轴的右侧,∴ab <0,∵与y 轴交于负半轴,∴c <0,∴abc >0, 故①正确;②∵a >0,x=﹣2ba <1,∴﹣b <2a ,∴2a+b >0,故②正确;③∵抛物线与x 轴有两个交点,∴b 2﹣4ac >0,故③正确;④当x=﹣1时,y >0,∴a ﹣b+c >0,故④正确.故选D .变式1-1.(2019·深圳市末)如图,已知二次函数()2y ax bx c a 0=++≠的图象如图所示,有下列5个结论 abc 0>①;b a c ->②;4a 2b c 0++>③;3a c >-④;()a b m am b (m 1+>+≠⑤的实数).其中正确结论的有( )A .①②③B .②③⑤C .②③④D .③④⑤【答案】B【提示】 由抛物线对称轴的位置判断ab 的符号,由抛物线与y 轴的交点判断c 的符号,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所给结论进行判断即可.【详解】 ①对称轴在y 轴的右侧,ab 0∴<,由图象可知:c 0>,abc 0∴<,故①不正确;②当x 1=-时,y a b c 0=-+<,b ac ∴->,故②正确;③由对称知,当x 2=时,函数值大于0,即y 4a 2b c 0=++>,故③正确;b x 12a=-=④, b 2a ∴=-,a b c 0-+<,a 2a c 0∴++<,3a c <-,故④不正确;⑤当x 1=时,y 的值最大.此时,y a b c =++,而当x m =时,2y am bm c =++,所以()2a b c am bm c m 1++>++≠, 故2a b am bm +>+,即()a b m am b +>+,故⑤正确,故②③⑤正确,故选B .【名师点睛】本题考查了图象与二次函数系数之间的关系,二次函数2y ax bx c =++系数符号由抛物线开口方向、对称轴和抛物线与y 轴的交点、抛物线与x 轴交点的个数确定,熟练掌握二次函数的性质是关键.变式1-2.(2019·济南市期中)如图,若二次函数y=ax 2+bx+c (a≠0)图象的对称轴为x=1,与y 轴交于点C ,与x 轴交于点A 、点B (﹣1,0),则①二次函数的最大值为a+b+c ;②a ﹣b+c <0;③b 2﹣4ac <0;④当y >0时,﹣1<x <3,其中正确的个数是( )A .1B .2C .3D .4【答案】B【解析】 详解:①∵二次函数y=ax 2+bx+c (a≠0)图象的对称轴为x=1,且开口向下,∴x=1时,y=a+b+c ,即二次函数的最大值为a+b+c ,故①正确;②当x=﹣1时,a ﹣b+c=0,故②错误;③图象与x 轴有2个交点,故b 2﹣4ac >0,故③错误;④∵图象的对称轴为x=1,与x 轴交于点A 、点B (﹣1,0),∴A (3,0),故当y >0时,﹣1<x <3,故④正确.故选B .名师点睛:此题主要考查了二次函数的性质以及二次函数最值等知识,正确得出A 点坐标是解题关键. 变式1-3.(2018·福州市期中)二次函数y =ax 2+bx +c (a ≠0)的图象如图,下列结论正确的是( )A .a <0B .b 2-4ac <0C .当-1<x <3时,y >0D .-2b a=1 【答案】D【解析】 试题提示:根据二次函数的图象和性质进行判断即可.解:∵抛物线开口向上,∴0a >∴A 选项错误,∵抛物线与x 轴有两个交点,∴240b ac ->∴B 选项错误,由图象可知,当-1<x <3时,y <0∴C 选项错误,由抛物线的轴对称性及与x 轴的两个交点分别为(-1,0)和(3,0)可知对称轴为1x =即-=1,∴D 选项正确,故选D.变式1-4.(2019宁波市期中)如图,已知二次函数y=ax 2+bx+c (a≠0)的图象如图所示,有下列5个结论:①abc <0;②b <a+c ;③4a+2b+c >0;④2c <3b ;⑤a+b <m (am+b )(m≠1的实数).其中正确结论的有( )A .①②③B .①③④C .③④⑤D .②③⑤【答案】B【解析】 试题提示:由抛物线的开口方向判断a 的符号,由抛物线与y 轴的交点判断c 的符号,然后根据对称轴及抛物线与x 轴交点情况进行推理,进而对所得结论进行判断.试题解析:①由图象可知:a <0,b >0,c >0,abc <0,故此选项正确;②当x=-1时,y=a-b+c <0,即b >a+c ,错误;③由对称知,当x=2时,函数值大于0,即y=4a+2b+c >0,故此选项正确;④当x=3时函数值小于0,y=9a+3b+c <0,且x=-2b a =1, 即a=-2b ,代入得9(-2b )+3b+c <0,得2c <3b ,故此选项正确; ⑤当x=1时,y 的值最大.此时,y=a+b+c ,而当x=m 时,y=am 2+bm+c ,所以a+b+c >am 2+bm+c ,故a+b >am 2+bm ,即a+b >m (am+b ),故此选项错误.故①③④正确.故选B .变式1-5.(2019·泉州市期末次函数2y ax bx c =++的图象如图所示,下列结论中正确的是( )① 0abc < ②240b ac -< ③2a b > ④22()a c b +<A .1个B .2个C .3个D .4个【答案】A 【提示】由函数图象可知a <0,对称轴-1<x <0,20b a ->;0b <,图象与y 轴的交点c >0,函数与x 轴有两个不同的交点;△=b 2-4ac >0;再由图象可知当x=1时,y <0,即a+b+c <0;当x=-1时,y >0,即a-b+c >0;即可求解.【详解】解:由函数图象可知0a <,对称轴10x -<<,图象与y 轴的交点0c >,函数与x 轴有两个不同的交点, ∴2b a >,0b <;③错误240b ac ∆=->;②错0abc >;①错误当1x =时,0y <,即0a b c ++<;当1x =-时,0y >,即0a b c -+>;∴()()0a b c a b c ++-+<,即22()a c b +<;∴只有④是正确的;故选:A .【名师点睛】本题考查二次函数的图象及性质;熟练掌握函数的图象及性质,能够通过图象获取信息,推导出a ,b ,c ,△,对称轴的关系是解题的关键.考查题型二 一次函数与二次函数的综合判定典例2(2018·烟台市期末)如图,函数221y ax x =-+和y ax a =-(a 是常数,且0a ≠)在同一平面直角坐标系的图象可能是( )A .B .C .D .【答案】B【解析】详解:A .由一次函数y =ax ﹣a 的图象可得:a <0,此时二次函数y =ax 2﹣2x +1的图象应该开口向下.故选项错误;B .由一次函数y =ax ﹣a 的图象可得:a >0,此时二次函数y =ax 2﹣2x +1的图象应该开口向上,对称轴x =﹣22a->0.故选项正确; C .由一次函数y =ax ﹣a 的图象可得:a >0,此时二次函数y =ax 2﹣2x +1的图象应该开口向上,对称轴x =﹣22a->0,和x 轴的正半轴相交.故选项错误; D .由一次函数y =ax ﹣a 的图象可得:a >0,此时二次函数y =ax 2﹣2x +1的图象应该开口向上.故选项错误.故选B .名师点睛:本题考查了二次函数以及一次函数的图象,解题的关键是熟记一次函数y =ax ﹣a 在不同情况下所在的象限,以及熟练掌握二次函数的有关性质:开口方向、对称轴、顶点坐标等.变式2-1.(2018·陇南市期中)当ab >0时,y =ax 2与y =ax +b 的图象大致是( )A .B .C .D .【答案】B【详解】∵ab >0,∴a 、b 同号.当a >0,b >0时,抛物线开口向上,顶点在原点,一次函数过一、二、三象限,没有图象符合要求;当a <0,b <0时,抛物线开口向下,顶点在原点,一次函数过二、三、四象限,B 图象符合要求. 故选B .变式2-2.(2020·无锡市期末)在同一坐标系内,一次函数y ax b =+与二次函数2y ax 8x b =++的图象可能是A .B .C .D .【答案】C【提示】x=0,求出两个函数图象在y 轴上相交于同一点,再根据抛物线开口方向向上确定出a >0,然后确定出一次函数图象经过第一三象限,从而得解.【详解】x=0时,两个函数的函数值y=b,所以,两个函数图象与y轴相交于同一点,故B、D选项错误;由A、C选项可知,抛物线开口方向向上,所以,a>0,所以,一次函数y=ax+b经过第一三象限,所以,A选项错误,C选项正确.故选C.变式2-3.(2018·巴彦淖尔市期中)在同一直角坐标系中,一次函数y=ax+c和二次函数y=ax2+c的图象大致为()A.B.C.D.【答案】D【提示】根据二次函数的开口方向,与y轴的交点;一次函数经过的象限,与y轴的交点可得相关图象.【详解】解:∵一次函数和二次函数都经过y轴上的(0,c),∴两个函数图象交于y轴上的同一点,故B选项错误;当a>0时,二次函数开口向上,一次函数经过一、三象限,故C选项错误;当a<0时,二次函数开口向下,一次函数经过二、四象限,故A错误,D选项正确;故选D.【名师点睛】本题考查二次函数及一次函数的图象的性质;用到的知识点为:二次函数和一次函数的常数项是图象与y 轴交点的纵坐标;一次函数的一次项系数大于0,图象经过一、三象限;小于0,经过二、四象限;二次函数的二次项系数大于0,图象开口向上;二次项系数小于0,图象开口向下.变式2-4.(2018·成都市期末)同一平面直角坐标系中,一次函数y=ax+b和二次函数y=ax2+bx+c的图象可能为()A .B .C .D .【答案】A【提示】本题可先由二次函数y=ax 2+bx+c 图象得到字母系数的正负,再与一次函数y=ax+b 的图象相比较看是否一致.【详解】A 、由抛物线可知,a <0,x=﹣2b a<0,得b <0,由直线可知,a <0,b <0,故本选项正确; B 、由抛物线可知,a >0,由直线可知,a <0,故本选项错误; C 、由抛物线可知,a >0,x=﹣2b a >0,得b <0,由直线可知,a >0,b >0,故本选项错误; D 、由抛物线可知,a >0,由直线可知,a <0,故本选项错误.故选A .考查题型三 用待定系数法求二次函数解析式典例3(2018·合肥市期末)已知二次函数的图象经过点(-1,-5),(0,-4)和(1,1),则这二次函数的表达式为( )A .y =-6x 2+3x +4B .y =-2x 2+3x -4C .y =x 2+2x -4D .y =2x 2+3x -4【答案】D【提示】利用待定系数法即可求出抛物线的解析式.【详解】解:设所求函数的解析式为y =ax 2+bx +c ,把(-1,-5),(0,-4),(1,1)分别代入, 得:541a b c c a b c -+-⎧⎪-⎨⎪++⎩===解得234a b c ⎧⎪⎨⎪-⎩===所求的函数的解析式为y =2x 2+3x -4.故选:D【名师点睛】 本题考查了用待定系数法求函数解析式的方法,同时还考查了方程组的解法等知识.变式3-1.(2019·青岛市期末)如图是某个二次函数的图象,根据图象可知,该二次函数的表达式是( )A .y=x 2﹣x ﹣2B .y=﹣12x 2﹣12x+2C .y=﹣12x 2﹣12x+1D .y=﹣x 2+x+2 【答案】D【提示】 根据开口方向、顶点坐标、对称轴逐项提示即可.【详解】A 、由图象可知开口向下,故a <0, 故A 错误;B 、抛物线过点(﹣1,0),(2,0),根据抛物线的对称性,顶点的横坐标是12, 而211222y x x =--+的顶点横坐标是﹣12, 故B 错误; C 、211122y x x =--+的顶点横坐标是﹣12, 故C 错误; D 、22y x x =-++的顶点横坐标是12,并且抛物线过点(﹣1,0),(2,0),故D 正确. 故选D.【名师点睛】本题考察了二次函数的图像和性质,对于二次函数y =ax 2+bx +c (a ,b ,c 为常数,a ≠0),当a >0时,抛物线开口向上,当a <0时,抛物线开口向下;其对称轴是直线:2b x a =-;若抛物线与轴的两个交点是A (x 1,0),B (x 2,0),则抛物线的对称轴是:122x x x +=. 变式3-2.(2018·海淀区期末)在平面直角坐标系xOy 中,四条抛物线如图所示,其解析式中的二次项系数一定小于1的是( )A .y 1B .y 2C .y 3D .y 4【答案】A【提示】 由图象的点的坐标,根据待定系数法求得解析式即可判定.【详解】由图象可知:抛物线y 1的顶点为(-2,-2),与y 轴的交点为(0,1),根据待定系数法求得y 1=34(x+2)2-2; 抛物线y 2的顶点为(0,-1),与x 轴的一个交点为(1,0),根据待定系数法求得y 2=x 2-1;抛物线y 3的顶点为(1,1),与y 轴的交点为(0,2),根据待定系数法求得y 3=(x-1)2+1;抛物线y 4的顶点为(1,-3),与y 轴的交点为(0,-1),根据待定系数法求得y 4=2(x-1)2-3;综上,解析式中的二次项系数一定小于1的是y 1故选A .【名师点睛】本题考查了二次函数的图象,二次函数的性质以及待定系数法求二次函数的解析式,根据点的坐标求得解析式是解题的关键.变式3-3.(2018·庆阳市期中)已知某二次函数的图象如图所示,则这个二次函数的解析式为( )A .22(1)8y x =++B .218(1)8y x =+-C .22(1)89y x =-+ D .22(1)8y x =-- 【答案】D【提示】顶点式:y=a (x-h )2+k (a ,h ,k 是常数,a≠0),其中(h ,k )为顶点坐标.【详解】解:由图知道,抛物线的顶点坐标是(1,-8)故二次函数的解析式为y=2(x-1)2-8故选:D .【名师点睛】本题考查由顶点坐标式看出抛物线的顶点坐标,y=a (x-h )2+k 的顶点坐标是(h ,k ).变式3-4.(2018·庆阳市期末)顶点在点M(﹣2,1),且图象经过原点的二次函数解析式是( )A .y =(x ﹣2)2+1B .y =﹣14(x+2)2+1C .y =(x+2)2+1D .y =14(x ﹣2)2+1 【答案】B【提示】二次函数图象的顶点在点M (-2,1),可设函数的解析式是y =a (x +2)2+1,再将原点的坐标代入求出a 的值即可.【详解】解:∵二次函数图象的顶点在点M (-2,1),可设函数的解析式是y =a (x +2)2+1,把点(0,0)代入得,4a +1=0,得:a =-14, 则此二次函数的解析式是y =-14(x +2)2+1, 故选B.【名师点睛】本题主要考查了待定系数法求二次函数的解析式,解决本题的关键是要熟练掌握待定系数法求二次函数解析式.变式3-5.(2019·吉林市期中)已知二次函数的图象如图所示,则这个二次函数的表达式为( )A .2 23y x x =-+B .2 23y x x =--C .2 23y x x =+-D .2 23y x x =++【答案】B【提示】根据题意,把抛物线经过的三点代入函数的表达式,列出方程组,解出各系数则可.【详解】根据题意,图象与y 轴交于负半轴,故c 为负数,又四个选项中,B 、C 的c 为-3,符合题意,故设二次函数的表达式为y=ax 2+bx+c ,抛物线过(-1,0),(0,-3),(3,0),所以0{3930a b c c a b c -+-++===,解得a=1,b=-2,c=-3,这个二次函数的表达式为y=x 2-2x-3.故选:B .【名师点睛】本题考查了用待定系数法求函数表达式的方法,同时还考查了方程组的解法等知识,是比较常见的题目.。
小专题(六) 二次函数的图象与字母系数之间的关系

小专题(六)二次函数图象与字母系数之间的关系抛物线y=ax2+bx+c的图象与字母系数a,b,c之间的关系:(1)当a>0时,开口向上,当a<0时,开口向下;(2)若对称轴在y轴的左边,则a,b同号,若对称轴在y轴的右边,则a,b异号;(3)若抛物线与y轴的正半轴相交,则c>0,若抛物线与y轴的负半轴相交,则c<0,若抛物线经过原点,则c =0;(4)当x=1时,y=ax2+bx+c=a+b+c;当x=-1时,y=ax2+bx+c=a-b+c;当x=2时,y=ax2+bx+c =4a+2b+c;当x=-2时,y=ax2+bx+c=4a-2b+c;…(5)当对称轴x=1时,x=-b2a=1,所以-b=2a,此时2a+b=0;当对称轴x=-1时,x=-b2a=-1,所以b=2a,此时2a-b=0;判断2a+b大于或等于0,看对称轴与1的大小关系;判断2a-b大于或等于0,看对称轴与-1的大小关系;(6)b2-4ac>0⇔二次函数与横轴有两个交点;b2-4ac=0⇔二次函数与横轴有一个交点;b2-4ac<0⇔二次函数与横轴无交点.1.若二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列选项正确的是(C)A.a>0 B.c>0C.ac>0 D.bc<02.二次函数y=ax2+bx+c的图象如图所示,给出以下结论:①a>0;②b>0;③c<0;④b2-4ac>0,其中所有正确结论的序号是(A)A.②④B.①③C.③④D.①②③3.(陕西中考)二次函数y=ax2+bx+c(a≠0)的图象如图所示,则下列结论中正确的是(D)A.c>-1 B.b>0C.2a+b≠0 D.9a+c>3b4.(龙岩中考)已知抛物线y=ax2+bx+c的图象如图所示,则|a-b+c|+|2a+b|=(D)A.a+b B.a-2bC.a-b D.3a5.(孝感中考)如图是抛物线y=ax2+bx+c的部分图象,其顶点坐标为(1,n),且与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论:①a-b+c>0;②3a+b=0;③b2=4a(c-n);④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.其中正确结论的个数是(C)A.1 B.2C.3 D.46.(扬州中考)如图,抛物线y=ax2+bx+c(a>0)的对称轴是过点(1,0)且平行于y轴的直线,若点P(4,0)在该抛物线上,则4a-2b+c的值为0.。
人教版九年级上 二次函数的图像和字母系数之间的关系(20张ppt)

当堂检测
1.抛物线 y=x2-6x+5 的顶点坐标为 A.(3,-4) B.(3,4) C.(-3,-4) D.(-3,4)
(A )
解 析 配方:y=x2-6x+5=(x-3)2-4,所以顶点坐 标为(3,-4),故选 A.
当堂检测
1.抛物线 y=x2-6x+5 的顶点坐标为 A.(3,-4) B.(3,4) C.(-3,-4) D.(-3,4)
抛物线有最低点,当 x 抛物线有最高点,当 x=
最值 =-2ba时,y 有最小值, -2ba时,y 有最大值,
y 最小值=4ac4-a b2.
y 最大值=4ac4-a b2.
字母
关键点回顾
1.a>0 时,开口向上;2.a<0 时,开口向下. a
|a|越大,抛物线的开口程度___越__小___,|a|越小,抛物线的开口程度___越__大___.
y
1、点(1,a+b+c) a+b+c>0
2、点 (-1,a-b+c) a-b+c=0
●
-2 -1 o 1 2
x
3、点 (2,4a+2b+c) 4a+2b+c>0
4、点 (-2,4a-2b+c) 4a-2b+c<0
…………… ……………
已知二次函数y=ax2+bx+c(a≠0)
的图象如图所示,下列结论:
() A.1 B.2 C.3 D.4
C
由-12<0,得抛物线开口向下,①正确;关系 式写成了顶点形式,因此对称轴为直线 x=-1,顶点坐标
为(-1,3),②错误;③正确;由-12<0,当 x>1>-1 时, y 随 x 的增大而减小,④正确.故选 C.
二次函数与字母系数的关系(教案)

(三)实践活动(用时10分钟)
1.分组讨论:学生们将分成若干小组,每组讨论一个与二次函数相关的问题,如“如何通过改变系数来得到特定的图像”。
(二)新课讲授(用时10分钟)
1.理论介绍:首先,我们要了解二次函数的基本概念。二次函数是形如y=ax^2+bx+c的函数,其中a、b、c是常数且a≠0。它在数学和物理学等多个领域都有广泛应用,如描述物体抛掷运动的轨迹。
2.案例分析:接下来,我们来看一个具体的案例。通过分析y=x^2和y=-2x^2+4x+1这两个函数的图像,了解系数a、b、c对图像的具体影响。
- b对图像对称轴的影响;
- c对图像与y轴交点的影响;
3.结合具体实例,通过调整系数,观察图像变化,总结规律;
4.解决实际问题,运用字母系数的关系解决二次函数相关问题。
二、核心素养目标
本节课的核心素养目标旨在培养学生的以下能力:
1.掌握二次函数图像的基本性质,提高学生的数形结合思维能力,强化几何直观;
最后,关于课堂总结部分,我觉得自己在引导学生们进行反思和总结时,还可以做得更好。在今后的教学中,我会更加注重这一点,让学生们在总结过程中,能够更好地梳理所学知识,提高他们的自主学习能力。
二次函数与字母系数的关系(教案)
一、教学内容
本节教学内容选自人教版《数学》八年级下册第11章“二次函数”,重点探讨二次函数y=ax^2+bx+c(a≠0)中字母系数a、b、c对函数图像的影响。具体内容包括:
1.二次函数图像的基本性质;
二次函数的图像与字母a、b、c的关系

课次教学方案教学过程:一、知识要点二次函数y=ax 2+bx+c 系数符号确实定:〔1〕a 由抛物线开口方向确定:开口方向向上,那么a >0;否那么a <0. 〔2〕b 由对称轴和a 的符号确定:由对称轴公式x=判断符号.〔3〕c 由抛物线与y 轴的交点确定:交点在y 轴正半轴,那么c >0;否那么c <0.〔4〕b 2-4ac 的符号由抛物线与x 轴交点的个数确定:2个交点,b 2-4ac >0;1个交点,b 2-4ac=0; 没有交点,b 2-4ac <0.〔5〕当x=1时,可确定a+b+c 的符号,当x=-1时,可确定a-b+c 的符号. 〔6〕由对称轴公式x=,可确定2a+b 的符号.二、根底练习1、抛物线y=ax 2+bx+c 〔a ≠0〕在平面直角坐标系中的位置如下图,那么以下结论中,正确的选项是〔 D 〕 A 、a >0 B 、b <0 C 、c <0 D 、a+b+c >02、二次函数y=ax 2+bx+c 的图象如图,其对称轴x=-1,给出以下结果①b 2>4ac ; ②abc >0;③2a+b=0; ④a+b+c >0;⑤a-b+c <0,那么正确的结论是〔 D 〕 A 、①②③④ B 、②④⑤ C 、②③④ D 、①④⑤任课教师学科 版本 年段 辅导类型 上课时间学生签名数学北师大初三课题二次函数y=a 2x +bx+c 系数符号确实定方法课次教学目标掌握二次函数中字母 a 、b 、c 三者与图象之间的关系。
教学策略 教学重点、难点:利用图形的性质与特殊性来确定字母a 、b 、c 三者之间的关系。
3、如图,二次函数y=ax 2+bx+c 的图象与y 轴正半轴相交,其顶点坐标为〔21,1〕,以下结论:①ac <0;②a+b=0;③4ac-b 2=4a ;④a+b+c <0.其中正确结论的个数是〔 C 〕1\2\3 A 、1 B 、2 C 、3 D 、44、二次函数y=ax 2+bx+c 的图象如下图,对称轴为直线x=1,那么以下结论正确的选项是〔B 〕 A 、ac >0 B 、方程ax 2+bx+c=0的两根是x 1=-1,x 2=3 C 、2a-b=0 D 、当x >0时,y 随x 的增大而减小5、二次函数y=ax 2+bx+c 〔a ,b ,c 为常数,a ≠0〕的图象如下图,有以下结论: ①abc >0,②2b -4ac <0,③a-b+c >0,④4a-2b+c <0,其中正确结论的个数是〔A4 〕 A 、1 B 、2 C 、3 D 、46、〔如下图的二次函数y=ax 2+bx+c 的图象中,刘星同学观察得出了下面四条信息: 〔1〕b 2-4ac >0;〔2〕c >1;〔3〕2a-b <0;〔4〕a+b+c <0.你认为其中错误的有〔D2〕 A 、2个 B 、3个 C 、4个 D 、1个7、抛物线y=ax 2+bx+c 〔a ≠0〕的图象如下图,那么以下说法正确的选项是〔C 〕 A 、b 2-4ac <0 B 、abc <0 C 、 -a2b<-1 D 、a-b+c <08、二次函数y=ax 2+bx+c 〔a ≠0〕的图象如下图,现有以下结论:①b 2-4ac >0 ②a >0 ③b >0 ④c >0 ⑤9a+3b+c <0,那么其中结论正确的个数是〔B 〕1/2/5 A 、2个 B 、3个 C 、4个 D 、5个9、二次函数y=ax 2的图象开口向上,那么直线y=ax-1经过的象限是〔D 〕 A 、第一、二、三象限 B 、第二、三、四象限 C 、第一、二、四象限 D 、第一、三、四象限10、二次函数y=ax 2+bx+c 的图象如下图,那么以下结论正确的选项是〔D 〕A 、a <0,b <0,c >0,b 2-4ac >0B 、a >0,b <0,c >0,b 2-4ac <0C 、a <0,b >0,c <0,b 2-4ac >0D 、a <0,b >0,c >0,b 2-4ac >011、二次函数y=ax 2+bx+c 的图象如下图,那么以下判断不正确的选项是〔B 〕 A 、ac <0 B 、a-b+c >0C 、b=-4aD 、关于x 的方程a 2x +bx+c=0的根是x 1=-1,x 2=512、二次函数y=ax 2+bx+c 的图象如下图,那么a ,b ,c 满足〔A 〕A 、a <0,b <0,c >0,2b -4ac >0 B 、a <0,b <0,c <0,2b -4ac >0 C 、a <0,b >0,c >0,2b -4ac <0 D 、a >0,b <0,c >0,2b -4ac >013、二次函数y=2ax +bx+c 〔a ≠0〕的图象如下图,有以下4个结论,其中正确的结论是〔B 〕 A 、abc >0 B 、b >a+c C 、2a-b=0 D 、2b -4ac <014、二次函数y=2ax +bx+c 〔a ≠0〕的图象如下图,那么以下结论: ①ac >0;②a-b+c <0;③当x <0时,y <0;④方程2ax +bx+c=0〔a ≠0〕有两个大于-1的实数根.其中错误的结论有〔C 〕 A 、②③ B 、②④ C 、①③ D 、①④15、如下图为二次函数y=ax 2+bx+c 〔a ≠0〕的图象,在以下选项中错误的选项是〔C 〕 A 、ac <0 B 、x >1时,y 随x 的增大而增大 C 、a+b+c >0 D 、方程ax 2+bx+c=0的根是1x =-1,2x =316、二次函数y=ax 2+bx+c 的图象如下图,以下结论错误的选项是〔B 〕 A 、ab <0 B 、ac <0C 、当x <2时,函数值随x 增大而增大;当x >2时,函数值随x 增大而减小D 、二次函数y=2ax +bx+c 的图象与x 轴交点的横坐标就是方程2ax +bx+c=0的根17、二次函数y=ax 2+bx+c 的图象如下图,那么以下结论正确的选项是〔D 〕 A 、a >0 B 、c <0 C 、b 2-4ac <0 D 、a+b+c >018、二次函数y=ax 2+bx+c 〔a ≠0〕的图象如下图,以下结论①a ,b 异号;②当x=1和x=3时,函数值相等; ③4a+b=0;④当y=4时,x 的取值只能为0,结论正确的个数有〔 C 〕个.1/2/3 A 、1 B 、2 C 、3 D 、4三、能力练习c bx ax y ++=2的图象如图 l -2-2所示,那么a 、b 、c 满足〔 〕 A .a <0,b <0,c >0 B .a <0,b <0,c <0C .a <0,b >0,c >0D .a >0,b <0,c >02.二次函数c bx ax y ++=2(a≠0〕且a <0,a -b+c >0,那么一定有〔 〕A .b 2-4ac >0B .b 2-4ac =0C .b 2-4ac <0D .b 2-4ac≤03.二次函数c bx ax y ++=2的图象如图1-2-10,那么点〔b ,c a〕在〔 〕A .第一象限B .第二象限C .第三象限D .第四象限4.假设二次函数c bx ax y ++=2的图象如图,那么ac_____0〔“<〞“>〞或“=〞〕第4题图5.二次函数c bx ax y ++=2的图象如图 1-2-14所示,那么以下关于a 、b 、c 间的关系判断正确的选项是〔 〕 A .ab <0 B 、bc <0 C .a+b +c >0 D .a -b 十c <0四、知识小结:例题.抛物线c bx ax y ++=2过三点〔-1,-1〕、〔0,-2〕、〔1,l 〕.〔1〕求抛物线所对应的二次函数的表达式; 〔2〕写出它的开口方向、对称轴和顶点坐标;〔3〕这个函数有最大值还是最小值? 这个值是多少?五、中考真题回忆:〔09佛山〕19.〔1〕请在坐标系中画出二次函数22y x x =-+的大致图象;〔2〕在同一个坐标系中画出22y x x =-+的图象向上平移两个单位后的图象; 〔3〕直接写出平移后的图象的解析式. 注:图中小正方形网格的边长为1.〔1〕画图〔略〕注:根本反映图形的特征〔如顶点、对称性、变化趋势、平滑〕给2分, 满足其中的两至三项给1分,满足一项以下给0分; 〔2〕画图、写解析式〔略〕注:画图总分值2分,同〔1〕的标准;写解析式2分〔无过程不扣分〕.〔11·佛山〕21.如图,二次函数y =ax 2+bx +c 的图像经过A 〔-1,-1〕、B 〔0,2〕、C 〔1,3〕; 〔1〕求二次函数的解析式; 〔2〕画出二次函数的图像;【答案】解:〔1〕根据题意,得⎩⎪⎨⎪⎧a -b +c =-1c =2a +b +c =3………………2分解得a =-1,b =2,c =2………………4分所以二次函数的解析式为y =-x 2+2x +2………………5分〔2〕二次函数的图象如图………………8分 给分要点:顶点、对称、光滑〔各1分〕〔12佛山〕xyO第19题图xyoABC1xyoABC122.(1)任选以下三个条件中的一个,求二次函数c bx ax y ++=2的解析式; ①y 随x 变化的局部数值规律如下表:②有序数对()0,1-、()4,1、()0,3满足c bx ax y ++=2; ③函数c bx ax y ++=2的图象的一局部〔如图〕. (2)直接写出二次函数c bx ax y ++=2的三个性质.解析:〔1〕方法一:由 可得:C=3,0=+-c b a ,4=++c b a ,所以1-=a ,2=b ,C=3,所以二次函数解析式为:322++-=x x y方法二:由②可得:0=+-c b a ,4=++c b a ,039=++c b a ,解之得:1-=a ,2=b ,C=3,所以二次函数解析式为:322++-=x x y 方法三:由③可得:C=3,0=+-c b a ,12=-ab,解之得:1-=a ,2=b ,C=3, 所以二次函数解析式为:322++-=x x y 〔三种选其一即可〕〔2〕1、对称轴为1=x , 2、开口向下 3、与x 轴有2个交点 4、交 y 轴正半轴考察知识:待定系数法求二次函数解析式、二次函数的性质及图像〔2021•佛山〕24.如图①,抛物线y=ax 2+bx+c 经过点A 〔0,3〕,B 〔3,0〕,C 〔4,3〕.x -1 0 1 2 3 y343〔1〕求抛物线的函数表达式;〔2〕求抛物线的顶点坐标和对称轴;〔3〕把抛物线向上平移,使得顶点落在x轴上,直接写出两条抛物线、对称轴和y轴围成的图形的面积S〔图②中阴影局部〕.分析:〔1〕把点A、B、C代入抛物线解析式y=ax2+bx+c利用待定系数法求解即可;〔2〕把抛物线解析式整理成顶点式形式,然后写出顶点坐标与对称轴即可;〔3〕根据顶点坐标求出向上平移的距离,再根据阴影局部的面积等于平行四边形的面积,列式进展计算即可得解.解:〔1〕∵抛物线y=ax2+bx+c经过点A〔0,3〕,B〔3,0〕,C〔4,3〕,∴,解得,所以抛物线的函数表达式为y=x2﹣4x+3;〔2〕∵y=x2﹣4x+3=〔x﹣2〕2﹣1,∴抛物线的顶点坐标为〔2,﹣1〕,对称轴为直线x=2;〔3〕如图,∵抛物线的顶点坐标为〔2,﹣1〕,∴PP′=1,阴影局部的面积等于平行四边形A′APP′的面积,平行四边形A′APP′的面积=1×2=2,∴阴影局部的面积=2.点评:此题考察了待定系数法求二次函数解析式,二次函数的性质,二次函数图象与几何变换,〔3〕根据平移的性质,把阴影局部的面积转化为平行四边形的面积是解题的关键.【本文档内容可以自由复制内容或自由编辑修改内容期待你的好评和关注,我们将会做得更好】。
专题:二次函数的图象与字母系数的关系

专题:二次函数y =ax 2+bx +c (a ≠0)的图象与字母系数的关系二次函数y =ax 2+bx +c (a ≠0)系数符号的确定:⑴a 由抛物线开口方向确定:开口方向向上,则a >0;否则a <0.⑵b 由对称轴和a 的符号确定:由对称轴公式x = -2ba判断符号(左同右异). ⑶c 由抛物线与y 轴的交点确定:交点在y 轴正半轴,则c >0;否则c <0.⑷b 2-4ac 的符号由抛物线与x 轴交点的个数确定:2个交点,b 2-4ac >0;1个交点,b 2-4ac =0;没有交点,b 2-4ac <0. ⑸当x =1时,y =a +b +c ,当x =-1时,y =a -b +c .故由点(1, a +b +c ) 所在的象限,可判断a +b +c 的符号;由点(-1, a -b +c ) 所在的象限,可判断a -b +c 的符号.同理,当x =2时,可确定4a +2b +c 的符号,当x =-2时,可确定4a -2b +c 的符号……⑹由对称轴x = -2b a 与x =±1的位置关系,可确定2a ±b 的符号.当x = -2b a =1时,b = -2a ,即2a +b =0;当x = -2ba=-1时,b = 2a ,即2a -b =0.例1.抛物线y =ax 2+bx +c 图象如图所示,则下列式子中正确的个数为( )①a <0;②b <0;③c >0;④a +b +c >0;⑤ 4a -2b +c <0;⑥2a +b >0;⑦b 2-4ac >0;⑧4a +c <0C .5D .6c 的图象如图所示,给出下列结论:①2a +b >0;②b >a >c ;③若-1<m <n <1,则m +n <-ba;④3|a |+|c |<2|b |.其中正确的结论是 (写出你认为正确的所有结论序号).例3.二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,与y 轴相交点C ,与x 轴负半轴相交点A ,且OA =OC ,下列5个结论:①abc >0;②b <a +c ;③4a +2b +c >0;④2a +b =0;⑤c +1a= -2,其中正确的结论有 .(请填序号)强化训练1.如图为二次函数y =ax 2+bx +c (a ≠0)的图象,则下列说法:①a >0②2a +b =0 ③a +b +c >0 ④当-1<x <3时,y >0,其中正确的个数为( )A .1 B .2 C .3 D .42.已知二次函数y =ax 2+bx +c +2的图象如图所示,顶点为(-1,0),下列结论:①abc <0;②b 2-4ac =0;③a >2;④4a -2b +c >0.其中正确结论的个数是( )A .1 B .2 C .3 D .43.已知二次函数y =ax 2+bx +c 的图象如图所示,则下列结论:①c =2;②b 2-4ac >0;③2a +b =0;④a -b +c <0.其中正确的为( )A .①②③ B .①②④ C .①② D .③④4.如图是二次函数y =ax 2+bx +c =(a ≠0)图象的一部分,对称轴是直线x =-2.关于下列结论:①ab <0;②b 2-4ac >0;③9a -3b +c <0;④b -4a =0;⑤方程ax 2+bx =0的两个根为x 1=0,x 2=-4,其中正确的结论有( ) A .①③④ B .②④⑤ C .①②⑤ D .②③⑤5.已知二次函数y =ax 2+bx +c (a ≠0)的图象如图所示,有下列5个结论:①abc >0;②b <a +c ;③4a +2b +c >0;④2c <3b ;⑤a +b >m (am +b )(m ≠1的实数).其中正确的结论有( ) A .2个 B .3个 C .4个 D .5个6.如图,抛物线y =ax 2+bx +c (a ≠0)过点(1,0)和点(0,-2),且顶点在第三象限,设P =a -b +c ,则P 的取值范围是( )A .-4<P <0 B .-4<P <-2 C .-2<P <0 D .-1<P <07.已知二次函数y =ax 2+bx +c 的图象与x 轴交于点(-2,0)、(x 1,0),且1<x 1<2,与y 轴的正半轴的交点在(0,2)的下方.下列结论:①4a -2b +c =0;②a -b +c <0;③2a +c >0;④2a -b +1>0.其中正确结论的个数是( )个.A .4个B .3个C .2个D .1个8.如图,已知二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点A (-1,0),对称轴为直线x =1,与y 轴的交点B 在(0,2)和(0,3)之间(包括这两点),下列结论:①当x >3时,y <0;②3a +b <0;③-1≤a ≤-23;④4ac -b 2>8a ;其中正确的结论是( )A .①③④ B .①②③ C .①②④ D .①②③④9. 如图,二次函数y =ax 2+bx +c (a ≠0)的图象经过点(1,2)且与x 轴交点的横坐标分别为x 1,x 2,其中-1<x 1<0,1<x 2<2,下列结论:4a +2b +c <0,2a +b <0,b 2+8a >4ac ,a <-1,其中结论正确的有( ) A .1个B .2个C .3个D .4个10.抛物线y =ax 2+bx +c (a ≠0)满足条件:(1)4a -b =0;(2)a -b +c >0;(3)与x 轴有两个交点,且两交点间的距离小于2.以下有四个结论:①a <0;②c >0;③a +b +c <0;④4c <a <3c,其中所有正确结论的序号是 .有已知二次函数y=ax2+bx+c的图象与x轴交于点(-2,0),(x1,0),且1<x1<2,与y轴正半轴的交点在(0,2)的下方,下列结论:①a<b<0;②2a+c>0;③4a+c<0;④2a-b+1>0.其中正确的结论是.(填写序号)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
模块二:图像与b2-4ac 间的关系
1.二次函数y=ax2+bx+c的图象 如图所示,那么关于x的方程ax2 +bx+c=0的Δ的情况是( ) AΔ<0 BΔ=0
CΔ>0 DΔ≥0
变式:若抛物线y=x2+2x+
a的顶点在x轴的下方,则a的
取值范围是( )
A.a>1
B.a<1
C.a≥1
D.a≤1
归纳:抛物线与x轴有两个交点 时,________;抛物线与x轴 只有一个交点时,________; 抛物线与x轴没有交点时, ________.
③a+c=1;④a>1.
其中正确 结论的序号是
O -1
1
x
-1
【精讲释疑】
例:已知二次函数y=ax2+bx+ c(c≠0)的图象如图所示,下列结论① b<0;②4a+2b+c<0;③a-b+ c>0;④(a+c)2<b2.其中正确的结论 是( ) A.①② B.①③ C.①③④ D.①②③④
课堂小结:
模块三:图像与2a+b,2a-b 间的关系
1.已知二次函数y=ax2+bx+c(a≠0) 的图象如图所示,下列结论:① abc>0;②2a+b<0;③a-b+c<0; ④a+c>0,其中正确结论的个数为
() A.4个 B.3个 C.2个 D.1个
2.已知:二次函数y=ax2+bx+c的
图象如图所示,下列结论中:①
这节课你有什么收获? 还有什么困惑?
总结体会
1.a,b,c等符号与二次函数y=ax2+bx+c
有密切的联系;
2.解决这类问题的关键是运用数形结合 思想,即会观察图象;如遇到2a+b,2ab要与对称轴联系等;
3.要注意灵活运用数学知识,具体问题
具体分析……
4.方法技巧
【当堂检测】
1.已知抛物线y=ax2+bx+ c(c≠0)在平面直角坐标系中的位 置如图所示,则下列结论中正确的 是( )
抛物线与字母系数 之间的关系
【学习目标】
1.让学生掌握二次函数的图象与字 母系数之间的关系.
2.能够根据字母间的关系式,判断 二次函数的性质。
3.增强学生解决问题能力。
【导入新ቤተ መጻሕፍቲ ባይዱ】
思考:二次函数的图象与系数a、 b、c之间还有怎样的关系呢?
【合作交流】
1.已知抛物线y=ax2+bx+ c(a≠0)在平面直角坐标系中的位 置如图所示,则有( ) A.a>0,b>0 B.a>0,c>0 C.b>0,c>0 D.a,b,c都小于0
变式: 二次函数y=ax2+bx+c的图象
如图所示,则点M( b ,a)在
()
cy
A、第一象限
B、第二象限
C、第三象限
o
x
D、第四象限
归纳:a的符号由抛物线的开口方向 决定,图象开口向上,a>0,图象 开口向下,a<0;b的符号由抛物线 的对称轴位置决定,当对称轴在y轴 的____侧时,a、b同号,对称轴在 y轴的____侧时,a、b异号,对称 轴在y轴,____;c的符号由图象与 y轴的交点位置决定.在y轴的正半 轴时,C___0,在y轴的负半轴时, C___0,在原点时,C___ 0.
abc>0;②b=2a;③a+b+c<0;
④a+b-c>0; ⑤a-b+c>0正确的个
数是 ( )
y
A、2个 B、3个
C、4个 D、5个
-1 o
10
1x
3.直击中考: 如图,二次函数
y=ax2+bx+c的图象开口向上,图象经
过点(-1,2)和(1,0),且与y
轴相交于负半轴. y
给出四个结论:
① abc<0;②2a+b>0; 2
A.a>0 B.b<0 C.c<0 D.a+b+c>0
2.图为二次函数y=ax2+bx+ c(a≠0)的图象,则下列说法:① a>0;②2a+b=0;③a+b+c>0; ④当-1<x<3时,y>0.其中正确的 个数为( )
A.1 B.2 C.3 D.4
3.如图,抛物线y=ax2+bx+ c(a>0)的对称轴是过点(1,0)且 平行于y轴的直线,若点P(4,0) 在该抛物线上,则4a-2b+c的 值为____.
