极限荷载计算
临塑荷载、临界荷载及极限荷载的理论公式计算

4.0
11.0 21.8 45.4 125
326
Nc
5.71 7.32 9.58 12.9
17.6 25.1 37.2 57.7 95.7 172.2
上述公式只适用于条形基础,对方形和圆形基础,太沙基建议按下列修正公式计算地基极限荷载:
方形基础:
整体剪切破坏:
局部剪切破坏:
圆形基础: 整体剪切破坏:
底以上土的加权平均重度; d---基底埋深,m ; b---基础宽度,m ; Nr、Nq、Nc---无量纲承载力系数,可根据内摩擦角从表 7-2 查出。 以上公式只适用于地基土整体剪切破坏情况,即地基土较密实,其 P-S 曲线有明显的转折点,破坏前沉
降不大等情况。对于松软土质,地基破坏是局部剪切破坏,沉降较大,其极限荷载较小。太沙基建议采用较
7.2.3 汉森公式
除了考虑基础形状对极限荷载的影响外,汉森比较仔细地考虑了基础埋深和荷载偏心,倾斜等的影响。 公式如下:
式中:Nc、Nq、Nr---承载力系数,查表 7-5 。
φ
Nr
Nq
Nc
0
0
5.14
1.00
2
0.01
5.69
1.20
4
0.05
6.17
1.43
6
0.14
6.82
1.72
8
0.27
φ(度)
0
2
4 6 8 10 12 14 16 18 20
Nr
0
0.03
0.06 0.10 0.14 0.18 0.23 0.29 0.36 0.43 0.51
Nq
1.00
1.12
1.25 1.39 1.55 1.73 1.94 2.17 2.43 2.72 3.06
结构力学专题十六(单跨梁极限荷载计算)

P
P
A
D
B
C
l/3 l/3 l/3
共有三种可能的破坏机构
Fpu
4 l
Mu
F1
5 l
Mu
F2
4 l
Mu
2.用试算法求解
F3
9 l
Mu
作业:
16—3、 16—4。
补:求图示结构的极限荷载, 材料极限弯矩为Mu。
M
A
C
B
3m
1m
(2)平衡弯矩法
Mmax 1.5FPu M u
FPu
2 3
Mu
2F
F
2m
2m
1m
小结: 静定梁极限荷载计算特点:
静定结构无多余约束,出现一个塑性铰即成为破 坏机构。这时结构上的荷载即为极限荷载。
塑性铰出现的位置应为截面弯矩与极限弯矩之比 的绝对值最大的截面。
求出塑性铰发生的截面后,令该截面的弯矩等于 极限弯矩,利用平衡条件即可求出极限荷载。
(1)可破坏荷载 Fp
对任一破坏机构,由平衡条件求出的荷载称为可破坏 荷载;
(2)可接受荷载 Fp
同时满足屈服条件和平衡条件的荷载称为可接受荷载;
(3)极限荷载 Fpu
同时满足三个条件的荷载称为极限荷载,即极限荷载 既是可破坏荷载,又是可接受荷载。
4、一般定理
(1)基本定理(预备定理)
可破坏荷载恒不小于可接受荷载 Fp Fp
第十六章 梁和刚架的极限荷载
§16-3 单跨梁极限荷载计算
一、静定梁 例2:求图示结构的极限荷载,
材料极限弯矩为Mu。 (1)机动法
2F
F
2m
2m
1m
塑性铰出现在支座处
14.5 连续梁的极限荷载
ql
各种可能 的单跨破 坏机构
A B l /2 l /2
q C l l
2ql
2ql
B D l A
Mu
C D
1.2 Mu 1.2Mu l /2 l /2
q ql 1.2 Mu A C Mu D A 2ql
ql
q 1.2Mu
2 ql 2.4Mu D
B 2 Mu
All Rights Reserved
重庆大学土木工程学院®
2) BC跨破坏时 跨破坏时
ql B A q Mu C D 1.2 Mu 1.2Mu l /2 l /2 2ql
ql ∆ = 1.2M uθ B + 1.2M uθC + M u (θ B + θC ) 2
θ B = θ C = 2∆ / l
Mu q C = 17.6 2 l
All Rights Reserved 重庆大学土木工程学院®
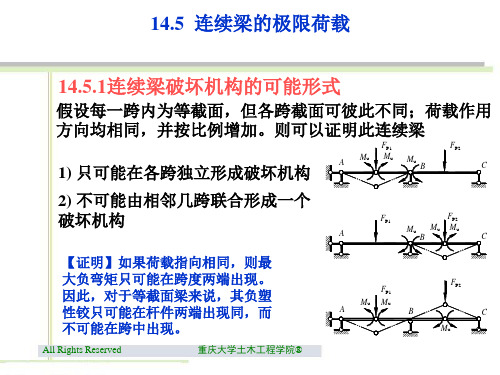
则可以证明此连续梁mumu不可能由相邻几跨联合形成一个破坏机构证明如果荷载指向相同则最大负弯矩只可能在跨度两端出现
14.5 连续梁的极限荷载 14.5.1连续梁破坏机构的可能形式 连续梁破坏机构的可能形式
假设每一跨内为等截面,但各跨截面可彼此不同; 假设每一跨内为等截面,但各跨截面可彼此不同;荷载作用 方向均相同,并按比例增加。 方向均相同,并按比例增加。则可以证明此连续梁 1) 只可能在各跨独立形成破坏机构 2) 不可能由相邻几跨联合形成一个 破坏机构
(1)先求出各跨独自破坏时的破坏荷载 先求出各跨独自破坏时的破坏荷载 1) AB跨破坏时 跨破坏时
A C Mu D q ql 1.2 Mu 2ql
极限承载力计算公式

极限承载力计算公式极限承载力是指结构或构件在达到其极限状态时所能承受的最大荷载。
计算极限承载力是结构设计中的重要环节,它直接关系到结构的安全性和可靠性。
本文将介绍几种常用的极限承载力计算公式及其应用。
1. 材料强度公式对于简单的材料,如钢材和混凝土,其极限承载力可以通过材料的屈服强度或抗压强度来计算。
对于受拉构件: [ F = A \times f_y ] 其中,( F ) 是极限承载力,( A ) 是横截面积,( f_y ) 是材料的屈服强度。
对于受压构件: [ F = A \times f_c ] 其中,( f_c ) 是材料的抗压强度。
2. 梁的弯矩公式对于受弯构件,如梁,其极限承载力可通过计算最大弯矩来确定。
对于简支梁: [ M = \frac{F \times L}{4} ] 其中,( M ) 是极限弯矩,( F ) 是集中荷载,( L ) 是梁的跨度。
3. 柱的稳定性公式柱的稳定性是影响其承载力的关键因素之一。
欧拉临界荷载公式用于计算理想弹性直杆的稳定性: [ P_{cr} = \frac{\pi^2 \times E \times I}{(K \timesL)^2} ] 其中,( P_{cr} ) 是临界荷载,( E ) 是材料的杨氏模量,( I ) 是截面惯性矩,( K ) 是长度系数,( L ) 是柱的长度。
4. 板的剪切公式对于板状构件,如楼板或基础板,其极限承载力可通过剪切应力来计算。
对于均匀受载的矩形板: [ V = t \times l \times \tau ] 其中,( V ) 是极限剪力,( t ) 是板厚,( l ) 是板的长度,( \tau ) 是允许的剪切应力。
5. 复合结构的相互作用公式在复合结构中,不同材料之间的相互作用会影响整体的承载力。
例如,钢筋混凝土结构中的钢筋和混凝土共同工作,其承载力可以通过以下公式估算: [ F = A_{sc} \times f_{sc} ] 其中,( A_{sc} ) 是钢筋混凝土的换算面积,( f_{sc} ) 是钢筋混凝土的组合强度。
16716-3超静定梁的极限荷载

1)第一跨破坏:
ql
q
θ
θ
1.5ql
Mu Δ
1.2M u
ql
ql
l 2
1.2Mu
M
u
2
q1
6.4 l2
Mu
2)第二跨破坏
ql
q
1.5ql
1.2M u θ Mu Δ θ 1.2M u
ql 2
ql 2
l 2
1.2Mu
1.2Mu
Mu
2
q2
17.6 l2
Mu
3)第三跨破坏 ql
q
1.5ql
θ
1.2M u
§16-3 超静定梁的极限荷载
1.超静定梁的破坏过程和极限荷载的特点
超静定梁由于有多余的约束,
必须出现多个塑性铰,
才能变成机构。
l/2
FP
l/2
以简例说明加载至极限状态的过程
(1)弹性阶段弯矩如图所示。 固端处弯矩最大。
A
3 16 FPl
(2)加载至A端达到Mu时, 第一个塑性铰形成。
MU A
FP
C
FP1
FP2
可能的破坏机构1
Mu
FP1
FP2
可能的破坏机构2
Mu
FP2 FP1 Mu
不可能出现的破坏形式
Mu
(2)连续梁极限荷载计算 —— 逐跨计算,比较最小者为FPU
[例1] 图示各跨等截面连续梁,第一、二跨正极限弯矩为Mu,
第三跨正极限弯矩为2Mu,各跨负极限弯矩为正极限弯
矩的1.2倍,求qu 。
B
5 32 FPl
FPS <FP<FPu
C
B
(3)继续加载至C达到Mu时, 第二个塑性铰形成, 结构变成机构而破坏。
极限承载力的计算

第三节 极限承载力的计算在土力学的发展中,已经提出了许多极限荷载公式,1920年普朗特首先根据塑性平衡理论导出了介质达到极限荷载时,沿着曲面发生滑动的数学方程,并认为介质的抗剪强度性质,可以用强度指标c ,ϕ表示,但是,他的研究结果只适用于无重量的介质的极限平衡平面课题。
随后不少学者根据他的研究结果,引用来求解地基土的极限荷载,并进一步作了不同形式的修正和补充,以便在工程中加以应用。
太沙基根据普朗特相似的概念,导出了考虑地基土自重影响的极限荷载公式。
但这些公式都忽略了基础底面以上覆盖土层的抗剪强度的影响,故只适用于计算浅基础的极限荷载。
梅耶霍夫进一步考虑了基础底面以上覆盖层的抗剪强度的影响,从而提出了浅基础和深基础的极限荷载公式。
一.普朗特尔极限承载力公式普朗特尔公式是求解宽度为b 的条形基础,置于地基表面,在中心荷载P 作用下的极限荷载Pu 值。
普朗特尔的基本假设及结果,归纳为如下几点:(1)地基土是均匀,各向同性的无重量介质,即认为土的0=γ,而只具有c ,ϕ的材料。
(2)基础底面光滑,即基础底面与土之间无摩擦力存在,所以基底的压应力垂直于地面。
(3)当地基处于极限平衡状态时,将出现连续的滑动面,其滑动区域将由朗肯主动区I ,径向剪切区II 或过渡区和朗肯被动区III 所组成。
其中滑动区I 边界BC 或AC 为直线,并与水平面成(45+ϕ/2)角;即三角形ABC 是主动应力状态区;滑动区II 的边界CE 或C D为对数螺旋曲线,其曲线方程为 θθtg e r r 0=,r 0为起始矢径;θ为射线r 与r 0夹角,滑动区III 的边界E G ,DF 为直线并与水平面成(45-φ/2)角。
(4)当基础有埋置深度d 时,将基础底面以上的两侧土体用相当的均布超载d q γ=来代替。
根据上述的基本假设,采用刚体平衡方法或特征线法,可以得到地基极限承载力为:c q u cN rdN p +=式中:r :基础两侧土的容重d :基础的埋置深度q N ,c N :承载力系数,它们是土的内摩擦角ϕ的函数,可查下表:其中)245(02ϕϕπ+=tg e Nq tgϕctg Nq Nc )1(-=二、斯肯普顿地基极限承载力公式对于矩形基础,斯肯普顿(1952年)给出的地基极限承载力公式为:d c p b d l b u 055)1)(1(5γ+++=c ——地基土粘聚力;b 、l ——分别为基础的宽度和长度;0γ——基础埋置深度d 范围内土的重度。
结构力学第17章结构的塑性分析与极限荷载

Mu
(
l
) 0
l
得:
FPu
6M u l
[例] 求梁的极限荷载,已知极限弯矩为Mu。
q
qu
A
C
B
l/2
l/2
A Mu
Mu l
C B
2 Mu
解:计算刚体虚功:
2
瞬变体系机构
W
l
y qu dx
Mu
Mu
Mu
qu
(
l
l
)
M u
qu l
M u
虚功方程:
qu l
M u
qu
16M u l2
FPu
M
' u
3 2l
Mu
9 2l
A
M ' u
A
2l /3
FPu
DC
Mu
D
l/3
FPu
l
(M u
M u )
A
3 2l
D
3 2l
3 l
9 2l
弯矩图如图,弯矩
MB=
1 2
(M
' u
Mu )
M
u
,即M
' u
3M u
时,此破坏形态就可实现。
M' u
1 2
(M
' u
-
M
u
)
FPu D
C
A
B
Mu
综上,当M
Mu
FP增大
A
C
B
FP继续增大,第二个塑性铰出现在C 截面,梁变为机构。弯矩 增量图相应于简支梁的弯矩图(如图)。
Mu
FP达到极限值FPu
钢筋混凝土梁的疲劳性能计算方法

钢筋混凝土梁的疲劳性能计算方法一、前言钢筋混凝土梁是结构工程中常用的结构构件,其在承载力和使用寿命方面的性能要求非常高。
在长期的使用过程中,其承载能力会逐渐下降,甚至发生疲劳破坏。
因此,研究钢筋混凝土梁的疲劳性能,对保障结构的安全性和延长使用寿命具有重要意义。
二、疲劳载荷作用下的钢筋混凝土梁疲劳载荷作用下的钢筋混凝土梁是指在长期重复荷载作用下,材料会逐渐疲劳损伤,导致梁的性能逐渐下降,最终发生疲劳破坏。
其荷载作用方式分为单向反复荷载和多向反复荷载。
钢筋混凝土梁的疲劳破坏主要表现为裂纹的产生和扩展,最终导致梁的破坏。
因此,研究钢筋混凝土梁的疲劳性能,需要关注裂纹的发生和扩展过程。
三、疲劳性能计算方法1. 疲劳极限荷载计算疲劳极限荷载是指在给定的疲劳寿命下,能够承受的最大荷载。
其计算方法如下:Wf = W0 × Kf × Kfs其中,W0为静载荷,Kf为荷载系数,Kfs为应力系数。
荷载系数Kf的计算公式如下:Kf = 1 + (Nf / N0) ^ b其中,Nf为疲劳寿命,N0为静载荷下的寿命,b为材料参数。
应力系数Kfs的计算公式如下:Kfs = 1 / (1 - R)其中,R为应力幅值与极限应力的比值。
2. 疲劳裂纹扩展速率计算疲劳裂纹扩展速率是指裂纹在疲劳荷载作用下每个循环内扩展的长度。
其计算方法如下:da / dN = C × ΔK ^ m其中,C和m为材料参数,ΔK为应力强度因子范围。
3. 疲劳寿命计算疲劳寿命是指在给定的荷载下,材料能够承受的循环次数。
其计算方法如下:Nf = (W / Wf) ^ (1 / b)其中,W为荷载,Wf为疲劳极限荷载,b为材料参数。
四、疲劳性能试验方法疲劳性能试验是评价钢筋混凝土梁疲劳性能的重要手段。
常用的试验方法包括疲劳试验和裂纹扩展试验。
1. 疲劳试验疲劳试验是通过在钢筋混凝土梁上施加重复荷载,模拟实际使用条件下的荷载作用,评估梁的疲劳性能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
载荷试验桩端一定在砂层上,所以桩端的qpk至少应取1500以上 .如果是硬塑的粘土,其qpk可取到1600~1800。 压的最大荷载 应取 按曲线捌点取有可能还要小一些 68米桩 17000 8500 7650 大约7300 65米桩 16000 8000 7200 大约7000
差很多呀
11632.51 14294.63 15775.91 7887.954 (qpk取1500) 桩端极限阻力=0.8736*1500*3.14*0.6*0.6=987.5174 1481.276 15282.15 7641.075 (qpk取1000) 13113.79 6556.893 单桩极限承载力=11632.51+987.5174=12620.03
土样 尺寸效应系数 吹填砂 0.8736 淤泥质粘土 0.9221 粉质粘土 0.9221 粉土 0.9221 粉质粘土 0.9221 粉细砂 0.8736 粉细砂 0.8736 粉质粘土 0.9221 粘土 0.9221 粉细砂 0.8736 粉质粘土 0.9221 粉质粘土 0.9221 粉细砂 0.8736 粉质粘土 0.9221
46 28 60 66 60 64 80 60 60 75 75 75 86 64
按规范 401.856 30 208.8741 20 123.377 50 217.8738 45 121.7172 45 251.5968 50 724.7386 70 109.5455 45 475.2503 45 150.6970 58.42426 75 3793.692 65
桩侧极限摩阻力=3.14*1.2*3087.184=11632.51
1481.276 14009.62 7004.812
我按照规范上的经验公式(5.3.6),计算出68米单桩极限承载力=12620.03,但我这个工程实例给出的单桩竖向承载力为8500,那它的极限承载力应该是17000,这跟我按公式计算的差很多呀
68米桩长 桩周土极限侧阻力 35 20 50 45 45 50 70 45 45 65 65 65 75 70
桩周土层厚度 10 8.09 2.23 3.58 2.2 4.5 10.37 1.98 8.59 2.3 2.97 3.68 6.52 0.99
305.76 149.19578 102.81415 148.55031 91.2879 196.56 634.14624 82.15911 356.437755 130.6032 178.011405 220.56632 427.1904 63.90153 3087.1841
按预制桩 35 25 55 50 50 55 75 50 50 70 70 70 75 80 70 75 80 80 305.76 186.4947 113.0956 165.0559 101.431 216.216 679.4424 91.2879 396.042 140.6496 191.7046 237.533 427.1904 73.03032 3324.933 12528.35
