新北师大版七年级下数学三角形全等证明典型习题
北师大版七年级数学下第四章 三角形 判定三角形全等的方法归纳 习题

七下数学第四章-判定三角形全等的基本方法归纳类型1:已知两边相等(选择的判定方法-SAS或SSS)1. 如图,已知AC=BD, 要使ΔABC≅ΔDCB, 则只需添加一个适合的条件是_________(填一个即可)2. 已知,AB=AD, AC=AE, 请添加一个条件,_______,使ΔABC≅ΔADE,并说明理由3. 已知,如图,∠BAC=∠DAM, AB=AN, AD=AM, 求证:∠B=∠ANM4. 如图,点D在AB上,点E在AC上,AB=AC, AD=AE, 试说明:BE=CD5. 如图,AB=AE, BD=EC, ∠BCA=80º, 求∠BDE的度数类型2:已知一边,一角相等(选择的判定方法-AAS,SAS,或ASA)6. 如图,AD和CB相交于点E, BE=DE, 请添加一个条件,使ΔABE≅ΔCDE, 你所添加的条件是___________7. 如图,点C, F, 在线段BE上,BF=EC, ∠1=∠2, 请你添加一个条件,使ΔABC≅ΔDEF, 并加以证明(不再添加辅助线和字母)8. 如图,四边形ABCD中,E点在AD上,其中∠BAE=∠BCE=∠ACD=90º, 且BC=CE, 请完整说明ΔABC与ΔDEC全等的理由9. 如图,已知AD=AE, ∠ACD=∠ABE, 求证:BD=CE类型3. 已知两角对应相等(选择判定方法ASA或AAS)10. 如图,ΔABC中,AD⊥BC, CE⊥AB, 垂足分别为D, E, AD, CE交于点H, 请你添加一个适当的条件:_________________________,使ΔAEH≅ΔCEB11. 如图,已知CE⊥AD于E, BF⊥AD于F, 你能说明ΔBDF和ΔCDE全等吗?若能,请你说明理由;若不能,在不用添加辅助线的情况下,请添加其中一个适当的条件,这个条件是________________,写出证明过程12. 如图,点A, C, D, B四点共线,且AC=BD, ∠A=∠B, ∠ADE=∠BCF, 求证:DE=CF13. 如图,已知∠ABC=∠DCB, BD, CA分别是∠ABC, ∠DCB 的平分线,求证:AB=DC类型4. 两次应用全等14. 如图,在ΔABC与ΔDCB中,AC与BD交于点E, 且∠BAC=∠CDB, ∠ACB=∠DBC, 分别延长BA与CD交于点F,求证:BF=CF类型5. 全等基本图形归纳(平移,旋转,翻折)15. 如图,ΔABC中,D, E, 分别为AB, AC 的中点,过点C作CF∥AB交DE的延长线于F, 求证:AB=2CF16. 如图,在ΔABC中,AD⊥BC于D, 若BD=AD, FD=CD, 求证(1)∠FBD=∠CAD(2) BE⊥AC17. 如图,四边形ABCD的对角线交于点O, AB∥CD, O是BD的中点(1)说明:ΔABO≅ΔCDO(2) 若BC=AC=4, BD=6, 求ΔBOC的周长18. 如图,AD⊥AB于点A, BE⊥AB于点B, 点C在AB上,且CD⊥CE., CD=CE, 试说明:AD=CB19. 如图,已知点B, E, C, F在一条直线上,AB=DF, AC=DE, ∠A=∠D(1) 说明:AC∥DE(2) 若BF=13, EC=5, 求BC的长20. 如图所示,将一长方形纸片ABCD折叠,使点C与点A重合,点D落在点E处,折痕为MN, 图中有全等三角形吗?,若有,请找出并证明21.如图(1)中,在ΔABC中,CD平分∠ACB, ∠A=2∠B, 试判断BC, AC, 和AD之间的数量关系小明发现,将ΔACD沿CD翻折,使点A落在BC边上的A.处,展开后连接D A., 则得到一对全等的三角形,从而将问题解决(如图2)根据小明的发现,写出BC, AC, 和AD之间的数量关系并说明理由。
北师大七年级下册数学全等三角形习题精选

FED CB A 第五章 全等三角形 A一、选择题1.下列三角形不一定全等的是( ) A .有两个角和一条边对应相等的三角形 B .有两条边和一个角对应相等的三角形C .斜边和一个锐角对应相等的两个直角三角形D .三条边对应相等的两个三角形 2.下列说法:①所有的等边三角形都全等 ②斜边相等的直角三角形全等③顶角和腰长对应相等的等腰三角形全等 ④有两个锐角相等的直角三角形全等 其中正确的个数是( )A .1个B .2个C .3个D .4个3.如图,AB 平分∠CAD ,E 为AB 上一点,若AC=AD ,则下列结论错误的是( )=BD =DE 平分∠CBD D.图中有两对全等三角形是△ABC 的角平分线,自D 向AB 、AC 两边作垂线,垂足为E 、F ,那么下 列结论中错误的是 ( )=DF =AF =CD D.∠ADE=∠ADF5.在△ABC 中,∠B=∠C ,与△ABC 全等的三角形有一个角是130°,那么△ABC 中与这个 角对应的角是( ).A .∠AB .∠BC .∠CD .∠B 或∠C6.如图所示,BE ⊥AC 于点D ,且AD=CD ,BD=ED ,若∠ABC=54°,则∠E=( ).A .25°B .27°C .30°D .45° 7.如右图,△ABC 中,∠C=90°,AC =BC ,AD 平分∠CAB 交BC 于点D ,DE⊥AB,且AB =10 cm ,则△BED 的周长为 ( ) A .5 cm B .10 cm; C .15 cm D .20 cm8.如图,AB=AC ,BE ⊥AC 于E ,CF ⊥AB 于F ,则①△ABE ≌△ACF ;②△BOF ≌△COE ;③点O 在∠BAC 的角平分线上,其中正确的结论有( )A .3个B .2个C .1个D .0个9.如图,在△ABC 中,AD 平分∠BAC ,过B 作BE ⊥AD 于E ,过E作EF ∥AC 交AB 于F ,则( ) A 、AF=2BF; B 、AF=BF; C 、AF>BF; D 、AF<BF E DCBAD A CE B CBAEF O二、填空题1.如果△ABC≌△A’B’C’,若AB =A’B’,∠B=50°,∠C=70°,则∠A’= °2.如图,若BD ⊥AE 于B ,DC ⊥AF 于C ,且DC=DC ,∠BAC=40°,∠ADG=130°,则∠DGF=________。
最新北师大版七年级下册三角形全等(SSS)的证明试题以及答案(共41道证明题)
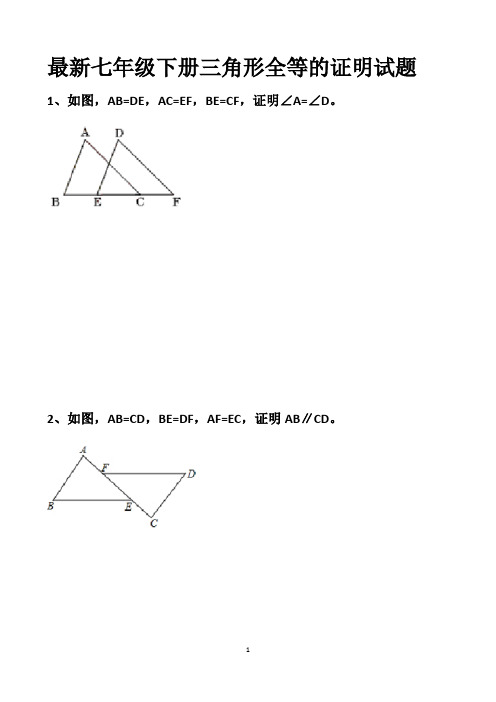
最新七年级下册三角形全等的证明试题1、如图,AB=DE,AC=EF,BE=CF,证明∠A=∠D。
2、如图,AB=CD,BE=DF,AF=EC,证明AB∥CD。
3、如图,AC=DF,EF=BC,AD=BE,证明∠F=∠C。
4、如图,AB=AC,AD=AE,BE=DC,证明∠ABD=∠AEC。
5、如图,AB=AD,AE=AC,BC=ED,证明∠ABE=∠ACD。
6、如图,AD=AB,DC=BC,证明∠B=∠D。
7、如图,AB=AC,BD=DC,证明∠1=∠2.8、如图,∠C=90°,AD=BD,DE=DC,AE=BC,说明AB和DE的关系。
9、如图,AB=DE,BC=EF,AF=CD,证明AB∥DE。
10、如图,AB=AC,D是BC的中点,证明AD⊥BC。
11、如图,AE=DF,AB=CD,CE=BF,证明AE∥DF。
12、如图,AB=AD,AE=AC,BC=DE,证明∠E=∠C。
13、如图,BC=BE,DE=DC,∠C=90°,证明(1)DE⊥AB(2)BD是∠ABC的角平分线。
14、如图,AB=EF,AD=CF,DE=BC,证明∠B=∠E。
15、如图,OA=OB,AC=BD,AD=BC,证明∠ACB=∠ADB。
16、如图,AD=BC,A0=OB,OC=OD,证明∠BAD=∠ABC。
17、如图,AD=BD,BE=AC,AD+DE=BC,AD⊥BC,证明BE⊥AC。
18、如图,AD=BC,AF=EC,DE=BF,证明DE∥BF,AD∥BC。
19、如图,AB=DC,AC=BD,AO=OD,证明∠B=∠C。
20、如图,AB=AD,AE=AC,BC=DE,证明∠1=∠2.21、如图,AC⊥CE,AC=CE,AB=CD,且AB+DE=BD,AB∥DE。
22、如图,AE=AB,AC=AF,EC=BF,证明∠BAE=∠CAF。
23、如图,AD=BC,AC=BD,证明∠ADO=∠BCO。
24、如图,AB=AC,BD=CE,AD=AE,证明∠ABC=∠ADE。
北师大版七年级下册三角形全等证明及其性质(试题集)

B ′C ′D ′O ′A ′图6图7 北师大版七年级下册三角形综合检测题一、选择填空题1.如图,为了使一扇旧木门不变形,木工师傅在木门的背面 加钉了一根木条,这样做的道理是 。
2.一个三角形的两边长为2和6,第三边为偶数.则这个 三角形的周长为 ( )A .10B .12C .14 D.163.适合条件∠A =∠B =∠C 的三角形一定是( )A.锐角三角形B.钝角三角形C.直角三角形D.任意三角形4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形 是( )A .锐角三角形B .钝角三角形C .直角三角形D .无法确定 5.下列语句:①面积相等的两个三角形全等; ②两个等边三角形一定是全等图形;③如果两个三角形全等,它们的形状和大小一定都相同; ④边数相同的图形一定能互相重合。
其中错误的说法有( )A 、4个B 、3个C 、2个D 、1个6.用直尺和圆规作一个角等于已知角的示意图如下,则要说明∠A′O′B′=∠,需要证明△A′O′B′≌△,则这两个三角形全等的依据是 (写出全等的简写)7.把一副三角板按如图所示放置,已知∠A =45º,∠E =30º,则两条斜边相交所成的钝角∠的度数为 度8.如图,∥、交于点O ,∠420,∠580则∠( )A .420B .580C .800D .1000 9.如图, Δ≌Δ和和是对应边,那么∠等于( ) A.∠ B.∠ C.∠ D.∠图1图11BCD 1 2图10图9图12图1310.如图,已知∠1=∠2,要说明⊿≌⊿,还需从下列条件中选一个,错误的选法是( )A 、∠∠B 、∠∠C C 、D 、11.如图,有两个长度相同的滑梯,左边滑梯的高度与右边滑梯水平 方向的长度相等,若∠320,则∠ ,∠ 。
12.如图,⊥,⊥,垂足分别为D 、E ,且=,则△与△全等的理由是( ). (A ) (B ) (C ) (D )13.小涛在家打扫卫生,一不小心把一块三角形的玻璃台板打碎了,如图所示,如果要配一块完全一样的玻璃,至少要带 块,序号分别是 。
北师大版数学七年级下册《全等三角形》练习题

北师大版数学七年级下册《全等三角形》练习题全等三角形练习题(3)一、选择题(每题3分,共18分)1.下列命题①同旁内角互补,两直线平行;②全等三角形的周长相等;③直角都相等;④等边对等角.它们的逆命题是真命题的个数是( )A.1个B.2个C.3个D.4个2.命题“到线段两端距离相等的点在这条线段的垂直平分线上”的结论是 ( )(A)在这条线段的垂直平分线上 (B)线段的垂直平分线上有个点(C)这点在这条线段的垂直平分线上 (D)这点在垂直平分线上3.下列命题中,真命题是()A.相等的角是直角B.不相交的两条线段平行C.两直线平行,同位角互补D.经过两点有具只有一条直线.4。
命题:①对顶角相等;②平面内垂直于同一条直线的两直线平行;③相等的角是对顶角;④同位角相等.其中假命题有()A 、1个B 、2个C 、3个D 、4个5.只用无刻度的直尺就能作出的图形是()A.延长线段AB 至C ,使BC =ABB.过直线L 上一点A 作L 的垂线C.作已知角的平分线D.从点O 再经过点P 作射线OP6.用尺规作已知角平分线,其根据是构造两个三角形全等,它所用到的识别方法是()A.SASB.ASAC.AASD.SSS二、填空题(每题3分,共15分)7.把命题“角平分线上的点到这个角两边的距离相等”改写成“如果……,那么…….”的形式:如果,那么 .8. 为说明“如果b a >,那么ba 11>”是假命题,你举出的反例是 . 9.命题“等边三角形的一个外角等于相邻内角的2倍”的逆命题是,这个逆命题是命题10.命题“垂直于同一条直线的两直线平行”的题设是______ _,命题“平行于同一条直线的两直线平行”的结论是____ __.11.定理“直角三角形的两直角平方和等于斜边的平方”的逆定理是三、选择题(每题4分,共20分)12.如图7所示,若△ABE ≌△A CF ,且AB =5,AE =2,则EC 的长为()A.2B.3C.5D.2.513.如图8,∠1=∠2,BC =EF ,欲证△ABC ≌△DEF ,则须补充一个条件是()A.AB =DEB.∠ACE =∠DFBC.BF =ECD.∠ABC =∠DEF14.如图10,△ABC 中,AD ⊥BC ,D 为BC 中点,则以下结论不正确的是()A.△ABD ≌△ACDB.∠B =∠CC.AD 是∠BAC 的平分线D.△ABC 是等边三角形图7 F E B A 图815.如图11,∠1=∠2,∠C =∠D ,AC 、A.∠DAE =∠CBEB.C.△DEA 不全等于△CBED.△16.如图12,在△ABC 中,AB >AC ,AC =10,△BCD 的周长为18,则BC A.8B.6C.4D.2四、填空题(每题3分,共24分)17.如图1,根据SAS ,如果AB =AC ,=,即可判定ΔABD ≌ΔACE .18.如图2,BD 垂直平分线段AC ,AE ⊥BC ,垂足为E ,交BD 于P 点,PE =3cm ,则P点到直线AB 的距离是___.19.如图3,在等腰Rt △ABC 中,∠C =90°,AC =BC ,AD 平分∠BAC 交BC 于D ,DE⊥AB 于D ,若AB =10,则△BDE 的周长等于____.20.如图4,△ABC ≌△DEB ,AB =DE ,∠E =∠ABC ,则∠C 的对应角为,BD的对应边为 .21.如图5,AD =AE ,∠1=∠2,BD =CE ,则有△ABD ≌ ,理由是,△ABE ≌△ ,理由是22.如图6,AD ⊥BC ,DE ⊥AB ,DF ⊥AC ,D 、E 、F 是垂足,BD =CD ,那么图中的全等三角形有_______.23.如图,直线l 过正方形ABCD 的顶点B ,点C A 、到直线l 的距离分别是1和2,则正方形的边长为 .24.如图,等边△ABC ,B 点在坐标原点,B 图11 2(12)C B A 1ED A 图2E C D P A B 图3 E DC B A 图1 ED C B A 图5图6 A F (8)C E DC 点的坐标为(6,0),点A 关于x 轴对称点A?′的坐标为_______.五、解答题(共24分)25.如图,在□ABCD 中,F E 、分别是边BC 和AD 上的点.请你补充一个条件,使CDF ABE ??≌,并给予证明.(9分)26.“太湖明珠”无锡要建特大城市,有人建议无锡(A )、江阴(B )、宜兴(C )三市共建一个国际机场,使飞机场到江阴、宜兴两城市距离相等,且到无锡市的距离最近.请你设计机场的位置(要保留作图痕迹哦!).(8分)27.ABC Δ的三边分别为a,b,c 且a=22n m -,b=2mn,c=22n m +(m>n,m,n 是正整数),ABC Δ是直角三角形吗?说明理由。
最新北师大版七年级下册三角形全等的证明练习题以及答案
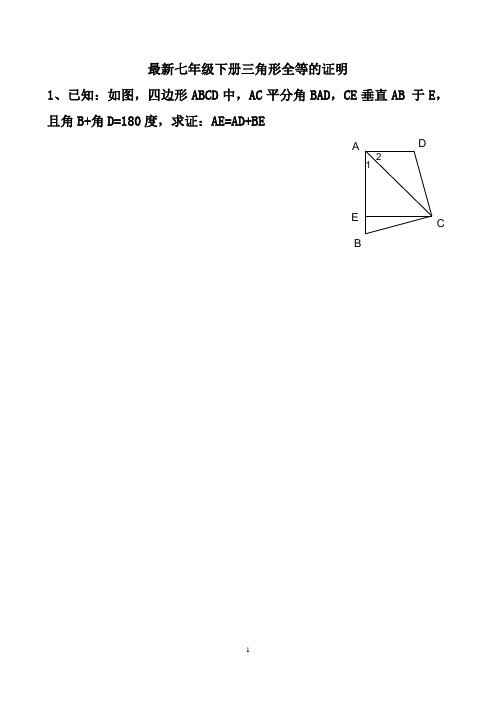
最新七年级下册三角形全等的证明1、已知:如图,四边形ABCD中,AC平分角BAD,CE垂直AB 于E,且角B+角D=180度,求证:AE=AD+BEA B DCE 122、已知,如图,AB=CD,DF⊥AC于F,BE⊥AC于E,DF=BE。
求证:AF=CE。
FE A CDB3、已知,如图,AB ⊥AC ,AB =AC ,AD ⊥AE ,AD =AE 。
求证:BE =CD 。
AEDC B4、如图,DE⊥AB,DF⊥AC,垂足分别为E、F,请你从下面三个条件中任选出两个作为已知条件,另一个为结论,推出一个正确的命题。
①AB=AC ②BD=CD ③BE=CFBD C5、如图,△ABC中,AB=AC,过A作GE∥BC,角平分线BD、CF 交于点H,它们的延长线分别交GE于E、G,试在图中找出三对全等三角形,并对其中一对给出证明。
E G6、如图,在△ABC中,点D在AB上,点E在BC上,BD=BE。
(1)请你再添加一个条件,使得△BEA≌△BDC,并给出证明。
你添加的条件是:________ ___(2)根据你添加的条件,再写出图中的一对全等三角形:______________(不再添加其他线段,不再标注或使用其他字母,不必写出证明过程)7、已知:如图,AB⊥BC,AD⊥DC,AB=AD,若E是AC上一点。
求证:EB=ED。
DA E CB8、已知:如图,AB、CD交于O点,CE//DF,CE=DF,AE=BF。
求证:∠ACE=∠BDF。
AB CDEFO9、已知:如图,△ABC中,AD⊥BC于D,E是AD上一点,BE的延长线交AC于F,若BD=AD,DE=DC。
求证:BF⊥AC。
AE FDB C10、. 已知:如图,△ABC 和△A 'B 'C '中,∠BAC=∠B 'A 'C ',∠B=∠B ',AD 、A 'D '分别是∠BAC 、∠B 'A 'C '的平分线,且AD=A 'D '。
求证:△ABC ≌△A’B’C’。
最新北师大版七年级下册三角形全等的证明单元测试试题以及答案

最新七年级下册三角形单元测试试题一、选择题1.一定在△ABC内部的线段是()。
A.锐角三角形的三条高、三条角平分线、三条中线B.钝角三角形的三条高、三条中线、一条角平分线C.任意三角形的一条中线、二条角平分线、三条高D.直角三角形的三条高、三条角平分线、三条中线2.下列说法中,正确的是()。
A.一个钝角三角形一定不是等腰三角形,也不是等边三角形B.一个等腰三角形一定是锐角三角形,或直角三角形C.一个直角三角形一定不是等腰三角形,也不是等边三角形D.一个等边三角形一定不是钝角三角形,也不是直角三角形3.如图,在△ABC中,D、E分别为BC上两点,且BD=DE=EC,则图中面积相等的三角形有()。
A.4对 B.5对 C.6对 D.7对4.如果一个三角形的三条高的交点恰是三角形的一个顶点,那么这个三角形是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.无法确定5.下列各题中给出的三条线段不能组成三角形的是()A.4厘米、5厘米、6厘米B.4厘米、4厘米、4厘米C.5厘米、13厘米、6厘米D.7厘米、9厘米、7厘米6.若等腰三角形的一边是7,另一边是4,则此等腰三角形的周长是()。
A.18 B.15 C.18或15 D.无法确定7.两根木棒分别为6cm和9cm,要选择第三根木棒,将它们钉成一个三角形,如果第三根木棒长为偶数,那么第三根木棒的取值情况有()种。
A.3 B.4 C.5 D.68.△ABC的三边a、b、c都是正整数,且满足a≤b≤c,如果b=4,那么这样的三角形共有()个。
A.4 B.6 C.8 D.109.各边长均为整数的不等边三角形的周长小于13,这样的三角形有()A.1个 B.2个 C.3个 D.4个10.三角形所有外角的和是()A.180° B.360° C.720° D.540°11.锐角三角形中,最大角α的取值范围是( ) A .0°<α<90°; B .60°<α<180°; C .60°<α<90°; D .60°≤α<90°12.如果三角形的一个外角不大于和它相邻的内角,那么这个三角形为( )A .锐角或直角三角形;B .钝角或锐角三角形C .直角三角形;D .钝角或直角三角形13.已知△ABC 中,∠ABC 与∠ACB 的平分线交于点O ,则∠BOC 一定( )A .小于直角;B .等于直角;C .大于直角;D .大于或等于直角 二、填空题1.如图:(1)AD ⊥BC ,垂足为D ,则AD 是________的高, ∠________=∠________=90°;(2)AE 平分∠BAC ,交BC 于点E ,则AE 叫________,∠________=∠________=∠________,AH叫________;(3)若AF =FC ,则△ABC 的中线是________;(4)若BG =GH =HF ,则AG 是________的中线,AH 是________的中线.212.如图,∠ABC=∠ADC=∠FEC=90°.(1)在△ABC中,BC边上的高是________;(2)在△AEC中,AE边上的高是________;(3)在△FEC中,EC边上的高是________;(4)若AB=CD=3,AE=5,则△AEC的面积为________.3.在等腰△ABC中,如果两边长分别为6cm、10cm,则这个等腰三角形的周长为________.4.五段线段长分别为1cm、2cm、3cm、4cm、5cm,以其中三条线段为边长共可以组成________个三角形.5.已知三角形的两边长分别为3和10,周长恰好是6的倍数,那么第三边长为________.6.一个等腰三角形的周长为5cm,如果它的三边长都是整数,那么它的腰长为________cm.7.在△ABC中,若∠A∶∠B∶∠C=5∶2∶3,则∠A=______;∠B =______;∠C=______.8.如图,△ABC中,∠ABC、∠ACB的平分线相交于点I.(1)若∠ABC=70°,∠ACB=50°,则∠BIC=________;(2)若∠ABC+∠ACB=120°,则∠BIC=________;(3)若∠A=60°,则∠BIC=________;(4)若∠A=100°,则∠BIC=________;(5)若∠A=n°,则∠BIC=________.三、解答题1.在△ABC中,∠BAC是钝角.画出:(1)∠ABC的平分线;(2)边AC上的中线;(3)边AC上的高.2.△ABC 的周长为16cm ,AB =AC ,BC 边上的中线AD 把△ABC 分成周长相等的两个三角形.若BD =3cm ,求AB 的长.3.如图,AB ∥CD ,BC ⊥AB ,若AB =4cm ,,求△ABD 中AB 边上的高.212cm =∆ABCS4.学校有一块菜地,如下图.现计划从点D 表示的位置(BD ∶DC =2∶1)开始挖一条小水沟,希望小水沟两边的菜地面积相等.有人说:如果D 是BC 的中点的话,由此点D 笔直地挖至点A 就可以了.现在D 不是BC 的中点,问题就无法解决了.但有人认为如果认真研究的话一定能办到.你认为上面两种意见哪一种正确,为什么?5.在直角△ABC 中,∠BAC =90°,如下图所示.作BC 边上的高,图中出现三个直角三角形(3=2×1+1);又作△ABD 中AB 边上的高,这时图中便出现五个不同的直角三角形(5=2×2+1);按照同样的方法作、、……、.当作出时,图中共有多少个不同的直角三角形?1DD 21D D 32D D k k D D 1-k k D D 1-6.一块三角形优良品种试验田,现引进四个良种进行对比实验,需将这块土地分成面积相等的四块.请你制订出两种以上的划分方案.7.一个三角形的周长为36cm,三边之比为a∶b∶c=2∶3∶4,求a、b、c.8.已知△ABC的周长为48cm,最大边与最小边之差为14cm,另一边与最小边之和为25cm,求△ABC各边的长.9.已知三角形三边的长分别为:5、10、a-2,求a的取值范围.10.已知等腰三角形中,AB=AC,一腰上的中线BD把这个三角形的周长分成18cm和9cm两部分,求这个等腰三角形的底边的长.11.如图,已知△ABC中,AB=AC,D在AC的延长线上.求证:BD-BC<AD-AB.12.如图,△ABC 中,D 是AB 上一点.求证:(1)AB +BC +CA >2CD ;(2)AB +2CD >AC +BC .13.如图,AB ∥CD ,∠BMN 与∠DNM 的平分线相交于点G ,(1)完成下面的证明:∵ MG 平分∠BMN ( ),∴ ∠GMN =∠BMN ( ),同理∠GNM =∠DNM .∵ AB ∥CD ( ),∴ ∠BMN +∠DNM =________( ).∴ ∠GMN +∠GNM =________.2121∵∠GMN+∠GNM+∠G=________(),∴∠G= ________.∴ MG与NG的位置关系是________.(2)把上面的题设和结论,用文字语言概括为一个命题:_________________________________________________.14.已知,如图D是△ABC中BC边延长线上一点,DF⊥AB交AB于F,交AC于E,∠A=46°,∠D=50°.求∠ACB的度数.15.已知,如图△ABC中,三条高AD、BE、CF相交于点O.若∠BAC =60°,求∠BOC的度数.16.已知,如图△ABC中,∠B=65°,∠C=45°,AD是BC边上的高,AE是∠BAC的平分线.求∠DAE的度数.17.已知,如图CE是△ABC的外角∠ACD的平分线,BE是∠ABC内任一射线,交CE于E.求证:∠EBC<∠ACE.18.画出图形,并完成证明:已知:AD是△ABC的外角∠EAC的平分线,且AD∥BC.求证:∠B=∠C.。
(完整版)新北师大版七年级下数学三角形全等证明典型习题

新北师大版七年级下数学三角形全等证明典型习题1.一个零件的形状如图,按规定∠A=90º ,∠ C=25º,∠B=25º, 检验已量得∠BCD=150º,就判断这个零件不合格, 运用三角形的有关知识说明零件不合格的理由。
2.已知,如图,在△ ABC 中,AD ,AE 分别是 △ ABC 的高和角平分线, 若∠B=30°,∠C=50°. (1)求∠DAE 的度数。
(2)试写出 ∠DAE 与∠C-∠B 有何关系?(不必证明)3.如图,已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交 AC 于E,∠A=35°,∠D=42°,求∠ACD 的度数.4.如图,在△ABC 中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED, 求∠CDE 的度数.5、有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D 使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?21.已知:如图,在△ABC 中,∠BAC=800,AD ⊥BC 于D ,AE 平分∠DAC ,∠B=600; 求∠AEC 的度数.CDAE CDBFDCBE ADCBEA6、已知:如图,AC BE BA DC ⊥=,于点AC DF E ⊥,于点F ,且BE=DF求证:AB ∥DCABCDE F8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠BCD , 且点E 在AD 上。
求证:BC=AB+DC 。
9、如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新北师大版七年级下数学三角形全等证明典型习题
1.一个零件的形状如图,按规定∠A=90o ,∠ C=25o ,∠B=25o , 检验已量得∠BCD=150o ,就判断这个零件不合格, 运用三角形的有关知识说明零件不合格的理由。
2.已知,如图,在△ ABC 中,AD ,AE 分别是 △ ABC 的高和角平分线, 若∠B=30°,∠C=50°. (1)求∠DAE 的度数。
(2)试写出 ∠DAE 与∠C-∠B 有何关系?(不必证明) 3.如图,已知D 为△ABC 边BC 延长线上一点,DF ⊥AB 于F 交 AC 于E,∠A=35°,∠D=42°,求∠ACD 的度数.
4.如图,在△ABC 中,∠B=∠C,∠BAD=40°,且∠ADE=∠AED, 求∠CDE 的度数.
5、有一座小山,现要在小山A 、B 的两端开一条隧道,施工队要知道A 、B
两端的距离,于是先在平地上取一个可以直接到达A 和B 的点C ,连接AC 并延长到D 使CD=CA ,连接BC 并延长到E ,使CE=CB ,连接DE ,那么量出DE 的长,就是A 、B 的距离,你能说说其中的道理吗?
21.已知:如图,在△ABC 中,∠BAC=800,AD ⊥BC 于D ,AE 平分∠DAC ,∠B=600
求∠AEC 的度数. 6、已知:如图,
AC BE BA DC ⊥=,于点AC DF E ⊥,于点F ,且BE=DF
求证:AB ∥DC
8. 如图,四边形ABCD 中,AB ∥DC ,BE 、CE 分别平分∠ABC 、∠
BCD , 且点E 在AD 上。
求证:BC=AB+DC 。
9、如图:AE 、BC 交于点M ,F 点在AM 上,BE ∥CF ,BE=CF 。
求证:AM 是△ABC 的中线。
10、AB=AC ,DB=DC ,F 是AD 的延长线上的一点。
求证:BF=CF
11.已知:如图所示,AB =AD ,BC =DC ,E 、F 分别是DC 、BC 12.已知:如图,AB =AC ,BD ?AC ,CE ?AB ,垂足分别为D 、E ,.
A
C
D
A。
