怎样求一次函数关系式
一次函数关系式的求解途径

【 例4 】 ( 2 0 1 7 ・ 荆州) 将直线 y = + 6 沿 轴向下
平 移 3个单 位 长度 , 点A( 一1 , 2) 关于y 轴 的 对称 点
【 分析 】 ( 1 ) 州 衷 r } ] 的数据 , 日期 每 增 『 J l 】 1 , , K , 、 增』 J u ( ) . 5 米, 昕 以1 是 的 … 玖 函 数.
m l : ( 6 >0 ) 平移或向下( 6 <0 ) 移 个F f 长嚏
5 2 I 策 略方 法
/
初学习 ・ 策 略 方 法
僻剑. 五、 利用 一次 函数 的图像 求解
注 意 的世 : 【 } 1 的 .
衷, J 段i < = . 必
i
线 段长 正( 如本 题中 线 段O B 长为l 4 f ) . 这 1
一
落在平 移 后的 直线 上 , 则b的值 为— — .
【 分析 】 将直线 + 厶 沿、 轴向下 、 g 3 1 、 单 长嘘 . 忻得直线 的函数天系式为 r + b - 3 . 再将
・ _A ( 一 1 , 2 ) 芙丁Y 轴的对称』 、 、 ( 1 , 2 ) 标 代 人直
解 途径
利 用一 次 函数 的定 义求 解 用所建 、 的 函 数 模 型远 离 已 知数 据 , 作 预 测
一
、
【 例1 】 已知函数 ’ = ( , n + 2 ) … 。 。 + 6 是 关于. 1 7 的 不 可 靠 的.
一
次 函数 , 试 求一 ; 欠函数 关 系式.
、 = O . 5 . r + l 9 . 5 . ( 2 ) t = 6 代入 ( 1 ) L 卜 I 求 僻 函 教 关 系
求一次函数的关系式

求一次函数的关系式资料编号:202204011450【自学指导】借助于课本和下面的讲解,弄清楚以下经过问题:(1)怎样用待定系数法求一次函数的关系式?(2)求一次函数的关系式都有哪些类型?相应的解题策略是什么?【重要知识点总结】求一次函数()0≠+=k b kx y 的关系式,就是求出b k ,的值,然后代入关系式即可.常用待定系数法求一次函数的关系式.用待定系数法求一次函数关系式的一般步骤:(1)设一次函数的关系式为b kx y +=,其中b k ,为待定的系数;(2)把两个已知点的坐标分别代入b kx y +=,建立关于b k ,的二元一次方程组;(3)用加减消元法求解方程组,求出b k ,的值;(4)将求出的b k ,的值代回所设的函数关系式,即得所求的函数关系式.说明对于一次函数()0≠+=k b kx y ,待确定的系数有两个,分别是k 和b ,如果知道其中一个系数的值,则只需知道函数图象上一个点的坐标,把该点的坐标代入函数关系式即可求得另一个系数的值;如果两个系数的值都不知道,则就需要知道函数图象上两个点的坐标,把这两个点的坐标分别代入关系式建立方程组求解.求一次函数关系式的类型及方法一、定义型例1. 已知函数()332+-=-m x m y 是一次函数,求这个一次函数的关系式.分析 根据一次函数的定义,其自变量的系数不等于0,自变量的次数为1,据此求出参数的值.解:由题意可知:⎩⎨⎧=-≠-1203m m 解之得:3-=m∴这个函数的关系式为36+-=x y .二、两点型知道一次函数的图象经过的两个点的坐标,用待定系数法求其函数关系式.例2. 已知一次函数的图象经过点()1,1和点()2,0,求该一次函数的关系式.分析 先设一次函数的关系式为b kx y +=,然后把两个点的坐标分别代入,从而建立关于b k ,的二元一次方程组求解.解:设该一次函数的关系式为b kx y +=把()1,1、()2,0分别代入b kx y +=得:⎩⎨⎧==+21b b k 解之得:⎩⎨⎧=-=21b k ∴该函数的关系式为2+-=x y .三、图象型知道一次函数图象上两个点的坐标(读图获得),用待定系数法求函数关系式.题目通常给出的是函数图象与两条坐标轴的交点坐标.例3. 已知一次函数的图象如图所示,求这个函数的关系式. yx32O解:设这个函数的关系式为b kx y +=由函数图象可知,其图象经过()0,2,()3,0-两点把()0,2,()3,0-分别代入b kx y +=得:⎩⎨⎧-==+302b b k 解之得:⎪⎩⎪⎨⎧-==323b k ∴这个函数的关系式为323-=x y . 四、平行型若两个一次函数的图象互相平行,则它们的k 值相等,b 值不相等.据此来确定系数k 的值.“平行型”题目的特征是:待求函数的图象与已知直线平行,且经过一个已知点.例4. 已知一次函数b kx y +=的图象平行于直线1+-=x y ,且经过点()4,0-,求这个一次函数的关系式.解:由题意可知:1-=k∴b x y +-=把()4,0-代入b x y +-=得: 4-=b∴这个一次函数的关系式为4--=x y .五、相交型同一平面内两条直线的位置关系有两种:平行和相交.确定相交的两条直线的函数关系式,要明确交点的意义,即两个一次函数图象的交点的横坐标和纵坐标,是由这两条直线的关系式组成的方程组的解.例5. 如图所示,正比例函数的图象与一次函数1+-=x y 的图象相交于点P ,求这个正比例函数的关系式.解:设正比例函数的关系式为kx y =对于1+-=x y令2=y ,则21=+-x解之得:1-=x∴()2,1-P把()2,1-P 代入kx y =得:2=-k解之得:2-=k∴这个正比例函数的关系式为x y 2-=.例6. 已知三条直线2,12,32-=+-=-=kx y x y x y 相交于一点,求该交点的坐标和第三条直线的表达式.分析 该交点的横、纵坐标是方程组⎩⎨⎧+-=-=1232x y x y 的解. 解:解方程组⎩⎨⎧+-=-=1232x y x y 得: ⎩⎨⎧-==11y x ∴该交点的坐标为()1,1-把()1,1-代入2-=kx y 得:12-=-k解之得:1=k∴第三条直线的表达式为2-=x y .六、面积型给出的条件中有直线的坐标三角形的面积,求直线的解析式,注意分类讨论.例7. 直线b kx y +=经过点⎪⎭⎫ ⎝⎛-0,23,且与坐标轴围成的直角三角形的面积为415,求直线的解析式.分析 题中的三角形就是坐标三角形,它是直角三角形,两条直角边的长度隐含在一次函数的图象与两条坐标轴的交点坐标中:与x 轴的交点的横坐标的绝对值是其中一条直角边的长,与y 轴的交点的纵坐标的绝对值是另一条直角边的长.解:直线b kx y +=与y 轴的交点坐标为()b ,0由题意可知:4152321=⨯-⨯b ∴5,5±==b b∴5+=kx y 或5-=kx y∵直线b kx y +=经过点⎪⎭⎫ ⎝⎛-0,23 ∴0523=+-k 或0523=--k 解之得:310=k 或310-=k ∴该直线的解析式为5310+=x y 或5310-=x y . 例8. 如图所示,在平面直角坐标系中,一次函数42+-=x y 的图象分别与x 轴、y 轴交于点A 、B ,点P 在x 轴上,若6=∆ABP S ,求直线PB 对应的函数关系式. yxABO分析:根据题意可得点P 可以在y 轴左边,也可以在y 轴右边,应分两种情况讨论.先求点A 和点B 的坐标,然后根据6=∆ABP S 确定点P 的位置,进而运用待定系数法可求出直线PB 对应的函数关系式.解:对于42+-=x y令0=y ,则042=+-x解之得:2=x∴()0,2A令0=x ,则4=y∴()4,0B∵6=∆ABP S ∴6421=⨯AP ,得3=AP ∴点P 的坐标为()0,1-或()0,5设直线PB 对应的函数关系式为b kx y +=∴⎩⎨⎧==+-40b b k 或⎩⎨⎧==+405b b k 解之得:⎩⎨⎧==44b k 或⎪⎩⎪⎨⎧=-=454b k ∴直线PB 对应的函数关系式为44+=x y 或454+-=x y . 七、范围型例9. 已知一次函数b kx y +=中,自变量x 的取值范围是1-≤x ≤4,相应函数值的范围是3-≤y ≤2,求此函数的表达式.分析 本题分为两种情况:(1)y 随x 的增大而增大;(2)y 随x 的增大而减小. 解:分为两种情况:①当0>k 时,y 随x 的增大而增大∴当1-=x 时,3-=y ;当4=x 时,2=y∴⎩⎨⎧=+-=+-243b k b k 解之得:⎩⎨⎧-==21b k ∴2-=x y ;②当0<k ,y 随x 的增大而减小∴当1-=x 时,2=y ;当4=x 时,3-=y∴⎩⎨⎧-=+=+-342b k b k 解之得:⎩⎨⎧=-=11b k∴1+-=x y .综上所述,此函数的表达式为2-=x y 或1+-=x y .八、表格型例10. 某农产品每件成本10元,试销阶段每件产品的销售价x (元)与产品的日销售量y (件)之间的关系如下表:若日销售量y 是销售价x 的一次函数,求出日销售量y (件)与销售价x (元)之间的函数关系式.解:设此一次函数的关系式为b kx y +=,则有⎩⎨⎧=+=+20202515b k b k 解之得:⎩⎨⎧=-=401b k ∴此一次函数的关系式为40+-=x y .九、其它类型例11. 已知y 与2+x 成正比例,当4=x 时,12=y ,求y 与x 之间的函数关系式,并判断y 是x 的什么函数.分析 正比例关系: 若A 与B 成正比例,则可设kB A =,其中k 为正比例系数.解:由题意可设()2+=x k y∵当4=x 时,12=y∴()1224=+k解之得:2=k∴()4222+=+=x x y .∴y 是x 的一次函数.例12. 已知两条直线111:b x k y l +=,222:b x k y l +=,若21l l ⊥,则121-=⋅k k .(1)应用:已知直线12+=x y 与直线1-=kx y 垂直,求k 的值;(2)一直线经过点()3,2A ,且与直线331+-=x y 垂直,求该直线的关系式. 分析 两个一次函数的图象互相垂直的条件一般地,对于两条直线 111:b x k y l +=,222:b x k y l +=若21l l ⊥,则121-=⋅k k .反过来亦成立.我们可以用此结论证明两个一次函数的图象互相垂直.解:(1)由题意可知:12-=k解之得:21-=k ; (2)设该直线的关系式为b ax y += 由题意可知:131-=-a 解之得:3=a∴b x y +=3把()3,2A 代入b x y +=3得:36=+b ,解之得:3-=b∴该直线的关系式为33-=x y .。
用二元一次方程组求一次函数关系式

议一议
A、B两地相距100 km,甲、乙两人骑自行车分别从A、B两地相
向而行。假设他们都保持匀速行驶,则他们各自到A地的距离 s(km) 都是骑车时间 t (h)的一次函数.
1 h后乙距A地80 km,
2 h后甲距A地 30 km. 问:经过多长时间两人相遇 ?
直线型图表示
甲 A
2 h,30 km
消去 s s 15t s 100 20t
t=
用方程解行程问题 1 h后乙距A地80 km,即乙的速度是 20 km/h, 2 h后甲距A地 30 km,故甲的速度是 15km/h,
小彬
由此可求出甲、乙两人的速度, 以及……
你明白他的想法吗? 用他的方法做一做, 看看和你的结果一致吗?
解(1)设y与x之间的函数表达式y=kx+b, (2)当y=0时,解得x=30 所以旅客最多可以 根据题意,得 免费携带30 kg的行李。 解得 所以y与x之间的函数表达式
随堂练习
如图中的两直线l1 ,l2 的交点坐标可以看作 方程组 的解
y
4
3 2
l1
l2 1 -1 0 -1 1 2 3 4 x
80 km
1h
B 乙
图象表示
可以分别作出两人s 与t 之间的关系图象,找出 交点的横坐标就行了! s 100 (B) 80 60 你明白他的想法吗? 用他的方法做一做, 看看和你的结果一致吗?
l2
l1
40
20 0 (A)
1 1 2 2
小明的方法求出的结果 准确吗?
3 3
4
5 t
求出s与t之间的关系式,联立解方程组
对于乙,s是t的一次函数,可设 s=kt+b。 当t=0时,s=100;当t=1时,s=80。 将它们分别代入s=kt+b中,可以求出k、b的值, 小颖 也即可以求出乙s与t之间的函数表达式。 同样可求出甲s与t之间的函数表达式。 再联立这两个表达式,求解方程组就行了。
一次函数解析式的常见求法

一次函数解析式的常见求法一、求函数解析式的几种方法:方法一:利用待定系数法。
解析:( 1)建立关于x, y的一元二次方程: y^2=2×x^2-8x+42,当x=0时,得到一次函数的解析式。
2.(解析:令y为所求函数的自变量,根据题意列出含有x的方程组即可解决。
) 3.(解析:注意所求的解不能超过两个,这样可以保证方程组有唯一解。
) 4.(解析:此法仅限于当y为已知实数时使用,且在自变量取定后,函数式能唯一确定的情况下使用。
)4.(解析:将y=f(x)-4y, f=x-4作为未知数代入( 1)中,可得y=f(x)-4y,而根据“同一平面内,两个函数的图象关于y轴对称”可知,所求函数的自变量必须是该函数的奇函数,因此只需要再令f=x-4,即可解决。
) 5.(解析:根据题目中已知条件,可列出关于x, y的一元二次方程,并对方程两边同时求导数。
当x=0时,二次函数的解析式为y=2x-6;当x=-3/2时,二次函数的解析式为y=-1/2-6/2。
利用待定系数法可得y=-x/2,或者直接根据两个函数的关系进行判断。
)6.(解析:设y为实际问题的一次函数,由已知条件知,二次函数与y有关,由待定系数法可知, y可取任意值。
)7.(解析:以点B为圆心, y=f(x)=kx-4为半径画圆,令f(y)与k是两个不同的自变量,则其图象关于y轴对称,即可解决问题。
)方法二:利用方程法。
解析:( 1)建立关于x, y的一元二次方程: y^2=2×x^2-8x+42,当x=0时,得到一次函数的解析式。
2.(解析:令y为所求函数的自变量,根据题意列出含有x的方程组即可解决。
) 3.(解析:注意所求的解不能超过两个,这样可以保证方程组有唯一解。
) 4.(解析:此法仅限于当y为已知实数时使用,且在自变量取定后,函数式能唯一确定的情况下使用。
) 5.(解析:根据题目中已知条件,可列出关于x, y的一元二次方程,并对方程两边同时求导数。
根据图象求一次函数关系式
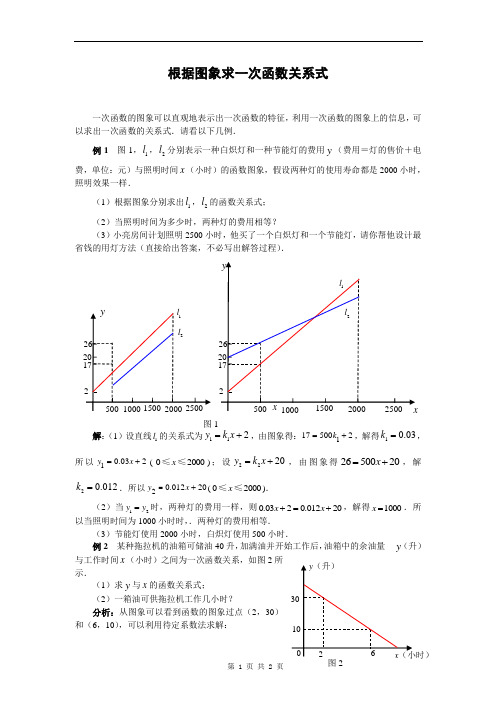
第 1 页 共 2 页 根据图象求一次函数关系式一次函数的图象可以直观地表示出一次函数的特征,利用一次函数的图象上的信息,可以求出一次函数的关系式.请看以下几例.例1 图1,1l ,2l 分别表示一种白炽灯和一种节能灯的费用y (费用=灯的售价+电费,单位:元)与照明时间x (小时)的函数图象,假设两种灯的使用寿命都是2000小时,照明效果一样.(1)根据图象分别求出1l ,2l 的函数关系式;(2)当照明时间为多少时,两种灯的费用相等?(3)小亮房间计划照明2500小时,他买了一个白炽灯和一个节能灯,请你帮他设计最省钱的用灯方法(直接给出答案,不必写出解答过程).解:(1)设直线1l 的关系式为112y k x =+,由图象得:1175002k =+,解得10.03k =,所以10.032y x =+(02000x ≤≤);设2220y k x =+,由图象得2650020x =+,解20.012k =.所以20.01220y x =+(02000x ≤≤).(2)当12y y =时,两种灯的费用一样,则0.0320.01220x x +=+,解得1000x =.所以当照明时间为1000小时时,.两种灯的费用相等.(3)节能灯使用2000小时,白炽灯使用500小时.例2 某种拖拉机的油箱可储油40升,加满油并开始工作后,油箱中的余油量 y (升)与工作时间x (小时)之间为一次函数关系,如图2所示.(1)求y 与x 的函数关系式;(2)一箱油可供拖拉机工作几小时?分析:从图象可以看到函数的图象过点(2,30)和(6,10),可以利用待定系数法求解:图1图2第 1 页 共 2 页 解:(1)设一次函数的关系式为y kx b =+,将条件代入,得230610.k b k b +=⎧⎨+=⎩,解得540.k b =-⎧⎨=⎩, 所以此函数的关系式为540y x =-+.(2)当0y =时,即5400x -+=,所以8x =.即一箱油可供拖拉机工作8小时. 例3某长途汽车客运站规定,乘客可以免费携带一定质量的行李,但超过该质量则需要购买行李票.且行李费y (元)是行李质量x (千克)的一次函数,如图3所示.(1)求y 与x 之间的函数关系式; (2)最多可免费携带多少质量的行李.解:(1)观察图象可知一次函数的图象经过(60,6),(80,10)两点,可设y kx b =+,将条件代入,得6068010.k b k b +=⎧⎨+=⎩, 解得156k b ⎧=⎪⎨⎪=-⎩,.所以函数的关系式为165y x =-. (2)当0y =时,30x =.即最多可免费携带30千克的行李.图3。
关于一次函数表达式的几种求法

关于一次函数表达式的几种求法用待定系数法求一次函数的解析式:待定系数法:先设待求函数关系式(其中含有未知常数,系数),再根据条件列出方程或方程组,求出未知系数,从而得到所求结果的方法。
用待定系数法求一次函数解析式的步骤:第一步:设关系式第二步:列方程(组)第三步:求出结果,写出关系式。
扩展资料一次函数应用常用公式:1、求函数图像的k值:(y1-y2)/(x1-x2)2、求与x轴平行线段的中点:(x1+x2)/23、求与y轴平行线段的中点:(y1+y2)/24、求任意线段的长:√[(x1-x2)2+(y1-y2)2]5、求两个一次函数式图像交点坐标:解两函数式两个一次函数y1=k1x+b1;y2=k2x+b2令y1=y2得k1x+b1=k2x+b2将解得的x=x0值代回y1=k1x+b1;y2=k2x+b2两式任一式得到y=y0则(x0,y0)即为y1=k1x+b1与y2=k2x+b2交点坐标。
6、求任意2点所连线段的中点坐标:[(x1+x2)/2,(y1+y2)/2]6、求任意2点的连线的一次函数解析式:(x-x1)/(x1-x2)=(y-y1)/(y1-y2)(x,y)为+,+(正,正)时该点在第一象限(x,y)为-,+(负,正)时该点在第二象限(x,y)为-,-(负,负)时该点在第三象限(x,y)为+,-(正,负)时该点在第四象限8、若两条直线y1=k1x+b1//y2=k2x+b2,则k1=k2,b1≠b29、如两条直线y1=k1x+b1⊥y2=k2x+b2,则k1×k2=-110、y=k(x-n)+b就是直线向右平移n个单位y=k(x+n)+b就是直线向左平移n个单位y=kx+b+n就是向上平移n个单位y=kx+b-n就是向下平移n个单位口决:左加右减相对于x,上加下减相对于b。
11、直线y=kx+b与x轴的交点:(-b/k,0)与y轴的交点:(0,b)。
求一次函数解析式的常用方法精选全文

可编辑修改精选全文完整版求一次函数解析式的常用方法一次函数是初中数学的重要内容之一,要学好它,首先会求它的解析式。
本文举例介绍求一次函数解析式的几种常用方法,供同学们学习时参考。
一、 定义法一次函数y=kx+b (k≠0)的x 的指数等于1,系数k≠0,据此求一次函数的解析式。
例1 求一次函数y=(p+1)x p2-3p-3+2p 的解析式解:由一次函数的定义可知p 2-3p-3=1∴p=4或p=-1又p+1≠0p=4所以所求解析式为y=5x+8点评:用定义法求一次函数解析式关键是抓住“一次”即未知数的指数等于1且它的系数不等于0。
二、 两点坐标法一次函数y=kx+b (k≠0)中,有两个字母需k 、b 要求,而将一次函数y=kx+b (k≠0)图象上的两点坐标代入y=kx+b (k≠0),得关于k 、b 的二元一次方程组解之可得k 、b1、已知两点坐标例2 已知一次函数的图像经过两点(-2,10),(4,-8),求该一次函数的解析式。
解:设所求一次函数解析式为y=kx+b (k≠0)将(-2,10),(4,-8)代入得⎩⎨⎧-=+=+-84102b k b k 解之得⎩⎨⎧-==34k b 所以所求一次函数的解析式为y=-3x+4点评:已知一次函数经过两点,把这两点坐标代入y=kx+b 解出k 、b 即可。
2、已知表格例3 某商店出售一种瓜子,其售价y (元)与瓜子质量x (kg )之间的关系如下表:由上表得y 与x 之间的关系式是 。
解:设所求关系式为y=kx+b将(2,)、(2,)代入得:⎩⎨⎧=+=+4.728.3b k b k 解得:⎩⎨⎧==6.32.0k b ∴y=+ 将(3,11),(4,)代入也适合故y 与x 之间的关系式是y=+点评:一次函数的关系由表格给出时,从表格中选出两组较简数字代入y=kx+b 解出k 、b 即可。
3、已知图像例4如下图是某出租车单程收费y (元)与行程x (km )之间的函数关系图像,求出收费y (元)与行程x (km )(x≥3)之间的函数关系,并求行驶10km 需收费多少元解:设y 与x 的关系是y=kx+b 将(3,5),(8,11)代入得⎩⎨⎧+=+=bk b k 81135 解得⎩⎨⎧==5756b k∴y=65x+75(x≥3) 当x=10时,y=65×10+ 75=12+ 75=1325故行驶10km 需收费13元4角。
一次函数的关系式

18.3 一次函数
4.求一次函数的关系式
回顾与思考
1
1.什么叫一次函数?
若两个变量x,y间的关系式可以表示成 y=kx+b(k,b为常数,k不为零)的形式,则称y 是x的一次函数x为自变量,y为因变量. 特别地,当b=0时,称y是x的正比例函数.
某物体沿一个斜坡下滑,它的速度v(米/秒)与其下滑时 间t(秒)的关系如图6—5所示。 (1)写出v与t 之间的关系式; (2)下滑3秒时物体的速度是多少?
① ② 得 0=2k-2 ∴k=1
∴这个一次函数的表达式为y=x-2
例 1: 在弹性限度内,弹簧的长度y(厘米)是所挂物体质量x (千克)的一次函数。一根弹簧不挂物体时长 14.5厘米; 当所挂物体的质量为3千克时,弹簧长16厘米。写出y与x 之间的关系式,并求当所挂物体的质量为4千克时弹簧的 长度。 设y=kx+b,根椐题意,得 14.5=b ① 16=3k+b ② 把b=14.5代入②,得 k=0.5 所以在弹性限度内:y=0.5x+14.5 当x=4时,y=0.5 × 4+14.5=16.5 即物体的质量为4千克时,弹簧长度为16.5
y=x+2
y
8 7 6 5 4 3 2 1
0
1 2 3
4
5
6 7 8
x
随堂练习
1.若一次函数y=2x+b的图象经过点A(-1,1),则b= 3 该函数图象过点B(1,5 )和点C( -1.5 ,0)。 2.如图,直线l是一次函数y=kx+b的图象,填空: 2 (1) b= 2 ,k= 3
(2)当x=30时,y= -18 (3) 当y=30时,x= -42
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
怎样求一次函数关系式?
广东 林伟杰
一次函数关系式)0(≠+=k b kx y 中有两个待定系数k 和b ,确定了它们就确定了一个一次函数,故一般需要两个条件才能确定一个一次函数.现结合实例介绍求一次函数关系式的方法,供同学们学习时参考.
一、利用代入坐标法求一次函数关系式
例1 已知一次函数的图象经过(1,5)和(3,9)两点,求此一次函数关系式. 分析:先设函数关系式为b kx y +=,然后代入坐标建立方程组,求出方程组的解后再代回所设关系式即可.
解:设所求函数关系式为b kx y +=,则由题意,得⎩⎨⎧+=+=,39,5b k b k 故⎩
⎨⎧==.3,2b k 故所求的函数关系式是32+=x y .
点评:图象上每一点的横坐标和纵坐标都是此函数中自变量与函数的一对对应值,据此可通过建立二元一次方程组来求一次函数关系式.
二、根据直线间的位置关系求一次函数关系式
例2 某一次函数的图象过点(2,1)且与直线32+-=x y 相交于y 轴上的同一点,求此一次函数的关系式.
分析:因直线32+-=x y 与y 轴的交点是(0,3),故设函数关系式为3+=kx y ,代入点(2,1)可求出k ,进而可得关系式.
解:因直线32+-=x y 交y 轴于点(0,3),故某一次函数的图象也与y 轴相交于点(0,3),故设其关系式为3+=kx y ,代入点(2,1),得321+=k ,故1-=k ,故关系式为3+-=x y . 点评:由已知条件得出图象与y 轴的交点坐标,进而正确设出所求关系式是解本题的关键.
三、根据表格信息求一次函数关系式
例3 商店出售某商品时,在进价的基础上加一定的利润,其数量x 与售价y 的关系如下表所示,请根据表中提供的信息求出y 与x 的函数关系式,并求出当数量是2.5千克时的售价.
分析:由表可知,当1=x 时, 4.08+=y ;当2=x 时,
)4.08(28.016+=+=y ;当3=x 时,
)4.08(32.124+=+=y ;当4=x 时,)4.08(46.132+=+=y ;…… 故x x y 4.8)4.08(=+=.
解:由表中信息可求得函数关系式是x x y 4.8)4.08(=+=(正比例函数是一次函数的特例).当5.2=x 千克时,214.85.2=⨯=y (元).
四、根据图象信息求一次函数关系式
例4 长途汽车客运公司规定旅客可随身携带一定重量的行李,若超过规定,则要购买
行李票,行李费用y (元)是行李重量x (千克)的一次函数,其图象如图所示,试求出y 与x 之间的函数关系式并求出自变量x 的取值范围.
分析:由图象可知,直线过点(60,6)和(80,10)两点,据此即可求出y 与x 间的函数关系式.
解:设函数关系式为b kx y +=,因为图象过点(60,6) 和(80,10),则有⎩⎨⎧+=+=,8010,606b k b k 故⎪⎩⎪⎨⎧-==.6,51b k 故函数关系式是 65
1-=x y .令0=y ,得30=x ,故自变量x 的取值范围是x ≥30
点评:直线与x 轴的交点的横坐标就是可免费携带行李的最大重量.解决本题的关键是读懂题意.此外,通过本题要注意掌握实际问题中自变量取值范围的确定方法,它包括:(1)使关系式有意义;(2)符合实际问题的需要.
五、根据一次函数的性质求其关系式
例5 一次函数b kx y +=的自变量的取值范围是-3≤x ≤6,相应函数值的取值范围是-5≤y ≤-2,求此一次函数的关系式.
分析:对一次函数b kx y +=,若y 随x 的增大而增大,则由题意知其图象过点(-3,-5)和(6,-2),由此可求其关系式;若y 随x 的增大而减小,则由题意知其图象过点(-3,-2)和(6,-5),由此可求其关系式,故本题应分两种情况求解.
略解:本题应分两种情况来解.设所求关系式为b kx y +=.(1)当y 随x 的增大而增大时,由题意知其图象过点(-3,-5)和(6,-2),由此可求得关系式是43
1-=x y (-3≤x ≤6);(2)当y 随x 的增大而减小时,由题意知其图象过点(-3,-2)和(6,-5),由此可求得关系式是33
1--=x y (-3≤x ≤6). 点评:本题题设只给出了一次函数的自变量与函数值的取值范围,在这种情况下应根据一次函数的性质来求其关系式,否则极易造成漏解.
x。
