北师大版初二上数学勾股定理与实数复习题
北师大版八年级数学上册勾股定理练习题
第一章勾股定理第1课时认识勾股定理1．若△ABC中，∠C=90°，（1）若a=5，b=12，则c= ；（2）若a=6，c=10，则b= ；（3）若a∶b=3∶4，c=10，则a= ，b= .2．某农舍的大门是一个木制的矩形栅栏，它的高为2 m，宽为1.5 m，现需要在相对的顶点间用一块木棒加固，木板的长为.3．直角三角形两直角边长分别为5 cm，12 cm，则斜边上的高为.4．等腰三角形的腰长为13 cm，底边长为10 cm，则面积为（）.A．30 cm2B．130 cm2C．120 cm2D．60 cm25．轮船从海中岛A出发，先向北航行9km，又往西航行9 km，由于遇到冰山，只好又向南航行4 km，再向西航行6 km，再折向北航行2 km，最后又向西航行9 km，到达目的地B，求AB两地间的距离.6．一棵9 m高的树被风折断，树顶落在离树根3 m之处，若要查看断痕，要从树底开始爬多高？7．折叠长方形ABCD 的一边AD ，使点D 落在BC 边的F 点处， 若AB =8 cm ，BC =10 cm ，求EC 的长.第2课时 验证勾股定理1.在两千多年前我国古算术上记载有“勾三股四弦五”.你知道它的意思吗？ 它的意思是说：如果一个直角三角形的两条直角边长分别为3和4个长度单位，那么它的斜边的长一定是5个长度单位，而且3、4、5这三个数有这样的关系：32+42=52.（1）请你动动脑筋，能否验证这个事实呢？该如何考虑呢？（2）请你观察下列图形，直角三角形ABC 的两条直角边的长分别为AC =7，BC =4，请你研究这个直角三角形的斜边AB 的长的平方是否等于42+72？2.下图甲是任意一个直角三角形ABC ，它的两条直角边的边长分别为a 、b ,斜边长为c .如图乙、丙那样分别取四个与直角三角形ABC 全等的三角形，放在边长为a +b 的正方形内. E CFB D A①图乙和图丙中（1）（2）（3）是否为正方形？为什么？②图中（1）（2）（3）的面积分别是多少？③图中（1）（2）的面积之和是多少？④图中（1）（2）的面积之和与正方形（3）的面积有什么关系？为什么？由此你能得到关于直角三角形三边长的关系吗？。
北师大版八年级上册数学复习题(经典)
第一章 勾股定理一、选择题1．等腰三角形的腰长为13cm ，底边长为10cm ，则面积为（ ）．A ．30 cm 2B ．130 cm 2C ．120 cm 2D ．60 cm 22．已知Rt △ABC 中，∠C ＝90°，若14=+b a cm ，10=c cm ，则Rt △ABC 的面积为（ ）．（A ）24cm 2 （B ）36cm 2 （C ）48cm 2 （D ）60cm 23．如图，分别以直角三角形的三边为边长向外作正方形，然后分别以三个正方形的中心为圆心，正方形边长的一半为半径作圆，记三个圆的面积分别为 S 1，S 2，S 3，则S 1，S 2，S 3之间的关系是（ ）． （A ）321S S S >+ （B ）321S S S =+（C ）321S S S <+ （D ）无法确定 4、以下列各组数为边长，能组成直角三角形的是（ ）A ．2，3，4B ．10，8，4C ．7，25，24D ．7，15，125、已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ）A ．25B ．14C ．7D ．7或256、以面积为9 cm 2的正方形对角线为边作正方形，其面积为（ ）A ．9 cm 2B ．13 cm 2C ．18 cm 2D ．24 cm 27、如图，直角△ABC 的周长为24，且AB:AC=5:3，则BC=（ ）A ．6B ．8C ．10D ．128、如图，一架云梯长25米，斜靠在一面墙上，梯子底端离墙7米，如果梯子的顶端下滑4米，那么梯子的底部在水平方向上滑动了（ ）A ．4米B ．6米C ．8米D ．10米9、将一根长24 cm 的筷子，置于底面直径为5cm 、高为12cm 的圆柱形水杯中，设筷子露在杯子外面的长为hcm ，则h 的取值范围是（ ）A ．5≤h ≤12B ．5≤h ≤24C ．11≤h ≤12D ．12≤h ≤2410、已知，如图，长方形ABCD 中，AB=3cm ，AD=9cm ，将此长方形折叠，使点B 与点D 重合，折痕为EF ，则△ABE 的面积为（ ）A ．6cm 2B ．8cm 2C ．10cm 2D ．12cm2 二：解答题11．一个长为10m 为梯子斜靠在墙上，梯子的顶端距地面的垂直高度为8m ，梯子的顶端下滑2m 后，底端滑动多少米？12．一棵9m 高的树被风折断，树顶落在离树根3m 之处，若要查看断痕，要从树底开始爬多高？13．折叠长方形ABCD 的一边AD ，使点D 落在BC 边的F 点处，若AB=8cm ，BC=10cm ，求EC的长.321S S S第二章 实数1一、填空题：1、()26-的算术平方根是__________。
(北师大版)八年级数学上(勾股定理、实数、四边形)
(北师大版)八年级数学上(勾股定理、实数、四边形)一、选择题1. 三角形三边长分别为6；8；10；那么它最短边上的高为……………（）A. 4B. 5C. 6D. 82. 三角形各边（从小到大）长度的平方比如下；其中不是直角三角形的是…………………………………………………………………………………（）A. 1:1:2B. 1:3:4C. 9:25:36D. 25:144:169﹡3. 设一个直角三角形的两条直角边长为a、b；斜边上的高为h；斜边长为c；则以c+h；a+b；h为边的三角形的形状是…………………………………（）A. 直角三角形B. 锐角三角形C. 钝角三角形D. 不能确定﹡4. △ABC中；∠A:∠B:∠C=1:2:3；则BC:AC:AB为……………………（）A. 1:2:3B. 1:2:3C. 1:3:2D. 3:1:25. △ABC中；AB=15；AC=13。
高AD=12。
则△ABC的周长是……………（）A. 42B. 32C. 42或32D. 37或33提示：两种情况。
二、填空题1. 若有两条线段；长度分别为8 cm；17cm；第三条线段长满足__________条件时；这三条线段才能组成一个直角三角形。
2. 木工做一个长方形桌面；量得桌面的长为60cm；宽为32cm；对角线长为68cm；这个桌面__________ （填“合格”或“不合格”）。
3. 如图；有一圆柱；其高为12cm；它的底面半径为3cm；在圆柱下底面A处有一只蚂蚁；它想得到上面B处的食物；则蚂蚁经过的最短距离为________ cm。
（π取3）4. 如图；有一块直角三角形纸片；两直角边AC=6cm；BC=8cm；现将直角边AC沿直线AD折叠；使它落在斜边AB上；且与AE重合；则CD等于________ 。
三、计算题1. 如图；公路MN和公路PQ在P点处交汇；点A处有一所中学；AP=160米；点A到公路MN的距离为80米；假使拖拉机行驶时；周围100米以内会受到噪音影响；那么拖拉机在公路MN上沿PN方向行驶时；学校是否会受到影响；请说明理由；如果受到影响；已知拖拉机的速度是18千米/小时；那么学校受到影响的时间为多少？2. 已知直角三角形的三边长分别为3；4；x；求x2。
2021年北师大版八年级实数及勾股定理复习题
初二数学科复习题一——实数及勾股定理一．选择题:(每题2分，共20分) 1. 2的算术平方根是( ) A ．4B. ±4C. 2D. 2±2. 在02）（-、22、0、9-、38、0.101001…、2π、722中，无理数的个数是( )A. 2B. 3C. 4D. 53. 下列计算正确的是( ) A. 532=+B. 2222=+C. 752863=+D.942188+=+ 4．下列能构成直角三角形三边长的是 ( ) A. 4、5、6 B. 3、4、5 C. 2、3、4 D. 1、2、3 5.直角三角形两边长分别是3、4，第三边是( ) A. 5 B. 7 C. 5或7 D. 无法确定6．与数轴上的点一一对应的数是 ( ) A. 无理数 B. 有理数 C. 实数 D. 整数 7.下列各数与2互为相反数的是 A.2(2) B.38 C.2 D.128.下列说法正确的是A. 4的平方根是2B.0的平方根是0C. 4的平方根是2D.2(3) 的算术平方根是3 9.下列说法正确的是A. 64的平方根是8B.64的立方根是4C.64的平方根不存在D.64的立方根不存在10.若195+x 的立方根是4，则72+x 的平方根是( )A.25B.-5C.5D.5±11.( )Ａ．6到7之间 Ｂ．7到8之间 Ｃ．8到9之间 Ｄ．9到10之间 12.( )A.aB.a ±C.D.二、填空题:(每小题3分，共30分) 13.3的倒数是______,相反数是_______.2的绝对值是_______,25的绝对值是_______.15.将下列各数填在对应的大括号内2351,,,3.14,0,3.333,3,64,2,2.10100100017整数集合: ｛______________________________________｝ 有理数集合:｛______________________________________｝ 无理数集合:｛______________________________________｝16.平方根等于它本身的数是_____；立方根等于它本身的数是_____ 17.将,0, 1.62用按照顺序连接_______________18.有这样一个问题:3与以下那个数相乘，结果是有理数？ A ．32 B ．32+C ．32+D ．3- E．32 F ．0(只须填字母): 19.4，则___a 4，则___m20.若实数a 、b 满足02)2(2=-+-a b a ，则=-3ab .21.要使式子1x 2-+3x 1- 有意义的x 取值范围是22.一个三角形的三边长分别为7、24、25，则其面积为 23.171,和59的大小___________ 1012()|3|1)_____2-⨯+-+= 02|1|432_____25.的位置三、解答题:26.计算题(每小题5分，共15分)(1) 2818327+-⨯ (2)2122213322）（-+- (3) 0(π3)8122解方程(每小题5分，共15分) (1)25119x(2)32412x (3)2313(5)3328x先化简，再求值(1)22(3)(2)(2)2x x x x +++--，其中x = (2) )(2)(2y x y y x -+- ，其中2,1==y x ．27．在矩形ABCD 中，对角线AC 、BD 相交于点O ，AB=OA=3㎝， 求BD 和AD 的长？28.一个无盖长方体盒子的长、宽、高分别是8cm ,8cm,12cm.(1)一只蚂蚁想从盒底的A 点爬到盒顶的B 点，有很多种走法。
北师大版八年级上实数及勾股定理综合测试题150分
实数及勾股定理综合测试：总分：150分得分：一、单选题（共15题；共45分）1、算术平方根比原数大的是( )｡A、正实数B、负实数C、大于0而小于1的数D、不存在2、下列计算中，正确的是（）A、B、C、D、3、下列说法错误的是（）A、5是25的算术平方根B、1是1的一个平方根C、（-4）2的平方根是-4D、0的平方根与算术平方根都是04、下列各式中不是二次根式的是（）A、B、C、D、5、化简的结果是（）A、3B、±3C、9D、±96、下列说确的个数有（）①2是8的立方根；②±4是64的立方根；③无限小数都是无理数；④带根号的数都是无理数．A、1个B、2个C、3个D、4个7、用计算器计算约为（）A、3.049B、3.050C、3.051D、3.0528、化简的结果为（）A、B、30C、D、309、下列运算正确的是（）A、+ =B、3 ﹣2 =1C、2+ =2D、a ﹣b =（a﹣b）10、下列计算正确的是（）A、×=B、=3C、（）（）=﹣2D、×=11、Rt△ABC中，斜边BC=2，则AB2+AC2+BC2的值为（）A．8 B．4 C．6 D．无法计算12、如图，已知两正方形的面积分别是25和169，则字母B所代表的正方形的面积是（）A．12 B．13 C．144 D．19413、已知一直角三角形的木板，三边的平方和为1800cm2，则斜边长为（）A．30cm B．80cm C．90cm D．120cm14、下列说确的是（）A．已知a、b、c是三角形的三边长，则a2+b2=c2B．在直角三角形中，两边的平方和等于第三边的平方C．在Rt△ABC中，∠C=90°，a、b、c分别是∠A，∠B，∠C的对边，则a2+b2=c2D．在Rt△ABC中，∠B=90°，a、b、c分别是∠A，∠B，∠C的对边，则a2+b2=c215、已知，如图长方形ABCD中，AB=3cm，AD=9cm，将此长方形折叠，使点B与点D重合，折痕为EF，则△ABE的面积为（）A．3cm2B．4cm2C．6cm2D．12cm2二、填空题（共15题；共30分）16、如图，有一个长为50cm，宽为30cm，高为40cm的长方体木箱，一根长70cm的木棍放入（填“能”或“不能”）．17、长方体的长、宽、高分别为8cm，4cm，5cm．一只蚂蚁沿着长方体的表面从点A爬到点B．则蚂蚁爬行的最短路径的长是cm．18、如图是一个三级台阶，它的每一级的长，宽，高分别为100cm，15cm和10cm，A和B 是这个台阶的两个相对的端点，A点上有一只蚂蚁想到B点去吃可口的食物，则它所走的最短路线长度为．19、如图，已知CD=6m，AD=8m，∠ADC=90°，BC=24m，AB=26m．图中阴影部分的面积=．20、如图，所有三角形都是直角三角形，所有四边形都是正方形，已知S1=9，S2=4，S3=8，S4=10，则S=．21、边长为7，24，25的△ABC有一点P到三边距离相等，则这个距离为．22、一个三角形的三边的比是3：4：5，它的周长是36，则它的面积是．23、下列各数：，，，1.414，，3.12122，，3.161661666…（每两个1之间依次多1个6）中，无理数有________个，有理数有________个，负数有________个，整数有________个． 24、用科学记算器计算，按键顺序的结果是________ ． 25、已知﹣1＜a ＜0，化简得________． 26、下列二次根式，不能与合并的是________（填写序号即可）．①；②；③；④；⑤． 27、﹣8的立方根是________．28、当x=2+时，式子x 2﹣4x+2017=________． 29、已知m=1+，n=1﹣，则代数式的值________． 30、化简：（+2）（﹣2）=________．三、解答题（共8题；共75分）31、化简（24分）：①44.1-21.1; ②2328-+;③92731⋅+; ④0)31(33122-++;⑤)32(-;1(-+; ⑥2)5)(12⑦2)332(-+.23)(22(+; ⑧)332、在：，，0，3.14，﹣，﹣，7.151551…（每相邻两个“1”之间依次多一个“5”）中（6分），整数集合{…}，分数集合{…}，无理数集合{…}．33、如图，已知四边形ABCD中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD的面积．（5分）34、如图，已知AC=4，BC=3，BD=12，AD=13，∠ACB=90°，试求阴影部分的面积．（5分）35、已知2m-3和m-12是数p 的平方根，试求p 的值。
北师大版八年级(上)数学《勾股定理》专题复习(含答案)
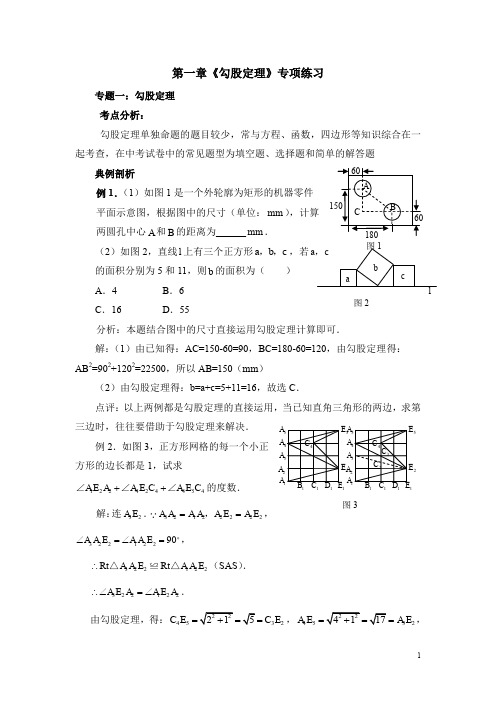
第一章《勾股定理》专项练习专题一：勾股定理考点分析：勾股定理单独命题的题目较少，常与方程、函数，四边形等知识综合在一起考查，在中考试卷中的常见题型为填空题、选择题和简单的解答题典例剖析例1．（1）如图1是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位：mm），计算两圆孔中心A和B的距离为______mm．（2）如图2，直线l上有三个正方形a b c，，，若的面积分别为5和11，则b的面积为（）A．4 B．6C．16 D．55分析：本题结合图中的尺寸直接运用勾股定理计算即可．解：（1）由已知得：AC=150-60=90，BC=180-60=120，由勾股定理得：AB2=902+1202=22500，所以AB=150（mm）（2）由勾股定理得：b=a+c=5+11=16，故选C．点评：以上两例都是勾股定理的直接运用，当已知直角三角形的两边，求第三边时，往往要借助于勾股定理来解决．例2．如图3，正方形网格的每一个小正方形的边长都是1，试求122424454A E A A E C A E C++∠∠∠的度数．解：连32A E．32122222A A A A A E A E==，，32212290A A E A A E∠=∠=，322122Rt RtA A E A A E∴△≌△（SAS）．322122A E A A E A∴∠=∠．由勾股定理，得：4532C E C E===，4532A E A E===，图21A2A3A4A5A5E2E11114C1A2A3A4A5A5E2E11114C3C2C图344332A C A C ==，445332A C E A C E ∴△≌△（SSS ）． 323454A E C A E C ∴∠=∠122424454324424323224A E A A E C A E C A E C A E C A E C A E C ∴∠+∠+∠=∠+∠+∠=∠．由图可知224E C C △为等腰直角三角形．22445A E C ∴∠=． 即12242445445A E A A E C A E C ∠+∠+∠=．点评：由于在正方形网格中，它有两个主要特征：（1）任何格点之间的线段都是某正方形或长方形的边或对角线，所以格点间的任何线段长度都能求得．（2）利用正方形的性质，我们很容易知道一些特殊的角，如450、900、1350，便一目了然．以上两例就是根据网格的直观性，再结合图形特点，运用勾股定理进行计算，易求得线段和角的特殊值，重点考查学生的直觉观察能力和数形结合的能力．专练一：1、△ABC 中，∠A ：∠B ：∠C=2：1：1，a ，b ，c 分别是∠A 、∠B 、∠C 的对边，则下列各等式中成立的是（ ）（A ）222a b c +=；（B ）222a b =； （C ）222c a =； （D ）222b a = 2、若直角三角形的三边长分别为2，4，x ，则x 的可能值有（ ） （A ）1个； （B ）2个； （C ）3个； （D ）4个3、一根旗杆在离底面4.5米的地方折断，旗杆顶端落在离旗杆底部6米处，则旗杆折断前高为（ ）（A ）10.5米； （B ）7.5米； （C ）12米； （D ）8米 4、下列说法中正确的有（ ）（1）如果∠A+∠B+∠C=3：4：5，则△ABC 是直角三角形；（2）如果∠A+∠B=∠C ，那么△ABC 是直角三角形；（3）如果三角形三边之比为6：8：10，则ABC 是直角三角形；（4）如果三边长分别是221,2,1(1)n n n n -+>，则ABC 是直角三角形。
北师大版八年级勾股定理练习题(含答案)
北师大版八年级数学上【1】勾股定理练习题一、基础达标:1. 下列说法正确的是（）A.若 a、b、c是△ABC的三边，则a2＋b2＝c2；B.若 a、b、c是Rt△ABC的三边，则a2＋b2＝c2；C.若 a、b、c是Rt△ABC的三边， 90∠A，则a2＋b2＝c2；=D.若 a、b、c是Rt△ABC的三边， 90∠C，则a2＋b2＝c2．=2. Rt△ABC的三条边长分别是a、b、c，则下列各式成立的是（）A．cb+ D.+ C. ca<bba>a=+ B. c2c22+a=b3．如果Rt△的两直角边长分别为k2－1，2k（k >1），那么它的斜边长是（）A、2kB、k+1C、k2－1D、k2+14. 已知a，b，c为△ABC三边，且满足(a2－b2)(a2+b2－c2)＝0，则它的形状为（）A.直角三角形B.等腰三角形C.等腰直角三角形D.等腰三角形或直角三角形5．直角三角形中一直角边的长为9，另两边为连续自然数，则直角三角形的周长为（）A．121B．120C．90D．不能确定6．△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长为（）A．42B．32C．42 或 32 D．37 或 337.※直角三角形的面积为S，斜边上的中线长为d，则这个三角形周长为（）（A2d（B d（C）2d（D）d8、在平面直角坐标系中，已知点P的坐标是(3,4)，则OP的长为（ ）A ：3 B ：4 C ：5 D ：79．若△ABC 中，AB=25cm ，AC=26cm 高AD=24,则BC 的长为（ ）A ．17 B.3 C.17或3 D.以上都不对10．已知a 、2(6)100a c --=则三角形的形状是（ ）A ：底与边不相等的等腰三角形B ：等边三角形C ：钝角三角形D ：直角三角形11．斜边的边长为cm 17，一条直角边长为cm 8的直角三角形的面积是．12. 等腰三角形的腰长为13，底边长为10，则顶角的平分线为＿＿.13. 一个直角三角形的三边长的平方和为200，则斜边长为14．一个三角形三边之比是6:8:10，则按角分类它是三角形．15. 一个三角形的三边之比为5∶12∶13，它的周长为60，则它的面积是＿＿＿.16. 在Rt △ABC 中，斜边AB=4，则AB 2＋BC 2＋AC 2=_____．17．若三角形的三个内角的比是3:2:1，最短边长为cm 1，最长边长为cm 2，则这个三角形三个角度数分别是，另外一边的平方是．18．如图，已知ABC ∆中，︒=∠90C ，15=BA ，12=AC ，以直角边BC 为直径作半圆，则这个半圆的面积是．19． 一长方形的一边长为cm 3，面积为212cm ，那么它的一条对角线长是． 二、综合发展:1．如图，一个高4m 、宽3m 的大门，需要在对角线的顶点间加固一个木条，求木条的长．2、有一个直角三角形纸片，两直角边AC=6cm,BC=8cm,现将直角边AE 重合， AC B你能求出CD 的长吗？3.一个三角形三条边的长分别为cm 15，cm 20，cm 25，这个三角形最长边上的高是多少？4．如图，要修建一个育苗棚，棚高h=3m ，棚宽a=4m ，棚的长为12m ，现要在棚顶上覆盖塑料薄膜，试求需要多少平方米塑料薄膜？5．如图，有一只小鸟在一棵高13m 的大树树梢上捉虫子，它的伙伴在离该树12m ，高8m 的一棵小树树梢上发出友好的叫声，它立刻以2m/s 的速度飞向小树树梢，它最短要飞多远？这只小鸟至少几秒才可能到达小树和伙伴在一起？15．“中华人民共和国道路交通管理条例”规定：小汽车在城街路上行驶速度不得超过70km/h.如图，，一辆小汽车在一条城市街路上直道行驶，某一时刻刚好行驶到路对面车速检测仪正前方30m 处，过了2s 后，测得小汽车与车速检测仪间距离为50m ，这辆小汽车超速了吗？答案:一、基础达标1. 解析:利用勾股定理正确书写三角形三边关系的关键是看清谁是直角．答案: D.2. 解析：本题考察三角形的三边关系和勾股定理.答案：B.3．解析：设另一条直角边为x ，则斜边为（x+1）利用勾股定理可得方程，可以求出x ．然后再求它的周长.答案：C ．4．解析：解决本题关键是要画出图形来，作图时应注意高AD 是在三角形的内部还是在三角形的外部，有两种情况，分别求解.答案：C.5． 解析: 勾股定理得到：22215817=-，另一条直角边是15， 小汽车 小汽车 B C 观测点所求直角三角形面积为21158602cm ⨯⨯=．答案:260cm ．6． 解析：本题目主要是强调直角三角形中直角对的边是最长边,反过来也是成立．答案:222c b a =+，c ，直角，斜，直角．7． 解析:本题由边长之比是6:8:10可知满足勾股定理，即是直角三角形．答案：直角．8． 解析：由三角形的内角和定理知三个角的度数,断定是直角三角形．答案：︒30、︒60、︒90，3．9．解析：由勾股定理知道：22222291215=-=-=AC AB BC ，所以以直角边9=BC 为直径的半圆面积为10.125π．答案：10.125π．10． 解析:长方形面积长×宽，即12长×3，长4=，所以一条对角线长为5．答案：cm 5．二、综合发展11．解析：木条长的平方=门高长的平方+门宽长的平方．答案：5m ．12解析：因为222252015=+，所以这三角形是直角三角形，设最长边（斜边）上的高为xcm ，由直角三角形面积关系，可得1115202522x ⨯⨯=⨯⋅，∴12=x ．答案：12cm 13．解析：透阳光最大面积是塑料薄膜的面积，需要求出它的另一边的长是多少，可以借助勾股定理求出.答案：在直角三角形中，由勾股定理可得：直角三角形的斜边长为5m,所以矩形塑料薄膜的面积是：5×20=100(m 2) ．14．解析：本题的关键是构造直角三角形，利用勾股定理求斜边的值是13m ，也就是两树树梢之间的距离是13m ，两再利用时间关系式求解.答案：6.5s ．15．解析：本题和14题相似，可以求出BC 的值，再利用速度等于路程除以时间后比较.BC=40米，时间是2s ，可得速度是20m/s=72km/h ＞70km/h ．答案：这辆小汽车超速了．。
初二数学上册知识点.复习及配套练习(新北师大版本)
.新北师大版八年级数学上册知识点复习第一章勾股定理1．勾股定理：直角三角形两直角边的平方和等于斜边的平方；即 2 2 2a b c 。
2．勾股定理的证明：用三个正方形的面积关系进行证明（两种方法）。
2 2 23．勾股定理逆定理：如果三角形的三边长a，b，c 满足a b c ，那么这个三角形是2 2 2直角三角形。
满足a b c 的三个正整数称为勾股数。
第二章实数1．平方根和算术平方根的概念及其性质：（1）概念：如果 2x a，那么x 是a 的平方根，记作： a ；其中 a 叫做a 的算术平方根。
（2）性质：①当a≥0 时， a ≥0；当a ＜０时， a 无意义；②2a ＝a ；③ 2a a 。
2．立方根的概念及其性质：（1）概念：若（2）性质：①33 a ；x a ，那么x 是a 的立方根，记作：33 a3 a ；② 3 a a；③ 3 a ＝ 3 a3．实数的概念及其分类：（1）概念：实数是有理数和无理数的统称；（2）分类：按定义分为有理数可分为整数的分数；按性质分为正数、负数和零。
无理数就是无限不循环小数；小数可分为有限小数、无限循环小数和无限不循环小数；其中有限小数和无限循环小数称为分数。
4．与实数有关的概念：在实数范围内，相反数，倒数，绝对值的意义与有理数范围内的意义完全一致；在实数范围内，有理数的运算法则和运算律同样成立。
每一个实数都可以用数轴上的一个点来表示；反过来，数轴上的每一个点都表示一个实数，即实数和数轴上的点是一一对应的。
因此，数轴正好可以被实数填满。
a a5．算术平方根的运算律：（a ≥0，b ≥0）；（a ≥0，b ＞0）。
a b a bb b第三章位置与坐标1．直角坐标系及坐标的相关知识。
2．点的坐标间的关系：如果点A、B横坐标相同，则AB ∥y 轴；如果点A、B 纵坐标相同，则AB∥x 轴。
3．将图形的纵坐标保持不变，横坐标变为原来的1倍，所得到的图形与原图形关于y 轴对称；将图形的横坐标保持不变，纵坐标变为原来的1倍，所得到的图形与原图形关于x 轴对称；将图形的横、纵坐标都变为原来的1倍，所得到的图形与原图形关于原点成中心对称。
北师大版数学八年级上册全册复习
例4 李老师让同学们讨论这样一个问题，如图1－3所示，有 一个长方体盒子，底面正方形的边长为2 cm，高为3 cm，在长
方体盒子下底面的A点处有一只蚂蚁，它想吃到上底面的F点处
的食物，则怎样爬行路程最短？最短路程是多少？
过了一会，李老师问同学们答案，甲生说：先由A点到B点， 再走对角线BF；乙生说：我认为应由A先走对角线AC，再走C到F 点；丙生说：将长方形ABCD与长方形BEFC展开成长方形AEFD， 利用勾股定理求AF的长；丁生说：将长方形ABCD与正方形CFGD 展开成长方形ABFG，利用勾股定理求AF的长．你认为哪位同学
则BF＝BC＋CF＝3＋2＝5(cm)，AB＝2 cm，连接AF，在 Rt△ABF中，AF2＝BF2＋AB2＝52＋22＝29≈5.392，
∴AF＝5.39 cm.连接AC， ∵AF<AC＋CF，
∴丁的方法比乙的好． 比较丙生与丁生的计算结果，知丙生的说法正确．
图1－4
图1－5
方法技巧
最短路径问题是勾股定理在立体几何中的应用，一般做法 是把长方体(或其他几何体)侧面展开，将立体图形问题转化为 平面图形问题，再根据两点之间线段最短，用勾股定理求解．
图1－19
15.一个棱长为6的木箱(如图1－20)，一只苍蝇位于左面的壁 上，且到该面上两侧棱距离相等的A处．一只蜘蛛位于右面壁上 ，且到该面与上、下底面两交线的距离相等的B处．已知A到下 底面的距离AA′＝4，B到一个侧面的距离BB′＝4，则蜘蛛沿这 个立方体木箱的内壁爬向苍蝇的最短路程为多少？
在 Rt△ECF 中，有 EF2＝a22＋a42＝156a2. 在 Rt△FDA 中，有 AF2＝a22＋a2＝54a2.
在 Rt△ABE 中，有 BE＝a－14a＝34a，
北师大版初中数学八年级数学上学期第1章勾股定理复习训练题有答案
一、填空题1．直角三角形两直角边长分别为5 和12，则斜边为________，斜边上的高为__________． 2．已知一个直角三角形的两边长分别为3和4，则第三边长是3. 已知等腰三角形的腰长是5cm ，底边长是6cm ，那么这个等腰三角形的面积是 .4．如图所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为8，正方形A 的面积是11，B 的面积是10，C 的面积是13，则D 的面积之为_______.5. 如图,有两棵树,一棵高8米,另一棵高2米,两树相距8米,一只小鸟从一棵树的树梢飞到另一棵树的树梢,则它至少要飞行___________米.6．如图，直线 l 过正方形 ABCD 的顶点 B , 点A 、C 到直线l 的距离分别是 1 和 2 , 则正方形的ABCD 的面积是 . 7. 如图是一个长方体长4、宽3、高12，则图中阴影部分的三角形的周长为__________。
8．在△ABC 中，∠90°，a 、b 、c 分别为∠A 、∠B 、∠C 的对边. (1)若a ＝6，c ＝10，则b ＝ ； (2)若a ＝12，b ＝5，则c ＝ ； (3)若c ＝15，b ＝12，则a ＝ 。
9．在△ABC 中，AB ＝AC ，AD ⊥BC ，若AB ＝13，BC ＝10，则AD ＝ 。
10．若一个直角三角形的三边长分别是6、8、a ，则a 2＝11．等腰三角形的腰长为10，底边上的高为6，则底边长为 。
12．小颖从学校出发向南走了150m ，接着向东走了80m 到书店，则学校与书店的距离是 。
13．飞机在空中水平飞行，某一时刻刚好到一个站着不动的女孩头顶正上方4000米处，过了20秒，飞机距离这个女孩头顶5000米处，则飞机飞行的速度为 千米/时。
二、选择题14．下列几组数中不能作为直角三角形三边长度的是 （ ） A ．7,24,25a b c === B ． 1.5,2, 2.5a b c ===ABCD8cm第9题312C．25,2,34 a b c===D．15,8,17a b c===15. 在下列以线段a，b，c的长为三边的三角形中，不能构成直角三角形的是()A. a＝9,b＝41,c＝40B. a＝5,b＝12, c＝13C. a:b:c＝3:4:5D. a＝11,b＝12,c＝1516. 若△ABC中，AB＝13，AC＝15，高AD＝12，则BC的长是()A. 14B. 4C. 14或4D. 以上都不对17.《勾股圆方图》，它是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，如果大正方形的面积是13，小正方形的面积是1，直角三角形的短直角边为a，较长直角边为b，那么(a＋b)2的值为()A. 13B. 19C.25D. 16918. 如图，已知矩形ABCD沿着直线BD折叠，使点C落在C'处，BC'交AD于E，AD＝8，AB＝4，则DE的长为()A. 3B. 4C. 5D. 619．两只小鼹鼠在地下打洞，一只朝正东方挖，每分钟挖8cm，另一只朝正南方挖，每分钟挖6cm，10分钟之后两只小鼹鼠相距（）A. 50cmB. 100cmC. 140cmD. 80cm20．如图一个圆桶儿，底面直径为24cm,高为32cm,则桶内能容下的最长的木棒为（）A. 20cmB. 50cmC. 40cmD. 45cm21. 如图将一根长24cm的筷子，置于底面直径为5cm，高为12cm的圆柱形水杯中，设筷子露在杯子外面的长度是为hcm，则h的取值范围是___________。
初中数学北师大版八年级上册 第一章 勾股定理单元测试(含答案)
第一章勾股定理一、选择题1. 若a，b，c为△ABC的三边长，则下列条件中不能判定△ABC是直角三角形的是( )A．a=1.5，b=2，c=2.5B．a:b:c=3:4:5C．∠A+∠B=∠C D．∠A:∠B:∠C=3:4:52. 在Rt△ABC中，若∠C=90∘，AC=3，BC=4，则点C到直线AB的距离为( )A．3B．4C．5D．2.43. 如图，四边形ABCD中，∠B=90∘，且AB=BC=2，CD=3，DA=1，则∠DAB的度数为( )A．90∘B．120∘C．135∘D．150∘4. 如图，在高为5 m，坡面长为13 m的楼梯表面铺地毯，地毯的长度至少需要( )A．17 m B．18 m C．25 m D．26 m5. 如图是一株美丽的勾股树，其中所有四边形都是正方形，所有的三角形都是直角三角形．若正方形A，B，C，D的面积分别为3，5，2，3，则最大正方形E的面积是( )A．47B．13C．11D．86. 如图，将一根长度为8 cm，自然伸直的弹性皮筋AB两端固定在水平的桌面上，然后把皮筋中点C竖直向上拉升3 cm到点D，则此时该弹性皮筋被拉长了( )A．6 cm B．5 cm C．4 cm D．2 cm7. 如图，为了测得湖两岸A点和B点之间的距离，一个观测者在C点设桩，使∠ABC=90∘，并测得BC长为16 m，若已知AC比AB长8 m，则A点和B点之间的距离为( )A．25 m B．12 m C．13 m D．43 m8. 如图，在三角形纸片ABC中，∠ACB=90∘，AC=4，BC=3，点D，E分别在AB，AC上，连接DE，将△ADE沿DE翻折，使点A的对应点F落在BC的延长线上．若FD平分∠EFB，则AD的长为( )A．259B．258C．157D．207二、填空题9. 在△ABC中，∠C=90∘．（1）已知a=10，b=24，那么c=．（2）已知b:c=4:5，a=9，那么b=，c=．10. 如图是“赵爽弦图”，△ABH，△BCG，△CDF和△DAE是四个全等的直角三角形，四边形ABCD和EFGH都是正方形，如果AH=6，EF=2，那么AB等于．11. 《九章算术》中的“折竹抵地”问题：今有竹高一丈，末折抵地，去根六尺．问折高者几何？意思是：一根竹子，原高一丈（一丈=10尺），一阵风将竹子折断，其竹梢恰好抵地，抵地处离竹子底部6尺远，问折断处离地面的高度是多少？设折断处离地面的高度为x尺，则可列方程为．12. 如图，一个长方体长4 cm，宽3 cm，高12 cm，则它上下两底面的对角线MN的长为cm．13. 已知a，b，c为△ABC的三边，且满足a2+b2+c2+338=10a+24b+26c，则可以判断△ABC的形状为．14. 如图所示的网格是正方形网格，则∠PAB+∠PBA=∘（点A，B，P是网格线的交点）．15. 对角线互相垂直的四边形叫做“垂美”四边形，现有如图所示的“垂美”四边形ABCD，对角线AC，BD交于点O．若AD=2，BC=4，则AB2+CD2=．三、解答题16. 在Rt△ABC中，∠C=90∘．(1) 已知a=8，c=17，求b．(2) 已知b=40，c=41，求a．17. 如图，在四边形ABCD中，∠DBC=90∘，AB=9，AD=12，BC=8，DC=17，求四边形ABCD的面积．18. 如图，滑竿在机械槽内运动，∠C=90∘，AB=2.5 m，BC=1.5 m，当底端B向右移动0.5 m时，顶端A下滑了多少米？19. 假期中，王强和同学到某海岛上去旅游．他们按照如图所示路线．在点A登陆后租借了自行车，骑车往东走8千米，又往北走2千米；遇到障碍后往西走3千米，再折向北走到6千米处往东拐，走了1千米到达景点B．登陆点A到景点B的直线距离是多少千米？20. 若正整数a，b，c（a<b<c）满足a2+b2=c2，则称（a，b，c）为一组“勾股数”．观察下列两类“勾股数”：第一类（a是奇数）：(3,4,5)，(5,12,13)，(7,24,25)，⋯⋯第二类（a是偶数）：(6,8,10)，(8,15,17)，(10,24,26)，⋯⋯(1) 请再写出两组勾股数，每类各写一组；(2) 分别就a为奇数、偶数两种情形，用a表示b和c，并选择其中一种情形证明(a,b,c)是“勾股数”．答案一、选择题1. D2. D3. C4. A5. B6. D7. B8. D二、填空题9. 26；12；1510. 1011. x2+62=(10−x)212. 1313. 直角三角形14. 4515. 20三、解答题16.(1) 15．(2) 9．17. ∵∠DBC=90∘，DC=17，BC=8，∴BD2=CD2−BC2=172−82=225=152，∴BD=15．∵AD2+AB2=122+92=144+81=225，BD 2=225， ∴AD 2+AB 2=BD 2，∴△ABD 是直角三角形，且 ∠A =90∘，∴ 四边形 ABCD 的面积 =△ABD 的面积 +∠CBD 的面积 =12×9×12+12×15×8=54+60=114．18. 依题意得 AB =DE =2.5 m ，BC =1.5 m ，∠C =90∘，∴AC 2+BC 2=AB 2，即 AC 2+1.52=2.52，解得 AC =2 m ． ∵BD =0.5 m ， ∴CD =2 m ．在 Rt △ECD 中，CE 2+CD 2=DE 2， ∴CE =1.5 m ， ∴AE =0.5 m ．答：顶端 A 下滑了 0.5 m ．19. 10 千米．20.(1) 第一组（a 是奇数）：9,40,41（答案不唯一）；第二组（a 是偶数）：12,35,37（答案不唯一）．(2) 当 a 为奇数时，b =a 2−12，c =a 2+12；当 a 为偶数时，b =a 24−1，c =a 24+1．证明：当 a 为奇数时，a 2+b 2=a 2+(a 2−12)2=(a 2+12)2=c 2，∴(a,b,c ) 是“勾股数”．当 a 为偶数时，a 2+b 2=a 2+(a 24−1)2=(a 24+1)2=c 2，∴(a,b,c ) 是“勾股数”．。
北师大版数学八年级上学期勾股定理总复习
八年级数学（上）勾股定理练习题【主要知识】1、勾股定理：直角三角形的两直角边的平方和等于_______________。
如果用b a ,和c 分别表示直角三角形的两直角边和斜边，那么________________【注】①直角三角形；②找准斜边、直角边。
2、（1）勾股定理的逆定理：如果三角形的三边长c b a ,,满足_____________，那么这个三角形是直角三角形。
（2）勾股数：满足222c b a =+的三个正整数，称为______________。
3、勾股定理的应用1、在Rt △ABC 中，∠C ＝90°，a ＝12，b ＝16，则c 的长为（ ）A ．26B ．18C ．20D ．212、在下列数组中，能构成一个直角三角形的有（ ） ①10，20，25；②10，24，25；③9，80，81；④8；15；17A 、4组B 、3组C 、2组D 、1组3、三角形的三边长ａ,ｂ,ｃ满足2ａｂ=(ａ+ｂ)2－ｃ2,则此三角形是 ( ). A 、钝角三角形 B 、锐角三角形 C 、直角三角形 D 、等边三角形 4、下列各组数：①0.3，0.4，0.5；②9，12，16；③4，5，6；④a 8，a 15，a 17（0≠a ）； ⑤9，40，41。
其中是勾股数的有（ ）组A 、1B 、2C 、3D 、45、将Rt △ABC 的三边都扩大为原来的2倍，得△A ’B ’C ’,则△A ’B ’C ’为( ) A 、 直角三角形 B 、锐角三角形 C 、钝角三角形 D 、无法确定6、在Rt △ABC 中，∠C ＝90°，∠B ＝45°,c ＝10，则a 的长为（ ）A ：5B ：10C ：25D ：57、已知a 、b 、c 是三角形的三边长，如果满足2(6)100a c --=，则三角形的形状是（ ）A ：底与边不相等的等腰三角形B ：等边三角形C ：钝角三角形D ：直角三角形S 3S 2S 1CBA8、将一根24cm 的筷子，置于底面直径为15cm ，高8cm 的圆柱形水杯中，如图所示，设筷子露在杯子外面的长度为hcm ，则h 的取 值范围是（ ）．A ．h ≤17cmB ．h ≥8cmC ．15cm ≤h ≤16cmD ．7cm ≤h ≤16cm1、有两棵树，一棵高6米，另一棵高2米，两树相距5米．一只小鸟从一棵树的树梢飞到.2、如图，把直角三角形ABC 的斜边AB 放在定直线l 上，按顺时针A 向在l 上转动两次，使它转到△A ’B ’C ’的位置．设BC ＝1，AC ＝3，则顶点A 运动到点A ’’的位置时，点A 经过的路线长是 （计算结果不取近似值）．3、如图所示，以Rt ABC 的三边向 外作正方形，其面积分别为123,,S S S ,且1234,8,S S S ===则 ；4、在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S1、S2、S3、S4，则 S1+S2+S3+S4=_______.5、木工师傅要做一个长方形桌面，做好后量得长为80cm ，宽为60cm ，对角线为100cm ， 则这个桌面 （填“合格”或“不合格”）；6、写出一组全是偶数的勾股数是 ；7、如图，为修通铁路凿通隧道AC ，量出∠A=40°∠B ＝50°，AB ＝5公里，BC ＝4公里，若每天凿隧道0.3公里，问几天才能把隧道AB 凿通？CADCAB D8、（本题10分）如图，某会展中心在会展期间准备将高5m ,长13m ，宽2m 的楼道上铺地毯,已知地毯平方米189、（本题10分）如图，每个小方格的边长都为1．求图中格点四边形ABCD 的面积。
北师大版八年级上册数学 勾股定理及实数综合练习3
八上勾股定理与实数综合练习31．实数（相邻两个1之间依次多一个0），其中无理数是（ ）个．A ． 1B ．2C ． 3D ．4 2．如图，在数轴上表示实数的点可能是（ ）A ． 点MB ． 点NC ．点P D ． 点Q 3．若x ，y 为实数，且|x+1|+=0，则（）2011的值是（ ）A ． 0B ． 1C ． ﹣1D ．﹣20114．如图，在Rt △ABC 中，∠ACB=90°，CD ⊥AB 于D ，已知BC=8，AC=6，则斜边AB 上的高是（ ）A ． 10B ． 5C ．D ． 5．如图．矩形纸片ABCD 中，已知AD=8，折叠纸片使AB 边与对角线AC 重合，点B 落在点F 处，折痕为AE ，且EF=3．则AB 的长为（ ）A ． 3B ． 4C ． 5D ． 66．如图是一块长，宽，高分别是6cm ，4cm 和3cm 的长方体木块一只蚂蚁要从长方体木块的一个顶点A 处，沿着长方体的表面到长方体上和A 相对的顶点B 处吃食物，那么它需要爬行的最短路径的长是（ ）A ． （3+2）cmB ． cmC ． cmD ． cm7．如图，在数轴上点A和点B之间的整数是_________．8．勾股定理是几何中的一个重要定理．在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入矩形内得到的，∠BAC=90°，AB=3，AC=4，点D，E，F，G，H，I都在矩形KLMJ的边上，则矩形KLMJ的面积为（）A ．90 B．100 C．110 D．1219.已知三角形相邻两边长分别为20cm和30cm，第三边上的高为10cm，则此三角形的面积为_________cm2．10、已知△ABC是边长为1的等腰直角三角形，以Rt△ABC的斜边AC为直角边，画第二个等腰Rt△ACD，再以Rt△ACD的斜边AD为直角边，画第三个等腰Rt△ADE，…，依此类推，第n个等腰直角三角形的斜边长是_________．11、已知：如图，以Rt△ABC的三边为斜边分别向外作等腰直角三角形．若斜边AB=3，则图中阴影部分的面积为_________．12．计算：+（﹣）+．（+）﹣（）﹣；13、解方程-10032)4()1(-=-x 381250x +=14. 若8+a 与()227-b 互为相反数，求33b a -的立方根.15、请阅读下列解题过程：已知a 、b 、c 为△ABC 的三边，且满足a 2c 2﹣b 2c 2=a 4﹣b 4，试判断△ABC 的形状．解：∵a 2c 2﹣b 2c 2=a 4﹣b 4，A∴c 2（a 2﹣b 2）=（a 2+b 2）（a 2﹣b 2），B∴c 2=a 2+b 2，C∴△ABC 为直角三角形．D问：（1）在上述解题过程中，从哪一步开始出现错误： _________ ；（2）错误的原因是： _________ ；（3）本题正确的结论是： ．16．已知：如图，在四边形ABCD 中，∠ABC=90°，CD ⊥AD ，AD 2+CD 2=2AB 2．（1）求证：AB=BC ；（2）当BE ⊥AD 于E 时，试证明：BE=AE+CD ．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
北师大版初二上数学勾
股定理与实数复习题 TTA standardization office【TTA 5AB- TTAK 08- TTA 2C】
北师大版初二上数学《勾股定理》与《实数》复习题
一、填空题：
1、已知直角三角形的三边长为6、8、x ，则以x
2、如右图：以直角三角形斜边为边的正方形面积是
3、9的算术平方根是 ， 0)
5(-的立方根是
4、在棱长为5
是 ；
5、210-的算术平方根是 ，16的平方根是 ；
6、计算：_________,1125
61
3
=- 7、若a 、b 互为相反数，c 、d 互为负倒数，则______3=++cd b a ； 8、37-的相反数是 ；绝对值等于3的数是 ； 9、把下列各数分别填入相应的集合里：
有理数集合：｛ ｝；无理数集合：｛ ｝； 负实数集合：
｛ ｝；
10、已知5-a +3+b =0，那么a —b= ； 11、有两棵树，一棵高6米，另一棵高2
5
米．一只小鸟从一棵树的树梢飞到另一棵了 米.
12、如图，把直角三角形ABC 的斜边AB 放在定直线L 上，按顺时针方
向在L 上转动两次，使它转到△A ”B ”C ”的位置．设BC ＝1，AC ＝3，则顶点A 运
F
第14
题
图
C 第13题
动到点A”的位置时，点A经过的路线长是（计算结果不取近似值）．
13、已知：如图（1），在Rt△ABC中，∠B=90°，D、E分别是边AB、AC的中点，
DE=4，AC=10，则AB=_____________.
14、一只蚂蚁从长、宽都是3，高是8的长方体纸箱的A点沿纸箱爬到B点，那么它所行的最短路线的长是_____________。
15、把一根长为10㎝的铁丝弯成一个直角三角形的两条直角边，如果要使三角形的面积是9㎝2，那么还要准备一根长为____的铁丝才能按要求把三角形做好。
二．选择题：
1、五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（）
2、在△ABC中，AB=15,AC=13,高AD=12,则三角形的周长是（）
（A）42 (B)32 (C)42或32 (D)37或33.
3、已知一直角三角形的木版，三边的平方和为1800cm2,则斜边长为（）.
（A）80cm (B)30cm (C)90cm (D120cm.
4、下列六种说法正确的个数是 ( )
(A) 1 ( B) 2 (C) 3 (D) 4
○1无限小数都是无理○2正数、负数统称有理数○3无理数的相反数还是无理数○4无理数与无理数的和一定还是无理数○5无理数与有理数的和一定是无理数○6无理数与有理数的积一定仍是无理数
5、下列语句中正确的是（）
(A) 9
- (B) 9的平方根是3
-的平方根是3
(C) 9的算术平方根是3
± (D) 9的算术平方根是3
6、下列运算中，错误的是 （ ） ①1251144251
=，②4)4(2±=-，③22222-=-=-，④20
9
5141251161=+=+ (A) 1个 ( B) 2个 (C) 3个 (D) 4个
7、若9,422==b a ，且0<ab ，则b a -的值为 （ ） (A) 2- (B) 5± (C) 5 (D) 5- 8、实数13 ，24 ，6π
中，分数的个数有（ ）
A 、0
B 、1
C 、2
D 、3
三．计算： 1、
24
612⨯ 2、)32)(32(-+
3、2)5
25(-
4、2224145-
5、 )81()64(-⨯-
6、
3
12
27-
7、348- 8、 ()
32
22143-⎪⎭
⎫
⎝⎛-⨯+
9、求x
（1）8)1(22=-x （2） 8)12(3-=-x 四．解答题：
1、一个长方形的长与宽的比是5：3，它的对角线长为68，求这个长方形的长与宽（结果保留两个有效数字）
2、已知a a a =-+-20052004，求22004-a 的值；
3、如图，每个小正方形的边长是1，在图中画出①一个面积是2的直角三角形；②一个面积是2的正方形。
4、自由下落的物体的高度h (米)与下落时间t (秒)的关系为h =2t .有一学生不慎让一个玻璃杯从米高的楼上自由下落, 刚好另有一学生站在与下落的玻璃杯同一直线的地面上, 在玻璃杯下落的同时楼上的学生惊叫一声. 问这时楼下的学生能躲开吗 (声音的速度为340米/秒)
5、如图, 一等边三角形的边长为10, 求它的面积. (精确到
6、如图, 在一圆筒里放入两种不同的物体, 并用一长方形的玻璃薄片(玻璃厚度忽略不计)分隔开来. 已知圆筒高30厘米, 容积为
9420厘米3, 问这长方形玻璃薄片的尺寸为多少 ( 取, 玻璃薄片的上边与圆筒的上底面持平) 7、如图, E 是长方形ABCD 边AD 的中点, AD=2AB=2,
求ΔBCE 的面积和周长.(结果精确到
8、如图，有一块塑料矩形模板ABCD ，长为10cm ，宽为5cm ，将你手中足够大的直角三角板 PHF 的直角顶点P 落在AD 边上（不与A 、D 重合），在
AD 上适当移动三角板顶点P ：
①能否使你的三角板两直角边分别通过点B 与点C ？若能，请你求出这时 AP 的长；若不能，请说明理由.
9、一架方梯长25米，如图，斜靠在一面墙上，梯子底端离墙7米，（1）这个梯子的顶端距地面有多高（
2）如果梯子的顶端下滑了4米，那么梯子的底端在水平方向滑动了几米（3）当梯子
的顶端下滑的距离与梯子的底端水平滑动的距离相等时，这时梯子的顶端距地面有多
高
A
A ′
A ′
O。