材料力学B试题6弯曲变形
材料力学—弯曲变形
判断方法：(两种方法)
左上右下为正
使研究对象顺时针转动为正
具体计算时：(黑色表示外力，蓝色表示内力)
S
F
S
F
S
F
S
F
F
判断方法：(两种方法)
左顺右逆为正 上凹下凸为正
具体计算时：（黑色表示外力，红色表示内力）
正： 负：
M
直接求解剪力和弯矩的法则：
1、 任意截面上的剪力=[∑一侧横向力代数值] 横向力：包含载荷、约束力、分布力、集中力 代数值：左上右下为正，反之为负
2、 任意截面上的弯矩=[∑一侧外力对截面形心之矩的代数值] 外力：包含载荷、约束力、分布力、集中力、集中力偶 代数值：左顺右逆为正，反之为负 截面形心：所求截面的截面形心
绘制剪力弯矩图的方法(从左往右绘制)：
q F F S s +=12所围成的面积 S F M M +=12所围成的面积。
材料力学B作业
第一章 绪 论一、选择题1、构件的强度是指_________，刚度是指_________，稳定性是指_________。
A. 在外力作用下构件抵抗变形的能力B. 在外力作用下构件保持其原有的平衡状态的能力C. 在外力作用下构件抵抗破坏的能力2、根据均匀性假设，可认为构件的________在各点处相同。
A. 应力B. 应变C. 材料的弹性常数D. 位移3、下列结论中正确的是________ 。
A. 内力是应力的代数和B. 应力是内力的平均值C. 应力是内力的集度D. 内力必大于应力4、下列说法中，正确的是________ 。
A. 内力随外力的改变而改变。
B. 内力与外力无关。
C. 内力在任意截面上都均匀分布。
D. 内力在各截面上是不变的。
5、图示两单元体虚线表示其受力后的变形情况,两单元体的切应变γ分别为________ 。
A. α，αB. 0，αC. 0，-2αD. α,2α二、计算题1、如图所示，在杆件的斜截面m-m上，任一点A处的应力p=120 MPa，其方位角θ=20°，试求该点处的正应力σ与切应力τ。
2、已知杆内截面上的内力主矢为F R与主矩M如图所示，且均位于x-y平面内。
试问杆件截面上存在哪种内力分量，并确定其大小。
图中之C点为截面形心。
3、板件ABCD的变形如图中虚线A’B’C’D’所示。
试求棱边AB与AD的平均正应变以及A点处直角BAD的切应变。
第二章 拉伸与压缩一、选择题和填空题1、轴向拉伸杆件如图所示，关于应力分布正确答案是_________。
A 1-1、2-2面上应力皆均匀分布；B 1-1面上应力非均匀分布，2-2面上应力均匀分布；C 1-1面上应力均匀分布，2-2面上应力非均匀分布；D 1-1、2-2面上应力皆非均匀分布。
2、图示阶梯杆AD 受三个集中力作用，设AB 、BC 、CD 段的横截面积分别为3A 、2A 、A ，则三段的横截面上 。
A 轴力和应力都相等B 轴力不等，应力相等C 轴力相等，应力不等D 轴力和应力都不等3、在低碳钢拉伸曲线中，其变形破坏全过程可分为4个变形阶段，它们依次是 、 、 、 。
第6节(弯曲变形)
Mechanics of Materials
中南大学土木建筑学院力学系
Department of Mechanics of School of Civil Engineering and Architecture of Central South University
第六章 弯曲变形 第一节 概述
Fx Fl
转角方程
EI(x)1Fx2FlxC
2 挠度方程
E Iv(x)1F x31F lx2C xD 62
EI
d2v dx2
Fx Fl
EI(x)1Fx2FlxC
2
E Iv(x)1F x31F lx2C xD 62
⑶ 确定积分常数
EI(0)1F02Fl0C0
2 E Iv(0 )1F 0 31F l0 2 C 0D 0
EI(x)b2F l x2C1
E I(x)b 2 F l x2F 2(xa)2C 2
挠度方程
EIv(x)b6F l x3C1xD1 E Iw (x ) b 6 F lx 3F 6(x a )3 C 2xD 2
⑶ 确定积分常数
v(0)E 1 I(b 6 F l03C 10D 1)0
v (l) E 1 I[ b 6 F ll3 F 6(l a )3 C 2 l D 2 ] 0
max
(0)
Fl2 3EI
(x) 0
x (3 3)l 3
(33)l F l3
F l3
vm a xv(
) 0 .0 6 4 2
3 93E I
E I
例：简支梁AB如图所示（图中a > b），承受集中载荷F作 用，梁的弯曲刚度为EI。求此梁的挠曲轴方程和转角方程， 并确定挠度的最大值。
材料力学第六章 弯曲变形
4
2
C
B
)
=
A
( A)q C
l q
( B )q
(b)
B
( wC )q
l
θ B ( θ B )q ( θ B ) M e
+
Me
(c)
Mel ql 24 EI 6 EI
3
A
B
( B ) M e
( A ) MC ( wC ) M
e
e
l
例题3
AB梁的EI为已知,求梁中间C截面挠度.
F1l 2 F2 la 0.4 400 200 B ( ) 16 EI 3 EI 210 1880 16 3 +0.423 10-4 （rad）
F1l a F2a F2a l wC 5.19 106 m 16 EI 3 EI 3 EI wmax w （3）校核刚度: l l
x A
dx
F
x
C' dω
B
d tg dx
二、挠曲线的微分方程
1.纯弯曲时曲率与弯矩的关系
M EI
1
横力弯曲时, M 和 都是x的函数.略去剪力对梁的位移的影 响, 则
1 M ( x) ( x) EI
2.由数学得到平面曲线的曲率
F
1 | w | 3 2 2 ( x) (1 w )
q
A x B
w w F wq
+
w wF wq
例1 已知：EI, F,q .求C点挠度 F q
A
C a a
B
Fa 3 ( wC )F 6 EI
材料力学第6章弯曲变形
M1 EIw1
Fb x1 l
2 x1
" EIw2
Fb M2 x2 F ( x2 a ) l
2 x2 2
EIw1
Fb C1 l 2
x2 a Fb F C2 (i) EIw2 l 2 2
工学院
§6.2 挠曲线的微分方程
纯弯曲情况下，弯矩与曲率 间的关系(5.1):
M EI
1
--(a)
横力弯曲时，梁截面上有弯矩也有剪力，对于跨 度远大于截面高度的梁，剪力对弯曲变形的影响可以 省略，(a)式便可以作为横力弯曲变形的基本方程。其 中，M和1/ρ都是x的函数。
工学院
§6.2 挠曲线的微分方程
(o) (p)
CB段 (a x2 l )
Fb 2 3l 2 2 2 l b 3 x ( x a ) 2 2 6l b Fb 2 l 2 2 3 EIw2 l b x x ( x a ) 2 2 6l b 2 EIw2
车床主轴的变形过大会影响 齿轮的啮合和轴承的配合， 造成磨损不匀，产生噪音， 降低寿命以及影响加工精度。
工学院
§6.1 工程中的弯曲变形问题
吊车梁的变形过大，会 使梁上小车行走困难， 出现爬坡现象，还会引 起较严重的振动。
变形超过允许数值，即 使在弹性范围内，也被 认为是一种失效现象。
工学院
§6.1 工程中的弯曲变形问题
l
2
b
2
3
工学院
§6.3 用积分法求弯曲变形—实例3
7). 讨论
上面得到最大挠度表达式为： 3 1 Fb 2 2 wmax l b 9 3 EIl
材料力学B试题6弯曲变形
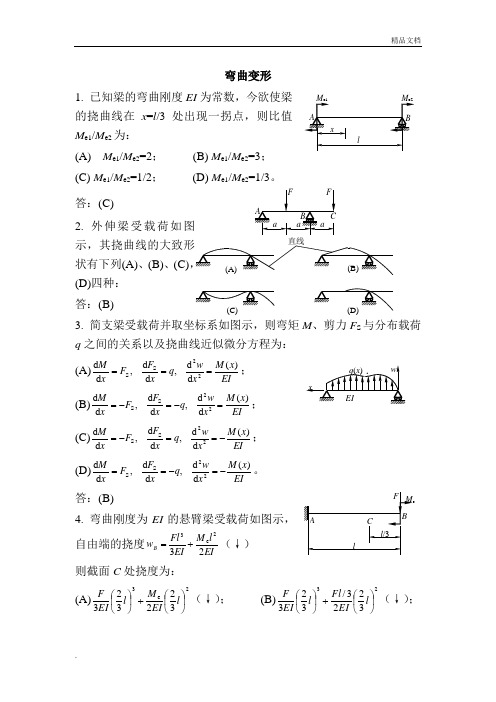
弯曲变形1. 已知梁的弯曲刚度EI 为常数，今欲使梁的挠曲线在x =l /3处出现一拐点，则比值M e1/M e2为：(A) M e1/M e2=2； (B) M e1/M e2=3； (C) M e1/M e2=1/2； (D) M e1/M e2=1/3。
答：(C)2. 外伸梁受载荷如图状有下列(A)、(B)、(C)(D)四种： 答：(B)3. 简支梁受载荷并取坐标系如图示，则弯矩M 、剪力F S 与分布载荷q 之间的关系以及挠曲线近似微分方程为：(A)EI x M xw q xF F xM)(d d ,d d ,dd 22SS ===； (B)EI x M xw q x F F x M)(d d ,d d ,d d 22SS =-=-=； (C)EI x M xw q x F F x M)(d d ,d d ,d d 22SS -==-=； (D)EI x M xw q xF F xM)(d d ,d d ,d d 22SS -=-==。
答：(B)4. 弯曲刚度为EI 的悬臂梁受载荷如图示，自由端的挠度EIl M EI Fl w B 232e 3+=（↓） 则截面C 处挠度为：(A)2e 3322323⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛l EI M l EI F （↓）； (B)233223/323⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l EI Fl l EI F （↓）；(C)2e 3322)3/(323⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛l EI Fl M l EI F （↓）；(D)2e 3322)3/(323⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛l EI Fl M l EI F （↓）。
答：(C)5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。
答：6.7.、(b)两种(A) (a)＞(b)； (B) (a)＜(b)； (C) (a)=(b)； (D) 不一定。
答：(C)8. 试写出图示等截面梁的位移边界条件，并定性地画出梁的挠曲线大致形状。
材料力学习题册答案_第6章_弯曲变形
得 x=0.519l
所以
W
m
ax
=0.00652
ql 4 EI
3 用叠加法求如图 7 所示各梁截面 A 的挠度和转角。EI 为已知常数。
解 A 截面的挠度为 P 单独作用与 M 0 单独作用所产生的挠度之和。 查表得：
y AP
Pl 3 24 EI
y = M 0l 2 Pl 3
AM 0
8EI
度 y = Fl 3 。 C 32 EI
4. 如图 4 所示两梁的横截面大小形状均相同，跨度为 l , 则两梁的力 图 相同 ，两梁的变形 不同 。（填“相同”或“不同”）
5. 提高梁的刚度措施有 提高Wz 、 降低 M MAX 等。 四、计算题 1 用积分法求图 5 所示梁 A 截面的挠度和 B 截面的转角。
8EI
y y 则 y A
AP
= Pl 3
AM0 12 EI
同理，A 截面的转角为 P 单独作用与 M 0 单独作用所产生的转角之和。
查表得
AP
Pl 2 8EI
对于 AM0 可求得该转角满足方程 EI =-Plx+C 边界条件 x=0 0 可得 C=0
现 4 个积分常数，这些积分常数需要用梁的 边界 条件和 光滑连
续 条件来确定。
2. 用积分法求图 2 所示梁变形法时，边界条件为：YA 0,A 0,YD 0 ；
连续条件为：
YA
1
YA
2
,
B
1
B
2
,
YC3.
如图
3
所示的外伸梁，已知
B
截面转角
B
=
Fl 2 16 EI
，则 C 截面的挠
于零的截面处。
材料力学弯曲变形
压杆稳定计算 1）根据压杆的约束条件确定长度系数 ）根据压杆的约束条件确定长度系数µ 2）计算杆件自身的柔度 ）计算杆件自身的柔度λ(10.7)，判断发生弯曲的平面 ， 也可由惯性矩来判断最大、最小刚度平面） （也可由惯性矩来判断最大、最小刚度平面） 3）通过比较 的大小，判断计算临界压力的公式 的大小， ）通过比较λ的大小
1. λ1与材料的性能有关，材料不同，λ1的数 与材料的性能有关，材料不同， 值也就不同； 越大，杆件越容易弯曲。 值也就不同；λ越大，杆件越容易弯曲。 2. 满足 1条件的杆件称为细长杆或大柔度杆； 满足λ≥λ 条件的杆件称为细长杆 大柔度杆； 细长杆或 也叫大柔度杆的分界条件。 也叫大柔度杆的分界条件。其临界应力可用欧 拉公式计算。 拉公式计算。 3. λ越大杆件越容易弯曲。 越大杆件越容易弯曲。 越大杆件越容易弯曲 解题步骤： 解题步骤： 1）由截面形状确定最大、最小刚度平面 ）由截面形状确定最大、 2）计算柔度，判断欧拉公式是否适用 ）计算柔度， 3）计算临界压力和临界应力 ）
σ =
P ≤ [σ ] st A
14
图示结构中， 为圆截面杆 直径d=80 mm，A端固 为圆截面杆， 例10.4 图示结构中，AB为圆截面杆，直径 ， 端固 端铰支； 是正方形截面杆 边长a=70 mm，C端也为 是正方形截面杆， 定，B端铰支；BC是正方形截面杆，边长 端铰支 ， 端也为 铰支； 和 杆可以独自发生弯曲变形而互不影响 杆可以独自发生弯曲变形而互不影响； 铰支；AB和BC杆可以独自发生弯曲变形而互不影响；两杆 的材料是A3钢 的材料是 钢，其λp=104 ，l=3 m，稳定安全系数 st=2.5 ； ，稳定安全系数n 求结构的许可载荷P。 求结构的许可载荷 。
π 2E Pcr = σ cr A = 2 ⋅ A = 269kN λ
《材料力学》第1到8章复习题
材料力学第一章复习题1，下列结论中正确的是（）A,内力是应力的代数和B,应力是内力的平均值C应力是内力的集度D内力必大于应力2. 一对自平衡的外载产生杆件的哪种基本变形只对杆件的某一局部存在影响。
( )A 拉伸与压缩B 剪切C扭转D弯曲3，已设计好的构件，若制造时仅对其材料进行更换通常不会影响其( )A稳定性 B 强度C几何尺寸D刚度4. 根据均匀性假设，可认为构件的下列各量中的( )在各点处都相同A屈服极限B材料的弹性常数C应力D应变第二章轴向拉伸压缩与剪切挤压的实用计算1.塑性材料的极限应力是A屈服极限B强度极限c比例极限D弹性极限2.脆性材料的极限应力是。
A屈服极限B比例极限C强度极限D弹性极限3.受轴向拉压的杆件内最大切应力为80 Mpa，则杆内最大正应力等于A160Mpa B 80Mpa C40Mpa D20Mpa4.在低碳钢Q235的拉伸试验中，材料暂时失去了抵抗变形能力是发生在哪个阶段A弹性B屈服C强化D缩颈断裂5材料进入强化阶段卸载，在室温中放置几天再重新加载可以获得更高的()。
A比例极限B强度极限C弹性变形D塑性变形6直径为d的圆截面钢杆受轴向拉力作用，已知其纵向线应变为e，弹性模量为E，杆轴力大小为()。
填空题(5.0分)7.在连接件上，剪切面和挤压面分别（)于外力方向8.连接件剪切强度的实用计算中去，许用切应力是由( )9.插销穿过水平放置的平板上的圆孔，在其下端受拉力F作用。
该插销的剪切面面积和挤压面面积分别等于( a)。
填空题(5.0分)10.低碳钢拉伸试验中滑移线是( )造成的。
11.外力消失后，变形也消失,这种变形为( )12.当延伸率小于( )时为脆性材料，当延伸率大于( )时为塑性材料13.一个结构中有三根拉压杆，设由这三根杆的强度条件确定的结构许用载荷分别为F1、F2、F3，且F1<F2<F3，则该结构的实际许可载荷[F]为判断题(5.0分)14低碳钢的抗拉能力小于抗剪能力（）A对 B 错15. 试求图中1-1，2-2，3-3截面上的轴力，并作轴力图。
《材料力学》第六章-弯曲变形
当载荷P处于梁中点，即ｂ=l／２时，ｘl=0.5l；
当载荷Ｐ移至支座B,即ｂ→０时
x1
l2 0.577l 3
即使在这种极端的情况下，最大挠度的位置距中 点只有0.077l，也就是说点的位置影响甚小，最大挠 度总是发生在梁跨中点的附近。可以认为在工程中 当有一集中力作用在简支梁上时，梁的最大挠度发 生在梁的中点，其结果误差不超过3％。
§6.1 工程中的弯曲变形问题
工程中有些受弯构件在载荷作用下虽能满足强度 要求，但由于弯曲变形过大，刚度不足，仍不能保证 构件的正常工作，成为弯曲变形问题。
出现“爬坡”现象
使齿轮啮合力沿齿宽分布极 不均匀，加速齿轮的磨损。
一、挠度和转角
构件的弯曲变形通常用截面的挠度和转角度量。
梁在横向力作用下发生弯曲变形， y
§6.3 用积分法求弯曲变形
一、积分法求弯曲变形 w Mx
EI
积分
挠曲线近似微分方程
w E 1IM xd x C
积分
转角方程
w E 1IM xd x CD x 挠曲线方程
式中C和D是待定的积分常数，可根据梁的具体条件来确定。
积分法计算梁的变形的步骤： 1.建立梁截面的弯矩方程式M(x)； 2.代人挠曲线近似微分方程式，并积分； 3.确定积分常数，得到具体的挠度和转角方程式； 4.求梁任一截面的转角和挠度。
令
w1 10 F 2lx b12-F 6lb l2-b2 0
当ａ>ｂ时，x1<a，wmax发生在AC段内。
得： x1
l2 -b2 3
wm若求最大转角，求θA、θB，比较大小，取其大者。
当
x1
l2 -b2 3
wmax-
Fb 9
材料力学典型例题及解析 6.弯曲变形典型习题解析
弯曲变形典型习题解析1 试用积分法写出图示梁的挠曲轴方程，说明用什么条件决定方程中积分常数，画出挠曲轴大致形状。
图中C 为中间铰。
为已知。
I E解题分析：梁上中间铰处，左、右挠度相等，转角不相等。
解：设支反力为，如图示。
yB A yA FM F、、1、建立各段挠曲轴近似微分方程并积分 将梁分为AC 、CB 、BD 段。
AC 段 a x ≤≤10挠曲轴近似微分方程 11x FM w I E yA A ⋅−=′′转角方程1211'12C x Fx Mw IE yA A+−= (a) 挠度方程1113121162D x C x F x M w I E y A A ++−=(b)CB 段 )(2b a x a +≤≤挠曲轴近似微分方程2"2x FMw I E yA A ⋅−=转角方程 222222C x F xM w I E yA A+−=′(c)挠度方程2223222262D x C xFx M w I E yA A++−= (d)BD 段 l x b a ≤≤+3)(挠曲轴近似微分方程[])(333b a x Fx FM w I E yB yA A+−+−=′′转角方程[]32323332)(2C b a x F x F x M w I E yB yA A++−+−=′ (e) 挠度方程[]33333332336)(62D x C b a x FxFxM w I E yB yA A+++−+−= (f)2、确定积分常数共有6个积分常数。
需要6个位移边界条件和光滑连续条件。
332211D C D C D C 、、、、、题1图M A边界条件：，代入(b)得 01=x 01=w 01=D (g)0'1=w 代入(a)得 01=C(h)b a x +=2，02=w (i)连续条件： ， a x x ==2121w w =(j) b a x x +==32， 32w w ′=′ (k) 32w w =(l)联立(i)、(j)、(k)、(l)，可求出。
材料力学-6-弯曲刚度
• 引言 • 弯曲刚度的基本原理 • 弯曲刚度的实验验证 • 弯曲刚度在工程中的应用 • 弯曲刚度的优化设计 • 结论与展望
01
引言
主题简介
01
弯曲刚度是材料力学中一个重要 的概念，主要研究材料在受到弯 曲力作用时的行为和性能。
02
弯曲刚度涉及到材料抵抗弯曲变 形的能力，对于工程结构的稳定 性、承载能力和使用寿命具有重 要意义。
车辆行驶安全
弯曲刚度影响桥梁的平顺性，从而 影响车辆行驶的安全性和舒适性。 弯曲刚度不足可能导致桥面不平整， 增加车辆颠簸和振动。
建筑度对其抗震性 能具有重要影响。在地震作用下， 具有较高弯曲刚度的建筑能够更 好地抵抗地震引起的振动，减少
破坏。
风载响应
弯曲刚度也决定了建筑结构对风 载的响应。弯曲刚度较大的建筑 能够更好地承受风力作用，减少
机械零件
在机械零件的设计中，弯曲刚度是评估零件性能的重要指标。例如，在汽车和 航空器的设计中，需要确保关键部件的弯曲刚度满足要求，以保证车辆和飞机 的安全性和稳定性。
03
弯曲刚度的实验验证
实验设备与材料
01
02
03
试样
选择具有代表性的材料试 样，如金属、塑料等。
实验设备
包括万能材料试验机、测 力计、测量工具等。
轻质材料
选择轻质材料，如铝合金、碳纤维复合材料等，以减小结构重量， 提高弯曲刚度。
高强度材料
选用高强度材料，如高强度钢、钛合金等，以提高结构承载能力， 降低弯曲变形。
材料属性优化
通过合金化、热处理等方法优化材料的力学性能，如提高弹性模量、 抗拉强度等，从而提高弯曲刚度。
结构设计优化
合理布局
材料力学期末试题选择题
材料力学期末试题选择题一、绪论1．各向同性假设认为，材料沿各个方向具有相同的A。
(A)力学性质；(B)外力；(C)变形；(D)位移。
2．均匀性假设认为，材料内部各点的C是相同的。
(A)应力；(B)应变；(C)位移；(C)力学性质。
3．构在外力作用下B的能力称为稳定性。
（A）不发生断裂；（B）保持原有平衡状态；（C）不产生变形；（D）保持静止。
4．杆的刚度是指D。
（A）杆的软硬程度；（B）的承载能力；（C）杆对弯曲变形的抵抗能力；（D）杆对弹性变形的抵抗能力。
二、拉压1．低碳钢材料在拉伸实验过程中，不发生明显的塑性变形时，承受的最大应力应当小于D的数值，（A）比例极限；（B）许用应力；（C）强度极限；（D）屈服极限。
2．对于低碳钢，当单向拉伸应力不大于C时，虎克定律σ=Eε成立。
(A)屈服极限σs；(B)弹性极限σe；(C)比例极限σp；(D)强度极限σb。
3．没有明显屈服平台的塑性材料，其破坏应力取材料的B。
（A）比例极限σp；（B）名义屈服极限σ0.2；（C）强度极限σb；（D）根据需要确定。
4．低碳钢的应力~应变曲线如图所示，其上C点的纵坐标值为该钢的强度极限sb。
3题图(A)e；(B)f；(C)g；(D)h。
5、三种材料的应力—应变曲线分别如图所示。
其中强度最高、刚度最大、塑性最好的材料分别是。
(A)a、b、c；(B)b、c、a；(C)b、a、c；(D)c、b、a。
5．材料的塑性指标有C。
(A)σs和δ；(B)σs和ψ；(C)δ和ψ；(D)σs,δ和ψ。
6．确定安全系数时不应考虑D。
(A)材料的素质；(B)工作应力的计算精度；(C)构的工作条；(D)载荷的大小。
7．低碳钢的许用力［σ］=C。
(A)σp/n；(B)σe/n；(C)σs/n；(D)σb/n。
8．系统的温度升高时，下列结构中的____A______不会产生温度应力。
9、图示两端固定阶梯形钢杆，当温度升高时D。
(A)AC段应力较大，C截面向左移；(B)AC段应力较大，C截面向右移；(C)CB段应力较大。
材料力学 第6章 弯曲变形
6-1 弯曲变形的实例
弯曲变形
摇臂钻床的摇臂或车床的主轴变形过大，就会 影响零件的加工精度，甚至会出现废品。
第6章
6-1 弯曲变形的实例
弯曲变形
桥式起重机的横梁变形过大,则会使小车行走困难， 出现爬坡现象。
第6章
6-1 弯曲变形的实例
弯曲变形
但在另外一些情况下，有时却要求构件具有较大的 弹性变形，以满足特定的工作需要。 例如，车辆上的板弹簧，要求有足够大的变形，以 缓解车辆受到的冲击和振动作用。
F l [ ( x a)3 x 3 (l 2 b 2 ) x] 6 EIl b
F l 1 [ ( x a) 2 x 2 (l 2 b 2 )] 2 EIl b 3
第6章
6-5 叠加法求梁的位移 叠加法求梁的挠曲线
弯曲变形
梁在若干个载荷共同作用时的挠度或转角， 等于在各个载荷单独作用时的挠度或转角的代 数和。这就是计算弯曲变形的叠加原理。
3. 增大梁的弯曲刚度：主要增大I值，在截面面积不变的情况下，采用
适当形状，尽量使面积分布在距中性轴较远的地方。例如：工字形、箱 形等。
q
A B l B l A
q
A
q
B
第6章
6-7 提高弯曲刚度的一些措施
弯曲变形
第6章
6-7 提高弯曲刚度的一些措施
弯曲变形
1) 支承条件：
y
w 0; w 0
弯曲变形
y
y
w0
F A
w0
2) 连续条件：挠曲线是光滑连续唯一的
C
B
w|
x C
w|
x C
， |
x C
|
(整理)材料力学试题库题解题6_弯曲应力
弯曲应力1.圆形截面简支梁A,B套成，A,B层间不计摩擦，材料的弹性模量E B=2E A求在外力偶矩M e作用下，A,B中最大正应力的比值^max有4个答案:Bmin1(A)-；61 (C)1；81(D)丄10答: B2.矩形截面纯弯梁，材料的抗拉弹性模量E t大于材料的抗压弹性模量E c，则正应力在截面上的分布图有以下4种答案：(A) (B) (C) (D) 答: C3.将厚度为2 mm的钢板尺与一曲面密实接触，已知测得钢尺点A处的应变为—，则该曲面在点A1000处的曲率半径为_________ m m。
答：999 mmP4.边长为a的正方形截面梁，按图示两种不同形式放置，在相同弯矩作用下，两者最大正应力之比匕丛= ___________(%x)bO(b)答：1/ , 25. 一工字截面梁，截面尺寸如图，h二b, b =10t。
试证明，此梁上，下翼缘承担的弯矩约为截面上总弯矩的88%证: — My M12MA y(ybdy) =1 820 罟3Iz4 l z=690tM1 Mt4 1勺8207 6904”88%I yh/2—- 丄h/2zt其中：积分限Bt? , A弓为翼缘弯矩6. 直径d =20 mm 的圆截面钢梁受力如图，已知弹性模量E = 200 GPa , a =200 mm ，欲将其中段AB 弯成 f m 的圆弧，试求所需载荷，并计算最大7. 钢筋横截面积为A ，密度为「，放在刚性平面上，一端加力F ，提起钢筋离 开地面长度-。
试问F 应多大?3解：截面C 曲率为零2Fl gA(l /3) 3 28. 矩形截面钢条长l ，总重为F ，放在刚性水平面上，在钢条A 端作用|向上的拉力时，试求钢条内最大正应力。
解：在截面C 处，有―罟丸弯曲正应力。
解：1 = M 而 M 二 Fa P EI Fmax64 =0.785 10 岀 m 4, 「旦 Pa = 0.654 kN21 Fad 21 3 3 0.654 1 03 0.2 20 10 2 0.785 10 出 = 167 MPa即M C =F Is3 l AC F (I AC )2 l 2 2l AC AC 段可视为受均布载荷q 作用的简支梁 max max 2q(U c ) /8 _ Fl bt 2/6 3bt 2iF/3 C9.图示组合梁由正方形的铝管和正方形钢杆套成，在两端用刚性平板牢固联接。
材料力学习题解答(弯曲变形)
+
ql 12
x13
+ C1x1
+
D1
⎨
⎪ ⎪⎩
EIv2
=
−
q(l
− x2 )4
24
+ C2 x2
+
D2
光滑连续条件： 求解得积分常数
x1 = 0 : v1 = 0, v1' = 0
x1
=
x2
=
l 2
:
v1 = v2 , v1' = v2'
C1 = D1 = 0
C2
=
−
7ql 3 48
D2
=
15ql 4 384
P
2EI
EI
A
l/2
C l/2
B
解：(1) 求约束反力
MA
2EI
P
EI
A
RA
x1
C
B
x2
RA = P M A = Pl
(2) 弯矩方程
M1(x1) = Px1 − Pl x ∈ (0, l / 2] M2 (x2 ) = Px2 − Pl x ∈[l / 2, l]
(3) 挠曲线近似微分方程
(4) 直接积分两次
x2 ∈[a, 2a)
(2) 挠曲线近似微分方程
(3) 直接积分两次
⎧⎪ ⎨ ⎪⎩
EIv1" EIv2"
= =
M1( x1) = −Px1 M2 ( x2 ) = −Px2
−
P ( x2
−
a)
⎧ ⎪⎪
EIv1'
⎨
⎪ ⎪⎩
EIv2'
= =
− −
材料力学习题弯曲变形
弯曲变形基本概念题一、选择题1.梁的受力情况如图所示，该梁变形后的挠曲线如图（）所示(图中挠曲线的虚线部分表示直线，实线部分表示曲线)。
2. 如图所示悬臂梁，若分别采用两种坐标系，则由积分法求得的挠度和转角的正负号为（）。
题2图题1图A．两组结果的正负号完全一致B．两组结果的正负号完全相反C．挠度的正负号相反，转角正负号一致D．挠度正负号一致，转角的正负号相反3.已知挠曲线方程y = q0x(l3 - 3lx2 +2 x3)∕(48EI)，如图所示，则两端点的约束可能为下列约束中的（）。
题3图4. 等截面梁如图所示，若用积分法求解梁的转角、挠度，则以下结论中（）是错误的。
A．该梁应分为AB、BC两段进行积分B．挠度积分表达式中，会出现4个积分常数-26-题4图 题5图 C ．积分常数由边界条件和连续条件来确定D ．边界条件和连续条件表达式为x = 0，y = 0；x = l ，0==右左y y ，0='y 5. 用积分法计算图所示梁的位移，边界条件和连续条件为( )A ．x = 0，y = 0；x = a + l ，y = 0；x = a ，右左y y =，右左y y '=' B ．x = 0，y = 0；x = a + l ，0='y ；x = a ，右左y y =，右左y y '=' C ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y =D ．x = 0，y = 0；x = a + l ，y = 0，0='y ；x = a ，右左y y '=' 6. 材料相同的悬臂梁I 、Ⅱ，所受荷载及截面尺寸如图所示。
关于它们的最大挠度有如下结论，正确的是（ ）。
A ． I 梁最大挠度是Ⅱ梁的41倍 B ．I 梁最大挠度是Ⅱ梁的21倍 C ． I 梁最大挠度与Ⅱ梁的相等 D ．I 梁最大挠度是Ⅱ梁的2倍题6图 题7图 7. 如图所示等截面梁，用叠加法求得外伸端C 截面的挠度为（ ）。
材料力学复习题
第一章 绪论1. 试求图示结构m-m 和n-n 两截面上的内力，并指出AB 和BC 两杆的变形属于何类基本变形。
2. 拉伸试样上A ，B 两点的距离l 称为标距。
受拉力作用后，用变形仪量出两点距离的增量为mm l 2105-⨯=∆。
若l 的原长为l ＝100mm ，试求A 与B 两点间的平均应变m ε。
第二章 轴向拉伸和压缩与剪切 一、选择题１.等直杆受力如图，其横截面面积Ａ＝１００2mm ，则横截面ｍｋ上的正应力为（ ）。
（Ａ）５０ＭＰａ（压应力）； （Ｂ）４０ＭＰａ（压应力）； （Ｃ）９０ＭＰａ（压应力）； （Ｄ）９０ＭＰａ（拉应力）。
2.低碳钢拉伸经过冷作硬化后，以下四种指标中哪种得到提高( )： （Ａ）强度极限； （Ｂ）比例极限；（Ｃ）断面收缩率； （Ｄ）伸长率（延伸率）。
3.图示等直杆，杆长为3a ，材料的抗拉刚度为EA ，受力如图。
杆中点横截面的铅垂位移为（ ）。
（Ａ）0；（Ｂ）Pa/(EA);（Ｃ）2 Pa/(EA);（Ｄ）3 Pa/(EA)。
4.图示铆钉联接，铆钉的挤压应力bsσ是（ ）。
（A ）2P/（2d π）； （B ）P/2dt;(C)P/2bt; (D)4p/(2d π)。
5.铆钉受力如图，其压力的计算有（ ） （A ）bs σ=p/(td);(B)bs σ=p/(dt/2);(C)bs σ=p/(πdt/2);(D)bs σ=p/(πdt/4)。
6.图示A 和B 的直径都为d,则两面三刀者中最大剪应力为（ ）(A)4bp/(2d απ);(B)4(αb+)P/(2d απ);(C)4(a b+)P/(2b d π); (D)4αP/(2b d π).7.图示两木杆（I 和II ）连接接头，承受轴向拉力作用，错误的是( ).（A ）1-1截面偏心受拉； （B ）2-2为受剪面；（C ）3-3为挤压面； （D ）4-4为挤压面。
二、填空题1.低碳钢的应力一应变曲线如图所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
弯曲变形1. 已知梁的弯曲刚度EI 为常数，今欲使梁的挠曲线在x =l /3处出现一拐点，则比值M e1/M e2为：(A) M e1/M e2=2； (B) M e1/M e2=3； (C) M e1/M e2=1/2； (D) M e1/M e2=1/3。
答：(C)2. 外伸梁受载荷如致形状有下列(A)(B)、(C)，(D)四种：答：(B)3. 简支梁受载荷并取坐标系如图示，则弯矩M 、剪力F S 与分布载荷q 之间的关系以及挠曲线近似微分方程为： (A)EI x M x w q xF F x M )(d d ,d d ,d d 22SS ===；(B)EI x M xw q x F F xM)(d d ,d d ,d d 22SS =-=-=； (C)EI x M x w q x F F x M )(d d ,d d ,d d 22SS -==-=；(D)EI x M x w q xF F x M )(d d ,d d ,d d 22SS -=-==。
答：(B)4. 弯曲刚度为EI 的悬臂梁受载荷如图示，自由端的挠度EIl M EI Fl w B 232e 3+=（↓）则截面C 处挠度为：(A)2e 3322323⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛l EI M l EI F （↓）；(B)233223/323⎪⎭⎫⎝⎛+⎪⎭⎫ ⎝⎛l EI Fl l EI F （↓）； (C)2e 3322)3/(323⎪⎭⎫ ⎝⎛++⎪⎭⎫ ⎝⎛l EI Fl M l EI F （↓）；(D)2e 3322)3/(323⎪⎭⎫ ⎝⎛-+⎪⎭⎫⎝⎛l EI Fl M l EI F （↓）。
答：(C)5. 画出(a)、(b)、(c)三种梁的挠曲线大致形状。
答：6.7.(a)、(b)刚度关系为下列中的哪一种： (A) (a)＞(b)； (B) (a)＜(b)；(C) (a)=(b)； (D) 不一定。
答：(C)8. 试写出图示等截面梁的位移边界条件，并定性地画出梁的挠曲线大致形状。
答：x =0, w 1=0,1w '=0；x =2a ，w 2w 2；x =2a ，32w w '='。
9. 试画出图示静定组合梁在集中力F 作用下挠曲线的大致形状。
(a)(b)(c)w ===θw w10. 画出图示各梁的挠曲线大致形状。
答：11.12.l。
⎢⎣⎡提示证：令外伸端长度为a，内跨长度为得b3 = 0即13. 等截面悬臂梁弯曲刚度EI为已知，梁下有一曲面，方程为w= -Ax3。
欲使梁变形后与该曲面密合（曲面不受力），试求梁的自由端处应施加的载荷。
解：EIAxwEIxM6)(-=''=F S(x)=-6EIAx=l，M=-6EIAlF=6EIA（↑），M e=6EIAl）14. 变截面悬臂梁受均布载荷ql 及弹性模量E 。
试求截面A 的挠度w A 解：x lhb h x b x I 1212)()(303== 由边界条件0,='==w w l x 得C3042h Eb ql w A -=（↓） ，30338h Eb ql C =θ（）15. 在刚性圆柱上放置一长2R 、宽b 、厚h 的钢板，已知钢板的弹性模量为E 。
试确定在铅垂载荷q 作用下，钢板不与圆柱接触部分的长度l 及其中之最大应力。
解：钢板与圆柱接触处有 EIql R 2/12= 故qREbh RqEI l 623==16. 弯曲刚度为EI的最大挠度及其挠曲线方程。
解：30)(6)(x l lq x M w EI --==''12024)(12043050lq x l q x l l q EIw -+--=w 17. 图示梁的左端可以自由上下移动，但不能左右移动及转动。
试用积分法求力F 作用处点A解：Fx Fl w EI -=''EIFl w A 33-=（↓）18. 简支梁上自A 至B 的分布载荷q (x )=-Kx 2，K 为常数。
试求挠曲线方程。
解：2)(Kx q x M -=='' 二次积分B Ax x K x M ++=412)( x =0， M =0， B =0 x =l ， M =0，123Kl A -=x =0， w =0， D =0 x =l ， w =0， 36045Kl C -=)45(3605336x l x l x EIKw +--=（↓） 19. 弯曲刚度为EI 的悬臂梁原有微小初曲率，其方程为y =Kx 3。
现在梁B 端作用一集中力，如图示。
当F 力逐渐增加接触。
若作用力为F ，试求： （1）梁与水平面的接触长度； （2）梁B 端与水平面的垂直距离。
解：(1) 受力前C 处曲率Ka a 6)(11=ρ，弯矩M (a )1 = 0受力后C 处曲率0)(12=a ρ，弯矩M (a )2 = -F (l - a ) (2)同理,受力前x 1截面处0)(),(6d d )(111122111=+=⎪⎪⎭⎫ ⎝⎛=+=x M x a K x y x xa x ρ受力后x 1截面处 )()(,d d )(1121211221x b F x M x y x --==ρ 积分二次D Cx EIFx EI Fbx Kx Kax y +++-+=132131211623C =0，D =020. 图示弯曲刚度为EI 的两端固定梁，其挠度方程为 式中A 、B 、C 、D 为积分常数。
试根据边界条件确定常数A 、B 、C 、D ，并绘制梁的剪力F S 、弯矩M 图。
解：x = 0，w = 0，D = 00,='=w l x 代入w '方程242ql B -=21. 已知承受均布载荷q 0图示受三角形分布载荷作用为w C = 。
答：EIl q 768540（↓）22. 试用叠加法计算图示梁A 点的挠度A 解：22)2/(3)2/(3)2/(233aEI a F EI a F EI a F w A ++= EIFa 48133=（↓）23. 试求图示梁BC 段中点的挠度。
解：EI a q EI a qa EI a qa w 384)2(53)3(3)(21433+⎪⎪⎭⎫ ⎝⎛+=EIqa8394=（↓）24. 已知梁的弯曲刚度EI 。
试用叠加法求图示梁截面C 的挠度w C 。
解：EIa a l q EI al q EI l a l q EI ql w C 96)2(256)2(96)2(76853434⋅-+-+--=EIa l qa 96)23(222-=（↓）25. 已知梁的弯曲刚度EI 为常数。
试用叠加法求图示梁B 截面的挠度和转角。
ql解： EI l q EI l q EI l q w B 12011308404040=-=（↓）EIl q EI l q EI l q B 8246303030=-=θ26. 试用叠加法求图示简支梁跨度中点C 的挠度。
解：+27. 试用叠加法求图示简支梁集中载荷作用点C 的挠度。
解：EIFlEI l F EI l F w w B B C 483)4/(413414333====（↓）28. 已知简支梁在均布载荷作用下跨中的挠度为EIql w C 38454=，用叠加法求图示梁中点C 的挠度。
解：()EIl q EI l q w C 76853842/54040=⋅=（↓）29.A解：A d θEI l q x x EIlq lA 10d 2304020==⎰θ）30. 弯曲刚度为EI 的等截面梁受载荷如图示，试用叠加法计算截面C 的挠度w C 。
解：EIl q q EI l q q w C 768)(53842/)(5421421+=⋅+⋅=q /23q 231. 如图所示两个转子，重量分别为P 1和P 2，安装在刚度分别为EI 1及EI 2的两个轴上，支承轴是A 、B 、C 、D 四个轴承。
B 、C 两轴承靠得极近以便于用轴套将此两轴连接在一起。
如果四个轴承的高度相同，两根轴在B 、C 处连接时将出现“蹩劲”现象。
为消除此现象可将A 处轴承抬高，试求抬高的高度。
解：121116EI l P B ⋅=θ， 222216EI l P C ⋅=θ点A 抬高的高度为131116EI l P +32. 图示梁AB 的左端固定，梁的横截面高度为h 膨胀系数为l α，若梁在安装后，顶面温度为t 1，底面温度为t 2（t 2＞t 1），试求此梁的约束力。
解：因温度变化而弯曲的挠曲线微分方程为ht t x w x l )(d d d d 1222-==αθ由A 处边界条件得 2122)(x ht t w l -=α而EIl F w B BF B33=33. 图示温度继电器中两种金属片粘结的组合梁，左端固定，右端自由。
两种材料的弹性模量分别为E 1与E 2。
线膨胀系数分别为1l α与2l α，并且1l α＞2l α起的挠度。
解：1l α＞2l α，梁上凸下凹弯曲平衡条件 F N1 = F N2 = F N M 1 + M 2 = F N h 变形协调 θ1 =θ2，2211E M E M =ε1 =ε2，即ε1N +ε1M +ε1t =ε2N +ε2M +ε2t 得t I E hM A E F t I E h M A E F l l 222222N21111111N 22αα+-=+- 其中 A 1 = A 2 = bh ，I 1 = I 2 =123bh则 F N1 = F N2 =21222121212114)()(E E E E E E E tbhE l l +++-αα M 1 =21222122122114)(E E E E E E tbh l l ++-ααM 2 =21222122122114)(E E E E E E tbh l l ++-αα故)14()(222122212212122221121E E E E h l E tE b I E l M I E l M w l l B ++-===αα 34. 单位长度重量为q ，弯曲刚度为EI 的均匀钢条放置在刚性平面上，钢条的一端伸出水平面一小段CD ，若伸出段的长度为a ，试求钢条抬高水平面BC 段的长度b 。
解：()062/2423=-=EIbqa EI qb B θ35. 图示将厚为h = 3 mm 的带钢围卷在半径R = 1.2 m 的刚性圆弧上，试求此时带钢所产生的最大弯曲正应力。
已知钢的弹性模量E = 210 GPa ，屈服极限s σ= 280 MPa ，为避免带钢产生塑性变形，圆弧面的半径R 应不小于多少？解：262maxmax ==ρσEy MPa ，hR Eh+=2s σ， R = 1.12 m 36. 一悬臂梁受分布载荷作用如图示，荷载集度x l q x q 2πcos )(0=，试用叠加原理求自由端处截面B 的挠度w B ，梁弯曲刚度EI 为常量。