快速构建Delaunay三角网算法研究及OpenGL下三维可视化
一次性构建约束Delaunay三角网的三维显示

一次性构建约束Delaunay三角网的三维显示摘要:本文主要介绍了一次性构建约束Delaunay三角网算法的具体步骤,在VC++6.0编程环境中利用该算法对大量离散数据点进行三维建模,并结合OpenGL对三角网模型进行三维显示。
关键词:约束;Delaunay;三角网;算法;VC++6.0;OpenGL1 前言地图数据往往是离散的数据点集,要生成三维地形图的技术路线是:(1)从地形图中取得离散点的高程数据;(2)采用约束Delaunay三角网对离散点进行三维建模;(3)采用OpenGL对所建模型进行三维图形生成和显示[1].传统构建约束Delaunay三角网的算法即所谓的“两步法”[2],将构建过程分为两步:第一步构建常规Delaunay三角剖分;第二步将约束边强行嵌入到常规Delaunay三角剖分结果中。
传统方法的缺点是要对无约束数据和约束数据进行分别管理,具有数据管理凌乱的缺点;而且,当常规三角网生成后再加入约束边数据重新修改三角网,具有固有的时间效率低的缺点。
笔者提出了一种一次性构建约束Delaunay三角网算法。
该算法没有继承传统的构建约束Delaunay三角网的“两步法”,而是先将约束边的点数据和无约束数据一起存入点数据链表,根据点的属性生成约束边链表,再以各约束边为基边生成左右三角形,构成初始三角网,然后以左右三角形的除约束边的另外两边为基边,用一步生长法生成新的一层三角形,再以新生成的一层三角形的边为新的基边用一步生长法生成新的三角形,直到生成完整的约束Delaunay三角网。
最后,用简化的LOP优化算法对三角网进行优化。
建立模型后,将OpenGL中的三个库(opengl32.lib、glut32.lib和glu32.lib)与VC相连,实现开发环境与OpenGL的结合,将点Z坐标值也参与构网,同时设计像素格式、选择视点及投影模式、选定光源、计算出每个点的法向量及进行光照渲染等各项处理,最终生成三维三角网。
快速构建 Delaunay 三角网算法研究及OpenGL下三维可视化

快速构建 Delaunay 三角网算法研究及OpenGL下三维可视化王星【摘要】对Delaunay三角网的构建算法进行研究.提出了一种基于网格索引的构网算法.借助于该算法的特点提出了一种新的点一块一三角形映射机制定位点所在三角形的方法.简化了三角网的优化过程,提高了三角网构建速度.同时在OpenGL 开放式三维环境下,进行光照渲染等处理,实现了地形的三维可视化.%The construction of TIN based on grid index is reseached. A new point-block-triangle mapping mechanism used to locate the location of point is put forward in virtue of algorithmic characters, which simplifies the LOP of TIN and improves the speed of the constructing net. At the same time, it realizes the terrain 3D visualization in OpenGL environment by lighting and colouring.【期刊名称】《科学技术与工程》【年(卷),期】2011(011)009【总页数】5页(P2070-2074)【关键词】Delaunay三角网;网格索引;三维可视化;OpenGL【作者】王星【作者单位】昆明理工大学,昆明,650031【正文语种】中文【中图分类】P217DTM(数字地面模型)是实现地形三维可视化一种很有效的途径。
栅格和TIN(不规则三角网)是表示DTM的两种主要数据格式。
与栅格方法对格网的周围采样点按照距离远近加权平均的思想不同,TIN方法采取的是一种更加忠实于原始数据的方法,它几乎完整地保留原始数据,按Delaunay原则将采样点直接连成网建立起模型。
Delaunay三角网生成算法的研究与实现(1).

Delaunay三角网生成算法的研究与实现(1)摘要 Delaunay三角网作为一种主要的数字地形模型表示法,经过二十多年来的研究,它的生成算法已趋于成熟。
本文在简单回顾和评价了分割—归并法、逐点插入法、三角网生长法等三类主流算法的基础上,介绍并实现了一个融以上算法优点于一体,兼顾空间与时间性能的合成算法。
关键字数字地层模型;三棱柱; Delaunay;三角网;生成算法0 引言计算机图形学是利用计算机研究图形的表示、生成、处理、显示的学科。
经过30多年的发展,科学可视化已成为计算机图形学中最活跃的分支之一,并得到了广泛的应用。
在地质领域,由于大量珍贵的地层钻探数据需要用有效的方式进行直观地表达,因而致使可视化技术成为地质研究和工程勘查领域必不可少的手段。
在建模中,2.5维的分析处理由DTM(数字地形模型)模型进行。
DTM主要由栅格与TIN(不规则三角网)两种数据格式来表示[1,2],而以后者更为重要。
TIN的生成算法中,最终有三种为普遍接受和采用,它们是分割—归并法、逐点插人法和逐步生长法。
本文在简要分析了上述算法所有缺点的基础上,实现了一种合成算法。
1 Delaunay三角网生成算法回顾Tsaj根据实现过程,把生成Delaunay三角网的各种算法分为三类:分治算法;逐点插入法;三角网生长法。
Tsai为比较算法性能,给出了一张各种算法的时间复杂度对照表,如表1所示。
表中,N为数据点数。
0(f(N))表示算法的时间复杂度,它以算法中频度最大的语句频度f(N)来度量。
上述三类算法中,三角网生长法在80年代中期以后就很少用到,较常见的是分治算法和逐点插入法,而这两类算法又各有其长处和短处。
逐点插入法虽然实现过程相对简单,所需内存较小,但它的时间复杂度高。
所以从时间复杂度方面看,分治算法最好。
但由于算法中存在递归,它需要较大内存空间。
在普通的计算机平台上,运行速度慢和占用较大内存都是应该尽量避免的。
本次设计中,我们引入并实现了一种合成算法,将逐点插入法植入到了分治算法中,互相取长补短,从而达到了较好的时空性能,也很好地体现了两者的优势。
Delaunay三角网制作流程
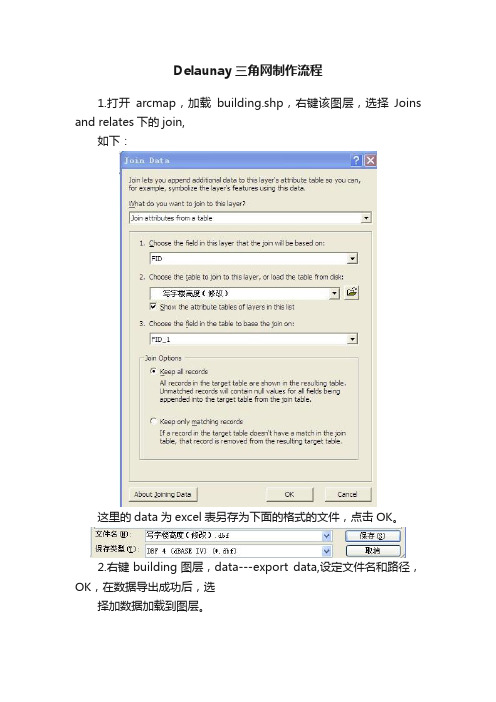
Delaunay三角网制作流程1.打开arcmap,加载building.shp,右键该图层,选择Joins and relates下的join,如下:这里的data为excel表另存为下面的格式的文件,点击OK。
2.右键building图层,data---export data,设定文件名和路径,OK,在数据导出成功后,选择加数据加载到图层。
3.对上步生成的点数据,在空间分析工具条下(3D analyst),选择create TIN from Features,生成TIN数据,具体步骤如下:4.右键单击生成的tin3,选择properties,在出现的面板中选择symbology,点击show下的add,,做如下选择:再次点击一次add,然后点击dismiss,确定即可。
5.要素图层在三维场景中的三种显示方式:1)使用属性设置图层的基准高程;2)在表面上叠加要素图层设置基准高程;3)突出要素。
6.右键点击tin3图层:选择properties,在base height下做以下修改:注:对于第四步操作,还可以采取下面方法创建Delaunay三角网在arctoolbox下,选择Tin Triangle:点击ok即可。
安装SketchUp6 ESRI 插件的方法1.双击“SketchUp6ESRI.exe”,开始安装,2.接受协议,点击“Next”3.第一个组件“GIS Plugin”,使用户能够在SketchUp中将模型以Multipatch要素的形式导入GDB。
第二个组件“3D Ana lyst SketchUp 3D Symbol Support”,用户可以在ArcMap中将GIS数据导入SketchUp 中。
上述两个组件的安装位置尽量不要改变,可能会导致在SketchUp 中导出3D模型失败。
4.执行组件安装(4)在ArcGIS环境中激活SketchUp6 ESRI插件1.启动ArcMap界面,在工具栏上选择“Customize”2.点击“Add from file”,找到SketchUp ArcGIS Plugin安装目录下的Features To SKP.dll (注:默认安装在C:\Program Files\ArcGIS\SketchUp6下)3.添加插件动态库后,在T oolbars项中可以找到SketchUp6的功能项。
VCOpenGL实现空间三维Delaunay三角剖分

注册|登录∙构建全球华人科学博客圈∙返回首页∙RSS订阅∙帮助MouStudio --- The Base of YANG Qing分享/u/moustudio爽的还是程序的人生∙博客首页∙动态∙记录∙博文∙相册∙主题∙分享∙好友∙留言板∙学术名片博文Captain Dialog 2009-09-18 VC+OpenGL 实现空间三维Delaunay三角剖分已有 4164 次阅读2009-9-19 14:43|个人分类:编程笔记|系统分类:科研笔记|关键词:Delaunay三角剖分,算法程序,VC++Captain Dialog 2009-09-18三维建模和等值面的绘制过程中,需要经常使用三角形网格对数据体进行构面。
而三角形的生成基于Delaunay三角剖分的算法实现的。
前段时间一直在考虑数据体的任意剖面切割该怎么做,但是一直被两个问题所困扰,一个就是交点问题,然后就是对所求交点进行绘制问题(三角形网格面构造)。
终于在半个月后有了一点收获。
1 Delaunay三角剖分原理三角剖分算法可以分为针对二维的局部剖分和三维的全局剖分算法。
在二维情况下建立的基于简单的三角形构面的方式,而三维情况下则是需要建立基于四面体的方式构造空间曲面。
在遇到三维空间散乱点的构面问题时,可以直接采用三维Delaunay剖分,亦可先将三维坐标预处理转换到二维坐标系中,间接的采用二维Delaunay剖分算法。
想着用最简单的方式实现功能的时候,就选择了第二种方式。
关于二维的Delaunay三角剖分原理,文献资料相当多,随便一搜就是一大堆,网上也有很不错的介绍:Delaunay三角剖分(Delaunay Triangulation)相关知识:/soroman/archive/2007/05/17/750430.html[图形算法]Delaunay三角剖分算法:/renliqq/archive/2008/02/06/1065399.html关于生成三角形网格的算法也是很多,我选择了稍微老套点的生长法,实现起来还算是思路清晰。
基于四叉树的Delaunay三角网的快速构建

天津城市建设学院学报 第 1 卷 第 4 20 年 1 月 3 期 07 2
Ju a o in n Is tt o b n C nt c o V 1 3 N . o r l fTaj ntue fUra o s ut n o. o4 e.20 n i i r i 1 D c 0 7
应 用打 下基础 .
并且具有地表重构精度高及对不规则区域数据点分
布适应能力强的特点. I 的实质是用一系列的互不 TN 交叉 、互 不重 复的三角 形逼 近地形 表 面…. I 的实 TN
现算法很 多 ,其 中 ,D l ny 三角 网是被普 遍认 eua a 可 ,并广泛应用于离散数据建模研究的有效工具. 尽 管许多学者已提出了较成熟 的各种算法 ,但大都是 以算法 的运行效率 为核心 ,数据结构多用链表或数
1 四叉树改进 的基于凸壳技术的 TN算法 I
基于凸壳技术的 TN 算法 ,首先对散乱点集按 I
扫描线方式排序 ,以排 序后的点为着眼点,通过依
次扫描各点快速地将有序点集进行三角联 网,最后 利用拓扑结构快速地将其优化为 TN2 这种算法利 I【 】 .
组实现,没有考虑建 TN 后要做的模型简化模板 函数 的
确 定 数 据 点 集 最 大 包 围 盒 建 立根 节 点R o N d ot oe
散数据点 集构建 了 D M 模 型,利 用四叉树结构和 c + T + 的标 准模板库 ( T S L)来组织地 形数 据 ,保证 了Deany构建程序的运行效率. l a u 关 键 词 :数字地面模型 ;De u a ;四叉树 ;S L l ny a T 文献标识码 :A 文章编号 :10 —8 32 0 )40 9 — 0 66 5 (0 70 —2 80 4 中图分类号 :P 0 28
Delaunay算法的研究与探讨

Delaunay算法的研究与探讨作者:高远来源:《硅谷》2011年第18期摘要:计算机图形学是一种用数学算法将二维或者三维图形转化为计算机显示器的栅格形式的科学。
其主要研究的基本内容就是如何在计算机中表示出图形,或怎样利用计算机来进行图形的计算处理以及显示的原理和算法。
当前,在计算机图形学中,科学可视化是最活跃的分支之一,得到普遍的应用。
特别是地质领域,其地质研究和工程勘查领域都离不开可视化技术,众多的珍贵地层钻探数据必须用有效的方式进行直观地表达。
Delaunay三角网是一种主要的数字地形模型表示法,它经过二十多年的发展,其生成算法已日趋成熟。
因此,就Delaunay 的基本概况、Delaunay方法的基本原理、Delaunay三角网生成算法、合成算法的研究与实现四个方面来对Delaunay算法探究。
关键词: Delaunay;三角剖分;基本原理;三角网;生成算法中图分类号:TP309 文献标识码:A 文章编号:1671-7597(2011)0920180-011 Delaunay算法的基本概况G.Voronoi在1907年时三角网格化问题,后来Delaunay在1932年首次提出了解决这一问题的方法。
近些年来,计算机图形学一直在密切关注平面任意点集的三角网格化(triangulation)问题,但真三维的地理信息系统的实现仍然存在诸多尚未解决的技术难题,一是空间三维数据的采集成本相当高昂;其次,真三维的地理信息系统空间数据量大,种类多,结构复杂;再次,三维空间的点、线、面和体之间的拓扑关系复杂,技术尚不熟练;最后,三维空间分析起来相当困难。
所以,在地理信息的三维可视化(特别是地形三维可视化)的探究中,大多都采用2.5维的GIS可视化的方法来实现地理信息的三维可视化,这种方法主要是以高质量的数字高程模型(DEM)和高逼真度的三维显示技术为基础。
在三维可视化中,对地形三维可视化的效果起关键作用的就是DEM的质量,而影响DTM质量的重要因素就是生成DEM的算法。
基于delaunay三角网的三维地形可视化仿真

取 、灾 害预 测 、军事及 游 戏等各 个 方面 …。因此 , 研 究如 何更好 、更快 的实现 地形 可视 化是 很有 必要
收 稿 日期:2 l— 1 1;修 改 日期 :2 1— 22 O2 0— 5 02 0— 2 基 金项 目:国家 83高 技术研 究发 展计划 (0 0 A12 0 ) 6 2 1A 220 作 者简 介:徐祥 龙(9 8 ) 18 一,男 ,山东 l 临沂人 ,硕 士生 ,主 要从事 地形 建模 与仿 真、 图形 图像 处理 研究 (— i x x 15 6 . m) Ema :u1 2 @13c ; l 6 o + 光耀(9 5 ) 李 16 一,男 ,安徽安 庆人 ,教授 ,博 导 ,主要 从事大 规模 城市 建模与 仿真 、图 形 图像 处理研 究 f. i ly oNi d. ) Em l g @tn . UC a : e n 谭 云兰(9 2 ) 17 一,女 ,江 西新 干人 ,副教 授 ,同济 大学在 读博 士生 ,主要 从事 图像 处理 ,计算 机图 形与科 学可 视化研 究 ( - i tn u l @ 1 3 o ) Em l a y na a : n 6.r; cn 李 超(99 ) 17 一,男 ,安徽合肥 人 ,博士 生 ,主要 从事 图像 处理 ,月表 地形仿 真研 究(. i 13 1 6 . m) E m l i 2 @13 o . a :c c
( o a Opi zt nPo e ue进行 优化 ,保证o
本 文 从地形 模拟 的角度 出发 ,对地 形 数据进 行
处理, 应用改进的 D l ny e ua 算法建立三维地形模型 a
中的不 规 则三角 网(I ,以此 来模 拟地 形表 面 。 TN) 并
RES EARCH oN D 3 TERRAI VI UALI N S ZATI oN BAS ED oN
