数字逻辑 第三章 加法器
数字逻辑 第三章 加法器.ppt
四位二进制并行加法器
三、四位二进制并加法器的外部特性和逻辑符号 1．外部特性
图中，A4、A3、A2、A1 ------- 二进制被加数； B4、B3、 B2、B1 ------- 二进制加数； F4、 F3、 F2、 F1 ------相加产生的和数； C0 --------------------来自低位的进位输入； FC4 -------------------向高位的进位输出。
a3b1
+) 乘积 Z5 a3b2 Z4 a2b2 Z3
a2b1
a1b2 Z2
a1b1
Z1
因为： ☆1位二进制数乘法 法则和逻辑“与”运算法 则相同，“积”项aibj(i =1，2，3；j=1，2)可用 两输入与门实现。 ☆对部分积求和可用 并行加法器实现。 所以：该乘法运算电 路可由6个两输入与门和1 b2 个4位二进制并行加法器构 成。逻辑电路图如右图所 示。
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。 1) 输入端A4、A3、A2、 A1输入8421码；
2) 而从另一输入端B4、 B3、B2、B1输入二进 制数0011； 3) 进位输入端C0接上“0”；
4) 可从输出端F4、F3、F2、 F1得到与输入8421码对
应的余3码。
四位二进制并行加法器
Z5 Z4 Z3 Z 2 Z1
F4 F3 F2 F 1 FC4 T 693 C0
0
A4 A3 A2 A1
B4 B 3 B2 B1
＆
＆
＆
＆
＆
＆
b1
a3
a2
a1 0 a 3
a2
a1
FA4
F3 C3
FA3
F2
数字电路实验报告实验三加法器
实验三加法器一、实验目的1、掌握用SSI器件实现全加器的方法。
2、掌握用MSI组合逻辑器件实现全加器的方法。
3、掌握集成加法器的应用。
二、实验设备及器件1、数字逻辑电路实验板1块2、74HC(LS)00（四二输入与非门）1片3、74HC(LS)86（四二输入异或门）1片4、74HC(LS)153（双四选一数据选择器）1片5、74HC(LS)283（4位二进制全加器）1片6、万用表1块三、实验原理组合逻辑电路是数字电路中最常见的逻辑电路之一。
组合逻辑电路的特点，就是在任意时刻电路的输出仅取决于该时刻的输入信号，而与信号作用前电路所处的状态无关。
本实验是根据给定的逻辑功能，设计出实现这些功能的组合逻辑电路。
不考虑低位进位，只本位相加，称半加。
实现半加的电路，为半加器。
考虑低位进位的加法称为全加。
实现全加的电路，为全加器。
实现三个输入变量（一位二进制数）全加运算功能的电路称为1位全加器。
实现多位二进制数相加有串行多位加法和并行多位加法两种形式，其中比较简单的一种电路是采用多个1位全加器并行相加，逐位进位的方式。
实验用器件管脚介绍：1、74HC(LS)00（四二输入与非门）管脚如下图所示。
2、74HC(LS)86（四二输入异或门）管脚如下图所示。
3、74HC(LS)153（双四选一数据选择器）管脚如下图所示。
4、74HC(LS)283（4位二进制全加器）管脚如下图所示。
四、 实验内容与步骤1、用门电路实现全加器（基本命题）参照表达式i i i i C B A S ⊕⊕=，i i i i i i B A C B A C +⊕=+)(1，其中i S 为本位和，i C 为低位向本位的进位，1+i C 为本位向高位进位，设计用与非门74HC(LS)00及异或门74HC(LS)86实现1位全加器的实验电路图，搭接电路，用LED 显示其输出，并记录结果在下表中。
1.1电路图1.2实验结果（基本命题）2、用数选器实现全加器输出Sn参照和实验内容与步骤1完全相同的逻辑功能，设计用与非门74HC(LS)00和数选器74HC(LS)153实现1位全加器输出S n的实验电路图，搭接电路，用LED显示其输出，观察电路的逻辑功能是否与设计功能一致。
加法器实验总结
加法器实验总结1. 引言加法器是计算机中一种关键的数字逻辑电路，用于实现数字数据的加法运算。
本文将对我们进行的加法器实验进行总结和分析，包括实验的目的、设计原理、具体实验步骤、实验结果以及实验总结和改进方向。
2. 实验目的本次实验的主要目的是通过设计和实现一个4位二进制加法器，加深理解数字逻辑电路的工作原理和设计方法，并通过实际操纵和观察实验现象来验证所学到的知识。
3. 设计原理一个基本的4位二进制加法器包含4个输入端口（两个4位的二进制数A和B）、一个输出端口（4位二进制数S）和一个进位输出端口（C）。
设计原理可以简述如下： - 每一位的加法运算由一个半加器（half adder）实现，用于计算每一位的和（S）和进位（C）。
- 第一位的和（S[0]）和进位（C[0]）直接由对应的输入端口A[0]和B[0]进行异或和与运算，得到结果。
- 对于其它位（i>=1），和（S[i]）的计算需要考虑前一位的进位（C[i-1]），即S[i] = A[i] ^ B[i] ^ C[i-1]，进位（C[i]）的计算需要考虑前一位的进位（C[i-1]）和当前位的进位（Carry）信号，即C[i] = (A[i] & B[i]) || (C[i-1] & (A[i] ^ B[i]))。
4. 实验步骤4.1 材料准备•集成电路芯片：4个半加器、4个或门、3个异或门。
•连线材料：导线、面包板等。
4.2 电路连接根据设计原理进行电路的连接，确保每个元件都正确连接并没有短路或接触不良的情况。
4.3 电路测试对搭建好的电路进行测试，将不同的二进制数输入A和B接入相应的输入端口，并观察输出端口S和进位输出端口C的结果是否符合预期。
5. 实验结果根据我们的实验步骤，我们成功完成了一个4位二进制加法器的设计和实现。
通过输入不同的二进制数A和B，我们观察到输出端口S和进位输出端口C都能正确地计算出4位二进制数的和。
加法器 逻辑公式
加法器逻辑公式
加法器是数字电路中常用的一种逻辑电路，它可以将两个数字相加。
在计算机中，加法器是必不可少的部分，因为它能够使计算机进
行加法运算，从而能够实现各种复杂的计算。
加法器的逻辑公式可以用如下的形式表示：S=A+B+C，其中A和B
是被加数，C是进位（Carry）。
这个公式表示，将A、B、C三个二进
制数相加，得到的结果为S。
这个过程可以通过一些基本门电路（如AND门、OR门、XOR门和NOT门）来实现。
具体来说，首先将A和B输入到一个全加器中，然后再将C输入
到这个全加器中，得到S和进位。
全加器也可以用一些基本门电路来
实现，比如利用两个半加器来实现。
在实际应用中，加法器的位数和进位方式都有很多种不同的选择，这取决于所需的精度和性能要求。
在一些高速的应用中，可以采用并
行加法器，使用多个加法器同时进行计算。
总之，加法器作为电路设计中最基本的模块之一，对于计算机的
工作起着至关重要的作用。
因此，对于电路设计和计算机工作原理的
学习，掌握和理解加法器的逻辑公式是至关重要的。
第3章 数字逻辑基础(4)
K4=C4=1 B=S+0110 无溢出
总结上表,可得: ① K4=1 时,需进行加6 (0110) 校正; ② K4=1 有三种情况: a. C4=1 (对应十进制数16,17,18,19) ; b. S4=S3=1 (对应十进制数12,13,14,15) ; c. S4=S2=1(对应十进制数10,11,14,15) . 所以: K4=C4+S4S3+S4S2
信号)
＝A －(2n －B补)
= A+B反+1 －2n
CI
7483
借位信号实现减2n 的功能: 当A+B反+1 的高位有进位时, 该进位信号和2n 相减使最高位为0, 反之为1。
2. 分两种情况讨论： (1)A－B≥1 设 A=0101 , B=0001 求补码相加演算过程如下： 0101 (A) + 1110 (B反) 1 (加1） 1 0100
A1 A2 A3 A4 B1 B2 B3 B4
0
C4 A1Σ A2 CO A3 A4 B1 B2 S4 B3 S3 B4 S2 CI S1
≥1
0
&
&
0
A4Σ A3 CO A2 A1
K4
0
B4 B3 B2 B1 CI
S4 S3 S2 S1
7483 8421码加/法器
7483
3.2.7 数值比较器 数值比较器用来判断两个二进制数的大小或相等. 1. 一位数值比较器 表达式: 真 值 表 A B Y(A>B) Y(A<B) Y(A=B) Y(A>B)=AB
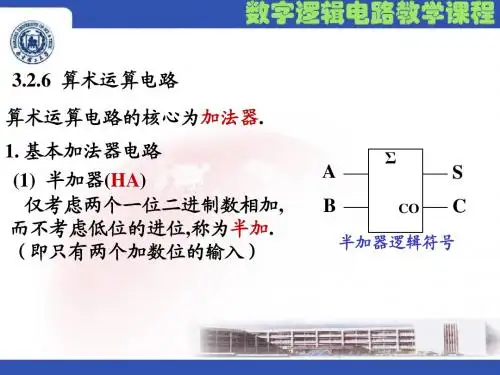
全加器逻辑符号
(3) 串行进位加法器
当有多位数相加时,可模仿笔算,用全加器构成串行进位 加法器.
加法器及其应用
l
l
用两片74LS283和必要的门电路实现两个8421BCD码求和运算，结果 仍为8421BCD码，要求画出逻辑功能图。
思考题
l
全部采用与非门设计，实现一位全加器。
实验报告要求
l l
实验原理、实验过程的描述。 整理实验数据，列写实验任务的设计过程，画出设计的逻辑电路图， 并注明所用集成电路的引脚号。
l l l
拟定记录测量结果的表格。 总结用门电路实现半加器和全加器的方法。 总结用四位二进制全加器74LS283设计代码转换电路的方法。
芯片分布
74LS32
74LS283
74LS08 +5v电源
数码管输入及电源
输入端A、B、C、D，最低位 是A，最高位是D
数码管电源 +5V，用一根 导线相连
C'
S'
A
B
输入：A（A3A2A1A0）+ B（B3B2B1B0） 输入范围： A : 0~9 B : 0~9
l
分析：和283直接输出的区别
C' S' C S
？
A B 相同 不同 A
283
B
0010+0101=0 0111 0110+0111=1 0011
0010+0101=0 0111 0110+0111=0 1101
A
B S
C
283（1）
A
B
C'=S3·S2+S3·S1
式子有没有问题？
C'=S3·S2+S3·S1+C
8421BCD码加法器 最终设计的电路：
74LS32（四2输入或门） 74lS08（四2输入与门）
加法器实验报告
加法器实验报告加法器实验报告概述：本次实验旨在设计和实现一个加法器电路，通过对电路的搭建和测试，验证加法器的正确性和可行性。
加法器是计算机中最基本的算术运算器之一，其在数字逻辑电路中扮演着重要的角色。
1. 实验背景加法器是一种基本的数字逻辑电路，用于实现数字的加法运算。
在计算机中，加法器被广泛应用于算术逻辑单元(ALU)和中央处理器(CPU)等部件中，用于进行各种数值计算和逻辑运算。
因此，了解和掌握加法器的工作原理和设计方法对于理解计算机原理和数字电路设计具有重要意义。
2. 实验目的本次实验的主要目的是通过设计和实现一个4位二进制加法器电路，验证加法器的正确性和可行性。
具体要求如下：- 设计并搭建一个4位二进制加法器电路；- 对电路进行测试，验证其加法运算的正确性；- 分析电路的性能和优化空间。
3. 实验原理加法器是通过逻辑门电路实现的。
在本次实验中，我们将使用全加器电路来实现4位二进制加法器。
全加器是一种能够实现两个二进制位相加并考虑进位的电路。
通过将多个全加器连接起来，可以实现更高位数的二进制加法器。
4. 实验步骤4.1 设计加法器电路的逻辑功能首先，我们需要确定加法器电路的逻辑功能。
在这个实验中，我们需要实现两个4位二进制数的相加运算，并输出结果。
具体的逻辑功能可以通过真值表或逻辑表达式来描述。
4.2 搭建电路根据逻辑功能的要求，我们可以使用逻辑门电路来搭建加法器。
在本次实验中，我们将使用多个全加器电路来实现4位二进制加法器。
通过将多个全加器连接起来，可以实现更高位数的二进制加法器。
4.3 进行电路测试在搭建完电路后，我们需要对电路进行测试，以验证其加法运算的正确性。
可以通过输入一些测试用例，并比较输出结果与预期结果是否一致来进行测试。
5. 实验结果与分析通过对加法器电路的测试，我们可以得到加法器的输出结果。
通过比较输出结果与预期结果，可以验证加法器的正确性。
同时，我们还可以分析电路的性能和优化空间，例如进一步提高加法器的速度和减少功耗等。
【西安交通大学】【数字逻辑实验】【实验三 组合电路与全加器设计实验】
输出
和数S 进位C 0 0 0 1
由真值表得逻辑表达式
S = A⊕ B C = A• B
Xi’an Jiaotong University
前面是由与非门构成的半加器 下图是由异或门、 下图是由异或门、与门构成的半加器
这两个电路同样实现两 个一位二进制数相加的功 是它们的和， 是向 能。S是它们的和，C是向 是它们的和 高位的进位。根据S和 的 高位的进位。根据 和C的 表达式， 表达式，将原电路图改画 成如图所示的逻辑图。 成如图所示的逻辑图。
S = A⊕ B C = A•B
Xi’an Jiaotong University
2.全加器 全加器 一般作二进制数加法时 除两个加数外， 作二进制数加法时， 一般作二进制数加法时，除两个加数外，还必须 考虑低位进位问题， 全加过程时被加数、 考虑低位进位问题， 全加过程时被加数、加数及低 位向本位进位数三者相加， 位向本位进位数三者相加，所以全加器有三个输入 端（被加数、加数和进位数），有两个输出端（本 被加数、加数和进位数），有两个输出端（ ），有两个输出端 位和及进位数）。 位和及进位数）。
1.使用 使用QUARTUS软件完成电路设计 使用 软件完成电路设计 2.先设计半加器电路，并进行仿真测试 先设计半加器电路， 先设计半加器电路 3.利用半加器电路再完成全加器电路设计，并进行 利用半加器电路再完成全加器电路设计， 利用半加器电路再完成全加器电路设计 仿真测试 4.下载后连线做硬件验证测试 下载后连线做硬件验证测试
Xi’an Jiaotong University 全加器电路参考图：ADDER_F.QDF
半加器电路参考图：ADDER_H.QDF
An
B C 为进位， 为本位和， 为向高位的进位； 为被加数， 为加数， 为被加数， n 为加数， n −1 为进位， S n 为本位和，Cn 为向高位的进位；
数字逻辑课件——加法器
综上所述，接法如图3-3-23(b)所示。与方法1比 较，多用了一个与非门，却省去两个“四选一” 选择器。“选择输入”端A1，A0，可接C，D， 也可接A，B或A，C或B，D或A，D或B，C， 相应的卡诺图略加变动，所得的D0，D1， D2， D3的表达式各不相同。经过各种方案的比较， 可得最佳的简化结构。
例3-6 用74153实现逻辑函数Z F (A, B) m(1, 3)
解：由最小项表达式得该函数的真值表，如表 3-3-12所示，用半片74153即可实现该逻辑函数， 接法如图3-3-20。
输入变量A，B分别送选择输入端A1，A0选通输 入，ST 应接0，数据输入D0，D1，D2，D3根据 真值表分别接0，1，0，1。这样，74153的输 出端Y 即逻辑函数Z。
逻辑图可以看出，数据输出Y 的逻辑表达 式为
Y ST[D0 ( A1 A0 ) D1( A1 A0 ) D2 ( A1 A0 ) D3 ( A1 A0 )]
即当选通输入 ST 0 时，若将选择输入A1，
A0分别为00，01，10，11则相应地把D0，D1，
D2，D3送到数据输出端Y去， 当
图3-3-21 例3-7图
25
①B当C BC =00时，Z = D0 ；由卡诺图可见，Z 此时 不②不A管管当01 AAB0000等 等C 于 于=01110001或 或时111011，， ，Z1ZZ001 =都都D等等1 于于；01由，，卡因因B0C 诺此此图以以S可AAT0110 输 输见D012入 入，7DY411DD此53D012。 。时D3
从图3-3-22可以发现，下层的片0和片3， 输出分别恒为0和1，故可省去片0和片3， 同时，片4的D0和D3分别改接0和1。因此， 在用74153实现逻辑函数时，必须根据具 体情况考虑简化结构的可能性。
数字电子技术-加法器
• 74LS283电路是一个四位加法器电路，可实现两个四位二进制 数的你相加，其逻辑符号如图2-23所示。
CO是向高位的进位
S3、S2、S1、S0是对应各位的和 CI是低位的进位
A3A2A1A0和B3B2B1B0是两个二进制待加
加法器
2.3 加法器(Accumulator)
算术运算是数字系统的基本功能，更是计算机中不可缺少的 组成单元。
本节介绍实现加法运算的逻辑电路。
完成加法运算的逻辑器件称为加法器。 加法器分为半加器和全加器。
2
2.3.1 全加器
在第1章中，我们讨论了半加运算电路
该电路实现两个一位二进制数相加的功能。S是它们的本位和，C是向高位的进位。 由于这一加法器电路没有考虑低位的进位，所以称该电路为半加器。
输 输出 入
AB SC
00 00 01 10 10 10 11 01
半加器的逻辑符号
在第1章中，我们还讨论了全加运算电路。
电路实现全加器FA(Full
全加器的逻辑符号
输入
AnBnCn-1
000 001 010 011 100 101 110 111
输出 Sn Cn
00 10 10 01 10 01 01 11
Adder)的逻辑功能。输入An 和Bn为一位二进制数，Cn-1 为低位的进位，输出Sn为本 位和，Cn为本位的进位。全
加器能把本位两个一位二进 制加数和来自低位的进位三 者相加，得到求和结果和该 位的进位信号。
由多个全加器，可构成多位加法运算电路。
2.3 加法器(Accumulator)
2.3.2 多位加法器
胡全连版数字逻辑第3章习题解答
f 习题三3.1写出如图判p3.1中各逻辑图的逻辑表达式，并化简成最简与或表达式。
BCBC(a) (b)AA C(c)(d)图p3.1题3.1逻辑图解：（a ）C B C B A C B C B A F +=•=(b) 1=)+(+)+(+)+(=+•+•+=C B B A C A C B B A C A F(c)CA BC AB C B A AB C B A AB F++=)⊕(+=)⊕(+=1 ABC C B A C B A C B A C B A F +++=⊕⊕=2(d)F=A⊙B⊙C= ABC C B A C B A C B A C AB B A C AB B A +++=•)+(+•+3.2、3.2、化简下列逻辑函数，并用与非门和或非门实现。
解：(1)∑)7,3,2,0(=),,(m C B A F与非门实现：BC B A BC B A F •=+=或非门实现：C B C A F +=,C B C A C B C A F F +++=)+)(+(== (2) C A C B AB C B A F ++=),,( 解：与非门实现：AB C AB C F •=+=或非门实现：C B C A F +=,C B C A C B C A F F +++=)+)(+(== ┏ (^ω^)=☞(3) ABD D C B C A B A D C B A F +++=),,,( 解：与非门实现：BCD AC AB BCD AC AB F ••=++= 或非门实现：C B D A C A B A F +++=,C BD A C A B A C B D A C A B A F F +++++++=)+)(+)(+)(+(==(4) ∑)15,14,10,8,2,0(=),,,(m D C B A F解：与非门实现：ABC BD ABC BD F •=+= 或非门实现：C B D B D A B A F +++=,C BD B D A B A C B D B D A B A F F +++++++=)+)(+)(+)(+(==（图略）3.3、分析如图p3.2所示组合逻辑电路，写出输出函数表达式，列出真值表，说明电路的逻辑功能。
逻辑电路中加法器的概念
逻辑电路中加法器的概念逻辑电路中的加法器是一种将两个二进制数相加的电路。
它被广泛应用于计算机、数字信号处理和通信系统等领域。
在计算机中，加法器用于执行整数运算，并且是所有算术操作的基础。
因此，对于理解和设计逻辑电路来说，加法器的概念至关重要。
加法器的基本原理是将两个二进制数的对应位相加，并得到相应的和与进位。
在加法器中，输入位称为"被加数"和"加数"，输出位称为"和"和"进位"。
加法器可以分为半加器和全加器两种类型。
半加器只能处理一位的二进制加法，而全加器可以处理两位的二进制加法。
半加器的原理很简单，它有两个输入位（被加数和加数）和两个输出位（和和进位）。
和的输出位等于两个输入位的异或运算结果，进位的输出位等于两个输入位的与运算结果。
全加器是由两个半加器和一个或门组成的。
它有三个输入位（被加数、加数和进位）和两个输出位（和和进位）。
和的输出位等于三个输入位的异或运算结果，进位的输出位等于三个输入位的与运算结果与进位输入位的异或运算结果进行或运算得到的值。
在实际应用中，为了进行更高位数的加法运算，可以将多个全加器连接起来形成级联的加法器。
这种级联的加法器称为Ripple Carry Adder（串行进位加法器）。
其中，每个全加器的进位输入位是上一个全加器的进位输出位，从而实现了加法器的级联操作。
此外，为了提高计算速度和减少器件的数量，还可以使用并行进位加法器（Carry Lookahead Adder）或进位选择加法器（Carry Select Adder）。
这些高级加法器利用了更复杂的电路结构来预先计算出进位，从而减少了级联操作所需的时间。
总的来说，加法器是逻辑电路中的一种基本组件，用于将两个二进制数相加。
它可以使用半加器、全加器或其它高级加法器来实现。
加法器的设计取决于所需的位数和性能要求。
在计算机和数字电路中，加法器是执行算术操作和实现数字逻辑功能的重要组成部分。
加法器的工作原理
加法器的工作原理加法器是一种常见的电子数字逻辑电路，用于对数字信号进行加法运算。
它可以将两个或多个数字信号相加，并输出它们的和。
在计算机和其他数字系统中，加法器是一种基本的逻辑单元，其工作原理对于理解数字电路和计算机原理至关重要。
加法器的基本原理是利用逻辑门来实现数字信号的加法运算。
在数字电路中，最常用的加法器是全加器，它可以对两个输入信号进行加法运算，并输出它们的和以及进位信号。
全加器通常由XOR 门、AND门和OR门组成，通过这些逻辑门的组合，可以实现数字信号的加法运算。
当我们输入两个数字信号时，全加器首先对它们进行加法运算。
XOR门用于计算两个输入信号的和，AND门用于计算进位信号，而OR门则用于将进位信号和求和信号相加，得到最终的输出结果。
通过这种方式，全加器可以对两个数字信号进行加法运算，并输出它们的和以及进位信号。
除了全加器之外，还有半加器和Ripple Carry加法器等其他类型的加法器。
半加器可以对两个输入信号进行简单的加法运算，但无法处理进位信号。
而Ripple Carry加法器则可以对多位数字进行加法运算，通过级联多个全加器来实现对多位数字的加法运算。
除了基本的加法器外，还有一些高级的加法器，如带有溢出检测功能的加法器、带有进位预置功能的加法器等。
这些高级加法器可以提供更多的功能和灵活性，使得数字信号的加法运算更加方便和高效。
总的来说，加法器是一种非常重要的数字逻辑电路，它可以对数字信号进行加法运算，并输出它们的和。
通过逻辑门的组合，加法器可以实现简单的加法运算，同时也可以扩展到多位数字的加法运算。
加法器的工作原理对于理解数字电路和计算机原理至关重要，它在数字系统和计算机中扮演着非常重要的角色。
数字逻辑课后答案 第三章
第三章 时序逻辑1.写出触发器的次态方程，并根据已给波形画出输出 Q 的波形。
解：2. 说明由RS 触发器组成的防抖动电路的工作原理，画出对应输入输出波形解：3. 已知JK 信号如图，请画出负边沿JK 触发器的输出波形（设触发器的初态为0）1)(1=+++=+c b a Qa cb Q nn4. 写出下图所示个触发器次态方程，指出CP 脉冲到来时，触发器置“1”的条件。
解：（1），若使触发器置“1”，则A 、B 取值相异。
（2），若使触发器置“1”，则A 、B 、C 、D 取值为奇数个1。
5.写出各触发器的次态方程，并按所给的CP 信号，画出各触发器的输出波形（设初态为0）解：6. 设计实现8位数据的串行→并行转换器。
B A B A D +=DC B A K J ⊕⊕⊕==Q AQ B Q D Q C Q E Q F Q7. 分析下图所示同步计数电路解：先写出激励方程，然后求得状态方程状态图如下：该计数器是五进制计数器，可以自启动。
8. 作出状态转移表和状态图，确定其输出序列。
解：求得状态方程如下故输出序列为：000119. 用D 触发器构成按循环码(000→001→011→111→101→100→000)规律工作的六进制同步计数器解：先列出真值表，然后求得激励方程PS NS 输出N0 0 0 0 0 1 00 0 1 0 1 1 0 0 1 1 1 1 1 0 1 1 1 1 0 1 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1化简得：逻辑电路图如下：n Q 2n Q 1n Q 012+n Q 11+n Q 10+n Q n n n nn n n n n n nnQ Q Q Q Q Q Q Q Q Q Q Q Z 121002*********+==+==+++nnn nnn nnnn QQ Q D QQ Q D QQ Q Q D 121211121122+====+==+++10. 用D 触发器设计3位二进制加法计数器，并画出波形图。
03实验三 加法器的设计与应用
4位二进制加 数A 输入端
向高位片的 进位输出 本位和输出端 相加结果读数为 C0S3S2S1S0
4位二进制加 数B 输入端 低位片进位输入端
74LS283逻辑符号
四、实验内容及步骤
1.用基本门电路实现全加器电路。
解：①逻辑抽象 输入变量： 被加数为A，加数为B 由低位来的进位为Ci 输出变量： 相加后本位和为S 往高位的进位为Co
i i
1
1
BCi A 00 01 0 1 1
11 1
1
10
1
Co A BC i A B C i AB C i ABC ( A B ) C i AB ( A B ) C i AB
四、实验内容及步骤
③逻辑电路图
用一片74LS00和一片74LS86即可实现。
四、实验内容及步骤
如：
要考虑低位 来的进位
0 0 0 1
全加器实现
+ 0 0 1 1
进位
1 1 01 0 0
不考虑低位 来的进位
半加器实现
三、实验原理
多个一位全加器进行级联可以得到多位全加器。 74ls283是采用快速进位的四位二进制全加器.与之 类似的还有 74ls83等。
83管脚图
三、实验原理
A4 A3 A2 A1 B4 B3 B2 B1 CI ∑ CO S4 S3 S2 S1 S4 S3 S2 S1
END
兰州交通大学 国家级电工电子实验教学示范中心
真值表
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
Ci 0 1 0 1 0 1 0 1
S 0 1 1 0 1 0 0 1
Co 0 0 0 1 0 1 1 1
数字电路中加法器和减法器逻辑图分析
数字电路中加法器和减法器逻辑图分析1.加法器，减法器都是从一位的二进制数开始进行例题讲解，逐渐扩展到多位二进制位数之间的运算。
在设计逻辑电路的过程中，根据所描述的功能构建好真值表。
出题者喜欢要求读者用与或门，与或非门构建函数表达式。
它的原因在于依据真值表写函数表达式，最标准的就是最小项表达式。
以下小图的逻辑图来看与或门，我们的头脑中不能老是思维定势，认为输入就是两个，在实际生活中，输入应该非常多，远非两个，在逻辑符号中，要清楚地认识与非门的多输入的画法，将与门分成了好几格，每一格代表一个与门电路。
下小图可以写成AB+CD+EF（不认真考虑前面的输入），由细小的门集成为更大的门，将某一部分单独来看，它们就是一个整体，如（AB+CD+EF），体现在逻辑图中就是一个角。
如果从全图的角度看，在最后一级门电路中，每一个小整体代表着输出。
最后一级的与门中，有两个输入，有三个输入，这都是可以的，最多输入的个数是依照初始的输入的个数来定，不可能超过这个数，只可能少于这个数，因为对于某一输出而言，并非所有的输入对它都是有效的。
从最左边的所有输入，经过逻辑电路图，在最右边得到了所有的输出。
还有一点，这是与或表达式的逻辑图，如果在写逻辑表达式，包括化简变化函数式时，采用了不同于与或形式的表达式，那么最终得到的逻辑图就和下面的与或形式的逻辑图完全不一样。
2.一位的全减器是指，两个一位的二进制数之间进行减法运算。
全减器的特例就是半减器。
多位二进制减法器，是由加法电路构成的；在加法电路的基础上，减法与加法采用同一套电路，实现加减法共用。
3.这里的多位二进制数的减法，是指无符号数，为什么？将减法运算转换为加法运算，采用的是补数的方法完成的。
这就解释了为什么两者能共用一套电路，是不是减法在转换时，我们需要在加法电路的基础上进行一些小的扩展，来进行减法的补码转换？N反是每一位都取反，没有符号位，下式当中，A-B是减法，通过形式转化，将-B化为B反+1-2n，B是正数，A和B均为无符号数，通过补码的转变，我们成功的将-B变为了固定的-2n，但是这还是有减号，该怎么解决？仔细观察下面这张图，A和B是两个四位二进制数相减。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
加数
和数
半
S
加
被加数 器 向高位进位 Ci＋1
图 3 – 10 半加器框图
A，B —输入变量，表示两个一位二进制数。
S —输出变量，相加后的和数。
C
i
—输出变量，向高位的进位数。
1
半加器
列真值表
表3-20 半加器真值表
AB
00 01 10 11
S
Ci+1
00
10
10
01
写表达式
S A B A B A B C i1 = A•B
0
0
1
1
1
1
1
Si=m（1，2，4，7）
Ci+1=m（3，5，6，7）
全加器
函数变换过程如下：
__ __
__
__
__ __
Si Ai Bi Ci Ai Bi Ci Ai Bi Ci Ai BiCi
__
__ __ __ __
( Ai Bi Ai Bi ) Ci ( Ai Bi Ai Bi )Ci
四位二进制并行加法器
三、四位二进制并加法器的外部特性和逻辑符号 1．外部特性
图中，A4、A3、A2、A1 ------- 二进制被加数； B4、B3、 B2、B1 ------- 二进制加数； F4、 F3、 F2、 F1 -----C0 --------------------来自低位的进位输入； FC4 -------------------向高位的进位输出。
总结一下：
C1～C4是Pi、Gi和C0的函数，即Ci=f(Pi,Gi,C0)； 而Pi、Gi又是 Ai、Bi的函数， Ai Bi Pi 所以，在提供输入Ai、Bi和C0之后，A 可i以Bi同 时产G生i C1～C4。 通常将根据Pi、Gi和C0形成C1～C4的逻辑电路称为先行进 位发生器。
超前进位二进制并行加法器特点： 根据输入信号同时形成各位向高位的进位； 同时产生各位的和。
是否可行？ 由全加器的结构可知：
Si Ai Bi Ci Ci1AiBiCi AiBiCi AiBiCi AiBiCi
（Ai Bi） Ci AiBi
关键是进位信号C
超前进位二进制并行加法器
例2 用4位二进制并行加法器设计一个4位二进制并行加 法/减法器。
解 分析：根据问题要求，设减法采用补码运算，并令
A = a4a3a2a1 ----- 为被加数(或被减数)； B = b4b3b2b1 ----- 为加数(或减数)； S = s4s3s2s1 ----- 为和数(或差数)；
M--- 为 功 能 选 择 变 量 .M=0 时 ， 执 行 A+B ； M=1时，执行A-B。
半加器
画逻辑图
用异或门
S AB Ci1 AB
A
=1 S
B
&
C i1
图 3 – 11 半加器逻辑图
A
S
A
S
HA
B
CO
Ci1 B
C i1
逻辑符号
惯用符号
全加器
多位二进制数加法的例子
0111 +) 1 1 0 1
0100 1111
被加数 加数 和 进位
2. 全加器
全加器
图 3-12 全加器框图
__ _________
( Ai Bi ) Ci Ai Bi Ci Ai Bi Ci
__
__
__
Ci1 Ai Bi Ci Ai Bi Ci Ai Bi Ci Ai BiCi
__ __
( Ai Bi Ai Bi )Ci Ai Bi ( Ai Bi )Ci Ai Bi
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。
1) 输入端A4、A3、A2、 A1输入8421码；
2) 而从另一输入端B4、 B3、B2、B1输入二进 制数0011；
3) 进位输入端C0接上“0”；
4) 可从输出端F4、F3、F2、 F1得到与输入8421码对 应的余3码。
四位二进制并行加法器
超前进位二进制并行加法器
C1P1C0G1
C 2 P 2 C 1 G 2 P 2 P 1 C 0 P 2 G 1 G 2 C 3 P 3 C 2 G 3 P 3 P 2 P 1 C 0 P 3 P 2 G 1 P 3 G 2 G 3
C 4 P 4 C 3 G 4 P 4 P 3 P 2 P 1 C 0 P 4 P 3 P 2 G 1 P 4 P 3 G 2 P 4 G 3 G 4
F3
F2
F1
FC4
FA4
C3
FA3
C2
FA2
C1
FA1
C0
A4 B4
A3 B3
A2 B2
A1 B1
图3-15 四位串行进位并行加法器的结构框图
串行进位并行加法器
串行进位二进制并行加法器的特点： 结构简单 被加数和加数的各位能同时并行到达各位的输入端,但是各位全加 器的进位输入则是按照由低位向高位逐级串行传递的，各进位形成一个 进位链。 由于每一位相加的和都与本位进位输入有关，所以，最高位必须等 到各低位全部相加完成并送来进位信号之后才能产生运算结果。
一.基本概念 加法器 ●定义：实现多位二进制数算术和运算的电路
●一位加法器：半加器和全加器
半加 — 两个一位二进制数相加，不考虑进位输入。
半加器 — 实现半加逻辑的电路。
全加 —加数、被加数和来自低位的进位数三者相 加。 全加器 — 实现全加逻辑的电路。
半加器与全加器
二.一位加法器
1. 半加器
A
B
输入变量：A i，B i — A、B两个数的第 i 位。 C i — 来自低位的进位。
输出变量：S i — 本位数和。 C i+1 — 向相邻高位进位数。
列真值表
Ai
0 0 0 0 1 1 1 1
全加器
表3-21 全加器真值表
பைடு நூலகம்
Bi
Ci
Si
C i+1
0
0
0
0
0
1
1
0
1
0
1
0
1
1
0
1
0
0
1
0
0
1
0
1
1
当M=0时， A+B+C0 (C0=0 )
当M=1时，A+B +C0 (C0=1 )
根据异或逻辑: B0B,B1B
B
B
=1
=1
B0
B1
21
四位二进制并行加法器
实现给定功能的逻辑电路图如下图所示。
例3 用一个4位二进制并行加法器和六个与门设计一个 乘法器，实现A×B,其中
A = a3a2a1 , B = b2b1 。
Ci1AiBiCiAiBiCiAiBiCiAiBiCi (AiBi)CiAiBi
令 则有
Ai Bi Pi （进位传递函数）
AiBi Gi
（进位产生函数）
Ci1P iCi Gi
当 i=1、2、3、4时，根据递推关系，可得到4位并行加法器 各位的进位输出函数表达式为：
C1P1C0G1
四位二进制并行加法器
四、应用举例 二进制并行加法器除实现二进制加法运算外，还可实
现代码转换、二进制减法运算、二进制乘法运算、十进制 加法运算等功能。
例1 用4位二进制并行加法器设计一个将8421码转换成 余3码的代码转换电路。
解 根据余3码的定义可知，余3码是由8421码加3后形 成的代码。所以，用4位二进制并行加法器实现8421码到余 3码的转换，只需从4位二进制并行加法器的输入端A4、A3、 A2和A1输入8421码，而从输入端B4、B3、B2和B1输入二进制 数0011，进位输入端C0接上“0”，便可从输出端F4、F3、 F2和F1得到与输入8421码对应的余3码。
显然，这种加法器运算速度较慢，而且位数越多,速度就越低。
如何提高加法器的运算速度?
必须设法减小或去除由于进位信号逐级传送所花费的时间 若能使各位的进位直接由加数和被加数来决定，而不需依赖低位进位。 那么就可以有所改进。
根据这一思想设计的加法器称为超前进位(又称先行进位)二进制并行加 法器。
超前进位二进制并行加法器
解 根据乘数和被乘数的取值范围，可知乘积范围处在 0～21之间。故该电路应有5个输出，设输出用Z5Z4Z3Z2Z1 表示，
×) 乘数 +)
a3b2
a3
a3b1 a2b2
a2 b2
a2b1 a1b2
a1 b1
a1b1
乘积 Z5 Z4
Z3
Z2
Z1
因为： ☆1位二进制数乘法 法则和逻辑“与”运算法 则相同，“积”项aibj(i =1，2，3；j=1，2)可用 两输入与门实现。
全加器
画逻辑图 用异或门实现
图 3 – 13 用异或门构成全加器
Ai
Si
Bi Ci
CI CO
Ci+1
逻辑符号
Ai
Bi
FA
Ci
Si Ci+1
惯用符号
多位加法器
三 多位加法器
多位加法器按照各位数相加方式不同可分为串行加法
器和并行加法器。
S n1
S0
C n 二进制并行加法器 C 0
An1 A0
B n1 B 0
☆对部分积求和可用 并行加法器实现。
所以：该乘法运算电 路可由6个两输入与门和1 b2 个4位二进制并行加法器构 成。逻辑电路图如右图所 示。