南师附中物理竞赛讲义 106光学例题t资料
初中物理竞赛辅导—光、热、声(教师使用)
竞赛辅导讲义——光、热、声 （教师使用）一、知识要点二、例题与练习[例1]处在赤道上某地的人在月落4h 后，还能看到一颗绕赤道平面轨道运行的人造卫星在其正上方，试求这颗卫星距地面高度最小约多少?(地球半径R=6.4X106m)分析与解答：忽略大气对光的折射，光沿直线传播。
能看到卫星，则卫星上必须有太阳的反射光线进入观察者的眼中，作出示意图如下：图中A 点处刚日落，地球自转4h ，原A 点转至A ’点，由圆的知识可得：α=244×360°=60° (1) 又：cos α=hR R+ (2)由（1）、（2）两式得:h=R （αcos 1-1）≈6.4×106（m ）[练习1]太阳和月亮位于如图所示的位置，请你根据光的直线传播规律，在图中画出当地球上的人分别处于什么空间区域时，可以看到月全食、日偏食和日环食? 分析与解答：如图所示1区——日全食 2区——日偏食 3区——日环食[例2]水平桌面上放置一平面镜，镜面与桌面成45°角，一个小球以V 匀速沿桌面向镜滚去，如图所示，问镜中小球的像将如何运动?分析与解答：根据平面镜成像规律可知，物像等大，物像对称。
小球沿桌面向镜主动的任一时刻，物像关系都符合此规律。
故小球的像将竖直向下运动。
1232太阳月亮[练习2]只要你稍微注意一下就会发现，除了大型客车外，绝大多数汽车的前窗都是倾斜的，你能从光学的原理解释这一情况吗?分析与解答：当汽车和前窗玻璃倾斜装置时，车内乘客经过玻璃反射成人像在车的前上方，而路上行人是不可能出现在上方空中的，这样就将车内乘客的像与路上的行人分离开来，司机就不会出现错误，尤其在夜间开车，车内开灯，造成外暗内亮的时候，大型客车较大，前窗离地面要比小汽车高得多，即使前窗玻璃竖直装，像是与窗同高的，而路上行人不可能出现在这个高度，则不会混淆。
[例3]一般人脸宽（包括两耳）约18cm，两眼的光心相距约7cm，两眼光心离头顶和下巴分别为10cm和13cm．当平面镜竖直放置时，则至少要用多大的平面镜（矩形），才能看到自己脸的全部？分析与解答：先求镜宽（如图）设Ａ１、Ａ２为两耳，Ｂ１、Ｂ２为两眼．因为Ａ１Ｂ１ＭＮ及Ａ２Ｂ２ＭＮ均为平行四边形，即，所以镜宽＝（18－7）／2cm＝5.5cm再求镜长（如图2）设人脸长，眼在Ｂ处，因为像长＝，所以镜长＝／2＝／2＝（10＋13）／2cm＝115cm[练习3]如图所示，水平地面上有一障碍物ABCD，较大的平面镜MN在某一高度上水平放置，试用作图法求出眼睛位于O点从平面镜中所能看到的障碍物后方地面的范围。
全国中学生物理竞赛真题汇编---光学 参考答案
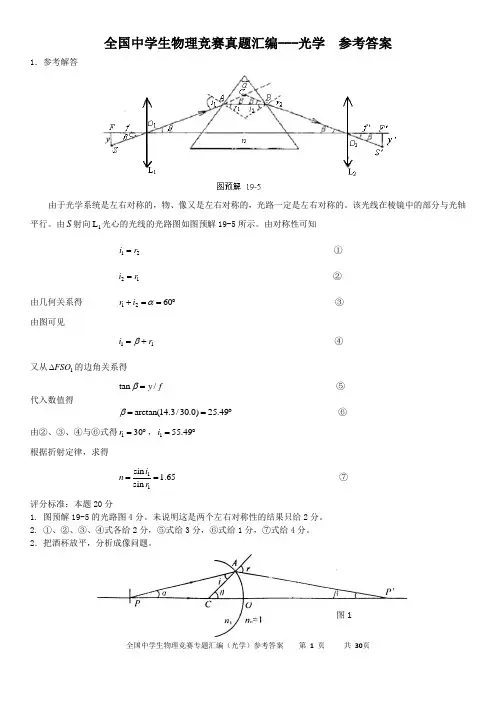
全国中学生物理竞赛真题汇编---光学 参考答案1．参考解答由于光学系统是左右对称的，物、像又是左右对称的，光路一定是左右对称的。
该光线在棱镜中的部分与光轴平行。
由S 射向1L 光心的光线的光路图如图预解19-5所示。
由对称性可知12i r = ①21i r = ②由几何关系得 1260r i α+==︒ ③ 由图可见11i r β=+ ④又从1FSO ∆的边角关系得tan /y f β= ⑤代入数值得arctan(14.3/30.0)25.49β==︒ ⑥由②、③、④与⑥式得130r =︒，155.49i =︒ 根据折射定律，求得11sin 1.65sin i n r == ⑦ 评分标准：本题20分1. 图预解19-5的光路图4分。
未说明这是两个左右对称性的结果只给2分。
2. ①、②、③、④式各给2分，⑤式给3分，⑥式给1分，⑦式给4分。
2．把酒杯放平，分析成像问题。
图11．未斟酒时，杯底凸球面的两侧介质的折射率分别为n 1和n 0＝1。
在图1中，P 为画片中心，由P 发出经过球心C 的光线PO 经过顶点不变方向进入空气中；由P 发出的与PO 成α 角的另一光线PA 在A 处折射。
设A 处入射角为i ，折射角为r ，半径CA 与PO 的夹角为θ ，由折射定律和几何关系可得n 1sin i ＝n 0sin r （1） θ ＝i +α （2）在△PAC 中，由正弦定理，有sin sin R PCiα= （3） 考虑近轴光线成像，α、i 、r 都是小角度，则有1n r i n =（4） Ri PCα=（5） 由（2）、（4）、（5）式、n 0、n l 、R 的数值及 4.8PC PO CO =-=cm 可得θ ＝1.31i （6） r ＝1.56i （7）由（6）、（7）式有r ＞θ （8）由上式及图1可知，折射线将与PO 延长线相交于P '，P ' 即为P 点的实像．画面将成实像于P ' 处。
高中物理竞赛讲座17(光学1word)
l x （2） sin i sin i l 2 R2 x2 2Rx cos i （3） 由式（1）和式（2）得 x nl 再由式（3）得 x2 n2 (R2 x2 2Rx cosi ) 设 M 点到 Ox 的距离为 h ，有 h R sin i
在 OMP 中
R cos i R2 R2 sin 2 i R2 h2 x2 得 2 R 2 x 2 2 x R 2 h2 n 1 x 2 (1 2 ) 2 x R 2 h2 R 2 0 n
光在两种介质的界面会发生反射和折射现象，分别符合反射定律和折射定律。 光在不均匀介质中要发生弯曲现象。研究办法：可以将介质分为很多薄层，每层的折 射率认为为定值，利用折射定律进行研究。 题、如图所示，一半径为 R 、折射率为 n 的玻璃半球，放在空气中，平表面中央半径 为 h0 的区域被涂黑． 一平行光束垂直入射到此平面上， 正好覆盖整个表面．Ox 为以球心 O 为原点，与平而垂直的坐标轴．通过计算，求出坐标轴 Ox 上玻璃半球右边有光线通过的 各点（有光线段）和无光线通过的各点（无光线段）的分界点的坐标．
的一段为有光线段，其它各点属于无光线段。 x0 与 xC 就是所要求的分界点，如图 评分标准：本题 20 分。求得式（7）并指出在 Ox 轴上 x x0 处无光线通过，给 10 分； 求得式（8）并指出在 Ox 轴上 x x0 处无光线通过，给 6 分；得到式（9）并指出 Ox 上有 光线段的位置，给 4 分。 题、如图所示，一个三棱镜 ABC 的顶角 α 小于 90°。假设光线在纸面内以任意入射 角入射到 AB 面上的 D 点，经一次折射后，又入射到 AC 面上，且能在 AC 面上发生全反射。 已知光线在 AC 面上发生全反射的临界角为θ（θ<45°） ，AC 边足够长。试求下列两种情 形下分别求三棱镜顶角 α 的取值范围： 2 （1）如果光线仅从 AB 面上法线的下方入射 900 （2）如果光线仅从 AB 面上法线的上方入射
江苏省南京师范大学附属中学物理竞赛讲义-12.1欧姆定律
12.1欧姆定律一、电阻的大小1、电阻的计算式（欧姆定律）U R I =2、电阻的决定式（电阻定律）l R Sρ= 微观解释：电阻产生的原因，是定向移动的自由电子与原子核碰撞。
长度越长，碰撞概率越大 横截面积越大，碰撞概率越小 3、电阻率与温度的关系：0(1)t ρρα=+微观解释：对于金属：温度高，分子热运动剧烈，碰撞概率大，电阻升高，α为正值 对于绝缘体：温度高，更多电子挣脱束缚，成为自由电子，电阻降低，α为负值二、网络电阻的化简1、利用电路的对称性进行折叠、翻转、合并拆分（1）设网络电阻的两端点为A 和B 。
AB 的这根对称轴两侧的对称是“完全对称”。
可以看成是两条支路并联，因此只需计算一条支路的电阻，并将总电阻除以2，相当于将原电路沿AB 折叠，电阻变粗，电阻值减半。
如果电阻就在对称轴上，相当于是中间一条支路上的电阻，则折叠过程中不受影响 （2）AB 中垂线的两侧具有不完全的对称性。
虽然电阻网络的分布是对称的，但是电路中电势的分布是不对称的，一边高一边低。
由这种不完全的对称性可以得到： <1>中垂线上各点电势相等①等电势的点之间，可以用导线任意连接②等势点间若存在电阻，则此支路上电流为0，可将此支路断开 <2>对称的支路上电流大小相等，因此可以将节点处的电路分离 2、利用电路的自相似性进行化简弄清究竟谁和谁自相似自相似性一般适用于半无限网络。
注意相似比的大小 3、等效电路在不改变电路性质的情况下，可以对电路进行变形、翻转，导线可以伸缩移动（节点移动不能跨过电路元件），三维图形可以“压扁”为二维图形。
4、电流注入法用均匀电阻线做成的正方形回路，如图，由九个相同的小正方形组成．小正方形每边的电阻均为r=8Ω．(1)在A 、B 两点问接入电池，电动势E=5.7V ，内阻不计，求流过电池的电流强度．(2)若用导线连接C 、D 两点，求通过此导线的电流(略去导线的电阻)．电阻丝无限网络如图所示，每一段金属丝的电阻均为r ，试求A 、B 两点间的等效电阻R AB ．由十二个相同的电阻连接成一个立方体框架，若每个电阻的阻值均为R 问从立方体八个顶点中的任意两个顶点测量时立方体的总电阻等于多少？1. 三个相同的金属圈两两相交地焊接成如图所示的形状，若每一金属圈的原长电阻（即它断开时测两端的电阻）为R ，试求图中A 、B 两点之间的电阻.【解析】从图看出，整个电阻网络相对A 、B 两点具有上、下对称性，因此可上、下压缩成如图所示的等效简化网络，其中r 为原金属圈长度部分的电阻，即有:r=R/4图网络中从A 点到O 点电流与从O 点到B 点的电流必相同；从A ′点到O 点的电流与从O 点到B ′点电流必相同.因此可将O 点断开，等效成图所示简化电路.B ′A ′AA继而再简化成如图所示的电路:最后可算得: R AB =1225512r r r -+=（） 即有R AB =5R/48.如图所示，无限旋转内接正方形金属丝网络由一种粗细一致、材料相同的金属丝构成，其中每个内接正方形的顶点都在外侧正方形四边中点上．已知与最外侧正方形边长相同的同种金属丝A'B'的电阻为R 0，求网络中：(1)A 、C 两端间等效电阻R AC ． (2)E 、G 两端间等效电阻R EG ．例1. 如图所示，框架是用同种金属丝制成的，单位长度的电阻为ρ，一连串内接等边三角形的数目可认为趋向无穷，取AB 边长为a ，以下每个三角形的边长依次减小一半，则框B ′BA ′AAB ′BA ′架上A 、B 两点间的电阻为多大？从对称性考虑原电路可以用如图所示的等效电路来代替，同时我们用电阻为2ABR 的电阻器来代替由无数层“格子”所构成的“内”三角，并且电阻是RAB 这样的，AB x R R =，R αρ=因此/2/2()()/2/2x x x x x RR RR R R R R R R R R R =+⋅++++解此方程得到：11)3AB x R R a ρ===如图所示是一个由电阻丝构成的平面正方形无穷网络，各小段的电阻为R ，求A 、B 两点间的等效电阻.若将A 、B 间的一小段电阻丝换成电阻为4R 的另一小段电阻丝.试问换后A 、B 间的等效电阻是多少?解析:设想内阻极大的电源加在A 和地(或无穷远)之间,使由A 点流进网络的电流为I ，则由对称性可知,流过AB 的电流为4I.假设拆去此电源,在B 点和地(或无究远)之间加上另一内AB B2/阻极大的电源,使由B 点流出网络的电流强度为I,由对称性可知,流过AB 的电流仍为4I.若把上述电源同时加上,则由叠加原理可知,流过AB 的电流为442I I I+=.设AB 间的等效电阻为R AB ，所以：2AB I IR R =⋅2AB R R =外的其它电阻丝构成的网络的电阻为R0，则整个电阻可以看成是除A 、B 间电阻丝与R0的并联.则:002AB R R RR R R ==+0R R =当A 、B 间的一小段电阻丝换成电阻为4R 时,则:004'0.84AB R RR R R R⋅==+.有一无限平面导体网络，它由大小相同的正六边形网眼组成，如图所示．所有六边形每边的电阻均为R 0． (1)求结点a 、b 间的电阻．(2)如果有电流I 由a 点流入网络，由g 点流出网络，那幺流过de 段电阻的电流I de 为多大?【解析】（1）设有电流I 自a 点流入，流到四面八方无穷远处，那么必有3/I 电流由a 流向c ，有6/I电流由c 流向b .再假设有电流I 由四面八方汇集b 点流出，那么必有6/I 电流由a 流向c ，有3/I电流由c 流向b .将以上两种情况综合，即有电流I 由a 点流入，自b 点流出，由电流叠加原理可知263II I I ac =+=（由a 流向c ） 263I I I I cb =+=（由c 流向b ）因此，a 、b 两点间等效电阻000R I R I R I I U R cb ac AB AB =+==（2）假如有电流I 从a 点流进网络，流向四面八方，根据对称性，可以设 A I I I I ===741B I I I I I I I ======986532应该有I I I A =+B 63因为b 、d 两点关于a 点对称，所以A be deI I I 21=='同理，假如有电流I 从四面八方汇集到g 点流出，应该有 BdeII =''最后，根据电流的叠加原理可知()I I I I I I I I B A B A de dede 61636121=+=+=''+'=如图，有一三角形的无穷长电路其中每个电阻阻值均为R ，求AB 间的等效电阻R AB 。
高中物理竞赛辅导讲义-第12篇-光学
高中物理竞赛辅导讲义
第 12 篇 光学
【知识梳理】 一、光的直线传播 1. 光在均匀媒质中是直线传播的，光在真空中的传播速度为 c=3.00×108m/s，在其他 媒质中的传播速度都小于 c。 2. 影 光射到不透明物体上，在背光面的后方形成一个光线照不到的黑暗区域，就是物体的 影。在这黑暗区域中完全照不到的区域叫做本影，只有一部分光照不到的区域叫做半影。 二、光的反射 1. 光的反射定律：反射光线与入射光线、法线在同一平面上，反射光线和入射光线分 居在法线的两侧，反射角等于入射角 。 2、光路可逆性：当光线逆着原来的反射光线（或折射光线）的方向射到媒质界面时， 必会逆着原来的入射方向反射（或折射）出去，这种性质叫光路可逆性或光路可逆原理。 三、平面镜 1. 平面镜只改变光的传播方向，不改变光的会聚或发散程度。 2. 平面镜成像特点：平面镜成像时，像和物关于镜面对称。 对于实物，平面镜使之成一个等大小的正立虚像；对于虚物，平面镜使之成一个等大 小的正立实像。 四、球面镜 1. 反射面是球面的一部分，这种镜叫球面镜。反射面如果是凹面的，叫做凹面镜，简 称凹镜；反射面是凸面的，叫做凸面镜，简称凸镜。 2. 球面的球心叫曲率中心，镜面的中心叫镜的顶点，顶点与曲率中心的连线称为主光 轴，简称主轴。 3. 球面镜的反射仍遵从反射定律。凹镜对光线有会聚作用，凸镜对光线有发散作用。 4. 一束近主轴的平行光线，经凹镜反射后将会聚于主轴上一点 F，这 F 点称为凹面镜 的焦点。 一束近主轴的平行光线经凸镜反射后将发散， 反向延长线可会聚于主轴上一点 F， 这 F 点称为凸镜的虚焦点。焦点 F 到镜面顶点 O 之间的距离叫做球面镜的焦距 f。可以证 明，对近轴光线，球面镜焦距等于球面半径的一半，即 f = R/2。 5. 球面镜成像作图中，常用的三条特殊光线为： （1）跟主轴平行的入射光线，其反射光线通过焦点。 （2）通过焦点的入射光线，其反射光线与主轴平行。 （3）通过曲率中心的入射光线，其反射光线和入射光线重合，但方向相反。 6. 球面镜成像公式为： 1 1 1 。符号法则为：实为正值，虚为负值。 u v f 7. 球面镜成像规律。 8. 成像放大率。
国中学生物理竞赛真题大全光学
全国中学生物理竞赛真题汇编---光学1.（19Y5）五、（20分）图预19-5中，三棱镜的顶角α为60，在三棱镜两侧对称位置上放置焦距均为30.0cmf=的两个完全相同的凸透镜L1和 L2．若在L1的前焦面上距主光轴下方14.3cmy=处放一单色点光源S，已知其像S'与S对该光学系统是左右对称的．试求该三棱镜的折射率．2.（21Y6）六、（15分）有一种高脚酒杯，如图所示。
杯内底面为一凸起的球面，球心在顶点O下方玻璃中的C点，球面的半径R＝，O到杯口平面的距离为。
在杯脚底中心处P点紧贴一张画片，P点距O点。
这种酒杯未斟酒时，若在杯口处向杯底方向观看，看不出画片上的景物，但如果斟了酒，再在杯口处向杯底方向观看，将看到画片上的景物。
已知玻璃的折射率n1＝，酒的折射率n2＝。
试通过分析计算与论证解释这一现象。
3．（22Y3）三、(18分)内表面只反射而不吸收光的圆筒内有一半径为尺的黑球，距球心为2R处有一点光源S，球心p和光源s.皆在圆筒轴线上，如图所示．若使点光源向右半边发出的光最后全被黑球吸收，则筒的内半径r最大为多少?4．（16F2）（25分）两个焦距分别是1f和2f的薄透镜1L和2L，相距为d，被共轴地安置在光具座上。
1.若要求入射光线和与之对应的出射光线相互平行，问该入射光线应满足什么条件？ 2. 根据所得结果，分别画出各种可能条件下的光路示意图。
5．（17F2）如图1所示，在真空中有一个折射率为ｎ（ｎ＞ｎ0，ｎ0为真空的折射率），半径为ｒ的质地均匀的小球，频率为ν的细激光束在真空中沿直线ＢＣ传播，直线BC与小球球心O的距离为ｌ（ｌ＜ｒ），光束于小球体表面的点Ｃ经折射进入小球（小球成为光传播的介质），并于小球表面的点D又经折射进入真空．设激光束的频率在上述两次折射后保持不变．求在两次折射过程中激光束中一个光子对小球作用的平均力的大小．图16.（17F6）、普通光纤是一种可传输光的圆柱形细丝，由具有圆形截面的纤芯Ａ和包层Ｂ组成，Ｂ的折射率小于Ａ的折射率，光纤的端面和圆柱体的轴垂直，由一端面射入的光在很长的光纤中传播时，在纤芯Ａ和包层Ｂ的分界面上发生多次全反射．现在利用普通光纤测量流体F的折射率．实验方法如下：让光纤的一端（出射端）浸在流体F中．令与光纤轴平行的单色平行光束经凸透镜折射后会聚光纤入射端面的中心Ｏ，经端面折射进入光纤，在光纤中传播．由点Ｏ出发的光束为圆锥形，已知其边缘光线和轴的夹角为α，如图3甲所示．最后光从另一端面出射进入流体Ｆ．在距出射端面ｈ1处放置一垂直于光纤轴的毛玻璃屏Ｄ，在Ｄ上出现一圆形光斑，测出其直径为ｄ1，然后移动光屏Ｄ至距光纤出射端面ｈ２处，再测出圆形光斑的直径ｄ２，如图3乙所示．图31．若已知Ａ和Ｂ的折射率分别为ｎＡ与ｎＢ，求被测流体F 的折射率ｎＦ的表达式．2．若ｎＡ、ｎＢ和α０均为未知量，如何通过进一步的实验以测出ｎＦ的值?7．(18F1)（22分）有一放在空气中的玻璃棒，折射率 1.5n =，中心轴线长45cm L =，一端是半径为110cm R =的凸球面．1．要使玻璃棒的作用相当于一架理想的天文望远镜（使主光轴上无限远处物成像于主光轴上无限远处的望远系统），取中心轴线为主光轴，玻璃棒另一端应磨成什么样的球面？2．对于这个玻璃棒，由无限远物点射来的平行入射光柬与玻璃棒的主光轴成小角度1φ时，从棒射出的平行光束与主光轴成小角度，求21/φφ（此比值等于此玻璃棒望远系统的视角放大率）．8．（19F5）（20分）薄凸透镜放在空气中，两侧焦点和透镜中心的距离相等。
物理竞赛真题分析(全国复赛篇)·光学(16—26届)(共65张PPT)
R2 h02 n R2 n2h02 n2 1
在轴上 x x0 处，无光线通过。
随 h 增大，球面上入
射角 i 增大，当 i 大
于临界角 iC 时，即会
发生全反射，没有折
射光线。与临界角 iC
相这应光的线光的线折有 射线hC与 R轴si线niC的交R 1n点处于xC
n2R
1
n2
n1
狭缝S：光源的光由此进入分光镜，观察到的谱线就是狭缝的像 透镜L1：与狭缝的距离为f1，使由狭缝射来的光束经L1后成为与圆 筒轴平行的平行光束． 分光棱镜：使由L1射来的平行光束中频率不同的单色光经棱镜后成 为沿不同方向出射的平行光束． 透镜L2：使各种单色平行光束经L2 成像在它的焦平面上，形成狭 缝的像（即光谱线）． 观察屏P：位于L2焦平面上，光源的谱线即在此屏上 透镜L3：与P的距离f3，是人眼观察光谱线所用的放大镜（目镜）
v与像长分别为
v fu u- f
y
v u
y0
f
f u y0
平面镜成像时，由于抛物液面最低点上升，物距为
u u h u R2 8f
像距与像长分别为 v -u 两像视角相同要求 y y
u v u - v
y
v u
y0
y0
即
1 2u u2
相距为d，被共轴地安置在光具座上。 1. 若要求入射光线和与之对应的出射光线相互平行，问该
入射光线应满足什么条件？
2. 根据所得结果，分别画出各种可能条件下的光路示意 图。
回顾1；像与物的概念： 发光物体上的每个发光点可视为一个“物点”即“物”。 一个物点上发出的光束，经一系列光学系统作用后，若 成为会聚光束，则会聚点为物的实像点；若成为发散光 束，则其反向延长线交点为物的虚像点；若为平行光束 则不成像。
江苏省南京师范大学附属中学高中物理竞赛讲义教程全集
1.1质点运动的基本概念运动的合成和分解一、图像法例1、蚂蚁离开巢沿直线爬行，它的速度与到蚁巢中心的距离成反此，当蚂蚁爬到距巢中心L1=1m的A点处时，速度是v1=2cm／s，试问：蚂蚁从A点爬到距巢中心L2=2m的B点所需的时间为多少?例2、已知一质点做变加速运动，初速度为v0，其加速度随位移线性减小的关系及加速过程中加速过程中加速度与位移之间的关系满足条件a=a0-ks，式中a为任意位置处的加速度，求当位移为s0是瞬时速度。
二、矢量运算1、矢量加法（矢量合成）（1）平行四边形法则已知两个矢量F1和F2的大小和夹角，求合矢量F合的大小和方向。
2212122cosF F F F Fθ=++212sintancosFF Fθαθ=+（2）三角形法则和多边形法则（接龙法则）（3）矢量式的脚标的接龙法则例如，人在车厢内走动，人相对于地的速度等于人相对于车的速度加上车相对于地的速度。
=+v v vr r r车车人地人地（4）矢量减法将减法变为加法然后再利用接龙法则。
例3：(1)无风的下雨天，小明坐在匀速行驶的车上，发现雨滴沿斜线下落，且与竖直方向成30 夹角，若车速为10m/s，则雨滴下落的速度为多大？(2)小明坐在以10m/s向东匀速行驶的车上，发现雨滴是竖直下落的，若雨滴对地速度为20m/s，则雨滴实际上是如何下落的？三、运动的合成和分解实例1：平抛运动实例2：滚动的车轮边缘上一个点的运动1、运动合成和分解其实就是位移、速度、加速度的合成和分解2、合运动的效果和若干个分运动的总效果相同（等效性）3、实际观察到的运动是合运动，分运动是人们为了方便研究而假想出来的。
四、运动分解的方法1、按效果分解2、正交分解：建立直角坐标系，将运动（位移、速度、加速度）分解在坐标轴方向。
例4、如图所示，在离水面高度为h的岸边，有人用绳子拉船靠岸，若人拉绳的速率恒为v0，试求船在离岸边s距离处时的速度。
例5、如图所示，质点A和质点B同时从A、B两点出发，分别以速度v1沿AB和以速度v2沿BC做匀速直线运动，BC和AB的夹角为α．开始时质点A和质点B相距为l，试求两质点之间的最短距离．例6、如图所示，几辆相同的汽车以等速度v，沿宽为c的直公路行驶，每车宽为b，前后两车头尾间距为a，则人能以最小速度沿一直线穿过马路所用的时间是多少？例7、有五个花样滑冰运动员表演一种节目，表演的动作规定为：开始时五人分别从边长为l的正五边形A 1A2A3A4A5的五个顶点出发，以相同速率v适动，如图所示．运动中A1始终朝着A3、，A3始终朝着A5，A5始终朝着A2，A2始终朝着A4，A4始终朝着A1，问：经过多长时间五人相聚?五、物体系统的运动学连接条件1、刚性杆、绷紧的不可伸长的绳上，各点在同一时刻，具有相同的沿杆、绳的分速度。
物理竞赛试题与解答(光学)
从图中几何关系，有
（1）
若光线1和2在球外相交，有条件 ，考虑到 和 都是锐角，此条件写成
（2）
根据折射定律，又有
（3）
联立式（2）、（3），再利用关系式 ，得
几何光学
7．证明：光线相继经过几个平行分介面的多层介质时，出射光线的方向只与入射方向及两边的折射率有关，与中间各层介质无关。
证：因为界面都是平行的，所以光线在同一层介质中上界面的折射角相等。如图所示，由折射定律有
……………..
由此可见，最后出射光线的方向只与当初入射方向及两边介质的折射率有关。
8．顶角α很小的棱镜称为光楔。证明光楔使垂直入射的光线产生偏向角 ，其中是光楔的折射率。
（2）对波长比 长的红光，n1和n2均小于1.5。对波长比 短的蓝光，n1和n2均大于1.5。所以入射角相同的、波长为 、 和 的三种不同光线经AD面折射后在介质中的折射光线如图2中所示， 折射角最小， 折射角最大。
再讨论一下光线抵达AC面的折射。对于波长 的光，有
即
对于波长 的光
因 ,所以
同理，对于波长 的光
所以此时ABC上被照区变为以DB为对称轴球面上一圆盘。
而当 时，由式（5）可得到n的值，再代回式（2），可以判定， 。即ABC上被照区仍为球面上一圆盘。
当n再大时，又变为球面上一圆环。
当 时，由式（2）和（5）可知， ，ABC上圆环趋于一圆线。这种情况，即QM光线 PA光线，入射光线只有一条光线PA才能经折射再与黑球相切射抵ABC球面，当 时，所有光线都照不到ABC球面上。
江苏省南京师范大学附属中学高中物理竞赛讲义教程全集
1.1质点运动的基本概念 运动的合成和分解一、图像法例1、蚂蚁离开巢沿直线爬行，它的速度与到蚁巢中心的距离成反此，当蚂蚁爬到距巢中心L 1=1m 的A 点处时，速度是v 1=2cm ／s ，试问：蚂蚁从A 点爬到距巢中心L 2=2m 的B 点所需的时间为多少?例2、已知一质点做变加速运动，初速度为v 0，其加速度随位移线性减小的关系及加速过程中加速过程中加速度与位移之间的关系满足条件a=a 0-ks ，式中a 为任意位置处的加速度，求当位移为s 0是瞬时速度。
二、矢量运算1、矢量加法（矢量合成）（1）平行四边形法则已知两个矢量F 1和F 2的大小和夹角，求合矢量F 合的大小和方向。
F =212sin tan cos F F F θαθ=+ （2）三角形法则和多边形法则（接龙法则）（3）矢量式的脚标的接龙法则例如，人在车厢内走动，人相对于地的速度等于人相对于车的速度加上车相对于地的速度。
=+v v v 车车人地人地（4）矢量减法将减法变为加法然后再利用接龙法则。
例3：(1)无风的下雨天，小明坐在匀速行驶的车上，发现雨滴沿斜线下落，且与竖直方向成30 夹角，若车速为10m/s，则雨滴下落的速度为多大？(2)小明坐在以10m/s向东匀速行驶的车上，发现雨滴是竖直下落的，若雨滴对地速度为20m/s，则雨滴实际上是如何下落的？三、运动的合成和分解实例1：平抛运动实例2：滚动的车轮边缘上一个点的运动1、运动合成和分解其实就是位移、速度、加速度的合成和分解2、合运动的效果和若干个分运动的总效果相同（等效性）3、实际观察到的运动是合运动，分运动是人们为了方便研究而假想出来的。
四、运动分解的方法1、按效果分解2、正交分解：建立直角坐标系，将运动（位移、速度、加速度）分解在坐标轴方向。
例4、如图所示，在离水面高度为h的岸边，有人用绳子拉船靠岸，若人拉绳的速率恒为v0，试求船在离岸边s距离处时的速度。
例5、如图所示，质点A和质点B同时从A、B两点出发，分别以速度v1沿AB和以速度v2沿BC做匀速直线运动，BC和AB的夹角为α．开始时质点A和质点B相距为l，试求两质点之间的最短距离．例6、如图所示，几辆相同的汽车以等速度v，沿宽为c的直公路行驶，每车宽为b，前后两车头尾间距为a，则人能以最小速度沿一直线穿过马路所用的时间是多少？例7、有五个花样滑冰运动员表演一种节目，表演的动作规定为：开始时五人分别从边长为l的正五边形A 1A2A3A4A5的五个顶点出发，以相同速率v适动，如图所示．运动中A1始终朝着A3、，A3始终朝着A5，A5始终朝着A2，A2始终朝着A4，A4始终朝着A1，问：经过多长时间五人相聚?五、物体系统的运动学连接条件1、刚性杆、绷紧的不可伸长的绳上，各点在同一时刻，具有相同的沿杆、绳的分速度。
江苏省南京师范大学附属中学物理竞赛讲义-12.6物质的导电性
12.6物质的导电性一、金属导电1、电流强度的微观表达式在加有电压的一段粗细均匀的导体AD上选取截面C，设导体的横截面积为S。
导体每单位体积内的自由电子数为n，每个电子的电荷量为e，电荷的定向移动速率为v 在时间t内，处于相距为vt 的两截面B、C间的所有自由电荷将通过截面C。
在时间t内通过导体某截面的电量为:Q = (vtS) ne形成的电流为：I = Q/t = neSv二、液体导电1、液体金属导电与金属导电类似2、溶液导电法拉第电解定律（参考黑皮的讲解）三、气体导电1、一般情况下，气体不导电。
2、气体导电分自激放电和被激放电。
被激放电是指有其他物质作为电离剂促使空气电离。
自激放电是由于碰撞产生离子，离子在强电场中高速运动，将其它气体分子撞散，产生新的离子，从而发生类似核裂变的连锁反应。
自激放电包括：(1)辉光放电：空气稀薄，分子间距大，离子动能大，易碰撞产生新的离子。
(2)火花放电：由于电场非常大，离子动能大，易碰撞产生新的离子。
(3)弧光放电：由于温度高，离子动能大，易碰撞产生新的离子。
(4)电晕放电：原理与火花放电类似，也是电场很强。
但火花放电是两个带电体之间的，而电晕放电是一个高电压导体表面进行放电，电流较小。
四、半导体1 、半导体的导电性能介于导体和绝缘体之间。
纯净的半导体经常由硅晶体制成。
半导体通常具有热敏和光敏特性，即温度升高，电阻率减小，光线照射，电阻率减小2、半导体的掺杂掺入三价硼，缺少电子，形成空穴。
（P型半导体）掺入五价磷，多余自由电子。
（N型半导体）空穴和自由电子均可导电（载流子），增强了半导体的导电性。
3、二极管一个半导体左右掺入不同杂质，一边为P型，另一边为N型。
在中间的结合部会形成“PN 结”。
在中间，左右的空穴和自由电子进行复合，从而形成无载流子的“空间电荷区”。
因此，可以看成中间变为绝缘体。
在二极管两端加电场：(1)P 连正极，N 连负极。
左边提供正电荷，右边提供负电荷，使空间电荷区变窄甚至消失。
高中物理竞赛讲义完整版
最新高中物理竞赛讲义（完整版）目录最新高中物理竞赛讲义（完整版） (1)第0部分绪言 (5)一、高中物理奥赛概况 (5)二、知识体系 (5)第一部分力＆物体的平衡 (6)第一讲力的处理 (6)第二讲物体的平衡 (8)第三讲习题课 (9)第四讲摩擦角及其它 (13)第二部分牛顿运动定律 (15)第一讲牛顿三定律 (16)第二讲牛顿定律的应用 (16)第二讲配套例题选讲 (24)第三部分运动学 (24)第一讲基本知识介绍 (24)第二讲运动的合成与分解、相对运动 (26)第四部分曲线运动万有引力 (28)第一讲基本知识介绍 (28)第二讲重要模型与专题 (30)第三讲典型例题解析 (38)第五部分动量和能量 (38)第一讲基本知识介绍 (38)第二讲重要模型与专题 (40)第三讲典型例题解析 (53)第六部分振动和波 (53)第一讲基本知识介绍 (53)第二讲重要模型与专题 (57)第三讲典型例题解析 (66)第七部分热学 (66)一、分子动理论 (66)二、热现象和基本热力学定律 (68)三、理想气体 (70)四、相变 (77)五、固体和液体 (80)第八部分静电场 (81)第一讲基本知识介绍 (81)第二讲重要模型与专题 (84)第九部分稳恒电流 (95)第一讲基本知识介绍 (95)第二讲重要模型和专题 (98)第十部分磁场 (107)第一讲基本知识介绍 (107)第二讲典型例题解析 (111)第十一部分电磁感应 (117)第一讲、基本定律 (117)第二讲感生电动势 (120)第三讲自感、互感及其它 (124)第十二部分量子论 (127)第一节黑体辐射 (127)第二节光电效应 (130)第三节波粒二象性 (136)第四节测不准关系 (139)第0部分绪言一、高中物理奥赛概况1、国际（International Physics Olympiad 简称IPhO）① 1967年第一届，（波兰）华沙，只有五国参加。
江苏省南京师范大学附属中学物理竞赛复习预测检测备考讲义-10.6光学例题
10.6费马原理 光学例题费马原理：光线在两点间的实际路径是使所需的传播时间为极值的路径。
在大部分情况下，此极值为极小值。
i i ixt t v ==∑∑i icn v =可得:i in x t c=∑我们定义折射率与路径长的乘积为光程,用l 表示,l nx =,于是,费马原理又可表述为:光线在两点之间的实际路径,是使光程为极值的路径.例1、如图所示，湖中有一小岛A ，A 与直湖岸的距离为d ，湖岸边的一点B ，B 沿湖岸方向与A 点的距离为l ，一人自A 点出发,要到达B 点。
已知他在水中游泳的速度为v 1，在岸上走的速度为v 2，且v 1<v 2，要求他由A 至B 所用的时间最短，此人当如何先择其运动的路线?【解析】根据费马原理,若要人由A 到B 的时间最短,则所走路径应类似于光线所走路径. 这时的水和岸相当于介质,折射率分别为n 1、n 2.设最短时间为如图所示路径.则等效光线由水到岸满足下式:1221sin sin 90v n C v n == 12sin v i v =这时的C 实际上为光线发生全反射的临界角. 所以,我们不难得到:当tan l d C >时,人所走的路径为如图所示的路径.即沿着和垂直于岸的方向成C 的角度游向岸边再在岸上走至B 点.当tan l d C ≤时,人由A 直接游到B 点.【点评】本题若从运动学角度分析,也可以作出解答,但比较麻烦.例1. 一曲率半径R=60cm 的凹面镜水平放置,使其凹面向上,并在其中装满水，水的折射率为43n =，假如装满水后水的的深度比半径R 小得多，试问平行光束成像于何处?【解析】法一:直接用折射定律和反射定律来做,未装水时,平行光束经镜面反射后通过焦点F ′,它离开镜面顶点的距离为30cm,若装有水,当α、β为小角度,由图可知:图16- 12tan sin a a f Rαα=== tan sin afββ==,由折射定律: sin sin 2Rn fβα== 22.52Rf cm n== 法二:用逐次成像法,物体先经过平面折射成像: 1110'n s s -= 再经球面反射成像: 22112's s R +=- 由于是水很浅,所以: 21's s =令1s →∞可得:2'2R s =- 再经平面折射: 3310'ns s -= 32's s =3''22.52Rf s cm n==-=- d26．如图所示，在焦距f=0.15m 的凸透镜L 主轴上有一小光源S ，凸透镜L 另一侧有两个反射面相向放置的平面镜OM 1和OM 2．平面镜OM 1和OM 2彼此垂直，且与透镜L 主轴成450，两平面镜的交线与透镜主轴垂直．已知小光源中心到两平面镜的交线距离SO=O.9m ，透镜到两平面镜的交线距离O 1O=O.3m ，试求： (1)小光源S 在透镜主轴上共成多少个像? (2)小光源S 在透镜主轴外共成多少个像? 分别指出像的虚实、位置及放大率．由折射率为n=1.5的玻璃制成的对称的双凸透镜，在空气中焦距为30cm （1）把它放在平面镜上形成一个折、反射系统，该系统的焦距为多少？（2）在透镜和平面镜之间注满水，水的折射率为4/3，这个系统的折射率为多少？【解析】(1)由于平面镜成像的对称性,从S 发出的光线经透镜折射,再经平面镜反射,相当于从镜中对称的像点S ′发出,经镜中透镜像折折射出的,最后再经透镜的折射成像.因此,它相当于两个相同的透镜组成的密接透镜组,如图所示.该透镜组的焦距为:'152ff cm == (2)当在平面镜与透镜间加水后,相当于原透镜跟一个水透镜(平凹)密接,再经平面镜反射就相当于两个双凸透镜与一个双凹水透镜的密接.在空气中的透镜焦距可按下式求得:12111(1)()f n r r =--双凸透镜及水透镜的折射面曲率半径相同,但凸透镜和凹透镜半径的符号相反.设玻璃双凸透镜焦距为f 1,水双凹透镜的焦距为f 2 (均对周围介质为空气来说).则:122111f n f n -=-- 式中n 1、n 2分别为玻璃和水的折射率. 密接透镜组等效焦距为f,则有: 1211111f f f f =++ 21111(2)1n f n -=-- 将n 1=1.5,n 2=43,f 1=30cm 代入得: f=22.5cm【答案】15cm ,22.5cm.【总结】此题要用到透镜的焦距公式,密接透镜的有关知识.此题非常困难,困难的原因就在于学生对这一块内容不熟悉,平时在这方面的练习不够.好象有点问题:中间的凹透镜的两个折射面的曲率均应为r 2?,答案题目把一个面的曲率看成是一个是r 1,另一个面的曲率看成是r 2,好象是值得研究了.研究的思路是:用四次平面折射来看看.例10、如图5所示，两个薄凸透镜12L L 、与一个平面镜及物屏共轴放在光具座上，每个凸透镜的两表面的曲率半径均为R ，12L L 、的焦距分别为12f f 、，它们之间的距离用d 表示，且1L 更靠近物屏。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
10.6费马原理 光学例题费马原理：光线在两点间的实际路径是使所需的传播时间为极值的路径。
在大部分情况下，此极值为极小值。
i i ixt t v ==∑∑i icn v =可得:i i n xt c=∑我们定义折射率与路径长的乘积为光程,用l 表示,l nx =,于是,费马原理又可表述为:光线在两点之间的实际路径,是使光程为极值的路径.例1、如图所示，湖中有一小岛A ，A 与直湖岸的距离为d ，湖岸边的一点B ，B 沿湖岸方向与A 点的距离为l ，一人自A 点出发,要到达B 点。
已知他在水中游泳的速度为v 1，在岸上走的速度为v 2，且v 1<v 2，要求他由A 至B 所用的时间最短，此人当如何先择其运动的路线?【解析】根据费马原理,若要人由A 到B 的时间最短,则所走路径应类似于光线所走路径. 这时的水和岸相当于介质,折射率分别为n 1、n 2.设最短时间为如图所示路径.则等效光线由水到岸满足下式:1221sin sin90v n Cv n ==o12sin v i v =这时的C 实际上为光线发生全反射的临界角. 所以,我们不难得到:当tan l d C >时,人所走的路径为如图所示的路径.即沿着和垂直于岸的方向成C 的角度游向岸边再在岸上走至B 点.当tan l d C ≤时,人由A 直接游到B 点.【点评】本题若从运动学角度分析,也可以作出解答,但比较麻烦.例1. 一曲率半径R=60cm 的凹面镜水平放置,使其凹面向上,并在其中装满水，水的折射率为43n =，假如装满水后水的的深度比半径R 小得多，试问平行光束成像于何处? 【解析】法一:直接用折射定律和反射定律来做,未装水时,平行光束经镜面反射后通过焦点F ′,它离开镜面顶点的距离为30cm,若装有水,当α、β为小角度,由图可知:l图16- 12tan sin a a f R αα=== tan sin afββ==,由折射定律: sin sin 2Rn fβα== 22.52Rf cm n== 法二:用逐次成像法,物体先经过平面折射成像:1110'n s s -= 再经球面反射成像:22112's s R+=- 由于是水很浅,所以:21's s =令1s →∞可得:2'2R s =- 再经平面折射:3310'ns s -= 32's s =3''22.52Rf s cm n==-=- d(b)(a)26．如图所示，在焦距f=0.15m 的凸透镜L 主轴上有一小光源S ，凸透镜L 另一侧有两个反射面相向放置的平面镜OM 1和OM 2．平面镜OM 1和OM 2彼此垂直，且与透镜L 主轴成450，两平面镜的交线与透镜主轴垂直．已知小光源中心到两平面镜的交线距离SO=O.9m ，透镜到两平面镜的交线距离O 1O=O.3m ，试求：(1)小光源S 在透镜主轴上共成多少个像? (2)小光源S 在透镜主轴外共成多少个像? 分别指出像的虚实、位置及放大率．由折射率为n=1.5的玻璃制成的对称的双凸透镜，在空气中焦距为30cm（1）把它放在平面镜上形成一个折、反射系统，该系统的焦距为多少？（2）在透镜和平面镜之间注满水，水的折射率为4/3，这个系统的折射率为多少？【解析】(1)由于平面镜成像的对称性,从S 发出的光线经透镜折射,再经平面镜反射,相当于从镜中对称的像点S ′发出,经镜中透镜像折折射出的,最后再经透镜的折射成像.因此,它相当于两个相同的透镜组成的密接透镜组,如图所示.该透镜组的焦距为:'152ff cm == (2)当在平面镜与透镜间加水后,相当于原透镜跟一个水透镜(平凹)密接,再经平面镜反射就相当于两个双凸透镜与一个双凹水透镜的密接.在空气中的透镜焦距可按下式求得:12111(1)()f n r r =--双凸透镜及水透镜的折射面曲率半径相同,但凸透镜和凹透镜半径的符号相反.设玻璃双凸透镜焦距为f 1,水双凹透镜的焦距为f 2 (均对周围介质为空气来说).则:122111f n fn -=-- 式中n 1、n 2分别为玻璃和水的折射率. 密接透镜组等效焦距为f,则有:1211111f f f f =++ 21111(2)1n f n -=-- 将n 1=1.5,n 2=43,f 1=30cm 代入得: f=22.5cm【答案】15cm ,22.5cm.【总结】此题要用到透镜的焦距公式,密接透镜的有关知识.此题非常困难,困难的原因就在于学生对这一块内容不熟悉,平时在这方面的练习不够.好象有点问题:中间的凹透镜的两个折射面的曲率均应为r 2?,答案题目把一个面的曲率看成是一个是r 1,另一个面的曲率看成是r 2,好象是值得研究了.研究的思路是:用四次平面折射来看看.例10、如图5所示，两个薄凸透镜12L L 、与一个平面镜及物屏共轴放在光具座上，每个凸透镜的两表面的曲率半径均为R ，12L L 、的焦距分别为12f f 、，它们之间的距离用d 表示，且1L 更靠近物屏。
物屏上开有一个箭形小孔，若左右移动物屏，同时改变d 的大小，发现在物屏上可以多次得到倒立的清晰像，且左右移动平面镜对像无影响。
问在物屏上能有几次得到这样的像，定量分析得到这些像的条件（在透镜面有部分光线发生反射，不考虑2次以上的反射成像）。
物屏上可以得到4个像。
1、凸透镜L 1的后有面反射达到自准直成像，光路如图，设物屏到L 1的距离为u 1.11/1/1/1f R u =-得 )/(111f R Rf u +=此情况一定能通过移动物屏观察到像2、L 2前表面反射达到自准直成像，光路如图，设物屏到L 1的距离为u 212/1)/(1/1f R d u =++ )/()(112f R d f R d u -++=此情况出现的条件为 R f d ->13、L 2后表面反射达到自准直成像，光路如图，设对L 2成像时的物距为u ，物屏与L 1距离为u 3，则2/1/1/1f R u =- 311/1/()1/u d u f +-=联立二式 )/(/)/(2212213f R Rf f d f R Rf d f u +--+-= 此情况出现的条件为： )/()/(22221f R Rf d f R Rf f d +<+->或 4、由平面镜反射达到自准直成像，光路如图，设物屏到L 1的距离为u 4124/1)/(1/1f f d u =-+)/()(12124f f d f f d u ---= 出现此情况的条件为： 221f d f f d <+>或例15、在焦距为20.00cm 的薄凸透镜的主轴上离透镜中心30.00cm 处有一小发光点S ，一个厚度可以忽略的光楔C （顶角a 很小的三棱镜）放在发光点与透镜之间，垂直于轴，与透镜的距离为2.00cm ，如图1-5-54所示，设光楔的折射率n=1.5，楔角a =0.028弧度。
在透镜另一侧离透镜中心46.25cm 处放一平面镜M ，其反射面向着透镜并垂直于主轴。
问最后形成的发光点的像相对发光点的位置在何处（只讨论近轴光线，小角度近似适用。
在分析计算过程中应作出必要的光路图）？分析:这是一个光具成像问题，厚度可忽略的光楔在成像过程中的作用相当于一使光线产生偏折的薄平板，平面镜使光线反射后再次经凸透镜成像，在这一过程中，我们再根据折射定律、透镜成像公式及有关数学近似进行一系列计算，就可得出最后结果。
解:共有五次成像过程。
（1）光楔使入射光线偏折，其偏向角（出射光线与入射光C LM S 图1-5-541i 1i '2i 2i 'δa线方向的夹角）用δ表示，由图1-5-55可知11sin sin i n i '=，22sin sin i n i '=，α='+'21i i 对近轴光线，1i 很小，有11i n i '=； 因a 也很小，同样有22ni i =' 故有 )()(2211i i i i -'+'-=δ αα)1(21-=-'+=n i i 代入数值，得rad rad 014.0028.0)15.1(=⨯-=δ 因δ与入射角大小无关，各成像光线经光楔后都偏折同样角度δ。
又因光楔厚度可忽略，所以作光路图时可画成一使光线产生偏折角δ的薄平板，图1-5-56。
光点S 经光楔成一虚像点1S '。
对近轴光线，1S '在S 正上方，到S 的距离为h ，离光楔距离cm l 00.28=。
l n l h αδ)1(-== 代入数据，得cm h 39.0=（2）1S '为透镜L 的实物，像点2S '的位置可由下式求出f u 111=+υ 以u=30.00cm,f=20.00cm 代入，得cm 00.60=υ将1S S '视为与光轴垂直的小物，由透镜的放大率公式u M υ=1 可求得SS 图1-5-56图1-5-57cm h M h 78.012==' 即像点2S '在光轴下方与光轴的距离为0.78cm ，与透镜的中心距离为60.00cm 处，图1-5-57。
（3）2S '在平面镜之后，对平面镜是虚物，经平面镜成像，像点3S '与2S '对称于平面镜（图1-5-57）cm d 75.13=cm h h 78.023='=' （4）3S '作为透镜的实物，经透镜折射后再次成像，设像点2S ''，2S ''及3S '与L 的距离分别为和u '，则cm u 50.32='，cmf u u f 00.52)(=-'='υ2S ''在透镜左侧，主轴上方，图1-5-58。
cm h M h 25.1222='='' （5）第二次经透镜折射后成像的光线还要经光楔偏折，再次成像，像点1S ''在2S ''正下方，离光楔距离为50cm ，离光轴的距离为（见图1-5-58）。
cm l h 70.0='=∆δcm h h h 55.02=∆-''=' 像点1S ''在光轴上的垂足与S 的距离为cm l l s 00.22=-'=∆即最后的像点在发光点S 左侧光轴上方，到光轴的距离为0.55cm ，其在光轴上的垂足到S 的距离为22.00cm 。
图1-5-58。