过抛物线的焦点的弦的一般性质
抛物线焦点弦的性质结论归纳与应用

抛物线焦点弦的性质结论归纳与应用抛物线焦点弦的性质结论归纳与应用如下:
首先,抛物线焦弦的性质决定了抛物线的几何特性。
抛物线的焦弦公式是y=4ax,这个式子定义了抛物线的性质,一般在其中,a是抛物线的两个焦点之间的距离,因此可以用这个性质来确定抛物线的几何特性。
其次,抛物线焦弦的性质也可以应用于统计学中。
在统计学中,抛物线焦弦是一种线性回归的拟合方法。
它能推断出两个变量之间的相关性,从而用于市场营销、供应链管理以及其他方面的数据预测和分析研究。
最后,抛物线焦弦的性质也可以用于科学研究中。
以抛物线焦弦为模型,可以表达出粒子动力学中问题的数学解。
例如在分子动力学中,用抛物线焦弦可以解释温度和粒子冲突频率之间的关系,从而为科学研究提供新的指导思想。
抛物线焦弦的性质使抛物线变得更加精妙。
它对于几何的解决、统计的分析以及科学研究的指导都具有重要的意义,为我们探究物理现象提供了新的可能性。
过焦点的抛物线弦的结论

过焦点的抛物线弦的结论
过焦点的抛物线弦的结论是:对于任意一条过抛物线焦点的弦,其两个端点和焦点构成的三角形总是一个等腰三角形。
抛物线是一个特殊的曲线,其定义是到焦点和直线的距离相等的点的轨迹。
抛物线有一个重要的性质,即焦点到抛物线上任意一点的距离等于该点到抛物线的准线的垂直距离。
考虑一条过抛物线焦点的弦,设其两个端点分别为A和B,焦点为F。
我们需要证明三角形ABF是一个等腰三角形。
首先,我们可以利用抛物线的性质得到焦点到A点和B点的距离相等,即AF = BF。
这是因为F是焦点,所以FA和FB到准线的垂直距离相等,而根据三角形AFB,我们知道FA=FB。
其次,我们注意到焦点到抛物线上任意一点的距离等于该点到抛物线准线的垂直距离。
假设弦AB与焦点F的连线与抛物线的准线相交于点C,则可以得到FA = FC以及FB = FC。
综上所述,我们得出结论:对于任意一条过抛物线焦点的弦AB,其两个端点和焦点F构成的三角形ABF是一个等腰三角形。
抛物线的焦点弦性质

法二:由题知AB不与x轴平行 p 设AB方程为x my ,(m R) 2 y 2 2 px p 2 p y 2 p (my ) 2 x my 2 y
即:y 2 pmy p 0
2 2
A
y1 y2 p (定值)
2
O
F B
1 当AB x轴时,
O B
F
x
20 AB斜率存在时设为k,(k 0)
2
y p 2 py 2 消元得y 2 ( p )即y p2 0 k 2 k 2 2 2 y1 y1 p 2 y1 y2 - p ;x1 x2 2 p 2 p 4
p 则直线AB方程为y=k(x- ) 代入抛物线方程y2 2 px 2
1 同理, k
以代k得B(2pk2, -2pk) .
1 2 x p ( k ) 0 k2 y p( 1 k ) 0 k
1 1 2 k 2 (k ) 2 k k
2
x0 y0 2 ( ) 2 p p
即 y02 = px0-2p2,
2 px y1 2 px1 y1 y2 2 px 2 px1 y y y1 y1 y2 y1 y2 y1 y2 y1 y2
2 2 px 4 p 2 y1 2 px1 , y1 y2 4 p2 y y1 y2 y1 y2
2 p | y1 y2 | 4 p2
当且仅当|y1|=|y2|=2p时,等号成立.
例3. A、B是抛物线 y2 = 2px(p>0)上的两点,且OA⊥OB, (5)求O在AB上的射影M轨迹方程. y (5)法一:设M(x3, y3), 则 kOM 3 x3 x
抛物线的焦点弦-经典性质及其证明过程
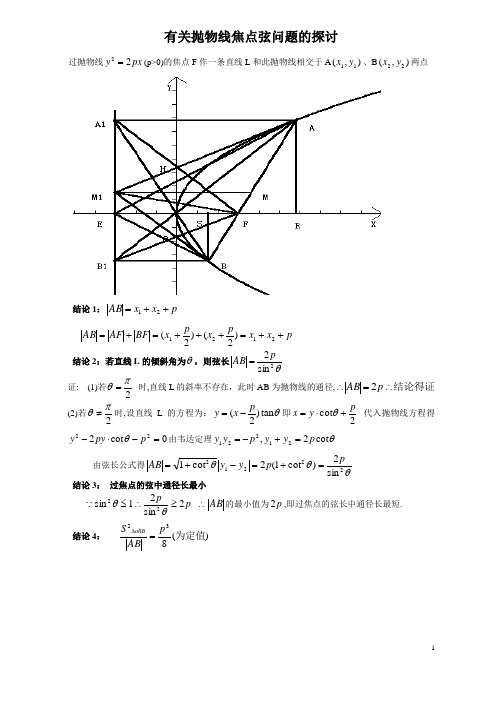
有关抛物线焦点弦问题的探讨过抛物线px y 22=(p>0)的焦点F 作一条直线L 和此抛物线相交于A ),(11y x 、B ),(22y x 两点结论1:p x x AB ++=21p x x px p x BF AF AB ++=+++=+=2121)2()2( 结论2:若直线L 的倾斜角为θ,则弦长θ2sin 2pAB =证: (1)若2πθ= 时,直线L 的斜率不存在,此时AB 为抛物线的通径,结论得证∴=∴p AB 2(2)若2πθ≠时,设直线L 的方程为:θtan )2(p x y -=即2cot py x +⋅=θ 代入抛物线方程得0cot 222=-⋅-p py y θ由韦达定理θcot 2,21221p y y p y y =+-=由弦长公式得θθθ22212sin 2)cot 1(2cot1pp y y AB =+=-+= 结论3: 过焦点的弦中通径长最小p p2sin 21sin 22≥∴≤θθ ∴AB 的最小值为p 2,即过焦点的弦长中通径长最短. 结论4: )(832为定值p AB S oAB =∆()8sin 2sin sin 2221sin 21sin 21sin 21sin 2132220P AB S p p p AB OF BF AF OF AF OF BF OF S S S OAB AF OBF OAB =∴=⋅⋅⋅=⋅⋅=+⋅=⋅⋅+⋅⋅=+=∆∆∆∆θθθθθϑθ结论5: (1) 221p y y -= (2) x 1x 2=42p证44)(,2,22222121222211P Py y x x p y x p y x ==∴== 结论6:以AB 为直径的圆与抛物线的准线相切证:设M 为AB 的中点,过A 点作准线的垂线AA 1, 过B 点作准线的垂线BB 1, 过M 点作准线的垂线MM 1,由梯形的中位线性质和抛物线的定义知 222111AB BFAF BB AA MM =+=+=故结论得证结论7:连接A 1F 、B 1 F 则 A 1F ⊥B 1FFA A FO A FO A F AA OF AA AFA F AA AF AA 11111111//,∠=∠∴∠=∠∴∠=∠∴=同理︒=∠∴∠=∠901111FB A FB B FO B ∴A 1F ⊥B 1 F 结论8:(1)AM 1⊥BM 1 (2)M 1F ⊥AB (3)BF AF FM ⋅=21(4)设AM 1 与A 1F 相交于H ,M 1B 与 FB 1相交于Q 则M 1,Q ,F ,H 四点共圆 (5)2121214M M B M AM =+证:由结论(6)知M 1 在以AB 为直径的圆上∴ AM 1⊥BM 111FB A ∆为直角三角形, M 1 是斜边A 1 B 1 的中点111111111AFA F AA F A M FA M F M M A ∠=∠∠=∠∴=∴︒=∠=∠+∠9011111M AA M FA F AA ︒=∠+∠∴90111FM A AFA∴M 1F ⊥ABBF AF F M ⋅=∴21 AM 1⊥BM 1 F B F A 90111⊥︒=∠∴ 又B AM︒=∠∴90FB A 11 所以M 1,Q ,F,H 四点共圆,22121AB B M AM =+()()()2121211242MM MM BB AABFAF ==+=+=结论9: (1)、A O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3)设直线AO 与抛物线的准线的交点为B 1,则BB 1平行于X 轴(4)设直线BO 与抛物线的准线的交点为A 1,则AA 1平行于X 轴证:因为p y p y k y p p y y x y k oB oA 2212111122,221-=-====,而221p y y -=所以122222oB oA k p y y ppk =-=-=所以三点共线。
抛物线“焦点弦的性质”及解题策略

03
解题策略
利用焦点弦性质解题
焦点弦性质
对于抛物线上的任意一点P,其到焦 点F的距离等于到准线的距离。利用这 一性质,可以快速找到与焦点弦相关 的点P的坐标。
解题方法
利用焦点弦性质,可以求出点P的坐 标,进而求出与焦点弦相关的其他量, 如弦长、面积等。
在抛物线中,焦点弦的倾斜角可以通过轴线的倾斜角和该弦与轴线的夹角的补角之和(或差)来计算 。这个补角等于该弦与轴线的夹角的两倍。当焦点弦与轴线垂直时,其倾斜角等于轴线的倾斜角。
焦点弦的倾斜角
解题策略
根据题目给出的条件,选择适当的方法计算焦点弦的长 度、中点坐标或倾斜角。
熟悉抛物线的定义和性质,理解焦点弦的意义和特点。
02
焦点弦的性质
焦点弦的长度
总结词
焦点弦的长度等于通径的长度,等于焦准距的平方根。
详细描述
在抛物线中,焦点弦是指通过焦点的弦,其长度可以通过通径的长度来计算。 通径是过焦点的最短的弦,其长度等于焦准距的平方根。当焦点弦与抛物线的 轴线不垂直时,其长度还会受到其他因素的影响。
焦点弦的中点坐标
总结词
焦点弦的中点坐标等于焦点坐标加上弦中点与轴线的垂直距 离。
详细描述
在抛物线中,焦点弦的中点坐标可以通过焦点坐标和弦中点 与轴线的垂直距离之和来计算。这个垂直距离等于弦的长度 的一半乘以该弦与轴线的夹角的正切值。
焦点弦的倾斜角
总结词
焦点弦的倾斜角等于轴线的倾斜角加上或减去该弦与轴线的夹角的补角。
详细描述
解题方法
利用代数方法,可以建立方程组、不等式组等,进而求解与抛物线相关的问题。在解题过程中,需要注意方程组 的解法、不等式的性质等。
过抛物线的焦点的弦的一般性质

《国际财务管理》章后练习题及答案第一章【题1—1】某跨国公司A,2006年11月兼并某亏损国有企业B。
B企业兼并时账面净资产为500万元,2005年亏损100万元(以前年度无亏损),评估确认的价值为550万元。
经双方协商,A跨国公司可以用以下两种方式兼并B企业。
甲方式:A公司以180万股和10万元人民币购买B企业(A公司股票市价为3元/股);乙方式:A公司以150万股和100万元人民币购买B企业。
兼并后A公司股票市价3.1元/股。
A公司共有已发行的股票2000万股(面值为1元/股)。
假设兼并后B企业的股东在A公司中所占的股份以后年度不发生变化,兼并后A公司企业每年未弥补亏损前应纳税所得额为900万元,增值后的资产的平均折旧年限为5年,行业平均利润率为10%。
所得税税率为33%。
请计算方式两种发方式的差异。
【题1—1】答案(1)甲方式:B企业不需将转让所得缴纳所得税;B 企业2005年的亏损可以由A公司弥补。
A公司当年应缴所得税=(900-100)×33%=264万元,与合并前相比少缴33万元所得税,但每年必须为增加的股权支付股利。
(2)乙方式:由于支付的非股权额(100万元)大于股权面值的20%(30万元)。
所以,被兼并企业B 应就转让所得缴纳所得税。
B企业应缴纳的所得税=(150 ×3 + 100- 500)×33% = 16.5(万元)B企业去年的亏损不能由A公司再弥补。
(3)A公司可按评估后的资产价值入帐,计提折旧,每年可减少所得税(550-500)/5×33%=3.3万元。
【题1—2】东方跨国公司有A、B、C、D四个下属公司,2006年四个公司计税所得额和所在国的所得税税率为:A公司:500万美元 33%B公司:400万美元 33%C公司:300万美元 24%D公司:-300万美元 15%东方公司的计税所得额为-100万美元,其所在地区的所得税税率为15%。
过抛物线焦点弦的性质及其应用

过抛物线焦点弦的性质及其应用过抛物线焦点的弦是每年高考的热点内容,能够迅速准确的将其解出,是同学们的共同愿望,本文从课本出发,引入两个重要公式,希望对大家有所帮助。
公式一、设AB 是过抛物线y 2=2px 的焦点的弦,若A (x A ,y A ),B(x B ,y则|AB |=x A +x B +p|AF |= x A +2p|BF|= x B +2p 所以|AB |=|AF|+|BF|=x A +x B +p例1、过抛物线y 2=4x 的焦点F 做直线l 与抛物线交于P (x 1,y 1),Q(x 2,y 2)两点,x 1+x 2=6,则|PQ |=_____(2007年广东高考模拟)解:由题可得p=2 ,代入公式一得|PQ|=x 1+x 2+p=6+2=8公式二、设AB 是过抛物线y 2=2px 的焦点F 的弦,弦AB的倾斜角为θ,则 (i )θcos 1p |FA |-=θc o s 1p |FB |+=(ii)|证明:在Rt △AFD ∵||||cos AF FD ==θ∴θθcos 2cos 2pp x x A A +=- 即 θθcos 1)cos 1(2-+=px A∴ϑϑθθcos 1cos 1)cos 1(2}cos 1(22||-=--++=+=p pp p AF x A 同理可得 θcos 1||+=pFBϑϑϑϑϑϑϑϑsin cos 22212)cos 1)(cos 1()cos 1()cos 1(cos 1cos 1||||||p p p p pp FB FA AB =-=-+++-=-++=+=例2、抛物线y 2=4x 焦点弦被焦点分成长是m 和n 两部分,则m 和n 的关系是( )A 、m+n=mnB 、m+n=4C 、mn=4D 、无法确定 解:由已知得p=2,代入公式二可得 ϑcos 12-=m ϑcos 12+=n则m+n=ϑsin24mn=ϑϑϑsin 24)cos 1)(cos 1(4=-+ 所以m+n=mn 故选A例3、如图所示 ,设O 为抛物线的顶点,F 为焦点且PQ 为过点F 的弦,已知|OF |=a ,|PQ|=b ,求△OPQ 的面积。
抛物线的焦点弦_经典性质及其证明过程

AB1 2 12 3有关抛物线焦点弦问题的探讨过抛物线 y 2= 2 px (p>0)的焦点 F 作一条直线 L 和此抛物线相交于 A (x , y ) 、B (x , y ) 两点1122结论 1: AB = x 1 + x 2 + pAB =AF + BF = (x + p ) + (x + p) = x + x + p1 2 2 21 22 p结论 2:若直线 L 的倾斜角为θ,则弦长 AB π=sin 2 θ证: (1)若θ= 时,直线 L 的斜率不存在,此时 AB 为抛物线的通径,∴ AB 2= 2 p ∴结论得证π(2)若θ≠时,设直线 L 的方程为: y = (x -2p ) tan θ即 x = y ⋅ cot θ+ p2 2代入抛物线方程得y 2 - 2 py ⋅ cot θ- p 2 = 0 由韦达定理 y y = - p 2 , y + y = 2 p cot θ 由弦长公式得 AB =y 1 - y 2 = 2 p (1 + cot 2θ) =2 p sin 2 θ结论 3: 过焦点的弦中通径长最小sin 2 θ≤ 1∴2 psin 2 θ≥ 2 p ∴ AB 的最小值为 2 p ,即过焦点的弦长中通径长最短.结论 4:S 2 ∆oAB = p (为定值) 8 1 + cot 2 θAF + BF 222 212 2 1 S= S+ S= 1OF ⋅ BF ⋅ sin θ+ 1OF ⋅ AF ⋅ sin ϑ ∆OAB∆OBF=1⋅ (+∆ 0 AF) 2 2 θ= 1 ⋅ ⋅ θ= 1 ⋅ ⋅ 2 p ⋅θ=p 2OF2 S 2AF= P 3 8 BFsin OF AB 2sin2 2 sin 2 θsin2 sin θ结论 5: (1) y 1 y 2 = - p p2 (2) x 1x 2=4y 2 y 2 ( y y )2 P 2证 x = 1 , x = 2 ,∴ x x =1 2 = 1 2 p 22 p1 2 4P 2 4结论 6:以 AB 为直径的圆与抛物线的准线相切证:设 M 为 AB 的中点,过 A 点作准线的垂线 AA 1, 过 B 点作准线的垂线 BB 1,过 M 点作准线的垂线 MM 1,由梯形的中位线性质和抛物线的定义知MM 1 == = 2 2 2故结论得证结论 7:连接 A 1F 、B 1 F 则 A 1F ⊥ B 1FAA 1 = AF ,∴∠AA 1 F = ∠AFA 1 AA 1 // OF ∴∠AA 1 F = ∠A 1 FO ∴∠A 1 FO = ∠A 1 FA同理∠B 1 FO = ∠B 1 FB ∴∠A 1 FB 1 = 90︒∴A 1F ⊥ B 1 F结论 8:(1)AM 1 ⊥ BM 1(2)M 1F ⊥ AB(3) M 1 F = (4) 设 AM 1 与 A 1F 相交于 H ,M 1B 与 FB 1 相交于 Q (5) AM 1+ M 1 B = 4 M 1 MAF ⋅ BF则 M 1,Q ,F ,H 四点共圆证:由结论(6)知 M 1 在以 AB 为直径的圆上∴ AM 1 ⊥ BM 1∆A 1 FB 1 为直角三角形, M 1 是斜边 A 1 B 1 的中点∴ A 1 M 1 = M 1 F ∴∠M 1 FA 1 = ∠M 1 A 1 F ∠AA 1 F = ∠AFA 1∠AA 1 F + ∠FA 1 M 1 = ∠AA 1 M 1 = 90︒∴M 1F ⊥ AB∴∠AFA 1 + ∠A 1 FM 1 = 90︒∴ M F 2= AF ⋅ BF AM 1 ⊥ BM 1 ∴∠AM 1 B = 90︒又 A 1F ⊥ B 1F∴∠A 1FB 1 = 90︒所以 M 1,Q ,F,H 四点共圆, AM 1 + M 1 B = AB2= ( A F + BF )2= ( AA+ BB 1 )2= (2 MM )2= 4 MM 2结论 9: (1) A 、O 、B 1 三点共线 (2)B ,O ,A 1 三点共线(3) 设直线 AO 与抛物线的准线的交点为 B 1,则 BB 1 平行于 X 轴 (4) 设直线 BO 与抛物线的准线的交点为 A 1,则 AA 1 平行于 X 轴AA 1 + BB 1 AB1 21FA FB AF FA FB BF FA B 1 E EA 1 AF BFAE BEAF BF 时⎪ y 1 y 1 1证:因为 k oA = x = y 2 = 2 p , k yoB 1 = y 2 - p = - 2 y 2 p ,而 y 1 y 2 = - p 21 1 12 p2 所以 k oA 结论 10:+=2 p- p 2y 2 1 = = - 2 y 2 p2 p= k oB 1所以三点共线。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
过抛物线的焦点的弦的一般性质
不妨设抛物线方程为)0(22>=p px y ,则焦点)0,2(p F ,准线l 的方程:2p x -=. 过焦点F 的直线交抛物线于A(x 1,y 1)、B(x 2,y 2)两点,又作AA 1⊥l , BB 1⊥l ,垂足分别为A 1、B 1.
基本概念:
1.若AB 垂直于抛物线的对称轴,则称线段AB 为抛物线的通径。
|AB|= .
2.设P(x 0,y 0)是抛物线y 2=2px(p>0)上的一点,则P 到抛物线焦点F 的距离|PF|称为P 点
的焦半径。
|PF|= ;直线AB 经过抛物线y 2=2px(p>0)的焦点,且与抛物线相
交于A(x 1,y 1)、B(x 2,y 2)(AB 则为抛物线的焦点弦).
结论1:4221p x x =⋅ (定值),2
2212k p p k x x +=+. 结论2:221p y y -=⋅ (定值),k p y y 221=
+.
结论3:(1)弦长p x x p x p x BB AA BF AF AB ++=+++=+=+=2121112
2||||||||||. (2) 若AB 所在的直线的倾斜角为α,则 α
2sin 2||p AB =.
结论4:若此焦点弦AB 被焦点F 分成n m ,两部分,则p n m 211=+.
结论5:抛物线)0(22>=p px y 的焦点弦中通径最小.
结论6:以焦点弦AB 为直径的圆与抛物线的准线l 相切.
结论7:以抛物线焦半径||AF 为直径的圆与y 轴相切.
结论8:F B F A 11⊥.
结论9:若M 为11B A 的中点,则AB MF ⊥.
结论10:在梯形AA 1B 1B 中,两对角线AB 1与BA 1相交于点抛物线顶点O .。
