《工程力学(工程静力学与材料力学)(第3版)》习题解答：第18章 聚合物的粘弹性行为
工程力学-静力学与材料力学课后习题答案
工程力学课后题答案1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB杆的受力图。
(a)B(b)(c)(d)A(e)A(a)(b)A(c)A(d)A(e)(c)(a)解：1-3 试画出以下各题中AB 梁的受力图。
解：(e)BB(a)B(b)(c)F B(a)(c)F (b)(d)(e)(a)F (b)W(c)1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：(d)D(e)F Bx(a)(b)(c)(d)D(e)W(f)(a)D(b)B(c)BFDF CWBF F BC1-5 试画出以下各题中指定物体的受力图。
(a) 结点A，结点B；(b) 圆柱A和B及整体；(c) 半拱AB，半拱BC及整体；(d) 杠杆AB，切刀CEF及整体；(e) 秤杆AB，秤盘架BCD及整体。
解：(a)(b)(c)(d)ATF BAF(b)(e)(c)(d)(e)C AA C’CDDB2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC ox BC ACAC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：(2)F 1F FDF F AF D211 1.1222D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第3章 力系的平衡
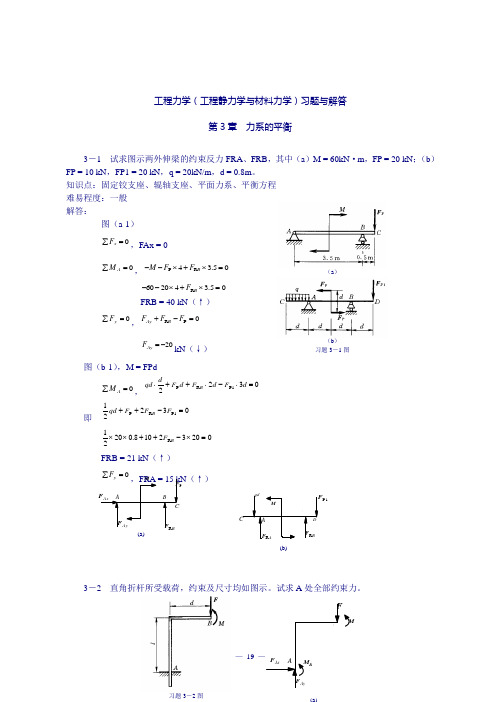
工程力学（工程静力学与材料力学）习题与解答第3章 力系的平衡3－1 试求图示两外伸梁的约束反力FRA 、FRB ，其中（a ）M = 60kN ·m ，FP = 20 kN ；（b ）FP = 10 kN ，FP1 = 20 kN ，q = 20kN/m ，d = 0.8m 。
知识点：固定铰支座、辊轴支座、平面力系、平衡方程 难易程度：一般 解答：图（a-1） 0=∑x F ，FAx = 00=∑A M ，05.34R P =⨯+⨯--B F F M 05.342060R =⨯+⨯--B F FRB = 40 kN （↑）=∑y F ，0P R =-+F F F B Ay20-=Ay F kN （↓）图（b-1），M = FPd 0=∑A M ，03221P R P =⋅-⋅++⋅d F d F d F dqd B即 032211P R P =-++F F F qd B 02032108.02021R =⨯-++⨯⨯B FFRB = 21 kN （↑）=∑y F ，FRA = 15 kN （↑）3－2 直角折杆所受载荷，约束及尺寸均如图示。
试求A 处全部约束力。
A MB Ay F B R F CAx F PF(a) M A B B R F A R F P 1F C qdBD(b)（a ）（b ） 习题3－1图FMB习题3－3图sF W A F ABF BF AN F(a)知识点：固定端约束、平面力系、平衡方程 难易程度：一般 解答： 图（a ）： 0=∑x F ，0=Ax F=∑y F ，=Ay F （↑）0=∑A M ，0=-+Fd M M AM Fd M A -=3－3 图示拖车重W = 20kN ，汽车对它的牵引力FS = 10 kN 。
试求拖车匀速直线行驶时，车轮A 、B 对地面的正压力。
知识点：固定端约束、平面力系、平衡方程 难易程度：一般解答： 图（a ）：0)(=∑F A M 08.214.1NB S =⨯+⨯-⨯-F F W6.13NB =F kN=∑y F ，4.6NA =F kN3－4 图示起重机ABC 具有铅垂转动轴AB ，起重机重W = 3.5kN ，重心在D 。
《工程力学(工程静力学与材料力学)(第3版)》习题解答：第1章 静力学基本概念
(a) (b)习题1-1图FACBAxF Ay F 工程力学（工程静力学与材料力学）第1章 静力学基本概念1－1 图a 、b 所示，Ox1y1与Ox2y2分别为正交与斜交坐标系。
试将同一方F 分别对两坐标系进行分解和投影，并比较分力与力的投影。
知识点：力的分力与投影 难易程度：易 解答：（a ），图（c ）：11 sin cos j i F ααF F += 分力：11 cos i F αF x = ， 11 sin j F αF y =投影：αcos 1F F x = ，αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
（b ），图（d ）： 分力：22)tan sin cos (i F ϕααF F x -= ，22sin sin j F ϕαF y =投影：αcos 2F F x = ，)cos(2αϕ-=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1－2 试画出图a 、b 两情形下各物体的受力图，并进行比较。
1y F xx F 1y F α1x F yF（c ）x F 2y F 2y 2x 2x F 2y F F（d ）Ay F F B C A Ax F 'F C(a-2)C D C F D R (a-3)AxF F F A C BD Ay F (b-1)习题1－3图知识点：受力分析与受力图 难易程度：易 解答： 比较：图（a-1）与图（b-1）不同，因两者之FRD 值大小也不同。
1－3 试画出图示各物体的受力图。
F Ax F AyF D C B A B F 或(a-2) F B F A F D C A (a-1)BF AxF A AyF C(b-1) W F B DC F F (c-1) F F C B BF A 或(b-2)αD AF A BC B F(d-1)C F C A AF (e-1)Ax F A Ay F D F D CαF BF FC D B F A习题1－4图难易程度：易 解答：1－4 图a 所示为三角架结构。
《工程力学》详细版习题参考答案
∑ Fx
=FAx
+
FBx
+
FCx
=− 1 2
F
+
F
−
1 2
F
=0
∑ Fy
= FAy
+
FBy
+
FCy
= − 3 2
F
+
3 F = 0 2
∑ M B= FBy ⋅ l=
3 Fl 2
因此，该力系的简化结果为一个力偶矩 M = 3Fl / 2 ，逆时针方向。
题 2-2 如图 2-19（a）所示，在钢架的 B 点作用有水平力 F，钢架重力忽 略不计。试求支座 A，D 的约束反力。
（a）
（b）
图 2-18
解：（1）如图 2-18（b）所示，建立直角坐标系 xBy。 （2）分别求出 A，B，C 各点处受力在 x，y 轴上的分力
思考题与练习题答案
FAx
= − 12 F ，FAy
= − 3 F 2
= FBx F= ，FBy 0
FCx
= − 12 F ，FCy
= 3 F 2
（3）求出各分力在 B 点处的合力和合力偶
（3）根据力偶系平衡条件列出方程，并求解未知量
∑ M =0 − aF + 2aFD =0
《工程力学》
可解得 F=Ay F=D F /2 。求得结果为正，说明 FAy 和 FD 的方向与假设方向相同。 题 2-3 如 图 2-20 （ a ） 所 示 ， 水 平 梁 上 作 用 有 两 个 力 偶 ， 分 别 为
3-4 什么是超静定问题？如何判断问题是静定还是超静定？请说明图 3-12 中哪些是静定问题，哪些是超静定问题？
（a）
工程力学课后习题答案【整理版】
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案 1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解� 1-2 试画出以下各题中A B 杆的受力图。
BA OW(a ) B A O WF(b ) OW (c ) AAO W(d ) BA O W (e ) BFB FABO W (a ) BA OW F(b ) F A F BAO W(c )FA FO AO W (d ) F B F A A O W (e ) BF B FA A WC B (c ) D(a ) AW CEB (b ) AW C DB《工程力学》习题选解 。
工程力学 静力学与材料力学 (单辉祖 谢传锋 著) 高等教育出版社 课后答案解�1-3试画出以下各题中A B 梁的受力图。
ABF (d ) CABW (e ) CAB W (e ) C FB FA AB F(d ) CFB F A (a ) FD FB FE DAW CEB (b ) AW CD B F D FB FA (c ) A WC B FB FA AWCB(a ) W ABCD(c ) AB Fq D (b ) C CABFW DA’ D ’ B’ (d ) AB Fq (e )解�1-4 试画出以下各题中指定物体的受力图。
(a ) 拱A B C D �(b ) 半拱A B 部分�(c ) 踏板A B �(d ) 杠杆A B �(e ) 方板A B C D �(f ) 节点B 。
解� A WCB(a ) FB FAA BFqD(b ) FC FD W ABC(c ) FC FB CAB F WD(d ) FB FA FD ABFq(e ) FB x FB y FA AB F (a ) D C WAF(b ) DB (c ) F ABD D ’ A B F(d ) C DW A B CD(e ) W A BC(f ) A BF(a ) D CWFA x FA y FD AF (b ) B FB FA (c ) FA B DF B FD1-5 试画出以下各题中指定物体的受力图。
《工程力学(工程静力学与材料力学)(第3版)》考试试卷(附答案)(10)
工程力学考试答卷（10）1．（5分）结构对称的梁在反对称载荷作用下：弯矩图对称，剪力图反对称；弯矩图反对称，剪力图对称；弯矩图和剪力图都对称；弯矩图和剪力图都反对称。
正确答案是B。
2．（5分）关于材料的力学一般性能，有如下结论，请判断哪一个是正确的：脆性材料的抗拉能力低于其抗压能力；（B）脆性材料的抗拉能力高于其抗压能力；（C）韧性材料的抗拉能力高于其抗压能力；正确答案是A。
（D）脆性材料的抗拉能力等于其抗压能力。
3．（5分）关于斜弯曲的主要特征有以下四种答案，请判断哪一种是正确的。
（A） My≠0，Mz≠0，FNx≠0；，中性轴与截面形心主轴不一致，且不通过截面形心；（B） My≠0，Mz≠0，FNx＝0，中性轴与截面形心主轴不一致，但通过截面形心；（C） My≠0，Mz≠0，FNx＝0，中性轴与截面形心主轴平行，但不通过截面形心；（D） My≠0，Mz≠0，FNx≠0，中性轴与截面形心主轴平行，但不通过截面形心。
正确答案是B。
4．（5分）两根长度相等、直径不等的圆轴受扭后，轴表面上母线转过相同的角度。
设直径大的轴和直径小的轴的横截面上的最大剪应力分别为τ1max和τ2max，材料的切变模量分别为G1和G2。
关于τ1max和τ2max的大小，有下列四种结论，请判断哪一种是正确的。
（A）τ1max>τ2max；（B）τ1max<τ2max；（C）若G1>G2，则有τ1max>τ2max；正确答案是C。
（D）若G1>G2，则有τ1max<τ2max。
5．（10分）截面为工字形的立柱受力如图所示。
试求此力向截面形心C平移的结果。
解：r =（-50, 125, 0）mm F =（0, 0, -100）kN F 向C 平移，得 FR =（0, 0, -100）kN1000000.1250.05-)(-=⨯==kj i F r F M M C C=（-12.5, -5, 0）kN ·m6．（10分）图示芯轴AB 与轴套CD 的轴线重合，二者在B 、C 处连成一体；在D 处无接触。
工程力学(静力学与材料力学)课后习题答案(单辉祖)
1-1试画出以下各题中圆柱或圆盘的受力图。
与其它物体接触处的摩擦力均略去。
解：1-2 试画出以下各题中AB杆的受力图。
A(BF((W(AW(F(F(F(FW(AW(F((B(DB解：1-3 试画出以下各题中AB 梁的受力图。
B(BB(F BF(FB (D B F F(FB(W(B F(A DBB1-4 试画出以下各题中指定物体的受力图。
(a) 拱ABCD ；(b) 半拱AB 部分；(c) 踏板AB ；(d) 杠杆AB ；(e) 方板ABCD ；(f) 节点B 。
解：B(BF (W((D(F Bx(DC(D((BC(WB(1-5 试画出以下各题中指定物体的受力图。
(a) 结点A ，结点B ；(b) 圆柱A 和B 及整体；(c) 半拱AB ，半拱BC 及整体；(d) 杠杆AB ，切刀CEF 及整体；(e) 秤杆AB ，秤盘架BCD 及整体。
(D CD(B(BF D(F CC(WB(F ABF BC((C(A(解：(a)(b)(c)AF ABF ATF AF BAFCC’CD((e)D DC’2-2 杆AC 、BC 在C 处铰接，另一端均与墙面铰接，如图所示，F 1和F 2作用在销钉C 上，F 1=445 N ，F 2=535 N ，不计杆重，试求两杆所受的力。
解：(1) 取节点C 为研究对象，画受力图，注意AC 、BC 都为二力杆，(2) 列平衡方程：12140 sin 600530 cos6005207 164 o y AC o x BC AC AC BC F F F F F F F F F N F N=⨯+-==⨯--=∴==∑∑ AC 与BC 两杆均受拉。
2-3 水平力F 作用在刚架的B 点，如图所示。
如不计刚架重量，试求支座A 和D 处的约束力。
解：(1) 取整体ABCD 为研究对象，受力分析如图，画封闭的力三角形：FF43xFDF F AF D(2) 由力三角形得211 1.122D A D D A F F FF F BC AB AC F F F F F =====∴===2-4 在简支梁AB 的中点C 作用一个倾斜45o 的力F ，力的大小等于20KN ，如图所示。
工程力学(静力学和材料力学)课后习题答案
工程力学（静力学与材料力学）习题详细解答(第1章)(a) (b) 习题1－1图第1章 静力学基础1一1 图a 和b 所示分别为正交坐标系11y Ox 与斜交坐标系22y Ox 。
试将同一个力F 分别在两中坐标系中分解和投影，比较两种情形下所得的分力与投影。
解：图（a ）：11 sin cos j i F ααF F +=分力：11 cos i F αF x = ， 11 sin j F αF y = 投影：αcos 1F F x = ， αsin 1F F y =讨论：ϕ= 90°时，投影与分力的模相等；分力是矢量，投影是代数量。
图（b ）： 分力：22)tan sin cos (i F ϕααF F x −= ， 22sin sin j F ϕαF y =投影：αcos 2F F x = ， )cos(2αϕ−=F F y讨论：ϕ≠90°时，投影与分量的模不等。
1一2 试画出图a 和b 两种情形下各构件的受力图，并加以比较。
比较：解a 图与解b 图，两种情形下受力不同，二者的F R D 值大小也不同。
DR习题1－2b 解图DR习题1－2a 解2图C习题1－2a 解1图(a) (b)习题1－2图1一3 试画出图示各构件的受力图。
习题1－3图B F 习题1－3a 解2图 B习题1－3a 解1图习题1－3b 解1图F Ay Ax 习题1－3c 解图 A习题1－3b 解2图习题1－3d 解1图习题1－3e 解1图习题1－3e 解2图1－4 图a 所示为三角架结构。
荷载F 1作用在B 铰上。
AB 杆不计自重，BD 杆自重为W ，作用在杆的中点。
试画出图b 、c 、d 所示的隔离体的受力图，并加以讨论。
习题1－4图1习题1－3f 解1图F习题1－3e 解3图'A习题1－3f 解2图1O 习题1－3f 解3图F F'F 1习题1－4d 解2图F y B 21习题1－4c 解1图 AA B 1B FDx y2B 习题1－4b 解2图 1习题1－4b 解3图 F y B 2习题1－4c 解2图 F A B1B FAxF'习题1－5b 解3图E D(a-3)E B F习题1－5b 解2图习题1－5b 解1图'AxFF B习题1－5c 解图1一5 试画出图示结构中各杆的受力图。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
工程力学（静力学与材料力学）习题 第18章 聚合物的粘弹性行为18－1 对于麦克斯韦模型，保持初始应力为0σ时的应变不变，试证明经过时间t 后其应力由下式给出：)exp()(0λσσtt -=并说明其中λ的含义。
知识点：粘弹性，麦克斯韦模型 难度：难 解答：解：麦克斯韦模型的本构方程是ησσε+=t k t d d 1d d t式中k为弹簧刚度，η为粘度，令0d d =t tε，得方程σησkt -=d d 分离变量 tk d d ησσ-=积分得tke C ησ-⋅=由t = 0时0σσ=，求得0σ=C 于是tk eησσ-⋅=0或 λσσte -⋅=0 式中kηλ=是粘度与刚度之比。
18－2 承受轴向拉伸的橡皮带，当横截面上应力0σ= 10MPa 时，其纵向正应变为0.5，然后保持应变不变，50天后应力减小为5MPa 。
试计算若保持同样应变，再经过50天后应力减少到什么数值。
知识点：粘弹性，麦克斯韦模型，应力松弛 难度：难 解答：解：此问题为串联模型，适用麦克斯韦模型方程0d d 1d d =+=ησσεt k t t利用上题结果，求得λλσσtteet --=⋅=10)(0由题给条件，当t = 50（天）时，应力由10MPa 下降至5MPa 。
于是有λλtee --=⋅=1010550，由此可知2ln 50=λ因而502ln 5021010)(ttet --⨯=⋅=σ（MPa ），t 以天为单位再令t = 100（天），可求得5.2210)100(2=⨯=-σ（MPa ）再经过50天（一共经过100天），应力减小到2.5MPa.18－3 对于开尔文模型，若粘弹性材料的弹性模量为E ，则在保持应力不变的情形下，经过时间t 后，其应变值由下式给出：⎥⎦⎤⎢⎣⎡-=)exp(1)(λσεt k t并说明其中λ的含义。
知识点：粘弹性，开尔文模型，蠕变 难度：难解答：解：开尔文模型的本构方程是tE t k d d d d εηεεηεσ⋅+=⋅+=对t求导，并令0d d =t σ有0d d d d 22=⋅+⋅t t E σηε此乃二阶线性齐次常系数微分方程，其特证方程为02=+Er r η对应特征根为01=r ，ηEr -=2于是通解为tE eC C t ηε-+=21)(利用初始条件，当t = 0时，ε= 0（因来不及发生应变）和ησε==0d d t t代入通解有⎪⎩⎪⎨⎧=-=+ηση2210C EC C求得EC σ-=2，EC σ=1，于是)1()(tE eE t ησε--=或)1()(λσεtekt --=式中k = E 为弹性模量，kEηηλ==是粘度与弹性模量之比。
18－4 图示线性粘弹性模型，包括一个刚度系数为k 的弹簧和一个粘度为η的粘性元件，如图所示。
试用拉普拉斯变换方法描述蠕变响应，其中应力为常数。
知识点：粘弹性，蠕变 难度：难 解答：解：σεεη=+k td d （常数）引入拉普拉斯变换tet f s f t Lf std )()()(0-+∞⎰==导数变换)0()()]([--⋅='f s f s t f L及变换公式，已知对上述微分方程引入拉普拉斯变换后有 sk s σεεεη=+--)]0([由于0)0(=-ε，于是有sk s σεη=+)(⎥⎦⎤⎢⎣⎡+-=+-⋅=+=ησηησσησε/11)(11)(k s s k k s k s k k s s于是]1[1)1(][)(111t kk e k s L s L k L t ηησσεε-----=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛+-==18－5 试证明习题18－4给出的并联模型不能用来描述应力松弛问题。
知识点：粘弹性，麦克斯韦模型，应力松弛 难度：难 解答：证：应力松弛问题是保持应变不变，即0d d =t ε，如果仍应用习题18－4的并联模型将导致εσk =是常数的结论，这显然是不对的，只有应用串联模型才能分析应力松弛现象。
18－6 图示麦克斯韦标准线性固体模型的弹簧刚度系数分别为k1和k2，粘度为1η。
试证明其本构方程为τσστεε+=++t k t k k d d d d )(212习题18-4图式中，11k ητ=。
知识点：粘弹性，麦克斯韦标准线性固体模型 难度：难 解答：证：对于右半部属于串联模型，其应力1σ与应变ε关系为1111d d 1d d ησσε+=t k t （1）左半部应力2σ与应变ε关系为εσ⋅=22k （εεε==21） （2）再利用σσσ=+21 （3）由（3）式，21σσσ-=代入（1）式得)(1d d d d 1d d 2121σσησσε-+⎥⎦⎤⎢⎣⎡-=t t k t再将（2）式代入上式得)(1d d d d 1d d 2121εσηεσεk t k t k t -+⎥⎦⎤⎢⎣⎡⋅-=移项得 σησεηε1112121d d 1d d )1(+=++t k k t k k或τσσετε+=++t k t k k d d d d )(212式中11k ητ=18－7 试证明麦克斯韦标准线性固体模型的蠕变柔量表达式为c21220c 111)()(τσεtek k k k t t C -⎥⎦⎤⎢⎣⎡-++==式中，ττ212c k k k +=。
知识点：粘弹性，麦克斯韦标准线性固体模型，蠕变柔量习题18-6图难度：一般 解答：证：蠕变柔量定义为c )()(σεt t C =由上题已经证明应变与应力关系为τσσετε+=++t k t k k d d d d )(221式中11k ητ=讨论蠕变问题时，控制应力σ为常数0σσ=，而0d d =t σ。
于是方程化为τσετε0221d d )(=++k t k k此方程的通解是εττσσεttk k k eC k eC k -+-+=+=12)(12212式中11221221)(k k k k k k k ηττε⋅+=+=利用初始条件t = 0时tk d d 11111εηεσ==222εσk =，且εεε==21，及210σσσ+=给出0210|)(=+=t k k εσ或2100|k k t +==σε 代入解中得12210C k k k +=+σσ∴ )11(22101k k k C -+=σ于是ετσσεte k k k k t --++=)11()(221020求得c21220c 111)()(τσεte k k k k t t C -⎥⎦⎤⎢⎣⎡-++==18－8 低碳奥氏体合金锻件在816℃时的应力—变形—时间关系试验曲线如图所示。
试求其在应力σ= 105MPa 时的最小蠕变率。
知识点：粘弹性，蠕变率 难度：一般 解答：解：查图8－1可知，当固定应力为σ= 105MPa 时，应变与时间关系如下表示ε（%） 0.1 0.2 0.5 1.0 t （h ）1.5815.85 100251 t∆∆ε（%/h ）0.0130.00350.0033可见最小蠕变率/h1033h /103.3h /%0033.0d d 65min--⨯=⨯=≈tε18－9 176℃时铝合金在两种应力水平下的蠕变曲线如图所示。
试求其在应力σ= 59MPa 时的最小蠕变率。
知识点：粘弹性，蠕变率 难度：一般习题18-8图习题18-9图解答：解：当σ= 55MPa 时，h/105.241526010)2.08.0(d d 6255--⨯=-⨯-=tε当σ= 62MPa 时，h/107.66015010)4.04.1(d d 6262--⨯=-⨯-=tε利用线性插值公式，可求得。
当应力σ= 59MPa 的最小蠕变率是)h (%106.48h /106.48h /10]5.247.66[74h /105.24d d d d 55625559d d d d 1466655625559-----⨯=⨯=⨯-+⨯=⎥⎥⎦⎤⎢⎢⎣⎡---+=ttttεεεε18－10 奥氏体钢制连杆750℃下工作，由蠕变试验测得这种材料在750℃下的数据列于表中。
假定连杆所承受的轴向载荷F = 35kN ，在10000h 内允许的蠕变总应变为1%，并要求安全因数3c =n 。
试求连杆的横截面面积。
知识点：粘弹性，伪弹性设计方法 难度：难 解答： 解：利用公式][σ≤A F其中c][n xσσ=，3c =n ，x σ由限制性条件)h (%1010h /10h 10000%1h /156---⨯==÷=ε 确定。
查表知，当σ= 70MPa 时，)h (%108h /15--⨯=ε当σ= 100MPa 时，)h (%1026h /14--⨯=ε利用线性插值易求得，当)h (%1010h /15--⨯=ε 时，对应的应力24.70)70100(826081070=-⨯--+=x σMPa于是4.23324.70][c===n xσσMPa1496)MPa (4.23)N (1035][3=⨯=≥σF A （mm2）18－11 长l = 1m 、横截面面积31029.1⨯=A mm2的拉杆由酰胺塑料制成。
假定酰胺塑料的蠕变应力—应变—时间关系可近似地由下式描述：nm t k k E)()(21σσσε++=其中，σ和ε分别为正应力和正应变，t 为时间，单位为d （天）。
现已知：E = 1.7GPa （注：原书为MPa ），91108.34-⨯=k m2/N ，m = 1.16，921041.3-⨯=k m2/（N ·d ），n = 0.75。
若要求拉杆在1年内的总伸长不超过6.94mm ，试确定许可轴向载荷。
知识点：粘弹性，伪弹性设计方法 难度：难 解答：解：刚度条件应写作无量钢形式如下：3211094.6][)()(-⨯=≤++=εσσσεn m t k k E式中E = 1.7GPa ，91108.34-⨯=k （1/Pa ）3108.34-⨯=（1/MPa ），321041.3-⨯=k /（MPa ·d ），n = 0.75，m = 1.16，若应力用MPa 作单位，则上式给出375.0316.1331094.6)3651041.3()108.34(107.1---⨯≤⨯⨯⨯+⨯+⨯σσσ或 375.0416.1441094.61011784102031088.5----⨯≤⨯+⨯+⨯σσσ这是一个关于σ的非线性方程（或不等式），利用迭代法可求出其近似值。
但考虑到左式的第三项占主要部分，不妨选初始值)0(σ，使之满足375.0)0(41094.61011784--⨯=⨯σ求得375.0143)0(1007.1)10117841094.6(---⨯=⨯⨯=σ（MPa ）简单迭代程序为75.01)(16.1)(3)1(]0005.00172.010889.5[k k k σσσ--⨯=-+选3)0(1007.1-⨯=σ于是75.01316.133)1(]1007.10005.0)1007.1(0172.010889.5[---⨯⨯-⨯⨯-⨯=σ75.01333]10000535.01000616.010889.5[---⨯-⨯-⨯=310062.1-⨯=（MPa ）3)2(1006.1-⨯=σ（MPa ）可取迭代值31006.1-⨯≤σ（MPa ）于是求得作用载荷37.11029.11006.133=⨯⨯⨯≤=-A P σ（N ） 许可轴向载荷 [P] = 1.37 N18－12 某种材料的σ= 100MPa 下的蠕变率可由下述方程确定：TBA -=e ε其中，A 、B 均为材料常数，T 为热力学温度，单位为K 。