武汉四环线汉江大桥抗风性能研究_郑群华
1999武汉江汉四桥合理施工状态的确定_颜东煌

第15卷第2期1999年6月 长 沙 交 通 学 院 学 报JOURNA L OF CHANG SHA COMUNICATIONS UNIVERSIT Y Vo.15No.2 J une 1999 文章编号:1000-9779(1999)02-0065-05武汉江汉四桥合理施工状态的确定颜东煌1,袁帅华2,郭奕众3(1.长沙交通学院,湖南长沙 410076;2.湘潭工学院,湖南湘潭 411100;3.广州港工程设计所,广东广州 510700)摘 要:采用正装迭代法确定武汉江汉四桥(不对称独塔PC 斜拉桥)的合理施工状态,准确模拟了主桥施工过程,分析了主桥合龙方案。
关键词:斜拉桥;施工状态;正装迭代法中图分类号:U448.27;U445 文献标识码:A Ξ图1 主跨主梁标准断面图 武汉江汉四桥主桥为不对称独塔双斜索面PC 斜拉桥。
汉口侧(主跨)跨度为232m 半封闭箱形截面(图1),汉阳侧(边跨)由75.4m (单箱三室箱形截面)+34.0m (实体截面)+28.6m (实体截面)3跨组成。
预应力混凝土A 形索塔高110.5m ,塔纵向两侧各26对索,索在江侧主梁上间距为8m ,在岸侧主梁上间距为8m 和3.4m 两种。
索塔截面为箱形。
在斜拉桥合理成桥状态确定后,如何选择施工方法,进而确定各施工状态的控制参数(控制张拉索力和主梁立模标高)———合理施工状态,成为设计及施工控制中需解决的关键问题[1]。
作者在参与本桥施工控制工作中,对该桥合理施工状态的确定进行了研究,并提出用正装迭代法来解决这一问题。
1 施工简介对于上述的斜拉桥结构体系,主跨采用前支点挂篮(或称牵索挂篮)悬臂现浇施工,岸侧采用落地支架现浇。
具体为:1)主跨箱梁悬臂浇筑段,即主跨1~26号索对应的梁段(M1~M26),长208.0m ,用挂篮进行悬臂浇筑施工;2)汉口侧主跨现浇段,即14号墩侧长9.2m 的梁段,进行支架现浇;3)主跨合龙段(即M27号梁段)长2.8m ,利用挂篮作底模,挂篮前端支在主孔现浇段的支架上,后端挂在M26号梁段上;4)汉阳侧梁段均在支架上浇筑施工。
大跨度悬索桥非线性静风稳定性优化迭代分析方法

PM 一 ,CM( ) 2 a b /
式 中 : n a , 、 a , ( ) 别 为 在 有 效 攻 角 下 c () C . ) C a 分 (
主 梁 的 阻 力 、 力 、 力 矩 系 数 , 效 攻 角 是 指 静 升 升 有 风初 始攻 角与 静 风作 用 引 起 的 主梁 扭 转 角之 和 ;
Vo1 4 No. .3 6
De . 20 c 10
大跨 度悬 索桥非线 性静 风稳定性优 化迭代分 析方法 *
张 文 明 葛 耀 君
( 济 大学 土 木 工程 防 灾 国 家 重 点 实验 室 上 海 2 0 9 ) 同 0 0 2
摘 要 : 合 考 虑 静 风 荷 载 非 线 性 和 几 何非 线性 , 用 大 跨 度 桥 梁 非 线 性 静 风 稳 定 分 析 理 论 , 过 引 综 引 通
且 可 能 出现 在 高 于 I 风 速 的 某 一 风 速 下 内 外 层 临界 迭代 均收敛 的情 况 , 此 不 能 准确 地 搜 索 到 临界 因
求解 如下 形式 的非线性 方程
[ “ + K ( ) 【 一 K () “ ], F P ()P ()P 口] [ H d , v a , M() () 2
承 重 桥 梁 存 在 静 风 失 稳 的 可 能 性 [= 所 谓 静 风 失 1. 。
P} 一 l Pv一
C}( ) / Ia h 2 C a12 v( ) / , () 1
稳 是指 结构在 给 定 风速 作 用 下 , 梁 发 生弯 曲和 主
扭 转 变 形 , 方 面 改 变 了 结 构 刚 度 , 一 方 面 因 结 一 另
1 静风 失 稳优 化 迭 代 分 析 方 法及 其 实 现
大跨悬索桥Π形加劲梁处风参数实测与风攻角修正

第50 卷第 11 期2023年11 月Vol.50,No.11Nov. 2023湖南大学学报(自然科学版)Journal of Hunan University(Natural Sciences)大跨悬索桥Π形加劲梁处风参数实测与风攻角修正刘志文1,2,3†,魏子然1,2,3,何法伟1,2,3,刘曙光4,万田保4,陈政清1,2,3[1.风工程与桥梁工程湖南省重点实验室(湖南大学),湖南长沙 410082;2.桥梁工程安全与韧性全国重点实验室(湖南大学),湖南长沙 410082;3.湖南大学土木工程学院,湖南长沙 410082;4.中铁大桥勘测设计院集团有限公司,湖北武汉 430056]摘要:以一座已建的大跨悬索桥为工程依托,基于现场实测与计算流体动力学(Compu⁃tational Fluid Dynamics, CFD)方法研究Π形加劲梁断面气动外形对桥面高度处实测风参数的影响,并提出实测风攻角的修正方法. 进行为期5个月的桥面高度处风速和风攻角现场实测,分析风参数沿桥轴线的分布规律,并比较了桥面高度处迎风侧与背风侧风速仪实测的风速和风攻角;采用计算流体动力学方法模拟气流流经静止加劲梁断面的流场,研究来流风攻角和风速对风速仪安装在加劲梁不同位置处风参数的影响;结合数值模拟结果,通过函数拟合得到Π形加劲梁断面风速仪实测风攻角的修正公式. 结果表明:实测风速在大桥主跨范围内较为接近,且边跨风速相较于主跨风速偏小;现场实测得到的迎风侧风攻角明显大于背风侧,两侧风速基本一致;迎风侧与背风侧的风参数数值模拟结果与现场实测具有一致性,主梁绕流对距主梁20 m范围内的风攻角监测结果均存在一定影响. 通过本文建立的风攻角修正方法,可以根据迎风侧风攻角的实测值得到较为合理的风攻角修正结果.关键词:桥梁工程;大跨悬索桥;Π形加劲梁;风参数;现场实测;计算流体动力学;修正方法中图分类号:U446.1 文献标志码:AField Measurements of Wind Parameters and Correction of Wind Angle of Attack at Π-shaped Stiffening Girder Level ofLarge-span Suspension BridgeLIU Zhiwen1,2,3†,WEI Ziran1,2,3,HE Fawei1,2,3,LIU Shuguang4,WAN Tianbao4,CHEN Zhengqing1,2,3[1.Key Laboratory for Wind and Bridge Engineering of Hunan Province(Hunan University),Changsha 410082, China;2.State Key Laboratory of Bridge Engineering Safety and Resilience(Hunan University),Changsha 410082, China;3.College of Civil Engineering, Hunan University, Changsha 410082, China;4.China Railway Major Bridge Reconnaissance & Design Institute Co., Ltd., Wuhan 430056, China]Abstract:Taking an existing large-span suspension bridge as the engineering background, the influence of the aerodynamic contour of a Π-shaped stiffening girder on the measured wind parameters at the main girder level was∗收稿日期:2022-11-03基金项目:国家自然科学基金资助项目(52178475, 51778225), National Natural Science Foundation of China(52178475, 51778225)作者简介:刘志文(1975—),男,山西阳高人,湖南大学教授,工学博士† 通信联系人,E-mail:*****************.cn文章编号:1674-2974(2023)11-0001-13DOI:10.16339/ki.hdxbzkb.2023119湖南大学学报(自然科学版)2023 年studied, and a correction method for the measured wind angle of attack (AOA) was proposed based on the field mea⁃surement and Computational Fluid Dynamics (CFD) method. Moreover, the field measurements of wind speeds and AOAs at different measurement points on the Π-shaped stiffening girder were carried out for five months. The distri⁃bution of wind parameters along the bridge axis was analyzed, and the wind speeds and the wind AOAs measured by the anemometers on the windward and leeward sides at the stiffening girder level were compared, respectively. Fur⁃thermore, the CFD method was utilized to simulate the flow field of the stationary girder to investigate the influence of incoming wind speeds and wind AOAs on the wind parameters measured by the anemometer installed at different positions of the Π-shaped stiffening girder. Additionally, a correction formula for the wind AOAs measured at the windward side of the Π-shaped stiffening girder was proposed based on the numerical simulation. The results show that the measured wind speeds are relatively close within the main span while those are lower at the side span. The wind AOAs measured on the windward side are significantly larger than those on the leeward side of the girder, while the wind speeds are almost the same on both sides. The numerical simulation results of the wind parameters mea⁃sured on the windward and leeward sides are consistent with the measured results, and the flow around the girder has a specific influence on the wind AOAs within 20 m of the girder. Via the wind AOAs data measured on the windward side, the rational wind AOAs results can be obtained based on the correction method proposed in this study. Key words:bridge engineering;large-span suspension bridge;Π-shaped stiffening girder;wind parameters;field measurement;computational fluid dynamics;correction method桥位风场特性对大跨桥梁抗风设计至关重要,主要研究方法有现场实测、风洞试验和数值模拟三类. 现场实测是研究桥位风场特性最为直接有效的手段,众多学者通过现场实测方法对桥位风场展开了大量研究. 郭增伟等[1-2]利用三峡库区青草背长江大桥桥位处实测风速序列,从定量上评价和描述了山区峡谷风场的非平稳程度. 辛亚兵等[3-5]、刘志文等[6]通过对赤石大桥桥位风场特性实测数据的分析,研究了桥位处下击暴流风特性. 李威霖等[7]利用西堠门大桥结构健康监测系统的风速实测数据,分析得到了桥位处的风特性参数,并采用规则化波矢量随机流生成法合成了符合强风特性的均质各向异性湍流.目前,现场实测在大跨径桥梁风场特性研究中的应用已经很多,风观测方法主要可以分为两类,一是在桥位处设置风观测塔,二是在桥面处架设风速仪. 第2种风观测方法已广泛应用于国内外多座大跨径桥梁的结构健康监测系统[8]. 在大型桥梁健康监测系统中,风速仪一般布置于主跨跨中、1/4跨以及桥塔塔顶等位置,在不同桥梁上风速仪的布置差异较大,部分未考虑主梁对风速仪测试数据的影响.如日本明石海峡大桥[9]风速仪布设于加劲梁端部上侧 11 m处(约为0.79H,H为加劲梁高度),浙江舟山西堠门大桥[10]风速仪布设于加劲梁端部上侧6 m高度处(约为1.84H),苏通长江大桥[11]风速仪布设于主跨跨中桥面上、下游距桥面2.28 m高度处(约为0.57H),丹麦大带东桥[12]风速仪布设于加劲梁端部上侧2 m高度处(约为0.50H),挪威Gjemnessund大桥[13]风速仪布设于加劲梁端部外侧,水平间距4.26 m (约为1.70H)、垂向间距1.61 m处(约为0.64H).由于主梁的存在,桥面上方一定高度范围内的风速测试数据会受到一定影响. Jensen等[14]发现在Sotra悬索桥(挪威)桥面上的风速仪在距主梁3 m高度处采集到的风速数据可能受到主梁结构的影响,但认为其误差很小,可以忽略.马帅飞[15]进行了厦漳大桥风参数实测研究,研究表明,迎风侧桥面超声波风速仪测得的风攻角明显大于背风侧,认为是风流经主梁断面时的绕流现象所致,并进行了主梁绕流数值模拟,建立了桥面风速仪监测的风速、风攻角与远端来流风速、风攻角的近似函数关系. Frandsen[12]在大带东桥风场特性研究中,结合现场实测数据及数值模拟结果,采用有限元方法估算得到无栏杆状态下主梁迎风侧不受流动分离干扰的最小高度约为2.3 m,而背风侧相较于迎风侧受干扰程度较小,在风场特性分析中也更倾向于使用背风侧的风参数采样数据. Cheynet等[16]通过统计、比较Lysefjord桥上2第 11 期刘志文等:大跨悬索桥Π形加劲梁处风参数实测与风攻角修正不同高度处(2.2H 、3.5H )迎风侧与背风侧的平均风特性,认为迎风侧风攻角相较于背风侧而言稍大,主梁结构在一定高度范围内对风速的竖向分量可能存在一定影响,而风速的横桥向分量可能不会受到影响. Andersen [13]通过比较Gjemnessund 桥主梁迎风侧与背风侧的脉动风功率谱,发现背风侧在高频段的波动大于迎风侧. Qin 等[17]对一个流线型箱梁截面进行了龙卷风涡流数值模拟,研究表明主梁对流场存在明显干扰,破坏了原有的龙卷风涡流结构,并在主梁上侧和下侧形成了2种不同的新流态,这种干扰对迎风侧的风攻角存在明显的影响,但对风速影响较小,且在此情况下测量实际来流风攻角是较为困难的.综上所述,现场实测方法在国内外应用较多,但目前国内外桥梁桥面处风速仪的布设位置并没有统一标准. 部分大桥桥面高度处的风速、风攻角实测数据可能会受到主梁绕流效应影响,迎风侧与背风侧的测量结果存在一定差异,与实际来流可能并不一致. 然而,在风场特性分析中,学者们对大桥主梁断面迎风侧与背风侧风参数测量数据的选择并不统一. 因此,结合现场实测与数值模拟方法,研究主梁绕流效应对桥面高度处风参数实测数据的影响十分必要.1 项目概况1.1 桥梁简介依托鹦鹉洲长江大桥工程,开展桥面高度处风速实测研究. 鹦鹉洲长江大桥是湖北省武汉市连接汉阳区和武昌区的过江通道,是武汉二环线的重要组成部分. 桥位处长江河道呈西南-东北走向,桥轴线与长江基本正交,与东-西向夹角约为36°. 主桥为三塔四跨Π形钢-混凝土结合加劲梁悬索桥,加劲梁跨度布置为(200+850+850+200) m=2 100 m ,主缆矢跨比为f /L =1/9.主缆跨径布置为(225+850+850+225) m ,两根主缆的中心间距为36 m. 加劲梁采用双铰式支承体系,中塔为钢-混凝土叠合结构,边塔为混凝土结构. 中塔下横梁及两边塔下横梁上设有主梁竖向支座和横向抗风支座.加劲梁为Π形钢-混凝土结合梁,其中钢梁采用工字形钢板梁,中心线处梁高H =2.423 m ,混凝土桥面板厚为20 cm. 加劲梁标准节段长为15 m ,吊索中心距为36 m ,两片钢梁的中心距为31.2 m ,钢梁外侧每隔3 m 设置一道牛腿,其上设有检修道和吊索锚点,且沿桥纵向每隔3 m 设置一道横梁,横梁的断面形式为I 形断面;索塔总高152 m. 加劲梁梁宽38 m ,桥轴线处梁高3 m. 主桥立面布置与加劲梁标准断面如图1所示. 考虑到Π形加劲梁断面的气动外形较钝,加劲梁自身对流场的干扰较大,因此有必要研究该桥主梁绕流效应对桥面高度处风参数实测的影响.1.2 风速仪布置情况2014—2021年期间,大桥于汉阳侧跨中及中塔塔顶设有二维机械式风速风向仪,采样频率为4.0 Hz. 2020年4月26日鹦鹉洲长江大桥出现涡激共振现(a )全桥立面图(b )加劲梁断面图图1 鹦鹉洲长江大桥立面布置与加劲梁标准断面图(单位:cm )Fig.1 Elevation layout and standard section of stiffening girder of Yingwuzhou Yangtze River Bridge (unit : cm )3湖南大学学报(自然科学版)2023 年象,为进一步掌握大桥桥位处风场特性,而二维机械式风速风向仪无法测量桥位处风攻角,因此从2022年起根据涡振情况对健康监测系统进行了优化:在加劲梁桥面处增设了16个三维超声波风速风向仪,采样频率为20 Hz.风速仪风速测试范围为0~65 m/s ,风速分辨率为0.01 m/s ;风向以正北方向为0°,正东方向为90°,采样风向范围为0°~360°,风向分辨率为0.1°.16个三维超声波风速风向仪编号分别UAN-01~UAN-16,其中UAN-01、UAN-02、UAN-15、UAN-16布设于边跨跨中;UAN-03~UAN-14分别布设于主跨L /4、L /2、3L /4跨位置.三维超声波风速风向仪距加劲梁断面垂向间距约为5.2 m (底座高0.2 m ,净高约为1.73H ,H 为加劲梁高度). 既有的机械式风速风向仪及新布设的16个三维超声波风速风向仪在桥面的分布位置如图2所示. 鉴于本文旨在研究Π形加劲梁断面对实测风参数的影响,考虑到风攻角实测数据的重要性,本文仅综合三维超声波风速风向仪UAN-01~UAN-16于2022年1月至2022年5月观测期内的风参数实测数据,对鹦鹉洲长江大桥的风特性进行分析.2 风参数实测结果2.1 实测数据处理由于风速风向仪采样频率较高,数据量较大,为方便处理,首先对风速、风攻角、风向角的采样结果进行了每分钟平均. 其中,求解平均风向角时采用矢量平均法[18],如式(1)所示. 考虑到反正切后的风向角范围为-90°~90°,而实际风向角为0°~360°,因此还需要根据uˉ和v ˉ的正负号对风向角进行还原. 最后,鉴于桥轴线东西向偏角约为36°,定义风向角A 为126°~216°时,加劲梁上游为迎风侧,下游为背风侧;反之则加劲梁下游为迎风侧,上游为背风侧.u ˉ=1n ∑i =1nsin A iv ˉ=1n ∑i =1ncos A iA =arctan(uˉvˉ)(1)式中:n 为单位时间采样数;u ˉ和v ˉ分别为东西和南北方位的风速平均分量;A i 为单位矢量风向角;A 为单位矢量平均风向角.考虑到实测结果容易受到环境噪声的影响,利用莱茵达(PauTa )准则[19],以3倍风参数的标准差作为极限取舍标准,对每分钟的风参数数据进行野点剔除. 当风参数的每分钟平均值满足条件式(2),即与10 min 内均值的差值大于3倍10 min 内标准差时,即将该风参数数据视为离群值,若任一分钟下风速、风向、风攻角3个参数均值中存在离群值,则将该时刻视为野点,并将该时刻的3个参数均从整体样本中剔除.|||x 1-x ˉ10σ|||>3(2)式中:x 1为风参数每分钟均值;x ˉ10为风参数10 min 内均值;σ为风参数10 min 内标准差.2.2 实测结果2.2.1 观测期平均风特性通过分析观测期间UAN-01~UAN-16位置处的平均风特性,可以得到风参数沿桥跨的分布规律.考(a )桥位处风速仪总体分布 (b )风速仪架设位置(汉阳侧跨中)图2 风速风向仪测点布置图Fig.2 Layout of the measuring position of anemometers4第 11 期刘志文等:大跨悬索桥Π形加劲梁处风参数实测与风攻角修正虑到当来流风向与桥轴线大致垂直时更容易发生一定的桥梁风致振动现象,首先针对东北风和西南风两个风况进行分析. 图3为当来流为东北风及西南风时UAN-01~UAN-16的风速和风攻角统计结果.其中,风速和风攻角均为各测点位置的统计样本均值.样本的来流风向与桥轴线大致垂直(误差在-15°~ +15°以内),风攻角样本还需满足一定的风速条件,即每分钟平均风速大于5 m/s.从图3(a)可知,东北风作用下的桥面高度处平均风速稍大于西南风,加劲梁断面上、下游测得风速结果总体而言吻合较为良好;同时,主桥结构边跨风速较主跨处偏小.由图3(b)可知,当来流为东北风时,加劲梁上游各测点的风攻角均值为-6.4°~3.6,下游各测点的风攻角均值为4.2°~14.6°;当来流为西南风时,加劲梁上游各测点的风攻角均值为3.1°~12.3°,下游各测点的风攻角均值为-2.3°~2.2°. 整体上看,当来流与桥轴线大致垂直时,加劲梁上、下游的风攻角实测结果存在明显差异,其特征表现为:迎风侧风攻角实测结果大于背风侧,且迎风侧风攻角常大于10°,而背风侧风攻角常为一定的负攻角,可能是主梁绕流效应所致.图4为UAN-01~UAN-16于2022年1月至5月20日期间风向频率玫瑰图. 总体上看,大桥桥位处主导风向为东北风和西南风,其中东北风的风向频率相较于西南风较大. 主导风向基本与桥轴线方向垂直. 图4中除UAN-03、UAN-04及UAN-11、UAN-12两组风向频率有小幅偏差,在其余桥跨同一位置上、下游处的风向频率统计结果基本一致,即可以认为主梁绕流效应对该桥风向实测结果影响较小.(a)风速(b)风攻角图3 不同风向下实测风参数统计结果Fig.3 Statistical results of the measured wind parameters in different wind directions图4 风向频率玫瑰图Fig.4 Rose diagram of frequency of wind direction5湖南大学学报(自然科学版)2023 年2.2.2 大风天气风特性分析为研究风参数沿桥轴线的分布规律,进一步研究主梁绕流效应对实测数据的影响,选择有代表性的风况对实测结果进行相应分析. 根据2022年采集得到的风参数数据,在观测期内大桥桥位处发生过多次风速超过10 m/s 的天气,如3月12日14:25—14:35、3月20日1:40—1:50、4月28日16:20—16:30. 其中3月12日为西南风,3月20日、4月28日为东北风,这3日风速最大时刻的平均风向近似垂直于桥轴线. 图5为各测点位置10 min 滑动平均风速时程图,图6为大风天气各测点位置风参数.由图5可知,对于本文所研究的Π形加劲梁断面,当风速仪位于桥面以上5.2 m (约1.73H )时,在不同时刻,大桥上、下游实测风速均吻合较好,主梁绕流效应对迎风侧与背风侧的风速实测结果影响相对较小. 这一特点与图6(a )中各测点位置处的风速结果具有较好的一致性. 从图6(a )可以看出,主跨各测点位置处风速较为接近,而边跨风速相对较小,可能的原因是边跨风速较易受到桥位周边建筑影响. 从图6(b )可知,迎风侧、背风侧风攻角实测结果差异明显,其特征表现为:迎风侧风攻角稍大,而背风侧风攻角相较于迎风侧较小. 图6(b )与图4风攻角误差表现出的特征一致,可见对该桥Π形加劲梁断面而言,主梁绕流效应的确存在对风攻角实测结果的干扰. 同时,测点位置处风速与实际来流风速的关系也需要通过主梁绕流数值模拟进行进一步研究.(a )3月12日(b )3月20日(c )4月28日图5 各测点位置10 min 滑动平均风速时程图Fig.5 Time history diagram of 10 min moving average wind speed at each measuring point6第 11 期刘志文等:大跨悬索桥Π形加劲梁处风参数实测与风攻角修正3 基于CFD 的实测风参数修正3.1 控制方程与计算模型3.1.1 流体控制方程对于黏性不可压缩流体,质量守恒方程(连续方程)的矢量形式可以表示为:∇⋅V =0(3)动量守恒方程,即N-S (Navier-Stokes )方程为:∂V ∂t+(V ⋅∇)V =f -1ρ∇p +μρ∇2V (4)式中:ρ为流体密度;V 为速度矢量;p 为压力;f 为单位体积流体受的外力,若只考虑重力,则f =ρg ;μ为动力黏度.3.1.2 计算域及边界条件文献[17]指出,来流的竖向和横桥向风速分量是风致振动问题中的主导因素,顺桥向风速分量影响较小. 虽然主梁绕流对风速的竖向、横桥向和顺桥向分量均有影响,但对顺桥向的风速分量的影响是十分有限的,因此,本文研究主梁绕流时仅针对来流垂直于加劲梁轴线的情况,且不计桥上车辆对流场的干扰[16].考虑阻塞率因素,结合以往经验确定加劲梁断面计算域采用35B ×20B 的矩形区域(B 为加劲梁断面宽度),如图7所示. 边界条件定义如下:入口设置为速度入口(velocity inlet ),出口设置为压力出口(pressure outlet ),加劲梁断面外壁采用无滑移的壁面边界(wall ),0°攻角时上边界和下边界设置为对称边界(symmetry ),非0°攻角时上边界或下边界设置为速度入口(velocity inlet )或压力出口(pressure out⁃let )边界. 首层网格高度为2 mm ,约为5×10-5B ,网格总计410 712个. 加劲梁断面几何缩尺比取为1∶50,湍流模型采用剪应力输运湍流模型(SST k-ω),计算时间步长Δt =0.001 s.加劲梁断面近壁面局部网格划分如图8所示.考虑到目前国内外大跨径桥梁风速仪的布设位置差异明显,一般位于主梁端部上侧或外侧,针对鹦鹉洲长江大桥Π形加劲梁断面设置多个虚拟风速仪进行主梁绕流CFD 数值模拟.加劲梁风速监测点设置如图9所示. 梁端上侧每侧布设24个风速监测点,对应编号1~24,竖向间距为0.5~1.0 m ;梁端外侧每侧布设48个风速监测点,对应编号25~72,竖向间距为1.0 m ,水平间距为1.0~2.0 m.图9中仅列出了迎风侧风速监测点位置,背风侧与迎风侧的风速监测点沿加劲梁中轴线对称,一共布设(48+24)×2=144个.3.2 计算结果图10为CFD 数值模拟得到的部分风速监测点位置处迎风侧的风速时程,各监测点的风速输出结果包括水平风量U x 和竖向分量U y ,其中h 0为风速监测点与加劲梁断面的垂向间距.计算开始后约2 s ,各监测点的风速结果逐渐趋于稳定. 从图10中可以看出,主梁静态绕流对风速的影响主要体现为改变了风速的竖向分量U y ,而水平分量U x受到的影响较图7 计算域示意图Fig.7 Computational domain(a )10 min 滑动平均最大风速 (b )风速最大时刻风攻角图6 大风天气各测点位置风参数Fig.6 Wind parameters of each measuring position in strong wind day7湖南大学学报(自然科学版)2023 年小. 对于距离加劲梁断面较远的风速监测点,竖向分量U y 受到的影响也逐渐减小. 为更直观地反映风速监测点的布设位置对风参数测试结果的影响,本文取计算开始后6~10 s 的U x 和U y 均值,换算得到各监测点位置处的风速U 和风攻角α,并进行进一步分析.由文献[15]可知,来流风速、风攻角均会对实测风攻角产生影响. 因此,为验证不同来流风速对鹦鹉洲长江大桥Π形加劲梁断面绕流效应的影响,分别在来流风速为10 m/s 、15 m/s 下进行0°、±3°风攻角的主梁绕流效应数值模拟研究. 图11为不同来流风速下各监测点位置处风速、风攻角的对比结果,限于篇幅,仅列出风速监测点编号1~9(现有风速仪竖向剖面近壁面位置)处风速、风攻角的数值模拟结果. 图11中h 0为风速监测点与加劲梁断面的垂向间距,折算风速为风速监测点测得风速与来流风速之比. 从图11中可以看,各监测点位置处的折算风速、风攻(a ) 来流攻角为0° (b ) 来流攻角为+3° (c ) 来流攻角为-3°图10 不同来流攻角下部分风速监测点处风速曲线Fig.10 Wind speed curves of some virtual anemometer under different incoming wind angle of attack(a )加劲梁整体网格划分(b )加劲梁前缘局部网格划分(c )中央栏杆处局部网格划分图8 加劲梁断面近壁面局部网格划分Fig.8 Local mesh division near the wall of the stiffening girdercross-section图9 加劲梁风速监测点设置图(单位:m )Fig.9 Wind speed monitoring position of thestiffening girder (unit :m )8第 11 期刘志文等:大跨悬索桥Π形加劲梁处风参数实测与风攻角修正角在来流风速分别为10 m/s 、15 m/s 下基本一致,即来流风速对大桥Π形加劲梁断面的实测风参数结果影响较小. 同时,迎风侧与背风侧的风参数结果存在一定差异,风速监测点高度h 0对风参数监测结果也存在一定影响.图12和图13分别为风速仪布设于加劲梁上侧(风速监测点编号1~24)和加劲梁外侧(风速监测点编号25~72)时,10 m/s 来流风速作用下的风参数数值模拟结果,图中l 0为风速监测点与加劲梁断面的水平间距. 从图12可知,风速仪布设于加劲梁上侧时,当风速仪布设高度增加时,迎风侧风速结果逐渐接近来流风速;当布设高度h 0较小时(小于H ~1.6H ),背风侧风速结果与来流风速误差较大,反之则误差较小. 当风速仪布设于24号风速监测点位置处(h 0≈7.1H )时,0°风攻角下迎风侧测得风速与来流风速误差为0.3%,+3°风攻角下误差为7.0%,-3°风攻角下误差为3.6%.当风速仪布设高度较小 (小于2H ) 时,迎风侧风攻角在各工况下均呈现为较大的正攻角;而背风侧风攻角在各工况下均在0°附近. 随着h 0增加,迎风侧与背风侧测得风攻角与来流风攻角的误差逐渐减小,当风速仪布设于24号风速监测点位置处时,0°风攻角下迎风侧测得风攻角为1.6°,+3°风攻角下为6.2°,-3°风攻角下为-1.8°. 总体上看,主梁绕流效应对风参数实测结果的影响主要表现为对风攻角的影响,即使将风速仪布设于距加劲梁断面较高的位置(如24号风速监测点,h 0=21.2 m≈7.1H ),风攻角的监测结果仍存在一定的误差.从图13可知,风速仪布设于加劲梁外侧时,增加风速仪与加劲梁断面的垂向间距h 0可以减小背风侧风速仪测得风速与来流风速的误差,而对迎风侧风速仪而言,当风速仪与加劲梁断面的水面间距l 0较大时(大于4H ),增加h 0已难以有效减小测得风速的误差,此时增加l 0可以使风速仪测得的风速逐渐接近于实际来流风速. 当风速仪布设于72号风速监测点位置处(l 0≈6.7H , h 0≈1.3H )时,0°风攻角下迎风侧测得风速与来流风速误差为0.3%,+3°风攻角下误差为0.2%,-3°风攻角下误差为0.2%,稍优于24号风速监测点位置.增加h 0对迎风侧风攻角的检测结果影响较小,而增加l 0可以有效减小+3°风攻角下迎风侧风攻角实测结果的误差,对于0°、-3°风攻角下的 (a )来流攻角为0°时各测点折算风速 (b )来流攻角为+3°时各测点折算风速 (c )来流攻角为-3°时各测点折算风速(d )来流攻角为0°时各测点风攻角 (e )来流攻角为+3°时各测点风攻角 (f )来流攻角为-3°时各测点风攻角图11 不同来流风速下风参数结果Fig.11 Results of wind parameters under different incoming wind speed9湖南大学学报(自然科学版)2023 年误差减小程度有限. 当风速仪布设于72号风速监测点位置处时,0°风攻角下迎风侧测得风攻角为0.2°,+3°风攻角下为6.5°,-3°风攻角下为-5.0°. 总体上看,当风速监测点布设于距加劲梁断面一定范围内(a )来流攻角为0°时各测点风速 (b )来流攻角为+3°时各测点风速 (c )来流攻角为-3°时各测点风速(d )来流攻角为0°时各测点风攻角 (e )来流攻角为+3°时各测点风攻角 (f )来流攻角为-3°时各测点风攻角图13 风速仪布设于加劲梁外侧时风参数结果Fig.13 Wind parameter results when the anemometer is arranged outside the stiffening girder(a )来流攻角为0°时各测点风速 (b )来流攻角为+3°时各测点风速 (c )来流攻角为-3°时各测点风速(d )来流攻角为0°时各测点风攻角 (e )来流攻角为+3°时各测点风攻角 (f )来流攻角为-3°时各测点风攻角图12 风速仪布设于加劲梁上侧时风参数结果Fig.12 Wind parameter results when the anemometer is arranged above the stiffening girder10。
温度对汉江特大桥线形和内力影响的试验研究
摘 要: 通过分析 台后 沉陷的原 因, 究 出整体 式盖板在 解决 u型桥 台台后填土沉 陷问题 的技术 , 研 实践证明该技术彻底 解决 了U型桥 台因台腔填土沉 陷导致侧墙 竖向开裂 的问题 , 值得在 实际工程 中广 泛应用和推广 。
关 键 词 : 体 盖 板 , 型桥 台 , 整 U 台后 沉 陷 , 梁 工 程 桥 中 图分 类 号 : 4 5 7 U 4 . 文 献 标 识 码 : A
0. 6 05 . O. 4
0
[
: 二 = 二 = 二竺 圯 = = == = = =I
大里程根部顶面
— —‘ - ;, ’ ZJ一 . J z A m.C -wn - . o O Ua - Iu / + io. ℃ 7o 6 :2 ~ 运 力
- :2C 一6 ,℃ O -0  ̄ 0 0
第3 6卷 第 3 1期 201 0年 11月
山 西 建 筑
SHANXI ARCHI TECTURE
Vo _ 6 No 31 l3 .
No . 2 1 v 0 0
・3 7 ・ 3
文章 编 号 :0 96 2 (o 0 3 —3 70 1o -8 5 2 1 ) 10 3 —2
. 路面 、 路基 和桥梁结 构物 产生进 一步 的损 坏 ; 车时 的冲击 力会 1 4 施 工措 施 不 当 跳 些 施工队盲 目追求高速度 , 没有 严格按施 工规程作业 。例 对车辆产生不利反力 。
一
对 当桥头产生跳车现象 时 , 需花 费大量 的人 力 、 物力 和财 力去 如 没 有 做 严格 的地 基 处 理 , 台背 填 料 不 加 选 择 和 没 有 把 好 质 量 压实度没有达到要求等等 。这些人 为因素使 高填土引道不 稳 维修养护 , 同时也会 产生 不 良的社会 影响 , 以在桥 头处需 要采 关 , 所 定 , 后沉降大 , 不均匀 。 工 且 取 比较有效的方法来避免或减轻桥头沉降。
武汉西四环汉江特大桥3#墩主塔快速施工技术

武汉西四环汉江特大桥3#墩主塔快速施工技术摘要:武汉西四环汉江特大桥3#墩主塔结构型式为H型钢筋混凝土结构,塔高(塔座顶面以上)为130.1m,塔柱采用6m节段液压爬模施工。
为确保主塔施工安全和加快主塔施工速度,采取一些具体有效的措施:1、合理选择塔吊、电梯型号及布置位置;2、主塔塔柱施工采用6m节段液压爬模.关键词:高速公路;主塔施工;爬模法1;工程概况汉江特大桥是武汉西四环线的控制性工程,位于东西湖区慈惠街与蔡甸区交界处,沿九通路跨慈惠街及汉江左岸东西湖大堤,近正交跨越汉江,桥位在汉江与长江交汇口上游约21.5km。
汉江特大桥全长909m,主桥为714m的五跨一联双塔双索面预应力混凝土斜拉桥,桥跨布置为(77+100+360+100+77)m,3号主塔由下塔柱、上塔柱、塔冠、上横梁、牛腿等组成。
塔柱形式是“H”型,3号主塔牛腿顶面以上塔高112.55m,3号主塔牛腿底面以下塔高12.55m,牛腿高5m,3号塔柱总高130.1m。
上塔柱横桥向宽5m,顺桥向宽7m,采用空心矩形截面,上塔柱锚室壁厚0.7m(横桥向)、1.2m(纵桥向);下塔柱为四面内倾多面体构造,纵桥向内侧、外侧倾斜度分别为1/11.2857和1/8.3158,横桥向倾斜度为1/25.28;下塔柱横桥向宽5~7m,顺桥向宽7~12m,采用矩形空心截面。
壁厚1.2m(横桥向)、1.5m(纵桥向)。
主塔设有劲性骨架,以便于钢筋施工定位,劲性骨架不参与受力,上塔柱斜拉索锚固区之劲性骨架,施工时结合索导管定位可适当调整[1],主塔结构示意图及主塔分节浇筑图详见图1。
2 汉江特大桥3#墩主塔快速施工技术斜拉桥梁体尺寸较小,桥梁的跨越能力较大;受桥下净空和桥面标高的限制少;抗风稳定性比悬索桥好;不需悬索桥那样的集中锚碇构造;便于悬臂施工等。
斜拉桥造型美观,较多城市桥梁选用斜拉桥设计,成为城市一道美丽的风景线。
其主塔施工是斜拉桥施工的关键工序,主塔结构复杂,施工周期长,主塔高空作业安全风险较高,因此能总结一套安全、快速的施工方案,为今后类似主塔快速施工提供借鉴很有必要。
铁路超级大桥的抗风稳定性研究

铁路超级大桥的抗风稳定性研究第一章引言铁路超级大桥作为现代桥梁工程领域的代表,其抗风稳定性一直是相关技术的重要研究方向。
随着我国铁路交通的不断发展,越来越多的超级大桥被建设和使用,同时,不断出现的自然灾害以及意外事故也给铁路超级大桥的抗风稳定性和安全带来了更高的要求和挑战。
因此,本文将从桥体结构和风荷载两个方面,对铁路超级大桥的抗风稳定性进行深入研究,为铁路超级大桥的安全运行提供更为可靠和有效的技术支持。
第二章桥体结构对抗风稳定性的影响2.1 桥梁结构的刚度及迎风面积桥体结构的刚度是影响超级大桥抗风稳定性的一个重要因素。
过度的柔度会导致结构在风力作用下产生过大的变形,进而影响超级大桥的安全性。
因此,在设计铁路超级大桥时,需要综合考虑刚度和结构的抗风刚度参数,使其达到适当的刚度条件,以保证桥体的稳定性和安全性。
此外,迎风面积也是影响超级大桥抗风稳定性的另一个重要因素。
当桥体的迎风面积增大时,桥面所受的风荷载就会增大,从而导致超级大桥易发生风振现象。
因此,在超级大桥的设计中,需要通过合理地设置桥面形态和结构参数,降低迎风面积,以提高超级大桥的抗风稳定性。
2.2 桥体结构的防振措施为了改善铁路超级大桥的抗风稳定性,可引入一些防振措施。
常见的防振措施有:振动减缓器、承重调整器、倾斜支撑器等。
它们的作用是通过改变结构的柔性和材料性能等方面的特点,从而改变结构的振动特性,减小结构振动的幅值和频率,提高超级大桥的抗风稳定性。
第三章风荷载对抗风稳定性的影响3.1 风力特性对超级大桥的影响风力特性是影响超级大桥抗风稳定性的一个关键因素。
风力的大小和方向对超级大桥所受风荷载大小和方向有着重要的影响。
在风力方向垂直于超级大桥的情况下,风荷载对超级大桥所造成的破坏作用最大,需要通过结构设计和构造方案等方面的优化,来减小超级大桥所受风荷载对桥体结构的影响。
3.2 风荷载对结构的破坏作用风荷载对超级大桥所造成的破坏作用包括疲劳破坏和静态破坏。
1--武汉天兴洲公铁两用长江大桥抗风性能研究
文章编号:1003-4722(2009)04-0001-04武汉天兴洲公铁两用长江大桥抗风性能研究郑史雄1,徐 伟2,高宗余2(1.西南交通大学土木工程学院,四川成都610031;2.中铁大桥勘测设计院有限公司,湖北武汉430050)摘 要:针对目前我国最大跨度钢桁梁斜拉桥武汉天兴洲公铁两用长江大桥主桥的抗风性能进行风洞试验及分析研究,包括气动参数测量风洞试验、主梁节段模型风洞试验、施工状态气弹模型风洞试验、斜拉索风雨振动风洞试验及塔梁交汇区风场对行车安全性影响分析等。
研究表明,无论成桥状态或施工状态,其主梁断面具备足够的抗风稳定性,在相应设计风速作用下,其抖振响应性能满足要求,斜拉索虽存在发生风雨振动的可能,但可以通过气动措施或机械措施加以改善,塔梁交汇处风场特性较为特殊,在强风作用下可能会引起驾乘人员不适。
关键词:铁路公路两用桥;斜拉桥;桁梁桥;风洞试验中图分类号:U448.27;U446文献标志码:AStudy of Wind 2R esistant Perform ance of Main B ridge of WuhanTianxingzhou Changjiang River R ail 2cum 2R oad B ridgeZH EN G Shi 2xiong 1,XU Wei 2,GAO Zong 2yu 2(1.School of Civil Engineering ,Southwest Jiaotong University ,Chengdu 610031,China ;2.ChinaZhongtie Major Bridge Reconnaissance &Design Institute Co.,Ltd.,Wuhan 430050,China )Abstract :The wind t unnel test and analytical st udy were made for t he wind 2resistant per 2formance of t he main bridge of Wuhan Tianxingzhou Changjiang River Rail 2cum 2Road Bridge ,currently t he longest span steel t russ girder cable 2stayed bridge in China ,in which t he aerody 2namic parameter measurement test ,t he main girder sectional model test ,t he aeroelastic model test for t he bridge in const ruction state ,t he stay cable rain vibration test as well as t he analysis of influence of t he wind field at junct ure area of t he girder and pylo n on t he safe t raveling of vehicles were included.The result s of t he st udy indicate t hat for t he bridge eit her in t he completion state or const ruction state ,t he section of t he main girder has sufficient stability of wind resistance.U nder t he action of t he corresponding designed wind velocity ,t he buffeting response of t he bridge can satisfy t he required performance.Though t he rain vibration of t he stay cables may oc 2cur ,t he vibration can be imp roved by t he aerodynamic or mechanical measures.The characteris 2tic of t he wind field at junct ure area of t he girder and pylon is rat her special and will po ssibly make t he passengers uncomfortable in case of st rong wind.K ey w ords :rail 2cum 2road bridge ;cable 2stayed bridge ;t russ girder bridge ;wind t unnel test收稿日期:2008-12-04基金项目:铁道部科技研究开发项目(2004G028-D )作者简介:郑史雄(1965-),男,教授,博士生导师,1985年毕业于西南交通大学土木工程学院铁道桥梁专业,工学学士,1988年毕业于西南交通大学土木工程学院桥梁、隧道及结构工程专业,工学硕士,1996年毕业于西南交通大学土木工程学院桥梁及结构工程专业,工学博士(zhengsx @ )。
1000kV汉江大跨越塔线体系风洞实验与风振响应分析
风偏角β/(°) 0 15 30 45 60 75 90
Cx 2.402 2.728 2.881 2.943 3.082 3.076 2.770
Cy 0.129 −0.106 −0.165 −0.143 −0.128 −0.039 −0.065
Cmx 0.124 −0.313 −0.354 −0.428 −0.378 −0.097 0.023
抖振是输电塔风致振动中的一种,其发振风速 较低,在施工及运营期间容易发生,长时间的抖振 将对结构的疲劳、电网的安全等产生影响。由于输 电线具有较强的几何非线性,大跨越输电塔线体系 在风荷载作用下表现出复杂的振动特性[3-4],两者的 耦合作用十分显著[5-6]。与频域分析不同的是,建立 在数值积分基础上的时域分析能充分考虑结构的 非线性对大跨越输电塔线体系空气动力特性的影 响,并且能观察到结构动力响应的整个过程,能更 好揭示抖振现象的发生及演变过程,也可分析输电 塔的疲劳及可靠性。
1 000 kV 汉江大跨越塔线体系 风洞实验与风振响应分析
肖正直,李正良,汪之松,晏致涛,韩枫
(重庆大学土木工程学院,重庆市 沙坪坝区 400044)
Wind Tunnel Tests and Wind-induced Responses Analysis of 1 000 kV Hanjiang Long Span Transmission Line System
(c) 塔线体系
图 1 输电塔单塔和塔线体系模型
Fig. 1 Models of transmission tower and
transmission line system
2 风振时域分析
2.1 风场模拟
对 1 000 kV 汉江大跨越输电塔线体系进行风振
汉江大桥主梁设计与受力分析
交
通
科
技
Tr n p ra i n S in e& Te h oo y a s o t t ce c o c n lg
Se ilN o. 0 ra 25 No. 1 Fe 2Ol b. 2
汉 江 大 桥 主梁 设 计 与 受 力 分 析
6车 道 。
厚 3 m, 度 为 0 0c 渐 变 , 桥 向 横 向加 5c 高 ~8 m 纵 劲 矮肋标 准 间距 4m。
3 主 梁 受 力 分 析
3 3 偏 载 布置 2车道 计算 结果 . 偏 载布 置 2车道 计 算 结 果 见 图 6 各 工 况 作 , 用 下受 力情 况见 表 l 。
4 m 渐变 至 1 0c 5c 2 m。在 斜拉 索锚 固处 设置 横 隔 板 , 隔 梁厚 5 m。端横 隔梁 的厚度 为 1 0c 横 0c 5 m。 横 隔板 悬臂 端 和非 拉 索 区节段 设 置 加 劲 矮 肋 , 加 劲 肋厚 3 m, 5c 高度 为 O 0 c 渐 变 。主梁标 准 ~8 m
距 丹 江 口大坝 约 9 . m。 3 7k
1 主梁 结构 设计
主 梁 为 预 应 力 混 凝 土 结 构 , 用 C 5混 凝 采 5 土 。主梁 顶 板宽 2 . I其 中悬臂 长 度 5 7 6 51 , T . 5m,
桥塔 处梁 高 7 2I , 中梁高 3 41 ; . I跨 T . I中跨 等 高度 T 段长 2 I桥 塔 处 段 长 6m; 跨 端 部 段 等 高度 4I , T 边 长 2 . l 余梁 段底 部按 1 8次 抛物 线变 化 , O 8r 。其 r .
压 力 分 散 型胶 体 锚 索 结 构试 验研 究 和 理 论 分 析 *
浅谈大跨度桥梁抗风设计研究的发展现状
浅谈大跨度桥梁抗风设计研究的发展现状随着我国提出建设交通强国,我国交通工程建设迎来新时代踏上新征程,其中桥梁工程作为我国交通工程的重要组成部分,特别是大跨度桥梁在过去几十年快速发展,已然使中国桥梁技术成为令全世界同行瞩目的中心。
该文对大跨度桥梁为何要进行抗风设计的必要性进行阐述分析,介绍风致振动的类型,并就目前大跨度桥梁如何提高其抗风性能的方法进行了介绍,还简介了目前部分斜拉桥、悬索桥、拱桥三大类桥型所采用的抗风设计方法。
标签:大跨度;桥梁;抗风;风致振动我国交通工程建设在过去的几十年里取得了举世瞩目的辉煌成就,党的十九大报告中更是对我国交通工程的总体建设目标提出了更高标准的要求,要在新时代开启建设交通强国的新征程。
纵观我国交通工程建设发展的这几十年,桥梁工程作为交通工程的重要组成部分,其迅猛的发展速度令人惊叹。
从1991年我国建成了第一座完全由我国自行设计、自行建造的主跨达423m的现代化桥梁——上海南浦大桥;2008年正式建成通车的主跨1088m的世界第二大跨径的斜拉桥——苏通大桥;2009年建成通车的采用分体式钢箱梁主跨1650m目前位居世界悬索桥第二的西堠门大桥;2014年正式开工,建成后其悬索桥跨度在国内排名第一、世界排名第二,跨度长达1700m的杨泗港长江大桥。
随着科学技术的不断发展,桥梁设计也加入了新的科学理论、正在探索新的研究方法、开发创新新的高性能材料、施工工艺不断推陈出新,在科学技术的强有力推动下,全世界必将有更多大跨度的桥梁在今后涌现。
1、抗风设计的必要性现代桥梁的跨径随着时代发展需要正在逐步增大,其整体结构也趋向于质轻柔和,这使得桥梁对风荷载的作用就变得更加敏感。
桥梁在设计风速下的抗风稳定性已经成为控制桥梁结构设计和现场施工的至关重要的因素之一。
从1818年至今,全球有记录的因风致振动被强风摧毁的大跨度桥梁就有近20座。
这其中就包括1940年主跨853m风振致毁的美国塔科马大桥,也就是从那时开始,桥梁设计者们才真正重视对大跨度桥梁进行抗风设计的研究。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
郑群华
(武 汉 西 四 环 线 高 速 公 路 建 设 管 理 有 限 公 司 武 汉 430015)
摘 要 为研究武汉四环线汉江大 桥 抗 风 性 能,计 算 了 施 工 状 态 和 成 桥 状 态 结 构 的 动 力 特 性 ,通 过试验测量主梁的三分力系数值,评价了汉江大桥的颤振和 涡 振 性 能,最 后 进 行 静 风 稳 定 性 分 析 。 试验及计算分析结果表明,汉江大桥 颤 振 临 界 风 速 高 于 检 验 风 速,涡 激 振 动 最 大 振 幅 小 于 规 范 容 许 值 ,静 风 失 稳 临 界 风 速 较 高 ,整 体 抗 风 性 能 良 好 。 关键词 斜拉桥 风洞试验 涡振 颤振 静风稳定
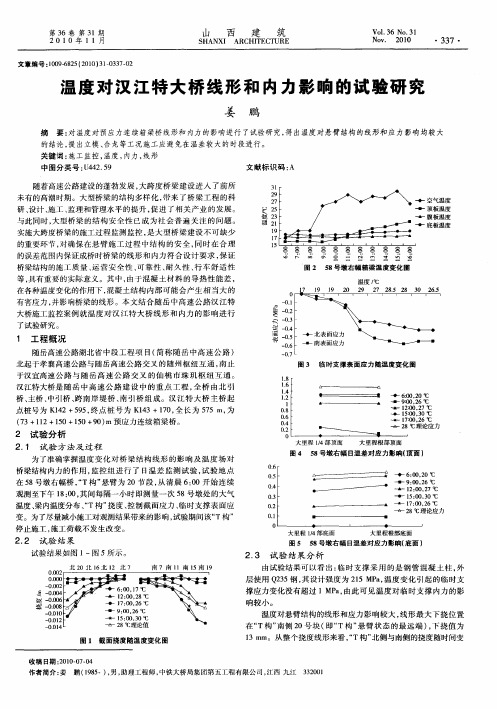
4 涡 激 振 动 试 验
涡激共振通常 发 生 在 较 低 的 风 速 下,其 振 动 形式通常为竖向涡振和扭转涡振。因为节段模型 缩尺比较大,模型 中 能 较 好 模 拟 出 各 种 影 响 涡 激 振动性能的细部 构 造,因 此 涡 激 振 动 性 能 的 评 定 以节段模型试验结果为依据。通过主梁节段模型 试验测定涡激振 动 的 发 振 风 速、振 幅,并 根 据 《公 路桥梁抗风设计规 范》对 主 梁 的 涡 激 振 动 特 性 作 出评价。图5~图9为成桥状 态 在 均 匀 流 工 况 下 各攻角涡激振动响应幅值与风速的关系。
总 第 282 期 2017 年 第 3 期
交 通 科 技 Transportation Science & Technology
DOI 10.3963/j.issn.1671-7570.2017.03.017
Serial No.282 No.3Jun.2017
武汉四环线汉江大桥抗风性能Fra bibliotek究图 4 动 力 模 型 试 验 照 片
采用直接测 量 法 进 行 颤 振 试 验 时,要 求 模 型 段模型的阻尼比根据《公路桥梁抗风设计规范桥》 系统满足动力节 段 模 型 的 相 似 律,即 要 求 模 型 与 (JTG D60-01-2004)的 建 议 值,偏 安 全 的 取 值 原型(实桥)之间 保 持 弹 性 参 数、惯 性 参 数 和 阻 尼 为1.0%。同时,通 过 全 桥 气 弹 模 型 风 洞 试 验,测 参数等3组无量纲参数一致。颤振稳定性试验节 定了该桥的颤振临界风速。表2列出了该桥具体
后程序自动在全域 内 进 行 搜 索,得 到 0°攻 角 下 三
维颤振分析的结 果,成 桥 状 态 和 施 工 状 态 的 颤 振
临界风速值 均 大 于 150 m/s,大 于 节 段 模 型 试 验
和全桥气弹模型 试 验 得 到 的 结 果,这 表 明 汉 江 大
桥 颤 振 性 能 良 好 ,安 全 富 余 度 高 。
56
郑 群 华 :武 汉 四 环 线 汉 江 大 桥 抗 风 性 能 研 究
2017 年 第 3 期
的颤振临界风速结果。
表 2 实 桥 颤 振 临 界 风 速
状态
成桥 状态
施工 状态
攻角
实 桥 临 界 风 速/(m·s-1)
/(°) 节段
全桥气弹
模型试验
模型试验
-5 74.8
>82
-3 75.9
图 3 施 工 状 态 主 梁 断 面 三 分 力 系 数 曲 线
3 颤 振 稳 定 性 试 验
颤振性能对桥梁结构的安全很重要。通过主 梁动力节段模型 风 洞 试 验,可 以 初 步 评 估 该 桥 的 抗风稳定性,试 验 在 西 南 交 通 大 学 XNJD-1 工 业 风洞第二试验段中进行。动力试验所用的节段模 型与静力试验的 模 型 相 同,并 在 模 型 两 端 设 置 端 板 ,以 保 证 主 梁 断 面 气 动 绕 流 的 二 维 特 性 ,由 8 根 拉伸弹簧悬挂在 支 架 上,形 成 可 竖 向 运 动 和 绕 模 型轴线转动的二自由度振动系统。试验支架置于 洞 壁 外 ,以 免 干 扰 流 场 ,见 图 4。
图6 攻角 -3°竖向涡振响应(成桥态) 图 7 攻 角 0°竖 向 涡 振 响 应 (成 桥 态 ) 图 8 攻 角 +3°竖 向 涡 振 响 应 (成 桥 态 )
图 5 攻 角 -5°竖 向 涡 振 响 应 (成 桥 态 )
图9 攻角 +5°竖向涡振响应(成桥态)
由图5~ 图 9 可 见,在 0°,-3°,-5°工 况 下, 没有出现明显 的 涡 激 共 振 现 象,在 +3°和 +5°工 况下出 现 了 竖 向 涡 激 共 振 现 象。 参 考 文 献 第 [1] 7.2.6条,基于人体舒适度的 考 虑,主 梁 涡 激 振 动 振幅须小于 规 定 的 容 许 值。 成 桥 状 态:主 梁 竖 向 涡振振幅容许值[ha]=0.056 8 m。 可 见,汉 江 大 桥的涡振性能满足要求。
臂 状 态 下 ,桥 梁 的 一 阶 振 型 表 现 为 主 梁 悬 臂 竖 摆 ,
二阶振型表现为 桥 塔 反 对 称 横 弯;在 最 大 单 悬 臂
状 态 下 ,桥 梁 的 一 阶 振 型 表 现 为 桥 塔 反 对 称 横 弯 ,
二阶振型表现为桥塔正对成横弯。
表 1 汉 江 大 桥 在 成 桥 状 态 和 施 工 状 态 时 的 动 力 特 性
武汉市 四 环 线 为 双 向 8 车 道,设 计 速 度 100 km/h 的 高 速 公 路 ,标 准 路 基 宽 度 为 41.0 m,荷 载 等级公路-I级。 汉 江 大 桥 连 接 武 汉 市 东 西 湖 区 和 蔡 甸 区 ,是 武 汉 市 四 环 线 的 重 要 过 江 通 道 、跨 越 汉江的控制性工程。主桥为双塔预应力混凝土边 箱 梁 斜 拉 桥 ,跨 径 组 成 为77 m+100 m+360 m+ 100m+77m,主桥 全 长 714 m,拉 索 采 用 平 行 双 索 面 布 置 ,锚 固 于 主 梁 两 侧 ;桥 塔 采 用 钢 筋 混 凝 土 H 型塔。由于拉索锚固区及风嘴需要占用一定 宽 度 ,主 桥 断 面 全 宽 43.6 m。
静力三分力系数是风致响应计算分析所必须 的气动力参数。试验在西南交通大学单回流串联 双试验段工业风 洞 的 第 二 试 验 段 中 进 行,试 验 来 流为均匀流,成桥 状 态 和 施 工 状 态 的 三 分 力 系 数 见图2和图3。试验结果 表 明,在 零 攻 角 情 况 下, 成 桥 状 态 主 梁 的 阻 力 系 数 为1.125 3,施 工 状 态 为 0.688 2。 无 论 在 成 桥 状 态 或 施 工 状 态 ,升 力 系 数 曲 线 和 力 矩 系 数 曲 线 的 斜 率 在 较 大 的 正 、负 攻 角
根据气象资料,大 桥 区 域 的 地 表 粗 糙 度 属 于 C 类,参阅《公路桥梁抗风设计规范》(JTG D60- 01-2004)[1],成桥状态桥面高度处的设计基 准 风 速为28.37m/s。如果取20 年重现 期,施 工 阶 段 的 设 计 基 准 风 速 为 24.96 m/s。
汉江大桥主桥 跨 度 大、桥 塔 高,桥 面 宽,为 缆 索 承 载 的 柔 性 桥 梁 体 系 ,这 种 桥 梁 相 对 刚 度 小 ,阻 尼低,是风致 振 动 的 敏 感 结 构[2-3],有 必 要 通 过 风 洞 试 验 和 必 要 的 计 算 分 析 ,考 察 主 梁 的 气 动 特 征 , 确保大桥的抗风 安 全 和 使 用 期 间 的 舒 适 性,必 要 时采取一定的气动措施 。 [4] 本文主要通过风 洞 试 验 [5],获 取 主 梁 的 静 力 系 数 、涡 激 振 动 和 颤 振 稳 定
主 梁 、桥 塔 和 桥 墩 离 散 为 空 间 梁 单 元 ,主 梁 的 质量和质量惯性 矩 则 采 用 质 量 点 单 元 来 模 拟;斜 拉索采用空间杆 单 元,并 直 接 与 主 梁 上 的 刚 臂 单 元进行联系;索 塔 各 构 件 均 采 用 空 间 梁 单 元。 在 计算过程中,不 考 虑 支 座 的 弹 性 和 位 移。 根 据 设 计 资 料 ,成 桥 状 态 结 构 的 边 界 约 束 条 件 为 :主 梁 顺 桥 向 自 由 度 放 松 ,主 梁 的 扭 转 自 由 度 约 束 ;竖 向 和 扭转自由度和辅助墩的竖向和扭转自由度设为主 从 约 束 关 系 ;主 梁 和 桥 塔 相 接 的 区 域 ,横 向 和 竖 向 为 主 从 约 束 关 系 ,顺 桥 向 约 束 放 松 ;所 有 桥 墩 底 部 设 置 为 固 定 约 束 ,不 考 虑 桩 - 水 - 土 的 相 互 作 用 。 图1为成桥状态、施 工 过 程 中 2 种 状 态 的 有 限 元 分析模型。
桥梁状态 振型序号
1
成桥状态
2
3
1
最大双悬臂
2
3
1
最大单悬臂
2
3
频 率/Hz 0.200 4 0.467 6 0.479 1 0.344 5 0.620 3 0.665 0 0.468 1 0.502 6 0.639 8
振型特点 主梁纵飘 桥塔反对称横弯 桥塔反对称横弯 主梁第一阶竖弯 桥塔反对称横弯 桥塔对称横弯 桥塔反对称横弯 桥塔对称横弯 主梁第一阶横弯
性等。
1 结 构 动 力 特 性 计 算 分 析
1.1 计 算 模 型 采用大 型 通 用 有 限 元 分 析 软 件 ANSYS,对
汉江大桥成桥状态和施工过程中的最大单悬臂、 最大双悬臂状态等3种工况进行建模分析。由于 该 桥 主 梁 约 束 扭 转 刚 度 的 影 响 较 小 ,因 此 采 用 “鱼 骨 式 ”单 主 梁 的 力 学 模 型 。
2017 年 第 3 期
郑 群 华 :武 汉 四 环 线 汉 江 大 桥 抗 风 性 能 研 究
57
5 静 风 稳 定 性 分 析
6 结 论
为检验汉江大 桥 的 静 风 稳 定 性 能,应 用 三 维 静 风 失 稳 模 型 ,在 综 合 考 虑 几 何 、静 风 荷 载 非 线 性 的 基 础 上 ,采 用 修 正 的 增 量 与 内 外 2 种 迭 代 方 法 , 编制了非线性静 风 稳 定 性 分 析 程 序,基 于 有 限 元 软件 ANSYS对桥梁从稳定到失稳的全过程进行 分析。 主 梁 静 风 响 应 随 风 速 变 化 过 程 见 图 10 及 图 11。
