SPSS与研究方法 CH13

圖13-5 「Discriminant Analysis: Classification」視窗設定
• 在「Discriminant Analysis」視窗中，按〔Sa ve〕，就會產生「Discriminant Analysis: Sa ve」視窗，我們選定的情形如圖13-6所示。
圖13-6 「Discriminant Analysis: Save」視窗設定
圖13-2 「Discriminant analysis: Define」視窗設定
• 將「經驗」、「在校成績」、「測驗成績」這 些自變數選入「Independents」（自變數）下 的方盒內，如圖13-3所示。可以用SPSS內定的 「Enter independents together」（使用所有 變數）或者「Use stepwise method」（使用逐 步方法）。
13.2 區別分析-區別二群
• 大海軟體公司裡面具有企管碩士學位的幹部30 名，分別有15名「前途光明」的幹部，15名 「前途黯淡」的幹部。該公司的總經理想要了 解，在人力資源管理中的員工錄用上，應特別 重視「經驗」、「在校成績」、「測驗成績」 中的什麼因素
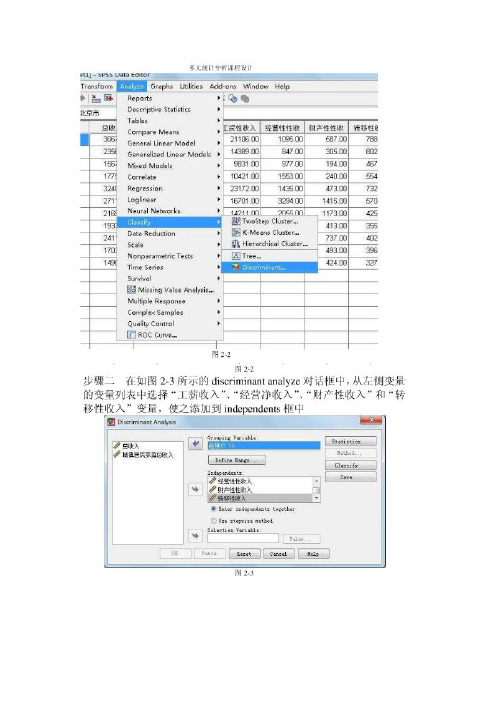
• 開啟檔案（檔案名稱：...\Chap13\Discriminant Two Groups.sav）。此檔案包括了組別（分為二組， 以1表示「前途光明」組，以2表示「前途黯淡」 組）、經驗（工作經驗）、在校成績（在校成績總 平均）、測驗成績（應徵測驗成績）。組別為名義 變數，其他的變數為區間變數。 • 進入SPSS，按〔Analyze〕、〔Classify〕、〔Dis criminant〕（〔分析〕〔分類〕〔判別〕），在 所產生的「Discriminant Analysis」視窗中，將 「組別」變數選入右邊的「Grouping Variable」 （分組變數）下的空格中，選取〔分組（??）〕， 按其下的〔Define Range〕（定義範圍），在「Di scriminant analysis: Define」視窗中的「Minim um:」（最小值）填入「1」，「Maximum:」（最大 值）填入「2」，如圖13-2所示。表示我們是將資 料分成二組。
• 區別分析是一種相依方法，其準則變數（依變
數）為事先訂定的類別或組別。其預測變數（自變 數）是區間資料或比率資料。 • 區別分析的目的是： 1. 找出預測變數（自變數）的線性組合，使組間變異 相對於組內變異的比值為最大。 2. 找出哪些預測變數具有最大的區別能力。 3. 根據新受試者的預測變數的數值，將該受試者指派 到某一群體。換句話說，在區別方程式建立之後， 研究者可將某人的有關資料（這些資料是在模式中 的變數）代入這個方程式中，以了解這個人被歸類 到哪一群。 4. 檢定各係數與0之間是否有顯著性的差異，以及檢 定各組的重心（centroid）是否有顯著性的差異。
• 區別函數的數目等於從分組數目減一與 自變數數目（有幾個自變數）中取最小 的數目。例如，分組數目有三個（分成 三組），自變數數目有三個，則區別函 數的數目等於Min（分組數目減一，自變 數數目）Min2。因此會有兩個區別函數。
• 在單因子多變量變異數分析的檢定達到顯著水 準之後，進一步可採用區別分析。區別分析適 用的情況是依變數有一個且為名義變數，自變 數可為區間變數或名義變數。如自變數為區間 變數，則可進行區別分析或者Logistic迴歸分 析，如果自變數為名義變數則要進行虛擬變數 區別分析，如圖13-1所示。
• 從「各組平均數的相等性檢定」表中可知，經驗 在二組（前途光明組及前途黯淡組）的平均數有 顯著差異，顯著性=0.003，達到顯著水準。在校 成績及測驗成績均未達顯著水準，表示在校成績 及測驗成績在二組（前途光明組及前途黯淡組） 的平均數均沒有顯著差異。
• Wilks‘ Lambda可用來檢定虛無假說。在下表中， 「經驗」、「在校成績」、「測驗成績」的顯著性分別為 0.003、0.870、0.594，在α=0.05之下， 我們要棄卻d1=0的虛無假設（經驗在二組上無顯著差異）， 而認為經驗在二組上有顯著差異。
• 圖13-7顯示了儲存的資料，SPSS的內定名稱是D is_1、Dis1_1、Dis1_2、Dis2_2。以第一名觀 察值來看，在SPSS處理後，他被分到第一組 （前途光明組），他的判別分數（discriminan t score）是3.58。他被分到第一組的機率是0. 98，被分到第二組的機率是0.02。 • 圖13-8顯示了SPSS的內定名稱Dis_1、Dis1_1、 Dis1_2、Dis2_2的註解（所代表的意義）。
• 描述性統計量（descriptives）：
• 矩陣（Matrices）：
• 區別函數係數（Function Coefficients）：
• 在「Discriminant Analysis」視窗中，按〔Class ify〕，就會產生「Discriminant Analysis: Clas sification」視窗，我們選定的情形如圖13-5所 示。 • 在「Prior Probabilities」（事前機率）的方盒下， 使用內定的「All groups equal」（所有組別大小均 等），也就是將所有組別的事前機率假設為相等。 • 在「Use Covariance Matrix」（使用共變異數矩陣）， 使用內定的「Within-groups」（組內變數），表示以組內 的共變異數矩陣來將觀察值加以分類。在「Display」 （顯示）下的方盒內，點選「Summary table」 （分類統計表）。
• 複區別分析的處理與13.2節所說明的大同小異。開 啟檔案（檔案名稱：...\Chap13\Discriminant Th ree Groups.sav）。此檔案包括了組別（分為三組， 以1表示「前途光明」組，以2表示「前途普通」組， 以3表示「前途黯淡」組）、經驗（工作經驗）、 在校成績（在校成績總平均）、測驗成績（應徵測 驗成績）。組別為名義變數，其他的變數為區間變 數。 • 首先進入SPSS，按〔Analyze〕、〔Classify〕、 〔Discriminant〕（〔分析〕〔分類〕〔判別〕）， 在所產生的「Discriminant Analysis」視窗中， 將「組別」變數選入右邊的「Grouping Variable」 （分組變數）下的空格中，選取〔分組（??）〕， 按其下的〔Define Range〕（定義範圍），在「Di scriminant analysis: Define」視窗中的「Minim um:」（最小值）填入「1」，「Maximum:」（最大 值）填入「3」，表示我們是將資料分成三組。
從典型區別函數係數來看，「經驗」的相對重要性較高。
• 結構矩陣（Structure Matrix）顯示，區別變 數和標準化典型區別函數之間的合併後組內相 關。變數係依函數內相關的絕對值大小加以排 序。相關係數的絕對值愈大者，表示此變數與 區別函數的相關愈高。從結構矩陣來看，「經 驗」與區別函數的相關最高。
• 「對數行列式」表中，如果變數之間具有高度多元共線 性問題，則對數行列式值（log determinant）會趨近 於0，而且等級（rank）會不等於自變數的數目。 • 此表顯示，「前途光明」組、「前途黯淡」組的對數行 列式值分別為12.783、12.657，與0距離相當大，而且等級 （=3），與自變數的數目（=3）相同，所以有理由相 信， 變數之間沒有高度多元共線性問題。
為了達成上述的目的，必須建立一個區別的直 線函數（linear function）如下：
• 在區別分析中，研究者常常將不同的人或個體分成 不同的群組，但是除此之外，我們還可以從區別函 數中來檢視各變數的相對重要性。假設我們用區別 分析對成功、不成功的管理者建立如下的區別函數：
• 其中，X1表示「與人相處的能力」、X2表示「對部 屬的激勵」、X3表示「專業技能」。由於區別函數 中的各係數值都經過標準化，我們可以說：在分辨 管理者的成功與否時，「與人相處的能力」的重要 性低於另外兩個變數
圖13-7 儲存的資料
圖13-8 SPSS的內定名稱Dis_1、Dis1_1、Dis1_2、Dis2_2 的註解（所代表的意義）
13.3 複區別分析
• 如前所述，如果所分類的二個群組，則會有一 個標準化的典型區別函數，如果所分類的是三 個群組，則會有二個標準化的典型區別函數。 • 由於每一個群組都會有一組Fisher's線性區別 函數，因此在三個群組下，會有三個Fisher's 線性區別函數。 • 如果必須分為三組（及以上），我們所涉及的 就是多元區別分析（multiple discriminant a nalysis）或稱複區別分析的問題。
• 在樣本數的要求上，全部觀察值數目最好是自變數（預 測變數）的10~20倍。每個自變數應有20個觀察值。
• 進行區別分析有以下的假定： 1. 自變數（預測變數）所屬母群體是常 態分配。 2.每組樣本均來自多變量常態分配的母群 體，亦即每一組內共變異數矩陣應大致 相等。 3.任何自變數（預測變數）都不是其他自 變數的線性組合，也就（Classification Results）表又稱為混淆矩 陣（Confusion Matrix）表。在我們的觀察值中，有15 名屬於前途光明組，有15名屬於前途黯淡組。經過分類 之後，前途光明組有11名，前途黯淡組有11名。每一組 都有4名被分到另外一組去了。正確分類的比率是73.3% （22/30）。
圖13-3 「Discriminant Analysis」視窗設定
• 在「Discriminant Analysis」視窗中，按〔Stati stics〕，就會產生「Discriminant Analysis: St atistics」視窗，我們選定的情形如圖13-4所示
圖13-4
「Discriminant Analysis: Statistics」視窗設定
• Wilks' Lambda值=0.710，顯著性=0.028>0.05， 表示區別函數對於依變數有顯著的解釋能力。