第1章例题详解
01章_热力学第一定律及其应用-例题和习题课解析

W V pdV p(V2 V1 ) 330.56 103 (40.00 15.00) 10 3 2864 J
1
V2
上一内容
下一内容
回主目录
返回
2018/12/28
例题
例: 10mol理想气体,压力为1000kPa,温度为300 K , 求下列 各种情况下的W: 1.在空气中( p )体积胀大1dm 3 ; 2.在空气中胀大到气体的压力也为p ; 3.等温可逆膨胀至气体的压力也为p。
3
1000 p1 10 8.314 300 ln 3.W nRT ln 100 p2 57.43kJ
上一内容
下一内容
回主目录
返回
2018/12/28
七、例题
例:气体He从0C, 5 105 Pa, 10dm3,经一绝热可逆 过程膨胀至10 Pa,试计算T2、Q、W、U和H。
物理化学电子教案—第一章
U Q W
上一内容
下一内容
回主目录
返回
2018/12/28
例题
例1:在25C时, 2molH 2的体积为15dm3,此气体 ( 1 )在定温下,反抗外压为105 Pa时,膨胀到体 积为50dm3 ; (2)在定温下可逆膨胀到体积为50dm3 , 试计算两种膨胀过程的功。
3
4865J
上一内容
下一内容
回主目录
返回
2018/12/28
例题
W
(2)
(3)
p(V2 V1 ) 105 (40.00 15.00) 103
2500 J
根据理想气体状态方程
pV nRT nRT 2 8.314 298.2 330.56kPa p 3 V 15.00 10
空间向量及其运算 高中数学例题课后习题详解

第一章空间向量与立体几何1.1空间向量及其运算1.1.1空间向量及其线性运算例1如图1.1-9,已知平行四边形ABCD ,过平面AC 外一点O 作射线OA ,OB ,OC ,OD ,在四条射线上分别取点E ,F ,G ,H ,使OE OF OG OH k OA OB OC OD====.求证:E ,F ,G ,H 四点共面.图1.1-9分析:欲证E ,F ,G ,H 四点共面,只需证明EH ,EF ,EG uuu r 共面.而由已知AD ,AB ,AC 共面,可以利用向量运算由AD ,AB ,AC共面的表达式推得EH ,EF ,EG uuu r 共面的表达式.证明:因为OE OF OG OH k OA OB OC OD====.所以OE kOA = ,OF kOB = ,OG kOC = ,OH kOD = .因为四边形ABCD 是平行四边形,所以AC AB AD =+ .因此EG OG OE kOC kOA k AC =-=-=()()k AB AD k OB OA OD OA =+=-+- OF OE OH OE EF EH=-+-=+ 由向量共面的充要条件可知,EH ,EF ,EG uuu r 共面,又EH ,EF ,EG uuu r 过同一点E ,从而E ,F ,G ,H 四点共面.练习1.举出一些表示三个不同在一个平面内的向量的实例.【答案】实例见解析;【解析】【分析】在空间几何体中,从一点出发的不同面的向量即可.【详解】在三棱锥P ABC -中,PA →,PB →,PC →不同在一个平面内;长方体ABCD A B C D ''''-中,从一个顶点A 引出的三个向量AB →,AD →,AA →'不同在一个平面内.2.如图,E ,F 分别是长方体ABCD A B C D ''''-的棱AB ,CD 的中点、化简下列表达式,并在图中标出化简结果的向量:(1)AA CB '- ;(2)AA AB BC '++ ;(3)AB AD B D ''-+ ;(4)AB CF + .【答案】(1)AD ' ;(2)AC ' ;(3)0 ;(4)A E【解析】【分析】根据空间向量加减运算的运算法则计算即可.【详解】(1)AA CB AA BC AA A D AD ''''''-=+=+= ;(2)AA AB B C AA A B B C AC '''''''++=++''= ;(3)0AB AD B D AB AD BD DB BD -+=-+=+''= ;(4)AB CF AB BE AE +=+= .3.在图中,用AB ,AD ,AA ' 表示A C ' ,BD ' 及DB ' .【答案】A C AB AD AA =+'-' ;BD AA AD AB ''-=+ ;DB AA AB AD ''=+- .【解析】【分析】根据空间向量的加减运算法则可转化.【详解】()A C A A AC AA AB AD AB AD AA =+=-''++=-''+ ,()()BD BD DD BA BC DD AB AD AA AA AD AB =+=++=-++=+-''''' ,()()DB DB BB DA DC BB AD AB AA AA AB AD =+=++=-++''''=-'+ .4.如图,已知四面体ABCD ,E ,F 分别是BC ,CD 的中点,化简下列表达式,并在图中标出化简结果的向量;(1)AB BC CD ++ ;(2)()12AB BD BC ++ ;(3)()12AF AB AC -+ .【答案】(1)AD ;(2)AF ;(3)EF【解析】【分析】根据空间向量的线性运算法则计算即可.【详解】(1)AB BC CD AC CD AD ++=+= ;(2)()12AB BD BC AB BF AF ++=+= ;(3)()12AF AB AC AF AE EF -+=-= .5.如图,已知正方体ABCD A B C D ''''-,E ,F 分别是上底面A C ''和侧面CD '的中心,求下列各式中x ,y 的值:(1)AC x AB BC CC →→→→⎛⎫''=++ ⎪⎝⎭(2)AE AA x AB y AD→→→→'=++(3)AF AD x AB y AA →→→→'=++【答案】(1)1x =;(2)12x y ==;(3)12x y ==.【解析】【分析】(1)化简+AC AB AD AA →→→→''=+即得解;(2)化简1()2AE AA AC →→→''=+即得解;(3)化简1122AF AD AC →→→'=+即得解.【详解】(1)+AC AB AD AA AB BC CC →→→→→→→'''=+=++,所以1x =;(2)1111111()()2222222AE AA AC AA AC AA AA AB AD AA AB AD →→→→→→→→→→→→'''''''=+=+=+++=++,所以12x y ==;(3)111111()222222AF AD AC AD AB AA AD AD AB AA →→→→→→→→→→'''=+=+++=++,所以12x y ==.1.1.2空间向量的数量积运算例2如图1.1-12,在平行六面体ABCD A B C D ''''-中,5AB =,3AD =,7AA '=,60BAD ∠=︒,45BAA DAA ''∠-∠=︒.求:图1.1-12(1)AB AD ⋅ ;(2)AC '的长(精确到0.1).解:(1)||||cos ,AB AD AB AD AB AD ⋅=〈〉,53cos 607.5=⨯⨯︒=;(2)()22AC AB AD AA ''=++ ()222||||2AB AD AA AB AD AB AA AD AA '''=+++⋅+⋅+⋅ ()222537253cos 6057cos 4537cos 45=+++⨯⨯︒+⨯⨯︒+⨯⨯︒98=+,所以13.3AC '≈.例3如图1.1-13,m ,n 是平面α内的两条相交直线.如果l m ⊥,l n ⊥,求证:l α⊥.图1.1-13分析:要证明l α⊥,就是要证明l 垂直于α内的任意一条直线g (直线与平面垂直的定义).如果我们能在g 和m ,n 之间建立某种联系,并由l m ⊥,l n ⊥,得到l g ⊥,那么就能解决此问题.证明:在平面α内作任意一条直线g ,分别在直线l ,m ,n ,g 上取非零向量l ,m ,n ,g .因为直线m 与n 相交,所以向量m ,n 不平行.由向量共面的充要条件可知,存在唯一的有序实数对(,)x y ,使g xm yn =+u r u r r .将上式两边分别与向量l作数量积运算,得l g xl m yl n ⋅=⋅+⋅ .因为0l m ⋅=r u r ,0l n ⋅=r r (为什么?),所以0l g ⋅=r u r.所以l g ⊥.这就证明了直线l 垂直于平面α内的任意一条直线,所以l α⊥.练习6.如图,在正三棱柱111ABC A B C -中,若1AB =,则1AB 与1BC 所成角的大小为()A.60︒B.90︒C.105︒D.75︒【答案】B【解析】【分析】取向量1,,BA BC BB 为空间向量的一组基底向量,表示出1AB 与1 BC ,再借助空间向量运算即可计算作答.【详解】在正三棱柱111ABC A B C -中,向量1,,BA BC BB 不共面,11AB BB BA =- ,11BC BC BB =+ ,令1||BB a = ,则||||BA BC == ,而1BB BA ⊥ ,1BC BB ⊥ ,于是得11112111()()AB BC BB BA BC BB BB BC BB BA BC BA BB ⋅=-⋅+=⋅+-⋅-⋅ 2cos 600a =-=,因此,11AB BC ⊥ ,所以1AB 与1BC 所成角的大小为90︒.故选:B7.如图,正方体ABCD A B C D ''''-的棱长为1,设AB a = ,AD b = ,AA c '= ,求:(1)()a b c ⋅+ ;(2)()a a b c ⋅++ ;(3)()()a b b c ⋅++ .【答案】(1)0;(2)1;(3)1【解析】【分析】在正方体中,根据线线关系,结合空间向量运算法则对每个小题进行运算即可.【详解】(1)在正方体中,AB AA ⊥',AB AD⊥故()0a b c a b a c →→→→→→→⋅+=⋅+⋅=(2)由(1)知,()()1a abc a a a b c →→→→→→→→→⋅++=⋅+⋅+=(3)由(1)及AD AA '⊥知,2()()()1a b b c a b c b b c →→→→→→→→→→++=⋅+++⋅=8.如图,在平行六面体ABCD A B C D ''''-中,4AB =,3AD =,5AA '=,90BAD ∠=︒,BAA '∠=60DAA '∠=︒.求:(1)AA AB '⋅ ;(2)AB '的长;(3)AC '的长.【答案】(1)10;(261;(385【解析】【分析】(1)根据数量积的定义即可计算;(2)由AB AA A B ''''=+ 平方即可求解;(3)由A AB AD A C A =+'+'即可求解.【详解】(1)1cos 6054102AA AB AA AB ''⋅=⋅⋅=⨯⨯= ;(2)AB AA A B ''''=+ ,()()222222252101661AB AA A B AA AB AA AA AB AB '''''''∴=+=+=+⋅+=+⨯+= ,61AB '= AB '61;(3) AC AC CC AB AD AA '''=+=++ ,()()222222AC AB AD AA AB AD AA AB AD AB AA AD AA '''''∴=++=+++⋅+⋅+⋅ 11169252054358522⎛⎫=++++⨯⨯+⨯⨯= ⎪⎝⎭,85AC '∴= AC '85.9.如图,线段AB ,BD 在平面α内,BD AB ⊥,AC α⊥,且AB a =,BD b =,AC c =.求C ,D 两点间的距离.222a b c ++【解析】【分析】连接AD ,可得222AD a b =+,根据AC AD ⊥可求.【详解】连接AD ,BD AB ⊥ ,22222AD AB BD a b ∴=+=+,AC α⊥,AD α⊂,AC AD ∴⊥,222222CD AD AC a b c ∴=+=++,222CD a b c ∴=++即C ,D 222a b c ++.习题1.1复习巩固10.如图,在长方体ABCD A B C D ''''-中,E 、F 分别为棱AA '、AB 的中点.(1)写出与向量BC 相等的向量;(2)写出与向量BC 相反的向量;(3)写出与向量EF 平行的向量.【答案】(1),,AD A D B C '''' ;(2),,,DA CB C B D A '''' ;(3),,,,D C CD A B BA FE'''' 【解析】【分析】(1)由相等向量的定义可判断;(2)由相反向量的定义可判断;(3)由平行向量的定义可判断.【详解】(1)由相等向量的定义知,大小相等,方向相同的两个向量为相等向量,所以与向量BC 相等的向量为,,AD A D B C '''' ;(2)由相反向量的定义知,大小相等,方向相反的两个向量为相反向量,所以与向量BC 相反的向量为,,,DA CB C B D A '''' ;(3)由平行向量的定义知,方向相同或相反的两个向量为平行向量,所以与向量EF 平行的向量为,,,,D C CD A B BA FE '''' .11.如图,已知平行六面体ABCD A B C D ''''-,化简下列表达式,并在图中标出化简结果的向量:(1)AB BC + ;(2)AB AD AA '++ ;(3)12AB AD CC '++ ;(4)()13AB AD AA '++ .【答案】(1)AC →,向量如图所示;(2)AC →',向量如图所示;(3)AE →,向量如图所示;(4)AF →,向量如图所示;【解析】【分析】根据平行六面体基本性质及空间向量基本运算化简每个小题即可.【详解】(1)AB BC AC →→→+=,向量如图所示;(2)在平行六面体ABCD A B C D ''''-中,有AD BC →→=,AA CC →→''=,故AB AD AA AB BC CC AC →→→→→→→'''++=++=,向量如图所示;(3)由AD BC →→=知,取CC '的中点为E ,12AB AD CC AB BC CE AE →→→→→→→'++=++=,向量如图所示;(4)由(2)知,取AC '的三等分点F 点,1()3AB AD AA AF →→→→'++=,向量如图所示;12.证明:如果向量a ,b 共线,那么向量2a b + 与a共线.【答案】证明见解析【解析】【分析】由向量共线定理可证明.【详解】如果向量a ,b 共线,则存在唯一实数λ,使得b a λ= ,则()222a b a a a λλ+=+=+ ,所以向量2a b + 与a 共线.13.如图,已知四面体ABCD 的所有棱长都等于a ,E ,F ,G 分别是棱AB ,AD ,DC 的中点.求:(1)AB AC ⋅uu u r uuu r ;(2)AD DB ⋅ ;(3)GF AC ⋅ ;(4)EF BC ⋅uu u r uu u r ;(5)FG BA ⋅ ;(6)GE GF ⋅ .【答案】(1)22a ;(2)22a -;(3)22a -;(4)24a ;(5)24a -;(6)24a 【解析】【分析】根据空间向量数量积的定义计算即可.【详解】 四面体ABCD 的所有棱长都等于a ,∴任意两条棱所在直线的夹角为3π, E ,F ,G 分别是棱AB ,AD ,DC 的中点,//,//,||||2a EF BD FG AC EF FG ∴==,(1)2cos 32a AB AC a a π⋅=⨯⨯= ;(2)22cos 32a AD DB a a π⋅=⨯⨯=- ;(3)2cos 22a a GF AC a π⋅=⨯⨯=- ;(4)//EF BD ,则直线BD 与直线BC 所成角就是直线EF 与直线BC 所成角,又3CBD π∠=,2cos 234a a EF BC a π⋅==∴⨯⨯ ;(5)//FG AC ,则直线AC 与直线AB 所成角就是直线FG 与直线BA 所成角,22cos 234a a FG BA a π⋅-∴=⨯⨯= ;(6)取BD 中点M ,连接AM ,CM ,则,AM BD CM BD ⊥⊥,AM CM M ⋂= ,BD ∴⊥平面ACM ,又AC ⊂平面ACM ,BD AC ∴⊥,//EF BD ,EF AC ∴⊥,又//AC FG ,EF FG ∴⊥,0EF FG ⋅= ,可知1122GF AC a ==,222()||024a a GE GF GF FE GF GF FE GF ⎛⎫⋅=+⋅=+⋅=+= ⎝⎭∴⎪ .综合运用14.如图,在平行六面体1111ABCD A B C D -中,AC 与BD 的交点为M .设11111,,,=== A B a A D b A A c ,则下列向量中与1B M 相等的向量是()A.1122a b c --+B.1122a b c -++C.1122a b c -+ D.1122a b c ++ 【答案】B【解析】【分析】根据1112=+=+B M B B BM c BD uuuu r uuu r uuu r r uu u r代入计算化简即可.【详解】()1111112222=+=+=++=-++B M B B BM c BD c BA BC a b c uuuu r uuu r uuu r r uu u r r uu r uu u r rr r 故选:B.15.已知E ,F ,G ,H 分别是空间四边形ABCD 的边AB ,BC ,CD ,DA 的中点,用向量法证明:E ,F ,G ,H 四点共面.【答案】证明见解析【解析】【分析】根据给定条件利用空间向量的线性运算,结合空间向量共面定理即可得解..【详解】如图,E ,F ,G ,H 分别是空间四边形ABCD 的边AB ,BC ,CD ,DA 的中点,12EH FG BD == ,于是得:EG EF FG EF EH =+=+ ,即,,EG EF EH 共面,它们有公共点E ,所以E ,F ,G ,H 四点共面.16.如图,正方体ABCD A B C D ''''-(1)求A B '和B C '的夹角;(2)求证A A B C ''⊥.【答案】(1)3π;(2)证明见解析;【解析】【分析】(1)联结CD ',B D '',则A B CD '' ,A B '和B C '的夹角即CD '和B C '的夹角B CD ''∠,由B D CD B C ''''==知,B CD ''△是等边三角形,故A B '和B C '的夹角为3π.(2)联结AB ',则AB A B ''⊥,又B C ''⊥平面ABB A '',B C A B '''⊥,从而有A B '⊥平面AB C '',从而证得A A B C ''⊥.【详解】(1)联结CD ',B D '',则A B CD '' ,A B '和B C '的夹角即CD '和B C '的夹角B CD ''∠,在正方体中,设棱长为a ,则B D CD B C ''''===,则B CD ''△是等边三角形,即3B CD π''∠=故A B '和B C '的夹角为3π(2)联结AB ',则AB A B ''⊥,又B C ''⊥平面ABB A '',A B '⊂平面ABB A '',则B C A B '''⊥,又B C AB B ''''⋂=故A B '⊥平面AB C '',又AC '⊂平面AB C '',所以A A B C ''⊥17.用向量方法证明:在平面内的一条直线,如果与这个平面的一条斜线在这个平面上的射影垂直,那么它也与这条直线垂直(三垂线)【答案】证明见解析;【解析】【分析】根据向量运算法则,数量积为0即可证得垂直.【详解】如图所示,在平面α内,OB →是OA →在面内的投影向量,则BA CD →→⊥,由题知,CD OB →→⊥,则()0CD OA CD OB BA CD OB CD BA →→→→→→→→→⋅=⋅+=⋅+⋅=,故CD OA →→⊥,所以CD OA ⊥,即证得结论.拓广探索18.如图,空间四边形OABC 中,,OA BC OB AC ⊥⊥.求证:OC AB ⊥.【答案】证明见解析【解析】【详解】试题分析:利用三个不共面的向量OA OB OC ,,作为基底,利用空间向量的数量积为0,证明向量垂直,即线线垂直.试题解析:∵OA BC ⊥,∴OA OB ⊥ .∵0OA OB ⋅= ,∴()0⋅-= OA OC OB .∴0⋅-=⋅ OA OC OA OB (1)同理:由OB AC ⊥得0⋅-=⋅ OC OB OA OB (2)由(1)-(2)得0⋅-=⋅ OA OC OC OB∴()0⋅=- OA OB OC ,∴0OC BA ⋅= ,∴OC BA ⊥u u u r u u u r,∴OC AB ⊥.19.如图,在四面体OABC 中,OA OB =,CA CB =,E ,F ,G ,H 分别是OA ,OB ,BC ,CA 的中点.求证:四边形EFGH 是矩形.【答案】证明见解析;【解析】【分析】取AB 的中点D ,联结OD ,CD ,证得AB ⊥平面ODC ,AB OC ⊥,从而有EH EF ⊥;又E ,F ,G ,H 分别是OA ,OB ,BC ,CA 的中点.从而有EF GH =,结合EH EF ⊥,证得四边形EFGH 是矩形.【详解】取AB 的中点D ,联结OD ,CD ,由OA OB =,CA CB =知,⊥OD AB ,CD AB ⊥,又OD CD D ⋂=,故AB ⊥平面ODC ,又OC ⊂平面ODC ,因此AB OC⊥又E ,F ,G ,H 分别是OA ,OB ,BC ,CA 的中点.则EF AD = ,GH AD =,故EF GH=,四边形EFGH是平行四边形同理EH GF=,且EH OC,又AB OC⊥所以EH EF⊥,四边形EFGH是矩形。
第一章 或有事项

• 【例1-9】乙企业20×1年1月1日与某外贸公司 签订了一项产品销售合同,约定在20×1年2月15 日以每件产品100元的价格向外贸公司提供10 000 件A产品,若不能按期交货,乙企业需要交纳300 000元的违约金。这批产品在签订合同时尚未开始 生产,但企业开始筹备原材料以生产这批产品时, 原材料价格突然上涨,预计生产每件产品的成本 升至125元。 此例中,乙企业生产产品的成本为每件125元, 而售价为每件100元,每销售1件产品亏损25元, 共计损失250 000元。因此,这项销售合同是一项 亏损合同。如果撤销合同,乙企业需要交纳300 000元的违约金。
• 【答案】A
【例题7· 单选题】Y公司与X公司签订合同,购买X公 司10件商品,合同价格每件5000元。市场上同类商 品每件为3500元。Y公司购买的商品全部出售给Z公 司,单价为4000元。如Y公司单方面撤销合同,应 支付违约金为5000元。商品尚未购入。如满足预计 负债确认条件,Y公司应确认预计负债( )元。 A.10000 B.5000 C.1000 D.50000 • 【答案】B • 【解析】执行合同发生的损失=(5000-4000) ×10=10000(元),撤销合同支付违约金为5000 元,Y公司应确认预计负债5000元。
• 【例题6】关于或有事项,下列说法中正确的是 ( )。 A.待执行合同变成亏损合同的,该亏损合同 产生的义务满足或有事项确认预计负债规定的, 应当确认为预计负债 B.待执行合同变成亏损合同的,应当确认为 预计负债 C.企业应当就未来经营亏损确认预计负债 D.企业在一定条件下应当将未来经营亏损确认 预计负债
2008典型例题解析--第1章 几何组成分析
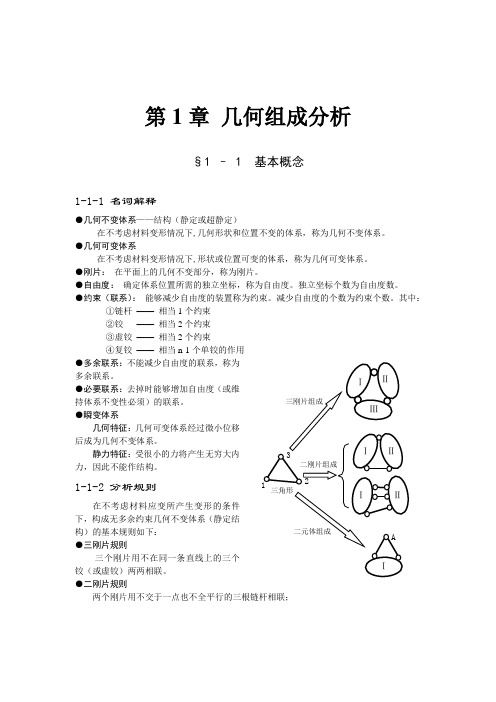
第1章几何组成分析§1 – 1 基本概念1-1-1 名词解释●几何不变体系——结构(静定或超静定)在不考虑材料变形情况下,几何形状和位置不变的体系,称为几何不变体系。
●几何可变体系在不考虑材料变形情况下,形状或位置可变的体系,称为几何可变体系。
●刚片:在平面上的几何不变部分,称为刚片。
●自由度:确定体系位置所需的独立坐标,称为自由度。
独立坐标个数为自由度数。
●约束(联系):能够减少自由度的装置称为约束。
减少自由度的个数为约束个数。
其中:①链杆——相当1个约束②铰——相当2个约束③虚铰——相当2个约束④复铰——相当n-1个单铰的作用●多余联系:不能减少自由度的联系,称为Array多余联系。
●必要联系:去掉时能够增加自由度(或维持体系不变性必须)的联系。
●瞬变体系几何特征:几何可变体系经过微小位移后成为几何不变体系。
静力特征:受很小的力将产生无穷大内力,因此不能作结构。
1-1-2 分析规则在不考虑材料应变所产生变形的条件下,构成无多余约束几何不变体系(静定结构)的基本规则如下:●三刚片规则三个刚片用不在同一条直线上的三个铰(或虚铰)两两相联。
●二刚片规则两个刚片用不交于一点也不全平行的三根链杆相联;2结构力学典型例题解析或:两个刚片用一个铰和不通过该铰心的链杆相联。
●二元体规则什么是二元体(二杆结点):两根不在同一条直线上的链杆联接一个新结点的装置,称为二元体。
在一个体系上增加或减少二元体不影响其几何不变性。
1-1-3 几何组成分析一般方法(步骤)(1)去二元体(二杆结点)。
(2)分析地基情况:上部体系与地基之间●当有满足二刚片规则的三个联系时,去掉地基,仅分析上部体系;●当少于三个联系时,必为几何常变体系;●当多于三个联系时,将地基当作一个刚片进行分析。
(3)利用规则找大刚片(最简单情况为:三个铰接杆件为刚片)。
(4)使用几何组成规则进行分析。
利用三刚片规则分析时:首先找出三个刚片,(满足三刚片规则的连接条件,即每两个刚片间有一个铰(或虚铰),然后再标出虚铰位置,最后看三个铰是否构成三角形。
第一章 习题讲解 PPT课件

2
3
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
0
5
10
15
20
25
[1sin( t)]sin(8 t)/
3
2
1.5
1
0.5
0
-0.5
-1
-1.5
-2
-15
-10
-5
0
5
10
15
[1sin( t)]sin(8 t)/
3
1.5
1
0.5
0
-0.5
-1
-1.5
-15
-10
-505来自1015[11sin( t)]sin(8 t)/
f (t)
E
sin ( T
t)
(0 t T )
0
(其 他 )
即 f (t) E sin ( t)[u (t) u (t T )] T
113绘出下列各时间函数的波形图
(1)f1(t)sin(t)u(t);(2)f2(t)sin[(tt0)]u(t) (3)f3(t)sin[(t)]u(tt0);(4)f2(t)sin[(tt0)]u(tt0)
(t
-
t0 )u(t
t0 )dt; 2
(4)
(t
-
t0 )u(t
t0 )dt 2
(5) (et t) (t 2)dt; (6) (t sin t) (t )dt
-
-
6
(7)
e jt[ (t) (t
-
t0 )]dt
解 : ( 1 )
f (t t0 ) (t ) d t
f (0 t0 )
第1章数据库系统概论习题及解答

第 1 章数据库系统概论1.1复习纲要本章介绍的主要内容:·数据管理技术的发展·数据模型·数据库系统结构1.1.1 数据管理技术的发展从20世纪50年代中期开始,数据管理技术大致经历了三个发展阶段:人工管理阶段、文件系统管理阶段和数据库系统管理阶段。
1. 人工管理阶段20世纪50年代中期以前,计算机主要从事计算工作,计算机处理的数据由程序员考虑与安排。
这一阶段的主要特点是:数据不长期保存;数据与程序不具有独立性;系统中没有对数据进行管理的软件。
2. 文件系统管理阶段20世纪50年代后期到60年代中后期,计算机系统中由文件系统管理数据。
其主要特点:数据以文件的形式可长期存储在磁盘上,供相应的程序多次存取;数据文件可脱离程序而独立存在,使得数据与程序之间具有设备独立性。
如果数据文件结构发生变化时,则对应的操作程序必须修改。
即文件系统管理文件缺乏数据独立性,并且数据冗余度大。
数据之间联系弱,无法实施数据统一管理标准。
这些都是文件系统管理的主要缺陷。
3.数据库系统管理阶段70年代初开始,计算机采用数据库管理系统管理大量数据,使计算机广泛应用于数据处理。
数据库系统管理数据的主要特点:·采用数据模型组织和管理数据,不仅有效地描述了数据本身的特性,而且描述了之间的联系。
·具有较高的数据独立性。
即数据格式、大小等发生了改变,使得应用程序不受影响。
·数据共享程度更高,冗余度比较小。
·由DBMS软件提供了对数据统一控制功能,如安全性控制、完整性控制、并发控制和恢复功能。
·由DBMS软件提供了用户方便使用的接口。
数据库系统管理数据是目前计算机管理数据的高级阶段,数据库技术已成为计算机领域中最重要的技术之一。
1.1.2 数据模型数据模型是构建数据库结构的基础,在构建时要经历从概念模型设计到DB逻辑模型和物理模型转换过程。
因此,数据模型可分为两类共4种,两类为概念模型和结构模型,其中结构模型又分为外部模型、逻辑模型和内部模型三种。
高考生物 学考例题解析及练习 第1章 遗传因子的发现2
女性正常4623男性正常4819避躲市安闲阳光实验学校第一章遗传因子的发现例题示范一、单项选择题(1-2小题每小题1分;3-4小题每小题2分) 【例1】 下列各组生物性状中,属于相对性状的是 ( ) A .草莓的红果和大果 B .狗的长毛和短腿 C .水稻的早熟和晚熟 D .棉花的短绒和粗绒【例2】家兔的毛色中白色和黑色是一对相对性状。
请你观察下列四种亲本杂交组合的亲子代性状,其中发生了性状分寓的一组是 ( )【例3】 已知厚壳紫种皮与薄壳红种皮落花生杂交(两对性状遗传),F1全 为厚壳紫种皮。
在F2中,稳定遗传的薄壳紫种皮落花生为3966株,则能稳定遗传的厚壳红种皮落花生株数大约为 ( )A. 1322B.1983C.3966D. 7932【例4】豌豆种子黄色对绿色为显性,圆粒对皱粒为显性(两对性状的遗传遵循自由组合定律)。
现用黄色皱粒与绿色圆粒两个纯系豌豆的亲本杂交得F1,F1自交,理论上F2植株中黄色皱粒纯合子豌豆数量比为 ( ) A. 1/3 B.2/3 C.3/16 D. 1/16二,双项选择题(在每小题给出的四个选项中,只有两个选项正确,全部选对得3分,选对一项得2分,有错选的得0分。
) 【例5】下图为鼠的毛色(灰色和白色)遗传图 解,已知6号是一只雌性鼠。
下列 说法正确的是 ( )A. 6号鼠是杂合子 B .鼠的灰色为显性性状C .鼠的白色为显性性状 D.7号鼠为杂合子的概率是2/3 三、复合选择题某生物研究小组的同学对一地区的人类遗传病进行调查,发现有一种遗传病表现出明显家族倾向,且往往是代代相传,下图为该研究小组绘制的该病在这个地区10000人中的发病情况图。
研究小组同学还对某一患该病男生的家族进行了分析,绘制出如下遗传系谱图:请分析上图回答例6—9小题:【例6】 由上图所示发病情况的调查结果可以推知,控制该病的基因最可能位于( )A .常染色体上B .X 染色体上C .Y 染色体上D .性染色体上【例7】 作出6题结论判断的主要理由是 ( ) A .男女患病几率均等 B .男患者多一点 C .男正常比女正常多 D .出现了女患者【例8】 分析上述系谱图,可以推知该患病男生与其患病姑姑的女儿基因型相同的概率是 ( )A.25%B.50%C.75%D. 100%【例9】 系谱图中的患病男生经手术治疗后表现正常,若他与表现型正常的女性婚配,你认为其后代还有可能患该病吗? ( )A .不能B .可能C .取决与环境D .取决于女方【例1】答案:C 【例2】答案C 【例3】答案C 【例4】答案D 【例5】答案BD 复合选择题答案 6. A 7.A 8.D 9.B 学业水平测试题一、单项选择题(1~9小题每小题1分,10~18小题每小题2分) 1.“种瓜得瓜,种豆得豆”这句俗语说明自然界中普遍存在着 ( ) A .生殖现象 B .遗传现象 C .进化现象 D .变异现象 2.生物的性状是指 ( )A .生物体的外在形状B .生物体的性别C .生物体的形态、生理特征D .生物体的大小 3.下列性状中属于相对性状的是 ( ) A .人的黑发和卷发 B .兔的长毛和短毛 C .猫的白毛与蓝眼 D .棉花的细绒与长绒 4.遗传的基本定律是指 ( )A .性状的传递规律B .蛋白质的传递规律C .基因的传递规律D .染色体的传递规律 5.下列表示测交的组合是 ( )A.AA×AaB.aa×aaC.Aa×aaD.Aa×Aa 6.下列属于等位基因的是 ( ) A .Ab B .Yy C .EE D .dd7.Aa 自交得F2,F2自交得F3,F3表型比为 ( ) A. 1:1 B.1:2:1 C.3:2:3 D.7:2:78.下图能正确表示基因分离定律实质的是 ( )9.基因型为DdTt 和ddTT 的亲本杂交,子代中不可能...出现的基因型是 ( ) A. DDTT B.ddTT C.DdTt D.ddTt10.一对肤色正常的夫妇生了一个白化病男孩。
高等数学第一章函数例题及答案
高等数学第一章 函数、极限、连续§1.1 函数一.求函数的定义域例1.求函数()2100ln ln ln x x x f -+=的定义域 例2.求5ln 1-+-=x x x y 的定义域例3.设()x f 的定义域为[]()0,>-a a a ,求()12-x f 的定义域 例4.设()⎩⎨⎧≤≤<≤=42 ,220 ,1x x x g 求()()()12-+=x g x g x f 的定义域,并求⎪⎭⎫ ⎝⎛23f 。
二.求函数的值域 例1.求3311-=x ey 的值域例2.求()()⎪⎩⎪⎨⎧>--≤≤---<-==2,2122,52,323x x x x x x x f y 的值域,并求它的反函数 三.求复合函数有关表达式 1.已知()x f 和()x g ,求()[]x g f 例1.已知()1-=x xx f ,求()⎥⎦⎤⎢⎣⎡-11x f f 例2.设()21x x x f +=,求()()[]()重复合n x f x f f f n =例3.设()⎩⎨⎧>≤-=2,02,42x x x x f ,求()[]x f f 2.已知()x g 和()[]x g f ,求()x f 例1.设()x e e e f x xx++=+21,求()x f例2.已知()xxxee f -=',且()01=f ,求()x f例3.设()x x fsin =,求()x f '例4.已知()x x f 2cos 3sin -=,求证()x x f 2cos 3cos += 3.已知()x f 和()[]x g f ,求()x g例.已知()()x x f +=1ln ,()[]x x g f =,求()x g 解:()[]x fx g 1-=实际上为求反函数问题()[]()[]x x g x g f =+=1ln ,()x e x g =+1 ()1-=x e x g 4.有关复合函数方程 例.设()x x f x x f 2311-=⎪⎭⎫⎝⎛-+,求()x f 四.有关四种性质例1.设()()x f x F =',则下列结论正确的是[ ](A )若()x f 为奇函数,则()x F 为偶函数。
(完整版)高数第一章例题及答案(终)理工类吴赣昌
第一章函数、极限与连续内容概要课后习题全解习题1-1★1.求下列函数的定义域:知识点:自然定义域指实数范围内使函数表达式有意义的自变量x 的取值的集合; 思路:常见的表达式有 ① a log □,( □0>) ② /N □, ( □0≠) ③(0)≥W④ arcsin W (W[]1,1-∈)等解:(1)[)(]1,00,11100101122⋃-∈⇒⎩⎨⎧≤≤-≠⇒⎩⎨⎧≥-≠⇒--=x x x x x x x y ;(2)31121121arcsin≤≤-⇒≤-≤-⇒-=x x x y ; (3)()()3,00,030031arctan 3⋃∞-∈⇒⎩⎨⎧≠≤⇒⎩⎨⎧≠≥-⇒+-=x x x x x x x y ;(4)()()3,11,1,,1310301lg 3⋃-∞-∈⇒⎩⎨⎧-<<<⇒⎩⎨⎧-<-<⇒-=-x x or x x x x x y x;(5)()()4,22,11601110)16(log 221⋃∈⇒⎪⎩⎪⎨⎧-<-≠-<⇒-=-x x x x x y x ; ★ 2.下列各题中,函数是否相同?为什么?(1)2lg )(x x f =与x x g lg 2)(=;(2)12+=x y 与12+=y x知识点:函数相等的条件;思路:函数的两个要素是f (作用法则)及定义域D (作用范围),当两个函数作用法则f 相同(化简后代数表达式相同)且定义域相同时,两函数相同;解:(1)2lg )(x x f =的定义域D={}R x x x ∈≠,0,x x g lg )(=的定义域{},0R x x x D ∈>=,虽然作用法则相同x x lg 2lg 2=,但显然两者定义域不同,故不是同一函数;(2)12+=x y ,以x 为自变量,显然定义域为实数R ;12+=y x ,以x 为自变量,显然定义域也为实数R ;两者作用法则相同“2□1+”与自变量用何记号表示无关,故两者为同一函数;★ 3.设⎪⎪⎩⎪⎪⎨⎧≥<=3,03,sin )(ππϕx x x x ,求)2()4()4()6(--ϕπϕπϕπϕ,,,,并做出函数)(x y ϕ=的图形知识点:分段函数;思路:注意自变量的不同范围; 解:216sin)6(==ππϕ,224sin 4==⎪⎭⎫⎝⎛ππϕ,224sin 4=⎪⎭⎫⎝⎛-=⎪⎭⎫ ⎝⎛-ππϕ()02=-ϕ;如图:★ 4.试证下列各函数在指定区间内的单调性 :(1)()1,1∞--=xxy (2)x x y ln 2+=,()+∞,0 知识点:单调性定义。
高一物理必修一第一章典型例题讲解
1.甲物体以乙物体为参考系是静止的,甲物体以丙物体为参考系又是运动的,那么,以乙物体为参考系,丙物体的运动情况是( )A .一定是静止的B .运动或静止都有可能C .一定是运动的D .条件不足,无法判断2.某人爬山,从山脚爬上山顶,然后又从原路返回到山脚,上山的平均速率为v 1,下山的平均速率为v 2,则往返的平均速度的大小和平均速率是( )A.v1+v22,v1+v22B.v1-v22,v1-v22C .0,v1-v2v1+v2D .0,2v1v2v1+v23.某物体作匀减速直线运动,其加速度为-2m/s 2,在任1秒中( )A .该秒末速度比前1秒初速度小2米/秒;B .末速度比初速度大2米/秒,方向与初速度方向相反;C .末速度比初速度小2米/秒,其加速度方向与初速度方向相反;D .末速度比初速度小2米/秒,其方向与初速度方向相反.4. 一物体做匀变速直线运动,某时刻速度的大小是4m/s ,1s 后的速度大小变成了10m/s ,在这1s 内该物体的( )A 、位移的大小可能小于4mB 、位移的大小可能大于10mC 、加速度的大小可能小于4m/s2D 、加速度的大小可能大于10m/s25.一辆汽车沿平直公路行驶,开始以20m/s 的速度行驶了全程的1/4,接着以v 的速度行驶了最后的3/4的路程,已知全程的平均速度是16m/s ,则v 等于( )A 、18m/sB 、36m/sC 、15m/sD 、17.1m/s6.列车长为L ,铁路桥长也是L ,列车沿平直轨道匀加速过桥,车头过桥头的速度是v1,车头过桥尾的速度是v2,则车尾通过桥尾时的速度为( )A .v 2B .2v 2-v 1 C. v21+v222 D. 2v22-v217.汽车刹车后做匀减速直线运动,最后停了下来,在汽车刹车的过程中,汽车前半程的平均速度与后半程的平均速度之比是( )A .(2+1)∶1B .2∶1C .1∶(2+1)D .1∶ 28.某物体做直线运动,物体的速度—时间图线如图所示,若初速度的大小为v0,末速度的大小为v ,则在时间t1内物体的平均速度是( )A .等于(v0+v)/2B .小于(v0+v)/2C .大于(v0+v)/2D .条件不足,无法比较9.如图5所示,小球从竖直砖墙某位置静止释放,用频闪照相机在同一底片上多次曝光,得到了图中1、2、3、4、5……所示小球运动过程中每次曝光的位置,连续两次曝光的时间间隔均为T ,每块砖的厚度为d.根据图中的信息,下列判断错误的是( )A .位置“1”是小球释放的初始位置B .小球做匀加速直线运动C .小球下落的加速度为d T2D .小球在位置“3”的速度为7d 2T10.小船匀速逆流而上,经过桥下时箱子落水了,船继续前进一段时间后才发现,并立即调头以相同的静水船速顺流而下,经过1h 在下游距桥7.2km 处追上.则河水流动速度为( )A .7.2km/hB .3.6km/hC .1m/sD .条件不足,无法确定11.一艘船以恒定的速度,往返于上、下游两码头之间.如果以时间t 1和t 2分别表示水的流速较小和较大时船往返一次所需的时间,那么,两时间的长短关系为( )A .t 1=t 2B .t 1>t 2C .t 1<t 2D .条件不足,不能判断12.下列给出的四组图象中,能够反映同一直线运动的是( )13.甲、乙两位同学多次进行百米赛跑,每次甲都比乙提前10m到达终点(近似匀速),现让甲远离起跑点10m,乙仍在起跑点起跑,则()A.甲先到达终点B.两人同时到达终点C.乙先到达终点D.不能确定14.相距12km的平直公路两端,甲乙两人同时出发相向而行,甲的速度是5km/h,乙的速度是3km/h,有一小狗以6km/h的速率,在甲、乙出发的同时,由甲处跑向乙,在途中与乙相遇,即返回跑向甲,遇到甲后,又转向乙.如此在甲乙之间往返跑动,直到甲、乙相遇,求在此过程中,小狗跑过的路程和位移.15.一辆客车在某高速公路上行驶,在经过某直线路段时,司机驾车做匀速直线运动.司机发现其正要通过正前方高山悬崖下的隧道,于是鸣笛,5s后听到回声;听到回声后又行驶10s司机第二次鸣笛,3s后听到回声.请根据以上数据帮助司机计算一下客车的速度,看客车是否超速行驶,以便提醒司机安全行驶.已知此高速公路的最高限速为110km/h,声音在空中的传播速度为340m/s.16.一根长L的细直杆AB原来紧贴y轴直立,当它的B端从坐标原点O开始从速度v沿着x 轴正方向匀速运动时,A端沿y轴运动的位移与时间的关系式如何?17.一列长 队伍,匀速行进速度为v,现有通讯员从队列的末尾跑步以匀速度u赶到队列前端传令,又立即以速度u返回队尾,在这段时间里,此列队伍前进的距离是多少?18.有小河流速是1m/s,船以划速3m/s逆水而行,忽有船上一顶草帽跌落水中立即随水漂流而去,10s后发觉,立即掉头以原划速顺水追赶,问再经几秒钟可追到草帽?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1章化学热力学基础[例1-1]用管道输送天然气,当输送压力为200kPa,温度25℃,管道内天然气的密度为多少?假设天然气可以看作是纯的甲烷。
解:p=(ρ/M) RT;ρ=pM/ RTp=200kpa, T=(25+273.15)K, M=16.04×10-3kg/mol, R=8.314 J·mol-1·K-1代入公式即可,ρ=1.294 kg/m3。
[例1-2]今有104.365kPa温度为300K的含水蒸气的烃类混合气体,其中水蒸气的分压为3.167kPa。
现欲得到除去水蒸气的1kmol干烃类混合气体,试求:(1)应从湿烃混合气体中除去水蒸气的物质的量;(2)所需湿烃类混合气体的初始体积解:(l)已知p=104.365kPa,T=300K,p A=3.167kPa,n B=1kmol则p B=p-p A =104.365 kPa-3.167 kPa=101.198kPa;p A=n A/V×RT,p B= n B/V×RTp A/p B=n A/n Bn A=p A/p B×n B=3.167/101.198×1000=31.30mol。
(2)p=n/V×R T,P、T已知,n=n A + n B=1000+31.30=1031.30 molV=nRT/p=1031.30×8.314×300/(104.365×1000)=24.65m3[例1-3]始态T=300K,p1=150kPa的某理想气体,n=2mol,经过下属两不同途径等温膨胀到同样的末态,其p2=50kPa。
求两途径的体积功:① 反抗50kPa的恒外压一次膨胀到末态;② 先反抗100kPa的恒外压膨胀到中间平衡态,再反抗50kPa的外压膨胀到末态。
解:两途径如图所示:两途径均属反抗恒外压膨胀:W =-p 外×ΔV根据理想气体状态方程计算出始、终及中间态的体积分别为33.26dm 3、99.78dm 3、49.89drn 3。
途径①的体积功:W =-p 外×ΔV =-3.326kJ 。
途径②的体积功:W =(-p 外’×ΔV 1)+(-p 外’’× ΔV 2)=-4.158kJ可以看出:①虽然两过程的始终态相同,但功却不相同,说明功与过程有关,功不是状态函数。
②保持始、终态相同,两次等温膨胀系统所做的功大于一次膨胀时系统所做的功。
[例1-4] 物质的量为n 的理想气体由始态p 1、V 1、T ,恒温变化压力、体积到终态p 2、V 2、T ,求过程的ΔH 。
解:ΔH =ΔU +Δ(pV )=ΔU +Δ(nRT )=0[例1-5] 始态T 1=298K ,p 1=500kPa ,体积为V 1=1dm 3的某理想气体等温可逆膨胀到最后压力为p 2=100Kpa 。
求体积功、热力学能的改变量和焓的改变量。
解:气体的物质的量为:由理想气体状态方程计算得n =pV/RT =0.204mol对等温可逆膨胀:ΔU =0,ΔH =0,Q =-W21lnp W nRT p ==0.204×8.314×ln(100/500)=-805.47 J Q = -W =805.47 J[例1-6] 设有0.1mol 正庚烷C 7H 16(l )在量热计中完全燃烧。
在25℃测得放热480.4kJ 。
分别计算下列两个方程的Δr H m 、Δr U m 。
(P151例5.8)解:在量热计中测出的是等容热效应,即ΔU =Q V =-480.4 KJ(1)716716()00.10.1()1n C H molmol C H ζν∆-∆===-480.44804/0.1r m U kJ U kJ mol ζ∆-∆===-∆ 114804/(117)8.314298r m r m B BH U RT kJ mol J K mol Kν--∆=∆+=-+-+⨯⋅⋅⨯∑4814/kJ mol =-(2)716716()00.10.05()2n C H molmol C H ζν∆-∆===-480.49608/0.05r m U kJ U kJ mol ζ∆-∆===-∆119608/(2214)8.314298r m r m B BH U RT kJ mol J K mol Kν--∆=∆+=-+-+⨯⋅⋅⨯∑9628/kJ mol =-可见,方程(2)的计量系数是方程(1)的两倍。
方程(2)的Δr H m 、Δr U m 也是方程(1)的两倍,因此,方程式的写法不同,其Δr H m 、Δr U m 也不同。
[例1-7] 已知下列反应的热效应:2212382231 () 393.5/2 393.5/1 (3) ()53+ 4 2219.9/m m m C O CO H kJ mol H kJ mol C H g O CO H kJ mol θθθ+=∆∆+=∆r 222r 2r ()石墨=-() H + 0.5O = H O(l) =-()H O(l)=- 求:2383()4 ?m C H C H H θ+=∆r 石墨=解:(1)×3 + (2)×4-(3)即为所求方程∴ 1234m m m m H H H H θθθθ∆∆+∆-∆r r r r =3=-130.93kJ/mol[例1-8] 利用标准摩尔生成焓数据,计算反应:CH 4(g )+2O 2(g )=CO 2(g )+2H 2O (l )的标准摩尔反应焓变。
解:从附录中查出各物质标准摩尔生成焓CH 4(g )+2O 2(g )=CO 2(g )+2H 2O (l )Δf H m θ kJ/mol -74.85 0 -393.5 -285.83 则:m m m H H H θθθ∆∆∆∑∑r ff 生成物反应物=-=-890.31 kJ/mol [例1-9] 已知25℃时:CO 2 (g) H 2O(l) C 2H 5OH(l)Δf H m θ /kJ·mol -1 -393.5 -285.83Δc H m θ/kJ·mol -1: -1366.8 求乙醇在25℃时Δf H m θ(C 2H 5OH ,l)。
解:乙醇的燃烧反应为:),(),(3),(2),()(3)(2)(3)(52225222252l OH H C H l O H H g CO H l OH H C H H l O H g CO g O l OH H C m f m f m f m c m r θθθθθ∆-∆+∆=∆=∆+=+∴ 252225(,)2(,)3(,)(,)f m f m f m c m H C H OH l H CO g H H O l H C H OH l θθθθ∆=∆+∆-∆=-277.69 kJ·mol -1[例1-10] 1mol 理想气体在298K 时等温膨胀,体积增大10倍,求系统的熵变。
假定膨胀过程:(1)可逆膨胀;(2)自由膨胀。
解:(1)可逆膨胀用V 2/V 1=10代入上式得:12lnV V nR S =∆=1mol×8.314J/K/mol×ln10=19.14J/K ΔS 为正值,并不意味着过程是不可逆的,因为它不是孤立系统。
考虑到环境熵变:10ln ln n 12rev nR V VR T Q S -===∆-环=-1mol×8.314J/K/mol×ln10=-19.14J/K 大孤立系统的总熵变:(ΔS)总=(ΔS)系 +(ΔS)环=0,所以该过程是可逆过程。
(2)自由膨胀是不可逆过程,不能用过程的热温商来计算。
但这个过程的始态、终态和过程(1)完全相同,所以系统的熵变仍是:ΔS=19.14J/K W=0,ΔU=0,Q =0,则0==∆TQ S -环大孤立系统的总熵变:(ΔS)总=(ΔS)系 +(ΔS)环=(ΔS)系=19.14 J/K>0 故理想气体等温自由膨胀是自发过程。
[例1-11] 1mol 理想气体在298K 时由1000kPa 等温膨胀至100kPa ,假设过程为:(1)可逆膨胀;(2)在等外压力100kPa 下膨胀;(3)向真空膨胀。
计算各过程的Q 、W 、ΔU、ΔH、ΔS 和ΔG。
解:(1)理想气体的等温膨胀,ΔU=0、ΔH=0Q =-W =J K K J mol p p nRT 7.5707kPa100kPa1000ln 15.298mol //314.81ln21=⨯⨯⨯= ΔS=Q rev/T =5707.7/298.15=19.14J/K ΔG=ΔH-TΔS=-5707.7J(2)等外压等温膨胀,ΔU=0、ΔH=0Q =-W =p 外×ΔV=p 外×(nRT/p2-nRT/p1)=2230.9J ΔS 和ΔG 和过程(1)可逆膨胀相同。
(3)向真空膨胀Q=0,W =0,ΔU、ΔH、ΔS 和ΔG 均和过程(1)可逆膨胀相同。
[例1-12] 分别计算反应C (s )+CO 2=2CO 在298K 和1173.15K 时(近似计算)的标准吉布斯函数变,并判断在此条件下能否自发进行。
解:1)计算298.15K 时的标准摩尔吉布斯函数变。
查表:C (s )+ CO 2 = 2CO Δf G m θ 0 -394.4 -137.2,不能自发)=()-(0mol /kJ 1204.39412.1372 )({>-⨯-⨯=∆⋅=∆∑B G G m f BB m r θθν2)计算1173.15K 时的标准摩尔吉布斯函数变。
)15.298()15.298()(θθθm r m r m r S T K H T G ∆∆=∆-查表: C (s )+ CO 2 = 2CO S m θ/J/K/mol 5.74 213.8 197.7 Δf H m θ/kJ/mol 0 -393.5 -110.5计算得: )15.298()15.298()(θθθm r m r m r S T K H T G ∆∆=∆-=-34.5 kJ/mol ,自发。
[例1-13] 已知在298.15K 时(1)CO (g )+ 0.5O 2 (g ) = CO 2(g );Δr G m θ=-257.19kJ/mol (2)C (石墨)+ O 2(g )= CO 2(g );Δr G m θ=-394.36kJ/mol 求反应(3):C (石墨)+ CO 2(g )= 2CO (g );Δr G m θ=?解:反应(3)=反应(2)-反应(1)×2则Δr G m3θ=Δr G m2θ-2Δr G m1θ=(-394.36)-2×(-257.19)=121.02 kJ/mol[例1-14] 分别计算反应C (s )+ CO 2(g ) =2CO (g ) 在298.15K 和1173.15K 时的K θ。
