高等数学各章知识结构复习课程

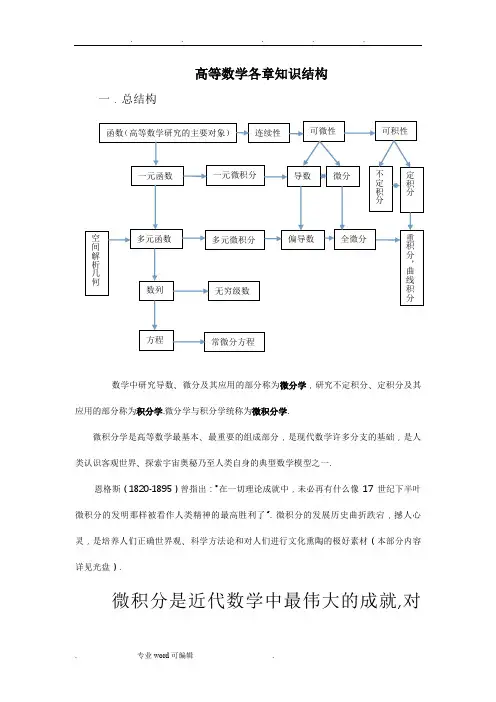
高等数学各章知识结构
一．总结构
数学中研究导数、微分及其应用的部分称为微分学，研究不定积分、定积分及其应用的部分称为积分学.微分学与积分学统称为微积分学.
微积分学是高等数学最基本、最重要的组成部分，是现代数学许多分支的基础，是人类认识客观世界、探索宇宙奥秘乃至人类自身的典型数学模型之一.
恩格斯（1820-1895）曾指出：“在一切理论成就中，未必再有什么像17世纪下半叶微积分的发明那样被看作人类精神的最高胜利了”. 微积分的发展历史曲折跌宕，撼人心灵，是培养人们正确世界观、科学方法论和对人们进行文化熏陶的极好素材（本部分内容详见光盘）.
微积分是近代数学中最伟大的成就,对它的重要性无论做怎样的估计都不会过分.
冯. 诺伊曼
注：冯. 诺依曼（John von Neumann，1903-1957，匈牙利人），20世纪最杰出的数学家之一，在纯粹数学、应用数学、计算数学等许多分支，从集合论、数学基础到量子理论与算子理论等作多方面，他都作出了重要贡献. 他与经济学家合著的《博弈论与经济行为》奠定了对策论的基础，他发明的“流程图”沟通了数学语言与计算机语言，制造了第一台计算机，被人称为“计算机之父”.
微积分中重要的思想和方法：
1．“极限”方法，它是贯穿整个《微积分》始终。

导数是一种特殊的函数极限；定积分是一种特殊和式的极限；级数归结为数列的极限；广义积分定义为常义积分的极限；各种重积分、曲线积分、曲面积分都分别是某种和式的极限。

所以，极限理论是整个《微积分》的基础。

尽管上述各种概念都是某种形式的极限，但是它们都有各自独特和十分丰富深刻的内容，这是《微积分》最有魅力的地方之一。

2．“逼近”思想，它在《微积分》处处体现。

在近似计算中，用容易求的割线代替切线，用若干个小矩形面积之和代替所求曲边梯形面积；用折线段的长代替所求曲线的长；用多项式代替连续函数等。

这种逼近思想在理论和实际中大量运用。

3．“求极限、求导数和求积分”是最基本的方法。

熟练掌握求极限、求导数和求积分的方法，学习《微积分》就不会遇到太多困难，甚至能做到得心应手。

4．“特色定理”是《微积分》的支柱。

夹逼定理、中值定理、微积分基本定理等是《微积分》中最深刻、最基本、最能体现《微积分》特色的定理，支撑起《微积分》的大厦。

5．“综合运用能力”是《微积分》学习的出发点和归宿。

充分注重综合运用极限概念与方法的能力、综合运用导数与积分相结合的各种方法的能力、综合运用定积分思想方法解决问题的能力、综合运用一元和多元相结合方法的能力、综合运用各种方法解决实际问题的能力。

二．函数、极限与连续
函数是现代数学的基本概念之一，是高等数学的主要研究对象. 极限概念是微积分的理论基础，极限方法是微积分的基本分析方法，因此，掌握、运用好极限方法是学好微积分的关键. 连续是函数的一个重要性态.
极限思想是由于求某些实际问题的精确解答而产生的. 例如，我国古代数学家刘徽（公元3世纪）利用圆内接正多边形来推算圆面积的方法----割圆术（参看光盘演示）, 就是极限思想在几何学上的应用. 又如，春秋战国时期的哲学家庄子（公元4世纪）在《庄子.天下篇》一书中对“截丈问题”（参看光盘演示）有一段名言：“一尺之棰, 日截其半, 万世不竭”，其中也隐含了深刻的极限思想.
极限是研究变量的变化趋势的基本工具，高等数学中许多基本概念，例如连续、导数、定积分、无穷级数等都是建立在极限的基础上. 极限方法又是研究函数的一种最基本的方法.
客观世界的许多现象和事物不仅是运动变化的，而且其运动变化的过程往往是连绵不断的，比如日月行空、岁月流逝、植物生长、物种变化等，这些连绵不断发展变化的事物在量的方面的反映就是函数的连续性. 连续函数就是刻画变量连续变化的数学模型.
16、17世纪微积分的酝酿和产生，直接肇始于对物体的连续运动的研究. 例如伽利略所研究的自由落体运动等都是连续变化的量. 但直到19世纪以前，数学家们对连续变量的研究仍停留在几何直观的层面上，即把能一笔画成的曲线所对应的函数称为连续函数. 19世纪
中叶，在柯西等数学家建立起严格的极限理论之后，才对连续函数作出了严格的数学表述.
连续函数不仅是微积分的研究对象，而且微积分中的主要概念、定理、公式法则等，往往都要求函数具有连续性.
我们将以极限为基础，介绍连续函数的概念、连续函数的运算及连续函数的一些性质.
从15世纪初文艺复兴时期起，欧洲的工业、农业、航海事业与商贸得到大规模的发展，形成了一个新的经济时代。

而16世纪的的欧洲，正处在资本主义的萌芽时期，生产力得到了很大的发展，生产实践的发展对自然科学提出了新的课题，迫切要求力学、天文学等基础科学的发展，而这些学科都是深刻依赖于数学的，因而也推动了数学的发展。

在各类学科对数学提出的种种要求下，下列三类问题导致了微分学的产生：
（1）求变速运动的*时速度；
（2）求曲线上一点处的切线；
（3）求最大值和最小值。

这三类实际问题的现实原型在数学上都可归纳为函数相对于自变量变化而变化的快慢程度，即所谓函数的变化率问题。

牛顿从第一个问题出发，莱布尼兹从第二个问题出发，分别给出了导数的概念。

在理论研究和实际应用中，常常又会遇到这样的问题：当自变量x有微小变化时，求函数)
y=的微小改变量
f
(x
f
y-
∆
∆.
=
+
f
(
)
)
(x
x
x
这个问题初看起来似乎只要做减法运算就可以了，然而，对于较复杂的函数)
(x
f，差值f-
x
+却是一个更复杂的表达式，不易求出其值。

一个想法是：我们设法将y∆表x
∆
)
(
)
(x
f
示成x
的线性函数，即线性化，从而把复杂问题化为简单问题。

微分就是实现这种线性化的一种数学模型。

数学中的转折点是笛卡尔的变数. 有了变数，
运动进入了数学；有了变数，辩证法进入了数学；
有了变数，微分和积分也就立刻成为必要的了，而
它们也就立刻产生，并且是有由牛顿和莱布尼茨大
体上完成的，但不是由他们发明的.
-------恩格斯
数学发展的动力主要来源于社会发展的环境力量. 17世纪，微积分的创立首先是为了解决当时数学面临的四类核心问题中的第四类问题，即求曲线的长度、曲线围成的面积、曲面围成的体积、物体的重心和引力等等. 此类问题的研究具有久远的历史，例如，古希腊人曾用穷竭法求出了某些图形的面积和体积，我国南北朝时期的祖冲之、祖恒也曾推导出某些图形的面积和体积，而在欧洲，对此类问题的研究兴起于17世纪，先是穷竭法被逐渐修改，后来由于微积分的创立彻底改变了解决这一大类问题的方法.
由求运动速度、曲线的切线和极值等问题产生了导数和微分，构成了微积分学的微分学部分；同时由已知速度求路程、已知切线求曲线以及上述求面积与体积等问题，产生了不定积分和定积分，构成了微积分学的积分学部分.
五．微分方程
六．向量代数与空间解析几何。