第24章太阳位置计算
黄帝内经:素问第24章 血气形志

血气形志篇原文和白话文翻译:【原文】夫人之常数,太阳常多血少气,少阳常少血多气,阳明常多气多血,少阴常少血多气,厥阴常多血少气,太阴常多气少血,此天之常数。
【翻译】人身各经气血多少,是有一定常数的。
如太阳经常多血少气,少阳经常少血多气,阳明经常多气多血,少阴经常少血多气,厥阴经常多血少气,太阴经常多气少血,这是先天禀赋之常数。
【原文】足太阳与少阴为表里,少阳与厥阴为表里,阳明与太阴为表里,是为足阴阳也。
手太阳与少阴为表里,少阳与心主为表里,阳明与太阴为表里,是为手之阴阳也。
今知手足阴阳所苦,凡治病必先去其血,乃去其所苦,伺之所欲,然后泻有余,补不足。
【翻译】足太阳膀胱经与足少阴肾经为表里,足少阳胆经与足厥阴肝经为表里,足阳明胃经与足太阴脾经为表里。
这是足三阳经和足三阴经之间的表里配合关系。
手太阳小肠经和手太阴心经为表里,手三阳三焦经与手厥阴心包经为表里,手阳明大肠经与手太阴肺经为表里,这是手三阳经和手三阴经之间的表里配合关系。
现以知道,疾病发生在手足阴阳使二经脉的那一经,其治疗方法,血脉雍盛的,必须先刺出其血,以减轻其病苦;再诊察其所欲,根据病情的虚实,然后泻其有余之实邪,补其不足之虚。
【原文】欲知背俞,先度其两乳间,中折之,更以他草度去半已,即以两隅相拄也,乃举以度其背,令其一隅居上,齐脊大柱,两隅在下,当其下隅者,肺之俞也。
复下一度,心之俞也。
复下一度,左角肝之俞也,右角脾之俞也。
复下一度,肾之俞也。
是谓五藏之俞,灸刺之度也。
【翻译】要想知道背部五脏俞穴的位置,先用草一根,度量两乳之间的距离,再从正中对折,另一草与前草同样长度,折掉一半之后,拿来支撑第一根草的两头,就成了一个三角形,然后用它量病人的背部,使其一个角朝上,和脊背部大椎穴相平,另外两个角在下,其下边左右两个角所指部位,就是肺俞穴所在。
再把上角移下一度,方在两肺俞连线的中点,则其下左右两角的位置是心俞的部位。
再移下一度,左角是肝俞,右角是脾俞。
从个问题到类问题的案例剖析 24 天文观测

视图一般以地球北极(或南极)上空俯视作为视角,以太阳为中心。在图a中,上合(位置
3)与下合(位置 1)均为日星地连成一线,但仅是俯视图上看起来如此,若在侧视视角中
(图d)太阳-金星-地球并不在同一直线上,因为共面性并不是所有行星在同一数学平面
上,而是在黄道平面附近略有高下参差,当然也有碰巧在同一平面的情况,比如下合时的“凌
在日月星辰不断东升西落的基础上,由于地球在宇宙空间进行绕日公转,太阳相对背景恒星
在缓慢移动,所以第二天的同一时刻恒星们整体往西方移动(约 1°)。月球的运动较复杂,
主要是两个方面:其一为地球自转导致东升西落,其二为月球绕地公转导致其自西向东运动,
前者的速度(360°/天)远大于后者(约 12.5°/天),所以月球总体表现为向西运动。月球
到月球、水星经过太阳表面的天象,则第二天正午三大天体在星空中的位置可能是( )
A.
B.
C.
D.
【参考答案与解析】
1. B 2.A 3.D
第 1 题,此题要用到月相知识,左图显示月相为蛾眉月,农历初二初三左右,月牙即将
遮盖木星,表明木星与月球重合,在地球上看来月球与木星连成一线。右图为经典的太阳系
极点俯视图,标出月球公转方向(与地球相同,逆时针),图中月球轨道 R 位置为刚过满月
时称为行星冲日,如“火星冲日”“木星冲日”等,火星冲日平均每 2 年发生一次,而木星
以外(含木星)的地外行星均每年发生一次冲日。某行星冲日时,日地星成 180°角,是观
测该行星时最好时机,因为太阳与该行星此升彼落,整晚可见该行星,当地子夜时它位于正
南(北半球)或正北(南半球)。
5.判方向是关键。天文观测类问题,判断方向是解题关键,也是落实地理实践力等核心
地理相关名词(赤纬角,太阳高度角,经纬度计算公式)

附件6:可参考的相关概念1. 太阳时()s t时间的计量以地球自转为依据,地球自转一周,计24太阳时,当太阳达到正南处为12:00。
钟表所指的时间也称为平太阳时(简称为平时),我国采用东经120度经圈上的平太阳时作为全国的标准时间,即“北京时间”。
(注:大同的经度为'18113o )。
(该定义摘自《太阳能应用技术》的第二章——太阳辐射)2. 时角()ω时角是以正午12点为0度开始算,每一小时为15度,上午为负下午为正,即10点和14点分别为-30度和30度。
因此,时角的计算公式为()(),1215度-=s t ω (1)其中s t 为太阳时(单位:小时)。
(该定义摘自《太阳能应用技术》的第二章——太阳辐射)3. 赤纬角()δ赤纬角也称为太阳赤纬,即太阳直射纬度,其计算公式近似为()(),3652842sin 45.23度⎪⎭⎫ ⎝⎛+=n πδ (2)其中n 为日期序号,例如,1月1日为1=n ,3月22日为81=n 。
(该定义摘自《太阳能应用技术》的第二章——太阳辐射)4. 太阳高度角()α太阳高度角是太阳相对于地平线的高度角,这是以太阳视盘面的几何中心和理想地平线所夹的角度。
太阳高度角可以使用下面的算式,经由计算得到很好的近似值:,cos cos cos sin sin sin ωδφδφα⋅⋅+⋅= (3)其中α为太阳高度角,ω为时角,δ为当时的太阳赤纬,φ为当地的纬度(大同的纬度为o 1.40)。
(该定义摘自维基百科)5. 太阳方位角()A 。
太阳方位角是太阳在方位上的角度,它通常被定义为从北方沿着地平线顺时针量度的角。
它可以利用下面的公式,经由计算得到良好的近似值,但是因为反正弦值,也就是()y x 1sin -=有两个以上的解,但只有一个是正确的,所以必需小心的处理。
.cos cos sin sin αδω⋅-=A (4) 下面的两个公式也可以用来计算近似的太阳方位角,不过因为公式是使用余弦函数,所以方位角永远是正值,因此,角度永远被解释为小于180度,而必须依据时角来修正。
计算月出和日出日落时间的几种数学模型

计算月出和日出日落时间的几种数学模型作者:陈素君来源:《现代职业教育.高职本科》 2016年第12期[摘要]利用天文学的基础知识和目前已有的天文资料,研究计算某地区月出与日落时刻的数学模型。
[关键词]月出时刻;日出日落时刻;检验[中图分类号] G642[文献标志码] A[文章编号] 2096-0603(2016)34-0038-02一、精确度较高的日落时刻计算模型我们把日落时刻定义为太阳每天从西方地平线降落的时刻。
日落的时间随着季节及纬度的不同而改变。
传统上认为在北半球,冬至时日落的时间最早,夏至时日落最晚。
但是实际上,由于黄赤交角与地球椭圆轨道的影响,日落最早的时间不会落在冬至,而是在12月初;日落最晚的时间也不会落在夏至,而是在6月底。
我们需要一种更精确的计算方法。
以下我们研究文献(详见参考文献[1])中的日落时刻计算模型:首先,日出日落时间指把地球假设为球形,圆盘太阳刚好到达地平线的时刻。
日落太阳的位置为h=-0.8333°,采用迭代法重新计算太阳的位置,直到满足要求的计算精度为止。
已知h=-0.8333°、经度Long、纬度Glat、时区Zone、第一次计算时间UT0=180。
(1)计算从格林威治时间公元2000年1月1日到计算日的天数days;(2)计算从格林威治时间公元2000年1月1日到计算日的世纪数t=■(3)计算太阳的平黄径L=280.460+36000.770×t(4)计算太阳的平近点角G=357.528+35999.050×t(5)计算太阳的黄道经度λ=L+1.915×sinG+0.020×sin(2G)(6)计算太阳的倾角ε=23.4393-0.0130×t(7)计算太阳的偏差δ=arcsin(sinε×sinλ)(8)计算格林威治时间的太阳的时间角GHA:GHA=UT0-180-1.915×sinG-0.020×sin (2G)+2.466×sin(2λ)-0.053×s in(4λ)(9)计算修正值e=arccos{■}(10)新的日落时间,西半球的经度Long为负数。
太阳位置计算

第24章太阳位置计算[许剑伟于家里 2008-3-30下午]一、低精度计算:当计算精度要求为0.01度,计算太阳位置时可假设地球运动是一个纯椭圆,也就说忽略月球及行星摄动,计算表达如下。
设JD是儒略日数,可以用第7章表述的方法计算。
T为J2000起算的儒略世纪数:T = (JD-2451545.0)/36525计算时要保留足够的小数位数,5位小数是不够的(除非所需的太阳黄经的精度要求不高),注意,T表达为儒略世纪数,所以T误差0.00001相当于0.37日。
接下来,太阳几何平黄经:Lo = 280°.46645 + 36000°.76983*T + 0°.0003032*T^2 (Date平分点起算)太阳平近点角: M = 357°.52910 + 35999°.05030*T - 0°.0001559*T^2 -0°.00000048*T^3地球轨道离心率: e = 0.0 - 0.000042037*T - 0.0000001236*T^2太阳中间方程:C = +(1°.914600 - 0°.004817*T -0°.000014*T*T) * sin(M)+(0°.019993 - 0°.000101*T) * sin(2M)+ 0°.000290*sin(3M)那么,太阳的真黄经是:Θ = Lo + C真近点角是: v = M + C日地距离的单位是"天文单位",距离表达为:R = 1.000001018 (1-e^2) / (1+e*cos(v)) ……24.5式式中的分子部分的值变化十分缓慢。
它的值是:0.9997190 1800年0.9997204 1900年0.9997218 2000年0.9997232 2100年太阳黄经Θ可由上述的方法算出,它是Date黄道分点坐标中的真几何黄经,需通过计算地心坐标星体位置也可算出。
【知识手册】高中地理全册必背章节知识清单(人教版2019选择性必修1)第一章 地球上的运动(背诵版)
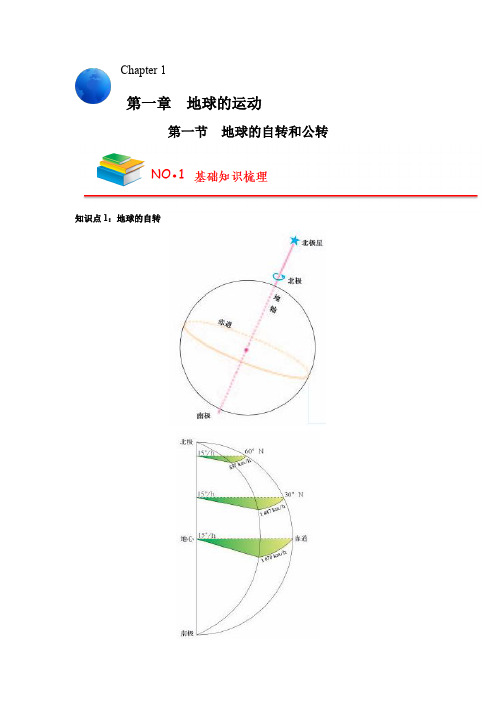
第一节地球的自转和公转知识点1:地球的自转Chapter 1第一章地球的运动1.概念:地球绕其自转轴的旋转运动。
2.运动特点特点自转轴地轴——北端始终指向北极星附近北半球纬度越高,北极星相对地平线的高度越高方向自西向东北极上空看呈逆时针,南极上空看呈顺时针周期太阳日:24时恒星日:23时56分4秒,地球自转的真正周期速度角速度:约为15°/h,除极点外都相等线速度:由赤道至两极递减知识点2:地球的公转1.概念:地球绕太阳的运动。
2.方向:自西向东。
3.周期:1回归年为365日5时48分46秒;1恒星年为365日6时9分10秒,是地球公转的真正周期。
4.轨道:近似正圆的椭圆轨道,太阳位于椭圆的一个焦点上。
5.速度位置时间速度A点近日点1月初线速度较快,角速度较快B点远日点7月初线速度较慢,角速度较慢知识点3:黄赤交角及其影响1.概念(1)赤道平面:过地心并与地轴垂直的平面。
(2)黄道平面:地球公转轨道平面。
(3)黄赤交角:赤道平面与黄道平面之间存在一个交角,叫黄赤交角,目前是23°26′。
2.影响:太阳直射点的回归运动(1)移动规律(北半球)(2)周期:1回归年,即365日5时48分46秒。
一、地球自转和公转运动的特征地球自转和公转运动的特征既有相同点也有不同点,还有相关性,具体如下表所示:运动形式自转公转概念绕地轴的旋转绕太阳的运动方向自西向东(从北极上空俯视——逆时针;从南极上空俯视——顺时针)地轴空间指向空间指向不变,北端始终指向北极星附近运动周期以遥远恒星为参照点1恒星日=23时56分4秒1恒星年=365日6时9分10秒以太阳为参照点1太阳日=24时(昼夜交替现象周期)1回归年=365日5时48分46秒(直射点回归运动周期)速度角速度除南北极点外,各地均约为15°/h(1°/4分钟)平均约1°/天近日点(1月初)快,远日点(7月初)慢线速度因纬度而异,自赤道(1 670 km/h)向两极(0 km/h)递减平均约30 km/s关系地球自转的平面(赤道平面)与公转轨道平面(黄道平面)目前存在23°26′的交角(黄赤交角)二、航天发射基地选址的条件气象条件晴天多、阴雨天少,风速小,湿度低,有利于发射和跟踪观测纬度因素纬度低,地球自转线速度大,可以节省燃料和降低成本地势因素地势越高,地球自转线速度越大地形因素地形平坦开阔,有利于跟踪观测海陆位置大陆内部气象条件好,隐蔽性强,人烟稀少,安全性强;海上人类活动少,安全性强交通条件对外交通便利,有利于大型航天装备的运输安全因素出于国防安全考虑,有的建在内陆山区、沙漠地区,有的建在地广人稀处三、我国航天发射基地区位条件评价思考方向答题术语西昌卫星发射中心纬度、地势纬度低(28.2°N),海拔高(1 500米),发射倾角好,地空距离短,既可充分利用地球自转的离心力,又可缩短地面到卫星轨道的距离,从而节省火箭的有效负荷地形峡谷地形,地形隐蔽,地质结构坚实,有利于发射场的总体布局气象多晴朗天气,“发射窗口”好。
太阳视运动规律及判读
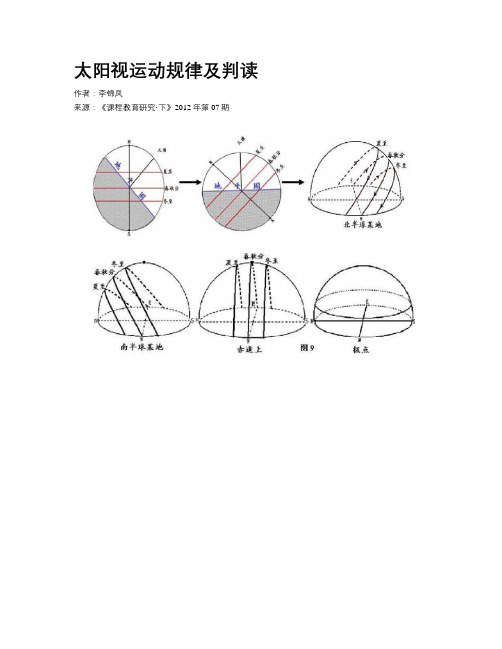
太阳视运动规律及判读作者:李锦凤来源:《课程教育研究·下》2012年第07期【中图分类号】G633.55 【文献标识码】A 【文章编号】2095-3089(2012)07-0174-02地球绕地轴自西向东自转,同时绕太阳自西向东公转,这样在我们的眼里,太阳一天中东升西落,同时在一年中每天东升西落又有规律地产生一定的变化,我们把太阳在天空中运动的轨迹,称为太阳的视运动。
太阳视运动知识比较抽象,学生不太容易理解,我结合日常生活经验和课本理论知识,总结出如下规律和做题技巧:一、太阳视运动图的作法1.画出观测地的地平圈,用椭圆形表示。
2.画出天穹,用弧线表示。
3.在地平圈上标出东南西北方向(为了更好的示意太阳出没方位,通常将南北方位标在左右两侧),地平圈方位是顺时针旋转。
4.标出东南西北方位的地方时(由于正午和子夜的地方时分别为12:00和24:00,所以正东和正西方位地方时分别为6:00和18:00)。
5.在地平圈上标出日出、日落及正午时的太阳,用平滑弧线连接三点即太阳视运动轨迹。
6.在视运动轨迹上用箭头示意日出和日落(偏东方位日出,偏西方位日落)。
二、太阳视运动规律1.太阳出没的方位(除极昼区外)。
规律1—1:二分日太阳出没方位:日出正东,日落正西(如图2)规律1—2:夏至日太阳出没方位:日出东北,日落西北(如图3)规律1—3:冬至日太阳出没方位:日出东南,日落西南2.正午太阳的方位。
正午太阳的位置一定位于正南、正北或天顶,这取决于太阳直射纬度与观测点纬度。
直射点偏南,正午太阳则偏南;直射点偏北,正午太阳偏北;如果太阳直射,则正午太阳于天顶。
规律2:北回归线以北各地,一年中正午太阳始终于正南方位;南回归线以南各地,一年中正午太阳始终于正北方位;南北回归线之间及线上各地,一年中正午太阳可能于正北、正南和天顶,要看直射纬度与观察者所处的纬度而定(以20°N为例,如图5):直射点于20°N—23°26′N时,正午太阳于正北;直射20°N纬线时,正午太阳于天顶;直射点于20°N—23°26′S时,正午太阳于正南。
九年级数学上第24章《相交、相切、相离》课件

知3-讲
解:如图,过点C作CD⊥AB于点D.
在Rt△ABC中,
AC=3 cm,BC=4 cm,∠ACB=90°,
∴AB= AC2 BC2 32 42 5(cm).
又∵S△ABC=
1 2
AB•CD=
1 2
AC•BC,
∴CD=2.4 cm.
∴r≥2.4 cm.
(来自《点拨》)
总结
知3-讲
(1)直线和圆的位置关系的应用过程实质是一种数形 结合思想的转化过程,它始终是“数”:圆心到 直线的距离与圆的半径大小,与“形”:直线和 圆的位置关系之间的相互转化.
知2-讲
例1 如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC =4 cm,以点C为圆心,2 cm为半径作圆,则⊙C与AB 的位置关系是( B ) A.相离 B.相切 C.相交 D.相切或相交
导引:本例若通过看公共点的个数来判断, 作图稍有不准,就会产生误判,因此需通过比较圆心到 直线的距离与半径的大小来判断.如图,过点C作CH⊥ AB于点H,在Rt△CHB中,易得CH=2 cm,即d=r=2 cm,所以⊙C与AB的位置关系是相切.
(2)圆心到直线的距离通常用勾股定理与面积相等法 求出。
(来自《点拨》)
知3-练
1 (中考·青岛)已知直线l与半径为r的⊙O相交,且点O到 直线l的距离为6,则r的取值范围是( C ) A.r<6 B.r=6 C.r>6 D.r≥6
2 如图,∠O=30°,P为边OA上的一点,且OP=5,若
以P为圆心,r为半径的圆与射线OB只有一个公共点,
归纳
知2-讲
如果画图后直线和圆的位置关系不明显,一般不 选用公共点个数来判断直线和圆的位置关系.应采 用比较圆心到直线的距离与半径大小的方法来确定 它们之间的位置关系;在没有给出d与r的具体数值 的情况下,可先利用图形条件及性质求出d与r的值, 再通过比较大小确定其位置关系.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第24章太阳位置计算[许剑伟于家里2008-3-30下午]一、低精度计算:当计算精度要求为0.01度,计算太阳位置时可假设地球运动是一个纯椭圆,也就说忽略月球及行星摄动,计算表达如下。
设JD是儒略日数,可以用第7章表述的方法计算。
T为J2000起算的儒略世纪数:T = (JD-2451545.0)/36525计算时要保留足够的小数位数,5位小数是不够的(除非所需的太阳黄经的精度要求不高),注意,T表达为儒略世纪数,所以T误差0.00001相当于0.37日。
接下来,太阳几何平黄经:Lo = 280°.46645 + 36000°.76983*T + 0°.0003032*T^2 (Date平分点起算)太阳平近点角: M = 357°.52910 + 35999°.05030*T - 0°.0001559*T^2 -0°.00000048*T^3 地球轨道离心率:e = 0.016708617 - 0.000042037*T - 0.0000001236*T^2太阳中间方程:C = +(1°.914600 - 0°.004817*T -0°.000014*T*T) * sin(M)+(0°.019993 - 0°.000101*T) * sin(2M)+ 0°.000290*sin(3M)那么,太阳的真黄经是:Θ= Lo + C真近点角是:v = M + C日地距离的单位是"天文单位",距离表达为:R = 1.000001018 (1-e^2) / (1+e*cos(v)) ……24.5式式中的分子部分的值变化十分缓慢。
它的值是:0.9997190 1800年0.9997204 1900年0.9997218 2000年0.9997232 2100年太阳黄经Θ可由上述的方法算出,它是Date黄道分点坐标中的真几何黄经,需通过计算地心坐标星体位置也可算出。
要取得Date黄道坐标中太阳的视黄经λ,还应对Θ进行章动修正及光行差修正。
如果精度要求不高,可用下式修正:Ω = 125°.04 - 1934°.136*Tλ = Θ - 0°.00569 -0°.00478*sin(Ω)某此时候,我们需要把太阳黄经转到J2000坐标中,在1900-2100年范围内可利用下式进行: Θ2000 = Θ- 0°.01397*(year-2000)如果还想取得更高的转换精度(优于0.01度),那么你可以使用第25章的方法进行坐标旋转。
Date黄道坐标中的太阳黄纬不超过1".2,如果对精度要求不是很高,可以置0。
因此,太阳的地心赤经α及赤纬δ可以用下式(24.6式,24.7式)计算,式中ε是黄赤交角(由21章的21.2式计算)。
tanα= cosεsinΘ/ cosΘ……24.6式sinδ= sinεsinΘ……24.7式如果要想得到太阳的视赤经及赤纬,以上二式中的Θ应换为λ,ε应加上修正量:+0.00256*cos(Ω)[译者注]:实际上就是对Θ补上黄经章动及光行差,ε补上交角章动后再转到赤道坐标中。
也可在赤道坐标中补章动及光行差,但公式不同。
公式24.6当然可以转为:tan(α) = cos(ε)*tan(Θ),接下来,我们要注意α与Θ应在同一象限。
然而,如果你使用计算机语中有ATN2函数(C语言是atan2),那最好保持24.6式不变,这样就可直接利用ATN2函数算出α,即:α= ATN2( cos(ε)*sin(Θ),cos(Θ) )例24.a——计算1992-10-13,0点,即力学时TD=JDE 2448908.5时刻的太阳位置。
我们算得:T = -0.072183436Lo= -2318°.19281 = 201°.80719M = -2241°.00604 = 278°.99396e = 0.016711651C = -1°.89732Θ= 199°.90987 = 199°54' 36"R = 0.99766Ω= 264°.65λ= 199°.90897 = 199°54' 32"εo= 23°26'24".83 = 23°.44023 (由21章的21.2式算得)ε= 23°.43999α视= -161°.61918 = +198°.38082 = 13h.225388 = 13h 13m 31s.4δ视= -7°.78507 = -7°47' 06"使用VSOP87行星理论计算出的的正确值是:(请与上面的结果做一下比较)Θ= 199°54' 26".18λ= 199°54' 21".56β= +0".72R = 0.99760853α视= 13h 13m 30s.749δ视= -7°47' 01".74二、高精计算在Bretagnon和Simon的书中给出一种计算太阳黄经的方法,其精度可以满足大部分应用.用他们的方法得到0—2800年的精度是0.0006度(2".2),-4000到+8000的精度是0.0009度(3".2),且计算时仅用到49个周期项。
有一个精度很高的,高达0.01角秒的方法,就是用31章要讲到的VSOP87理论进行计算,但对于地球,该理论用了2425个周期项(1080个黄经周期项,348个黄纬周期项,997个距离周期项)。
显然这么的数量无法复制到本书,因此我们只从VSOP87中取出一些主要项(详见附录II),利用它计算得到的太阳位置在-2000到6000年范围内精度是1"。
计算步骤如下:使用附录II的地球数据,可计算出给定时刻的日心黄经L、黄纬B及距离R,具体详见第31章。
别忘了,时间τ是JDE 2451545.0(即J2000.0)起算的儒略千年数,而不是世纪数,最后得到的结果L和B是弧度单位。
要取得地心黄经Θ及黄纬β,应按下式计算:Θ= L + 180°, β=-B转换到FK5系统。
太阳黄经Θ及黄纬β是P.Bretagnon的VSOP行星理论定义的动力学黄道坐标。
这个参考系与标准的FK5坐标系统(详见20章)仅存在很小的差别。
可按以下方法把Θ、β转换到FK5坐标系统中,其中T是J2000起算的儒略世纪数,或T=10τ。
先计算λ' = Θ- 1°.397*T - 0°.00031*T^2接下来Θ及β的修正量是:ΔΘ= -0".09033 ……24.9式Δβ= +0".03916*( cos(λ') - sin(λ') )仅在需要很精确计算时才进行这个修正。
如果使用附录II中提供的被削减了一些项的VSOP87,那么此项修正可省略。
********译者注:VSOP动力学的黄道与FK5黄道有一点小差别,所以作以上修正。
J2000.0动力学黄道和FK5黄道或赤道可以均可看作惯性系。
这两种参考系存在小量差别。
J2000.0的VSOP 黄道与J2000.0的FK5黄道存在一个很小的夹角E = 0".0554左右,VSOP黄道经过FK5黄道的升交点为N,N在春风点西侧135度。
根据以上说明,易得VSOP的Date黄道与FK5的Date黄道的变换关系:Δβ=0.0554*sin(Θ+135-p),(式中p是Date黄道上的岁差)……24.E1式由于两个黄道之间的夹角很小,Δβ也可看作在春分点处两道的垂直距离(看作直线AB),设Date赤道与两黄道交于分别交于A、C,这样三角形ABC直角小三角形,B角是90度,于是有:Θ=0时,AB = Δβ= 0".0554*sin(135-p)易得两个春风点相差,ΔΘ=AB/tan(ε)ε可值为常数23.44度,那么ΔΘ=0".1278*sin(135-p) ……14.E2式当计算的时间跨度不大时(如几百年),p取0即可,那么ΔΘ=0".09035实际上,原文的λ' = Θ- p代入24.E1式得:Δβ= +0".03916*( cos(λ') - sin(λ') )**********太阳的视位置。
到止,我们得到的太阳黄经Θ是Date黄道分点坐标的真几何黄经。
要取得视黄经λ,还应加上精确的黄经章动及光行差。
章动处理:根据第21章算出ΔΨ,并加到Θ中即可。
太阳地心黄经光行差修正项是: -20".4898/R ……20.10式式中R是日地距离(天文单位)。
分子是光行差常数(K=20".49552)乘以a*(1-e^2),与24.5式的分子相同。
因此24.10中的分子中其实是一个缓慢变化的数,在0年是20".4893,在+4000年是20".4904。
但重要的是,24.10式本身不是一个严格的准确的表达式,因为它是假设地球轨道是不受摄动的标准椭圆。
当受到摄动是,月球的摄动可引起0".01的误差。
当需要进行高精度计算时(比使用附录II计算精度要求更高时),可用以下方法进行光行差修正。
找个太阳黄经的修正参数Δλ(单位是角秒/日),光行差修正量为:-0.005775518*R*Δλ式中的R同上述的,是日地距离,单位是天文单位。
常数部分是1个距离单位的光行时间,单位是"日",(=8.3分)。
在章动与光行差修正之后,我们就得到了太阳的视黄经λ。
太阳的视黄经λ及视黄纬β可以由12.3式及12.4式转换为视赤经α及视纬δ,式中ε是真黄赤交角,含交角章动Δε。
太阳的地心黄经修正用的参数Δλ,单位是角秒/日,在J2000黄道坐标中,可由下页的公式计算,式中τ是J2000.0起算的儒略千年数,正弦内的角度的单位是度。
表达式中,仅保留了几个主要的周期项,因此结果不很严格,但Δλ最多只有0".1误差,用于光行差修正,误差只有0".001。
如果某些其它应用中,Δλ须是在Date黄道中的,则应把常数项3548.193换为3548.330Δλ的计算式J2000坐标, τ是J2000.0起算的儒略千年数, sin()的角度量的单位是度Δλ= 3548.193+ 118.568 sin( 87.5287 + 359993.7286τ)+ 2.476 sin( 85.0561 + 719987.4571τ)+ 1.376 sin( 27.8502 +4452671.1152τ)+ 0.119 sin( 73.1375 + 450368.8564τ )+ 0.114 sin( 337.2264 + 329644.6718τ )+ 0.086 sin( 222.5400 + 659289.3436τ )+ 0.078 sin( 162.8136 +9224659.7915τ )+ 0.054 sin( 82.5823 +1079981.1857τ )+ 0.052 sin( 171.5189 + 225184.4282τ )+ 0.034 sin( 30.3214 +4092677.3866τ )+ 0.033 sin( 119.8105 + 337181.4711τ )+ 0.023 sin( 247.5418 + 299295.6151τ )+ 0.023 sin( 325.1526 + 315559.5560τ )+ 0.021 sin( 155.1241 + 675553.2846τ )+ 7.311τsin( 333.4515 + 359993.7286τ )+ 0.305τsin( 330.9814 + 719987.4571τ )+ 0.010τsin( 328.5170 +1079981.1857τ)+ 0.309τ^2 sin( 241.4518 + 359993.7286τ)+ 0.021τ^2 sin( 205.0482 + 719987.4571τ)+ 0.004τ^2 sin( 297.8610 +4452671.1152τ)+ 0.010τ^3 sin( 154.7066 + 359993.7286τ)τ的系数为359993.7、719987或1079981的周期项,与地球离心率相关。
