理论力学竞赛辅导全
理论力学竞赛辅导2运动学

问题3:当平面运动刚体的角速度或角加速度分别为零时, 如何确定加速度瞬心的位置?
2020/6/8
5
BUAA
例题与思考题
习题4:点M做平面曲线运动,已知该点速度的大小 v=at (a>0), 速度的方向与 x 轴的夹角θ=0.5bt2(b>0),求任意时刻(t>0) 动点M的加速度在y轴上的投影以及轨迹的曲率半径。
aOn
vO2 R
r
(r)2
3r
12r
3
aPnO 2r
aPn
aOn
aPnO
42r
3
vP2 aPn
( 2r ) 2 42r
3r
2020/6/8 3
an
P PO
r
O
an O R
14
BUAA
例题与思考题
问题14:圆盘上哪点的加速度的模最大(小)?
为
o
常
量
A
aA O
Ca
B D
aB
CV
纯滚动
OA R, AB 2R
vB vA vBA
2、速度投影法
vB
AB
vA
AB
3、速度瞬心法
vM vMCV , vM MCV
思考题1:上述三种方法的内 在联系和区别是什么?
Ax’y’为平移动系,B为动点
y
y' vBA vB B
A
r0
B
A
vA
x'
o
vA x
M
vM
CV
2020/6/8
4
BUAA
二、刚体的平面运动
4、平面图形上各点的加速度
y
et (t t)
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题

B A
二力矩式
F F F x 0 , M A () 0 , M B () 0
FR x
(x 轴不得垂直于A、B 两点的连线)
是否存在三投影式?
三力矩式
F x1 0
M A ( F ) 0 , M B ( F ) 0 , M C ( F ) 0 Fra bibliotekFx2
0
(A、B、C 三点不得共线)
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题
理论力学(专题部分)
专题1: 虚位移原理
掌握虚位移、虚功的概念;掌握质点系的自由度、 广义坐标的概念;会应用质点系虚位移原理。
专题2: 碰撞问题
(1) 掌握碰撞问题的特征及其简化条件。掌握恢复因 数概念
(2) 会求解两物体对心碰撞以及定轴转动刚体和平面 运动刚体的碰撞问题。
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题
§2 平面任意力系的平衡条件和平衡方程
n
F xi 0
i1
} FR′ =0
Mo=0
n
F yi 0
i1
n
M O (F i) 0
i1
平衡方程
平面任意力系平衡的解析条件:所有各力在两个任选的坐标轴
上的投影的代数和分别等于零,以及各力对于任意一点矩的代
公理2 二力平衡条件
★ 作用在刚体上的两个力,使刚体保持平衡的充要条件是: 这两个力的大小相等,方向相反,且在同一直线上。
B A
F2
F1= F2
F1
注意: 公理对于刚体的平衡是充要条件,而对变形体仅为
平衡的必要条件;
全国周培源大学生力学竞赛辅导力学竞赛-静力学专题
公理3 加减平衡力系原理
★ 在已知力系上加上或减去任意的平衡力系,并不改变原力系
周培源大学生力学竞赛辅导材料

t 2H / g
e=1时,根据落下与反弹的轨迹对称性,设小球与地面碰撞N次,于是有
S=2NvBt,
S 2N 2gR(1 cos ) 2H / g
(3)假设小球击中CD杆上的E点,为了使悬挂点C处的冲量尽可能小,试确 定小球的号码及静止释放时的θ,此时CE的距离是多少?冲量有多大? 根据碰撞的理论,当冲量IE与杆垂直,且
解:1. 圆环不是匀质的,质心不在圆环的中心。开始滚动角速度大,圆环一跳 一跳地向前滚动;随后角速度减小,所以圆环不离开地面向前滚动。
2.(1)圆环能自己滚回的条件:圆环初瞬时环心速度为v0,角速度大小为ω0,以后 为v 和ω。圆环与地面接触点的速度大小为 u=v+rω (1) 第一阶段,u>0,圆环与地面有相对滑动,摩擦力F=fsFN,式中FN=mg 。 由质心运动定理 解得 由 解得 由于摩擦力存在,v 和ω都随时间而减小。 第二阶段,由(1),(3),(5)式解得 u = (v 0 + r ω 0) −2 f s gt v=v0-fsgt
S 2 gR(1 cos )t 1 1 2 H H gt 2 2
把参数带入小球的位移表达式,有
S的限制为
S 2HR
(2)假设某小球击中CD杆上的E点,为了使E点尽可能远离D点,试确 定小球的号码及静止释放时的θ,此时CE的距离是多少? 直观上看,当e=1(小球的号码为9)时反弹得最高,有可能击中C点。 此时E点离D点最远,距离为CE=0。 根据运动方程,在竖直方向,小球离开B点后与地面碰撞的时间为
不失一般性,设乘员的前脚向左蹬板,蹬板时前脚掌必自然倾斜使左侧略高于右 侧,并带动前板绕x轴逆时针偏转φ1角,前轮平面随同前板相对垂直平面偏转φ1角.此 时地面在P1点处作用的法向约束力N1必偏离前轮平面,其沿前轮平面法线方向的投影 为N1 sinφ1,仅保留φ1的一次项时,简化为N1φ1.此分量以a cosβ为力臂,产生绕前轮架 转轴z1;负方向的力矩M1,力矩的模为
全国周培源大学生力学竞赛辅导力学竞赛-静力学平衡方程
0.5 m C P
FAx FAy
FBy
解:研究系统,受力如图,由方程:∑Fx=0,∑Fy=0,∑MA=0,可 解得FAx=0、FAy=20 kN、MA=20 kN· m。
研究杆BEC,受力如图,由方程:∑Fx=0,∑Fy=0,∑MB=0,可 解得FBx=0、FBy=-20 kN、FDE=40 kN· m。
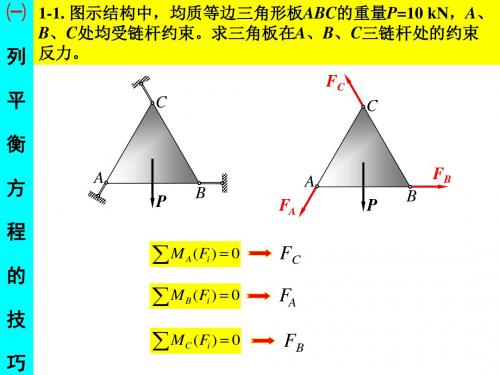
㈠ 1-1. 图示结构中,均质等边三角形板ABC的重量P=10 kN,A、
B、C处均受链杆约束。求三角板在A、B、C三链杆处的约束 列 反力。 FC 平 C C
衡 方 程 的 技 巧
A P
B
( Fi ) 0 ( Fi ) 0 (Fi ) 0
A FA P
FB B
M M M
A
FC FA
A A C B
D
FA
E
F P FC C FB
B
A FA D FD
C
B
E
F P
㈢ 3-1. 图示结构,已知P=20 kN,求支座A处反力及杆 物 DE的受力。 体 系 平 衡 问 题 基 本 解 法
B FBx 0.5 m A 0.5 m D B E C P D MA A B E C P
0.5 m
E FDE
0.6 m 0.6 m
A C
B
0.8 m
0.6 m
0.6 m
D
F
0.6 m 0.6 m
E
A M C
B
0.8 m
P 4-2′图示结构,已知 P=10 kN,求支座A、E处反力及 杆CF、BF的受力。 0.6 m 0.6 m
A M C
B
0.8 m
D P
F
0.6 m 0.6 m
力学竞赛辅导讲解

an a
a
an
a
1.2 曲率半径的物理求法
an
v2
v2 an
y
椭圆的曲率半径:
B
轨道方程:
x2 a2
y2 b2
1
对应运动方程: xy
a b
cos t sin t
b Oa
Ax
A点:v vy,max b,
A
v2 an
b2 a
an ax,max a2
v02 h
sin3
h v0
y
x
例1.8 如图示,一半径为R的半圆柱体沿水平方向
以速度v0作匀速运动。求杆与半圆柱体的接触点P
的角位置为 时竖直杆运动的速度和加速度。
vP
P
R
y
v0
O xA
解:y R2 x2
dy dy dx
dy
vP dt dx dt v0 dx v0
反映速度(大小和方向) 变化快慢的物理量
a v
a
t lim
t 0
v t
dv dt
d 2r dt 2
x
a x
dvx dt
d2x dt2
a y
dvy dt
d2y dt 2
z A
vA B
rA
vB
rB
O
y
(a)
vA v
vB (b)
加速度与速度的方向一般不同。
H
ymax
v02 sin2
2g
力学竞赛辅导讲义

力学竞赛辅导讲义——虚位移原理一、内容要点精讲1、约束与约束方程(1)约束。
限制非自由质点或质点系运动的各种条件称为约束。
(2)约束方程。
约束对质点系运动的限制可以通过质点系中各质点的坐标和速度以及时间的数学关系式或方程来表示。
这种方程通常称为约束方程。
2、约束分类(1)几何约束与运动约束。
只限制质点或质点系几何位置的约束称为几何约束;对于不仅限制质点系的位置,而且还限制质点系中质点的速度的这类约束称为运动约束。
(2)定常约束(稳定约束)与非定常约束(不稳定约束)。
约束方程中不显含时间t 的约束称为定常约束(或稳定约束);约束方程中显含时间t 的约束称为非定常约束(或不稳定约束)。
(3)完整约束与非完整约束:约束方程中不包含坐标对时间的导数,或者方程中的微分项可以积分为有限形式,这类约束称为完整约束;约束方程中包含坐标对时间的导数,而且方程中的微分项不能积分为有限形式,这类约束称为非完整约束。
(4)单侧约束(可离约束)与双侧约束(不可离约束)。
由不等式表示的约束称为单侧约束(或可离约束);由等式表示的约束称为双侧约束(或不可离约束)3、虚位移在某瞬时,质点系在约束允许的条件下,可能实现的无限小位移称为虚位移。
虚位移可以是线位移,也可以是角位移。
在定常约束条件下,微小实位移是虚位移之一。
4、虚位移与实位移的差别和联系(1) 差别。
虚位移是纯粹的几何概念,它与质点或质点系是否实际发生运动无关。
它不涉及运动时间、运动的初始条件和作用力等,只是约束许可的想像中的微小位移。
而实位移除与约束有关外,还与运动时间、运动初始条件和作用力、质量等有关;虚位移是微小的位移,而实位移可能是微小的,也可能是有限的;虚位移可以有多种不同的方向,而实位移只有惟一确定的方向,指向真实运动的一边。
(2) 联系。
在定常约束条件下,微小的实位移是虚位移中的一种情形。
在非定常约束条件下,微小的实位移一般不是虚位移中的一种情形。
为区别起见,虚位移用变分符表示,如r (投影为x,y,z),s 等,而微小的实位移用微分符号d表示,如dr (投影为dx,dy,dz),ds,d等。
理论力学竞赛辅导5综合应用PPT精品文档19页

01.06.2020
11
BUAA
动力学的应用
1、电机的驱动力矩M 应用动能定理微分形式:
T1 2m Cv21 2m Av21 2JAR v2 dWM d
T m Cv am Av aJAR v2aW MMRv
M(mCRmARR J)a
C θ
mCg
a A
F
2、求倾角θ 应用动静法:研究车身
M A0, FICmCa
01.06.2020
1、 若钢板能进入碾轧机,利 用的是什么力学概念? 2、轧轮和钢板间的摩擦系数 为f,确定a,b,d ,f间的关系。
ftam na x tan
5
BUAA
运动学的应用
问题5:已知车队以速度V 匀速行驶,车宽为b,车距为a, 若人要
匀速沿直线行走穿过马路,求人过马路的最小速度u,并确定过
马路的方向。
au
b
V
V ta(uco )ts f() a s i n b c os
(usin )tb
f'() a co b s si 0 n
uasinVbbcos
tan a
b
u Vb a2 b2
01.06.2020
6
BUAA
运动学的应用
问题6:设计一个机构,使得将转动转换成往复移动或摇动。
01.06.2020 问题3:该磅秤在设计上存在还哪些不足,如何改进2 。
BUAA
静力学的应用
问题3:该磅秤在设计上存在还哪些不足,如何改进。
01.06.2020
3
BUAA
静力学的应用
01.06.2020
4
BUAA
静力学的应用
问题4:轧钢机械中的力学问题
理论力学竞赛辅导动力学
试题范围(专题部分)
(一) 虚位移原理 掌握虚位移、虚功旳概念;掌握质点系旳自由度、广义坐 标旳概念;会应用质点系虚位移原理。 (二) 碰撞问题 (1) 掌握碰撞问题旳特征及其简化条件。掌握恢复因数概念 (2) 会求解两物体对心碰撞以及定轴转动刚体和平面运动刚 体旳碰撞问题。
基本概念—质心速度
Fgox (miaix) 如图11-2所示旳四杆机构中,各均质杆质量均为,
F2
v2 v1 N PF1 F2
N P F1 F2 v2 v1
定常流动时,管内流体在单位时间内流出动量与流入动量之差等于作用 于管内流体上旳全部外力之矢量和。流体流动欧拉定理
pv v t Wp (p1 p2)V
静约束力 附加动约束力
21
定常流动中旳能量方程(动能定理在流体中旳应用)
Fgoz 0 J yz
FAx
1 AB
My
FRxOB
Mgoy
FgoxOB
mi yi z i
M goy miaix zi mi ( 2 xi yi )zi J xz 2 J yz
M goz mi ai t riz mi riz2 J z
2 mi xi mi yi m(xC 2 yC )
根据本题旳启示,设计一种力学小魔术:不依托任何外力矩, 倒立摆可在任何倾角处保持不动甚至能从倾斜状态竖立起来。
魔术师旳表演(25分)第六届预赛样题
魔术师要表演一种节目。其中一种道具是边长为a旳不透明立方体箱子,质量为M; 另一种道具是长为L旳均质刚性板AB,质量为2M,可绕光滑旳A铰转动;最终一种 道具是半径为R旳刚性球,质量为3M,放在刚性旳水平面上。魔术师首先把刚性板 AB水平放置在圆球上,板和圆球都能够保持平衡,且圆心O和接触点B旳连线与垂 线夹角为ϕ。然后魔术师又把箱子固定在AB板旳中间位置,系统仍能够保持平衡, 如图3所示。 魔术师用魔棒轻轻向右推了一下圆球,居然轻易地就把圆球推开了。 更令人惊讶旳是,当圆球离开AB板后,AB板及其箱子仍能在水平位置保持平衡。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
II
B
A I
选择题28: 长方体I面上的A点作用 一该平面内的汇交力系,II面上的B 点也作用有一该面内的汇交力系,则 该力系最多有几个独立的平衡方程? A:2个 B:3个 C:4个 D:5个
B A
地面光滑
18
BUAA
虚位移原理
虚位移原理:具有双面、完整、 定常、理想约束的静止的 质点系, 在给定位置保持平衡的充要条件是:该质点系所 有主动力在系统的任何虚位移上所作的虚功之和等于零。
思考题13:判断在图示位置系统是否 有可能平衡.(F,M 均不为零)
C
CF
AM
B
A F
2020/10/18
0
MOx(F ) 0
MOy(F ) 0
M x(F) 0 M y (F ) 0,
Fz 0
MOz(F ) 0
M z(F) 0
注:正交条件是充分的,不是必要的。
2020/10/18
9
BUAA
空间汇交力系的平衡条件
空间汇交力系平衡条件的讨论
FR FRxi FRy j FRzk 0
A
O RC
mg
1. 不倒翁的质量m 2. 半圆球的半径R 3. 重力加速度g 4. 重心的位置h
2020/10/18
21
BUAA
静力学的思考题与例题
题15:在下列图示结构中,构件AC上作用有一已知力偶(构 件自重不计),试确定铰链A处约束力的方向。
AB AC, AC AB
思考题16:上述结构中,哪个结构中A点的约束力最大?
FR FR2x FR2y FR2z 0
FRx Fx FRy Fy FRz Fz
空 FRx Fx 0
间
力
FRy
Fy 0
系
FRz
Fz
0
有三个独立的平衡方程
z
?
x y
问题6:三根轴必须垂直吗?
2020/10/18
10
BUAA
三、刚体系与结构的平衡
•静 定 问 题 ( statically determinate problem): 未知量的数目= 独立平衡方程的数目
12
BUAA
四、虚位移原理
•元功: W F •vdt F •dr
等效力系作功定理: 若作用于刚体上的力系等效
即: {F1, F2,, Fn} {P1,, Pm} {FR , Mo}
n
m
则 W (Fi ) W (Pj ) W (FR ) W (MO )
i1
j 1
问题9: 如何求纯滚动圆盘轮心移动S距离时, 力F 所作的功。
7
BUAA 一、基本概念与基本原理和定理
选择题2: 力偶系和一个力构成的力系简化的最简结果可能是: A:平衡力系、B:力偶、C:合力、D:力螺旋
选择题3: 两个平面汇交力系构成的平面力系简化的最简 结果可能是: A:平衡力系、B:力偶、C:合力、D:力螺旋
选择题4: 图中的两个力构成的力
系简化的最简结果可能是: A:平衡力系、B:力偶、
M1 B
I
M B
I
II M2 A
F A
问题22:该 系统是否是 静定结构?
思考题21:重为W的均质正方体用球铰链约束,其上作用有一 个力和一个力偶(如图所示),求平衡时力与力偶的关系。设 正方体的棱长为L。
2020/10/18
25
BUAA
静力学的思考题与例题
问题23:空间汇交力系的平衡方程独立的充分必要条件:
F1
II I
C:合力、 D:力螺旋
F2
选择题5: 若作用在立方体上的力系由作用在I面和II面上的两
个平面任意力系构成,该力系简化的最简结果可能是:
A:平衡力系、B:力偶、C:合力、D:力螺旋
2020/10/18
8
BUAA 二、空间任意力系的平衡条件
空间任意力系简化 {F1, F2,, Fn} {FR, MO}
M l1 0 M l2 0
l2
M l3 0
l4
M l4 0 M l5 0
M l6 0
Mo 0
? FR 0
2020/10/18
27
BUAA
静力学的思考题与例题
选择题27: 长方体I面上的A点作用一 该平面内的汇交力系,II面上的B点也 作用有一该面内的汇交力系,则该力 系最多有几个独立的平衡方程? A:2个 B:3个 C:4个 D:5个
BUAA
问题10: 图示系统具有什 么类型的约束?试确定系 统的自由度和广义坐标。
RA
B r
图 1 齿轮机构
2020/10/18
约束的分类
o
yA sin t
A
x
l
y 图2B
A
B O
图 3 圆盘放置在光滑地面上 16
BUAA
虚位移与理想约束
•虚位移: 在给定瞬时,质点或质点系为 约束容许 的 任何 微
n
Fi • ri 0
i 1
M B
F
F
19
BUAA
平衡位置的稳定性
设质点系的势能函数为:V V (q1, q2,, qk )
质点系在势力场中的平衡充分必要条件是:
V 0,( j 1,, k) q j
质点系势能函数取得 极值是平衡的充分条件
定理:质点系在势力场中的平衡位置是稳定的充分必要 条件是系统在平衡位置的势能为极小值。
确定三根轴的位置
26
BUAA
静力学的思考题与例题
思考题26:长正方体上作用有一空间任意力系,对 其中的六个轴取矩方程均成立,该力系是否是平衡 力系。
MO
l3 FR
l5
MO
l3 FR
o
l6 l2
l6 o
l1
l4
l1
{F1, F2 ,, Fn} {FR , Mo}
平衡条件:FR 0 Mo 0
l5
•等效力系(equivalent force system): 对同一刚体产生相同作用效果的力系. Fn
F3
{F1, F2 ,, Fn} {P1, P2 ,, Pm} F1
F2
{F1, F2 ,, Fn} {FR}
Pm
P2 •合力(resultant force) :与某力系等效的力
P1
FR 称为该力系的合力,Fi(i=1,2,…n)称为合力的分力
R
F
Mr o
F
s
2020/10/18
13
BUAA
x
lM
y
约束的分类
x
l
M
y
xA A xA sin t
x
y
M
x2 y2 l2
x2 y2 l2
(x sin t)2 y2 l2
•双面约束:约束方程为等式的约束 •单面约束:约束方程为不等式的约束
•定常约束:约束方程中不显含时间t 的约束
•非定常约束:约束方程中显含时间t 的约束
FR 0, MO 0
平衡
n
n
FR Fi ' Fi
FR ( Fx )2 ( Fy )2 ( Fz )2
i1
i1
n
n
MO Mi ri Fi
MO ( MOx )2 ( MOy )2 ( MOz )2
i1
i1
空间任意力系的平衡条件:
FR
0
Fx 0
Fy 0
MO
2020/10/18
力螺旋
6
BUAA
一、基本概念与基本原理和定理
• 判断力系简化的最简结果的基本步骤:
– 计算力系的主矢 – 计算力系向某一点简化的主矩 – 分析主矢与主矩的几何关系
主要采用定性分析的方法
选择题1: 空间平行力系简化的最简结果可能是: A:平衡力系、B:力偶、C:合力、D:力螺旋
2020/10/18
华大学出版社
2020/10/18
2
BUAA
力学竞赛辅导
第一讲 静力学
• 静力学的基本概念与方法 • 平衡方程 • 虚位移原理 • 例题、思考题、问题(35个)
2020/10/18
3
BUAA 一、基本概念与基本原理和定理
•力系(force system): 作用在物体上的一组力 {F1, F2 ,, Fn}
思考题17:在下列图示结构中,构件AC上的D点作用有一已 知力(构件自重不计),回答上述问题。
2020/10/18
22
BUAA
静力学的思考题与例题
思考题18:下面哪些系统是可以保持平衡的结构?
A
D
A
D
B
L
L
A
(1)
F C
L
D
B
L
A
L (2)
F C
LDLeabharlann BL(3)L
2020/10/18
F C
L
B
L
(4)L
小位移。r
rA A rA
rA A rA
900 O
rB B rB
O
rB B rB
虚 1、不同瞬时或位置,虚位移不同
位 移 特
2、必须满足约束条件 3、是无限小的,不是有限位移
[rA ]AB [rB ]AB
点 4、虚位移不只有一个或一组 {rA,rB} {rA,rB}
2020/10/18
17
BUAA
F
C
L 23
BUAA
静力学的思考题与例题
A 思考题19:确定图示结构
D
中哪个二力杆受拉以及铰
链B的约束力FB的方向。
B
F
不计构件自重
L
(2)L
