有理数 - 教师版
初中数学有理数教案5篇
初中数学有理数教案5篇关于初中数学有理数教案5篇初中数学有理数教案（篇1）教学目标：1、知识与技能:(1)通过学生熟悉的问题情景，以过探索有理数减法法则得出的过程，理解有理数减法法则的合理性。
(2)精通有理数的减法。
2、过程与方法通过实例，归纳出有理数的减法法则，培养学生的逻辑思维能力和运算能力，通过减法到加法的转化，让学生初步体会人归的数学思想。
重点、难点1.重点:有理数减法规则及其应用。
2.难点:有理数减法规则的应用改变了符号。
教学过程：一、创设情景，导入新课1、有理数加法运算是怎样做的?(-5)+3= —3+(—5)=—3+(+5)=2、-(-2)= -[-(+23)]=，+[-(-2)]=3、20__的某天，北京市的最高气温是-20C,最低气温是-100C，这天北京市的温差是多少?导语：可见，有理数的减法运算在现实生活中也有着很广泛的应用。
(出示课题)二、合作交流，解读探究1(-2)-(-10)=8=(-2)+82:珠穆朗玛峰海拔高度为8848米，与吐鲁番盆地海拔高度为-155米，珠穆朗玛峰比吐鲁番盆地高多少米?3、通过以上列式，你能发现减法运算与加法运算的关系吗?(学生分组讨论，大胆发言，总结有理数的.减法法则)减去一个数等于加上这个数的相反数教师提问、启发：(1)法则中的“减去一个数”，这个数指的是哪个数?“减去”两字怎样理解?(2)法则中的“加上这个数的相反数”“加上”两字怎样理解?“这个数的相反数”又怎样理解?(3)你能用字母表示有理数减法法则吗?三、应用迁移，巩固提高1、P.24例1 计算：(1) 0-(-3.18)(2)(-10)-(-6)(3)-解：(1)0-(-3.18)=0+3.18=3.18(2)(-10)-(-6)=(-10)+6=-4(3)-=+=12、课内练习：P.241、2、33、游戏：两人一组，用扑克牌做有理数减法运算游戏(每人27张牌，黑牌点数为正数，红牌点数为负数，王牌点数为0。
1.2.1 有理数(教师版)
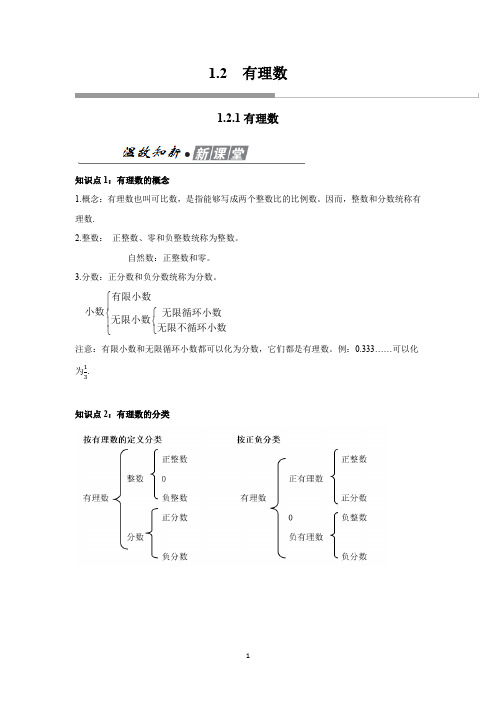
1.2 有理数1.2.1有理数知识点1：有理数的概念1.概念：有理数也叫可比数，是指能够写成两个整数比的比例数。
因而，整数和分数统称有理数.2.整数： 正整数、零和负整数统称为整数。
自然数：正整数和零。
3.分数：正分数和负分数统称为分数。
⎧⎪⎧⎨⎨⎪⎩⎩有限小数小数无限循环小数无限小数无限不循环小数 注意：有限小数和无限循环小数都可以化为分数，它们都是有理数。
例：0.333……可以化为.知识点2：有理数的分类知识点3：四非数①正整数、0统称为非负整数（也叫自然数）②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数考点梳理·新认知考点1 有理数的辨别例1在-,π,0,-0.74四个数中,有理数的个数是()A.1B.2C.3D.4【解析】-,0,-0.74是有理数,而π是无限不循环小数,不是有理数,故选C.总结：1.整数和分数统称为有理数.凡是能写成（p,q为整数，且q≠0）形式的数，都是有理数.2.有限小数与无限循环小数都能表示成分数形式，无限不循环小数不是有理数，如π不是有理数．考点2 有理数的分类例2把下列各数填在相应的集合中：－7，3.5，－3.14，0，1713，0.03%，－314，10．自然数集合：{ …}；整数集合：{ …}；负数集合：{ …}；正分数集合：{ …}；正有理数集合：{ …}．【解析】解：在所给的所有数中，①自然数集合为{0，10…}；②整数集合为{-7，0，10…}；③负数集合为{-7，-3.14，－314…}；④正分数集合为{3.5，1713，0.03%…}；⑤正有理数集合为{0.03%，1713，3.5，10…}．总结:对有理数进行分类，首先要理解以下数的概念：1.正数：像3,1.8%,3.5这样大于0的数叫做正数．正数的前面可以加上正号（即加号）“+”来表示2.负数：在正数前加上“-”的数叫做负数；3.整数：像-2，-1，0，1，2这样的数叫做整数；4.分数：把单位“1”平均分成若干份，表示这样的一份或几份的数叫做分数．考点3 带非字的数例3﹣5，0，﹣3.14，，﹣12，0.1010010001…,+1．99，﹣（1）非负数集合：{ …}（2）非负整数数集合：{ …}（3）非正数集合：{ …}（4）非正整数数集合：{ …}【解析】解：在所给的所有数中，（1）非负数集合：{ 0，，0.1010010001…,+1．99，…}（2）非负整数数集合：{ 0 …}（3）非正数集合：{﹣5，﹣3.14，﹣12，﹣…}（4）非正整数数集合：{ ﹣5，﹣12，…}总结：1.有理数分为正数、0和负数三类，正数和0统称非负数；负数和0统称非正数．2.一个数不是0，则它可能是正数或负数；若一个数不是正数，则它可能是负数或者0；若一个数不是负数，则它可能是正数或者0.基础训练1．下列各数：-1，，4.112134，0，，3.14，其中有理数有（ ）A ．6个B ．5个C ．4个D ．3个 【解析】解：在-1，2π ，4.112134，0，227 ，3.14中不是有理数是2π：故选B ．2. 在下列数， ，2.010010001…，25%，3.1415926，0， …中，属于分数的有（ ）A ．2个B ．3个C ．4个D ．5个【解析】解：属于分数的有25%，3.1415926，-0.222…， 故选B ． 3. 下列表述中，正确的是（ ）A ．有理数有最大的数，也有最小的数B ．有理数有最大的数，但没有最小的数C ．有理数有最小的数，但没有最大的数D ．有理数既没有最大的数，也没有最小的数 【解析】解：有理数既没有最大的数，也没有最小的数． 故选D ． 4. 下列说法正确的是（ ）A ．一个有理数不是整数就是分数B ．正整数和负整数统称为整数C ．正整数、负整数、正分数、负分数统称为有理数D ．0不是有理数【解析】解：A 、一个有理数不是整数就是分数，故本选项正确； B 、正整数和负整数和0统称为整数，故本选项错误； C 、正整数、负整数、正分数、负分数和0统称为有理数，故本选项错误； D 、0是有理数，故本选项错误；故选A ．5.下列说法：①-2.5既是负数、分数，也是有理数；②-7既是负数也是整数，但不是自然数；③0既不是正数也不是负数；④0是非负数．其中正确的个数是（ ） A ．1 B ．2 C ．3 D ．4【解析】解：①-2.5既是负数、分数，也是有理数，正确；②-7既是负数也是整数，但不是自然数，，正确；③0既不是正数也不是负数，正确；④0是非负数，正确， 则正确的个数是4，故选D ．6. 把下列各数填在相应的大括号内:5，7-8，-10，0，2.4，+3，227，-3.01.正数集合{…};非负数集合{…};整数集合{…};负分数集合{…}.【解析】正数集合,.,,,…;非负数集合,,.,,,…; 整数集合{5,-10,0,+3,…};负分数集合-,-.,….能力晋升1．设三个互不相等的有理数，既可表示为1、a+b、a的形式，又可表示为0、ba、b的形式，则b的值为（）A．0 B．-1 C．1 D．2【解析】解：由题意可知：a+b，a中有一个为0，且ba，b中有一个为1，当a=0时，则ba没有意义，不成立；∴b=1．故选C．2.下列判断正确的个数是（）①一个有理数不是整数就是分数②一个有理数不是正数就是负数③一个整数不是正数就是负数④一个分数不是正数就是负数⑤一个偶数不是正偶数就是负偶数A．1 B．2 C．3 D．4【解析】解：①一个有理数不是整数就是分数，正确；②一个有理数不是正数就是负数，错误，也可能是0；③一个整数不是正数就是负数，错误，也可能是0；④一个分数不是正数就是负数，正确；⑤一个偶数不是正偶数就是负偶数，错误，也可能是0；故选B．3. 在有理数集合中，最小的正整数是，最大的负整数是．【解析】解：在有理数集合中，最小的正整数是1，最大的负整数是-1．故答案为1；-1．4. 在-2，1.5，+，0，27，100，-2.1，18，-，-30中,是非负整数的是.【解析】0，27，100，18.5. 在-2，5，-，0.63，0，7，-0.05，-6，9，，，1中,正分数有个,负分数有个,自然数有个,整数有个.【解析】正分数是0.63，，，有3个;负分数是-，-0.05，有2个;自然数是5，0，7，9，1，有5个;整数是-2，5，0，7，-6，9，1，有7个.6.把下列各数分别填入相应的集合内：-2，-3.14，0.3，0，，，-0.1212212221…．（1）正数集合：{ }；（2）负数集合：{ }；（3）分数集合：{ }；（4）有理数集合：{ }．【解析】解：（1）正数集合：{0.3，，}；（2）负数集合：{ -2，-3.14，-0.1212212221…}；（3）分数集合：{ -3.14，0.3，}；（4）有理数集合：{ -2，-3.14，0.3，0，}．同步检测·新导向1．（2019•武汉模拟）下列各数中，属于正有理数的是（）A．π B．0 C．-1 D．2【解析】解：由题意得：π是无理数，故选项A错误；0是有理数，但不是正数，故选项B错误；-1是负有理数，故选项C错误；2是正有理数，故选项D正确；故选D．2.（2019•沙坪坝区校级模拟）下列四个数中，是正整数的是（）A．-2 B．-1 C．1 D．1 2【解析】解：A、-2是负整数，故选项错误；B、-1是负整数，故选项错误；C、1是正整数，故选项正确；D、12是非正整数，故选项错误．故选C．3．（2019•渝中区校级模拟）下列各数中是负整数的是（）A．-2 B．5 C．12D．2-5【解析】解：A、-2为负整数，故选项正确；B、5为正整数，故选项错误；C、12为正分数，故选项错误；D、2-5为负分数，故选项错误．故选A．4．（2018秋•沈河区期末）在-4，227，0，2，3.14159，1.3，0.1010010001…有理数的个数有（ ）A ．2个B ．3个C ．4个D ．5个【解析】解：2，0.1010010001…不是有理数，故选D ．5．（2018秋•卢龙县期末）下列说法正确的是（ ） A ．0是最小的有理数 B ．一个有理数不是正数就是负数 C ．分数不是有理数 D ．没有最大的负数【解析】解：A 、没有最小的有理数，故本选项错误；B 、一个有理数不是正数就是负数或0，故本选项错误；C 、分数是有理数，故本选项错误；D 、没有最大的负数，故本选项正确； 故选D ．6.（2018秋•门头沟区期末）在有理数-0.2，-3，0，132，-5，1中，非负整数有 ． 【解析】解：非负整数有0，1， 故答案为：0，1．7．（2018秋•仪征市期中）有三个有理数，分别是-1、a 、a +b ，或者写成0、-b a、b ，那么数b 的值是 ．【解析】解：由题意可知：a +b ，a 中有一个为0，且-b a ，b 中有一个为-1，当a =0时，则-b a没有意义，不成立；∴b =-1． 故答案为：-1． 8. （2018秋•武邑县校级月考）在数1-13，20%，227，0.3，0，-1.7，21，-2，1.0101001…，+6，π中，分数有 个． 【解析】解：分数有1-13，20%，227，0.3，-1.7， 故答案为：5。
有理数计算题专项练习(每日8题)-教师版
有理数专项练习每日8题1.(-1.2)+[1-(-0.3)]【答案】原式=-1.2+1.3=0.1．2.(-2)+(+30)-(-15)-(+27)【答案】原式=(-2)+(+30)+(+15)+(-27)=[(-2)+(-27)]+[(+30)+(+15)]=(-29)+(+45)=16.3.12-1 +13-12 +14-13 +⋯+12020-12019 【答案】原式=1-12 +12-13 +13-14 +⋯+12018-12019 +12019-12020 =1-12020=201920204.-(+1.5)--414 +3.75-+812 【答案】原式=-112+414+334-812=-112-812 +414+334=-10+8=-2．5.10×-211 -2×211+(-3)×-211 【答案】原式=-211×(10+2-3)=-211×9=-1811；6.-3÷-12 ÷-12【答案】【详解】原式-3×(-2)×(-2)=-3×2×2=-12，7.15÷-115 ×-216 【答案】原式=15×-56 ×-136 =1336；8.(-2)3--32 +-12-0.5 ×23【答案】原式=-8-(-9)+-1-0.5 ×23=-8+9+-1.5 ×23=-8+9+1=29.12-(-6)+(-9)【答案】原式=12+6+(-9)=18+(-9)=9；10.-9+5-(-12)+(-3)【答案】原式=-9+5+12-3=5；11.-23 +516 +-416 -913【答案】原式=-23-913 +516-416 =-10+1=-912.614-3.3-(-6)--334 +4+3.3【答案】原式=614--334+(3.3-3.3)+[4-(-6)]=10+0+10=2013.-2+-3 +-4 ×-5【答案】原式=-5+20=1514.112÷12-13+14【答案】112÷12-13+14 =112÷512=112×125=1515.1÷4×(-25)×(-6)×16【答案】原式=14×(-25)×(-6)×16=254．16.-14+3-5 -16÷-2 ×12【答案】原式=-1+2-16×-12 ×12=-1+2+4=5【答案】原式=(-1-2+7-4)+-14-13+56-12 =-14，=-61+71-8=-69+71=2．18.(-7)-(-10)+(-8)-(+2)【答案】原式=-7+10-8-2=-7；19.-3310 +-112 +235-212 【答案】原式=(-3-1+2-2)+-310-12+35-12=-4+-710 =-4710．20.(-0.5)-234-+214【答案】原式=(-0.5)+-234-214=-0.5-5=-5.5；21.-2 3+-9+-3 2 ×13【答案】原式=-8+-9+9 ×13=-822.(-18)÷(-6)2【答案】原式=-18÷36=-12，23.6×(-2)-12÷(-4)【答案】原式=-12+3=-9.24.722×-317+713 -3÷-3 2【答案】原式=722×-227 +722×223-3÷9=-1+73-13=1【答案】原式=3+15=18．26.(-7)-(+5)+(-4)-(-10)【答案】原式=-7-5-4+10=-627.-313--587 +-97 -+323 【答案】原式=-313-323 +587-97=-21+7=-14；28.123+212-334+13-4.25【答案】原式=123+212+-334 +13+-414=-312．29.-34+712-58×(-24)【答案】原式=18-14+15=19；30.(-16.8)÷(-3)【答案】原式=16.8÷3=5.6；31.-313 ÷-123 ×-25【答案】原式=-103×-35 ×-25 =-103×35×25=-45．32.14-14÷(-2)+7×(-3)【答案】原式=14-(-7)+(-21)=21-21=033.-8-12【答案】原式=-20；34.-17+(-33)-10-(-16)【答案】原式=-50-10+16=-4435.+13 +-12 -+34 --23 【答案】原式=+13+23 +-12-34 =1-114=-14．36.75--314 -(+0.5)+-712【答案】原式=(-1-2+7-4)+-14-13+56-12 =-14，= 2.75+314 +-0.5-712 =6-8=-2．37.-23-|-3|+4--38×(-3)【答案】原式=-8-3+4-98=-818．38.-54 ÷-45【答案】原式=-54 ×-54 = 2516；39.-347÷-123 ×-423【答案】原式=-257×-35 ×-143=-10；40.-3--4+1-1.6×58÷(-2) ÷2【答案】原式=-3-{[-4+(1-1)]÷(-2)}÷2=-3-[(-4)÷(-2)]÷2=-3-1=-4=-3-2÷241.10-(-5)+(-8)【答案】原式=10+5-8=7；42.|-7|-4+(-2)-|-4|+(-9)【答案】原式=7-4-2-4-9=-1243.+56 +-23 ++116 +-13 【答案】原式=56+-23 +116+-13 =1；44.613+(-4.6)+-25 -2.3--23【答案】原式=613+23-4.6-0.4-2.3=7-7.3=-0.3；45.(-48)×-12-58+712【答案】原式=(-48)×-12 +(-48)×-58 +(-48)×712=24+30-28=26；46.(+1.25)÷(-0.5)÷-58 【答案】原式=+54 ×(-2)×-85 =4.47.113×-256 ÷-414【答案】原式=+43×176÷174=43×176×417=8948.-12018+(-2)4×12 3-|-0.28|+-1102【答案】原式=-1+16×18-0.28+0.01=-1+2-0.28+0.01=-1-0.28+2+0.01=-1.28+2.01=0.7349.-3.8 -+7【答案】原式=-3.8-7=-10.8；50.1-(+2)+3-(+4)+5-(+6)⋯+2015-(+2016)【答案】原式=(1-2)+(3-4)+⋯+(2015-2016)=-1+(-1)+⋯(-1)=-100851.-3310 +-112 +235--212 【答案】原式=-3-310 +-1-12 +2+35 +2+12 =(-3-1+2+2)+-310-12+35+12 =0+310=310；52.1918+-534 +-918-1.25．【答案】原式=1918-918-534-1.25=10-7=3．53.-23 2×(-9)+|π-4|【答案】解：-23 2×(-9)+|π-4|=49×(-9)+4-π=-4+4-π=π，54.0.9÷313【答案】原式=910×310=27100,55.-212÷(-10)×313÷-56【答案】原式=-52×110×103×65=-1．56.-14+(-3)2×-23 -44÷|-4|．【答案】原式=-1+9×-23-256÷4，=-1-6-64，=-71．57.-5+8 +24+-3【答案】原式=3+24-3=24；58.(-4)-(+13)+(-5)-(-9)+7【答案】原式=-17-5+9+7=-659.-200056 +-199923 +400023+-112 【答案】原式=-2000-56 +-1999-23 +4000+23 +-1-12 =(-2000-1999+4000-1)+-56-23+23-12 =0-113=-113．60.+134 -+613 -2.25+103【答案】原式=74-94-193+103=-12-3=-72；61.14+16-12 ×12【答案】原式=14×12+16×12-12×12=3+2-6=-1；62.-34÷5【答案】原式=-34×15=-320,63.-7 ÷78×87×-21 【答案】原式=-7 ÷78 ×87×-21 =-8 ×-24=192．64.-32÷(-2)2×-113 ×6+(-2)3．【答案】原式=-9÷4×43×6+(-8)=-94×43×6+(-8)=(-18)+(-8)=-26．65.13-23+1【答案】原式=13+1-23=43-23=2366.(-25)+34+156+(-65)【答案】原式=(-25-65)+(34+156)=-90+190=100；67.-556 +-923 +1734+-312 【答案】原式=(-5)+-56 +(-9)+-23 +17+34 +(-3)+-12=[(-5)+(-9)+17+(-3)]+-56 +-23 +34+-12 =0+-114 =-11468.-34 --12 ++34++8.5 【答案】原式=-34 ++34 +--12++8.5 =0+9=9．69.-993536×18【答案】原式=136-100×18=136×18-100×18=12-1800=-179912；70.-18÷-145【答案】原式=18×59=10,71.-2.5 ÷-58×-0.25 【答案】原式=-2.5×85×0.25=-1；72.(-1)10×2+(-2)3÷4【答案】原式=1×2+(-8)÷4=2-2=0．73.|-3.2|+|0.5|-1+215【答案】原式=3.2+0.5-1-2.2=(3.2-2.2)-1+0.5=1-1+0.5=0.5；74.(-52)+24-(+74)+12【答案】原式=(-52+12)+(24-74)=-40-50=-90；75.-114+-213 +756+-412【答案】原式=(-1-2+7-4)+-14-13+56-12 =-14，76.-14+-2 +-13+-9 【答案】原式=-1-2-13+9=173．77.-214 ×-49【答案】原式=94×49=1；78.-32324÷-112【答案】原式=9524×12=952.79.+2831 ×-127 ×+2115 ×-412【答案】原式=7031×97×3115×92=27．80.-914+127-521 ÷-142 +32×|-110-(-3)2|【答案】原式=-914+97-521 ×(-42)+32×|-1-9|=27-54+10+32×10=-17+15=-2．82.(-13)+(-7)-(+20)-(-40)+(+16)【答案】原式=(-13)+(-7)+(-20)+40+16=16；83.-201723 +201634+-201556 +1612．【答案】原式=(-2017+2016-2015+16)+-23+34-56+12=-2000-14=-20001484.(-3.125)+(+4.75)+-978 ++514 +-423【答案】原式=-3.125+978 + 4.75+514 -423=-13+10-423=-723．85.7×(-4)×(-5)【答案】原式=7×20=140；86.(-8)×(-5)×(-2)×516【答案】原式=-25；87.3×-56 ÷-34【答案】原式=3×56×43=103．88.-4+5÷(-2)×12-9×2-13-29【答案】原式=-4-54-9×2+9×13+9×29=-4-54-18+3+2．90.(+1.9)+3.6-(-10.1)+1.4【答案】原式=1.9+3.6+10.1+1.4=17；91.+32 -512-52+-712【答案】原式=32-52-512-712=-1-1=-2；92.56+-34 -(+0.25)--16【答案】原式=56+-34 +-14 +16=56+16 +-34-14=1+(-1)=0．93.(-5)×(-8)×(-10)×(-15)×0【答案】原式=0．94.-1.25×(-5)×3×(-8)【答案】原式=-1.25×8 ×5×3 =-150.95.-34-59+712 ÷136【答案】原式=-34-59+712 ×36=-34×36-59×36+712×36=-27-20+21=-26；96.-27911 ÷9-12+23-34-1112×-24 【答案】原式=-27-911 ×19-12×-24 +23×-24 -34×-24 -1112×-24 =-27×19-911×19--12-16+18+22 =-3-111+12+16-18-22=-1511197.12+-23【答案】原式=-12-23=-1698.12-(-18)+(-7)-15【答案】原式=12+18-7-15=30-22=8；99.9+-25 -1--135【答案】原式=9-1-25+85=8+65=465；100.512+23-34×(-12)【答案】原式=512×-12 +23×-12 -34×-12 =-5-8+9=-4.101.-14×(-19)-12×19-34×(-19)【答案】原式=-14×-19 +12×-19 -34×-19 ,=-14+12-34×-19 =-12×-19 =192.102.-27 ÷-514 ÷-56,【答案】原式=-27×-145 ×-65,=45×-65,=-2425,103.-0.25÷-37 ×45【答案】原式=-14×-73 ×45=715；104.(-15)÷13-12×6【答案】原式=(-15)÷-16 ×6=(-15)×(-6)×6=90×6=540．105.(-4.7)+3.9【答案】原式=-(4.7-3.9)=-0.8106.(-5.5)+|-2.5|+(-3.2)-(+4.8)【答案】原式=-5.5+2.5-3.2-4.8=-3-8=-11；107.-14+56+23-12【答案】原式=56+23-14-12=32-34=34108.14×-89 【答案】原式=-29；109.--43×-1.5 【答案】原式=--43 ×-32 =-43×32 =-2；110.213÷-116【答案】原式=73÷-76 =73×-67 =-2111.(-1.5)×45÷-25 ×34【答案】原式=-32×45×-52 ×34=94．112.-15 ÷13-32-3 ×6【答案】原式=-15 ÷-256×6=-15 ×-625 ×6=185×6=1085．113.(-5)--34 +14【答案】原式=-5+34+14=-5+1=-4；114.-3+8-15-6【答案】原式=-16；115.-479 --316 -+229 +-616【答案】原式=-479+229 +316-616=-7-3=-10；116.-6×(-5)×(-7)【答案】原式=-210；117.1×(-0.001)×(-1)【答案】原式=0.0001118.134-78-716 ÷-78【答案】原式=134-78-716 ×-87=134×-87 -78×-87 -716×-87=-2+1+12=-12．119.-23÷8-14×(-2)2【答案】原式=-8÷8-14×4=-1-1=-2．120.-14-1-12 2×15×2+-3 3 【答案】原式=-1-12 2×15×(2-27)=-1-14×15×(-25)=-1+54=14．【答案】原式=-9-11+19=-1．122.+-2.1 +0.8+3.5+-2.1 +0.8+3.5【答案】原式=-2.1+0.8+3.5-2.1+0.8+3.5=-4.2+1.6+7=4.4；123.-56 ×-310 【答案】原式=14124.-2415×25【答案】原式=-3415×25=-1703；125.115+-56 --712×(-60)【答案】原式=115×(-60)+-56 ×(-60)--712 ×(-60)=-4+50-35=11．126.134-78-712 ÷-78【答案】原式=74-78-712 ×-87 =74×-87 -78×-87 -712×-87 =-2+1+23=-13；127.-32+5×(-6)-(-4)2÷(-2)【答案】原式=-9+(-30)-16×-12 =-9+(-30)+8=(-39)+8=-31．128.5÷(-1)2000-33×-29【答案】原式=5-9×-29 =5+2=7；【答案】原式=-20+3+5-7=-19；130.-5+6-7+8-9+10-⋯-2015+2016-2017+2018【答案】原式=(-5+6)+(-7+8)+(-9+10)+⋯+(-2017+2018)=1+1+⋯+1(1007个1相加)=1007，131.(-0.3)×-137 【答案】原式=310×107=37132.-2×3×(-4)【答案】原式=24133.-23 2017×(1.5)2018【答案】原式=-23 2017×32 2017×32=-23 ×32 2017×32=-1×32=-32. 134.512+23-34×(-12)【答案】原式=512×-12 +23×-12 -34×-12 =-5-8+9=-4.135.-23 ÷-85÷(-0.25)【答案】原式=-23 ÷-85 ÷-14 =-23 ×-58 ×-4 =512×-4 =-53；136.-22×5--2 3÷4【答案】原式=-4×5-(-8)÷4=-20+2=-18．137.-4.2+5.7-8.4+10【答案】原式=5.7+10-4.2-8.4=15.7-12.6=3.1138.6.1-3.7-4.9+1.8【答案】原式=6.1+1.8-3.7-4.9=7.9-8.6=-0.7139.(-100)×(-1)×(-3)×(-0.5)【答案】原式=150；140.(-17)×(-49)×0×(-13)×37【答案】原式=0141.722×-5 +-722 ×9+722×8【答案】原式=722×-5 -722×9+722×8=722×-5-9+8 =722×-6 =-2111；142.-9+3+12-23 ×12+32【答案】原式=-9+3+12×12-23×12+9=-9+3+6-8+9=1143.-49-512+16 ÷-136【答案】原式=-49-512+16 ×-36 =-49×-36 +-512 ×-36 +16×-36 =16+15-6=25．144.-32+1-47÷2×-4 2-2 【答案】原式=-9+37×12×16-2 =-9+37×12×14=-9+3=-6．145.0-(+2)-(-1)+(+4)-(-5)【答案】原式=0-2+1+4+5=8；146.+5.7+(-8.4)+(-4.2)-(-10)【答案】原式=5.7-8.4-4.2+10=(5.7+10)+(-8.4-4.2)=15.7-12.6=3.1；147.-4120×1.25×(-8)【答案】原式=8120×54×8=8110；148.(-10)×(-8.24)×(-0.1)【答案】原式=-8.24149.-56×2.4×35【答案】原式=-56×125×35=-65=-1.2；150.-32-(-1)2020×13-14+-3【答案】原式=-9-1×412-312+3=-6-112=-6112151.-72+2×-32+-6÷-1 32【答案】原式=-49+2×9+-6÷19=-49+18-54=-85．152.32÷-34+-272×21【答案】原式=-32×43+449×21=-2+127=-27；153.27-18+(-7)-32【答案】原式=27-18-7-32=-30；154.12-(-18)+(-7)-20【答案】原式=12+18-7-20=30-27=3；155.-|-2.5|×--225 【答案】原式=-52×225=-15；156.45×-256 ×-710 【答案】原式=45×256×710=73；157.54×-1.2 ×-19 【答案】原式=54×65×19=16．158.7+(-6)-(-4)×3【答案】原式=7+(-6)-(-12)=7+(-6)+12=13；159.-16+34-112×(-48)【答案】原式=-16×(-48)+34×(-48)-112×(-48)=8-36+4=-24．160.-65 ×-23 +-65 ÷317【答案】原式=65×23-65×173=45-345=-6161.1+-2 +-2-3 -5--9 【答案】原式=1-2+5-5+9=8.162.711516×(-8)【答案】原式=-71×8+1516×8 =-568+152 =-575.5.163.12×12-13+14【答案】原式=12×12-12×13+12×14=6-4+3=5；164.-12+56-79×18【答案】原式=-9+15-14=-8．165.|-1.25|×(-8)×4【答案】原式=-1.25×8×4=-40；166.(-4)×(-5)×0.25【答案】原式=(-4)×0.25×(-5)=-1×(-5)=5；167.-14-17×[2-(-3)2]【答案】原式=-1-17×(2-9)=-1-17×(-7)=-1+1=0；168.113×13-12 ×311÷54【答案】原式=113×-16 ×311×45=113×311×-16 ×45=-215.169.-36 ×-54+43-112【答案】原式=45-48+3=0；170.-12×(-8)+(-6)2【答案】原式=4+36=40；171.512+23+34×(-12)【答案】原式=512×(-12)+23×(-12)+34×(-12)=-5-8-9=-22；172.-37 ×-45 ×-712【答案】原式=-37 ×-712 ×-45 =14×-45 =-15；173.(-5)×-332 ×730×0×(-325)【答案】原式=0．174.-3 +22×-15【答案】原式=3+4×-15 =3-45=215；175.45×513+-35 ×513+513×-135【答案】原式=513×45-35-135 =513×-75 =-713．176.-13×23-0.34×27+13×(-13)-57×0.34【答案】原式=(-13)×23+13+0.34×-27-57 =(-13)×1+0.34×(-1)=-13-0.34=-13.34．177.-2 2+18--3 ×2 ÷4【答案】原式=4+18--6 ÷4=4+24÷4=4+6=10；178.-24+-223 ×2-512÷-16+-1 【答案】原式=-16+-83 ×2-112×-6 +1=-16-163+33+1=383；。
有理数的减法(一) - 教师版
有理数的减法（一）预习归纳1．有理数的减法法则：减去一个数等于加上这个数的____________，即()a b a b -=+-． 【答案】相反数 基础过关知识点一：有理数的减法法则 1．计算23-的结果是（ ）A ．5-B ．1-C ．1D ．5【答案】B2．计算()25--的结果是（ ） A ．3 B ．3-C ．7-D ．7【答案】D3．计算05-的结果是（ ）A ．5B ．5-C ．0D ．5±【答案】B4．下列计算正确的是（ ）A ．()325---=-B ．()532--=C ．330--=D ．541--=【答案】D 5．计算：（1）56-=_________ （2）()48---=________ （3）79---=________ （4）3______6--= 【答案】（1）1-；（2）4；（3）2-；（4）9- 6．计算：（1）()316--+ （2）113242⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭【答案】19- 【答案】354-（3）1444⎛⎫--- ⎪⎝⎭ （4）()()()963--+-+-【答案】14【答案】0（5）()()056---+ （6）()36--- 【答案】1- 【答案】3知识点二：有理数减法法则的应用 1．比2小3的数是（ ）A ．5B ．1C ．1-D ．0 【答案】C2．某地某天的最高气温是2-℃，最低气温是12-℃，则该地这一天的温差是（ ）A ．14-℃B ．10-℃C ．14℃D ．10℃ 【答案】D3．矿井下A ，B 两处的高度分别是48-米，128-米，A 处比B 处高_______米． 【答案】804．一种零件，标明直径的要求是0.040.0350+-Φ（单位：mm ），这种零件的合格品的最大直径比最小直径大多少？【答案】()0.040.030.07--=（mm ） 能力提升1．在1-，1，2-这三个数中，任意两个数的差最大是（ ）A ．0B ．1C ．2D ．3【答案】D2．若()______23--=，则横线处应该填上的数是（ ）A ．1-B ．1C ．5D ．5-【答案】B3．若1x =-，则4x -的值是为_________． 【答案】54．若130x y y +-++=，则x y -的值为_________． 【答案】75．已知7x =，2y =，且x y ＜，则x y -的值为_________． 【答案】9-或5-6．计算：（1）11123326⎛⎫⎛⎫---- ⎪ ⎪⎝⎭⎝⎭ （2）()()22.4425⎛⎫---+- ⎪⎝⎭【答案】1 【答案】07．如右图，数a ，b ，c 对应的点在数轴上，且a b =．（1）_____0a b +，_____0c b -，______0a c -； （2）2a =，4c =，求()a b c -+-的值； （3）化简：a c -及c b -．【答案】（1）=，＜，＞；（2）可得2a =，2b =-，4c =-，()8a b c -+-= （3）a c -，b c -8．若12a -=，13b +=，0a ＜，0b ＞，求a b -的值．【答案】1a =-，2b =，123a b -=--=-综合拓展1．已知点A 、B 在数轴上分别表示有理数a 、b ． （1）对照数轴，填写下表：（2）若A 、B 两点间的距离记为d ，试问d 和a 、b 之间有何数量关系？用数学式子表示． （3）求所有到表示数5和5-的距离之和为10的整数的和．列式计算．（4）若数轴上点C 表示的数为x ，当点C 在什么位置时，|1||2|x x ++-的值最小？最小值是多少？直接写出结论．【答案】解：（1）填表如下：（2）d 和a 、b 之间有的数量关系：||d a b =-； （3）5(5)5510--=+=Q ，∴点P 为5-、4-、3-、2-、1-、0、1、2、3、4、5，543210123450-----++++++=；（4）1-Q 到2的距离是2(1)213--=+=，∴点C 在1-到2之间时，|1||2|x x ++-取得的值最小，最小值是3．。
有理数的混合运算-教师版
【例1】 计算：()115555-+÷⨯． 【难度】★ 【答案】25-． 【解析】原式=11055-÷⨯=125-⨯=25-． 【总结】本题考查有理数的运算能力，注意掌握运算顺序和去括号法则．【例2】 计算：()2154832-÷+-⨯．【难度】★ 【答案】652． 【解析】原式=1116515921518322222-+⨯=-+==． 【总结】本题考查有理数的混合运算，熟练掌握运算法则是解题关键．【例3】 计算：()225339⎡⎤⎛⎫-⨯-+- ⎪⎢⎥⎝⎭⎣⎦． 【难度】★【答案】-11． 【解析】原式259()9()651139=⨯-+⨯-=--=-． 【总结】本题考查有理数的乘法，利用运算定律可以使计算更加简便．【例4】 计算：23121111113382⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫---÷-⨯-⎢⎥ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦．【难度】★★ 【答案】72． 【解析】原式=2325834402728277[()]()()()()()339292782782-⨯⨯-=-⨯-=-⨯-=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【例5】 计算：11110.252346⎧⎫⎡⎤⎛⎫-----+-⎨⎬ ⎪⎢⎥⎝⎭⎣⎦⎩⎭．【难度】★★【答案】0． 【解析】原式111111111[()]()()04231242444=-----+=---+=---=． 【总结】本题考查有理数运算法则，依次从小、中、大括号计算．【例6】 计算：643517.852171353⎛⎫⎛⎫-⨯--⨯- ⎪ ⎪⎝⎭⎝⎭． 【难度】★★ 【答案】998130-． 【解析】原式176301633299(17)()()68201713151013130=-+⨯--⨯-=---=-． 【总结】此类题目可以采用交换律、分配律、结合律等，主要目的就是能够做到整除，便 于计算．【例7】 计算：424211113333⎛⎫⎛⎫⎛⎫-÷--÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． 【难度】★★【答案】2-． 【解析】原式424211()3311233=-⨯-⨯=--=-． 【总结】本题考查有理数的乘方运算．【例8】 计算：()()444222131773⎛⎫-⨯-⨯⨯-⨯ ⎪⎝⎭． 【难度】★★【答案】2． 【解析】原式1882()(3)7()(37)27321=-⨯-⨯=-⨯-⨯=． 【总结】本题考查有理数混合运算．【例9】 计算：()34152********⎛⎫⎛⎫⨯-+⨯--- ⎪ ⎪⎝⎭⎝⎭． 【难度】★★ 【答案】1310．【解析】原式1131311521010=-++==． 【总结】本题考查有理数混合运算．【例10】 计算：()2111411 1.35332353⎡⎤⎛⎫⎛⎫⎛⎫--+⨯-⨯-⨯+⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎣⎦． 【难度】★★ 【答案】8711270． 【解析】原式16131621613628711()(5)()(5)91061596015270=-+⨯⨯-⨯=-+⨯-⨯=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【例11】 计算：2213825325⎡⎤⎛⎫⎛⎫÷⨯-⨯- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦． 【难度】★★【答案】140-． 【解析】原式2211(8)(153)414414022=⨯⨯--=-=-． 【总结】本题考查有理数的混合运算，注意运算的顺序和运算符号的判定．【例12】 计算：()2271158413505127113417512⎡⎤⎛⎫⨯+÷++--⨯⨯ ⎪⎢⎥⎝⎭⎣⎦． 【难度】★★ 【答案】533． 【解析】原式2256425553011671151233=⨯++⨯⨯=+=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【例13】 计算：()3111413832354453⎡⎤⎛⎫⎛⎫--+⨯⨯--⨯-÷ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦． 【难度】★★【答案】7415． 【解析】原式1121374119(1)31935555=⨯⨯+⨯=⨯⨯=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减．【例14】 计算：()()4233920.125-⨯⨯-．【难度】★★【答案】162 【解析】原式4321(6)2()1628=-⨯⨯-=． 【总结】本题主要考查有理数的乘方运算，注意法则的准确运用．【例15】 计算：()()()3.75 4.2336125 2.80.423-⨯⨯-+⨯-⨯．【难度】★★【答案】423．【解析】原式 3.75 4.2336125 2.80.423 4.23(3.7536125 2.80.1)=⨯⨯-⨯⨯=⨯⨯-⨯⨯ 4.23(3.754912540.70.1) 4.23100423=⨯⨯⨯-⨯⨯⨯=⨯=．【总结】本题考查乘法分配律的运用．【例16】 计算：2255977979⎛⎫⎛⎫+÷+ ⎪ ⎪⎝⎭⎝⎭． 【难度】★★【答案】13． 【解析】原式6565555555()()13()()1379797979=+÷+=⨯+÷+=． 【总结】本题主要考查有理数的运算，注意有括号时先算括号里面的．【例17】 计算：23453456137137⨯+⨯++⨯． 【难度】★★ 【答案】15313． 【解析】原式6126930754215313713713713=+++=+=．【总结】本题考查有理数混合运算．【例18】 计算：3971225.229113171451010-⨯⨯÷÷÷． 【难度】★★【答案】1.92． 【解析】原式12614811910112521212 1.92551037171425-⨯⨯⨯⨯⨯=-=． 【总结】本题考查有理数运算法则和乘法交换律的综合运用．【例19】 计算：131415415161344556⨯+⨯+⨯． 【难度】★★【答案】123． 【解析】原式435465(40)(50)(60)301401501123344556=+⨯++⨯++⨯=+++++=． 【总结】本题的关键是将算式中的带分数进行合适的分解，然后进行巧算．【例20】 计算：()2492154.66 5.34505694378⎛⎫-⨯-÷+⨯+÷⨯ ⎪⎝⎭． 【难度】★★ 【答案】209-． 【解析】原式=4444204.66 5.3450( 4.66 5.345)99999-⨯-⨯+⨯+=⨯--+=-． 【总结】本题是有理数的混合运算的题目，主要考查了学生对有理数的混合运算法则的掌握 情况，让学生学会运用法则来解题，提高学生的解题能力．【例21】 计算：()()2221111131313192222⎛⎫+⨯-+⨯-+-⨯+-⨯ ⎪⎝⎭． 【难度】★★【答案】11 【解析】原式1111119(11)29112222=++⨯-+-+-=+=．【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【例22】 计算：()()351155731436121827127118+-⨯+--⨯． 【难度】★★【答案】38 【解析】原式115573436251436381827127118=+--++++=+-+=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减．【例23】 计算：237970.71 6.6 2.20.7 3.31173118⨯-⨯-÷+⨯+÷． 【难度】★★【答案】1.4． 【解析】原式1333980.7 6.6 2.20.7 3.31177117=⨯-⨯-⨯+⨯+⨯ 1393 3.380.7()(6.6 2.2) 1.4111177⨯=⨯+-⨯++=． 【总结】此题考查的是有理数的混合运算，有理数的运算律，乘法分配律的应用．掌握有理 数的混合运算的法则和运算律并灵活运用时解题的关键，在此题中直接进行乘除运算显然很 麻烦，根据各个加数中的数的特点，分成两组逆用乘法分配律简化计算．【例24】 计算：()()()22324323295521651321690+⨯⨯-+÷+． 【难度】★★★ 【答案】185． 【解析】原式91821310894(41)131083610818166513516906513130131305⨯⨯⨯+⨯=⨯+⨯+=+=+=⨯． 【总结】本题考查了有理数的混合运算，属于基本题型，要熟练掌握．【例25】 计算：()()()()()2423320.2522830.33210--⨯+⨯÷⎡⎤-⨯+---÷-⎣⎦． 【难度】★★★ 【答案】1013-． 【解析】原式13416213210480.9(98)(10)0.9 1.7 2.613-⨯+⨯÷-+===-=--++÷---． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【例26】 计算：4324320.410.310.710.810.0410.0310.0710.081+++． 【难度】★★★【答案】11110．【解析】原式=432432432(0.04110)(0.03110)(0.07110)1010101010111100.0410.0310.071⨯⨯⨯+++=+++=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【例27】 计算：1994199499319921995994⨯-⨯．【难度】★★★【答案】1995994．【解析】原式19941993100119921994100119941001(19931992)=⨯⨯-⨯⨯=⨯⨯-=1994×1001=1995994．【总结】这道题考查的是整数四则混合运算的简便计算，发现19931993=1993×1001， 19941994=1994×1001是解题关键，本题中的数由于数据较大，数位较多，计算结果要细心， 数清数的位数．【例28】 计算：()()22111093444010.52224144433⎛⎫⎡⎤-⨯+÷-÷⨯-⨯-- ⎪⎣⎦⎝⎭． 【难度】★★★【答案】289．【解析】原式81180109444(2)028********+=-⨯⨯-⨯⨯-⨯=． 【总结】本题考查的是有理数的运算能力，注意计算顺序和去括号法则．【例29】 计算：()1010.5 5.214.69.2 5.2 5.4 3.7 4.6 1.5-÷⨯-⨯+⨯-⨯⎡⎤⎣⎦．【难度】★★★【答案】9.3【解析】原式=10-10.5÷（5.2×14.6-9.2×5.2-5.4×3.7+4.6×1.5）=10-10.5÷[5.2×（14.6-9.2）-5.4×3.7+4.6×1.5]=10-10.5÷（5.2×5.4-5.4×3.7+4.6×1.5）=10-10.5÷（5.4×1.5+4.6×1.5）=10-0.7=9.3【总结】解题关键是掌握小数乘除法的计算方法以及四则混合运算的顺序．【例30】 计算：4.29430430 4.274294292304.293⨯-⨯-． 【难度】★★★【答案】1990．【解析】原式 4.294301001 4.2742910012304.293⨯⨯-⨯⨯=- 1001(4.29430 4.27429)2304.293⨯⨯-⨯=- 4294.292304.291990=-=【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【习题1】 计算：()2411236⎡⎤--⨯--⎣⎦． 【难度】★【答案】16． 【解析】原式1711(29)1666=--⨯-=-+=． 【总结】本题考查有理数运算法则．随堂检测【习题2】 计算：()()()3351418325217⎛⎫⎡⎤---⨯+-÷-+ ⎪⎣⎦⎝⎭． 【难度】★★【答案】2． 【解析】原式1741(27)(325)1212217=-+⨯+-÷-+=-++=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【习题3】 计算：422511185418222⎧⎫⎡⎤⎪⎪⎛⎫⎛⎫⨯-⨯--⨯-+÷-⎢⎥⎨⎬ ⎪ ⎪⎝⎭⎝⎭⎢⎥⎪⎪⎣⎦⎩⎭． 【难度】★★ 【答案】109． 【解析】原式511510[(2516)]41822189=⨯--⨯-+=⨯=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【习题4】 计算：()()()()203233616-⨯-⨯-+-⨯．【难度】★★【答案】0【解析】原式236660=-⨯+=．【总结】本题考查有理数运算法则．【习题5】 计算：()()235.78 3.510.70.211⎡⎤+-÷⨯⎣⎦． 【难度】★★【答案】12100．【解析】原式(5.78 3.510.49)0.008118.80.0081112100=+-÷⨯=÷⨯=．【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【习题6】 计算：211350.62513136658⎛⎫⨯++÷- ⎪⎝⎭． 【难度】★★ 【答案】52． 【解析】原式5191855291550.625()3665886688=⨯++÷-=⨯+⨯-150554882=-=． 【总结】本题的关键是先将小数化为分数后找到式中相同的数，然后进行巧算．【习题7】 计算：33332542258125164816⨯+⨯+⨯． 【难度】★★【答案】5109． 【解析】原式333(325)4(225)8(125)164816=+⨯++⨯++⨯ 1300318003200035109=+++++=．【总结】本题关键是把三个带分数化成整数加上一个真分数，再利用乘法分配律进行简化．【习题8】 计算：()()2221134313450.01 3.45524⎛⎫-+÷--÷ ⎪⎝⎭． 【难度】★★ 【答案】134500． 【解析】原式222221132177(431)3451345(1)345 3.45345524524=-+÷+÷=-++÷=÷=134500． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【习题9】 计算：63.85(52) 1.257317(1) 1.1739⨯-÷+÷⨯． 【难度】★★★【答案】145． 【解析】原式153.85 1.258.25 1.251473473125() 1.1() 1.173977⨯÷÷===+÷⨯+⨯． 【总结】对繁分数的化简，分子分母同时计算，能约分的要约分，达到化简的目的．【习题10】 计算：()()322220.217012231440126327⎛⎫⎛⎫÷-⨯+⨯÷- ⎪ ⎪⎝⎭-⎝⎭． 【难度】★★★【答案】0【解析】原式222230.008112()12101262704970=⨯-⨯⨯-⨯⨯⨯ 222290.08112()1200704970=--=⨯=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【作业1】 计算：()35414772⎛⎫⎛⎫⎛⎫-⨯-÷-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭． 【难度】★【答案】418-． 【解析】原式5711414574888-⨯⨯-=--=-． 【总结】本题考查有理数混合运算法则．课后作业【作业2】 计算：()()()222322323⨯-+-⨯+-+．【难度】★【答案】49【解析】原式1236149=++=．【总结】本题考查有理数运算．【作业3】 计算：()()22131352404354⎡⎤⎛⎫-⨯⨯-⨯--÷-⨯ ⎪⎢⎥⎝⎭⎣⎦． 【难度】★★【答案】0【解析】原式3(1515)0=-⨯-+=．【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【作业4】 计算：()4211322272⨯+-⨯÷． 【难度】★★【答案】2【解析】原式312=-=．【总结】本题考查有理数的混合运算，注意法则的准确运用．【作业5】 计算：22755411353845235⎡⎤⎛⎫⨯+÷⨯-⨯-⨯⎢⎥ ⎪⎝⎭⎢⎥⎣⎦．【难度】★★ 【答案】2330． 【解析】原式1421323()15518530=+-⨯=． 【总结】本题考查有理数的混合运算，注意法则的准确运用．【作业6】 计算：()2232422 2.516348355⎛⎫⎛⎫-⨯⨯+⨯-⨯ ⎪ ⎪⎝⎭⎝⎭． 【难度】★★【答案】39.351 【解析】原式32161253128164039.3518325528125=-⨯⨯+⨯=-+=【作业7】 计算：()()21115160.0125387.524571615⨯-⨯-÷⨯+--． 【难度】★★ 【答案】1409225． 【解析】原式1161175161614098805721515225=⨯+⨯⨯⨯-=． 【总结】本题考查有理数的混合运算，注意法则的准确运用．【作业8】 计算：82390.8518180.85177717⎛⎫-⨯+⨯-⨯-⨯ ⎪⎝⎭． 【难度】★★ 【答案】367140-． 【解析】原式823998230.8518180.850.85()18()177717171777=-⨯+⨯-⨯+⨯=⨯-+⨯- 111183670.8518177207140=⨯-⨯=--=-． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．【作业9】 计算：()()()321145550.125813131313⎛⎫⎛⎫-⨯+-⨯--⨯+⨯-⨯- ⎪ ⎪⎝⎭⎝⎭． 【难度】★★ 【答案】413． 【解析】原式32114101445()0.125813131313131313=-⨯-++⨯⨯=-+=． 【总结】本题考查有理数的四则运算法则，能简便计算就简便计算．【作业10】 计算：()7577.5351326 4.035139618⎛⎫⨯-⨯+-+-⨯ ⎪⎝⎭． 【难度】★★★ 【答案】131318． 【解析】原式75713(7.535 4.035)213()9618=⨯--⨯⨯+-22171313 3.51345311392918=⨯-⨯=-=． 【总结】本题考查有理数的四则运算法则，先乘除，后加减，如果有括号就先算括号内再算 括号外，同一级运算注意符号，能简便计算就简便计算．。
有理数教案(精彩8篇)
有理数教案（精彩8篇）有理数教案篇一1、要求学生会进行有理数的加法运算；2、使学生更多经历有关知识发生、规律发现过程。
重点：对乘法运算法则的运用，对积的确定。
难点：如何在该知识中注重知识体系的延续。
一、知识导向：有理数的乘法是小学所学乘法运算的延续，也是在学习了有理数的加法法则与有理数的减法法则的基础上所学习的，所以应注意到各种法则间的必然联系，在本节中应注重学生学习的过程，多让学生经历知识、规律发现的过程。
在学习中应掌握有理数的乘法法则。
二、新课：1、知识基础：其一：小学所学过的乘法运算方法；其二：有关在加法运算中结果的确定方法与步骤。
2、知识形成：(引例)一只小虫沿一条东西向的跑道，以每分钟3米的速度爬行。
情形1：小虫向东爬行2分钟，那么它现在位于原来位置的哪个方向？相距出发地点多少米？列式：即：小虫位于原来出发位置的东方6米处拓展：如果规定向东为正，向西为负情形2：小虫向西爬行2分钟，那么它现在位于原来位置的哪个方向？相距出发地点多少米？列式：即：小虫位于原来出发位置的西方6米处发现：当我们把中的一个因数3换成它的相反数-3时，所得的积是原来的积6的相反数-6同理，如果我们把中的一个因数2换成它的相反数-2时，所得的积是原来的。
积6的相反数-6概括：把一个因数换成它的相反数，所得的积是原来的积的相反数3、设疑：如果我们把中的一个因数2换成它的相反数-2时，所得的积又会有什么变化？当然，当其中的一个因数为0时，所得的积还是等于0。
综合：有理数乘法法则：两数相乘，同号得正，异号得负，并把绝对值相乘；任何数与零相乘，都得零。
例：计算：(1)(2)三、巩固训练：p52.1、2、3四、知识小结：本节课从实际情形入手，对多种情形进行分析，从一般中找到规律，从而得到有关有理数乘法的运算法则。
在运算中应强调注意如何正确得到积的结果。
五、家庭作业：p57.1、2，3六、每日预题：1、小学多学过哪些乘法的运算律？2、在对有理数的简便运算中，一般应考虑到哪些可能的情况？有理数教案篇二知识与技能：熟记有理数的减法法则，能熟练进行有理数减法运算。
2019-2020学年七年级数学上册《有理数》导学案(教师版)-华东师大版
2019-2020学年七年级数学上册《有理数》导学案（教师版） 华东师大版预习课（时段：晚自习 时间：20分钟） 1、旧知链接：（1）刚刚学习过的正数和负数。
（2）总结已经学习过哪些数。
2、新知预习: 1 .用15分钟的时间阅读教材18~20页的内容，进行知识梳理，熟记基础知识，自主高效预习。
2. 完成教材助读设置的问题，然后结合课本的基础知识和例题，完成预习自测题。
3. 将预习中部能解决的问题用红笔标出来，便于讨论时共同探究，合作交流。
探究课（时段：正课 时间：50分钟） 【学习目标】：1、 熟练掌握有理数的意义，并能够按照不同的方式将有理数分类，提高归纳能力。
2、通过独立学，合作探究，感受解决与有理数有关的问题的规律和方法。
3、积极投入，培养严密的数学思维习惯，感悟数学知识与现实生活的密切联系。
【学习重点】：按照不同的方式将有理数分类【学习难点】：熟练按照不同的方式将有理数分类 学情检测： 1、既不是正数，也不是负数的数是 ，_____、_____、______统称为整数，_____和____统称为分数，______和______统称有理数。
2、下列各数哪些是正整数？哪些是非正数？哪些是负整数？哪些是负分数？ +5，－7，21，－61，+5.2，89，－43，－58，－1.5，－100，0。
探究案：探究点一：有理数的有关概念问题1：正整数、_______、_______统称整数，正分数和负分数统称_______。
问题2：_______和 ______统称有理数。
问题3：把一些数放在一起，就组成一个数的_______，简称数集。
所有的有理数组成的数集叫做_______。
类似地，所有的整数组成的数集叫做_______，所有的正数组成的数集叫做_______，所有的负数组成的数集叫做_______，所有的_______组成的数集叫做自然数集。
问题4：下列说法错误的是（ ）A 、零是非负数B 、零是整数C 、零是自然数D 、零的倒数是零 问题5：数－125不是（ ）A 、有理数B 、整数C 、负有理数D 、自然数 探究点二：有理数的分类例 1、把下列各数填在相应的括号里： －7，53，2003，0，－31，＋8.4，－5％，－0.0103，－0.12 学法指导：在进行有理数分类时，要严格按照分类标准，做到不重不漏。
(word完整版)有理数的运算技巧-教师版
“显示有理数的混合运算（1）有理数的加法：①同号两数相加，取相同的符号，并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数符号，并用较大的绝对值减去较小的绝对值.③一个数同0相加，仍得这个数.（2)有理数的减法:减去一个数，等于加这个数的相反数。
()a b a b -=+-(3）有理数的乘法：两数相乘，同号得正,异号得负，并把绝对值相乘.任何数同0相乘，都得0. （4)有理数的除法：除以一个不等于0的数,等于乘这个数的倒数.1a b a b÷=⋅ （0b ≠ ） (5）有理数的乘方：求n 个相同因数的积的运算叫做乘方。
一、有理数的加法运算技巧（1）分数与小数均有时，应先化为统一形式. （2）带分数可分为整数与分数两部分参与运算。
（3）多个加数相加时，若有互为相反数的两个数,可先结合相加得零。
（4)若有可以凑整的数，即相加得整数时，可先结合相加。
（5）若有同分母的分数或易通分的分数，应先结合在一起. (6）符号相同的数可以先结合在一起。
二、有理数的混合运算步骤（1）在进行有理数加法运算时，优先确定符号，然后在计算绝对值，这样就不容易出错。
减法转化为加法。
（2）作带分数加法时，可将整数部分与分数部分分开相加,然后再把结果相加。
（3）既有分数，又有小数时，通常把小数化成分数。
（4）有理数相乘,先确定积的符号，再确定积的绝对值;除法转化为乘法进行计算.(5）要正确解答乘方运算，必须切实弄清乘方定义，它是求n 个相同因数的积的运算，n a a n ≠⋅，2(1)1n -=，21(1)1n +-=-.（6)带分数进行乘方运算时，一般要把带分数化为假分数，注意不能犯如下错误：211(3)924=。
三、有理数的混合运算注意要点有理数混合运算,应注意以下几点：（1）先乘方，再乘除，最后加减; （2）同级运算，从左到右进行；有理数的运算技巧知识回顾知识讲解（3）如有括号，先做括号内的运算,按小括号,中括号，大括号的顺序依次进行（4)恰当地运用交换律，结合律、分配率有时可以使计算简便（5）进行分数的乘除运算时,一般要把带分数化为假分数，把除法转化为乘法进行有理数混合运算时易错点有:(1）符号错误；如2(2)4-=-，224-=等；（2）运算顺序发生错误，如1232123÷⨯=÷=等；（3）知识理解错误，如326=;（4）去括号法则，如112(2)222415 22-⨯-=-⨯-⨯=--=-一、有理数的加减运算【例1】计算：⑴11(28)(17)42++-⑵3510.75(2)(0.125)(12)(4)478+-+++-+-⑶3378 1.25644412-++-⑷11( 2.125)(3)(5)( 3.2)58-+++++-⑸112(3)( 2.4)()(4)335-+-++--⑹232(3)(2)(1) 1.75343------⑺219 17887.21435312.792121-++-【答案】⑴原式=1113 28(17)()11()104244 +-++-=+-=⑵原式=33151(2)(12)(4)44878+-++-+-=33151()()()(2)(12)(4)44878+-++-+-+-+-+-=5187-⑶原式=3137816444412-++-=3137(8)16(4)()()44412-+++-+-+++-=11(5)()533-+-=-⑷原式=1111(2)(3)(5)(3)8585-+++++-=11(2)5()88-++-+=3⑸原式=1212(3)(2)()(4)3535-+-++--=1212(3)(2)4()()3535-+-++-+-++=1-⑹原式=2323(3)(2)(1)(1)3434-+++-=2323(3)21(1)()()3434-+++-+-+++-=1-⑺原式=219178(87)4353(12)(0.21)(0.79)2121 +-+++-+-+-++=175【变式练习】计算：⑴12114()(3)(2)2735+-+-+-⑵5221(2000)(1999)4000(1)6332-+-++-⑶2(3)( 5.7)( 1.5)( 3.4)( 4.2)5----++++-⑷8110.8231033-+-+⑸113.125()()( 5.25)248--+--++⑹35713.2()()4612--+--同步练习【答案】⑴原式=12114(3)(2)()()()2725+-+-++-+-+-=17(1)()35-+-⑵原式=5221 (2000)(1999)4000(1)()()()6332-+-++-+-+-++-=43-⑶原式=27121 (3)5(1)3(4)510255 -++-++-=27121 (3)5(1)3(4)()()()510255-++-++-+-++-++-=0⑷原式=4411(2)35533-++-+=11(2)3()33-++-+=1⑸原式=11113()(5)28484++-+-+=11113(5)2()()8484+-++++-+-=0⑹原式=13571354612+++=13571354612++++=711330+=111530二、有理数加减运算解决实际问题【例2】超市新进了10箱橙子,每箱标准重量为50kg，到货后超市复秤结果如下（超市标准重量的千克数记为正数，不足的千克数记为负数）：0.5+、0.3+、0.9-、0.1+、0.4+、0.2-、0.7-、0.8+、0.3+、0.1+那么超市购进的橙子共多少千克?【答案】(0.5)(0.3)(0.9)(0.1)(0.4)(0.2)(0.7)(0.8)(0.3)(0.1)+++-+++++-+-++++++=[0.50.30.1(0.9)][0.80.1(0.2)(0.7)](0.40.3)+++-+++-+-++=0.750100.7500.7⨯+=()kg即橙子共有500.7千克【例3】数轴的原点O上有一个蜗牛,第1次向正方向爬1个单位长度，紧接着第2次反向爬2个单位长度，第3次向正方向爬3个单位长度，第4次反向爬4个单位长度……，依次规律爬下去,当它爬完第100次处在B点．①求O、B两点之间的距离(用单位长度表示)．②若点C与原点相距50个单位长度，蜗牛的速度为每分钟2个单位长度，需要多少时间才能到达？③若蜗牛的速度为每分钟2个单位长度，经过1小时蜗牛离O点多远？【答案】①1(2)3(4)99(100)50+-++-+++-=-，故O、B两点之间的距离为50个单位长度．②分两种情况，第一种情况：点C在数轴的正半轴，观察规律可知：除去第一次,依次每两次结合相当于向正方向前进1米，所以再经过(501)298-⨯=(次)运动即可前进50米，到达B地；用时为：(1239899)22475++++÷=（分钟）．第二种情况：点C在数轴的负半轴,观察规律可知，每两次结合相当于向负半轴前进1米,故经过100次运动即可前进50米，到达B地，用时为：(12100)22525+++÷=（分钟）．③设第n次运动时，正好60分钟,那么有12345660 2222222n+++++++=(word 完整版)有理数的运算技巧-教师版所以15n =，此时它离A 点：1234561314158-+-+-++-+=（米）．【变式练习】A 市的出租车无起步价，每公里收费2元，不足1公里的按1公里计价，9月4号上午A 市 某出租司机在南北大道上载人，其承载乘客的里程记录为：2.3、7.2-、 6.1-、8、9.3、 1.8-（单位：公里，向北行驶记为正,向南行驶记为负）,车每公里耗油0.1升，每升油4元，那么他这一上午的净收入是多少元？他最后距离出发点多远？【答案】因为每公里收费2元，且不足1公里的按1公里计算所以出租车司机的收入为收入：(3878102)276+++++⨯=(元) 出租车所行驶的路程为2.37.2 6.189.3 1.834.7+-+-+++-=公里 汽油成本:34.70.1413.88⨯⨯=（元)，收入7613.8862.12-=（元）。
有理数的运算-幻方专题-教师版
有理数的运算-幻方专题1．在“幻方拓展课程”探索中，小明在如图的33⨯方格内填入了一些表示数的代数式，若图中各行、各列及对角线上的三个数之和都相等，则2x y -=（ ）A ．2B ．4C ．6D ．8【答案】解：各行、各列及对角线上的三个数之和都相等， 206(2)y y y ∴++=++-，20(2)0y y x ++=+-+， 34y y ∴=+，32y x =-，解得2y =，8x =， 2x y ∴- 822=-⨯ 84=-4=故选：B ．2．将2n 个正整数1、2、3、⋯、2n 填入n n ⨯方格中，使其每行、每列、每条对角线上的数的和都相等，这个正方形叫做n 阶幻方．记()f n 为n 阶幻方对角线上数的和．如图就是一个3阶幻方，可知f （3）15=．则f （4）等于（ ）A ．36B ．42C ．34D ．44【答案】解：根据题意可知： 3阶幻方所有数之和为： 21233S =+++⋯+ 221(13)32=+⨯ 45=，f ∴（3）451533S ===； 4阶幻方所有数之和为：21234S =+++⋯+ 221(14)42=+⨯ 136=，f ∴（4）1363444S ===． 故选：C ．3．据记载，“九宫图”源于我国古代的“洛书”，是世界上最早的矩阵，又称“幻方”．如图所示，由33⨯的方格构成，每一行、每一列以及每一条对角线上的三个数字或字母的和均相等，则()a b -+的值为（ ）A ．3-B ．3C ．1-D ．1【答案】解：由题意可得：4523a +=-=， 解得：1a =-， 故323b +-=， 解得：2b =， 故()1a b -+=-． 故选：C ．4．把夏禹时代的“洛书”用数学符号翻译出来就是一个三阶幻方，它的每行、每列、每条对角线上三个数之和均相等，则幻方中a 的值是（ ）A ．6B ．12C ．18D ．24【答案】解：设中心数为x ，根据题意得，6164++=++，x x a∴=，18a故选：C．5．学习了“探寻神奇的幻方”后，小明也找了九个数字做成一个三阶幻方，如图所示是这个幻方的一部分，则a=，b=．【答案】解：由题意知2113+=+，b aa a b+=++，1921则21138a=+-=，b=-=，819216故答案为：6，8．6．我国的《洛书》中记载着世界最古老的一个幻方：将1~9这九个数字填入33⨯的方格中使三行、三列、两对角线上的三个数之和都相等，如图的幻方中，字母m所表示的数是．【答案】解：根据“每行、每列、每条对角线上的三个数之和相等”，可知三行、三列、两对角线上的三个数之和都等于15，--=，∴第3列第三个数为：15852∴=--=．15276m故答案为：6．7．将9个数填入幻方的九个格中，使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等，如表一．如表二：将满足条件的另外9个数中的三个数填入了表二，则这9个数的和为（用含a的整式表示）【答案】解：如图所示：++-++-=+++，a a x a x a a x2531027解得2=+，x a+++=+++=+，a a x a a a727239a a+=+．3(39)927故答案为：927a+．8．幻方是相当古老的数学问题，我国古代的《洛书》中记载了最早的幻方--九宫图．将数字1~9分别填入如图所示的幻方中，要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15，则m的值为．【答案】解：依题意，得：2415++=，m解得：9m=．故答案为：9．9．（1）在学习有理数的加减法时，教材第20页中有这样一个题目：你能将4-、3-、2-、1-、0、1、2、3、4这9个数分别填入如图1所示的幻方的9个空格里，使得处于同一横行、同一竖列、同一斜对角线上的3个数相加都得0吗？（2）填完（1）中的幻方后，请你将2-，0，1，2，3，4，5，6，8分别填入如图2所示的幻方的9个空格里，使得处于同一横行、同一竖列、同一斜对角线上的3个数相加都相等．【答案】解：（1）能，如图1；（2）将题中的9个数分别乘以2填入幻方，如图2．10．请完成如图所示的4阶幻方．【答案】解：1、先把1放在四阶幻方4个角的任意一个角格，按同一个方向按顺序依次填写其余数．如图：按行从左向右顺序排数．2、以中心点对称互换数字．（有两种对称交换的方法）1)、以中心点对称交换对角线上的数（即116-互换），完成幻方，-、710-、611-、413幻和值34=．2)、以中心点对称交换非对角线上的数（即215-、89-互换），完成幻方，-、512-、314幻和值34=故答案为：11．将九个数填在33⨯（三行三列）的方格中，如果满足每个横行、每个竖列和每条对角线上的三个数之和都相等，如图1，我们称这样的图为三阶幻方．如图2中的三阶幻方中已知三个数，请填上其余6个数．【答案】解：设第一行第三列的数为x，则三个数之和为11x+，根据题意得，113(1)+=-，x x解得7x=．所以，其余6个数如图2所示：12．请将“2，4，6，7，9，11，12，14，16”共9个数，填入到下面33⨯的方格中，使得每行、每列、每条对角线上的三个数之和相等，构成一个三阶幻方．（至少三种不同的填法）【答案】解：如图所示．。
1-1-1(10年秋)有理数基本概念讲义教师版
内容 基本要求略高要求较高要求有理数 理解有理数的意义会比较有理数的大小 数轴能用数轴上的点表示有理数；知道实数与数轴上的点的对应关系 会借助数轴比较有理数的大小相反数 会用有理数表示具有相反意义的量，借助数轴理解相反数的意义，会求实数的相反数掌握相反数的性质绝对值 借助数轴理解绝对值的意义，会求实数的绝对值会利用绝对值的知识解决简单的化简问题板块一、正数、负数、有理数随着同学们视野的拓展，小学学过的自然数、分数和小数已经不能满足认知需要了.譬如一些具有相反意义的量，收入300元和支出200元，向东50米和向西30米，零上6C ︒和零下4C ︒等等，它们不但意义相反，而且表示一定的数量，怎么表示它们呢？我们把一种意义的量规定为正的，把另一种和它意义相反的量规定为负的，这样就产生了正数和负数.正数：像3、1、0.33+等的数，叫做正数.在小学学过的数，除0外都是正数.正数都大于0.负数：像1-、 3.12-、175-、2008-等在正数前加上“－”（读作负）号的数，叫做负数.负数都小于0. 0既不是正数，也不是负数.一个数字前面的“＋”，“－”号叫做它的符号.正数前面的“＋”可以省略，注意3与3+表示是同一个正数.用正、负数表示相反意义的量：例题精讲中考要求有理数基本概念及运算如果正数表示某种意义，那么负数表示它的相反的意义，反之亦然.譬如：用正数表示向南，那么向北3km可以用负数表示为3km-.“相反意义的量”包括两个方面的含意：一是相反意义；二是相反意义的基础上要有量. 有理数:按定义整数与分数统称有理数.()⎧⎧⎫⎪⎬⎪⎨⎭⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数自然数整数零有理数按定义分类负整数正分数分数负分数()()⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数按符号分类零零既不是正数,也不是负数负整数负有理数负分数注：⑴正数和零统称为非负数；⑵负数和零统称为非正数；⑶正整数和零统称为非负整数；⑷负整数和零统称为非正整数.【例1】⑴如果收入2000元，可以记作2000+元，那么支出5000元，记为.⑵高于海平面300米的高度记为海拔300+米，则海拔高度为600-米表示.⑶某地区5月平均温度为20C︒，记录表上有5月份5天的记录分别为 2.7+，0， 1.4+，3-， 4.7-，那么这5项记录表示的实际温度分别是.⑷向南走200-米，表示.【考点】正负数的概念【难度】1星【题型】填空【关键词】【解析】略【答案】⑴5000-元；⑵低于海平面600米的高度；⑶22.7C︒，20C︒，21.4C︒，17C︒，15.3C︒；⑷向北走200米【巩固】珠穆朗玛峰海拔高度为8848米，吐鲁番盆地海拔高度为155-米，则海平面为【考点】正负数的概念【难度】1星【题型】填空【关键词】【解析】略【答案】0米【例2】下列说法正确的是（）A．a-一定是负数B．一个数不是正数就是负数C．0-是负数D．在正数前面加“-”号，就成了负数【考点】正负数的概念【难度】1星【题型】选择【关键词】2008年，厦门中考【解析】a-负数不一定是负数；一个数不是正数，有可能是负数和0；0-既不是正数也不是负数。
有理数的加法法则(教师版)
有理数的运算法则1. 理解并掌握重要的有理数的运算法则。
2. 认识和掌握列有理数加法法则的几个注意事项。
1、代数式：用运算符号“＋ － × ÷ …… ”连接数及表示数的字母的式子称为代数式。
注意：用字母表示数有一定的限制，首先字母所取得数应保证它所在的式子有意义，其次字母所取得数还应使实际生活或生产有意义；单独一个数或一个字母也是代数式。
2、列代数式的几个注意事项：（1）数与字母相乘，或字母与字母相乘通常使用“· ” 乘，或省略不写。
（2）数与数相乘，仍应使用“×”乘，不用“· ”乘，也不能省略乘号。
（3）数与字母相乘时，一般在结果中把数写在字母前面，如a×5应写成5a 。
（4）在代数式中出现除法运算时，一般用分数线将被除式和除式联系，如3÷a 写成a3的形式；（5）a 与b 的差写作a-b ，要注意字母顺序；若只说两数的差，当分别设两数为a 、b 时，则应分类，写做a-b 和b-a . 3、几个重要的代数式：（1）a 与b 的平方差是：a 2-b 2； a 与b 差的平方是：（a-b ）2。
（2）若a 、b 、c 是正整数，则两位整数是：10a+b ；则三位整数是：100a+10b+c 。
（3）若m 、n 是整数，则被5除商m 余n 的数是：5m+n ；偶数是：2n ，奇数是：2n+1；三个连续整数是：n-1、n 、n+1。
（4）若b ＞0，则正数是:a 2+b ，负数是：-a 2-b ，非负数是：b 2，非正数是：-b 2。
有理数 1、有理数： (1)凡能写成ab（a 、b 都是整数且a≠0）形式的数，都是有理数。
正整数、0、负整数统称整数；正分数、负分数统称分数；整数和分数统称有理数。
（注意：0即不是正数，也不是负数；-a 不一定是负数，+a 也不一定是正数；p 不是有理数）(2)有理数中，1、0、-1是三个特殊的数，它们有自己的特性；这三个数把数轴上的数分成四个区域，这四个区域的数也有自己的特性。
有理数的概念（教师教案）
有理数的概念（教师教案）【开课】今天的内容主要包括以下几部分：一．有理数的基本概念[课程目标]1理解有理数的基本概念，知道有理数的分类，有理数在数轴上的表示，理解相反数、倒数以及绝对值的概念并解决实际问题；[课程安排]老师先将第一段练习发给每一位学生，学生做题时老师必须巡视，了解学生做题情况。
学生完成练习后，老师讲解。
【教师讲课要求】教师简要介绍本次课程的关键点，同学做题，然后教师讲解（第一段例题）。
老师总结，学生做综合练习（第二段），然后老师讲解。
[知识点总结]1正数和负数正数就是带有正号的数(正号可以省略不写)，是大于零的数；而负数是带有负号的数，是比零小的数。
2有理数：整数和分数统称有理数。
⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数零负整数有理数正分数分数负分数(2) 而按照正、负数来分又有如下分类：⎧⎧⎪⎨⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数有理数零负整数负有理数负分数3数轴是这样的东西：规定了零点，正方向，单位长度的直线叫做数轴．4只有符号不同的两个数，叫做互为相反数。
5如果两个数的乘积为1，那么这两个数互为倒数．6相反数的数轴表现：在数轴上，位于原点两边，并且到原点的距离相等的数互为相反数；7一个数在数轴上所对应的点与原点的距离，叫做这个数的绝对值。
用符号∣а∣表示数a 的绝对值。
||00||0aa aa a a a a a a a >⎧≥⎧⎪===⎨⎨-<⎩⎪-<⎩或者说第一段典型例题第一部分【课程目标】：理解有理数的基本概念，知道有理数的分类，有理数在数轴上的表示，理解相反数、倒数以及绝对值的概念并解决实际问题【教师讲课要求】范例1．（1）最大的负整数是；最小的正整数是；（2）既不是整数，也不是正数的有理数是；（3）所有的小数都能化成分数吗？。
答案：(1)负整数是小于零的整数，所以最大的负整数是－1，同样可以得到最小的正整数是l(2)不是整数的数是分数，不是正数的数是负数和零，从而既不是整数也不是正数的有理数是负分数；(3)只有有限小数和循环小数可以化为分数．而无限不循环小数是不能化为分数的，例如，我们知道著名的圆周率 就不能化为分数．[教师总结知识点]有限小数和循环小数可以化为分数，他们是有理数．范例2 已知A在数轴上表示－2的点，在数轴上标出与点A的距离是2个长度单位的点，并读出这样的点所表示的数答案：(1)先在数轴上找到表示－2的点A；(2)在数轴上距离点A 2个长度单位的点有左右两个，一个在A的右侧，一个在A的左侧；(3)从A出发往右走两步得到的就是零点O，而往左走两步得到的是－4，就是图中的B点，从而图中的O和B就是我们要找的点，同时这两个数分别是0和－4．[教师总结知识点]利用数轴我们可以方便的找到一些我们要找的数．范例3 判断下列直线[图4-2（1）]是否是数轴？(1)-2 -1 0 1 2(2)图4-2（1）答案: (1)缺少正方向（2）缺少单位长度；有理数的概念(教师教案)Page 3 of 8（3）缺少原点．范例4 若3a +的相反数是－8，则a 的相反数是多少？解 因为 8的相反数是－8，根据题意，得3a +＝8．解方程，得a ＝5．所以a 的相反数是－5．范例5 若一个数与这个数的相反数的差为2，那么这个数是多少呢?答案：(1)设这个数是a,那么a 的相反数是－a ；(2)原问题转化为“a 与－a 的差为2,求a 的值”；(3)列出方程：a －(－a)＝2,也就是a ＋a ＝2；(4)最后得到以a ＝1．范例6已知以a<0，计算l+2a+∣1－2a ∣的值．分析: 还是要判断绝对值之中数的符号，也就是要判断l －2a 的符号．答案:(1)因为a ＜0，所以2a ＜0，从而1—2a 必然大于0，从而|1－2a|＝1－2a (2)1＋2a+ |1－2a|＝1+2a ＋1—2a ＝2．范例7 已知|2x ＋5|＋|x －y|＝0，试求x,y 的值．答案:(1)由于|2x ＋5|，|x －y|都是非负数，而它们的和又是0，所以只有2x ＋5＝x －y ＝0；(2)由2x ＋5＝0得到x ＝－，又由x －y ＝0得到y ＝x ＝－；5252(3)从而x ，y 的值都是－．52范例8 如果a ≠0,则有可能取什么样的值呢？||aa 答案: 我们知道∣a ∣有可能等于a 也有可能等于－a ，从而有可能等于1和－1；||aa [教师总结知识点]一个非零数和它的绝对值的商为1或者－1范例9 把下列各数，按从小到大的次序，用“＜”号连接起来：＋2，－2，＋3，－3，0，＋，－．21143分析：比较几个有理数的大小，可以先用数轴上的点来表示这些数（如果题目没有特别要求，只要画一个大致的草图即可），然后按照数轴上左边的数较小，右边的数较大的原理把这些数按从小到大的次序用“＜”连接起来．答案：把题中的各数表示在轴上，得到有理数的概念(教师教案)Page 4 of 8－＜－3＜－2＜0＜＋＜＋2＜＋3．14321[教师总结知识点] 数轴上的点从左到右的排列次序与有理数大小的排列顺序是一致的．解这类习题时，特别要注意审题清楚，即这些数的比较是按从小到大次序排列还是按从大到小的次序排列．范例10．比较－和－0.28的大小；27分折：比较两个负数的大小，可先比较这两个负数的绝对值的大小，最后根据“两个负数，绝对值大的反而小”下结论．解 （１）方法一：∣－∣＝＝， ∣－0.28∣＝＝＝．2727501752810072549175∵＞， ∴－＜－0.28 ．501754917527方法二：∣－∣＝＝， ∣－0.28∣＝＝．27271449281001450∵＞， ∴－＜－0.28 ．1449145027方法三：∣－∣＝＝0．281…, ∣－0.28∣＝0.28．2727∵0.281…＞0.28,∴－＜－0.28 ．27[教师总结知识点] 解本题的三种方法都是应用同一条法则进行比较的，区别在于比较绝对值大小的方法不同．方法一是化作分母相同的分数进行经较；方法二是变成分子相同的分数进行比较；方法三则是把分数化成小数，再按小数大小比较的法则进行的(实际比较时，分数化小数，只要取比已知小数多保留一位的近似值即可)．范例11．已知：|a|＝3，|b|＝2，且a ＞b ，求a+b 的值．．分析:由绝对值的含义可知：a ＝±3，b ＝±2．又a ＞b ，所以a ＝－3不能取，只能取3，又±2＜3，所以b 可以取±2．答案: 解 由|a|＝3得到a ＝±3，由|b|＝2得到b ＝±2，因为a ＞b ，所以a ＝3，b ＝±2，即a+b=5或a+b=1．[教师总结知识点] 一个数的绝对值等于一个正数，这个数应该是这个正数或它的相反数，在本题中另外要注意的是题目听“a ＞b ”这个条件，不能盲目地得出a ＝±3，必须排除a ＝－3这一可能性．范例12．(1)已知：|x|=x ，求x 的取值范围；（2）已知，求x 的取值范围．1||xx =-分析 : 第（1）小题由“一个正数的绝对值是它本身”和“零的绝对值是零”可知：一个数的绝对值等于这个数，这个数就是正数或零．第（2）小题中|x|= -x 时，（但这里的x ≠0），由“一个负数的绝对值是它的相反1||xx =-数”可知：这里的x 只能取负数．答案:解 （1）x 的取值范围为正数或零，即x ≥0．(2)x 的取值范围为负数，即x ＜0．[教师总结知识点]在第（1）题中应注意零和正数的绝对值就是它们本身，不能忽视了“零”;第（2）小题中应注意零与负数的绝对值就是它们的相反数，因为零不能为除数，所以这里的x 不能为零，如果是单纯的|x|= -x ，那么x 的取值应是x ≤0．范例13．已知三个有理数a 、b 、c ，b 是a 的相反数，c 是b 的倒数，比较a b +和ac 的大小？并简要说明理由．解：∵a 、互为相反数，∴a+b ＝0．∵c 是b 的倒数, c 是a -的倒数．∴()1c a ⋅-=，那ac ＝1．∵0＞－1, ∴a b +＞ac ．[中考链接]1请你在数轴上用“．”表示出比1小2的数．(2006 吉林)-3 -2 -1 0 1 22若m,n 互为相反数,则m+n= (2006 江西)答案:03若x 的相反数是3,∣y ∣=5,则x+y 的值是( ) (2006 哈尔滨)(A)-8 (B)2 (C)8或-2 (D)-8或2答案:D第二段一．填空题1．满足b≤3的整数b 是 ___________________答案: －3,－2,－1,0,1,2,32．规定了 ， ， 的直线叫做数轴．答案: 原点 、正方向 、单位长度．3．如果0a <，那么a--＝答案:a4．如果2m +与－3互为相反数，那么m ＝答案:15．如果0a b >>，那么a b--＝答案: a b + ．6．与互为相反数，与互为倒数．1313答案: －, 3137．比较大小：10(1)-101-．（填“＞”、“＜”或“＝”号）答案: ＞二、判断题．1．互为相反数的两个数的绝对值的和一定大于零．2．所有的有理数都能在数轴上找到与它对应的点．3．对于任意有理数0x <，0y <，都有x y x y+=+．4．1-的n 次方与1-的1n +次方互为相反数．答案:1（ × ）2（ √ ）3 （ × ）4( √ )三、选择题：1．在理数中，一个数的相反数等于它本身的有（ ）Ａ．０个； B ．１个； C ．２个； D ．无数个．答案:B2．下列说法正确的是（ ）Ａ．－a 一定是负数；B ．数轴上原点两旁的数是相反数；C ．一个数的绝对值是正数；D ．．任何有理数都有相反数．答案:D3．有a 、b 、－a 、－b 四个非零数，下列不等式不能成立的是（ ）有理数的概念(教师教案)Page 7 of 8Ａ．b a a b -<-<< ；B ．b a a b <<-<- ；C ．a b b a <-<<-；D ． a b a b -<-<<． 答案:D4．下列说法错误的是（ ）（A ）正数的倒数是正数； （B ）负数的倒数是负数； （C ）0没有相反数； （D ）0没有倒数．答案:C5．如果a ＞b ，那么下列结论正确的是（ ）（A ）2a ＞2b ；（B ）2a ＜2b ；（C ）2a ≠2b ；（D ）以上答案都有错误．答案:D四、比较下列每组的大小：（1）和；4534（2）0．87和；78-(3)比较和的大小．9991000-998999-(4)已知10a +<，试比较a 、－a 、１、－１的大小． 答案:(1) ＞； （2）0.87＞；453478-(3) ＜； (4) 11a a ->>->．9991000-998999-五化简：（１）y x y x-++； （２）x y y x-+-；（３）121a a a-+++，其中2a <-．答案：(1)y x y x-++＝2x ； （２）x y y x-+-＝22x y-(3)121a a a-+++＝－4a ． 六综合题1．已知6a =，3b =，a b b a-=-，求a 、b 的值．答案： 6a =-、33b =-或 2．已知，求x 的取值范围．|2|2x x--有理数的概念(教师教案)Page 8 of 8答案：2x <3．一个数的绝对值的倒数等于，这个数的绝对值是多少528答案：8214．设a 、b 、c 三个有理数在数轴上对应的点A 、B 、C 的位置如图所示，请化简：a b b c c a---+-．答案：22a b-七、简答题：(1)已知甲数的绝对值大于乙数的绝对值，能断定甲数一定大于乙数吗？举例说明．答：不能，如|-5|＞|-3|，但－５＜－３ ．(2) 已知甲数小于乙数，能断定甲数的绝对值一定小于乙数的绝对值吗？举例说明．答：不能，如－５＜－３，但|-5|＞|-3|．(３)如果甲乙两数的绝对值相等，甲乙两数的关系有哪几种可能？举例说明．答：两种可能：一种可能是相等（如|2|= |2|）；另一种可能是互为相反数（|2|= |-2|）．。
第02讲 认识有理数(教师版)
第二讲认识有理数【课程解读】————初中课程解读————【知识衔接】————初中知识与典例链接————一、正数和负数1．负数的概念：若把小学学过的数(0除外)叫做正数，则把在正数前面加上“－”号的数叫做负数．“－”号读作“负”．如“－5”读作“负五”．2．0的意义：0既不是正数，也不是负数．注：在小学里，0通常表示没有．当引入负数后，不能说0表示没有了．正整数、负整数、零统称为整数．正分数、负分数统称为分数．零是整数，也是偶数，非负数就是零和正数．【典例分析】例1．用正负数表示下列各题中具有相反意义的量．（1）如果用+15元表示收入15元，那么用去12元记作什么？（2）食堂购进100千克面粉记作+100千克，那么－20千克表示什么？【答案】（1）﹣12（2）用去20千克面粉【解析】用正负数表示两种具有相反意义的量．具有相反意义的量都是互相依存的两个量，它包含两个要素，一是它们的意义相反，二是它们都是数量【变式】（1）如果－10t 表示运出10t ，那么+30t 表示 ； （2）负债100元也可以说成是拥有 元； （3）如果规定向东方向为正，那么－200米表示什么意义？ －（－200）米表示什么意义？ 【答案】（1）运进30t （2）﹣100（3）向西200米；向东200米例2．下列各数中,哪些是正数? 哪些是负数?（正负数的判断）+7；-9；-4.5；0；722；-3.14；998；-999 【答案】正数：+7；722；998； 负数：-9；-4.5；-3.14；-999【解析】所有大于零的数都是正数，所有小于零的数都是负数思路点拨：对于正数和负数的意义，不能简单地理解为带“＋”号的数是正数，带“－”号的数是负数．而应该理解为“所有大于零的数都是正数，所有小于零的数都是负数”． 二、有理数1、有理数的概念：整数和分数统称为有理数． 把能够写成分数形式mn（m ，n 为整数，m≠0）的数叫做有理数2、无理数的概念：无限不循环小数叫做无理数．小结：分数、有限小数、循环小数都是有理数。
第1讲 数学教师讲义1(有理数的概念)
第1讲 与有理数有关的概念（教师讲义）一、教学目标1．了解负数的产生过程，能够用正、负数表示具有相反意义的量.2．会进行有理的分类，体会并运用数学中的分类思想.3．理解数轴、相反数、绝对值、倒数的意义．会用数轴比较两个有理数的大小，会求一个数的相反数、绝对值、倒数.二、例子【例1】写出下列各语句表示的实际意义⑴向前－7米 ⑵收人－50元 ⑶体重增加－3千克【解法指导】相反意义的量包合两个要素：一是它们的意义相反．二是它们具有数量．【变式题组】1．如果＋10%表示增加10%，那么减少8%可以记作（ ）A ． －18%B ． －8%C ． ＋2%D ． ＋8%2．（金华）如果＋3吨表示运入仓库的大米吨数，那么运出5吨大米表示为( )A ． －5吨B ． ＋5吨C ． －3吨D ． ＋3吨【例２】在－227，π，0，0.033.3这四个数中有理数的个数（ ) A ． 1个 B ． 2个 C ． 3个 D ． 4个【解法指导】有理数的分类：按整数、分数分、按正负性分类有理数⎧⎧⎪⎪⎨⎪⎪⎪⎨⎩⎪⎧⎪⎨⎪⎩⎩正整数整数0负整数正分数分数负分数， 有理数0⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩正整数正有理数正分数负整数负有理数负份数；其中分数包括有限小数和无限循环小数，因为π＝3.1415926…是无限不循环小数，它不能写成分数的形式，所以π不是有理数，－227是分数0.033.3是无限循环小数可以化成分数形式，0是整数，所以都是有理数，故选C ．【变式题组】01．在7，0．1 5，－12，－301.31.25，－18，100.l ，－3 001中，负分数为 ，整数为 ，正整数 .02．（河北秦皇岛）请把下列各数填入图中适当位置15，－19，215，－138，0.1．－5.32，123, 2.333【例３】（宁夏）有一列数为－1，12，－13，14．－15，16，…，找规律到第2007个数是 . 【解法指导】从一系列的数中发现规律，首先找出不变量和变量，再依变量去发现规律．击归纳去猜想，然后进行验证.解本题会有这样的规律：⑴各数的分子部是1；⑵各数的分母依次为1，2，3，4，5，6，…⑶处于奇数位置的数是负数，处于偶数位置的数是正数，所以第2007个数的分子也是1．分母是2007，并且是一个负数，故答案为－12007. 【变式题组】01．（湖北宜宾）数学解密：第一个数是3＝2 ＋1，第二个数是5＝3 ＋2，第三个数是9＝5＋4，第四个数是17＝9＋8…观察并精想第六个数是 .02．（茂名）有一组数l ，2，5，10，17，26…请观察规律，则第8个数为____.【例４】（2008年河北张家口）若1＋m 2的相反数是－3，则m 的相反数是____. 【解法指导】理解相反数的代数意义和几何意义，代数意义只有符号不同的两个数叫互为相反数.几何意义：在数轴上原点的两旁且离原点的距离相等的两个点所表示的数叫互为相反数，本题m 2＝－4,m ＝－8 【变式题组】01．已知a 与b 互为相反数，c 与d 互为倒数，则a ＋b ＋cd ＝______02．如图为一个正方体纸盒的展开图，若在其中的三个正方形A 、B 、C 内分别填人适当的数，使得它们折成正方体.若相对的面上的两个数互为相反数，则填人正方形A 、B 、C 内的三个数依次为( )A ． － 1 ,2，0B ． 0，－2，1C ． －2，0，1D ． 2，1，0【例５】（湖北）a 、b 为有理数，且a ＞0，b ＜0，|b |＞a ，则a ,b 、－a ,－b 的大小顺序是( )A ． b ＜－a ＜a ＜－bB ． –a ＜b ＜a ＜－bC ． –b ＜a ＜－a ＜bD ． –a ＜a ＜－b ＜b【解法指导】理解绝对值的几何意义：一个数的绝对值就是数轴上表示a 的点到原点的距离,即|a |,用式子表示为|a |＝0)0(0)(0)a a a a a >⎧⎪=⎨⎪-<⎩(.本题注意数形结合思想，画一条数轴标出a 、b ,依相反数的意义标出－b ,－a ,故选A ．【变式题组】01．推理①若a ＝b ，则|a |＝|b |；②若|a |＝|b |，则a ＝b ；③若a ≠b ，则|a |≠|b |；④若|a |≠|b |，则a ≠b ，其中正确的个数为（ ）A ． 4个B ． 3个C ． 2个D ． 1个02．a 、b 、c 三个数在数轴上的位置如图，则|a |a ＋|b |b ＋|c |c＝ .03．a 、b 、c 为不等于O 的有理散，则a |a |＋b |b |＋c |c |的值可能是____. 【例６】（江西课改）已知|a －4|＋|b －8|＝0，则a +b ab的值. 【解法指导】本题主要考查绝对值概念的运用，因为任何有理数a 的绝对值都是非负数，即|a |≥0．所以|a －4|≥0，|b －8|≥0.而两个非负数之和为0，则两数均为0.a解：因为|a －4|≥0，|b －8|≥0，又|a －4|＋|b －8|＝0，∴|a －4|＝0，|b －8|＝0即a －4＝0，b －8＝0，a ＝4，b ＝8.故a +b ab ＝1232＝38【变式题组】01．已知|a |＝1，|b |＝2，|c |＝3，且a ＞b ＞c ，求a ＋b ＋C ．02．（毕节）若|m －3|＋|n ＋2|＝0，则m ＋2n 的值为( )A ． －4B ． －1C ． 0D ． 403．已知|a |＝8，|b |＝2，且|a －b |＝b －a ，求a 和b 的值三、练习01．观察下列有规律的数12,16,112,120,130,142…根据其规律可知第9个数是( ) A ． 156 B ． 172 C ． 190 D ． 111002．在－227,π,8..0.3四个数中，有理数的个数为( ) A ． 1个 B ． 2个 C ． 3个 D ． 4个03．若一个数的相反数为a ＋b ，则这个数是( )A ． a －bB ． b －aC ． –a ＋bD ． –a －b04．数轴上表示互为相反数的两点之间距离是6，这两个数是( )A ． 0和6B ． 0和－6C ． 3和－3D ． 0和305．若－a 不是负数，则a ( )A ． 是正数B ． 不是负数C ． 是负数D ． 不是正数06．下列结论中，正确的是( )①若a ＝b ,则|a |＝|b | ②若a ＝－b ,则|a |＝|b |③若|a |＝|b |，则a ＝－b ④若|a |＝|b |,则a ＝bA ． ①②B ． ③④C ． ①④D ． ②③07．有理数a 、b 在数轴上的对应点的位置如图所示,则a 、b ，－a ，|b |的大小关系正确的是( )A ． |b |＞a ＞－a ＞bB ． |b | ＞b ＞a ＞－aC ． a ＞|b |＞b ＞－aD ． a ＞|b |＞－a ＞b8.零是（ ） A 、正有理数 B 、正数 C 、非正数 D 、有理数9.下列说法不正确的是（ ） A 、 0小于所有正数 B 、0大于所有负数C 、0既不是正数也不是负数D 、0没有绝对值10.在数轴上,原点及原点右边的点表示的数是( )A.正数B.负数C.非正数D.非负数11.下列说法正确的是( )A.-a 一定是负数;B.│a │一定是正数;C.│a │一定不是负数;D.-│a │一定是负数12.有理数a 、b 在数轴上的位置如图1-1所示,那么下列式子中成立的是( )A.a>bB.a<bC.ab>0D.0a b 13.下列说法正确的是( )A.所有的整数都是正数B.不是正数的数一定是负数C.0不是最小的有理数D.正有理数包括整数和分数14．一个数在数轴上的点向右移动5个单位后，得到它的相反数的对应点，则该数是____.15.－5的相反数是 ，－5的倒数是 ，－10的绝对值是 ；16.比较大小：0 －0.01，2334 - ⎽⎽⎽⎽⎽⎽-；－[－（－0.3）]_______－∣－31∣ 17.简化符号：1(71)2--= ，8--= ；18.最大的负整数是 ;绝对值最小的有理数是 ；最小的自然数是______19.数轴上到原点的距离是3个单位长度的点表示的数是 .20.若│a │=5,则a= .21.绝对值小于3的所有的负整数是 ；它们的和为_________22. -3.5的倒数数是 。
维思教育--有理数(从自然数到有理数1-4课时)教师版
答案：1．+0.2；–0.3；+0.039；–0.019；2．–8m；向东运动6m。
4．小资料：
世界各国对负数的认识和接受也有一个过程。如1484年法国数学家曾得到二次方程的一个负根，但他不承认它，说负数是荒谬的数。1545年卡尔丹承认方程中可以有负根，但认为它是“假数”。直到1831年还有数学家认为负数是“虚构”的，他还特意举了一个“特例”来说明他的观点：“父亲56岁，他儿子29岁，问什么时候父亲的岁数将是儿子的两倍？”，通过列方程解得x=―2，他认为这个结果是荒唐的，他不懂得x=―2正是说明两年前父亲的岁数将是儿子的两倍。
5．例题；把下列各数填入表示它所在的数集的圈里：
―18， ，3.1416，0，2001， ，―0.142857，95℅.
解：
，3.1416,2001, 95℅.–18, ,―0.142857
正数集负数集
―18， ，3.1416，0，
―18，0，2001 2001， ，―0.142857，95℅
整数集有理数集
例2：把下列各数填入相应集合的括号内：
29，―5.5，2002， ，―1，90%，3.14，0，―2 ，―0.01，―2，1
（1）整数集合：{29，2002，―1，0，―2，1 }
（2）分数集合：{―5.5， ，90%，3.14，―2 ，―0.01 }
（3）正数集合：{29，2002， ，90%，3.14，1 }
大家听过天气预报吧？经常听到气温25ºC，10ºC，零下10ºC，零下30ºC。那么我们怎么表示呢？截下来就是我们要学习的相反意义的量。
(完整)有理数教案
博大教育个性化教案（简案） 编号： 科目: 教师： 学生： 年级： 教学课题：
有理数
教学目标：
1.借助生活中的实例，了解从自然数、分数到有理数的扩展过程，体会有理数应用的广泛性，体验数学和现实生活的紧密联系，提高学习的兴趣.
2。
能判断一个数是不是有理数
3。
会用正数、负数、零表示生活中具有相反意义的量.
4.能将有理数进行正确的分类。
重点难点：
重点:自然数和分数的意义及运用自然数、分数的计算解决简单的实际问题。
难点：有理数、正数、负数的概念.
教学内容：
1、自然数有计数、测量结果、标号、排序的功能
2、为了表示具有相反意义的量,我们把一种意义的量规定为正,用过去学过的数,如123,298等来表示，这样的数就叫做正数,把另一种与之意义相反的量规定为负，在学过的数（零除外）前放上负号“—”表示，如—235，-478等，这样的数就叫做负数。
3、零既不是正数也不是负数。
4、正整数、零和负整数统称为整数；正分数、负分数统称为分数;整数和分数统称为有理数。
5、
正整数
整数 零 自然数
有理数 负整数
分数 正分数 可化为有限小数
负分数 或无限循环小数
⎧⎧⎨⎪⎩⎪⎪⎨⎪⎧⎪⎨⎪⎩⎩
正整数正有理数正分数有理数零负整数负有理数负分数
授课时间： 年 月 日 时 分至 时
博大教育个性化教案。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
有理数
预习归纳
1．有理数的分类：
（1）
_________
_________
______
_____
______
⎧⎧
⎪⎪
⎨
⎪
⎪⎪
⎨⎩
⎪
⎧
⎪⎨
⎪⎩
⎩
整数
负整数
有理数（2）
_________
_________
_________
_________
__________
__________
⎧⎧
⎨
⎪
⎩
⎪
⎪
⎨
⎪⎧
⎪⎨
⎪⎩
⎩
有理数
负有理数
【答案】（1）分数，正整数、0、正分数、负分数；
（2）正有理数、0、正整数、正分数、负整数、负分数2．__________和_________统称为非负数；
_________和__________统称为非正数；
_________和__________统称为非正整数；
_________和__________统称为非负整数．
【答案】0、正数；0、负数；0、负整数；0、正整数
基础过关
知识点一：有理数的概念
1．下列说法错误的是（）
A．3-是负有理数B．0不是整数
C．2
3
是正有理数D．0.15
-是负分数
【答案】B
2．下列各数中，既是分数又是正数的是（）
A．2+B．
1
4
3
+C．0D． 2.3
-
【答案】B
3．在下列各数中：3-，2.5，0，
2
5
-，0.6
-，10，负分数有（）
A．1个B．2个C．3个D．4个【答案】B
知识点二：有理数的分类
1．下列说法正确的是（）
A．非负有理数就是正有理数B．零表示没有，不是自然数
C．正整数和负整数统称为整数D．整数和分数统称为有理数【答案】D
2．下列说法不正确的是（ ）
A ． 3.14-既是负数，分数，也是有理数
B ．0既不是正数，也不是负数，是整数
C ．2020-既是负数，也是整数，但不是有理数
D ．0是非正数 【答案】C
3．给出下列说法：①0是整数；②1
23
-是负分数；③4.2不是正数；④自然数一定是正数；
⑤负分数一定是负有理数．其中正确的有（ ） A ．1个
B ．2个
C ．3个
D ．4个
【答案】C
4．把下列各数分别填在相应的横线上：1，0.21-，1
35
，325，789-，0，23.13-，0.618，
π，2020-．
正数有________________________；分数有__________________________； 负数有________________________；正整数有__________________________； 非正数有______________________；负整数有__________________________； 非负数有______________________；负分数有__________________________． 【答案】
正数：1，135，325，0.618，π；分数：0.21-，1
35
，23.13-，0.618；
负数：0.21-，789-，23.13-，2020-；正整数：1，325；
非正数：0.21-，789-，0，23.13-，2020-；负整数：789-，2020-；
非负数：1，1
35
，325，0，0.618，π；负分数：0.21-，23.13-．
能力提升
1．下列语句：①所有整数都是正数；②分数是有理数；③所有的正数都是整数；④在有理数中，除了负数就是正数，其中正确的结论个数为（ ）
A ．1个
B ．2个
C ．3个
D ．4个
【答案】A
2．下列说法中：①0是偶数；② 2.3-是负分数；③3.6不是正数；④自然数一定是正数； ⑤负分数一定是负有理数．其中正确的有（ ）
A ．1个
B ．2个
C ．3个
D ．4个
【答案】C
3．下列各数中：4-，3.2，3
4
-，0.5，0，既不是正数，又不是分数的有___________．
【答案】4-，0
4．在有理数中，是负数但不是分数的数是____________． 【答案】负整数
5．任意写出3个数（不能重复），同时满足下列三个条件：
①其中2个数是非正数；②其中2个数是非负数；③3个数都是有理数． 【答案】0，2020-，2020
6．把下列各数填入相应的大括号内． 7-，3.5， 3.1415-，π，0，
1317，0.03，132-，10，0.68-&&，42
-．
自然数集合：{ }；整数集合：{ }； 正分数集合：{ }；非正数集合：{ }； 有理数集合：{ }． 【答案】
自然数集合：0，10；整数集合：7-，0，10，4
2
-；
正分数集合：3.5，
1317，0.03；非正数集合：7-， 3.1415-，0，132-，0.68-&&，42
- 有理数集合：7-，3.5， 3.1415-，0，1317，0.03，132-，10，0.68-&&，42
-． 7．在下列适当的空格中画上“√”．
综合拓展
1．观察有规律的整数1-，2，3-，4，5-，6，⋯按照如图所示的方式排成的数阵．
（1）按照该数阵呈现的规律排下去，那么第n 行共有_______个数，其中最左侧的一个是_______，最右侧的一个是_________（用含有n 的代数式表示）；
（2）按照该数阵呈现的规律排下去，那么第10行从左数第9个数是_________； （3）第n 行所有数字之和是_________________________（用含有n 的代数式表示）． 【答案】（1）21n -，2(1)[(1)1]n n --+，2(1)n n -；（2）90；（3）2(1)(1)n n n --+ 【解析】（1）第1行共有1个数，其中最左侧的一个是1-，最右侧的一个是1-； 第2行共有3个数，其中最左侧的一个是22(1)[(21)1]--+，最右侧的一个是22(1)2-⨯； 第3行共有5个数，其中最左侧的一个是32(1)[(31)1]--+，最右侧的一个是32(1)3-⨯；
⋯
所以第n 行共有(21)n -个数， 其中最左侧的一个是2(1)[(1)1]n n --+ 最右侧的一个是2(1)n n -；
故答案为：(21)n -，2(1)[(1)1]n n --+，2(1)n n -； （2）根据（1）所得结论可知： 第10行从左数第1个数是82， 第10行从左数第9个数是90； 故答案为90；
（3）第n 行所有数字之和是： 221
{(1)[(1)1]((1)}2
n n n n --++- 2(1)(1)n n n =--+．
故答案为：2(1)(1)n n n --+．。