线性代数实验题04-交通网络的流量分析
线性代数实验题04-交通网络的流量分析
数学实验报告学号: , 姓名: , 得分: 实验内容:实验题：交通网络流量分析问题（线性方程组应用）城市道路网中每条道路、每个交叉路口的车流量调查，是分析、评价及改善城市交通状况的基础。
问题：某城市有下图所示的交通图，每条道路都是单行线，需要调查每条道路每小时的车流量。
图中的数字表示该条路段的车流数。
如果每个交叉路口进入和离开的车数相等，整个图中进入和离开的车数相等。
求（1）建立确定每条道路流量的线性方程组；（2）分析哪些流量数据是多余的；（3）为了唯一确定未知流量，需要增添哪几条道路的流量统计。
解：（1）由题意得：x1+ x7=400x1+ x9= x2+300x2+100=300+ x11x3+ x7=350+ x8x4+ x10= x9+ x3x11+500= x4+ x12x8+ x5=310x6+400= x10+ x5x12+150= x6+290整理得：x1+ x7=400x1- x2+ x9=300x2+ x11=200x3+ x7- x8=350-x3+x4+ x10- x9=0-x4+x11- x12=-500x5 +x8=310-x5+x6- x10=-400-x6+ x12= 140将方程组写成矩阵向量形式为AX = b1 0 0 0 0 0 1 0 0 0 0 0 400 x11 -1 0 0 0 0 0 0 1 0 0 0 300 x20 1 0 0 0 0 0 0 0 0 1 0 200 x3A= 0 0 1 0 0 0 1 -1 0 0 0 0 b= 350 X= x40 0 -1 1 0 0 0 0 -1 1 0 0 0 x50 0 0 -1 0 0 0 0 0 0 1 -1 -500 x60 0 0 0 1 0 0 1 0 0 0 0 310 x70 0 0 0 -1 1 0 0 0 -1 0 0 -400 x80 0 0 0 0 -1 0 0 0 0 0 1 140 x9x10x11x12在MATLAB环境中，首先输入方程组的系数矩阵A和方程组右端向量bA=[1,0,0,0,0,0,1,0,0,0,0,0;1,-1,0,0,0,0,0,0,1,0,0,0;0,1,0,0 ,0,0,0,0,0,0,1,0;0,0,1,0,0,0,1,-1,0,0,0,0;0,0,-1,1,0,0,0,0, -1,1,0,0;0,0,0,-1,0,0,0,0,0,0,1,-1;0,0,0,0,1,0,0,1,0,0,0,0; 0,0,0,0,-1,1,0,0,0,-1,0,0;0,0,0,0,-1,0,0,0,0,0,1]b = [400;300;200;350;0;500;310;-400;140]x9+500解得x1=-x2=200x3=- x9+ x10- x12。
应用线性代数解决实际问题
应用线性代数解决实际问题线性代数作为数学的一个重要分支，广泛应用于各个领域，包括计算机科学、物理学、经济学等。
它不仅是数学家们研究的重要工具，更是解决实际问题的有效途径。
本文将通过具体案例，介绍线性代数在实际问题中的应用，从而展示其强大的解决能力。
案例一：网络流量优化现代社会离不开互联网，而网络流量的优化是提高互联网服务质量的重要问题之一。
假设我们有一组服务器，每个服务器的带宽和消耗成本有所不同，现在需要将用户的请求合理地分配到这些服务器上，以最大化带宽利用率并最小化消耗成本。
这就可以转化为一个线性代数中的线性规划问题。
首先，我们可以用一个向量表示服务器的带宽，用另一个向量表示服务器的消耗成本。
设请求到达的向量为x，那么我们的目标就是最大化带宽利用率和最小化消耗成本，可以构建如下优化模型：maximize cᵀx subject to Ax ≤ b其中，c是服务器的消耗成本向量，x是请求到达的向量，A是服务器带宽的矩阵，b是服务器的带宽上限。
通过求解这个线性规划问题，我们可以得到最佳的请求分配方案，从而实现网络流量的优化。
案例二：图像处理线性代数在图像处理中有着广泛的应用。
以黑白图片为例，可以将其表示为一个矩阵，其中的元素代表每个像素点的灰度值。
通过矩阵的加减、乘除运算，以及线性变换等操作，可以实现图像的平移、旋转、缩放等处理效果。
举个例子，假设我们想要将一张黑白图片的亮度增加一倍。
我们可以将这张图片表示为一个矩阵A，然后构造一个倍增矩阵B，即每个元素都是2。
通过这两个矩阵的乘法运算，即可实现亮度的增加。
这个过程可以用下面的表达式表示：A' = BA其中，A'表示亮度增加后的图像矩阵。
通过线性代数的运算，我们可以方便地实现图像处理中的各种效果。
总结线性代数作为数学的重要分支，具有广泛的应用领域。
本文通过网络流量优化和图像处理两个具体案例，展示了线性代数在实际问题中的应用。
线性代数的强大解决能力不仅能帮助我们解决现实生活中的问题，同时也为我们提供了一种思维方式和方法论。
交通流量调查与分析
道路交通量调查方法时间安排实习时间：2012年6月18-22日调查日期：交通调查的日期为2012年21日星期四正常工作日调查时间：上午7:30至8:30调差地点平安南大街和槐安路交叉口（珠光灯饰城站）实习目的交通调查是交通工程学科中的一个重要组成部分，交通工程学的发展在一定程度上依靠交通调查工作的开展和数据资料的积累与利用。
交通调查就是通过对多种交通现象进行调查，提供准确的数据信息，为交通规划、交通设施建设、交通控制与管理、交通安全、交通环境保护和交通流理论研究等各方面服务。
交通调查实习是在交通工程专业相关主干专业课学习结束之后进行的，该实习在于帮助学生增强感性认识，更好地理解和掌握交通调查的基本原理、内容与方法，培养学生实践和组织能力，帮助学生掌握交通调查技术和技能，为学生今后更好地参加工作打下牢固的业务基础。
调查内容1、交叉口交通量调查：采用人工计数法，实地调查记录十字型各进口道各流向的车数，调查早高峰交通量的情况。
2、交通延迟调查：采用点样本法实地调查某交叉口延误，并现场记录表。
调查流程周一：动员大会，宣布调查任务，周二：完成人员分配，设计调查方案（下午4点组长到交通办公室开会）周三: 确定调查方案（上午8点全体学生到教室开会）周四: 实地调查（7：30——8：30）周五：统计调查数据，撰写实习报告人员配备及分工调查班级：交通L092班（共26人）组长：郭志勇、杨盼盼调查南进口交通延误调查尚兵、陈铁仁、丁海明、张雪峰北进口交通延误调查张金铜、马立辉、宋阳、耿贺明注意安全1. 调查同学站在人行道上，不准站在机动车与非机动车的隔离带上。
2．禁止横穿马路，一定要走十字路口的人行横道。
交叉口基本情况调查交叉口几何条件调查平安南大街与槐安路交叉口平安南大街与槐安路交叉口卫星图平安南大街与槐安路交叉口概况：南北向的平安南大街是城市主干道，全段为沥青混凝土路面，北进口为4车道设有直右混合车道，直左混合车道。
交通流量问题
实验序号.2日期：2005年5月23日
班级
应用数学12级
姓名
罗望
学号
1217020220
实验名称
交通流量问题
问题背景描述：
已知某城市单行道的交通流量（每小时过车数）如下图：
）
假设：1.全部流入网络的流量等于全部流出网络的流量
2．全部流入一个节点的流量等于全部流出此节电的流量
试建立数学模型确定该交通网络未知部分的具体流量
所以：方程有无穷解。
3.求对应的齐次同解方程组通解：
4求特解
特解 =
5.那么，方程的解是X= +k +l （其中，k，l是常数学）
实验结果报告与实验总结：
通过本次实验进一步熟悉建立数学模型的方法，巩固了MATLAB的简单操作。
并能够用MATLAB求线性方程组的通解.不过在实验之中还遇到一些建模方面的问题，我会在以后的实验中不断总结和学习，争取不在同一个地方跌倒。
3.求通解。
4.将增广距阵最简化得t，求特解。
5.求非齐次的通解
实验过程记录（含：基本步骤、主要程序清单及异常情况记录等）：
2.在MATLAB2012a下实现：
>> A=[0 1 -1 1 0 0 0 0 0 0 ;0 0 0 1 1 0 0 0 0 0 ;0 0 0 0 0 -1 1 0 0 0 ;1 1 0 0 0 0 0 0 0 0 ;1 0 0 0 1 0 0 0 0 0 ;0 0 0 0 0 0 1 1 0 0 ;0 0 0 0 0 0 0 0 1 0 ;0 0 0 0 0 0 0 0 -1 1;0 0 0 0 0 0 0 0 0 1;0 0 1 0 0 1 0 1 0 0 ]
思考与深入：
线性方程组应用实例
1.1 交通流量
图 4-1 是某城市的公路交通网络图，交叉路口由两条单向车道组成．图中给出了交通高 峰时段每小时进入和离开路口的车辆数，试计算两个交叉路口间车辆的数量．
1.1 交通流量
解：在每一路口，进入车辆与离开车辆肯定相等，所以得到非齐次线性方程组：
x1 450 x2 610 ， x1 x2
0 0
1 0
0 1
1 1
170
210
1 0 0 1 330 0 0 0 0 0
得同解方程组
x1 x2
x4 x4
330 170
， ，
x3 x4 210 ．
若知道某一路口的车辆数量，则其他路口的车辆数量即可求得．
1.2 化学方程式
在光合作用下，植物利用太阳提供的辐射能，将二氧化碳和水转化为葡萄糖和氧气，该 化学反应的方程式为
160 ，
x2 x3
520 390
x3 x4
480 600
， ，即
x2 x3 40 ， x3 x4 210 ，
x4 640 x1 310 ， x1
x4 330 ，
则有
1 1 0 0 160 1 0 0 1 330
A
0 0
1 1 0 0 1 1
40 210
0， 0，
2x2
12x4 ， 2x2
12x4 0 ，
得到 x1 x2 x3 6x4 ．若令 x4 1 ，则 x1 x2 x3 6 ，化学方程式的形式为 6CO2 6H2O 6O2 C6H12O6 ．
注：在实际问题中，要考虑各变量的实际意义．例如，化学方程式中的各变量应为非负
整数．
线性代数
x1CO2 x2H2O x3O2 x4C6H12O6 ． 为了平衡该方程式，需适当选择 x1 ，x2 ，x3 ，x4 ，使得方程式两边的碳、氢、氧原子数量 分别相等．
交通网络
就是说x1, x2, x3, x4这四个未知量中, 任意 一个未知量的值统计出来之后都可以确定 出其他三个未知量的值。
Matlab练习题 某城市有下图所示的交通图, 每条道路都是 单行线, 需要调查每条道路每小时的车流量. 图 中的数字表示该条路段的车流数. 如果每个交叉 路口进入和离开的车数相等, 整个图中进入和离 开的车数相等。 现在需要解决如下问题： （1）建立确定每条道路流量的线性方程组。 （2）分析哪些流量数据是多余的。 （3）为了唯一确定未知流量, 需要增添哪 几条道路的流量统计 。
案例1 交通网络流量分析问题
城市道路网中每条道路、每个交叉 路口的车流量调查，是分析、评价及改 善城市交通状况的基础。根据实际车流 量信息可以设计流量控制方案，必要时 设置单行线，以免大量车辆长时间拥堵。
下图为某城市的局部单行示意图
【问题描述】： 某城市单行线如下图所示, 其中的数字表示该路段每小时按箭头方向行 驶的车流量(单位: 辆).
【模型求解】根据上述等式可得如下线性方 程组。 500 x1 x 2
x1 x4 100 x 2 x3 300 x3 x 4 3 0 0
其增广矩阵
1 1 0 0 1 0 500 0 0 1 100 初等行变换 1 1 0 300 0 1 1 300 0 1 0 0 0 0 0 1 100 1 0 1 600 0 1 1 300 0 0 0 0
(A, b) =
由此可得
x1 x 4 1 0 0 x2 x4 600 x x 300 4 3
x1 x 4 1 0 0 x2 x4 600 x x 300 4 3
线性代数的应用
四、信号流图模型
信号流图是用来表示和分析复杂系统内的信号 变换关系的工具。 x1 G1 x2 u 右图方程如下： x1 = u G2 x2， -G2
x2 = G1 x1
写成矩阵方程 x=Qx+Pu 移项整理，可以得到求信号向量x的公式。
x1 0 G 2 x1 x = G x + 2 1 0 2
4000 2200 6000
四、产品成本的计算
将M和P相乘，得到的矩阵设为Q，Q的第一行 第一列元素为 Q(1,1)=0.1×4000+0.3×2000+0.15×5800=1870
1870 Q = 3450 1670 2220 4020 1940 2070 3810 1830 1960 3580 1740
0 0.9200 -0.7071 -0.3162 lamda = , e = 0.7071 -0.9487 0 1.0000
三、人口迁徙模型
令
1 1 u1 = , u2 = 1 3
它是特征向量的整数化，得到
x k = A x0 = 0.25u2 0.05(0.92) u1
一、药方配制问题
u7=[100;55;0;35;6;50;25;10;20]; U=[u1,u2,u3,u4,u5,u6,u7] [U0,r]=rref(U) 计算结果为
一、药方配制问题
U0= 101000 012003 000101 000011 000000 四个零行 0 0 0 0 1 r= 1 2 4 5 7 从最简行阶梯型U0中可以看 出，R（U）=5，向量组线性 相关，一个最大无关组为 u1，u2，u4，u5，u7， u3=u1+2u2 u6=3u2+u4+u5 故可以配制新药
线性代数数学建模案例(1)
其增广矩阵
(A, b) =
1 1 0 0 500
1 0 0 1 100
1
0 0
0 1 0
0 1 1
1 0 1
100
300 300
初等行变换
0
0 0
1 0 0
0 1 0
1 1 0
600
300 0
由此可得
x1 x4 100
百甚至上千未知量和线性方程。
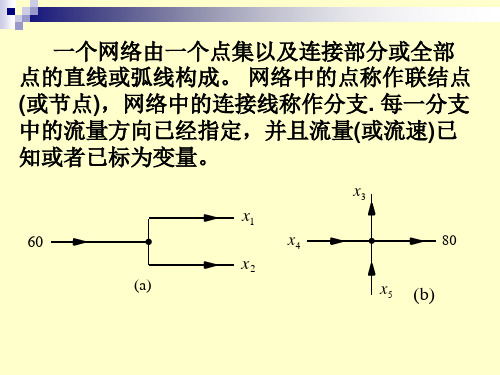
一个网络由一个点集以及连接部分或全部 点的直线或弧线构成。 网络中的点称作联结点
(或节点)，网络中的连接线称作分支. 每一分支 中的流量方向已经指定，并且流量(或流速)已 知或者已标为变量。
x3
x1
60
x4
80
x2
(a)
x5 (b)
网络流的基本假设是（1）网络中流入与流 出的总量相等；（2）每个节点上流入和流出 的总量也相等。例如，上面两图（a）、（b）。 流量在每个节点守恒。 在类似的网络模式中， 每个结点的流量都可以用一个线性方程来表示。
线性代数数学建模案例 （1）
一、网络流模型
网络流模型广泛应用于交通、运输、通讯、电力 分配、城市规划、任务分派以及计算机辅助设计等众 多领域。当科学家、工程师和经济学家研究某种网络 中的流量问题时,线性方程组就自然产生了,例如,城市 规划设计人员和交通工程师监控城市道路网格内的交 通流量,电气工程师计算电路中流经的电流,经济学家 分析产品通过批发商和零售商网络从生产者到消费者 的分配等. 大多数网络流模型中的方程组都包含了数
Matlab练习题
某城市有下图所示的交通图, 每条道路都是 单行线, 需要调查每条道路每小时的车流量. 图 中的数字表示该条路段的车流数. 如果每个交叉 路口进入和离开的车数相等, 整个图中进入和离 开的车数相等。
线性代数在交通流控制中的应用
文献标识 码： Ａ
文章编号 ： １ ６ ７ １ 一ｌ ４ ４ ０ （ ２ Ｏ ｌ ７ ） ０ ６ ｒ ＿ ＿ ０ Ｏ ７ ２ ＿ ＿ ０ ３
１ 单 行 道 交 通 网络 的 交通 流 量 平 衡 条 件
随着 计 算 机 的飞 速 发展 ， 我们 已然 生活 在 数
字化 时代 。 大数 据 、 云计算 的 出现极 大地 提升 了海
Ａ
ｘ４
１ ３
ｌ
Ｂ
Ｘ ３
图１
本 文针对几种 常见 的城市 交通局域 网络类 型 ， 探讨局 域 网各 结 点 交通 流 量 的 计算 方 法 并 给出
ｘ５
在 交通 流 量 平衡 条 件 下的 一组 流 量值 ， 交 通管制
条件下 流量控制 的可行 性 。
２ 不 同网络交叉点 的交通流量 的计算 。流量单
位： （ 辆Ｉ ｌ ｌ ＇ ， 时） ２ ． １ 含 丁 字 路 口的
体 系。 由于城市 车辆 的增 长和 路 网密 度 的增加 ， 交 叉 口之 问 的相 关性 逐渐 增 强 将 城 市 路 网 中 的多
个 交叉 口作 为 一 个 局域 网 ． 根 据交 通 流最平 衡条
反） 。 各 方 向的交通 流量 控制 ， 与单 行道 方法 相 同 。 各
路 口的交通 信号都 是分 别控 制各 行车 道 ，控 制 方法 与单行 道完 全一致 。 因此 ， 本 文不 再另 行探讨 。 交 通 流 量平 衡值 ， 流 量 的速 度 是交 通 信 号灯 的 控制时间 的重要 依据 。
中 国 ・包 头
职 大 学 报
２ ０ １ ７ 年 第 ６期
线性 代数 在 交通 流控 制 中的应 用
交通流量2
x 2 x3 x4 300 x 4 x5 500 x7 x6 200 800 x1 x 2 800 x1 x5 x7 x8 1000 400 x9 200 x10 x9 x10 600 x8 x3 x6 1000
数学实验报告
实验序号： 班级 信计 2 班 实验名称 交通流量问题 问 题 背 景 描 述 ： 已 知 某 城 市 单 行 道 的 交 通 流 量 （ 每 小 时 过 车 数 姓名 日期：2005 年 5 月 25 日星设：1.全部流入网络的流量等于全部流出网络的流量 2．全部流入一个节点的流量等于全部流出此节电的流量 试建立数学模型确定该交通网络未知部分的具体流量 实验目的：学会用线性代数中线性方程组的有关知识建立交通流量数学模型，并用数学 软件求其问题的全部解。 实验原理与数学模型： 1 由已知条件及假设建立 10 元线行方程组 2 用 MATLAB 软件求其通解 由网络流量假设,所给问题满足如下线行方程组
0 0 0 0 0 η 2= 1 1 1 0 0
赋值给自由未知量（x5,x6）为（0，0）得非齐次方程组的特解
x*
800 0 200 500 0 = 800 1000 0 400 600
0 1 -1 0 0
300 500 200 800 800 1000 400 200 600 1000
0 1 0 0 0 0 0
0 0 1 0 0 0 0
0 0 0 Columns 4 through 6 0 0 0 1 0 0 0 0 0 0 Columns 7 through 9 0 0 0 0 0 1 0 0 0 0 Columns 10 through 11 0 0 0 0 0 0 0 1 0 0 >>
数学理论在交通流量分析中的应用
数学理论在交通流量分析中的应用在现代社会，交通流量的分析对于优化交通系统、提高道路安全性和缓解拥堵至关重要。
数学理论在这一领域发挥着不可或缺的作用，为我们理解和预测交通流量提供了强大的工具。
首先，概率论在交通流量分析中有着广泛的应用。
交通流量是一个充满不确定性的现象，车辆的到达时间、行驶速度以及道路上的突发事件等都具有随机性。
通过概率论，我们可以对这些随机因素进行建模和分析。
例如，假设在某一路段上，车辆的平均到达率是每小时 100 辆，且符合泊松分布。
那么，我们可以计算在给定的时间段内，到达车辆数量的概率分布。
这有助于交通管理者预估在高峰时段可能出现的交通流量峰值，从而提前做好交通疏导的准备。
排队论也是交通流量分析中的重要数学工具。
当车辆在路口等待信号灯、在收费站排队缴费或者在停车场寻找停车位时，都形成了排队系统。
排队论可以帮助我们确定最优的信号灯时长、收费站通道数量以及停车场的规模等。
以路口信号灯为例，通过排队论的分析，可以计算出在不同信号灯周期下，车辆的平均等待时间和排队长度。
通过优化信号灯周期，能够最大程度地减少车辆的等待时间，提高道路的通行效率。
微分方程在交通流量模型中也占有一席之地。
交通流可以被看作是一种连续的流体，其流动特性可以用流体力学中的微分方程来描述。
例如，LighthillWhithamRichards （LWR）模型就是一个基于偏微分方程的交通流模型。
这个模型可以描述交通密度和交通流量之间的关系，帮助我们理解交通拥堵的形成和传播机制。
通过求解这些微分方程，我们可以预测交通拥堵的发生和发展，为制定有效的交通管控策略提供依据。
数学中的优化理论在交通流量分析中同样发挥着关键作用。
在交通网络中，如何分配交通流量以最小化总旅行时间或总油耗，是一个典型的优化问题。
线性规划、非线性规划和整数规划等优化方法可以用来解决这类问题。
例如，在城市道路网络中，通过优化理论，可以确定最优的道路扩建方案或者公交线路的布局，以提高整个交通系统的性能。
线性方程组在对交通流量分析的简单应用
1. 能否用单环的性质来研究多环；
2. 是否存在某种特殊结构网络其本身内部情 况不会对外部照成影响；
3. 大网络与小网络之间是否存在一定的状态 转移关系,使得一个庞大的网络可以划归为 小的、基本的网络来讨论。
1 0 0 0 0 0 0 0
0 0 0 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0
0 1 0 0 0 0 0
0 0 0 0 1 0 0 1 1 0 0 0 0 0
0 0 0 1
1 0 1
O3 I3 O1 O4 I1 I 4 O3 O2 I 3 O4 I1 I 2 O1 I 4 O3 I1
X 1 X 5 I1 X X O 6 3 2 X 3 X 7 I3 X 4 X 8 O1 X 1 X 7 O4 X 2 X 8 I4 X 3 X 5 O2 X X I 6 2 4
1 0 0 0 A 1 0 0 0
应用数学系 齐宇明 2012年12月22日制
介绍实例对象
问题分析 建立模型与求解 模型拓展 猜想
某市将耗资对城 市交通做规划。以 下是该市某路段简 易单行线如图所示， 箭头方向表示车流 的方向，适当收集 一些数据处理后找 出关于这个交通网 的一些结论。
E1 E2 O2 X1 X2 O1
E1+E2=O1+O2
0 0 0 1 0 0 0 I1 1 0 0 0 1 0 0 O3 0 1 0 0 0 1 0 I3 0 0 1 0 0 0 1 O1 0 0 0 0 0 1 0 O4 1 0 0 0 0 0 1 I4 0 1 0 1 0 0 0 O2 0 0 1 0 1 0 0 I2
线性方程组关于交通流量应用实例分析论文
线性方程组关于交通流量的应用实例分析【摘要】通过对福州某地段单行道交通网络实地调查，利用线性方程组分析其交通流量特性，借助Matlab计算工具提出了可变车道的设计方案，以求达到缓解该地段交通拥挤状况的目的.【关键词】线性方程组；交通流；Matlab引言线性代数是代数的一个主要分支，以向量空间与线性变换为研究对象，就其在数学、物理学以及经济学等分支的应用来说，线性代数的离化思想具有非常特殊的作用，为此也成为作为大学生的我们必修的公共基础课之一. 在现代大量的科学技术问题，最终往往归结为解线性方程组. 因此在线性方程组的数值解法得到发展的同时，线性方程组解的结构等理论性工作也取得了令人满意的进展. 现在，线性方程组的数值解法在计算数学中占有重要地位. 因此如何去解线性方程组，怎么去运用线性方程组成为了我们线性代数的学习基础.科学在发展，我们不仅要研究单个变量之间的关系，还要进一步研究多个变量之间的关系，各种实际问题在大多数情况下可以线性化，而由于计算机的发展，线性化了的问题又可以计算出来，线性代数正是解决这些问题的有力工具，就线性代数的思想而言，也十分适应于计算机的编程等方面，就产生了用Matlab来解决线性代数问题的思想，它与线性代数有着紧密的联系.线性方程组是线性代数最基本的内容之一，而经常见到的就是求解线性方程组，早在中国古代的数学著作《九章算术方程》章中已作了比较完整的论述. 其中所述方法实质上相当于现代的对方程组的增广矩阵施行初等行变换从而消去未知量的方法，即高斯消元法. 在西方，线性方程组的研究是在 17 世纪后期由莱布尼茨开创的.他曾研究含两个未知量的三个线性方程组组成的方程组. 麦克劳林在 18 世纪上半叶研究了具有二、三、四个未知量的线性方程组，得到了现在称为克莱姆法则的结果. 克莱姆不久也发表了这个法则. 18世纪下半叶，法国数学家贝祖对线性方程组理论进行了一系列研究，证明了元齐次线性方程组有非零解的条件是系数行列式等于零； 19 世纪，英国数学家史密斯 (H.Smith) 和道奇森 (C-L.Dodgson) 继续研究线性方程组理论，前者引进了方程组的增广矩阵和非增广矩阵的概念，后者证明了n个未知数n个方程的方程组相容的充要条件是系数矩阵和增广矩阵的秩相同，这正是现代方程组理论中的重要结果之一. [6]在行车道上经常会出现塞车的现象，在城市的车流高峰期尤为常见. 以单行道为例，在得知交通网络的车辆流向的前提下，经过对交通网络各个路口的交通流量的实际交通调查，统计出主要进出口的车辆总数大致相同的情况下，可以得出交通网络的平衡方程组，通过对线性方程组的解得分析，得出该交通网络的交通网络在某一段时间的车况受哪些车道路况影响，本文在以上条件下，提供了一种利用线性方程组来研究单行道路况的方法，也就是在列出交通网络的平衡方程通时，基于Matlab计算工具分析网络平衡方程的解，在得出问题车道后，提出了在拥堵的车道设计可控制的变向车道，以求缓解交通拥挤的状况，虽然未经实践实用，但具有一定的应用价值.1.基本概念与结论本节主要介绍线性方程组的一些基本概念与结论，以便后文使用.定理1.1[3] n 元齐次线性方程组m n ⨯=A x 0有非零解的充分必要条件是其系数矩阵的秩()r n <A 且其通解式中带有()n r -A 个任意参数; 只有零解的充分必要条件是()r n =A .定理1.2[3] n n ⨯齐次线性方程组=AX 0有非零解的充分必要条件是=A 0；它只有零解的充分必要条件是≠A 0.定理1.3[3] n 元非齐次线性方程组m n ⨯=A x b 有解的充分必要条件是其系数矩阵A 的秩等于增广矩阵=⎡⎤⎣⎦A A b 的秩.定理1.4[1] 对于n 元非齐次线性方程组m n ⨯=A x b 有如下结论：(1) 当()()r r =A A 时，方程组有解.这时，若()()r r n ==A A ，则方程组有唯一解 若()()r r n =<A A ，则方程组有无限多个解，且其通解式中带有()n r -A 个任意参数.(2) 当()()r r <A A 时，方程组无解.由于下文用到Matlab 来解线性方程组的，有必要说明一下几个命令：（1） 计算矩阵的秩——命令：rank （矩阵）；（2） 化矩阵为行阶梯形求解线性方程组——命令：rref （矩阵）例 求解线性方程组123412341234030230x x x x x x x x x x x x --+=⎧⎪-+-=⎨⎪--+=⎩ 具体操作：>> A=[1 -1 -1 1;1 -1 1 -3;1 -1 -2 3]A =1 -1 -1 1 1 -1 1 -3 1 -1 -23 >> rref(A)ans =1 -1 0 -1 0 0 1 -2 0 0 0 0即得与原方程组同解的方程组：12434020x x x x x --=⎧⎨-=⎩ 令4122,x c x c ==，可得通解为1122231412x c c x c x c x c ==+⎧⎪=⎪⎨=⎪⎪⎩其中12,c c 为任意常数2. 交通流量应用分析汽车在道路上连续行驶形成的车流，我们称之为交通流.广义上还包括其他车辆的车流和人流. 在某段时间内，在不受横向交叉影响的路段上，交通流呈连续流状态；在遇到路口信号灯管制时，呈断续流状态. 城市道路网中每条路、每个交叉路口的车流量调查是分析、评价及改善城市交通状况的基础. 根据实际车流量的信息可以设计流量控制方案，必要时设置单行线，以免大量车辆长时间堵车.2.1 问题提出据悉福州市在公路、铁路、港口等方面都将有大投资，其中拟投资约140亿元规划建设长约150 公里的高速公路，许多市内单行车道面临整改，市民出行将更加便捷，是否可以在原有的单行车道基础上做适当改造也能达到相应的效果呢？以下是福州某路段简易单行线如图(1)所示，箭头方向表示车流的方向，适当收集一些数据后我们是否可以得出关于这个交通网的一些结论.图（1）2.2模型分析为了便于接下来的分析，我们对车流图做如图(2)处理:a 2mjb 13a 4k2nEDCBA图（2）其中14~a a 表示各相交道路的进口交通量，13~b b 表示各相交道路的出口交通量，j k l m n r、、、、、表示通过图示各交通干道的车辆数.2.3 数据收集由于工具有限，我们只对进出口交通量（即14~a a 和13~b b ）进行实时统计，统计图表如下：表1 14~a a 进口交通流量表2 13~b b 出口交通流量2.4数据分析从表1和表2中可以看出在观察的时间段内各个进口的交通流量之和与各个出口的交通流量之和大致相同，即1234123a a a a b b b +++≈++，为了便于分析我们把进出口的交通流量按平均值折算为每小时的车流量，补正取367b =结果如下：进口交通流量：13612432a =⨯=（辆/小时） 23312396a =⨯=（辆/小时） 3157121884a =⨯=（辆/小时） 47012840a =⨯=（辆/小时）进入网络的车的总量(辆/小时)：43239618848403552+++= 出口交通流量：1155121860b =⨯=（辆/小时） 27412888b =⨯=（辆/小时） 36712804b =⨯=（辆/小时）离开交通网络的车总量（辆/小时）：18608888043552++=从交通流量平衡条件，对于每一个道路交叉点我们都可以写出一个流量平衡方程：A 路口：12a a j r +=+B 路口：1j k b n +=+C 路口：43a l b k +=+D 路口：2m n l b +=+E 路口：3a r m +=从而我们可以得到一个反应网络交通流量的线性代数方程：43239618608408048881884j r j k n l k m n l r m+=+⎧⎪+=+⎪⎪+=+⎨⎪+=+⎪+=⎪⎩ 化简得：8281860368881884j r j k n k l m n l m r +=⎧⎪+-=⎪⎪-=⎨⎪+-=⎪-=⎪⎩ 写成矩阵形式为：=Ax b10001110010011000001110000101⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥-⎢⎥⎢⎥-⎣⎦A ，[]T j klm n r =x ，[]8281860368881884T=b增广矩阵118281100101860011000360011108880001011884⎡⎤⎢⎥-⎢⎥⎢⎥=-⎢⎥-⎢⎥⎢⎥-⎣⎦A由于()()46rank rank ==<A A ，故方程组有无穷多个解，且其参数中带有2个任意参数运用Matlab 求解可得方程组的通解,求解步骤如下： >> B=[0 0 0 1 0 1 828; 0 0 -1 0 1 1 1860; -1 0 0 0 1 0 36; -1 1 1 0 0 0 888; 0 1 0 -1 0 0 1884]B =0 0 0 1 0 1 828 0 0 -1 0 1 1 1860-1 0 0 0 1 0 36 -1 1 1 0 0 0 888 0 1 0 -1 0 0 1884 >> rank(B) ans = 4 >> rref(B) ans =1 0 0 0 -1 0 -36 0 1 0 0 0 1 2712 0 0 1 0 -1 -1 -1860 0 0 0 1 0 1 828 0 0 0 0 0 0 0 即等价的原方程组的通解：12211213627121860828c c c c c c c ⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥+-⎢⎥-⎢⎥⎣⎦，其中12c c 、可以取任意实数，方程组有无限多个解. 是不是真的是无穷多个解呢？答案是否定的，注意到我们研究的是实际车道上的车流量，是不存在负数的，因此以上变量还需满足：12211210036027120186008280j c k c l c m c n c c r c =≥⎧⎪=≥⎪⎪=-≥⎪⎨=-≥⎪⎪=+-≥⎪=-≥⎪⎩ ① 即：21123608281860c c c c ≥⎧⎪≤≤⎨⎪+≥⎩，其中12c c 、为整数 也就是说：I ．只要追加统计出j k l m n r 、、、、、中任意2个数值的，就可以求出其他未知量数值. II ．该交通网络中，若每小时通过CB 段的车辆不超过36辆、通过AB 与CB 段的车辆总数之和不超过1860辆、通过AB 段的车辆多于828辆三种情况中出现一种整个网络平衡就会被破坏，即出现塞车的现象.2.5模型改进根据上述分析，上述的交通网络中若出现网络平衡被破坏了，我们可以采取合适的方法进行改进，使得网络重新回归平衡.交通网络还是图（1）网络.若112,2712,36j c c k c =>=≥这是造成网络失去平衡的一种情况：依据线性方程组①，我们可以得出12211210036027120186008280j c k c l c m c n c c r c =≥⎧⎪=≥⎪⎪=-≥⎪⎨=-<⎪⎪=+-≥⎪=-<⎪⎩ ②即：每小时通过ED ，AD 段的车流量出现负值的现象，现在做如变动，进出口的交通流量与之前一致变化如图（3）所示：a 213jb 1b 3a 4k2nmEDCBA图（3）变动说明：即把ED 、EA 段的车流方向改为与原来方向相反. 此时交通网络是否恢复了平衡了呢？ 若平衡，依据前文计算方法可得平衡线性方程组：43239618608408048881884r j j k n l k n l m m r++=⎧⎪+=+⎪⎪+=+⎨⎪=++⎪+=⎪⎩ 即8281860368881884r j n j k k l m n l m r =-⎧⎪=+-⎪⎪-=⎨⎪=--⎪=-⎪⎩ 化简后可得通解：12211213627121860828c c c c c c c ⎡⎤⎢⎥⎢⎥⎢⎥-⎢⎥-⎢⎥⎢⎥+-⎢⎥-⎢⎥⎣⎦其中12c c 、为满足假设的正整数不难发现：1221121271203603602712018602712361860082827128280j c k c l c m c n c c r c =>>=≥>=-≥=->=+->+->=->->均为正实数， 即现在网络是平衡的交通网络. 112,2712,36j c c k c =>=≥这是造成网络失去平衡的情况中的一种， 其他情况研究的方法类似在此就不一一列举.我们可以得出这样一个结论，在已知进出口车流总量的单行车道中当网络出现平衡被破坏时，也就是车道上的车流量出现负值时，可以把该干道车流方向变更为之前方向相反例如:在“A →B ”的车流量超过了2712，“C →B ”段的车流量超过36, 若按之前平衡方程进行分析，“E →D ”、“A →E ”流向车流量出现了负值现象，若要使网络恢复平衡，更改这两个车流方向即可，即：“E →D ”车流向变更为“D →E ” “A →E ” 车流向变更为“E →A ”网络就可恢复平衡，也就是各个交通要道车流量恢复了正值.在实际行车中，可以对经常出现交通紧张的车道进行可变车道改造，改造设计如图（4）所示：图（4）改造说明：将车道变更如图所示，道路进出口处标示“可变车道”，并设制正反向通行指示灯，需要注意的是此车道为单行车道同一时间段只允许一个方向的车通行. 可变车道的正反向的启动时间可根据电子监测设备采集的交通实时数据进行动态调整，也可引进相应的交通控制软件进行动态控制.2.6模型缺点（1） 城市交通路口的交通状况十分复杂，交通量尤其是高峰小时期的交通量很大，调查员在进行实际调查有一定的困难.（2） 对于各交通路口同一时段的车流量的即时统计存在一定的困难，需借助一定的测流工具，工具存在一定的误差，而且此次观察时间较短.（3） 该模型需要满足进出口的交通流量总量大致一致，要求比较苛刻（4） 该模型只适用于单车道模型，对于现在交通干道普遍存在的双车道的模型不适用. （5） 后文提到的解决单行车道道路堵塞问题存在可行性,但未进行实践应用，未能看出其实用价值.3. 结语本文主要通过一个简易的交通流量图，介绍了线性方程组的思想在交通流量方面的应用，提供了一种运用线性方程的思想去分析城市单行车道的交通状况的方法，并提出了一种解决交通堵塞的方法，其实线性方程组解决交通实际交通问题已经不是少见的事了，在统计城市三路交叉口、四路交叉口等等都会用到线性方程组的方法. 在科学、工程、化学、交通等各个领域中包含的众多数学问题中都，大都会遇到解线性方程组的问题，可见线性方程组的应用之广泛.参考文献[1] 丘维声.高等代数（上册）[M]. 北京：高等教育出版社，2007，90-97.[2] 王坤，周岩. 线性代数及其应用[M]. 北京：机械工业出版社，2007，125-127.[3] 刘剑平，施劲松，钱夕元. 线性代数及其应用[M]. 上海：华东理工大学出版社，2005，63-69.[4] 王亮，冯国臣，王兵团. 基于MATLAB的线性代数实用教程[M]. 北京：科学出版社，2008，63-89.[5] David C. Linear Algebra and Its Applications,Third Edition[M]. 北京：机械工业出版社，2005，59-88.[6] 徐品芳. 数学简明史[M]. 北京：学苑出版社，1992，63-72.[7] 姚喜研，王济荣. 线性代数[M]. 北京：北京大学出版社，2009，64-102.[8] 王建军. 线性代数及其应用[M]. 上海：上海交通大学出版社，2005，80-88.Applications of Linear Equations to AnalysePractical Examples on Traffic FlowHongdehuo 105012007003 Advisor:Zhou dexuMajor in Pure and Applied Mathematics College of Mathematics and Computer Science【Abstract】By surveying one-way traffic network on the spot in Fuzhou, we apply linear equations to analyse the traffic flow characteristics, and propose a design of variable lane relying on Matlab so that it is convenient to alleviate the status of traffic congestion in this place.【Key words】Linear equations; traffic flow; Matlab。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
数学实验报告
学号: , 姓名: , 得分:
实验内容:实验题：交通网络流量分析问题（线性方程组应用）
城市道路网中每条道路、每个交叉路口的车流量调查，是分析、评价及改善城市交通状况的基础。
问题：某城市有下图所示的交通图，每条道路都是单行线，需要调查每条道路每小时的车流量。
图中的数字表示该条路段的车流数。
如果每个交叉路口进入和离开的车数相等，整个图中进入和离开的车数相等。
求（1）建立确定每条道路流量的线性方程组；
（2）分析哪些流量数据是多余的；
（3）为了唯一确定未知流量，需要增添哪几条道路的流量统计。
解：
（1）由题意得：x1+ x7=400
x1+ x9= x2+300
x2+100=300+ x11
x3+ x7=350+ x8
x4+ x10= x9+ x3
x11+500= x4+ x12
x8+ x5=310
x6+400= x10+ x5
x12+150= x6+290
整理得： x 1+ x 7=400 x 1- x 2+ x 9=300
x 2+ x 11=200
x 3+ x 7- x 8=350
-x 3+x 4+ x 10- x 9=0 -x 4+x 11- x 12=-500 x 5 +x 8=310 - x 5+x 6- x 10=-400 -x 6+ x 12= 140
将方程组写成矩阵向量形式为AX = b
1 0 0 0 0 0 1 0 0 0 0 0 400 x 1
1 -1 0 0 0 0 0 0 1 0 0 0 300 x 2
0 1 0 0 0 0 0 0 0 0 1 0 200 x 3
A= 0 0 1 0 0 0 1 -1 0 0 0 0 b= 350 X= x 4
0 0 -1 1 0 0 0 0 -1 1 0 0 0 x 5
0 0 0 -1 0 0 0 0 0 0 1 -1 -500 x 6
0 0 0 0 1 0 0 1 0 0 0 0 310 x 7
0 0 0 0 -1 1 0 0 0 -1 0 0 -400 x 8
0 0 0 0 0 -1 0 0 0 0 0 1 140 x 9 x 10 x 11 x 12
在MATLAB 环境中，首先输入方程组的系数矩阵A 和方程组右端向量b
A=[1,0,0,0,0,0,1,0,0,0,0,0;1,-1,0,0,0,0,0,0,1,0,0,0;0,1,0,0,0,0,0,0,0,0,1,0;0,0,1,0,0,0,1,-1,0,0,0,0;0,0,-1,1,0,0,0,0,-1,1,0,0;0,0,0,-1,0,0,0,0,0,0,1,-1;0,0,0,0,1,0,0,1,0,0,0,0;0,0,0,0,-1,1,0,0,0,-1,0,0;0,0,0,0,-1,0,0,0,0,0,1] b = [400;300;200;350;0;500;310;-400;140]
解得 x 1=- x 9+500 x 2=200 x 3=- x 9+ x 10- x 12。