流体力学与传热习题:solutions
流体力学与传热习题:problems and solutions forchapter1,2

1.3 A differential manometer as shown in Fig. is sometimes used to measure small pressuredifference. When the reading is zero, the levels in two reservoirs are equal. Assume that fluid B ismethane (甲烷), that liquid C in the reservoirs is kerosene (specific gravity = 0.815), and thatliquid A in the U tube is water. The inside diameters of the reservoirs and U tube are 51mm and6.5mm , respectively. If the reading of the manometer is145mm., what is the pressure differenceover the instrument In meters of water, (a) when the change in the level in the reservoirs isneglected, (b) when the change in the levels in the reservoirs is taken into account? What is thepercent error in the answer to the part (a)?Solution :p a =1000kg/m 3 p c =815kg/m 3 p b =0.77kg/m 3 D/d=8 R=0.145mWhen the pressure difference between two reservoirs is increased, the volumetric changes in the reservoirs and U tubesR d x D 2244ππ= (1) so R D d x 2⎪⎭⎫ ⎝⎛= (2) and hydrostatic equilibrium gives following relationshipg R g x p g R p A c c ρρρ++=+21 (3)sog R g x p p c A c )(21ρρρ-+=- (4)substituting the equation (2) for x into equation (4) givesg R g R D d p p c A c )(221ρρρ-+⎪⎭⎫ ⎝⎛=- (5) (a )when the change in the level in the reservoirs is neglected,()Pa g R g R g R D d p p c A c A c 26381.98151000145.0)()(221=⨯-=-≈-+⎪⎭⎫ ⎝⎛=-ρρρρρ(b )when the change in the levels in the reservoirs is taken into account()Pa g R g R D d g R g R D d p p c A c c A c 8.28181.98151000145.081.9815145.0515.6)()(22221=⨯-+⨯⨯⨯⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛=-ρρρρρρ error=%=7.68.2812638.281-1.4 There are two U-tube manometers fixed on the fluid bed reactor, as shown in the figure. The readings of two U-tube manometers are R 1=400mm ,R 2=50mm, respectively. The indicating liquid is mercury. The top of the manometer is filled with the water to prevent from the mercury vapor diffusing into the air, and the height R 3=50mm. Try to calculate the pressure at point A and B .Solution: There is a gaseous mixture in the U-tube manometer meter. The densities of fluids are denoted by Hg O H g ρρρ,,2, respectively. The pressure at point A is given by hydrostatic equilibriumg R R g R g R p g Hg O H A )(32232+-+=ρρρg ρis small and negligible in comparison with Hg ρand ρH2O , equation above can be simplifiedc A p p ≈=232gR gR Hg O H ρρ+=1000×9.81×0.05+13600×9.81×0.05=7161N/m²1gR p p p Hg A D B ρ+=≈=7161+13600×9.81×0.4=60527N/mFigure for problem 1.41.5 Water discharges from the reservoir through the drainpipe, which the throat diameter is d. The ratio of D to d equals 1.25. The vertical distance h between the tank A and axis of the drainpipe is 2m. What height H from the centerline of the drainpipe to the water level in reservoir is required for drawing the water from the tank A to the throat of the pipe? Assume that fluid flow is a potential flow. The reservoir, tank A and the exit ofdrainpipe are all open to air.Solution: Bernoulli equation is written between stations 1-1 and 2-2, with station 2-2 being reference plane: 2222222111u gz p u gz p ++=++ρρ Where p 1=0, p 2=0, and u 1=0, simplification of the equation1The relationship between the velocity at outlet and velocity u o at throat can be derived by the continuity equation:22⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛D d u u o 22⎪⎭⎫ ⎝⎛=d D u u o 2 Bernoulli equation is written between the throat and the station 2-23 Combining equation 1,2,and 3 gives222u Hg =222200u u p =+ρSolving for HH=1.39m1.6 A liquid with a constant density ρ kg/m 3 is flowing at an unknown velocity V 1 m/s through a horizontal pipe of cross-sectional area A 1 m 2 at a pressure p 1 N/m 2, and then it passes to a section of the pipe in which the area is reduced gradually to A 2 m 2 and the pressure is p2. Assuming no friction losses, calculate the velocities V 1 and V 2 if the pressure difference (p 1 - p 2) is measured. Solution :In Fig1.6, the flow diagram is shown with pressure taps to measure p 1 and p 2. From the mass-balance continuity equation , for constant ρ where ρ1 = ρ2 = ρ,2112A A V V = For the items in the Bernoulli equation , for a horizontal pipe,z 1=z 2=0Then Bernoulli equation becomes, after substituting 2112A A V V = for V 2, ρρ22121211212020p A A V p V ++=++ ()===144.281.92100081.910002125.11112442-⨯⨯⨯--⎪⎭⎫ ⎝⎛==ρρg h d D u HgRearranging,2)1(21212121-=-A A V p p ρ ⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-12221211A A p p V ρ=Performing the same derivation but in terms of V 2,⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--21221212A A p p V ρ=1.7 A liquid whose coefficient of viscosity is µ flows below the critical velocity for laminar flow in a circular pipe of diameter d and with mean velocity V . Show that the pressure loss in a length of pipe L p ∆ is 232dV μ. Oil of viscosity 0.05 Pas flows through a pipe of diameter 0.1m with a average velocity of 0.6m/s. Calculate the loss of pressure in a length of 120m.Solution :The average velocity V for a cross section is found by summing up all the velocities over the cross section and dividing by the cross-sectional area1From velocity profile equation for laminar flow2 substituting equation 2 for u into equation 1 and integrating3 rearranging equation 3 gives ⎰⎰==R R rdr u R udA A V 020211ππ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--=22014R r R L p p u L μ2032D L p p V L μ-=1.8. In a vertical pipe carrying water, pressure gauges areinserted at points A and B where the pipe diameters are0.15m and 0.075m respectively. The point B is 2.5m belowA and when the flow rate down the pipe is 0.02 m 3/s, thepressure at B is 14715 N/m 2 greater than that at A.Assuming the losses in the pipe between A and B can beexpressed as g V k 22where V is the velocity at A, find the value of k . If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres.Solution:d A =0.15m; d B =0.075mz A -z B =l =2.5mQ =0.02 m 3/s,p B -p A =14715 N/m 2s m d QV V d Q A A AA /132.115.0785.002.044222=⨯===ππs m d QV V d Q B B BB /529.4075.0785.002.044222=⨯===ππWhen the fluid flows down, writing mechanical balance equation222222A B B B A A A V k V g z p V g z p +++=++ρρ 213.1253.4100014715213.181.95.2222k ++=+⨯ Figure for problem 1.8 232d V L p μ=∆Pa d VL p 115201.01206.005.0323222=⨯⨯⨯==∆μk 638.0260.10715.14638.0525.24++=+=k 0.295making the static equilibriumgR g x g l p g R g x p Hg A B ρρρρρ+∆++=+∆+()()mm g g l p p R g H A B 7981.91260081.910005.214715-=⨯⨯⨯-=---=ρρρ1.9.The liquid vertically flows down through the tube from thestation a to the station b , then horizontally through the tube fromthe station c to the station d , as shown in figure. Two segments ofthe tube, both ab and cd ,have the same length, the diameter androughness.Find:(1)the expressions of g p ab ρ∆, h fab , g p cd ρ∆ and h fcd , respectively. (2)the relationship between readings R 1and R 2 in the U tube.Solution:(1) From Fanning equationandsoFluid flows from station a to station b , mechanical energy conservation giveshence2from station c to station dFigure for problem 1.922V d l h fab λ=22V d l h fcd λ=fcdfab h h =fab b a h p p +=+ρρlg fab b a h p p =+-lg ρfcd d c h p p +=ρρhence3From static equationp a -p b =R 1(ρˊ-ρ)g -l ρg 4p c -p d =R 2(ρˊ-ρ)g 5Substituting equation 4 in equation 2 ,thentherefore6Substituting equation 5 in equation 3 ,then7ThusR 1=R 21.10 Water passes through a pipe of diameter d i=0.004 m with the average velocity 0.4 m/s, as shown in Figure.1) What is the pressure drop –∆P when water flows through the pipe length L =2 m, in m H 2O column?2) Find the maximum velocity and point r at which it occurs.3) Find the point r at which the average velocityequals the local velocity. 4)if kerosene flows through this pipe ,how do thevariables above change ?(the viscosity and density of Water are 0.001 Pasand 1000 kg/m 3,respectively ;and the viscosityand density of kerosene are 0.003 Pas and 800kg/m 3,respectively )solution:1)1600001.01000004.04.0Re =⨯⨯==μρud fcd d c h p p =-ρfab h g l g R =+--'lg 1ρρρρ)(g R h fab ρρρ-'=1g R h fcd ρρρ-'=2Figure for problem 1.10from Hagen-Poiseuille equation1600004.0001.024.0323222=⨯⨯⨯==∆d uL P μ m g p h 163.081.910001600=⨯=∆=ρ 2)maximum velocity occurs at the center of pipe, from equation 1.4-19max 0.5V u = so u max =0.4×2=0.8m3)when u=V=0.4m/s Eq. 1.4-172max 1⎪⎪⎭⎫ ⎝⎛-=wr r u u 5.0004.01max2=⎪⎭⎫ ⎝⎛-u V r = m r 00284.071.0004.05.0004.0=⨯== 4) kerosene:427003.0800004.04.0Re =⨯⨯==μρud Pa p p 4800001.0003.01600=='∆='∆μμ m g p h 611.081.98004800=⨯=''∆='ρ1.12 As shown in the figure, the water level in the reservoir keeps constant. A steel drainpipe (with the inside diameter of 100mm) is connected to the bottom of the reservoir. One arm of the U-tube manometer is connected to the drainpipe at the position 15m away from the bottom of the reservoir, and the other is opened to the air, the U tube is filled with mercury and the left-side arm of the U tube above the mercury is filled with water. The distance between the upstream tap and the outlet of the pipeline is 20m.a) When the gate valve is closed, R=600mm, h=1500mm; when the gate valve is opened partly, R=400mm, h=1400mm. The friction coefficient λ is 0.025, and the loss coefficient of the entranceis 0.5. Calculate the flow rate of water when the gate valve is opened partly. (in m³/h)b) When the gate valve is widely open, calculate the static pressure at the tap (in gauge pressure, N/m²). l e /d ≈15 when the gate valve is widely open, and the friction coefficient λ is still 0.025.Solution :(1) When the gate valve is opened partially, the water discharge isSet up Bernoulli equation between the surface of reservoir 1—1’ and the section of pressure point 2—2’,and take the center of section 2—2’ as the referring plane, then ∑+++=++21,2222121122—f h p u gZ p u gZ ρρ (a ) In the equation 01=p (the gauge pressure)222/396304.181.910004.081.913600m N gh gR p O H Hg =⨯⨯-⨯⨯=-=ρρ0021=≈Z uWhen the gate valve is fully closed, the height of water level in the reservoir can be related to h (the distance between the center of pipe and the meniscus of left arm of U tube).gR h Z g Hg O H ρρ=+)(12 (b )where h=1.5mR=0.6mSubstitute the known variables into equation b 2222_1,113.22)5.01.015025.0(2)(66.65.110006.013600V V V K d l h m Z c f =+⨯=+==-⨯=∑λ Substitute the known variables equation a9.81×6.66=2213.21000396302V V ++ the velocity is V =3.13m/s Figure for problem 1.12the flow rate of water is h m V d V h /5.8813.312.0436004360032=⨯⨯⨯=⨯=ππ2) the pressure of the point where pressure is measured when the gate valve is wide-open. Write mechanical energy balance equation between the stations 1—1’ and 3-3´,then∑+++=++31,3233121122—f h p V gZ p V gZ ρρ (c ) since m Z 66.61=311300p p u Z =≈=2223_1,81.4 2]5.0)151.035(025.0[ 2)(V V V K d l l h c e f =++=++=∑λ input the above data into equation c ,9.8122V 81.4266.6+=⨯V the velocity is: V =3.51 m/sWrite mechanical energy balance equation between thestations 1—1’ and 2——2’, for the same situation of water level ∑+++=++21,2222121122—f h p V gZ p V gZ ρρ (d )since m Z 66.61=212103.51/0(page pressure Z u u m s p =≈≈=)kg J V K d l hc f /2.26251.3)5.01.015025.0(2)(222_1,=+⨯=+=∑λ input the above data into equationd , 9.81×6.66=2.261000251.322++pthe pressure is: 329702=p1.14 Water at 20℃ passes through a steel pipe with an inside diameter of 300mm and 2m long. There is a attached-pipe (Φ60⨯3.5mm) which is parallel with the main pipe. The total length including the equivalent length of all form losses of the attached-pipe is 10m. A rotameter is installed in the branch pipe. When the reading of the rotameter is2.72m 3/h, try to calculate the flow rate in the main pipe and the total flow rate, respectively. The frictional coefficient of the main pipe and the attached-pipe is 0.018 and 0.03, respectively.Solution : The variables of main pipe are denoted by a subscript 1, and branch pipe by subscript 2.The friction loss for parallel pipelines is2121S S s f f V V V h h +==∑∑The energy loss in the branch pipe is 22222222u d l l h e f ∑∑+=λ In the equation 03.02=λs m u d ml l e /343.0053.04360072.2053.01022222=⨯⨯===+∑πinput the data into equation ckg J h f /333.02343.0053.01003.022=⨯⨯=∑The energy loss in the main pipe is 333.022111121===∑∑u d l h h f f λ So s m u /36.22018.023.0333.01=⨯⨯⨯= The water discharge of main pipe is h m V h /60136.23.043600321=⨯⨯⨯=π Total water discharge ish m V h /7.60372.26013≈+=1.16 A Venturimeter is used for measuring flow of water along a pipe. The diameter of the Venturi throat is two fifths the diameter of the pipe. The inlet and throat are connected by water filled tubes to a mercury U-tube manometer. The velocity of flow along the pipe is found to be R 5.2 m/s, where R is the manometer reading in metres of mercury. Determine the loss of head between inlet and throat of the Venturi when R is 0.49m. (Relative density of mercury is 13.6). Solution: Writing mechanical energy balance equation between the inlet 1 and throat o for Venturi meterf o o hg z V p g z V p +++=++22121122ρρ 1 rearranging the equation above, and set (z 2-z 1)=xf o oh xg V V p p ++-=-22121ρ 2 from continuity equation 11221125.625V V d d V V o o =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛= 3 substituting equation 3 for V o into equation 2 gives()f f f f oh xg R h xg R h V h xg V V p p ++=++=+=++-=-94.1185.203.1903.19206.3922121211ρ 4from the hydrostatic equilibrium for manometerg x g R p p Hg o ρρρ+-=-)(1 5substituting equation 5 for pressure difference into equation 4 obtainsf Hgh xg R gx g R ++=+-94.118)(ρρρρ 6 rearranging equation 6 kg J R R R R g R h Hg f /288.267.494.11861.12394.118)(==-=--=ρρρFigure for problem 1.161.17.Sulphuric acid of specific gravity 1.3 is flowing through a pipe of 50 mm internal diameter. A thin-lipped orifice, 10mm, is fitted in the pipe and the differential pressure shown by a mercury manometer is 10cm. Assuming that the leads to the manometer are filled with the acid,calculate (a)the weight of acid flowing per second, and (b) the approximate friction loss in pressure caused by the orifice.The coefficient of the orifice may be taken as 0.61, the specific gravity of mercury as 13.6, and the density of water as 1000 kg/m 3Solution: a)2.0501010==D D =⨯-=-=-81.9)130013600(1.0)(21g R p p Hg ρρ12066.3pas kg V D m /268.0130063.201.0442220=⨯⨯⨯==πρπb) approximate pressure drop=⨯-=-=-81.9)130013600(1.0)(21g R p p Hg ρρ12066.3Pa pressure difference due to increase of velocity in passing through the orificePa D D V V V V p p o 8.44882)2.01(63.213002242412222212221=-=⎪⎪⎭⎫ ⎝⎛-=-=-ρρ pressure drop caused by friction lossPa p f 5.75778.44883.12066=-=∆2.1 Water is used to test for the performances of pump. The gauge pressure at the discharge connection is 152 kPa and the reading of vacuum gauge at the suction connection of the pump is 24.7 kPa as the flow rate is 26m 3/h. The shaft power is 2.45kw while the centrifugal pump operates at the speed of 2900r/min. If the vertical distance between the suction connection and discharge connection is 0.4m, the diameters of both the suction and discharge line are the same. Calculate the mechanical efficiency of pump and list the performance of the pump under this operating condition. ()s m p p D D C V o /63.231.461.056.1861.0130081.9)130013600(1.022.0161.021*******=⨯=≈⨯-⨯-=-⎪⎪⎭⎫ ⎝⎛-=ρSolution:Write the mechanical energy balance equation between the suction connection and discharge connection 2_1,2222121122f H gp g u Z H g p g u Z +++=+++ρρ wherem Z Z 4.012=-(Pa 1052.1(Pa 1047.22_1,215241≈=⨯=⨯-=f H u u pressure gauge p pressure gauge p ))total heads of pump is m H 41.1881.9100010247.01052.14.055=⨯⨯+⨯+= efficiency of pump is N N e /=ηsince kW g QH N e 3.1360081.9100041.18263600=⨯⨯⨯==ρ N=2.45kWThen mechanical efficiency %1.53%10045.23.1=⨯=η The performance of pump is Flow rate ,m³/h26 Total heads ,m18.41 Shaft power ,kW2.45 Efficiency ,%53.12.2 Water is transported by apump from reactor, which has200 mm Hg vacuum, to thetank, in which the gaugepressure is 0.5 kgf/cm 2, asshown in Fig. The totalequivalent length of pipe is200 m including all localfrictional loss. The pipeline isφ57×3.5 mm , the orificecoefficient of C o and orificediameter d o are 0.62 and 25mm, respectively. Frictionalcoefficient λ is 0.025. Calculate: Developed head H of pump, in m (the reading R of U pressure gauge in orifice meter is 168 mm Hg)Solution:Equation(1.6-9)Mass flow rates kg S V m o o /02.21000025.0414.312.42=⨯⨯⨯==ρ 2) Fluid flow through the pipe from the reactor to tank, the Bernoulli equation is as follows for V 1=V 2f H z gp p H +∆+-=ρ12 ∆z=10mPa p 7570710013.17602001081.95.054=⨯⨯+⨯⨯=∆ ∆p/ρg=7.7mThe relation between the hole velocity and velocity of pipeFriction losssoH=7.7+10+5.1=22.8m2.3 . A centrifugal pump is to be used to extract water from a condenser in which the vacuum is 640 mm of mercury, as shown in figure. At the rated discharge, the netpositive suction head must be at least 3m above the cavitation vaporpressure of 710mm mercury vacuum. If losses in the suction pipeaccounted for a head of 1.5m. What must be the least height of the liquid level in the condenser above the pump inlet?Solution :From an energy balance,s m Rg D d C V f /12.444.69375.062.01000)100013600(81.9168.025025162.02144000=⨯=-⨯⨯⎪⎭⎫ ⎝⎛-=-⎪⎭⎫ ⎝⎛-=ρρρ)(s m D d V V /12112.42200=⎪⎭⎫ ⎝⎛⨯=⎪⎭⎫ ⎝⎛=m g u d l f H f 1.581.92105.0200025.02422=⨯⨯==NPSH H gp p H f v o g ---=ρWhereP o =760-640=120mmHgP v =760-710=50mmHgUse of the equation will give the minimum height H g as2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half, what will the new flowrate be ?• Density of acid 1840kg/m 3• Viscosity of acid 25×10-3 PasSolution: Velocity of acid in the pipe:s m d m d mpipe of area tional cross flowrate volumetric u /32.3025.01840785.03785.04sec 222=⨯⨯===-=ρπρReynolds number:6109102532.31840025.0Re 3=⨯⨯⨯==-μρud from Fig.1.22 for a smooth pipe when Re=6109, f=0.0085 pressure drop is calculated from equation 1.4-9kg J u d l f ph f /450232.3025.0600085.042422=⨯==∆=ρ kPa p 5.8271840450=⨯=∆ or friction factor is calculated from equation1.4-25kg J u d l u d l f ph f /426232.3025.0606109046.042Re 046.042422.022.02=⨯⨯⨯==∆=--=ρkPa p 84.7831840426=⨯=∆ if the pressure drop falls to 783.84/2=391.92kPam NPSH H g p p H f v o g 55.335.181.9100081.913600)05.012.0-=--⨯⨯⨯-=---=(ρ8.18.12.12.038.12.12.022.0012.089.1079`2025.060102518401840046.042046.042Re 046.043919202u u u d l u d l p p =⎪⎭⎫ ⎝⎛⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯==∆='∆----ρμρρ= so s m u /27.236.489..1079012.03919208.18.1==⨯= new mass flowrate=0.785d 2u ρ=0.785×0.0252×2.27×1840=2.05kg/s2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half on assumption that the change of friction factor is negligible, what will the new flowrate be ?Density of acid 1840kg/m 3Viscosity of acid 25×10-3 Pa Friction factor 32.0Re500.00056.0+=f for hydraulically smooth pipe Solution: Write energy balance equation:f hg u z g p H g u z g p +++=+++2222222111ρρ gu d l g p h H f 22λρ=∆== 342=ρπu ds m d u /32.31840025.014.3124322=⨯⨯=⨯=ρπ 611510251840025.032.3Re 3=⨯⨯⨯=- 0087.061155.00056.0Re 500.00056.032.032.0=+=+=f 92.4681.9232.3025.0600087.04222=⨯⨯==∆==g u d l g p h H f λρ Δp=46.92×1840×9.81=847.0kpa2.6 The fluid is pumped through the horizontal pipe from section A to B with the φ38⨯2.5mm diameter and length of 30 meters, shown as figure. The orifice meter of 16.4mm diameter is used to measure the flow rate. Orifice coefficient C o =0.63. the permanent loss in pressure is3.5×104N/m 2, the friction coefficient λ=0.024. find:(1) What is the pressure drop along the pipe AB?(2)What is the ratio of power obliterated in pipe AB to total power supplied to the fluid when the shaft work is 500W, 60%efficiency? (The density of fluid is 870kg/m 3 )solution :∑+++=+++f A A A A AA h u p g z w u p g z 2222ρρ ρλρ022p u d l h p p f BA ∆+==-∑ 247.0334.162=⎪⎭⎫ ⎝⎛=A A o ()()s m gR C u /5.8870870136006.081.9297.063.02247.01200=-⨯⨯=''--=ρρρ ∴u = (16.4/33)2×8.5=2.1m/s∴242/76855105.321.2033.030870024.0m N h p p f B A =⨯+⨯==-∑ρ (2)W u d p Wm 1381.2033.0785.0768554Ne 22=⨯⨯⨯=∆==ρπρ sothe ratio of power obliterated in friction losses in AB to total power supplied to the fluid %%=461006.0500138⨯⨯。
流体力学与传热作业-(含答案)
1、当地大气压为745mmHg 测得一容器内的绝对压强为350mmHg ,则真空度为 mmHg 。
测得另一容器内的表压强为1360 mmHg ,则其绝对压强为 mmHg 。
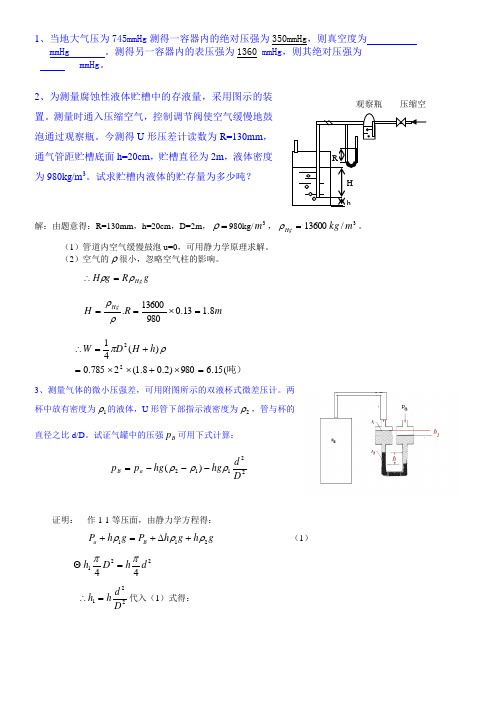
2、为测量腐蚀性液体贮槽中的存液量,采用图示的装置。
测量时通入压缩空气,控制调节阀使空气缓慢地鼓泡通过观察瓶。
今测得U 形压差计读数为R=130mm ,通气管距贮槽底面h=20cm ,贮槽直径为2m ,液体密度为980kg/m 3。
试求贮槽内液体的贮存量为多少吨?解:由题意得:R=130mm ,h=20cm ,D=2m ,=ρ980kg/3m ,=Hg ρ3/13600m kg 。
(1)管道内空气缓慢鼓泡u=0,可用静力学原理求解。
(2)空气的ρ很小,忽略空气柱的影响。
g R g H Hg ρρ=∴ m R H Hg 8.113.098013600.=⨯==ρρ 吨)(15.6980)2.08.1(2785.0)(4122=⨯+⨯⨯=+=∴ρπh H D W 3、测量气体的微小压强差,可用附图所示的双液杯式微差压计。
两杯中放有密度为1ρ的液体,U 形管下部指示液密度为2ρ,管与杯的直径之比d/D 。
试证气罐中的压强B p 可用下式计算:22112)(Dd hg hg p p a B ρρρ---=证明: 作1-1等压面,由静力学方程得:g h g h P g h P B a 211ρρρ+∆+=+ (1) 22144d hD h ππ=221Dd h h =∴代入(1)式得:g h g D d h P g h P B a 21221ρρρ++=+即22112)(Dd hg g hg P P a B ρρρ---=3、查阅资料,写出比重计(密度计)的设计原理4、本题附图所示的开口容器内盛有油和水。
油层高度h 1=0.7m 、密度ρ1=800kg/m 3,水层高度h 2=0.6m 、密度ρ2=1000kg/m 3。
(1)判断下列两关系是否成立,即 p A =p'A p B =p'B(2)计算水在玻璃管内的高度h 。
流体力学与热传递在工程设计中的应用考核试卷

1.流体在圆形管道中做层流运动时,流速分布呈_______状。
()
2.热对流的基本方程是_______方程。
()
3.在热辐射中,黑体的辐射强度与温度的_______成正比。
()
4.流体的粘度与温度的关系是_______。
()
D.流体粘性很小,雷诺数小于2000
4.在热传递中,热对流的主要影响因素是:()
A.流体的热导率
B.流体的速度
C.流体的比热容
D.流体与固体表面的温差
5.对于热辐射,以下哪种说法是正确的:()
A.热辐射不需要介质就可以传播
B.热辐射的强度与物体温度成反比
C.热辐射在真空中不能传播
D.热辐射的强度只与物体颜色有关
A.热边界层是温度梯度的过渡层
B.热边界层厚度随流体速度增加而减小
C.热边界层厚度与流体的热导率有关
D.热边界层厚度与流体与固体表面的温差有关
20.在流体力学中,以下哪些方程用于描述流体的运动:()
A.纳维-斯托克斯方程
B.连续性方程
C.能量方程
D.动量方程
(以上为多选题部分,以下是其他题型,请根据需要自行补充)
4.热对流是依靠流体的宏观运动进行热量传递的。()
5.热辐射的强度与物体的表面积成正比。()
6.在热交换器中,增加流体流速会降低传热效率。()
7.热力学第二定律表明,热能总是自发地从高温物体传递到低温物体。()
8.湍流流动的流线是平行的,层流流动的流线是弯曲的。()
9.热边界层的厚度与流体的热导率成反比。()
四、判断题
1. ×
2. √
流体力学与传热习题参考解答(英文).

1. Water is pumped at a constant velocity 1m/s from large reservoir resting on the floor to the open top of an absorption tower. The point of discharge is 4 meter above the floor, and the friction losses from the reservoir to the tower amount to 30 J/kg. At what height in the reservoir must the water level be kept if the pump can develop only60 J/kg?2222112f 1U P U P w=Z g+h (Z g+)22ρρ++-+ U 1=0 12P =P 10Z = W=60j/kg f h 30/kg =2U =1m/s 2(60300.5)/g 3m Z =--=21Z Z Z 431m ∆=-=-=2. The fluid (density 1200 kg/m 3 ) is pumped at a constant rate 20 m 3 /h from the large reservoir to the evaporator. The pressure above the reservoir maintains atmosphere pressure and the pressure of the evaporator keeps 200 mmHg (vacuum). The distance between the level of liquid in the reservoir and the exit of evaporator is 15 meter and frictional loss in the pipe is 120 J/kg not including the exit of evaporator, what is the pump effective work and power if the diameter of pipe is 60 mm?22112212f U U Z g+W Z g+h 22ρρP P ++=++ 10P = 5422200P x1.013x10 2.67x10N /m 760=-=- 31200Kg /m ρ= 1U 0= f h 120J /kg =22V 20U 1.97m /s A 3600*4006===π/*. 1Z 0= 2Z 15= 422.67x101.97W 15x9.81120246.88J /kg 12002=-+++= N W Q 246.88x1200x20/3600=1646W ρ==3. Water comes out of the pipe (Φ108x4 mm), as shown in Fig. The friction loss of the pipeline which does not cover the loss at the exit of pipe can be calculated by the following equation:h f =6.5U 2where U is the velocity in the pipe, finda. water velocity at section A-A'.b. water flow rate, in m 3 /h.22112212f U U Z g+Z g+h 22ρρP P +=++ 1U 0= 12P =P 1Z 6m = 2Z 0=2f h 6.5U = 22U 6x9.81 6.5U 2=+ U 2.9m/s = 23V=UA=2.94x01x360082m /h =π/.4. Water passes through the variable pipe. The velocity in the small pipe is 2.5 m/s. The vertical glass tubes are inserted respectively at the section A and B to measure the pressure (see fig.) If the friction loss between two section is 15 J/kg, what is the water column difference between two glass tubes? By the way, draw the relative liquid column height of two tubes in the Fig.a ab b U A U A = 2b U 2.5*(33/47)1.23m /s == 22a a b b a b f U U Z g+Z g+h 22ρρP P +=++ a b Z =Z 22a b b a f U U h 22ρρP P -=-+221.23/2 2.5/21512.63=-+= a b P P R g ρ-=∆ 3312.63R=1.29x10m 9.8x10-∆=5. A centrifugal pump takes brine (density 1180 kg/m 3 , viscosity 1.2 cp) from the bottom of a supply tankand delivers it into another tank. The line between the tanks is 300 m of 25 mm diameter pipe (inner diameter). The flow rate is 2 m 3 /h. In this line, there are two gate valves, four elbows (90o ) and one return bend, what is the friction loss if the roughness of pipe is 0.025 mm?22f fst flocal U U h h h 4f k d 22l ∑=+=+∑ 31180kg /m ρ= 300m, d=0.025m l =3-3v 2m /h =1.2cp=1.2x10Pa.s μ=k=0.025mm k/d=0.025/25=0.001c l r k =0.4 k =1 k =2x0.07=0.14el re k 4x0.75 3 k 1.5-2.2===2u v /A 2/(3600x /4x0.025)1.13m /s π===4u d Re 2.78x10ρμ== f 0.063= 2f 2h 4x0.0063x300/0.025x1.13/2+(0.4+1+2x0.07+4x0.7+1.5)x1.13/2 =197.86J/kg∑=6. The orifice meter (diameter of orifice 0.0001 m) is installed for measuring the flow rate. The indicating liquid of orifice is mercury if U shape pressure gauge reading is 0.6 meter and orifice coefficient can be takenas 0.61, what is the flow rate of water?o u c =20o 0V u s 0.61x /4x0.0001π==835.8x10m /s -=7. Water flows through a pipe with a diameter di 100 mm as shown in figure.a. when the valve is closed, R is 600 mm and h equals 1500 mm. While the valve opens partially, R=400 mm and h=1400 mm, f=0.00625 (Finning factor) and k c =0.5 (contraction coefficient), what is the flow rate of water, in m 3 /h?b. If the valve opens fully, what is the pressure of section 2-2', in N/m 2 ? The equivalent length of the valve is1.5 m and the Fanning factor f keeps the same?(ρH2O =1000kg/m 3, ρHg =13600kg/m 3)(1) the valve opens partially ,for selection 1-1’ and 2-2’ , we have 22112212f 1-2u u gZ gZ h 22ρρP P ++=+++ 2212Hg H o 0 g(R h)39630N/m ρρP =P =-= 2212f1-2c u u u 0 Z =0 h 4f +k 2.13u d 22===l We can get Z1 from the valve closed21Hg H O h=1.5m R=0.6m Z gR/h 6.66m ρρ=-=229.81x6.66u /2 2.13u 39630/1000=++23h u=3.13m/s V 3600x /4x0.1x3.1388.5m /h π==(2) when the valve opens fully, for section 1-1’ and 3-3’, we have 22331113f1-3u u gZ gZ h 22ρρP P ++=+++ 311Z 0 Z 6.66m u =0== 22e f1-3c u 3.1.5h (4f k )(4x0.00625x +0.5) 4.81u d 20.01l l ++=+== 229.81x6.66u /2 4.81u =+ u 3.51m/s =For section 1-1’ and 2-2’22112212f1-2u u gZ gZ h 22ρρP P ++=+++ 112120 Z 6.66 Z 0 u 0 u 3.51P ===== 22f1-2c l u h (4f k )(4x0.00625x15/0.10.5)3.51/226.2J /kg d 2=+=+= 22229.81x6.66 3.15/226.2N 32970mρP =++P =8. The rotameter is installed to measure the water flow rate, as shown in figure. If the total length including equivalent length of pipeline A is 10 m and the reading of rotameter is 2.72 m 3 /h, what is the flow rate for pipeline B? (f A =0.0075, f B =0.0045)For parallel pipe line fA fB total A B22A fA A 2A h h V V +V u (l+le) 2.72h 4f 4x0.0075x10/0.053/2()d 23600x /4x0.053π∑=∑=∑∑== 0.333J /kg = 22B fB B B B 23B B B B u (l+le)h 4f 4x0.0045x2/0.3/2xu 0.333d 2u 2.36m /s V =u A 2.36x /4x0.23600m /h π∑∑======10. A flat furnace wall is constructed of 120 mm layer of sil-o-cel brick, with a thermal conductivity 0.08 w/(m o C), backed by a 150 mm of common brick, of conductivity 0.8 w/(m o C), the temperature of inner face of the wall is 1400 o , and that of the outer face is 200o C.a. What is the heat loss through the wall in w per square meter.b. To reduce the heat loss to 600 w/m 2 by adding a layer of cork with k 0.2 w/(m o C) on the outside of common brick, how many meters of cork are requied? a. 2Q t 1400200711N /m 11L R 0.080.80.120.15∑∆-===∑+ b. 600=(1400-200)/(0.12/0.08+0.15/0.8+x/0.2)x=0.0625m13. Air at the normal pressure passes through the pipe (d i 20 mm) and is heated from 20o C to 100o C. What is the film heat transfer coefficient between the air and pipe wall if the average velocity of air is 10 m/s? The properties of air at 60 o C are as follows:density 1.06 kg/m 3 , viscosity 0.02 cp, conductivity 0.0289 w/(m o C), and heat capacity 1 kJ/kg-K443u d 10x0.02x1.06 Re=1.06x10100.02x10ρμ-==>12T +T 20100T=6022+==℃ 0.141ωμμ⎛⎫= ⎪⎝⎭10000.020.0010.6920.0289p c x x k μ==Pr= ()()0.81/3081/34Nu 0027Re Pr 0.027x 1.06x10x 0.69239.66==.=. ()2i i i h d 39.66 h 39.66x0.0289/0.02=57.22w/m .k k ==14. A hot fluid with a mass flow rate 2250 kg/h passes through a ∅25x2.5 mm tube. The physical properties of fluid are as follows:k=0.5 w/(m o C), C p =4 kJ/kg-K, viscosity 10-3 N-s/m 2 , density 1000 kg/m 3 Find:a. Heat transfer film coefficient h i , in w/(m 2 -K).b. If the flow rate decreases to 1125 kg/h and other conditions are the same, what is the h i ?c. If the diameter of tube (inside diameter) decreases to 10 mm, and the velocity u keeps the same as that of case a, calculate h i .d. When the average temperature of fluid and quantity of heat flow per meter of tube are 40 o C and 400 w/m, respectively, what is the average temperature of pipe wall for case a?e. From this problem, in order to increase the heat transfer film coefficient and enhance heat transfer, what kinds of methods can you use and which is better, explain?Hint: for laminar flow, Nu=1.86[Re Pr]1/3for turbulent flow Nu=0.023Re 0.8 Pr 1/3 (1) 444N 2250x4u d Gd d 3600x x0.02Re 3.98x10100.001ρππμμμ=====> ()()1/30.8081/3424Nu 0023Re Pr 0.023x 3.98x10220.10.5Nuk 220.1x0.5hi 5500w /m k d 0.02⎛⎫== ⎪⎝⎭===.=. (2) 12w 2w = 4421Re Re /2=2x1010=> 0.80.82211Nu Re 0.5Nu Re ⎛⎫== ⎪⎝⎭ 0.8i2i1h 0.5h = ()0.82i2h 5500x0.53159w /m k == (3) 44333u d 2000x0.01Re 2x10100.001ρμ===> 0.81/3Nu 0.023Re Pr = ()2hi=6347w/m k(4)i i w w Q=h A (t-t )=400=500x2x0.02(t-t )πw t=40t 39.41=℃ ℃(5) there methods : increase u or hi or decrease dThe first is better15. In a double pipe exchange (Φ23x2 mm), the cold fluid (Cp=1 kJ/kg, flow rate 500 kg/h) passes throughthe pipe and the hot fluid goes through the outside. The inlet and outlet temperatures of cold fluid are 20 and 80 o , and the inlet and outlet temperatures of hot fluid are 150 and 90o , respectively. The h i (film coefficient inside pipe) is 700 w/(m 2 o C)and overall heat transfer coefficient U o (based on the outside surface of pipe) is 300w/(m 2 o C), respectively. If the heat loss is ignored and the conductivity of pipe wall (steel) is taken as 45 w/(m o C), find:(1) heat transfer film coefficient outside the pipe h o ?(2) the pipe length required for counter flow, in m?(3) what is the pipe length required if the heating medium changes to saturated vapor(140 o C) and it condenses to saturated liquid and other conditions keep unchanged?(4) When the exchanger is used for a year, it is found that it cannot meet the need of production (the outlet temperature of cold fluid cannot reach 80 o C), explain why? (a) 0m o 0i i m d l d 111230.002x23h Vo h d kd 300700x1945x21⎛⎫=-+=-- ⎪⎝⎭ 1/h0=1/U0-(do/hidi+bdo/kdm)=1/300-23/700*19-0.002*23/45*21()20h 642.9w/m k =12t +t LMTD=702∆∆℃= Q=UoAo ∆Tm=mcCp(Tcb-Tca) 300*2π*0.023*70L=500/3600*1000*(80-20)L=5.4m(c) 8020LMTD=86.514020ln 14080-=--℃ 1122L t 70/86.5L t ∆==∆ 2L 0.81L1 4.4m == (d) scale is formed on the outside ,V 0 is decreased16. Water flows turbulently in the pipe of Φ25x2.5 mm shell tube exchanger. When the velocity of water u is 1 m/s, overall heat transfer coefficient Uo (based on the outer surface area of pipe) is 2115 w/(m 2 o C). If the u becomes 1.5 m/s and other conditions keep unchanged, Uo is 2660 w/( m 2 o C ). What is the film coefficient ho outside the pipe? (Heat resistances of pipe wall and scale are ignored)o i h h Uo 111+= (1) oi o h h U 1'1'1+= (2) (1)-(2)= 0.80.80.80.81211111121152660u C u C 1C 1.5C-=-=- C=2859 io h Uo h 111-= ho=8127W/(m2K)17. Water and oil pass parallelly through an exchanger which is 1 m long. The inlet and outlet temperatures of water are 15 and 40 o C, and those of oil are 150 and 100 o C, respectively. If the outlet temperature of oil decreases to 80 o C, and the flow rates and physical properties and inlet temperatures of water and oil maintain the same, what is the pipe length of new exchanger? (Heat loss and pipe wall resistance are neglected) ()()h h 12c c 21m Q W C T -T W C t t VA t ==-=∆()()h h 12c c 21W C T -T 'W C t 't =-2150100401515080t 15--=-- 2t 50=℃ 212m1112m2L T T 't 1508092.51.85L T T t 15010069.8-∆-===-∆- 2m1m2L 1.85m L1=1m t 92.5 t 69.8=∆=∆=18. Air which passes through the pipe in turbulent flow is heated from 20 to 80 o C. The saturated vapor at 116.3 o C condenses to saturated water outside the pipe. If air flow rate increases to 120% of the origin and inlet and outlet temperatures of air stay constant, what kind of method can you employ in order to do that? (Heat resistance of pipe wall and scale can be ignored))(111ca cb pc c m i i T T C m T A h -=∆=1Q)'(2212ca cb pc c m i T T C m T A h -=∆=2Q 128.012112i22.12.1h m m c c m i m T T m m T h T ∆∆===∆∆ )803.116/()203.116ln(20801---=∆m T )80/()20ln(20802---=∆h h m T T T Th=118.5oC19. Water flows through the pipe of a Φ25x2.5 mm shell-tube exchanger from 20 to 50 o C. The hot fluid (C p1.9 kJ/kg o C, flow rate 1.25 kg/s) goes along the shell and the temperatures change from 80 to 30 o C. Film coefficients of water and hot fluid are 0.85kw/(m 2 o C) and 1.7 kw/(m 2 o C). What is the overall heat transfer coefficient Uo and heat transfer area if the scale resistance can be ignored? (the conductivity of steel is 45w/(m o C).W=1.25Kg/s Cp=1.9Kj/kg ℃()()2h p 12Q W C T T 1.25x1.9x 80-30119Kw =-==m 3010t 30ln 10-∆= ()200m 00i i m 1V 472w/m k d l d 1h h d kd ++==32i 0m Q 119x10A 13.9m V t 472x18.2===∆20. A spherical particle (density 2650 kg/m 3) settles freely in air at 20 o C (density of air 1.205 kg/m 3 , viscosity 1x10-5 Pa.s). Calculate the maximum diameter of particle if the settle obeys the Stoke s’ Law?Re ≤1 ()2p t p D g U 18D ρρμμρP -== ()23p 18D g μρρρP =- ()1/3-10p 18x10D 1.205x9.81x 2650-1.205⎛⎫= ⎪ ⎪⎝⎭=3.85x10-521. A filter press(A=0.1 m 2 ) is used for filtering slurry. The vacuum inside the filter is 500 mm Hg. One liter filtrate can be got after filtering of 5 min and 0.6 more liter filtrate is obtained after 5 more min. How much filtrate will be got after filtering of 5 more min?for filter press 22e V 2VV =KA θ+5 min 22e 12V 0.1x5K +=(1)10min 22e 1.62x1.6V 0.1x10K +=(2)From (1) (2),we can see Ve=0.7 K=4815 min 22V 2x0.7V=48x0.1x15+ V=2.07m 3/h22. The following data are obtained for a filter press (A=0.0093 m 2) in a lab.------------------------------------------------------------------------------------------------pressure difference (kg f /cm 2 ) filtering time (s) filtrate volume (m 3 )1.05 502.27⨯10-3660 9.10⨯10-33.50 17.1 2.27⨯10-3233 9.10⨯10-3Find1) filtering constant K, q e , t e at pressure difference 1.05 kg f /cm 2 ?2) if the frame of filter is filled with the cake at 660 s, what is the end filtering rate (dV/dt)E at P 1.05 kg f /cm 2 ?3) compressible constant of cake s?For p=1.05Kg/cm 22e 2e 2e q 2qq K 0.002270.0002272x q 50K 0.00930.000930.000910.000912x q 660K 0.000930.00093θ+=⎛⎫+= ⎪⎝⎭⎛⎫+= ⎪⎝⎭We can see K=0.015 qe=0.026For p=3.5Kg/cm 21-s K=2k ∆P 1-s K'=2k '∆P 1s K 'K '-∆P ⎛⎫= ⎪∆P ⎝⎭ ()2E e V KA 2V+V d d θ⎛⎫= ⎪⎝⎭23. A slurry is filtered by a 0.1 m 2 filter press at constant pressure if the cake is incompressible. The filter basic equation is as follows:(q+10)2 = 250(t+ 0.4)where q---l/m 2 t----minfind (1) how much filtrate is got after 249.6 min?(2) if the pressure difference is double and the resistance of cake is constant, how much filtrate can be obtained after 249.6 min? (cake is imcompressible)(1)let θ=249.6 ()()2q+10250x 249.60.4=+ q=240 V=qA=240*0.1=24(2) K 2k =∆P K'2k '=∆P'2∆P =∆P K'2K 500== ()()2q'+10500x 249.60.4=+ q ’=343.6 v=34.36。
(完整版)流体力学练习题及答案

(完整版)流体力学练习题及答案-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN流体力学练习题及答案一、单项选择题1、下列各力中,不属于表面力的是( )。
A .惯性力B .粘滞力C .压力D .表面张力2、下列关于流体粘性的说法中,不准确的说法是( )。
A .粘性是实际流体的物性之一B .构成流体粘性的因素是流体分子间的吸引力C .流体粘性具有阻碍流体流动的能力D .流体运动粘度的国际单位制单位是m 2/s3、在流体研究的欧拉法中,流体质点的加速度包括当地加速度和迁移加速度,迁移加速度反映( )。
A .由于流体质点运动改变了空间位置而引起的速度变化率B .流体速度场的不稳定性C .流体质点在流场某一固定空间位置上的速度变化率D .流体的膨胀性4、重力场中平衡流体的势函数为( )。
A .gz -=πB .gz =πC .z ρπ-=D .z ρπ=5、无旋流动是指( )流动。
A .平行B .不可压缩流体平面C .旋涡强度为零的D .流线是直线的6、流体内摩擦力的量纲[]F 是( )。
A . []1-MLtB . []21--t MLC . []11--t ML D . []2-MLt 7、已知不可压缩流体的流速场为xyj zi x 2V 2+= ,则流动属于( )。
A .三向稳定流动B .二维非稳定流动C .三维稳定流动D .二维稳定流动8、动量方程 的不适用于(??? ??) 的流场。
A .理想流体作定常流动B .粘性流体作定常流动C .不可压缩流体作定常流动D .流体作非定常流动9、不可压缩实际流体在重力场中的水平等径管道内作稳定流动时,以下陈述错误的是:沿流动方向 ( ) 。
A .流量逐渐减少B .阻力损失量与流经的长度成正比C .压强逐渐下降D .雷诺数维持不变10、串联管道系统中,其各支管内单位质量流体的能量损失( )。
A .一定不相等B .之和为单位质量流体的总能量损失C .一定相等D .相等与否取决于支管长度是否相等11、边界层的基本特征之一是( )。
流体力学与传热学考试题目

流体力学与传热学考试题目1-1 下图所示的两个U 形管压差计中,同一水平面上的两点A 、B 或C 、D 的压强是否相等?答:在图1—1所示的倒U 形管压差计顶部划出一微小空气柱。
空气柱静止不动,说明两侧的压强相等,设为P 。
由流体静力学基本方程式: 11gh gh p p A 水空气ρρ++=11gh gh p p B 空气空气ρρ++=空气水ρρ>∴BA p p >即A 、B 两点压强不等。
而 1gh p p C 空气ρ+=1gh p p D 空气ρ+=也就是说,Cp 、D p 都等于顶部的压强p 加上1h 高空气柱所引起的压强,所以C 、D 两点压强相等。
同理,左侧U 形管压差计中,B A p p ≠ 而DC p p =。
分析:等压面成立的条件—静止、等高、连通着的同一种流体。
两个U 形管压差计的A 、B 两点虽然在静止流体的同一水平面上,但终因不满足连通着的同一种流体的条件而非等压。
1-2 容器中的水静止不动。
为了测量A 、B 两水平面的压差,安装一U 形管压差计。
图示这种测量方法是否可行?为什么? 答:如图1—2,取1—1/为等压面。
由1'1p p =可知:)(2H R g p O H B ++ρ=gRH h g p Hg O H A ρρ+++)(2ghp p O H A B 2ρ+=将其代入上式,整理得 0)(2=-gR O H Hg ρρ∵2≠-OHHg ρρ ∴0=RR 等于零,即压差计无读数,所以图示这种测量方法不可行。
分析:为什么压差计的读数为零?难道A 、B 两个截面间没有压差存在吗?显然这不符合事实。
A 、B 两个截面间确有压差存在,即h 高的水柱所引起的压强。
问题出在这种测量方法上,是由于导管内充满了被测流体的缘故。
连接A 平面测压口的导管中的水在下行过程中,位能不断地转化为静压能。
此时,U 型管压差计所测得的并非单独压差,而是包括位能影响在内的“虚拟压强”之差。
流体力学与传热习题参考解答(英文)(完整资料).doc

【最新整理,下载后即可编辑】1. Water is pumped at a constant velocity 1m/s from large reservoir resting on the floor to the open top of an absorption tower. The point of discharge is 4 meter above the floor, and the friction losses from the reservoir to the tower amount to 30 J/kg. At what height in the reservoir must the water level be kept if the pump can develop only60 J/kg?2222112f 1U P U P w=Z g+h (Z g+)22ρρ++-+U 1=012P =P10Z =W=60j/kg f h 30/kg = 2U =1m/s 2(60300.5)/g 3m Z =--= 21Z Z Z 431m ∆=-=-=2. The fluid (density 1200 kg/m 3 ) is pumped at a constant rate 20 m 3 /h from the large reservoir to the evaporator. The pressure above the reservoir maintains atmosphere pressure and the pressure of the evaporator keeps 200 mmHg (vacuum). The distance between the level of liquid in the reservoir and the exit of evaporator is 15 meter and frictional loss in the pipe is 120 J/kg not including the exit of evaporator, what is the pump effective work and power if the diameter of pipe is 60 mm?22112212f U UZ g+W Z g+h 22ρρP P ++=++10P =5422200P x1.013x10 2.67x10N /m 760=-=- 31200Kg /m ρ= 1U 0= f h 120J /kg =22V 20U 1.97m /s A 3600*4006===π/*.1Z 0=2Z 15=422.67x101.97W 15x9.81120246.88J /kg 12002=-+++=N W Q 246.88x1200x20/3600=1646W ρ==3. Water comes out of the pipe (Φ108x4 mm), as shown in Fig. The friction loss of the pipeline which does not cover the loss at the exit of pipe can be calculated by the following equation: h f =6.5U 2where U is the velocity in the pipe, find a. water velocity at section A-A'. b. water flow rate, in m 3 /h.22112212f U UZ g+Z g+h 22ρρP P +=++1U 0=12P =P1Z 6m =2Z 0=2f h 6.5U=22U 6x9.81 6.5U 2=+U 2.9m/s = 23V=UA=2.94x01x360082m /h =π/.4. Water passes through the variable pipe. The velocity in the small pipe is 2.5 m/s. The vertical glass tubes are inserted respectively at the section A and B to measure thepressure (see fig.) If the friction loss between two section is 15 J/kg, what is the water column difference between two glass tubes? By the way, draw the relative liquid column height of two tubes in the Fig.a ab b U A U A =2b U 2.5*(33/47)1.23m /s ==22aa b b a b f U U Z g+Z g+h 22ρρP P +=++a b Z =Z22abb a f U U h 22ρρP P -=-+221.23/2 2.5/21512.63=-+= a b P P R g ρ-=∆ 3312.63R=1.29x10m 9.8x10-∆=5. A centrifugal pump takes brine (density 1180 kg/m 3 , viscosity 1.2 cp) from the bottom of a supply tank and delivers it into another tank. The line between the tanks is 300 m of 25 mm diameter pipe (inner diameter). The flow rate is 2 m 3 /h. In this line, there are two gate valves, four elbows (90o ) and one return bend, what is the friction loss if the roughness of pipe is 0.025 mm?22f fst flocalU U h h h 4f k d 22l ∑=+=+∑31180kg /m ρ=300m, d=0.025m l =3-3v 2m /h =1.2cp=1.2x10Pa.s μ=k=0.025mm k/d=0.025/25=0.001c l r k =0.4 k =1 k =2x0.07=0.14 el re k 4x0.75 3 k 1.5-2.2===2u v /A 2/(3600x /4x0.025)1.13m /s π===4u dRe 2.78x10ρμ==f 0.063=2f 2h 4x0.0063x300/0.025x1.13/2+(0.4+1+2x0.07+4x0.7+1.5)x1.13/2 =197.86J/kg∑=6. The orifice meter (diameter of orifice 0.0001 m) is installed for measuring the flow rate. The indicating liquid of orifice is mercury if U shape pressure gauge reading is 0.6 meter and orifice coefficient can be taken as 0.61, what is the flow rate of water?0o o2gR()u c ρρρ-=20o 02gx0.6x(136001000)V u s 0.61x /4x0.0001x1000π-==835.8x10m /s -=7. Water flows through a pipe with a diameter di 100 mm as shown in figure.a. when the valve is closed, R is 600 mm and h equals 1500 mm. While the valve opens partially, R=400 mm and h=1400 mm, f=0.00625 (Finning factor) and k c =0.5 (contraction coefficient), what is the flow rate of water, in m 3 /h?b. If the valve opens fully, what is the pressure of section 2-2', in N/m 2 ? The equivalent length of the valve is 1.5 m and the Fanning factor f keeps the same?(ρH2O =1000kg/m 3, ρHg =13600kg/m 3)(1) the valve opens partially ,for selection 1-1’ and 2-2’ , we have22112212f 1-2u u gZ gZ h 22ρρP P ++=+++2212Hg H o 0 g(R h)39630N/m ρρP =P =-=2212f1-2c u u u 0 Z =0 h 4f +k 2.13ud 22===lWe can get Z1 from the valve closed21Hg H O h=1.5m R=0.6m Z gR/h 6.66m ρρ=-=229.81x6.66u /2 2.13u 39630/1000=++23h u=3.13m/s V 3600x /4x0.1x3.1388.5m /h π==(2) when the valve opens fully, for section 1-1’ and 3-3’, we have 22331113f1-3u u gZ gZ h 22ρρP P ++=+++311Z 0 Z 6.66m u =0==22e f1-3c u 3.1.5h (4f k )(4x0.00625x +0.5) 4.81ud 20.01l l ++=+==229.81x6.66u /2 4.81u =+ u 3.51m/s =For section 1-1’ and 2-2’22112212f1-2u u gZ gZ h 22ρρP P ++=+++112120 Z 6.66 Z 0 u 0 u 3.51P =====22f1-2c l u h (4f k )(4x0.00625x15/0.10.5)3.51/226.2J /kg d 2=+=+=22229.81x6.66 3.15/226.2N 32970m ρP=++P =8. The rotameter is installed to measure the water flow rate, as shown in figure. If the total length including equivalent length of pipeline A is 10 m and the reading of rotameter is 2.72 m 3 /h, what is the flow rate for pipeline B? (f A =0.0075, f B =0.0045)For parallel pipe linefA fB total A B 22A fAA 2A h h V V +V u (l+le) 2.72h 4f 4x0.0075x10/0.053/2()d 23600x /4x0.053π∑=∑=∑∑== 0.333J /kg =22B fB B B B 23B B B B u (l+le)h 4f 4x0.0045x2/0.3/2xu 0.333d 2u 2.36m /s V =u A 2.36x /4x0.23600m /hπ∑∑======10. A flat furnace wall is constructed of 120 mm layer of sil-o-cel brick, with a thermal conductivity 0.08 w/(m o C), backed by a 150 mm of common brick, of conductivity 0.8 w/(m o C), the temperature of inner face of the wall is 1400 o , and that of the outer face is 200o C.a. What is the heat loss through the wall in w per square meter.b. To reduce the heat loss to 600 w/m 2 by adding a layer of cork with k 0.2 w/(m o C) on the outside of common brick, how many meters of cork are requied? a.2Q t 1400200711N /m 11L R 0.080.80.120.15∑∆-===∑+b. 600=(1400-200)/(0.12/0.08+0.15/0.8+x/0.2) x=0.0625m13. Air at the normal pressure passes through the pipe (d i 20 mm) and is heated from 20o C to 100o C. What is the film heat transfer coefficient between the air and pipe wall if the average velocity of air is 10 m/s? The properties of air at 60 o C are as follows:density 1.06 kg/m 3 , viscosity 0.02 cp, conductivity 0.0289 w/(m o C), and heat capacity 1 kJ/kg-K443u d10x0.02x1.06 Re=1.06x10100.02x10ρμ-==> 12T +T 20100T=6022+==℃ 0.141ωμμ⎛⎫= ⎪⎝⎭10000.020.0010.6920.0289p c x x k μ==Pr=()()0.81/3081/34Nu 0027Re Pr0.027x 1.06x10x 0.69239.66==.=.()2i ii h d 39.66 h 39.66x0.0289/0.02=57.22w/m .k k==14. A hot fluid with a mass flow rate 2250 kg/h passes through a ∅25x2.5 mm tube. The physical properties of fluid are as follows:k=0.5 w/(m o C), C p =4 kJ/kg-K, viscosity 10-3 N-s/m 2 , density 1000 kg/m 3 Find:a. Heat transfer film coefficient h i , in w/(m 2 -K).b. If the flow rate decreases to 1125 kg/h and other conditions are the same, what is the h i ?c. If the diameter of tube (inside diameter) decreases to 10 mm, and the velocity u keeps the same as that of case a, calculate h i .d. When the average temperature of fluid and quantity of heat flow per meter of tube are 40 o C and 400 w/m, respectively, what is the average temperature of pipe wall for case a?e. From this problem, in order to increase the heat transfer film coefficient and enhance heat transfer, what kinds of methods can you use and which is better, explain?Hint: for laminar flow, Nu=1.86[Re Pr]1/3for turbulent flow Nu=0.023Re 0.8 Pr 1/3 (1)444N 2250x4u d Gd d 3600x x0.02Re 3.98x10100.001ρππμμμ=====>()()1/30.8081/3424Nu 0023Re Pr 0.023x 3.98x10220.10.5Nuk 220.1x0.5hi 5500w /m k d 0.02⎛⎫== ⎪⎝⎭===.=.(2)12w 2w =4421Re Re /2=2x1010=>0.80.82211Nu Re 0.5Nu Re ⎛⎫== ⎪⎝⎭0.8i2i1h 0.5h = ()0.82i2h 5500x0.53159w /m k ==(3) 44333u d 2000x0.01Re 2x10100.001ρμ===>0.81/3Nu 0.023Re Pr =()2hi=6347w/m k(4)i i w w Q=h A (t-t )=400=500x2x0.02(t-t )πw t=40t 39.41=℃ ℃(5) there methods : increase u or hi or decrease d The first is better15. In a double pipe exchange (Φ23x2 mm), the cold fluid (Cp=1 kJ/kg, flow rate 500 kg/h) passes through the pipe and the hot fluid goes through the outside. The inlet and outlet temperatures of cold fluid are 20 and 80 o , and the inlet and outlet temperatures of hot fluid are 150 and 90o , respectively. The h i (film coefficient inside pipe) is 700 w/(m 2 o C)and overall heat transfer coefficient U o (based on the outside surface of pipe) is 300w/(m 2 o C), respectively. If the heat loss is ignored and the conductivity of pipe wall (steel) is taken as 45 w/(m o C), find: (1) heat transfer film coefficient outside the pipe h o ?(2) the pipe length required for counter flow, in m?(3) what is the pipe length required if the heating medium changes to saturatedvapor(140 o C) and it condenses to saturated liquid and other conditions keep unchanged?(4) When the exchanger is used for a year, it is found that it cannot meet the need of production (the outlet temperature of cold fluid cannot reach 80 o C), explain why? (a)0m o 0i i m d l d 111230.002x23h Vo h d kd 300700x1945x21⎛⎫=-+=-- ⎪⎝⎭ 1/h0=1/U0-(do/hidi+bdo/kdm)=1/300-23/700*19-0.002*23/45*21 ()20h 642.9w/m k =12t +t LMTD=702∆∆℃=Q=UoAo ∆Tm=mcCp(Tcb-Tca)300*2π*0.023*70L=500/3600*1000*(80-20)L=5.4m (c) 8020LMTD=86.514020ln14080-=--℃1122L t 70/86.5L t ∆==∆ 2L 0.81L1 4.4m == (d) scale is formed on the outside ,V 0 is decreased16. Water flows turbulently in the pipe of Φ25x2.5 mm shell tube exchanger. When the velocity of water u is 1 m/s, overall heat transfer coefficient Uo (based on the outer surface area of pipe) is 2115 w/(m 2 o C). If the u becomes 1.5 m/s and other conditions keep unchanged, Uo is 2660 w/( m 2 o C ). What is the film coefficient ho outside the pipe? (Heat resistances of pipe wall and scale are ignored)oi h h Uo 111+= (1)o i o h h U 1'1'1+= (2) (1)-(2)=0.80.80.80.81211111121152660u C u C 1C 1.5C-=-=-C=2859 io h Uo h 111-= ho=8127W/(m2K)17. Water and oil pass parallelly through an exchanger which is 1 m long. The inlet andoutlet temperatures of water are 15 and 40 o C, and those of oil are 150 and 100 o C, respectively. If the outlet temperature of oil decreases to 80 o C, and the flow rates and physical properties and inlet temperatures of water and oil maintain the same, what is the pipe length of new exchanger? (Heat loss and pipe wall resistance are neglected) ()()h h 12c c 21m Q W C T -T W C t t VA t ==-=∆ ()()h h 12c c 21W C T -T 'W C t 't =- 2150100401515080t 15--=-- 2t 50=℃212m1112m2L T T 't 1508092.51.85L T T t 15010069.8-∆-===-∆- 2m1m2L 1.85m L1=1m t 92.5 t 69.8=∆=∆=18. Air which passes through the pipe in turbulent flow is heated from 20 to 80 o C. The saturated vapor at 116.3 o C condenses to saturated water outside the pipe. If air flow rate increases to 120% of the origin and inlet and outlet temperatures of air stay constant, what kind of method can you employ in order to do that? (Heat resistance of pipe wall and scale can be ignored))(111ca cb pc c m i i T T C m T A h -=∆=1Q)'(2212ca cb pc c m i T T C m T A h -=∆=2Q 128.012112i22.12.1h m m c c m i m T T m m T h T ∆∆===∆∆ )803.116/()203.116ln(20801---=∆m T)80/()20ln(20802---=∆h h m T T TTh=118.5oC19. Water flows through the pipe of a Φ25x2.5 mm shell-tube exchanger from 20 to 50 o C. The hot fluid (C p 1.9 kJ/kg o C, flow rate 1.25 kg/s) goes along the shell and the temperatures change from 80 to 30 o C. Film coefficients of water and hot fluid are0.85kw/(m 2 o C) and 1.7 kw/(m 2 o C). What is the overall heat transfer coefficient Uo and heat transfer area if the scale resistance can be ignored? (the conductivity of steel is 45w/(m o C).W=1.25Kg/s Cp=1.9Kj/kg ℃()()2h p 12Q W C T T 1.25x1.9x 80-30119Kw =-==m 3010t 30ln 10-∆= ()200m 00i i m 1V 472w/m k d l d 1h h d kd ++==32i 0m Q 119x10A 13.9m V t 472x18.2===∆20. A spherical particle (density 2650 kg/m 3) settles freely in air at 20 o C (density of air 1.205 kg/m 3 , viscosity 1x10-5 Pa.s). Calculate the maximum diameter of particle if the settle obeys the Stoke s’ Law?Re ≤1 ()2p t p D g U 18D ρρμμρP -== ()23p 18D g μρρρP =-()1/3-10p 18x10D 1.205x9.81x 2650-1.205⎛⎫= ⎪ ⎪⎝⎭=3.85x10-521. A filter press(A=0.1 m 2 ) is used for filtering slurry. The vacuum inside the filter is 500 mm Hg. One liter filtrate can be got after filtering of 5 min and 0.6 more liter filtrate is obtained after 5 more min. How much filtrate will be got after filtering of 5 more min?for filter press 22e V 2VV =KA θ+5 min 22e 12V 0.1x5K +=(1)10min 22e 1.62x1.6V 0.1x10K +=(2)From (1) (2),we can see Ve=0.7 K=4815 min 22V 2x0.7V=48x0.1x15+ V=2.07m 3/h22. The following data are obtained for a filter press (A=0.0093 m 2) in a lab.------------------------------------------------------------------------------------------------pressure difference (kg f /cm 2 ) filtering time (s) filtrate volume (m 3 )1.05 502.27⨯10-3660 9.10⨯10-33.50 17.1 2.27⨯10-3233 9.10⨯10-3Find1) filtering constant K, q e , t e at pressure difference 1.05 kg f /cm 2 ?2) if the frame of filter is filled with the cake at 660 s, what is the end filtering rate (dV/dt)E at P 1.05 kg f /cm 2 ?3) compressible constant of cake s?For p=1.05Kg/cm 22e 2e 2e q 2qq K 0.002270.0002272x q 50K 0.00930.000930.000910.000912x q 660K 0.000930.00093θ+=⎛⎫+= ⎪⎝⎭⎛⎫+= ⎪⎝⎭ We can see K=0.015 qe=0.026For p=3.5Kg/cm 21-s K=2k ∆P 1-s K'=2k '∆P1s K 'K '-∆P ⎛⎫= ⎪∆P ⎝⎭ ()2E e V KA 2V+V d d θ⎛⎫= ⎪⎝⎭23. A slurry is filtered by a 0.1 m 2 filter press at constant pressure if the cake is incompressible. The filter basic equation is as follows:(q+10)2 = 250(t+ 0.4)where q---l/m 2 t----minfind (1) how much filtrate is got after 249.6 min?(2) if the pressure difference is double and the resistance of cake is constant, how much filtrate can be obtained after 249.6 min? (cake is imcompressible)(1)let θ=249.6 ()()2q+10250x 249.60.4=+q=240 V=qA=240*0.1=24 (2) K2k=∆P=∆P K'2k'∆P=∆P K'2K500'2==()()2q'+10500x249.60.4=+q’=343.6 v=34.36。
(完整版)流体力学与传热学试题及答案

流体力学与传热学试题及参考答案一、填空题:(每空1分)1、对流传热总是概括地着眼于壁面和流体主体之间的热传递,也就是将边界层的 和边界层外的 合并考虑,并命名为给热。
答案:热传导;对流传热2、在工程计算中,对两侧温度分别为t1,t2的固体,通常采用平均导热系数进行热传导计算。
平均导热系数的两种表示方法是 或 。
答案;221λλλ+=-;221t t +=-λ3、图3-2表示固定管板式换热器的两块管板。
由图可知,此换热器为 管程,管程流体的走向为 或 。
1 2 3图3-2 3-18 附图答案:4;2→4 →1→5→3;3→5→1→4→24、黑体的表面温度从300℃升至600℃,其辐射能力增大到原来的 倍. 答案: 5.39分析: 斯蒂芬-波尔兹曼定律表明黑体的辐射能力与绝对温度的4次方成正比, 而非摄氏温度,即4273300273600⎪⎭⎫⎝⎛++=5.39。
5、3-24 用0.1Mpa 的饱和水蒸气在套管换热器中加热空气。
空气走管内,由20℃升至60℃,则管内壁的温度约为 。
答案:100℃6、热油和水在一套管换热器中换热,水由20℃升至75℃。
若冷流体为最小值流体,传热效率0.65,则油的入口温度为 。
答案:104℃ 分析: ε=2020751--T =0.65 ∴1T =104℃1 2 37、因次分析法的基础是 ,又称因次的和谐性。
答案:因次的一致性8、粘度的物理意义是促使流体产生单位速度梯度的_____________。
答案:剪应力9、如果管内流体流量增大1倍以后,仍处于滞流状态,则流动阻力增大到原来的 倍。
答案:210、在滞流区,若总流量不变,规格相同的两根管子串联时的压降为并联时的 倍。
答案:411、流体沿壁面流动时,在边界层内垂直于流动方向上存在着显著的_______________,即使____________很小,____________仍然很大,不容忽视。
答案:速度梯度;粘度;内摩擦应力 12、雷诺数的物理意义实际上就是与阻力有关的两个作用力的比值,即流体流动时的______ 与__ ____ 之比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.3Solution :p a =1000kg/m 3 p c =815kg/m 3 p b =0.77kg/m 3 D/d=8 R=0.145mWhen the pressure difference between two reservoirs is increased, the volumetric changes in the reservoirs and U tubesR d x D 2244ππ= (1) so R D d x 2⎪⎭⎫ ⎝⎛= (2) and hydrostatic equilibrium gives following relationshipg R g x p g R p A c c ρρρ++=+21 (3)sog R g x p p c A c )(21ρρρ-+=- (4)substituting the equation (2) for x into equation (4) givesg R g R D d p p c A c )(221ρρρ-+⎪⎭⎫ ⎝⎛=- (5) (a )when the change in the level in the reservoirs is neglected,()Pa g R g R g R D d p p c A c A c 26381.98151000145.0)()(221=⨯-=-≈-+⎪⎭⎫ ⎝⎛=-ρρρρρ(b )when the change in the levels in the reservoirs is taken into account()Pa g R g R D d g R g R D d p p c A c c A c 8.28181.98151000145.081.9815145.0515.6)()(22221=⨯-+⨯⨯⨯⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛=-+⎪⎭⎫ ⎝⎛=-ρρρρρρ error=%=7.68.2812638.281-1.4Solution: There is a gaseous mixture in the U-tube manometer meter. The densities of fluids are denoted by Hg O H g ρρρ,,2, respectively. The pressure at point A is given by hydrostatic equilibriumg R R g R g R p g Hg O H A )(32232+-+=ρρρg ρis small and negligible in comparison with Hg ρand ρH2O , equation above can be simplifiedc A p p ≈=232gR gR Hg O H ρρ+=1000×9.81×0.05+13600×9.81×0.05=7161N/m²1gR p p p Hg A D B ρ+=≈=7161+13600×9.81×0.4=60527N/mFigure for problem 1.41.5Solution: Bernoulli equation is written between stations 1-1 and 2-2, with station 2-2 being reference plane: 2222222111u gz p u gz p ++=++ρρ Where p 1=0, p 2=0, and u 1=0, simplification of the equation1The relationship between the velocity at outlet and velocity u o at throat can be derived by the continuity equation:22⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛D d u u o 22⎪⎭⎫ ⎝⎛=d D u u o 2 Bernoulli equation is written between the throat and the station 2-23 Combining equation 1,2,and 3 gives222u Hg =222200u u p =+ρSolving for HH=1.39m1.6Solution :In Fig1.6, the flow diagram is shown with pressure taps to measure p 1 and p 2. From the mass-balance continuity equation , for constant ρ where ρ1 = ρ2 = ρ,2112A A V V = For the items in the Bernoulli equation , for a horizontal pipe,z 1=z 2=0Then Bernoulli equation becomes, after substituting 2112A A V V = for V 2, ρρ22121211212020p A A V p V ++=++ Rearranging,()===144.281.92100081.910002125.11112442-⨯⨯⨯--⎪⎭⎫ ⎝⎛==ρρg h d D u Hg2)1(21212121-=-A A V p p ρ ⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎪⎭⎫ ⎝⎛-12221211A A p p V ρ=Performing the same derivation but in terms of V 2,⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛--21221212A A p p V ρ=1.7Solution :The average velocity V for a cross section is found by summing up all the velocities over the cross section and dividing by the cross-sectional area1From velocity profile equation for laminar flow2 substituting equation 2 for u into equation 1 and integrating3rearranging equation 3 gives ⎰⎰==R R rdr u R udA A V 020211ππ⎪⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛--=22014R r R L p p u L μ2032D L p p V L μ-=232d V L p μ=∆1.8. In a vertical pipe carrying water, pressure gauges areinserted at points A and B where the pipe diameters are0.15m and 0.075m respectively. The point B is 2.5m belowA and when the flow rate down the pipe is 0.02 m 3/s, thepressure at B is 14715 N/m 2 greater than that at A.Assuming the losses in the pipe between A and B can beexpressed as g V k 22where V is the velocity at A, find the value of k . If the gauges at A and B are replaced by tubes filled with water and connected to a U-tube containing mercury of relative density 13.6, give a sketch showing how the levels in the two limbs of the U-tube differ and calculate the value of this difference in metres.Solution:d A =0.15m; d B =0.075mz A -z B =l =2.5mQ =0.02 m 3/s,p B -p A =14715 N/m 2s m d QV V d Q A A AA /132.115.0785.002.044222=⨯===ππs m d QV V d Q B B BB /529.4075.0785.002.044222=⨯===ππWhen the fluid flows down, writing mechanical balance equation222222A B B B A A A V k V g z p V g z p +++=++ρρ 213.1253.4100014715213.181.95.2222k ++=+⨯ Figure for problem 1.8 Pa d VL p 115201.01206.005.0323222=⨯⨯⨯==∆μk 638.0260.10715.14638.0525.24++=+=k 0.295making the static equilibriumgR g x g l p g R g x p Hg A B ρρρρρ+∆++=+∆+()()mm g g l p p R g H A B 7981.91260081.910005.214715-=⨯⨯⨯-=---=ρρρ1.9..Solution:(1) From Fanning equationandsoFluid flows from station a to station b , mechanical energy conservation giveshence2from station c to station dhence3From static equationp a -p b =R 1(ρˊ-ρ)g -l ρg 4p c -p d =R 2(ρˊ-ρ)g 5Substituting equation 4 in equation 2 ,then Figure for problem 1.9 22V d l h fab λ=22V d l h fcd λ=fcdfab h h =fab b a h p p +=+ρρlg fab b a h p p =+-lg ρfcd d c h p p +=ρρfcd d c h p p =-ρtherefore6Substituting equation 5 in equation 3 ,then7ThusR 1=R 21.10solution:1)1600001.01000004.04.0Re =⨯⨯==μρud from Hagen-Poiseuille equation1600004.0001.024.0323222=⨯⨯⨯==∆d uL P μ m g p h 163.081.910001600=⨯=∆=ρ 2)maximum velocity occurs at the center of pipe, from equation 1.4-19max 0.5V u = so u max =0.4×2=0.8m3)when u=V=0.4m/s Eq. 1.4-172max 1⎪⎪⎭⎫ ⎝⎛-=wr r u u 5.0004.01max2=⎪⎭⎫ ⎝⎛-u V r = m r 00284.071.0004.05.0004.0=⨯==fab h g l g R =+--'lg 1ρρρρ)(g R h fab ρρρ-'=1g R h fcd ρρρ-'=2Figure for problem 1.104) kerosene:427003.0800004.04.0Re =⨯⨯==μρud Pa p p 4800001.0003.01600=='∆='∆μμ m g p h 611.081.98004800=⨯=''∆='ρSolution :(1) When the gate valve is opened partially, the water discharge isSet up Bernoulli equation between the surface of reservoir 1—1’ and the section of pressure point 2—2’,and take the center of section 2—2’ as the referring plane, then∑+++=++21,2222121122—f h p u gZ p u gZ ρρ (a ) In the equation 01=p (the gauge pressure)222/396304.181.910004.081.913600m N gh gR p O H Hg =⨯⨯-⨯⨯=-=ρρ0021=≈Z uWhen the gate valve is fully closed, the height of water level in the reservoir can be related to h (the distance between the center of pipe and the meniscus of left arm of U tube).gR h Z g Hg O H ρρ=+)(12 (b )where h=1.5mR=0.6mSubstitute the known variables into equation bFigure for problem 1.122222_1,113.22)5.01.015025.0(2)(66.65.110006.013600V V V K d l h m Z c f =+⨯=+==-⨯=∑λ Substitute the known variables equation a9.81×6.66=2213.21000396302V V ++ the velocity is V =3.13m/sthe flow rate of water is h m V d V h /5.8813.312.0436004360032=⨯⨯⨯=⨯=ππ2) the pressure of the point where pressure is measured when the gate valve is wide-open. Write mechanical energy balance equation between the stations 1—1’ and 3-3´,then∑+++=++31,3233121122—f h p V gZ p V gZ ρρ (c ) since m Z 66.61=311300p p u Z =≈=2223_1,81.4 2]5.0)151.035(025.0[ 2)(V V V K d l l h c e f =++=++=∑λ input the above data into equation c ,9.8122V 81.4266.6+=⨯V the velocity is: V =3.51 m/sWrite mechanical energy balance equation between thestations 1—1’ and 2——2’, for the same situation of water level ∑+++=++21,2222121122—f h p V gZ p V gZ ρρ (d )since m Z 66.61=2121003.51/0(page pressure Z u u m sp =≈≈=)kg J V K d l hc f /2.26251.3)5.01.015025.0(2)(222_1,=+⨯=+=∑λinput the above data into equation d ,9.81×6.66=2.261000251.322++p the pressure is: 329702=p1.14 Solution : The variables of main pipe are denoted by a subscript1, and branch pipe by subscript2.The friction loss for parallel pipelines is 2121S S s f f V V V h h+==∑∑The energy loss in the branch pipe is22222222u d l l he f ∑∑+=λ In the equation 03.02=λsm u d ml l e /343.0053.04360072.2053.01022222=⨯⨯===+∑πinput the data into equation c kg J hf /333.02343.0053.01003.022=⨯⨯=∑The energy loss in the main pipe is333.022111121===∑∑u d l h hf f λSo s m u /36.22018.023.0333.01=⨯⨯⨯=The water discharge of main pipe ish m V h /60136.23.043600321=⨯⨯⨯=πTotal water discharge ish m V h /7.60372.26013≈+=1.16 Solution:Writing mechanical energy balance equation between the inlet 1 and throat of o o h V p V p ++=+222211ρρ 1 rearranging the equation abovef o oh V V p p +-=-22121ρ2from continuity equation11221125.625V V dd V V o o =⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛= 3 substituting equation 3 for V o into equation 2 gives()ff f f oh R h Rh V h V V p p +=+=+=+-=-94.1185.203.1903.19206.3922121211ρ4from the hydrostatic equilibriumg R p p O H Hg o )(21ρρ-=- 5substituting equation 5 for pressure difference into equation 4 obtainsf OH O H Hg h R gR +=-94.118)(22ρρρ 6rearranging equation 6kg J R R R R gR h OH O H Hg f /288.267.494.11861.12394.118)(22==-=--=ρρρ1.17.Solution: a)2.0501010==D D =⨯-=-=-81.9)1300013600(1.0)(21g R p p Hg ρρs kg V D m /187.013000183.001.0442220=⨯⨯⨯==πρπb) approximate pressure drop=⨯-=-=-81.9)1300013600(1.0)(21g R p p Hg ρρ588.6Pa2.1Solution:Write the mechanical energy balance equation between the suction connection and discharge connection2_1,2222121122f H gp g u Z H g p g u Z +++=+++ρρwherem Z Z 4.012=-Figure for problem 1.17()s m p p D D C V o /183.030.061.00906.061.01300081.9)1300013600(1.022.0161.021*******=⨯=≈⨯-⨯-=-⎪⎪⎭⎫ ⎝⎛-=ρ(Pa 1052.1(Pa 1047.22_1,215241≈=⨯=⨯-=f H u u pressure gauge p pressure gauge p ))total heads of pump is m H 41.1881.9100010247.01052.14.055=⨯⨯+⨯+= efficiency of pump is N N e /=η since kW g QH N e 3.1360081.9100041.18263600=⨯⨯⨯==ρ N=2.45kWThen mechanical efficiency%1.53%10045.23.1=⨯=η The performance of pump isFlow rate ,m³/h 26 Total heads ,m 18.41 Shaft power ,kW 2.45 Efficiency ,%53.12.2Solution:Equation(1.6-9)sm Rg D d C V f /12.444.69375.062.01000)100013600(81.9168.025025162.02144000=⨯=-⨯⨯⎪⎭⎫ ⎝⎛-=-⎪⎭⎫⎝⎛-=ρρρ)(Mass flow rates kg S V m o o /02.21000025.0414.312.42=⨯⨯⨯==ρ 2) Fluid flow through the pipe from the reactor to tank, the Bernoulli equation is as follows for V 1=V 2f H z gp p H +∆+-=ρ12 ∆z=10mPa p 7570710013.17602001081.95.054=⨯⨯+⨯⨯=∆ ∆p/ρg=7.7mThe relation between the hole velocity and velocity of pipeFriction losssoH=7.7+10+5.1=22.8m2.3 .. Solution :From an energy balance,WhereP o =760-640=120mmHgP v =760-710=50mmHgUse of the equation will give the minimum height H g as2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half, what will the new flowrate be ?s m D d V V /12112.42200=⎪⎭⎫⎝⎛⨯=⎪⎭⎫ ⎝⎛=m g u d l fH f 1.581.92105.0200025.02422=⨯⨯==NPSH H gp p H f vog ---=ρmNPSH H gp p H f vo g 55.335.181.9100081.913600)05.012.0-=--⨯⨯⨯-=---=(ρ• Density of acid 1840kg/m 3 • Viscosity of acid 25×10-3 PasSolution:Velocity of acid in the pipe:s m d m d mpipe of area tional cross flowrate volumetric u /32.3025.01840785.03785.04sec 222=⨯⨯===-=ρπρReynolds number:6109102532.31840025.0Re 3=⨯⨯⨯==-μρudfrom Fig.1.22 for a smooth pipe when Re=6109, f=0.0085 pressure drop is calculated from equation 1.4-9kg J u d l f ph f /450232.3025.0600085.042422=⨯==∆=ρkPa p 5.8271840450=⨯=∆or friction factor is calculated from equation1.4-25kgJ u d l u d l f ph f /426232.3025.0606109046.042Re 046.042422.022.02=⨯⨯⨯==∆=--=ρkPa p 84.7831840426=⨯=∆if the pressure drop falls to 783.84/2=391.92kPa8.18.12.12.038.12.12.022.0012.089.1079`2025.060102518401840046.042046.042Re 046.043919202u u u dl u d l p p =⎪⎭⎫ ⎝⎛⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯==∆='∆----ρμρρ=sos m u /27.236.489..1079012.03919208.18.1==⨯=new mass flowrate=0.785d 2u ρ=0.785×0.0252×2.27×1840=2.05kg/s2.4 Sulphuric acid is pumped at 3 kg/s through a 60m length of smooth 25 mm pipe. Calculate the drop in pressure. If the pressure drop falls by one half on assumption that the change of friction factor is negligible, what will the new flowrate be ?Density of acid 1840kg/m 3Viscosity of acid 25×10-3 Pa Friction factor 32.0Re 500.00056.0+=f for hydraulically smooth pipeSolution:Write energy balance equation:f h gu z g p H g u z g p +++=+++2222222111ρρ gu d l g p h H f 22λρ=∆==342=ρπu ds m d u /32.31840025.014.3124322=⨯⨯=⨯=ρπ 611510251840025.032.3Re 3=⨯⨯⨯=- 0087.061155.00056.0Re 500.00056.032.032.0=+=+=f 92.4681.9232.3025.0600087.04222=⨯⨯==∆==g u d l g p h H f λρΔp=46.92×1840×9.81=847.0kpa2.6solution :∑+++=+++f AA A A AA h u p g z w u p g z 2222ρρρλρ022p u d l h p p f BA ∆+==-∑247.0334.162=⎪⎭⎫⎝⎛=A A o ()()s m gR C u /5.8870870136006.081.9297.063.02247.01200=-⨯⨯=''--=ρρρ∴u = (16.4/33)2×8.5=2.1m/s∴242/76855105.321.2033.030870024.0m N h p p f B A =⨯+⨯==-∑ρ (2)W u d p Wm 1381.2033.0785.0768554Ne 22=⨯⨯⨯=∆==ρπρ sothe ratio of power obliterated in friction losses in AB to total power supplied to the fluid%%=461006.0500138⨯⨯3.2Solution:The gravity settling is followed Stocks ’ law, so maximum diameter of particle settled can be calculated from Re that is set to 11Re ==μρt c t u d , thenρμc t d u =equation 3.2-16 for the terminal velocityμρρρμ18)(2g d d S c c -=solving for critical diameter32)(224.1gd S c ρρμ-=Check up the appendixThe density of 20℃ air ρ=1.205 kg/m³ and viscosity µ=1.81×10-3N ·s/m 2mm d c μ3.571073.5205.1)205.12650()1081.1(224.15323=⨯=⨯-⨯=--when Reynolds number ≥1000, the flow pattern follows Newton ’s law and terminal velocity can be calculated by equation 3.2-19()ρρρ-=p p t gd u 75.1 1critical Reynolds number is 1000Re ='=μρt ct u d , 2rearranging the equation 2 givesρμct d u '=1000 3 combination of equation 1 with equation 3ρρρρμg d d S c c )(74.11000-'=' solving for critical diameter32)(3.32μρρρ-='S cdumm d c151210512.1205.1)205.12650()1081.1(3.323323=⨯=⨯-⨯='--3.3solution:to calculate terminal velocity from the equation 3.2-16()μρρ182g d u p pt -=The density of 21℃ air ρ=1.205 kg/m³ and viscosity µ=1.81×10-5N ·s/m 2()s m g d u p pt /181.01081.11881.9)205.12403()1050(185262=⨯⨯⨯-⨯-=--=μρρt BLu Q = so286.20181.0605.226m u Q BL t =⨯==1 from equation3.3-4tu H u L = the maximum permissible velocity of the air is 3m/s181.03HL =H L 58.16= 2set B to be 3m , then from equation 1 L =7m And H =0.42m3.4 Solution: D =0.4m B =D /4=0.1m h =D /2=0.2ms m hB Q u i /9.131.02.036001000=⨯⨯==According to the equation3.3-12 for N=5:m m u N B d i p c μπρρπμ81089.13)02300(5)1.0)(106.3(9)(965=⨯=⨯-⨯≈-=--3.6Solution:The equation for the constant-pressure filtrationt KA VV V m 222=+5min .1l 51.02122⨯=+K V m 10min .6.1l 101.06.126.122⨯⨯=⨯+K V msolving the equations above for V m and K7.0=m V and K =48For min 15=t 151.0487.0222⨯⨯=⨯⨯+V VSolving for V =2.073 l3.7 The following data are obtained for a filter press of 0.0093 m 2 filtering area in the test(1) filtration constant K , V m at the pressure difference of 1.05(2) if the frame of the filter is filled with the cake at 660s, what is the final rate of filtration Edt dV ⎪⎭⎫ ⎝⎛ (3) and what is the compressible constant of cake n ?solution:①from equation 3.4-19aKt qq q m =+22 For pressure difference 05.1=p ㎏/㎝2500093.01027.220093.01027.2323⨯=⨯⨯+⎪⎪⎭⎫ ⎝⎛⨯--K q m 1 6600093.0101.920093.0101.9323⨯=⨯⨯+⎪⎪⎭⎫ ⎝⎛⨯--K q m 2 solving the equations 1 and 2 gives s m K mm q m /1056.10379.02323-⨯==② )(22m E V V KA dt dV +=⎪⎭⎫ ⎝⎛=s m /1014.736-⨯For pressure difference 5.3=p ㎏/㎝271.10093.01027.220093.01027.2323⨯'='⨯⨯+⎪⎪⎭⎫ ⎝⎛⨯--K q m 3 2330093.0101.920093.0101.9323⨯'='⨯⨯+⎪⎪⎭⎫ ⎝⎛⨯--K q m 4 solving the equations 3 and 4 gives s m K m m q m /1037.40309.02323-⨯='='n p p -⎪⎪⎭⎫ ⎝⎛∆'∆=K K '1 then n ---⎪⎭⎫ ⎝⎛=⨯⨯13305.15.31056.11037.433.3ln 8.2ln 1=-n solving for n =0.1423.8solution:(1)22250)4.06.249(250)4.0(250)10(=+=+=+t qq=240 l/m 2V=24 l (2) the pressure difference is double2=∆'∆='pp K K soK ´=500210102=⎪⎪⎭⎫ ⎝⎛++'q q 2/5.3421025041.110)10(2m l q q =-⨯=-+='V=34.25 lSolution:Area of filtration: A =2×0.32×20=3.6m 2Δp =248.7kN/m 2t 1=300s, V 1=1/4×0.7=0.175m 3t 2-t 1=1800s, ΔV=0.7-0.175=0.525m 3or t 2 =2100s, V 2=0.7m 3KV andKt KA V m m 21006.37.027.03006.3175.02175.022222⨯=⨯+⨯==⨯+V m =0.2627m 3 And 522101517.3210096.122627.04.149.021006.34.17.0-⨯=⨯⨯+=⨯+=m V K capacitys m Q /10692.250021007.034-⨯=+=for the rotary drum filterArea of filtration: A =πdL =3.14×2.2×1.5=10.362m 2Operating pressure:Δp =70kN/m 2Andthe drum submerged : φ=25%For rotary drum filter the filtration coefficient: keep V m unchanged, K changes with changing in pressure difference6510871.87.24870101517.3--⨯=⨯=∆'∆='p p K K the capacity of rotary drum filter is equal to that of press filter⎪⎪⎭⎫ ⎝⎛-+⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛-+'==⨯--2627.02627.025.0362.1010871.810692.2226224n n V V n A K n nV m m ϕSolving for n from the equation above by trial and error⎪⎪⎭⎫ ⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+'==⨯-2627.0069.00002381.010692.2224n n V V n A K n nV m m ϕ n=0.0088=0.048rpm(转/min)Solution:From equation4.2-11 (a) heat loss:22211/89.68838.1229.0138.0114.06.76760m W k B k B T R T A q i i =+-=+∆=∆=∑∑ (b) the temperature at interface:211/89.688138.0114.0760m W t k B T A q =-=∆= t=191℃(c) contact resistance is 0.088°C·m 2/W, heat loss:22211/4.683088.038.1229.0138.0114.06.76760088.0m W k B k B T R T A q i i =++-=++∆=∆=∑∑4.4.Solution :Similar to compound resistances in series through the flat wall, the total resistance across insulating layer is as followsLL kA B R m 2357.0)426.0/278.1ln(/)426.0278.1(615.0426.0=-⨯==π Heat loss per meter tube through the wall ism W R T L q /7.5892357.038177=-=∆= and temperature distribution is()m W r r t R T L q /7.589213.0ln 213.02615.0177=-⨯-=∆=π()213.0ln213.05.2277177r r t --=4.7. Solution:106001002.006.11002.0Re 3=⨯⨯⨯==-μρdu 692.00289.01002.01000Pr 3=⨯⨯==-k c p μ 6.47863.05.166003324.0692.01060002.00289.0023.0Pr Re 023.04.08.04.08.0=⨯⨯=⨯⨯==i i d k h 4.8. Methyl alcohol flowing in the inner pipe of a double-pipe exchanger is cooled with water flowing in the jacket. The inner pipe is made from 25-mm Schedule 40 steel pipe. The thermalconductivity of steel is 45 W/(m·o C). The individual coefficients and fouling factors are given in the following Table. What is the overall coefficient, based on the outside area of the inner pipe? TABLE Data for Problem 8Coefficient/ W/(m 2·°C)Alcohol coefficient h i 1020Water coefficient h o 1700Inside fouling factor h di 5680Outside fouling factor h do 2840Solution: From equation (4.3-37)od o m o i i o di i o o h h d d k b h d d h d d U 111++++= from appendix 3, the wall thickness is 3.25mm and outside diameter is 33.5mm for nominal diameter 25mm Schedule 40 standard steel pipemm d m 25.302275.33=+=Cm W U o o 244534/4.40710521.310882.510998.710216.110184.21284011700125.305.334500325.01020275.335680275.331=⨯+⨯+⨯+⨯+⨯=+++⨯+⨯=-----4.9.Solution:Outside diameter of inner tube d o =19mm, inside diameter of outer tube Di=32mmThe equivalent diameter of annular space of double tube de ismm d D d D d D d o i o i o i e 131932)()(4422=-=-=+-=ππfrom equation4.08.0023.0⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=k c u d d k h p e e μμρ 1 C t o m 5022080=+= the properties of benzene: µ=0.45×10-3Pas ,c p =1.81kJ/kg.℃,k=0.138W/m ℃,ρ= 850kg/m 3 at average temperature of 50℃andaverage velocity of benzene flowing through the annular space of double tube is calculated as followu d D mo i )(422-=πρ()s m d D m u o i /13.1019.0032.0850360018004)(42222=-⨯⨯⨯=-=ππρ Substituting the variables into equation 1 givesC)·W/(m 17809.527748244.0138.01045.01081.11045.085013.1013.0013.0138.0023.0023.024.08.04.0338.034.08.0︒⨯⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯⎪⎭⎫ ⎝⎛⨯⨯⨯⎪⎪⎭⎫ ⎝⎛⎪⎪⎭⎫ ⎝⎛=--==k c u d d kh p e e μμρ4.13Solution:From the appendix 6, we obtain the latent heat of the saturated vapor, 2256.7kJ/kg at 100 o C.The average temperature of the condensate film=(100+92)/2=96℃The properties of the saturated water at 96 o C are as follows:µ=0.282×10-3Pas(from appendix 8); ρ=958kg/m 3; k=0.68W/m.K(from appendix5)from equation (4.5-12)()())/(5471101327.1943.010282.05.292100107.225681.995868.0943.0943.0241154133234123C m W L T g k h o f o f f ⋅=⨯=⎪⎪⎭⎫ ⎝⎛⨯⨯⨯-⨯⨯⨯⨯=⎪⎪⎭⎫ ⎝⎛∆=-μλρ()h kg s kg t t hA m w s /8.20/005785.0107.2256921005.2038.05471)(3==⨯-⨯⨯⨯=-=πλ Check the flow pattern:)/(04848.0038.014.3005785.0ms kg d m o =⨯==Γπ 68810282.004848.044Re 3=⨯⨯=Γ=-μ(laminar flow) If the tube is placed horizontally, then from equation (4.5-14)4123729.0⎪⎪⎭⎫ ⎝⎛∆='f o o f f d T g k h μλρ then2.2848.2773.0038.05.2773.0943.0729.04141=⨯=⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛='od L h h h´=2.2h=2.2×5471=12036.2W/m 2℃hence,hh m m '=' m´=2.2×20.8=45.8kg/h4.14.Solution: (1)From equation (4.3-37)3001212345002.070011923111=++=++=o o m o i i o o h h d d k b h d d U 300110868.4001729.015=+⨯+-ohh o =642.8 W/m 2℃(2) write energy balance equationm o o m o o p t L d U t A U t t mc ∆=∆=-π)(12 1logarithmic mean temperature difference for countercurrent flow∆t 1=150-80=70 o C ; ∆t 2=90-20=70 o C so ∆t m =70 o Ccalculate the length of double tube from equation 1m t d U t t mc L m o o p 5.570023.03003600)2080(1000500)(12=⨯⨯⨯-⨯=∆-=ππ (3)∆t 1=140-80=60 o C ; ∆t 2=140-20=120 o C so2121ln t t t t t m ∆∆-=∆ m t t d U mc t t t t d U t t mc t d U t t mc L o o p o o p m o o p 4.412060ln 023.030036001000500ln ln )()(2121211212=⨯⨯⨯-=∆∆=∆∆--=∆-='ππππ(4) the scale depositing on the surfaces of the tube to give additional thermal resistances4.15.Solution:From equation (4.3-37), neglecting thermal resistance of tube wall giveso i o h h U 111+=when the velocity of water is 1m/s, the individual coefficient of water to wall of tubes is h i , overall coefficient2115111=+=o i o h h U 1when the velocity of water is 1.5m/s, the individual coefficient of water to wall of tubes is h ´i , and h ´i related to h i by equation(4.4-25)383.15.18.08.0==⎪⎭⎫ ⎝⎛'='u u h h i iand overall coefficient is26601383.111111=+=+'=o i o i o h h h h U 2solving equation 1 and 2 for h i and h o h i =2858 W/( m 2⋅ o C ); h o =8135 W/( m 2⋅ o C )4.22Solution :(1)Write energy balance equation211212ln )(t T t T t t A U t A U t t mc o o m o o p ---=∆=- sopo o mc A U t T t T =--21ln set U o =h i because the thermal resistance from saturated vapor to wall of tube and resistance of wall are very small and negligible 608.0100025.1203817030170ln 2=⨯⨯=--t 837.1100025.12038170301702=⨯⨯=--t t 2=93.8 o Cthe rate of condensate for one condenser ()s kg t t mc m p h /0388.010002054308.93100025.1)(121=⨯-⨯=-=λ sum of condensate for two condensers in parallel m h =2m h1=2×0.0388=0.0776kg/s(2) two condensers operate in series heat transfer coefficient between the air and wall of tubes 74.128.08.0==⎪⎭⎫ ⎝⎛'=⎪⎪⎭⎫ ⎝⎛'='u u h h U U i i o oU ´o =1.74U o =1.74×38=66.12 W/m 2⋅K. po o mc A U t T t T 2ln21⨯'='-- so 058.110005.24012.6617030170ln 2=⨯⨯='--t 88.2170301702='--t t´2=121.4 o C()s kg t t c m m p h /111.010*********.12110005.2)(12=⨯-⨯=-''=λ。
