拉格朗日插值定理习题
练习题三 插值法
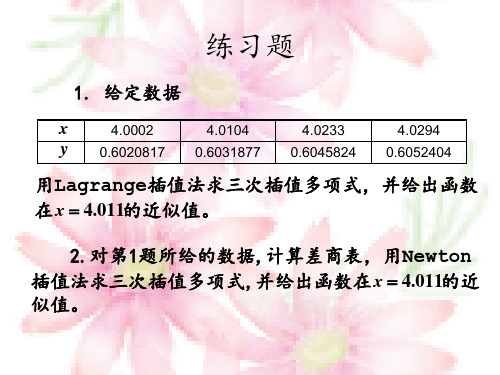
用Lagrange插值法求三次插值多项式,并给出函数 插值法求三次插值多项式, 插值法求三次插值多项式 的近似值。 在 x = 4.011的近似值。 2.对第1题所给的数据,计算差商表, 2.对第1题所给的数据,计算差商表,用Newton 对第 插值法求三次插值多项式, 插值法求三次插值多项式,并给出函数在 x = 4.011的近 似值。 似值。
(4)用 的近似值, (4)用3次样条插值求 f ( x ) 在 x = 0.425的近似值, 并与准确值作比较; 并与准确值作比较; 取值如下, 5. 已知函数 f ( x )取值如下,试求
x f (x) 0 .25 0 .5000 0 . 30 0 .5477 0 . 39 0 .6245 0 .45 0 .6708 0 .53 0 .7280
对第1题所给的数据计算差商表用newton插值法求三次插值多项式并给出函数在对函数在区间选取不同个数的等距插值节点用分段线性插值代替次插值函数观察插值节点增多时误差的变化情况
练习题
1. 给定数据
x y
4.0002 0.6020817 4.0104 0.6031877 4.0233 0.6045824 4.0294 0.6052404
1 − 3. 对函数 2 在区间 [−4,4] 选取不同个数的等 1+ x 距插值节点, 次插值函数, 距插值节点,用分段线性插值代替 n 次插值函数,观
察插值节点增多时误差的变化情况。 察插值节点增多时误差的变化情况。 4. 给出 f ( x ) = sin x 在 xk = 0.1k , k = 0,1,L,10 的函 数值 f ( xk ) = yk 。 (1)用9次Lagrange插值多项式求 f ( x ) 在 x = 0.425 (1)用 插值多项式求 的近似值,并与准确值作比较; 的近似值,并与准确值作比较; (2)用 (2)用9次Newton插值多项式计算 f ( x ) 在 x = 0.425 插值多项式计算 的近似值,并与准确值作比较; 的近似值,并与准确值作比较; (3)用分段线性插值求 的近似值, (3)用分段线性插值求 f ( x ) 在 x = 0.425的近似值, 并与准确值作比较; 并与准确值作比较;
数学分析6.1拉格朗日定理和函数的单调性(练习)

第六章微分中值定理及其应用1 拉格朗日定理和函数的单调性练习题1、试讨论下列函数在指定区间内是否存在一个点ξ,使f’(ξ)=0.(1)f(x)=xsin1x, 0<x≤1π0, x=0;(2)f(x)=|x|, -1≤x≤1.解:(1)∵f(x)在[0,1π]上连续,在(0,1π)内可导,且f(0)=f(1π),根据罗尔中值定理知,存在一个点ξ∈(0,1π),使f’(ξ)=0.(2)∵f(x)在[-1,1]连续,且f(-1)=f(1),但f(x)在(-1,1)内x=0点不可导,根据罗尔中值定理知,不一定存在一个点ξ∈(-1,1),使f’(ξ)=0.又f’(x)=1, x>0−1, x<0,∴不存在一个点ξ∈(-1,1),使f’(ξ)=0.2、证明:(1)方程x3-3x+c=0(c为常数)在区间[0,1]内不可能有两个不同的实根;(2)方程x n+px+q=0(n为自然数,p,q为实数)当n为偶数时至多有两个实根;当n为奇数时至多有三个实根。
证:(1)记f(x)=x3-3x+c,若f(x)=0在[0,1]有两个不同的实根a,b,则f(a)=f(b),又f(x)在[0,1]上连续,且在(0,1)内可导;根据罗尔中值定理知,存在一个点ξ∈(0,1),使f’(ξ)=0.但f’(x)=3(x2-1)只有两个实根x=±1,矛盾,结论得证。
(2)记f(x)=x n+px+q(n为自然数,p,q为实数).当n=2k(k=1,2,…)时,若f(x)=0至少有三个实根a,b,c,设a<b<c,由罗尔中值定理知,存在点ξ1∈(a,b),ξ2∈(b,c),使f’(ξ1)=2kξ12k-1+p=0, f’(ξ2)=2kξ22k-1+p=0,即f’(ξ1)= f’(ξ2).又f’(x)=2kx2k-1+p在R上严格增,矛盾,可得结论1:当n为偶数时,x n+px+q=0至多有两个实根.当n=2k-1(k=1,2,…)时,若k=1,结论成立;若k=2,3…,设f(x)=0至少有四个实根,由罗尔中值定理知,f’(x)=(2k+1)x2k+p=0,即x2k+0x+p=0有三个实根,与结论1矛盾,2k+1结论2:当n为奇数时,x n+px+q=0至多有三个实根.3、证明:若函数f和g在区间I上均可导,且f’(x)≡g’(x),x∈I,则在区间I上f(x)与g(x)只相差一个常数,即f(x)=g(x)+c (c为常数).证:记F(x)=f(x)-g(x),则F(x)在I上可导,且F’(x)=f’(x)-g’(x)≡0.∴F(x)为常量函数,设F(x)=c(c为常数),即f(x)-g(x)=c,∴f(x)=g(x)+c.4、证明:(1)若函数f在[a,b]上可导,且f’(x)≥m,则f(b)≥f(a)+m(b-a);(2)若函数f在[a,b]上可导,且|f’(x)|≤M,则|f(b)-f(a)|≤M(b-a);(3)对任意实数x1,x2都有|sinx1-sinx2|≤|x1-x2|.;证:(1)∵f在[a,b]上可导,∴存在一点ξ∈(a,b),使f’(ξ)=f b−f(a)b−a≥m,∴f(b)≥f(a)+m(b-a).又f’(ξ)≥m,即f b−f(a)b−a;(2)∵f在[a,b]上可导,∴存在一点ξ∈(a,b),使f’(ξ)=f b−f(a)b−a≤M,∴|f(b)-f(a)|≤M(b-a).又|f’(ξ)|≤M,即|f b−f a|b−a(3)证法1:当x1=x2时,结论成立;当x1≠x2时,∵sinx在R连续且可导,∴对任意实数x1,x2,设x2<x1,∴存在一点ξ∈(x2,x1),使(sinξ)’=sin x1−sin x2.x1−x2又(sinξ)’=cosξ,且|cosξ|≤1,∴|sin x1−sin x2|x1−x2≤1,即|sinx1-sinx2|≤x1-x2. 同理,设x1<x2,有|sinx1-sinx2|≤x2-x1.∴对任意实数x1,x2都有|sinx1-sinx2|≤|x1-x2|.证法2:利用(2)的结论,∵|(sin x)’|=|cosξ|≤1,∴对任意实数x1,x2都有|sinx1-sinx2|≤|x1-x2|.5、应用拉格朗日中值定理证明下列不等式:(1)b−ab <ln ba<b−aa, 其中0<a<b;(2)h1+h2<arctanh<h, 其中h>0.证:(1)ln ba=lnb-lna,∵lnx在[a,b]内连续,且在(a,b)内可导,∴存在一点ξ∈(a,b),使lnb-lna=(lnξ)’(b-a)=b−aξ.又b−ab <b−aξ<b−aa,∴b−ab<ln ba<b−aa.(2)arctanh=arctanh-arctan0,∵arctanh在[0,h]内连续,在(0,h)内可导,∴存在一点ξ∈(0,h),使arctanh-arctan0=h(arctanξ)’=h1+ξ2.又h1+h2<h1+ξ2<h,∴h1+h2<arctanh<h.6、确定下列函数的单调区间:(1)f(x)=3x-x3;(2)f(x)=2x2-lnx;(3)f(x)=2x−x2;(4)f(x)=x2−1x. 解:(1)f’(x)=3-3x2. 当f’(x)=0时,x=±1.∴f在[1,-1]上递增,在(-∞,-1]∪[1,+∞)上递减.(2)f的定义域为(0,+∞). f’(x)=4x−1x =4x2−1x.当f’(x)=0时,x=±12(负数舍去);当f’(x)>0时,x>12;当f’(x)<0时,0<x<12;∴f在(0,12]上递减,在[12,+∞)上递增.(3)f的定义域为[0,2]. f’(x)=2x−x2.当x=1时,f’(x)=0;当x<1时,f’(x)>0;当x>1时,f’(x)<0. ∴f在[0,1]上递增,在[1,2]上递减.(4) f的定义域为x≠0. f’(x)=x2−1x ′=x−1x′=1+1x2>0.∴f在(-∞,0)∪(0,+∞)上递增.7、应用函数的单调性证明下列不等式:(1)tanx>x−x33, x∈(0,π3);(2)2xπ<sinx<x, x∈(0,π2);(3)x−x22<ln(1+x)<x−x22(1+x), x>0.证:(1)记f(x)=tanx-(x−x 33)=tanx-x+x33,则f’(x)=sec2x-1+x2=tan2x+x2>0,∴f(x)在(0,π3)内严格递增. 又f(x)在x=0处连续,且f(0)=0,∴当0<x<π3时,f(x)>0,即tanx>x−x33.(2)记f(x)=sinxx ,x∈(0,π2);则f’(x)=(x−tanx)cosxx2.令g(x)=x-tanx,x∈(0,π2);则g’(x)=-tan2x<0,∴g(x)在(0,π2)严格递减.又g(x)在x=0处连续,且g(0)=0,∴g(x)<0. ∴f’(x)<0. ∴f(x)在(0,π2)严格递减.又limx→0sinxx=1,∴sinπ2π2<sinxx<1,即2xπ<sinx<x.(3)记f(x)=ln(1+x)-(x−x22)=ln(1+x)-x+x22,x>0;则f’(x)=11+x-1+x=x21+x>0.∴f(x)在(0,+∞)严格递增. 又f(x)在x=0处连续,且f(0)=0,∴f(x)>0,即ln(1+x)>x−x22.记g(x)=ln(1+x)-(x−x 22(1+x))=ln(1+x)−2x+x22(1+x),x>0;则g’(x)=11+x −2+2x1+x−(2x+x2)2(1+x)2=11+x−x2+2x+22(1+x)2=−x22(1+x)2<0∴g(x)在(0,+∞)严格递减. 又g(x)在x=0处连续,且g(0)=0,∴g(x)<0,即ln(1+x)<x−x22(1+x).8、以S(x)记由(a,f(a)),(b,f(b)),(x,f(x))三点组成的三角形面积,试对S(x)应用罗尔中值定理证明拉格朗日中值定理.证:S(x)=12a f(a)1b f(b)1x f(x)1,若f(x)在[a,b]上连续,在(a,b)上可导,则S(x)在[a,b]上连续,在(a,b)上可导,且S(a)=S(b)=0,由罗尔中值定理知:至少存在一点ξ∈(a,b),使S’(ξ)=0.又S’(x)=12a f(a)1b−a f b−f(a)01f′(x)0=12[f’(x)(b-a)-(f(b)-f(a))].∴S’(ξ)=12[f’(ξ)(b-a)-(f(b)-f(a))]=0,即f(b)-f(a)=f’(ξ)(b-a).拉格朗日中值定理得证.9、设f为[a,b]上的二阶可导函数,f(a)=f(b)=0,并存在一点c∈(a,b),使得f(c)>0,证明:至少存在一点ξ∈(a,b),使f”(ξ)<0.证:由拉格朗日中值定理可知:f(c)=f(c)-f(a)=f’(ξ1)(c-a)>0,a<ξ1<c.-f(c)=f(b)-f(c)=f’(ξ2)(b-c)<0,c<ξ2<b. ∴f’(ξ1)>0,f’(ξ2)<0,∴f’(ξ2)-f’(ξ1)<0,ξ2-ξ1>0,又由拉格朗日中值定理知:至少存在一点ξ∈(ξ1,ξ2)⊂(a,b),使f”(ξ)=fξ2−f(ξ1)ξ2−ξ1<0.10、设f在(a,b)上可导,且f’单调,证明:f’在(a,b)内连续. 证:不妨设f’在(a,b)内单调递增,则对任一x0∈(a,b),必存在的x0某一邻域U(x0)⊂(a,b).∵f’在U+(x0)内单递增,∴有下界f’(x0),又f’在U-(x0)内单递增,∴有上界f’(x0),∴lim x→x0+f’(x)和limx→x0−f’(x)都存在。
matlab拉格朗日插值多项式例题

文章主题:探索MATLAB中的拉格朗日插值多项式在现代科学与工程领域中,数值分析和插值方法是相当重要的研究方向之一。
它们在数据处理、图像处理、信号处理等领域都有着广泛的应用。
而MATLAB作为一个功能强大的数值计算软件,自然也包括了丰富的插值方法。
本文将重点探讨MATLAB中的拉格朗日插值多项式,通过具体例题来展示其应用与解决问题的能力。
一、拉格朗日插值多项式概述拉格朗日插值多项式是一种基本的插值方法,它的基本思想是在给定数据点的情况下,通过构造一个满足通过所有数据点的多项式来逼近实际函数。
具体而言,对于给定的n+1个不同的数据点(x0, y0), (x1,y1), …, (xn, yn),拉格朗日插值多项式可以表示为\[L(x) = \sum_{i=0}^{n} y_i l_i(x)\]其中,li(x)为拉格朗日基函数,它的表达式为\[l_i(x) = \prod_{j=0, j\neq i}^{n} \frac{x-x_j}{x_i-x_j}\]根据拉格朗日插值多项式的构造方式,我们可以看到它通过n+1个数据点构建了一个n次多项式来逼近实际函数,从而实现了插值的目的。
二、MATLAB中的拉格朗日插值多项式函数在MATLAB中,可以利用“lagrange”函数来实现拉格朗日插值多项式的计算。
对于给定的数据点和函数值,我们可以使用下面的MATLAB代码来实现拉格朗日插值多项式的计算:```matlabx = [1, 2, 3, 4, 5];y = [1, 4, 9, 16, 25];xi = 2.5;yi = lagrange(x, y, xi);disp(yi);```在上面的例子中,我们给定了数据点(1, 1), (2, 4), (3, 9), (4, 16), (5, 25),然后利用“lagrange”函数计算了在xi=2.5处的插值结果yi。
通过这样简单的几行代码,就可以实现拉格朗日插值多项式的计算与应用。
数值计算课后答案4

习 题 四 解 答1、设010,1x x ==,写出()x f x e -=的一次插值多项式1()L x ,并估计插值误差。
解:根据已知条件,有设插值函数为1()L x ax b =+,由插值条件,建立线性方程组为解之得111a eb -⎧=-⎨=⎩则11()(1)1L x e x -=-+ 因为(),()x x y x e y x e --'''=-= 所以,插值余项为 所以010101()max max (1)2111248x r x e x x e ξξ-≤≤≤≤-≤-=⨯⨯=。
2、给定函数表选用合适的三次插值多项式来近似计算f(0.2)和f(0.8)。
解:设三次插值多项式为230123()f x a a x a x a x =+++,由插值条件,建立方程组为 即解之得则所求的三次多项式为23()0.41 6.29 3.489.98f x x x x =--+。
所以3、设(0,1,2,,)i x i n =是 n+1个互异节点,证明:(1)0()(0,1,2,,)n k k i i i x l x x k n ===∑;(2)0()()0(0,1,2,,)nk i i i x x l x k n =-==∑。
证明: (1)由拉格朗日插值定理,以x 0,x 1,x 2,…x n 为插值节点,对y=f(x)=x k 作n 次插值,插值多项式为0()()nn i i i p x l x y ==∑,而y i =x i k ,所以0()()()nnk n i i i i i i p x l x y l x x ====∑∑同时,插值余项 所以()nk k i i l x x x =∑结论得证。
(2)取函数()(),0,1,2,,k f x x t k n =-=对此函数取节点(0,1,2,,)i x i n =,则对应的插值多项式为0()()()nk n i i i p x x t l x ==-∑,由余项公式,得(1)(1)011()()()()()()()()0(1)!(1)!nn kk n ki i i r x x t x t l x f x x t x n n ξξππ++==---==-=++∑所以令t=x ,4、给定数据(()f x =(1)试用线性插值计算f(2.3)的近似值,并估计误差;(2)试用二次Newton 插值多项式计算f(2.15)的近似值,并估计误差。
数值分析习题解答

解:(1) 由Lagrange 插值公式00112233()()()()()L x f l x f l x f l x f l x =⋅+⋅+⋅+⋅其中()()()()()()()()()()123001020311112233122x x x x x x x x x x x x l x x x x x x x ⎛⎫⎛⎫---- ⎪ ⎪---⎝⎭⎝⎭===----⎛⎫-⋅-⋅- ⎪⎝⎭()()()()()()()()()()()()02311012131111221112112x x x x x x x x x l x x x x x x x x x x ⎛⎫+-- ⎪---⎛⎫⎝⎭===+-- ⎪---⎛⎫⎝⎭⋅-⋅- ⎪⎝⎭()()()()()()()()()()()0132202123118113113222x x x x x x x x x x x x l x x x x x x x ---+-+-===----⎛⎫⋅- ⎪⎝⎭可得()231()12L x x x ⎛⎫=-+ ⎪⎝⎭(2)同理,利用Lagrange 插值公式可得231()2L x x x ⎛⎫=- ⎪⎝⎭方法二:由于题设有4 个条件(4个点),故只能确定一个至多3次的多项式,所以不妨设()()312L x x x Ax B ⎛⎫=-+ ⎪⎝⎭ (又120f f ==⇒1x 和2x 为()3L x 的根)又由()()33312112L L ⎧-=-⎪⎪⎨⎪=⎪⎩ ⇒()()()3312211122A B A B ⎧⎛⎫---+=- ⎪⎪⎪⎝⎭⎨⎛⎫⎪+= ⎪⎪⎝⎭⎩⇒10A B =⎧⎨=⎩ 所以()231122L x x x x x x ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭证明:(1)由于(),i jij l xδ=,故()()0nkn ii i L x x l x ==∑,当j x x =时,有(),0,1,,kn j j L x x j n ==,()n L x 即为kx 的插值多项式.由唯一性,可得()0nk ki i i x l x x ==∑,0,1,,k n =.(2)利用Newton 插值多项式()()[]()[]()()0010001,,,n n n N x f x f x x x x f x x x x x x -=+-++--,()*()()()()()()10010n n x x x x f x l x x x x x --==--差商表()f x一阶 二阶N 阶0x11x011x x-2x()()01011x x x x --n x0 0 0()()()010101n x x x x x x ---代入()*,有()()()()()()()01001010101n n n x x x x x x x x N x x x x x x x x x ----=+++---- ()0l x 为n 次代数多项式,由插值多项式的唯一性,得()()0n l x N x =解:作()f x 以,,a a b ε+为节点的Lagrange 插值多项式,有()()22()f x L x R x =+其中:()()()()()()()()()()()()()()()()()()2x a x b x a x a x a x b L x fa f a fb a b a b b a b a εεεεεεε-+---+--=+++--+---+()()()()()()23!f R x x a x a x b ξε'''=--+- a b ξ<<令0ξ→()()()()()226f R x R x x a x b ξ'''→=--又()()()()()()()()()()()()()()()()()()()()()()()()()()22222x a x a x a x a L x b x f a f a f a f a b a b a b a b a x a x a f b b a b a b x x b a b x x a x a f a f a f b P x b a b a b a εεεεεεεεεεε⎡⎤⎢⎥⎡⎤⎡⎤⎡⎤⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦⎡⎤⎣⎦⎡⎤⎣⎦-+---=-+-+-+--+-+-+--++--+-+----'→++=---故当0→ε时,公式()()()x R x P x f +=成立. 2.4解:设()f x 的插值多项式为: ()00n n p x a a x a x =+++则20010200210112212012n n n n nnn n n f a a x a x a x f a a x a x a x f a a x a x ax ⎧=++++⎪=++++⎪⎨⎪⎪=++++⎩ 添加一个方程后,得:00001001011101()n n n n nn nn n n p x a a x a x f a a x a x f a a x a x f a a x ax ⎧=+++⎪=+++⎪⎪=+++⎨⎪⎪⎪=+++⎩线性方程组有非零解()01,,,Tn a a - ,因而行列式000()1101nn n nnnp x xx f x x f x x =或者001100010111()011n nnn n n nnn nnx x xx x x f x x p x x x f x x ⋅+=记01()j i i j nC x x ≤<≤-=-∏ ,得0011()1nn n nx f x p x Cfx = .2.5略 2.6解:73()1f x x x =++ ,有(7)()17!f ξ= , (8)017017()[3,3,,3][2,2,,2]08!f f f η===2.7证明:1.1()f x a x=- .利用数学归纳法证明: (1) 当1n = 时,有001[]f x a x =-显然成立; (2) 假设n k = 时,有01011[,,,]()()()k k f x x x a x a x a x =--- 成立,则当1n k =+ 时,有:11010111011011001011101001110[,,,][,,,][,,,,]11()()()()()()()()()()()()()()()()()k k k k k k k k k k k k k k k k k k f x x x f x x x f x x x x x x a x a x a x a x a x a x x x a x a x a x a x a x a x x x x x a x a x a x a x x x +++++++++++-=--------=--------=------=-0111()()()()k k a x a x a x a x +=----也成立 综上(1)(2),故原等式成立 所以01011[,,,]()()()n n f x x x a x a x a x =---2.由01011[,,,]()()()n n f x x x a x a x a x =---可得:01011[,,,,]()()()()n n f x x x x a x a x a x a x =----因为()()[]()[]()()()()001000100,,,[,,,]n n n n f x f x f x x x x f x x xx x x f x x x x x x x -=+-++--+--故有0000101()()11()()()()()n x x x x x x a x a x a x a x a x a x a x ---=+++-------2.8 2.9 证明:(1)0n = 时,结论显然成立. 假设结论对0n ≥ 成立,即0(1)nnk ki n n i k k f C f +-=∆=-∑ 下面考虑 1n i f +∆()111001111101111111111(1)(1)(1)(1)(1)(1)(1)()n n n n i i i innkkk knn i k n n i kk k nn kkk k nn i k n n i kk k n n kk k k n i nn i k n n i k k k k k k n i n n n i f f f f C f C f C f C f f C f C f f C C f ++++-+-==+--++-++-==+-++++-++-==-++++∆=∆∆=∆-∆=---=---=+-+-=+-+∑∑∑∑∑∑111111111110(1)(1)(1)(1)nn nk n ik nk k n n i n n i k i k n k k n n i k k C f f C f f C f +-=++++++-=++++-=+-=+-+-=-∑∑∑即结论对也成立.由数学归纳法可得原等式成立. (2)。
52第二节 拉格朗日插值多项式

数学学院 信息与计算科学系
( t ) f ( t ) Ln ( t ) K ( x ) n1 ( t )
由式
n+1(xk)=0 和式 Ln(xk)=yk( k=0,1,…,n ),以及
Rn ( x ) f ( x ) Ln ( x ) K ( x ) n1 ( x )
O
l1 ( x) x1 x
O
x0
x0
x1 x
数学学院 信息与计算科学系
n=2时的二次基函数及图形为 ( x x0 )( x x2 ) ( x x1 )( x x2 ) l0 ( x ) , l1 ( x ) , ( x0 x1 )( x0 x2 ) ( x1 x0 )( x1 x2 )
可知:x0 , x1, , xn 和x 是(t)在区间[a,b]上的n+2个 互异零点, 因此根据罗尔(Rolle)定理, 至少存在一点 =(x) (a,b),使 ( n 1) f ( ) ( n1) 即 K ( x) ( ) 0 ( n 1)! ( n 1) f ( ) 所以 Rn ( x ) f ( x ) Ln ( x ) n 1 ( x )
1 3 | ( x 2)( x 2.5)( x 4) | 6 8 1 3 | R(3) || f (3) L2 (3) | | (3 2)(3 2.5)(3 4) | 6 8 0.03125
数学学院 信息与计算科学系
例4 已知sin0.32=0.314567, sin0.34=0.333487 有6位有效数字。 (1) 用线性插值求sin0.33的近似值; (2) 证明在区间[0.32, 0.34]上用线性插值计算sinx时 至少有4位有效数字. 解 (1)用线性插值 0.33 0.34 sin 0.33 L1 (0.33) 0.314567 0.32 0.34 0.33 0.32 1 0.333487 (0.314567 0.333487) 0.34 0.32 2 0.324027
第三章多项式插值方法习题

4、经过点(0,1),(1,2),(2,5)的插值多项式 P(x) ( D )
(A) x
(B) x 1
(C) 2x 1 (D) x2 1
x 0 2 51
5、已知函数 y f (x) 的数据表
,
y 3 6 9 0
则 y f (x) 的拉格朗日插值基函数 l2 (x) ( A )
(A) x(x 2)( x 1) (B) (x 2)( x 5)( x 1)
第三章 习 题
1、 n 次拉格朗日插值多项式的余项是( A )
(A) Rn (x)
f (n (n
1) ( )
1)!
n1
(
x)
(B) Rn (x)
f
(n)
n
(
!
)
n
(
x)
f (n1) ( )
(C) Rn (x) (n 1)!
(D)
Rn (x)
f (n) ( )
n!
x 0 0.5 1 1.5 2 1 1 x x 1 x 2 1 x3 3 x2 1。
2
2
22
又: R3 x f x px 满足: R0 1, R1 2, R2 3, R0 0 ,
使
xi
x
xi1 ,
令 h xi1 xi ,则: R(x)
f
'' (
2
)
(x
xi
)(x
xi1 )
,
解:对
x
[0,
2
]
,必有某个
x
i
使
xi
x
xi1 ,
令 h xi1 xi ,则: R(x)
f
'' (
拉格朗日插值_逐次线性插值法 (2)

第二章 插值与拟合
例2.1 已知 100 10 , 121 11 , 利用线性插值求 y 115
解: 这里x0=100,y0=10,x1=121,y1=11, 利用线 性插值
x 121 x 100 L1 ( x) 10 11 100 121 121 100
第二章 插值与拟合
例1:已知x0=100, x1=121, x2=144, 求 f ( x)
x
在x=115时的近似值。
x 121 x 100 L1 ( x ) 10 11 100 121 121 100
x 144 x 121 ~ L1 ( x ) 11 12 121 144 144 121
为克服这一缺点,通常可用逐次线性插值方法求得高次插 值。例如在例2.1-2.1*中:
115 121 115 100 11 10.714 100 121 121 100 115 144 115 121 ~ 115 L1 (115) 11 12 10.739 121 144 144 121 115 L1 (115) 10
x x0 x x1 x x2 x x3 x x4
第二章 插值与拟合
例:已知 sin 1 , sin 1 , sin 3 6 2 4 2 3 2 分别利用 sin x 的1次、2次 Lagrange 插值和牛顿插 值计算 sin 50。
