《电路基础》第22讲 正弦稳态电路的计算
合集下载
电路理论课本讲解----正弦稳态电路分析
U
k
I
km
0
0
例1. 图示正弦交流电路中，电压表V1、V2读数均为
100V，电压u1、 u2的初相位分别为 0 及 90
求电压表V的读数，并画电压相量图。 解：由相量形式的KVL，得
U U1 U2
1000 100(90 )
u1
V V1 V2
（振幅相量）
o
Im
x
Um
y
o
Im
x
y
I
o
I m cos(t )
Im 有效值相量 I 2
相量图
I
x
例1. 写出下列三个正弦量的相量并绘相量图 。
i1 (t ) 5cos(314t 60 ) A
i2 (t ) 10sin(314t 60 ) A
例4. 已知正弦交流电路中电流表读数分别为A1：5A；A2：20A；
A3：25A。求： （1）图中电流表A的读数； （2）如果维持A1的读数不变，而把电源频率提高一倍，再求 电流表 A的读数。
A1
I1
I
A
A2
I2
A3
+
U
I3
-
7.5 阻抗和导纳
一、阻抗
I
I
+ U 线性 Z 阻抗（Ω） U 无源 I 若 U U u , I I i U +j 则 Z u i | Z | Z R jX I U 其中 | Z | 阻抗模（Ω） I Z Z u i 阻抗角 [180 ,180 ]
U j LI
U LI
U
u
i
k
I
km
0
0
例1. 图示正弦交流电路中，电压表V1、V2读数均为
100V，电压u1、 u2的初相位分别为 0 及 90
求电压表V的读数，并画电压相量图。 解：由相量形式的KVL，得
U U1 U2
1000 100(90 )
u1
V V1 V2
（振幅相量）
o
Im
x
Um
y
o
Im
x
y
I
o
I m cos(t )
Im 有效值相量 I 2
相量图
I
x
例1. 写出下列三个正弦量的相量并绘相量图 。
i1 (t ) 5cos(314t 60 ) A
i2 (t ) 10sin(314t 60 ) A
例4. 已知正弦交流电路中电流表读数分别为A1：5A；A2：20A；
A3：25A。求： （1）图中电流表A的读数； （2）如果维持A1的读数不变，而把电源频率提高一倍，再求 电流表 A的读数。
A1
I1
I
A
A2
I2
A3
+
U
I3
-
7.5 阻抗和导纳
一、阻抗
I
I
+ U 线性 Z 阻抗（Ω） U 无源 I 若 U U u , I I i U +j 则 Z u i | Z | Z R jX I U 其中 | Z | 阻抗模（Ω） I Z Z u i 阻抗角 [180 ,180 ]
U j LI
U LI
U
u
i
电路设计--正弦稳态电路的功率讲解
2U cos(t u )×
2I cos( t i )
UI cos( u i ) UI cos(2t u i )
u i
为电压和电流之间的相位差
p UI cos UI cos(2t u i )
瞬时功率有两个分量： 第一个为恒定分量，第二个为正弦分量。
§9.4 正弦稳态电路的功率
一、瞬时功率
一端口内部不含独立电 源，仅含电阻、电感和 电容等无源元件。
+ u i N0
它吸收的瞬时功率 p 等于电压 u 和电流 i 的乘积 p =u i 在正弦稳态情况下，设
u
2U cos( t u )
i
2I cos( t i )
瞬时功率 p= 令
另一种解法
而 R = 30 Ω I R 30 Z R 2 (L) 2
2
故可求得： L 502 302 = 40Ω 40 L = 127 mH
解：
u 10
i 50 2 sin(314t 45 )=50 2 cos(314t 45 )
i 45
故：P UI cos(u i )=300 50cos55 8610(W )
例9－17：测量电感线圈R、L的实验电路，已知电压 表的读数为50V，电流表的读数为1A，功率表读数为 30W，电源的频率f =50Hz。试求R、L之值。
PC=UIcos =UIcos(-90)=0
电容不消耗有功 且QC<0
1 2 QC UI I wCU 2 wC
* 电感、电容的无功功率具有互相补偿的作用
例9-16： 求平均功率P。 已知u, i关联取向，且： u 300 2 cos(314t 10 )(V) i 50 2 sin(314t 45 )(A)
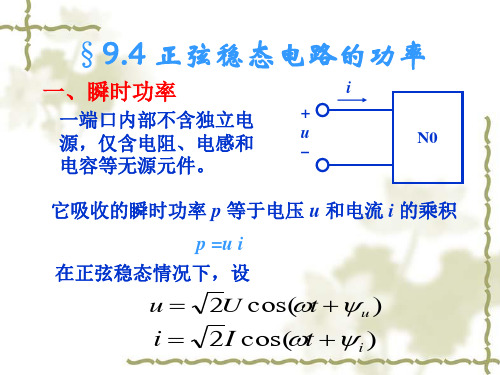
2I cos( t i )
UI cos( u i ) UI cos(2t u i )
u i
为电压和电流之间的相位差
p UI cos UI cos(2t u i )
瞬时功率有两个分量： 第一个为恒定分量，第二个为正弦分量。
§9.4 正弦稳态电路的功率
一、瞬时功率
一端口内部不含独立电 源，仅含电阻、电感和 电容等无源元件。
+ u i N0
它吸收的瞬时功率 p 等于电压 u 和电流 i 的乘积 p =u i 在正弦稳态情况下，设
u
2U cos( t u )
i
2I cos( t i )
瞬时功率 p= 令
另一种解法
而 R = 30 Ω I R 30 Z R 2 (L) 2
2
故可求得： L 502 302 = 40Ω 40 L = 127 mH
解：
u 10
i 50 2 sin(314t 45 )=50 2 cos(314t 45 )
i 45
故：P UI cos(u i )=300 50cos55 8610(W )
例9－17：测量电感线圈R、L的实验电路，已知电压 表的读数为50V，电流表的读数为1A，功率表读数为 30W，电源的频率f =50Hz。试求R、L之值。
PC=UIcos =UIcos(-90)=0
电容不消耗有功 且QC<0
1 2 QC UI I wCU 2 wC
* 电感、电容的无功功率具有互相补偿的作用
例9-16： 求平均功率P。 已知u, i关联取向，且： u 300 2 cos(314t 10 )(V) i 50 2 sin(314t 45 )(A)
正弦稳态电路
I L I L i
u L I LmL sin(t U L I LL i
2
i )
2
jLI L i
U L jL I L jX L I L
相量图如图
. U
. I
3.电感元件的功率
iL I Lm sin t u L U Lm sin(t ) 2
相量图如图（b）所示 3.电阻元件的功率 瞬时功率p ：元件上电压的瞬时值与电流的瞬时值的乘 积叫做该元件的瞬时功率。 有功功率P：计算瞬时功率的平均值, 即平均功率， 又叫有功功率。
功率的单位为瓦(W）, 工程上也常用千瓦（kW）
瞬时功率
p ui pR uRiR U Rm sin t I Rm sin t U Rm I Rm U Rm I Rm sin t (1 cos2t ) 2 U R I R (1 cos2t )
I Ie
.
j (t i )
I i
注：正弦量与相量一一对应。
２、相量图
相量图就是把正弦量的相量画在复平面上。
例： 已知正弦电压u1(t)=141 sin(ωt+π/3) V， u2(t)=70.5 sin(ωt-π/6) V， 写出u1和u2的相量， 并画出相 . 141 量图。 解：
相位差
φ12 =(ωt+ φ 1 )―(ωt+ φ2 )= φ1 ― φ2
由此得： 相位差＝初相之差 同频率正弦量的几种相位关系： （１）超前关系
φ12= φ 1 -φ 2>0且|φ12|≤π弧度，称第一量超前第二量
（２）滞后关系 φ12= φ 1 -φ 2 <0且|φ12|≤π弧度，称第一量滞后第二量， 即，称第二量超前第一量。
u L I LmL sin(t U L I LL i
2
i )
2
jLI L i
U L jL I L jX L I L
相量图如图
. U
. I
3.电感元件的功率
iL I Lm sin t u L U Lm sin(t ) 2
相量图如图（b）所示 3.电阻元件的功率 瞬时功率p ：元件上电压的瞬时值与电流的瞬时值的乘 积叫做该元件的瞬时功率。 有功功率P：计算瞬时功率的平均值, 即平均功率， 又叫有功功率。
功率的单位为瓦(W）, 工程上也常用千瓦（kW）
瞬时功率
p ui pR uRiR U Rm sin t I Rm sin t U Rm I Rm U Rm I Rm sin t (1 cos2t ) 2 U R I R (1 cos2t )
I Ie
.
j (t i )
I i
注：正弦量与相量一一对应。
２、相量图
相量图就是把正弦量的相量画在复平面上。
例： 已知正弦电压u1(t)=141 sin(ωt+π/3) V， u2(t)=70.5 sin(ωt-π/6) V， 写出u1和u2的相量， 并画出相 . 141 量图。 解：
相位差
φ12 =(ωt+ φ 1 )―(ωt+ φ2 )= φ1 ― φ2
由此得： 相位差＝初相之差 同频率正弦量的几种相位关系： （１）超前关系
φ12= φ 1 -φ 2>0且|φ12|≤π弧度，称第一量超前第二量
（２）滞后关系 φ12= φ 1 -φ 2 <0且|φ12|≤π弧度，称第一量滞后第二量， 即，称第二量超前第一量。
正弦电流电路的稳态分析基础知识讲解
dt t
T 1T
0
0
2
20 2
I
1 T
I
2 m
T 2
Im 2
0.707Im
Im 2I
i(t ) Im sin(wt Ψ ) 2I sin(wt Ψ )
同理，可得正弦电压有效值与最大值的关系：
1 U 2 Um
或
U m 2U
若一交流电压有效值为U=220V，则其最大值为Um311V；
U=380V，
二、正弦量的相量表示
两个正弦量 i1 2 I1 sin(wt y1 )
u, i
角频率： 有效值：
i1
w
i1
i2
wi2
I1
I2
初相位：
1 O 2
i2 2 I2 sin(wt y2 )
i1+i3i2 i3
w
I3
wt3
无论是波形图逐点相加，或用三角函数做都很繁。
因同频的正弦量相加仍得到同频的正弦量，所以，只 要确定初相位和有效值(或最大值)就行了。于是想到复数， 复数向量也包含一个模和一个幅角，因此，我们可以把正 弦量与复数对应起来，以复数计算来代替正弦量的计算， 使计算变得较简单。
解：
•
I
10030o
A
•
U 220 60o V
试用相量表示i, u .
例2.
•
已知I
5015
A,
f 50Hz .
试写出电流的瞬时值表达式。
解：i 50 2sin(314t 15 ) A
相量图(相量和复数一样可以在平面上用向量表示)：
•
U
•
I
i(t) 2Isin(ω t ) I I u(t) 2Usin(ωt θ ) U Uθ
T 1T
0
0
2
20 2
I
1 T
I
2 m
T 2
Im 2
0.707Im
Im 2I
i(t ) Im sin(wt Ψ ) 2I sin(wt Ψ )
同理，可得正弦电压有效值与最大值的关系：
1 U 2 Um
或
U m 2U
若一交流电压有效值为U=220V，则其最大值为Um311V；
U=380V，
二、正弦量的相量表示
两个正弦量 i1 2 I1 sin(wt y1 )
u, i
角频率： 有效值：
i1
w
i1
i2
wi2
I1
I2
初相位：
1 O 2
i2 2 I2 sin(wt y2 )
i1+i3i2 i3
w
I3
wt3
无论是波形图逐点相加，或用三角函数做都很繁。
因同频的正弦量相加仍得到同频的正弦量，所以，只 要确定初相位和有效值(或最大值)就行了。于是想到复数， 复数向量也包含一个模和一个幅角，因此，我们可以把正 弦量与复数对应起来，以复数计算来代替正弦量的计算， 使计算变得较简单。
解：
•
I
10030o
A
•
U 220 60o V
试用相量表示i, u .
例2.
•
已知I
5015
A,
f 50Hz .
试写出电流的瞬时值表达式。
解：i 50 2sin(314t 15 ) A
相量图(相量和复数一样可以在平面上用向量表示)：
•
U
•
I
i(t) 2Isin(ω t ) I I u(t) 2Usin(ωt θ ) U Uθ
电路正弦稳态电路课件
由电路参数决定。
电路参数与电路性质的关系：
由于:
U U U u Z Z u i I I i I
其中,
Z Z R j X L XC ＝Ｒ＋ｊＸ
呈感性
当 XL >XC 时， > 0 ，u 超前 i
当 XL < XC 时 ， < 0 ， u 滞后 i
R jX 1 1 Y G jB Z R jX R 2 X 2 X G 2R 2 , B 2 R X R X 2 1 | Y | , y z |Z |
一般情况 G1/R B1/X。若Z为感性，X>0，则B<0， 即仍为感性。
同样，若由Y求Z，则有：
令
. I I i I Y . i u G jB | Y | y U U u U
Y— 复导纳；G—电导(导纳的实部)；B—电纳(导纳的虚部)； |Y|—复导纳的模； y—导纳角。 |Y| 关系： G=|Y|cosy B | Y | G 2 B 2 y 或 B B=|Y|siny y arctg G G 导纳三角形 反映i ,u 幅度关系。 |Y|=I/U y = i- u 反映i ,u 相位关系。 好好理 解喽! 1 | Y | , y z |Z|
G
L
C
LL
BC= ω C BL=1/ ω L
当 C > 1/ L ，B>0， y >0，电路为容性，i 领先u；
当 C<1/ L ，B<0， y <0，电路为感性，i 落后u；
当C=1/ L ，B=0， y =0，电路为电阻性，i 与u同相。
阻抗与导纳
画相量图：选电压为参考向量(设C < 1/ L， y <0 )
电路参数与电路性质的关系：
由于:
U U U u Z Z u i I I i I
其中,
Z Z R j X L XC ＝Ｒ＋ｊＸ
呈感性
当 XL >XC 时， > 0 ，u 超前 i
当 XL < XC 时 ， < 0 ， u 滞后 i
R jX 1 1 Y G jB Z R jX R 2 X 2 X G 2R 2 , B 2 R X R X 2 1 | Y | , y z |Z |
一般情况 G1/R B1/X。若Z为感性，X>0，则B<0， 即仍为感性。
同样，若由Y求Z，则有：
令
. I I i I Y . i u G jB | Y | y U U u U
Y— 复导纳；G—电导(导纳的实部)；B—电纳(导纳的虚部)； |Y|—复导纳的模； y—导纳角。 |Y| 关系： G=|Y|cosy B | Y | G 2 B 2 y 或 B B=|Y|siny y arctg G G 导纳三角形 反映i ,u 幅度关系。 |Y|=I/U y = i- u 反映i ,u 相位关系。 好好理 解喽! 1 | Y | , y z |Z|
G
L
C
LL
BC= ω C BL=1/ ω L
当 C > 1/ L ，B>0， y >0，电路为容性，i 领先u；
当 C<1/ L ，B<0， y <0，电路为感性，i 落后u；
当C=1/ L ，B=0， y =0，电路为电阻性，i 与u同相。
阻抗与导纳
画相量图：选电压为参考向量(设C < 1/ L， y <0 )
正弦稳态电路的功率公式
正弦稳态电路的功率公式在电路中，功率是电能转换的重要指标之一。
而对于正弦稳态电路，我们可以通过一条简单而有效的公式来计算其功率。
本文将详细介绍正弦稳态电路的功率公式，并解释其背后的原理和应用。
一、正弦稳态电路的功率公式正弦稳态电路是指电路中的电流和电压都是正弦波形式，并且其频率保持不变。
在这种情况下，我们可以使用以下功率公式来计算电路中的功率：P = Vrms * Irms * cos(θ)其中，P表示电路的功率，Vrms表示电压的有效值，Irms表示电流的有效值，θ表示电压和电流之间的相位差。
二、功率公式的原理解释为了更好地理解功率公式的原理，我们可以从电能转换的角度来解释。
在正弦稳态电路中，电流和电压都是周期性变化的，而功率则是电能转化的速率。
根据能量守恒定律，电路中产生的功率等于电能的消耗速率。
在公式中，Vrms和Irms分别表示电压和电流的有效值。
有效值是指在一个周期内，电压和电流的平方值的平均值的平方根。
有效值可以反映电压和电流的实际大小，而不受正弦波形式的影响。
而c os(θ)则表示电压和电流之间的相位差。
相位差是指电压和电流的波形之间的时间差，它可以是正值、负值或零值。
当相位差为零时，电压和电流完全同相，功率取得最大值。
当相位差为正值或负值时，电压和电流存在一定的错位，功率将减小。
因此，正弦稳态电路的功率公式可以通过电压和电流的有效值以及它们之间的相位差来计算电路的功率。
三、功率公式的应用功率公式在电路分析和设计中有着广泛的应用。
它可以帮助我们计算电路中的功率消耗，并进一步优化电路的设计。
功率公式可以用于计算电路中不同元件的功率消耗。
例如，我们可以通过测量电压和电流的有效值，并计算它们之间的相位差，来确定电阻、电容或电感元件的功率消耗。
功率公式可以用于分析电路中的功率传递和传输效率。
通过计算电路中不同节点的功率，我们可以了解能量在电路中的分布情况，找出能量损失的原因，并进一步改进电路的效率。
正弦稳态电路分析和功率计算
仍为感性。
(5) 导纳三角形
Y G B
2 2
|Y|
|Y|
|B| G
(6) 导纳是频率的函数
Y(j) = G() + jB()
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 2 cos 500 t V 2 cos 3000 t V 为 120 与 120 时的稳态电 流 i(t)，并画出相量图。
1 I 记为 Y。 即 Y 。单位：西门子（S）. Z U
元件
I
Y
U
I Y U
—— 欧姆定律的相量形式
U Z I
1 I Y Z U
一端口
+ U
I
N0
—— 输入阻抗 (导纳)
N 只含阻抗与受控源
3. 分析
I Y U
(1) 元件与不含独立源的一端口的 VCR 统一表达为： ，不再表现为微积分的关系； I Y U I (2) Y 为一复数，记为 Y = G + jB . U 其中： G — 电导分量 (S)； B — 电纳分量 (S) 1 BL — 感纳 BC = C — 容纳； L I I I 2 2 (3) Y Y i u Y G B U U U
正弦稳态电路：（ m个网孔，m个网孔电流 Im1 , Im2 , … Imm）
Z Im Im2 Z Im m U 11 1 Z 12 1 m S 11 I Z I Z I U Z 21 m 1 22 m 2 2m m m S22 Z I Z I Z I U 1 m 1 m 2 m 2 m mm m Sm m m
电路原理 正弦稳态电路的计算
j10Ω I
A
A
I1
I2 C1
B
5Ω j5Ω V
分析：已知电容支路的电流、电压和部分参数
求总电流和电压 解题方法有两种： (1) 用相量(复数)计算
(2) 利用相量图分析求解
15
j10Ω I
A
I1
A I2 C1
B
5Ω j5Ω V
已知：I1= 10A、 UAB =100V，
求：A、V 的读数
解法1: 用相量计算
•
US 1
+
•
U s1 -
j
X
L
I2
I3
R
•
US
2
- I1 I2 I3 0
- j2I1 5I3 100
j5I2 5I3 j100
R
•
I3
②
3.6.2图(b)
•
I2 +
•
U s2 -
8
(2)回路电流法
•
I
1
jX C
jX L
+
•
•
U s1
Ia
-
•
Ib
R
•
I3
R - j X C
Ia
RIb
IC2 UC1
IR2 UR1 1
U2C 2 I1 C 1
U2 R2
I1 R1
•
I1
R1
C1
•
IC2
U + +
•
U1
•
-
3
R2
C2
•
+ •
U2
-
I R2
-
3.6.4例5图(a)
•
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
已知：U=115V , U1=55.4V ,
U2=80V , R1=32 , f=50Hz 求： 线圈的电阻R2和电感L2 。
解一： I U1 / R1 55.4 / 32
U
I
(R1 R2 )2 (L)2
U2
I
R22 (L)2
115
55.4
(32 R2 )2 (314L)2 32
80
55.4
i2 0.182 2 cos(314t 20) A
i3 0.57 2 cos(314 t 70) A
14
例4. 已知：IS 490o A , Z1 Z 2 j30Ω
Z3 30Ω , Z 45Ω 求：I.
Z2 I
解： 法一：电源变换
IS
Z1 Z3 Z
Z1
//
Z3
30( j30) 30 j30
∑i (t) = 0 ∀t ∑I= 0
∑u (t) = 0 ∀t ∑U= 0
3. 基本元件VCR（VAR）的相量形式
UR RIR
UR RIR
UL jL IL
U L LIL
UC
1
jC
IC
j
1
C
IC
UC
1
C
IC
∑Im = 0 ∑Um = 0
u i
u
i
2
u
i
2
7
3. 感抗、容抗、电抗、复阻抗、感纳、容纳、电纳、复导纳
i2 R1 i1
i3 C
+
R2
_u
L
I1 I2 R1
I3
j 1 C
+
R2
U _
Z1
Z2
jL
解：画出电路的相量模型
Z1
R1 ( R1
j
1
C
)
j
1
C
1000 ( j318.5) 1000 j318.5
318.5 103 90 1049 17.67
303.6 72.32 92.20 j289.3
jF Im
b
F
|F|
0
a Re
-F
-jF
旋转因子: j，-j，-1
设 F F e j
则 jF e j90 F F e j( 90)
jF e F j(90) F e j( 90)
F e F j(180) F e j( 180)
3
复数运算
(a)加减运算——直角坐标
F1±F2=(a1±a2)+j(b1±b2) (b) 乘除运算——极坐标
③ 求解
10
例1. 列写电路的回路电流方程 _ US +
I1 jL
R1
R2
I3
I4
1
IS
I2
R4
R3
jc
解：
(R1 R2 jL)I1 (R1 jL)I2 R2 I3 US
( R1 R3 R4 jL)I2 (R1 jL)I1 R3 I3 0
(R2
I4
R3
IS
1
jC
)I3
F1 F2 F1 e j1 F2 e j2
F1
F e j(1 2 ) 2
F1 F2 1 2
a F cos , b F sin
F a2 b2 , arctan b
a
F1 F2
F1 e j1 F2 e j2
F e 1 j(1 2 ) F2
F1 F2
1 2
4
u(t) Um cos(t u )
R2 I1
R3 I2
1
jC
I4
0
11
例2. 列写电路的节点电压方程
1 Y3 2
Y1
IS1
Y4
Y5
Y2
+
•
U _ S4
•+ U _S5
解：
(Y2 Y3 )U1 Y3U2 IS1 Y3U1 (Y3 Y4 Y5 )U2 Y4US4 Y5US5
12
例 3: 已知: R1 1000 , R2 10 , L 500mH , C 10F , U 100V , 314rad / s , 求:各支路电流。
Z2
Z1 Z3= Z2 Zx
Zx
Z3
R1(R3+j L3)=R2(Rx+j Lx)
∴ Rx=R1R3 /R2 Lx=L3 R1/R2
17
例6.
•
I
+
•
U_S
已知：Z=10+j50 , Z1=400+j1000。
Z
问：β 等于多少时，I1和US相位差90o ?
•
I1
Z1
•
β I1
分析：找出I1和US关系：US Z转 I1， Z转实部为零, 相位差为90o.
第22讲 正弦稳态电路的计算
学习重点： 掌握正弦稳态电路的分析步骤和方法。
1
回顾：
1. 正弦量与相量
u(t) Um cos(t u )
2U cos(t u )
三 要
i(t) Im cos(t i ) 2I cos(t i ) 素
复数及运算 虚数单位 j 1
欧拉公式: e j cos j sin
线性电阻电路
i 0 u0
u Ri i G u
网孔法
节点法
等效电源定理
正弦稳态电路(相量模型)
I 0 U 0
U Z I I Y U
网孔法
节点法
等效电源定理
9
相量法分析正弦稳态电路的步骤:
① 画出电路的相量模型
R
i , u U , I
L
C
② 列相量代数方程
I 0 , U 0
R
jL
1
jC
U Z I, I Y U
22
第22讲 正弦稳态电路的计算
结束
作业: P268 4-14 P269 4-17 、4-18
预习: 正弦稳态电路的功率
23
15
j15
I
IS(Z1 // Z3 ) Z1 // Z3 Z2 Z
j4(15 j15) 15 j15 j3045
5.65745o 5 - 36.9o
1.1381.9o A
Z2
Z1Z3
I
+
Z
( Z1 // Z 3 )IS
-
15
法二：戴维南等效变换
•
I
Z0
•+
Z
IS
U0
-
Z2 Z1 Z3 U0
求开路电压： U0 IS (Z1 // Z3 )
根据振幅相量可写出正弦量的瞬时值表达式。
5
U m 2U Um 2U 有效值相量
相量运算
（1）同频率正弦量相加减
u(t) u1 (t) u2 (t) U U1 U2
（2） 正弦量的微分、积分运算
i(t) I
di j I
dt
idt
1
j
I
6
2. KCL和KVL的相量形式
时域形式 ⇔ 有效值相量形式⇔ 振幅相量形式
U R2 U2 cos 2 80 cos 64.9 33.94V
•
I U1 / R1 55.4 / 32 1.731A
R2 UR2 I 33.94 1.731 19.6
I R1
+
+
_ U1 R2
+
L2 UL2 I 72.45 1.731 41.85
U _
U2 L2 _
L2 41.85 314 0.133 H
Z2 R2 jL 10 j157Ω
13
I1 I2 R1
I3
j 1 C
+
U _
Z1
R2
jL
Z Z1 Z2
167.2 52.31
Z2
I1
I2
U 0.59852.3 A Z
j
1
C
1
I1 0.182
20.0
A
R1 j C
I3
R1
R1 j 1
C
I1 0.57070.0 A
i1 0.598 2 cos(314 t 52.3) A
R22 (314L)2 32
R2 19.6 L2 0.133H
19
解二： U U1 U2 U1 UR2 UL2
U
U2
U
2 1
U
2 2
2U1U 2
cos
U1
U2 UL
2 UR2 I
cos 0.4237 115.1 2 180 64.9
U L2 U2 sin 2 80 sin64.9 72.45V
F (t ) U m cos(t u ) jU m sin(t u )
U m e j(tu )
u(t) Re F(t) Re Ume j(tu )
Re Ume ju e jt
令：Um Ume ju Umu 称为振幅相量
振幅相量包含振幅和初相，在已知角频率的情况下，
84.8645o V
求等效阻抗： Z0 Z1 // Z3 Z2
15 j45Ω
I U0 84.8645 1.1381.9o A
Z0 Z 15 j45 45
16
例5. 已知平衡电桥Z1=R1 , Z2=R2 , Z3=R3+j L3 。 求：Zx=Rx+jLx。
解： 由平衡条件：
Z1
感抗 X L L
容抗
XC
1
C
电抗X
感纳
BL
1
L
容纳 BC C
电纳B