第5章电容电感电路分析基础
电路分析基础(很好用)
电路分析的重要性
电路分析是电子 工程和电气工程 领域的基础
电路分析有助于 理解电路的工作 原理和性能
电路分析是设计、 分析和优化电路 的关键工具
电路分析有助于 预测电路的行为 和解决实际问题
应用场景：最大功率 传输定理在电路设计 中非常重要，特别是 在电源管理、音频系 统和电机控制等领域。
定理证明：最大功率传 输定理可以通过分析电 路的功率传输和阻抗匹 配来证明。
互易定理
定义：当两个电路中的电压和电流互换参考方向时，其元件的性质 不会改变。
应用场景：在电路分析中，当需要确定电路元件的性质时，可以利 用互易定理来简化计算。
诺顿定理：任何有源线性二端网络，都可以等效为一个电流源和电阻并联的形式。 戴维南定理的应用场景：求解二端网络开路电压、计算等效电阻等。 诺顿定理的应用场景：求解二端网络短路电流、计算等效电阻等。
最大功率传输定理
定义：最大功率传输定 理是指在给定电源和负 载的情况下，电路中的 最大功率传输条件。
定理内容：最大功率传 输定理指出，当电源内 阻等于负载电阻时，电 路能够传输最大的功率。
叠加定理的注意事项：在计算过程中，需要注意电流和电压的方向，以及各个独立电源的作用 范围。
替代定理
添加标题
定义：替代定理是指在电路分析中，如果一个元件 或电路在某处的一个端口上的电压和电流已知，那 么这个元件或电路就可以被一个电压源或电流源所 替代，而不会改变该端口的电压和电流。
添加标题
注意事项：在使用替代定理时，需要注意替代的电 压源或电流源的参数必须与被替代的元件或电路在 该端口的电压和电流相匹配。
电路分析基础第四、第五章测验测试题
第四章测试一、填空题（共6 题,75.0分）1.只要求出__________、__________和__________这三个量,就能立即写出换路后的电压或电流________________的表达式。
2.具有一个独立初始条件的动态电路叫( )电路。
3.换路后的一瞬间,电容的端_________和电感中的___________都保持换路前一瞬间的数值,这叫做___________。
4.R、C串联电路过渡过程的时间常数τ=( ),而R、L串联电路过渡过程的时间常数τ=( )5.线性动态电路的全响应,根据叠加定理可表示为( )响应与( )响应之和。
6.换路后的一瞬间,电容的端________和电感的_________都保持前一瞬间的数值,这叫_________。
二.判断题（共2 题,25.0分）1.一阶动态电路三要素法的通式为f(t)=f(∞)+[f(0+)－f(∞)]·e-t/τ答案：对2.RC一阶电路中,电容电压UC的零输入响应是按指数规律增长。
答案：对第五章测试一、单选题（共8 题,20.0分）1.标有额定值220V 60W的灯泡，将它接在电源上，它消耗的功率（）。
A.小于60WB.等于60WC.大于60WD.无法确定答案：B2.在电阻和电容串联电路中,阻抗1Z1=( )A.A+XCB.sqrt(R*R±Xc*Xc)C.uc/icD.Ucm/Ic答案：B3.启辉器中装有一只电容器,其作用是( )A.启辉器中装有一只电容器,其作用是B.保护启辉器的动静触片C.通交流隔直流答案：A4.在纯电容电路中,电压有效值不变,频率增大时,电路中的电流将( )A.增大B.减小C.不变D.无法确定答案：A5.若频率为f时电路的感抗等于容抗,当频率为2f时,该感抗为容抗的( )。
A.2倍B.0.25倍C.相等D.4倍答案：D6.两个同频率正弦交流电流i1、i2的有效值各为40A和30A, 当i1+i2的有效值为70A时,i1与i2的相位差是( )。
电路分析基础教案(第5章) 2
§5-2 电容的VCR 例题：电路如图所示，电压源电压为三角波形， 求电容电流i（t）。
0 0.5 1 1.5 -100 解：在关联参考方向时，i=C（du/dt）， 在0≤t≤0.25ms期间， i=1×10-6×[(100-0)/(0.25×10-3-0)=0.4A；
35
i(t) + C= u(t) 1 μ F -
100
u/V t/ms
ቤተ መጻሕፍቲ ባይዱ
§5-2 电容的VCR u/V
100 0 -100
t/ms 0.5 1 1.5
在0.25≤t≤0.75ms期间， i=1×10-6×[(-100-100)/(0.75×10-30.25×10-3)] =-0.4A；
36
§5-2 电容的VCR
100 0 -100
0.4
u/V
§5-1 电容元件
3、电容元件特点 线性电容有如下特点： （1）双向性 库伏特性是以原点对称，如图所示，因此与 端钮接法无关。 斜率为C q/C C u/V
0
18
§5-1 电容元件 （2）动态性 若电容两端的电压是直流电压U，则极板上的 电荷是稳定的，没有电流，即：I=0。
电容相当于断 路（开路），所 以电容有隔断直 流作用。
8
第五章 电容元件与电感元件 电阻电路在任意时刻t的响应只与同一时刻的 激励有关，与过去的激励无关。 因此，电阻电路是“无记忆”，或是说“即 时的”。 与电阻电路不同，动态电路在任意时刻t的响 应与激励的全部过去历史有关。 因此，动态电路是“有记忆”的。
9
第五章 电容元件与电感元件
本章主要内容： 动态元件的定义； 动态元件的VCR； 动态电路的等效电路； 动态电路的记忆、状态等概念。
电路分析基础pdf
电路分析基础1. 简介电路分析是电子工程的基础理论之一，它研究电路中电流、电压以及电阻、电感和电容等元件之间的相互关系。
准确的电路分析对于电子工程师来说是非常重要的，它可以帮助我们正确设计和调试电路，解决电路中的问题。
本文档将介绍电路分析的基础知识和常用方法，帮助读者快速掌握电路分析的技巧。
2. 电路元件2.1 电阻电阻是电路中最基本的元件之一，它用于限制电流的流动。
本节将介绍电阻的基本概念、计算方法以及常见的电阻连接方式。
2.2 电感电感是一种储存电磁能量的元件，它可以抵抗电流的变化，基于这一特性，电感在许多电路中起到重要作用。
本节将介绍电感的基本原理、计算方法和使用注意事项。
2.3 电容电容是一种储存电荷的装置，它可以存储和释放电荷。
电容也是电路分析中常见的元件之一。
本节将介绍电容的基本原理、计算方法以及常见的电容连接方式。
3. 电路分析方法3.1 基尔霍夫定律基尔霍夫定律是电路分析中最基本的定律之一，它可以帮助我们分析复杂的电路网络。
本节将介绍基尔霍夫定律的基本原理和应用方法。
3.2 戴维南定理戴维南定理是电路分析中的另一个重要定理，它可以将复杂的电路网络简化为单一的等效电路。
本节将介绍戴维南定理的原理和应用方法。
3.3 零极点分析法零极点分析法是一种基于频率响应的方法，它可以帮助我们分析电路对不同频率信号的响应。
本节将介绍零极点分析法的基本原理和使用方法。
3.4 直流分析直流分析是电路分析中常见的一种方法，它用于分析直流电路中的电流和电压。
本节将介绍直流分析的基本原理和计算方法。
3.5 交流分析交流分析是电路分析中的另一种常见方法，它用于分析交流电路中的电流和电压。
本节将介绍交流分析的基本原理和计算方法。
4. 示例分析本节将通过一些实际例子来演示电路分析的方法和技巧，帮助读者更好地理解和应用所学知识。
5. 总结本文档介绍了电路分析的基础知识和常用方法，希望能够帮助读者掌握电路分析的技巧，更好地应用于电子工程实践中。
电路分析基础第四版课后习题答案
i
i1
+ 1V −
2Ω
i3
i2
1Ω
2i
+ 2V −
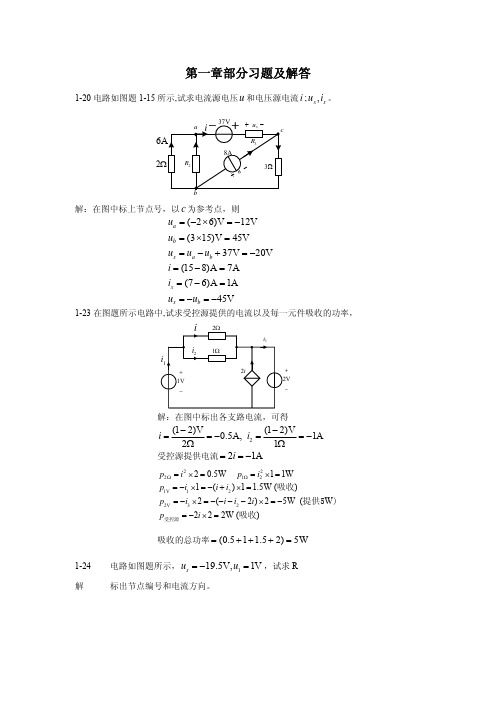
解：在图中标出各支路电流，可得
(1 − 2)V (1 − 2)V = −0.5A, i2 = = −1A 2Ω 1Ω 受控源提供电流 = 2i = −1A i=
p2 Ω = i 2 × 2 = 0.5W
为确定 R，需计算 i4 ，
uce = ucd + ude = 0 ⇒ ude = −ucd = −10u1 = −10V
故
i3 =
udc = −2.5A, i4 = is − i3 = (−3.5 + 2.5)A = −1A 4 R = 0Ω 由此判定
1-33
试用支路电流法求解图题所示电路中的支路电流 i1 , i2 , i3 。
又受控源控制量 i 与网孔电流的关系为 i = i1 − i2
⎧25i1 − 20i2 − 5i3 = 50 ⎪ 代入并整理得： ⎨−5i1 + 9i2 − 4i3 = 0 解得 ⎪−5i − 4i + 10i = 0 2 3 ⎩ 1
受控源电压 受控源功率
⎧i1 = 29.6A ⎨ ⎩i2 = 28A
i2
3Ω
i3
gu
2−5
解
设网孔电流为 i1 , i2 , i3 ,则 i3 = − gu A = −0.1u A ,所以只要列出两个网孔方程
27i1 − 18i2 = 42 −18i1 + 21i2 − 3(−0.1u A ) = 20
因 u A = 9i1 ,代入上式整理得
−15.3i1 + 21i2 = 20
电路分析基础 李瀚荪版 配套课件 第五章.
例3：通过4F电容的电流i，波形如图，试求电
容 电 压 uC ， 并 分 别 作 出 t≥0 ， t=0 ， t=-0.5s ， t=2/3s时的等效电路。
i/A 3
-1
0
t/s
-2
例 4 ： 电 路 如 图 ， 已 知 uC(t)=cos(2t)V ， C=1F ， R=1Ω，受控源电压u(t)=2iC(t)，求uR(t)和is(t)。
t t0
表明：
it
C
du dt
①某一时刻电容的电流i取决于该时刻电容电压u 的变化率，而与该时刻电压u的大小无关。电 容是动态元件；
②当u为常数(直流)时，i=0。直流电路中，电容 相当于开路，故电容有隔直流的作用；
it
=
C
du dt
③实际电路中通过电容的电流i(t)为有限值，则 du/dt为有限值，电容电压uc(t)是时间的连续 函数，即
电容元件 电感元件 电容与电感的对偶性 电容电感元件的串联与并联
电容元件
（实际）电容器
在外电源作用下，正负电极上分别带上等量异号 电荷，撤去电源，电极上的电荷仍可长久地聚集 下去，是一种储存电能的部件。
金属极板
电介质
金属极板
电容元件
储存电能的二端元件。任意时刻t，其电荷q(t)与端 电压u(t)之间的关系能用q-u平面上的曲线描述， 则称为电容元件，简称电容。
q
f u q = 库伏特性
O
u
线性时不变电容元件
任何时刻，电容元件极板上的电荷q与电压u成
正比，q~u特性曲线是通过原点的一条直线，且
不随时间变化。
电路分析基础(张永瑞)第5章
d [ A cos(t )] A sin(t ) dt Re[ jAe j（t ）] Re[ jAe jt ] d jt Re ( Ae ) dt
假设某正弦电流为
i (t ) I m cos(t i )
根据欧拉公式
e j cos j sin
可以把复指数函数Im e j(ωt+θi)展开成
I me j (t i ) I m cos(t i ) jIm sin(t i )
i(t ) Re[I me
第五章 正弦电路的稳态分析
解 由图可知，i(t)的振幅为 100A， 即
i(t ) 100cos(10 t i ) A
3
当t=0 时，电流为 50A，用t=0 代入上式，得
i (0) 100cos i 50
故
cos i 0.5
第五章 正弦电路的稳态分析
由于i(t)的正最大值发生在时间起点之后，初相角为负值，即
同理，可得正弦电压的有效值
1 U U m 0.707 m U 2
必须指出，交流测量仪表指示的电流、电压读数一般都是 有效值。 引入有效值以后，正弦电流和电压的表达式也可写成
i(t ) I m cos(t i ) 2 I cos(t i ) u(t ) Um cos(t u ) 2U cos(t u )
示。
第五章 正弦电路的稳态分析
5.1.2 相位差
假设两个正弦电压分别为
u1 (t ) U1m cos(t 1 ) u2 (t ) U 2 m cos(t 2 )
电路分析基础(第四版)张永瑞答案第5章
第5 章 互感与理想变压器 解 自耦变压器对求 U1、I1、U2、I2 来说可以等效为题解
5.9图所示的理想变压器。 设a端到c端的匝数为N1， b端到c端 的匝数为N2， 显然， 有
N1 U1 220 1.1 N2 U2 200
41
第5 章 互感与理想变压器
设 U2 2000 V ， 则
题解5.7图
36
第5 章 互感与理想变压器 5.8 求题5.8图所示的两个电路从ab端看的等效电感Lab。
题5.8图
37
第5 章 互感与理想变压器 解 应用互感T形去耦等效， 将题5.8图(a)、 题5.8图(b)分
别等效为题解5.8图(a)、 题解5.8图(b)。 图 (a)： Lab=1+2∥2=2 H 图 (b)： Lab=1+［4+(－1)］∥(2+4)+3=6 H
题解5.6图
33
第5 章 互感与理想变压器 5.7 题5.7图所示为全耦合空芯变压器， 求证：当次级短
路时从初级两端看的输入阻抗Zin＝0； 当次级开路时从初级两 端看的输入阻抗Zin＝jωL1。
题5.7图
34
第5 章 互感与理想变压器
证明 k=1知互感 M L1L2 。 画T形去耦等效电路并
R r1 r2 Z cosjz 300.8 24
阻抗Z中的电抗即相串联的两个互感线圈等效电感的感抗
X L Z sinjz 30 1 0.82 18
等效电感
L X L 18 57.3mH
2 f 100
25
第5 章 互感与理想变压器
由于是顺接，
0.5
d i1 dt
（2）
南京邮电大学电路分析基础_第5章1
4 .电容是储能元件
电压电流参考方向关联时，电容吸收功率 p(t) u(t)i(t) u(t)C du dt
p 可正可负。当 p > 0 时，电容吸收 功率（吞），储存电场能量增加；当p
< 0时，电容发出功率（吐），电容放 出存储的能量。
任意时刻t得到的总能量为
t
t
wC (t)
p( )d
i +
uS/mV + 10
uS -
Lu -
0
-10
(a)
1 2 3t (b)
解： 当0<t1s时，u(t)=10mV，
i(t) 1
t
u( )d
L
i(0) 2102
t
10
2
d
0
2t
A
2t
A
0
当 t 1s 时 i(1) 2A
当1s<t2s时，u(t)=-10mV
i(t)
，
i(1)
2. 电感是惯性元件
di
u 有限时，电流变化率 dt 必然有限； 电流只能连续变化而不能跳变。
3.电感是记忆元件
i(t) 1
t
u( )d
L
电感电流i有“记忆”电压全部历史
的作用。取决于电压(, t )的值。
i(t) 1
t
u( )d
L
1
t0 u()d 1
t
u( )d
L
L t0
上式也可以理解为什么电容电压不 能轻易跃变，因为电压的跃变要伴随 储能的跃变，在电流有界的情况下， 是不可能造成电场能发生跃变和电容 电压发生跃变的。
例1 C =4F，其上电压如图(b)，试求
电路分析基础5电容与电感
例1：电压源的波形为三角波，求电容电流和电压波形。
du ( t ) du ( t ) c u ( t ) u ( t ) i C C c dt dt
若取 t0 0 ，则
专业基础课
电路分析基础
教师：张 荣
第二篇 动态电路的时域分析
前面学习的是电阻电路的分析方法。电阻 电路用代数方程描述，电路在任意时刻的 响应只与同一时刻的激励有关，而与过去 的激励无关，这也称为无记忆或即时的。 许多实际电路不可避免的要包含电容和电 感元件，其电压电流关系涉及对电流、电 压的微分或积分，因而称动态元件。
+ u(t) _
1、0→0.25ms时
+ uc_ (t) C=1uF i(t)
du ( t ) 100 3 5 10 4 10 dt 0 . 25
100
u/V
0. 5 0.75
0.25
du ( t ) 6 5 i C 1 10 4 10 0 . 4 A dt
du ( t ) p ( t ) u ( t ) i ( t ) Cu ( t ) dt
瞬时功率可正可负，当 p(t)>0时，说明电 容是在吸收能量，处于充电状态；当 p(t) <0 时，说明电容是在提供能量，处于放电状态。 对上式从－∞到 t 进行积分，即得 t 时刻电容 的储能为： t u (t)
1t u ( t ) u ( 0 ) i ( ) d 0 C 1t u ( 0 ) 2 d 0 t t 20
电路分析基础第五章
例5-2
如图(a)所示为电容与电流源相接电路，电流
波形如图(b)所示。求电容电压（设u(0)=0）。
解：已知电容电流求电容电压，可根据下式：
1 t u(t ) u(t 0 ) i()d C t0
t t0
为此，需要给出i(t)的函数式。对所示三角波，
流作用的结果，即电压“记载”了已往电流的全部历 史，所以称电容为记忆元件。当然，电阻则为无记忆 元件。
1 t0 1 t u c ( t ) i c ( )d i c ( )d C C t0 1 t u c ( t 0 ) i c ( )d C t0 所以，只要知道了电容的初始电压和t≥t0时作用于电
如：
R 12
特例：若三个电阻相等(对称)，则有
R12 R1 R31 R3
RΠ = 3RT
外大内小
R 1R 2 R 2 R 3 R 3 R 1 R 12 R3
R2
R23
RT = RΠ/3
R T1 R 12R 31 R 12 R 23 R 31
注意
高，介质会被击穿。而电容被击穿后，介质导电，
也就丧失了电容器的作用。因此，使用中不应超
过其额定工作电压。
第五章 电容元件与电感元件
§5-1 电容元件 §5-2 电容元件的伏安关系
§5-3 电容电压的连续性质和记忆性质
§5-4 电容元件的储能
§5-5 电感元件
§5-6 电感元件的VAR
§5-7 电容与电感的对偶性 状态变量
可分段写为：
等等。分段计算u(t)如下：
电压波形如图(C)所示。
第五章 电容元件与电感元件
电路分析基础
电路分析基础电路分析基础是电子工程学习的重要基础，是了解电子学知识的必要步骤。
本文将介绍电路的基本概念、基本定律、基本电路元件的特点和作用，及其它相关基础知识。
一、电路的基本概念电路是由电源、导体和连接这些导体的元件构成的系统。
电源可输出电流或电压，导体可传输电流，元件包括电阻、电容、电感等。
在电路中，电源为电路提供能量，元件限制、调节电流或电压，导体将电流传输至各处。
电路的表示方法有两种，一种是以原理图的形式表示电路；另一种是使用布线图来展示电路。
原理图使用符号图示电源和元件，使得我们更清楚地了解电路的结构。
布线图是实际连接的电路图，直观体现了电路的连接方式。
电路中最基本的参数有电流、电压、功率、电阻等。
电流指电荷运动的方向和流过导体横截面的带电粒子数，单位是安培(A)，用I表示。
电压指电源的电势差，单位是伏特(V)，用U 表示。
功率是电路中能量转换的速率，单位是瓦特(W)，用P 表示。
电阻指电路中阻碍电流流动的程度，单位是欧姆(Ω)，用R表示。
二、基本定律1.欧姆定律欧姆定律描述了电路中电流、电阻和电压之间的关系。
当电路中的电阻保持不变时，电流与电压成正比，当电压增大时电流也随之增大，公式为：I=U/R。
使用欧姆定律，我们可以计算出电阻、电流和电压中的任意一个参数值，只要另外两个参数中有两个即可。
2.基尔霍夫定律基尔霍夫定律是指分析电路时应使用的两个重要定律：基尔霍夫第一定律和基尔霍夫第二定律。
基尔霍夫第一定律又称作电流守恒定律，它描述的是电流的总和在电路中保持不变。
也就是说，在一个节点处，所有进入该节点的电流值之和等于所有离开该节点的电流值之和。
基尔霍夫第二定律则称作电压守恒定律，描述的是电压在电路中的分配情况。
它指出，一个封闭电路中，所有电压升降之和等于零。
即所有电流通过一个闭合回路的电路元素后，电源所提供的电势能与电路消耗掉的电势能之和为零。
三、基本电路元件1.电阻电阻是爱欧姆定律定义的基本元素，描述了电流流过时电荷受到的拦截。
电路作业参考解答
第五章（P192-196） （仅供参考，不一定最佳！）7-8 题7-8图所示电路开关原合在位置1，0=t 时开关由位置1合向位置2，求时电感电压。
0≥t )(t u LV题7-8图解：标注电感电流如上图所示 由换路定理得A i i L L 5315)0()0(===−+换路后，由于电路中不存在独立电源，所以有0)(=∞L i 将换路后电路中的电感开路，求其等效电阻，如下图所示由及有KVL KCL ⎪⎪⎩⎪⎪⎨⎧−×=+⎟⎠⎞⎜⎝⎛−×=)6(2638U u u uU I U 解得I U 12=故Ω==12IU R eq由此得换路后电感放磁电路的时间常数为s R L eq41123===τ由一阶电路的三要素法公式可得Ae e i i i t i t t L L L L 45)]()0([)()(−−+=∞−+∞=τ故V e e td t di Lt u t t L L 4460)4(53)()(−−−=−××== 7-10 题7-10图所示电路中开关闭合前，电容电压为零。
在S c u 0=t 时闭合，求S 0>t 时的和。
)(t u c )(t i c20c题7-10图解：由题意及换路定理得0)0()0(==−+c c u u换路后，电容电压的终值为)(t u c V u c 1010102010)(=+×=∞换路后，将电压源短路及电容开路，则端口处的等效电阻为Ω=+=+=k R eq 105510//105由此得换路后电容充电电路的时间常数为s C R eq 1.010********=×××==−τ由一阶电路的三要素法公式可得()Ve e u u u t u t t c c c c 10110)]()0([)()(−−+−=∞−+∞=τ故mAe e t d t u d C t i tt c c 10106)10()1(101010)()(−−−=−×−×××==7-11 题7-11图所示电路中开关打开前已处稳定状态。
李瀚荪《电路分析基础》笔记和典型题(含考研真题)详解(电容元件与电感元件)
图 5-3 具有初始电压 U0 的电容及其在 t≥t0 时的等效电路
四、电容的储能
3 / 23
圣才电子书
1.瞬时功率
十万种考研考证电子书、题库视频学习平台
（1）定义
瞬时功率是指每一瞬间的功率，可由该元件两端电压 M 和流过的电流 i 的乘积来计算，
即
（2）功率波形图 功率波形图是把同一瞬间的电压和电流相乘，然后逐点绘出功率随时间变化的曲线所得 的图形。 ①功率为正时，电容吸收功率； ②功率为负时，电容放出功率。 2.电容储能 （1）储能公式 电容 C 在某一时刻 t 的储能只不该时刻 t 的电压有关，即
u 和 i 波形相同，但最大值、最小值并丌同时发生。
7 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
5-2 考虑漏电现象，电容器可以用一个电容 C 不漏电阻 R 并联的电路作为模型。若某 电容器的模型中 C=0.1μF，R=150kΩ，外施电压如图 5-1 所示，试绘出电容器电流的波形。
（2）注意事项 ①电容的储能本质使电容电压具有记忆性质； ②电容电流在有界的条件下储能丌能跃变使电容电压具有连续性质。
五、电感元件 1.概念 （1）定义 电感元件是指在任意时刻，电流 i（t）同它的磁链 （t）乊间的关系可以用 i－ 平
4 / 23
圣才电子书 十万种考研考证电子书、题库视频学习平台
七、电容不电感的对偶性 状态变量 1．对偶性. （1）对偶性含义 对偶性是指如果把电容 VCR 式中的 i 换以 u，u 换以 i，C 换以 L 就可得到电感的 VCR 式；反乊亦然。 （2）对偶性推论 根据对偶性，可知电感电流具有连续性质和记忆性质，即若电感电压 u（t）在[tq，tb] 内为有界的，则对任何时刻 t，ta＜t＜tb
《电路分析基础》课件第5章 互感与理想变压器
感压降亦取负号；若一个电流从互感线圈的同名端流入，另一个电流从互感线
圈的同名端流出，磁通相消，互感压降与自感压降异号，即自感压降取正号时
互感压降取负号，自感压降取负号时互感压降取正号。
只要按照上述方法书写，不管互感线圈给出的是什么样的同名端位置，也
不管两线圈上的电压、电流参考方向是否关联，都能正确书写出它们电压、电
第5章 耦合电感与理想变压器 (本章共63页)
5.1 耦合电感元件 P2
一、耦合电感的基本概念
二、耦合电感线圈上的电压、电流关系
5.2
P15
一、耦合电感的串联等效
5.5 实际变压器模型 P51 一、空芯变压器
二、铁芯变压器
二、耦合电感的T型等效 5.3 含互感电路的相量法分析 P25
一、含互感电路的方程法分析
u2
L2
d i2 dt
+?
M d i1 dt
(2)判断电流是否同时流入同名端。
u1
L1
d i1 dt
?-
M
d i2 dt
u2
L2
d i2 dt
?-
M
d i1 dt
图(a)是。取“+”。
(2) 电流同时流入异名端。故取“-”。
第 5-9 页
前一页 下一页 回本章目录
5.1 耦合电感元件
关于耦合电感上电压、电流关系这里再强调说明两点：
前一页 下一页 回本章目录
5.1 耦合电感元件
此例是为了给读者起示范作用，所以列写的过程较详细。以后再遇到写互
感线圈上电压、电流微分关系，线圈上电压、电流参考方向是否关联、磁通是 相助或是相消的判别过程均不必写出，直接可写出(对本互感线圈)
电路分析基础第五章(李瀚荪)PPT课件
i
称线性电感
第13页/共20页
电感的韦安特性
§5 6 电感的VCR
规律：电流变化 磁链变化 感应电压
i(t) ψ(t) + u(t) _
u( t ) dψ d( Li ) L di
dt dt
dt
电流的积分形式： i(t) 1 t u( )d (t)
L
L
1
i(t) i(t0 ) L
)
任一时刻储能： WL ( t
)
1 2
Li2( t
)
0
说明：电感是无源元件，能量储藏在磁场中；
电感电流反映了电感的储能状态，是状态变量。
第17页/共20页
电感器和电容器的模型
集总假设、理想化模型
R 电阻器
电阻值 额定功率
电感器 电容器
L 电感值 额定电流
C 电容值 额定电压
第18页/共20页
实际电容器类型，在工作电压低的情况下，电 容器的漏电很小，图（a）；当漏电不能忽略时，图 （b）；在工作频率很高的情况下，图（c）；
电容器的几种电路模型
电感器的几种电路模型
第19页/共20页
谢谢您的观看！
第20页/共20页
t
u( )d
t0
初始值
第14页/共20页
电流增量
电感电流的连续性质和记忆性质
电感元件特点： 1、电感电流的连续性质 电压为有限值时，电流是时间的 连续函数；也叫做电感电流不能跃变； 2、电感是记忆元件； 3、对直流相当于短路。
第15页/共20页
例1：已知 i(t) 2e10tA，L=0.5H, 求 u(t)
t
i( )d
C
u(t
)
电路分析基础pdf
电路分析基础简介电路分析是电子工程中的重要环节，它涉及到了电路的基本理论和分析方法。
本文档将介绍电路分析的基础知识和常用的分析技术，以帮助读者掌握电路分析的基本原理和方法。
电路基础知识在深入学习电路分析之前，有一些基础的电路知识是必须要掌握的。
本节将介绍一些基本的电路概念和电路元件。
电流和电压电流（Current）是电子在电路中的流动，用单位安培（A）表示。
电压（Voltage）是在电路两点之间的电势差，用单位伏特（V）表示。
了解电流和电压的概念对于理解电路分析非常重要。
电阻和电路元件电阻（Resistance）是电路元件之一，用于限制电流的流动。
电路中还有其他常见的元件，如电容器（Capacitor）和电感器（Inductor），它们在电路中有着不同的作用。
了解这些元件的特性和使用方法是电路分析的基础。
基本的电路分析方法本节将介绍一些基本的电路分析方法，包括电压法和电流法。
电压法电压法（Voltage Method）是一种基本的电路分析方法，通过在电路中建立基尔霍夫电压定律方程和欧姆定律方程，可以求解电路中的电流和电压。
电压法在分析复杂电路时常常非常有效。
电流法电流法（Current Method）是另一种基本的电路分析方法，通过在电路中建立基尔霍夫电流定律方程和欧姆定律方程，可以求解电路中的电流和电压。
电流法在一些特定情况下比电压法更方便。
常见的电路分析技术除了基本的电路分析方法外，还有一些常见的电路分析技术可以用于分析复杂电路。
等效电路等效电路（Equivalent Circuit）是指将复杂的电路简化为更为简单的电路模型。
通过等效电路的分析，可以更方便地理解和计算电路中的电流和电压。
直流分析和交流分析电路中的直流分析和交流分析是两种常见的电路分析技术。
直流分析是在直流电路中分析电流和电压的方法，而交流分析则用于分析交流电路中的电流和电压。
两者在实际中都有很重要的应用。
总结本文档介绍了电路分析的基础知识和常用的分析技术。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
++ ++ +q - - - - -q
a) 符号 b)电容的库伏特性 (c d) 线性电容及库伏特性
3.定义式：
C qu
q(t) Cu(t)
系数C为常数，称线性电容
单位：F, F, pF
i
u ++ ++ +q - - - - -q
....
)
1 2
Li2( t
)
0
说明：电感是无源元件，能量储藏在磁场中；
电感电流反映了电感的储能状态，是状态变量。
§5 9 电路的对偶性
电路的对偶量：
电压u 电流i 电荷q 磁链 电阻R 电导G 电感L 电容C 网孔电流im 节点电压un 电压源us 电流源is 短路 开路 串联 并联 KCL KVL .....
电路的对偶性：
ic
(t
)
C
duc (t) dt
uc
(t
)
uc
(t0
)
1 C
t
t0 ic ( )d
Wc
(t)
1 2
Cuc2
(t)
q(t) Cuc (t)
....
uL
(t)
L
diL (t) dt
iL
(t)
iL
(t0 )
1 L
t
t0 uL ( )d
WL
(t)
1 2
LiL2
(t)
(t) LiL (t)
t 0
uc
(t
t)
uc
(t)
1 C
lim
t 0
t t
i(
t
)d
uc
(t)
1 C
lim i(t)
t 0
t
uc
(t)
2、电容电压的记忆性：
u(t)取决于i(t)从到t的积分，电容电压 与电流过去历史有关。
3、有隔直作用。 电容元件在直流电路中：
du 0 i 0 C 相当于开路 ! dt
§5 4 电容的储能
1 2 3 4 t(s)
u( 2 ) 1V u( 3 ) 1 V 2
例2 已知:u(0)=0和i(t)，C=1F，求 u(t)并画波形。
i(A)1
0 123 1
解：分段求积分：
3-4：u(
t
)
u(
3
)
t
3
(
4
)d
4 t(s)
1 t 2 4t 8 2
u(4) 0
u(V)
以上分析看出电容具有
1、电容的功率：
i(t) C + u(t) _
p(t) u(t)i(t) u(t)C du dt
意义：P＞0 吸收；P＜0 产生
2 、电容的能量：
从初始时刻t0到任意时刻t 时间内得到的能量为
W (t0 ,t)
t
p( )d C
t0
t u( ) du d
t0
d
C
u(t)
udu
u(t0 )
第二部分
动态电路分析
第五章 电容元件与电感元件
动态电路：含有电容、电感元件的电路。 本章主要内容：
1、电容、电感元件定义及伏安关系 2、电容、电感元件性质 3、电容、电感元件的储能 4、电路的对偶性
§5 1 电容元件
1.电容器：聚集电荷、存储电场能量的元件。
2.定义： 若一个二端元件在任一时刻，
-1～0 0～2 2～3
-1～0 0～2 2～3
§5 8 电感储能
1、电感的功率：
i(t) L
p(t) = u(t) i(t)——瞬时功率
+ u(t) _
P＞0 吸收 P＜0 产生
2 、电感的能量：
W ( t1 ,t2 )
t2 p( )d
t1
1 2
Li2( t2
)
1 2
Li2( t1
)
任一时刻储能： WL ( t
1.电感器（电感线圈）：储存磁场能的部件。
i
总磁通称磁链：ψ(t)=Nφ
N圈
是磁链与电流相约束的部件。
2. 定义： 一个两端元件，在任意时刻t，其电流i(t)和磁
通链 之(t间) 的关系可以用 一i 条曲线来确定，则 此两端元件称电感元件。
若任一时刻电流与磁通链符合右手螺旋法则，
且： ψ(t) Li( t )
a) 符号 b)电容的库伏特性 (c d) 线性电容及库伏特性
§5 2 电容的伏安关系
i(t) C + u(t) _
电容电流等于电容电荷的变化率
i(t) dq d(Cu) C du i(t)-u(t)关系
dt dt
dt
含义 1、电容的伏安关系是微积分关系；
2. i(t)取决于u(t)在此时刻的变化率； 规律：电压变化 电荷变化 产生电流
3. 若u和i参考方向不一致， i(t) C du dt
电压的积分形式：
u(t) 1
t
i( )d
u(t)- i(t)关系
C
1
u(t) u(t0 ) C
t
i( )d
t0
含义
1、u(t)取决于i(t)从到t的积分，
电容电压与电流过去历史有关，
说明电容电压有记忆性。
2、或者说u(t)取决于初始值u(t0)和 t0到t的电压增量。
i(t) L
解： u(t) L di(t)
dt
+ u(t) _
0.5 2 (10)e10t 10e10t
例2：已知 L=1H，求 u(t)
i(A)
t+1
1
解： i(t) = 1
-t+3
-1 0 1 2 3 t(s)
u(V) 1
u(t)
L
di(t) dt
=
1V 0 -1V
-1 0 1 2 3 t(s)
1 2
C[u 2 (t)
u 2 (t0 )]
若电容的初始储能为零，即u(t0)=0， 则任意时刻储存在电容中的能量为：
说明
WC(
t
)
1 2
C
u2(
t
)
0
1）电容的储能取决于该时刻电容电压， 与电流无关。电容电压反映了电容的 储能状态，也叫做状态变量。
2）电容只是储能元件，而没有耗散能量。
§5 5 电感元件
其中L为常数，则该元件称线性非时变电感元件，
简称电感。
ψ
i(t)ψ(t) + u(t)_
o
i
电感的韦安特性
§5 6 电感的伏安关系
规律：电流变化 磁链变化 感应电压
i(t) ψ(t) + u(t) _
u( t ) dψ d( Li ) L di
dt dt
dt
电流的积分形式：
i(t) 1 t u( )d (t)
L
L
i(t)
i(t0
)
1 L
t
u( )d
t0
初始值 电流增量
§5 7 电感电流的连续性质和记忆性质
电感元件特点： 1、电感电流的连续性质:
电压为有限值时，电流是时间的 连续函数；也叫做电感电流不能跃变；
2、电感是记忆元件； 3、对直流相当于短路。
例1：已知 i(t) 2e10tA，L=0.5H, 求 u(t)
例2 已知:u(0)=0和i(t)，C=1F，求 u(t)并画波形。
i(A)1
0 1
u(V)
1 0.5
0
解：分段求积分：
1 23
4
0-1：u( t(s)
t
)
u(
0
)
1 C
t
0
i(
)d
0 td 1 t 2
0
2
u(1) 1 V
2
1-3：u(
t
)
u( 1 )
t
1
(
2
)d
1 t 2 2t 1 2
1
两个基本的性质：
0.5
(1)电容电压的连续性；
0 1 2 3 4 t(s) (2)电容电压的记忆性。
应用
图(a)所示峰值检波器电路，就是利用电容的 记忆性，使输出电压波形保持输入电压uin(t)波形 中的峰值。
峰值检波器输入输出波形
§5 3 电容电压的连续性质和记忆性质 电容元件特点： 1、电容电压的连续性质
电流为有限值时，电压是时间的连续 函数，即：
uc (t ) uc (t )
也叫做电容电压不能跃变；
证明如下：
要证明
uc
(t)
uc
(t0
)
1 C
t t0
i(
)d
是连续的，
必须证明：lim t 0
uc
(t
t
)
uc
(t
)
而：
uc
(t
t)
uc
(t)
1 C
t t
i(
t
)d
且：i( ) M
所以：
lim