电磁感应计算题专项训练及答案
【物理】高中物理电磁感应经典习题(含答案)
【物理】高中物理电磁感应经典习题(含答案)题一题目：一个导线截面积为$2.5\times10^{-4}m^2$，长度为$0.3m$，放在磁感应强度为$0.5T$的均匀磁场中，将导线两端连接到一个电阻为$2\Omega$的电阻器上，求电阻器中的电流。
解析：根据电磁感应定律，导线中的感应电动势与导线长度、磁感应强度以及导线的运动速度有关。
在此题中，导线不运动，所以感应电动势为零。
因此，电路中的电流完全由电源提供，根据欧姆定律，可以使用$U=IR$求解电流。
答案：电路中的电流为0A。
题二题目：一个充满磁感应强度为$1T$的磁场的金属环，直径为$0.2m$，环的厚度可以忽略不计。
当磁场方向垂直于环的平面并向上时，将环从磁场中抽出后，环中的磁场强度变为多少？解析：根据法拉第电磁感应定律，当闭合回路中的磁通量发生变化时，环中会产生感应电动势导致感应电流的产生。
在此题中，环被抽出磁场后，磁通量减小，从而产生感应电动势。
根据安培环路定理和比奥-萨伐尔定律，感应电动势的方向与磁场的变化方向相反，因此感应电流会生成一磁场。
根据安培定律和环形线圈的磁场公式，可以计算出环中的新的磁场强度。
答案：环中的新磁场强度需要通过计算得出。
具体计算过程请参考相关物理教材或参考书籍。
题三题目：一根长度为$0.5m$的直导线与一个磁场相垂直，导线两端的电动势为$2V$，导线的电阻为$4\Omega$，求导线在磁场中运动的速度。
解析：根据电磁感应定律，导线中的感应电动势与导线长度、磁场强度以及导线的运动速度有关。
在此题中，导线的电动势和电阻已知，可以使用欧姆定律$U=IR$解出电流，并使用感应电动势的公式$E=Bvl$解出运动速度。
答案：导线在磁场中的运动速度需要通过计算得出。
具体计算过程请参考相关物理教材或参考书籍。
(完整版)电磁感应综合练习题(基本题型,含答案)
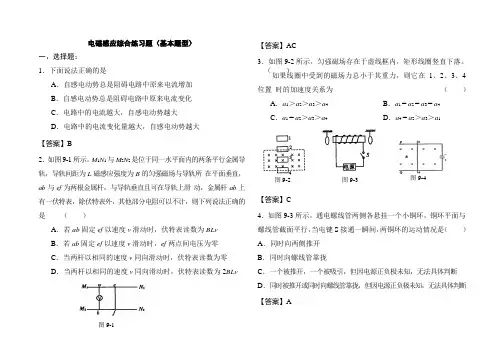
电磁感应综合练习题（基本题型）一、选择题： 1．下面说法正确的是（ ）A ．自感电动势总是阻碍电路中原来电流增加B ．自感电动势总是阻碍电路中原来电流变化C ．电路中的电流越大，自感电动势越大D ．电路中的电流变化量越大，自感电动势越大【答案】B2．如图9-1所示，M 1N 1与M 2N 2是位于同一水平面内的两条平行金属导轨，导轨间距为L 磁感应强度为B 的匀强磁场与导轨所 在平面垂直，ab 与ef 为两根金属杆，与导轨垂直且可在导轨上滑 动，金属杆ab 上有一伏特表，除伏特表外，其他部分电阻可以不计，则下列说法正确的是 （ ） A ．若ab 固定ef 以速度v 滑动时，伏特表读数为BLvB ．若ab 固定ef 以速度v 滑动时，ef 两点间电压为零C ．当两杆以相同的速度v 同向滑动时，伏特表读数为零D ．当两杆以相同的速度v 同向滑动时，伏特表读数为2BLv【答案】AC3．如图9-2所示，匀强磁场存在于虚线框内，矩形线圈竖直下落。
如果线圈中受到的磁场力总小于其重力，则它在1、2、3、4位置 时的加速度关系为 （ ） A ．a 1＞a 2＞a 3＞a 4 B ．a 1 = a 2 = a 3 = a 4C ．a 1 = a 2＞a 3＞a 4D ．a 4 = a 2＞a 3＞a 1【答案】C4．如图9-3所示，通电螺线管两侧各悬挂一个小铜环，铜环平面与螺线管截面平行，当电键S 接通一瞬间，两铜环的运动情况是（ ） A ．同时向两侧推开 B ．同时向螺线管靠拢C ．一个被推开，一个被吸引，但因电源正负极未知，无法具体判断D ．同时被推开或同时向螺线管靠拢，但因电源正负极未知，无法具体判断 【答案】 A图9-2图9-3图9-4图9-15．如图9-4所示，在U形金属架上串入一电容器，金属棒ab在金属架上无摩擦地以速度v向右运动一段距离后突然断开开关，并使ab停在金属架上，停止后，ab不再受外力作用。
电磁感应练习50题
电磁感应练习50题（含答案）1、如图所示，在匀强磁场中有一倾斜的平行金属导轨，导轨间距为L=0.2m，长为2d，d=0.5m，上半段d导轨光滑，下半段d导轨的动摩擦因素为μ=，导轨平面与水平面的夹角为θ=30°．匀强磁场的磁感应强度大小为B=5T，方向与导轨平面垂直．质量为m=0.2kg的导体棒从导轨的顶端由静止释放，在粗糙的下半段一直做匀速运动，导体棒始终与导轨垂直，接在两导轨间的电阻为R=3Ω，导体棒的电阻为r=1Ω，其他部分的电阻均不计，重力加速度取g=10m/s2，求：（1）导体棒到达轨道底端时的速度大小；（2）导体棒进入粗糙轨道前，通过电阻R上的电量q；（3）整个运动过程中，电阻R产生的焦耳热Q．答案分析：（1）研究导体棒在粗糙轨道上匀速运动过程，受力平衡，根据平衡条件即可求解速度大小．（2）进入粗糙导轨前，由法拉第电磁感应定律、欧姆定律和电量公式结合求解电量．（3）导体棒在滑动时摩擦生热为Q f=2μmgdcosθ，再根据能量守恒定律求解电阻产生的焦耳热Q．解答：解：（1）导体棒在粗糙轨道上受力平衡：由 mgsin θ=μmgcos θ+BIL得：I=0.5A由BLv=I（R+r）代入数据得：v=2m/s（2）进入粗糙导轨前，导体棒中的平均电动势为： ==导体棒中的平均电流为： ==所以，通过导体棒的电量为：q=△t==0.125C（3）由能量守恒定律得：2mgdsin θ=Q电+μmgdcos θ+mv2得回路中产生的焦耳热为：Q电=0.35J所以，电阻R上产生的焦耳热为：Q=Q电=0.2625J答：（1）导体棒到达轨道底端时的速度大小是2m/s；（2）导体棒进入粗糙轨道前，通过电阻R上的电量q是0.35C；（3）整个运动过程中，电阻R产生的焦耳热Q是0.2625J．点评：本题实质是力学的共点力平衡与电磁感应的综合，都要求正确分析受力情况，运用平衡条件列方程，关键要正确推导出安培力与速度的关系式，分析出能量是怎样转化的．2、如图所示，两平行金属导轨间的距离L=0.40m，金属导轨所在的平面与水平面夹角θ=37º，在导轨所在平面内，分布着磁感应强度B=0.50T、方向垂直于导轨所在平面的匀强磁场。
磁场,感应计算题有详细答案(快考试了,希望对同学们有所帮助)
稳恒磁场计算题144.稳恒磁学计算题144、如下图所示，AB 、CD 为长直导线BC 为圆心在O 点的一段圆弧形导线，其半径为R ．若通以电流I ，求O点的磁感应强度．解：如图所示，O 点磁场由DC 、CB 、BA 三部分电流产生，其中：DC 产生 )21(4)2sin 4(sin45cos 40001-=-=RI R IB πμπππμ 方向向里 CB 产生 RIR I B 16224002μμππ== 方向向里 BA 产生 03=BRIR I B B B B O 16)12(400321μπμ+-=++= 方向向里145、如图所示，一载流导线中间部分被弯成半圆弧状，其圆心点为O ，圆弧半径为R 。
若导线的流过电流I ，求圆心O 处的磁感应强度。
解：两段直电流部分在O 点产生的磁场01=B弧线电流在O 点产生的磁场 RIB 2202μπα=RI R I B B B O παμπαμ42220021==+=∴146、载流体如图所示，求两半圆的圆心点P 处的磁感应强度。
解：水平直电流产生01=B大半圆 产生1024R IB μ=方向向里小半圆 产生2034R IB μ=方向向里竖直直电流产生2044R I B πμ=方向向外4321B B B B B O +++=∴ )111(44442210202010R R R I R I R IR IB O πμπμμμ-+=-+=方向向里147、在真空中，有两根互相平行的无限长直导线相距0.1m ，通有方向相反的电流，I 1=20A,I 2=10A ，如图所示．试求空间磁感应强度分布，指明方向和磁感应强度为零的点的位置．、解：取垂直纸面向里为正，如图设X 轴。
)1.0(102102)(2272010x x xx d I x I B --⨯=-+=-πμπμ 在电流1I 左侧，B方向垂直纸面向外在电流1I 、2I 之间，B方向垂直纸面向里在电流2I 右侧，当m x 2.0<时，B方向垂直纸面向外当m x 2.0>时，B方向垂直纸面向里当0=B 时，即0)1.0(1021027=--⨯-x x x则 m x 2.0=处的B为0。
磁感应习题与解答
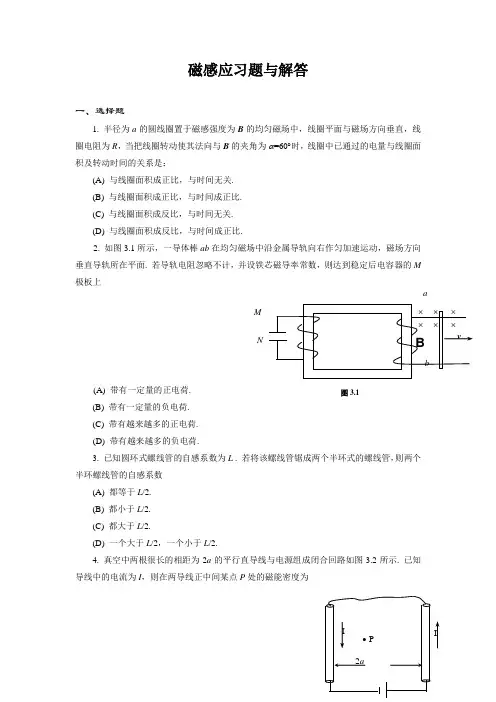
磁感应习题与解答一、选择题1. 半径为a 的圆线圈置于磁感强度为B 的均匀磁场中，线圈平面与磁场方向垂直，线圈电阻为R ，当把线圈转动使其法向与B 的夹角为α=60︒时，线圈中已通过的电量与线圈面积及转动时间的关系是：(A) 与线圈面积成正比，与时间无关. (B) 与线圈面积成正比，与时间成正比. (C) 与线圈面积成反比，与时间无关. (D) 与线圈面积成反比，与时间成正比.2. 如图3.1所示，一导体棒ab 在均匀磁场中沿金属导轨向右作匀加速运动，磁场方向垂直导轨所在平面. 若导轨电阻忽略不计，并设铁芯磁导率常数，则达到稳定后电容器的M 极板上(A) 带有一定量的正电荷. (B) 带有一定量的负电荷. (C) 带有越来越多的正电荷. (D) 带有越来越多的负电荷.3. 已知圆环式螺线管的自感系数为L . 若将该螺线管锯成两个半环式的螺线管，则两个半环螺线管的自感系数(A) 都等于L /2. (B) 都小于L /2. (C) 都大于L /2.(D) 一个大于L /2，一个小于L /2.4. 真空中两根很长的相距为2a 的平行直导线与电源组成闭合回路如图3.2所示. 已知导线中的电流为I ，则在两导线正中间某点P 处的磁能密度为NMa图3.1I(A) 200)2(1aIπμμ.(B) 200)2(21aIπμμ.(C) 200)(21a Iπμμ.(D) 0 .5. 一导体圆线圈在均匀磁场中运动，能使其中产生感应电流的一种情况是 （Ａ）线圈绕自身直径轴转动，轴与磁场方向平行． （Ｂ）线圈绕自身直径轴转动，轴与磁场方向垂直． （Ｃ）线圈平面垂直于磁场并沿垂直磁场方向平移． （Ｄ）线圈平面平行于磁场并沿垂直磁场方向平移．二、填空题1.在磁感强度为的磁场中，以速率ｖ垂直切割磁力线运动的一长度为Ｌ的金属杆，相当于____________，它的电动势ε＝____________，产生此电动势的非静电力是___________．2. 半径为a 的无限长密绕螺线管，单位长度上的匝数为ｎ，通以交变电流i ＝Ｉmsin ωｔ，则围在管外的同轴圆形回路(半径为r ）上的感生电动势为 .三、证明题:证明：自感系数为Ｌ的线圈通有电流Ｉ0时，线圈内贮存的磁能为LI 02/2．练习三 电磁感应习题答案一.选择题：1.A 2.B 3.B 4.C 5.B二.填空题: 1. 一个电源; vBl; 洛伦兹力 2.-mnpa 2wIcoswt 三.证明题:dt LdI I I i /,0-=→εε大小为过程中从线圈中作功为电源反抗L ε221LILIdI Idt A tI i m⎰⎰==-=ε221,LIW m =此能量全部转变为磁能由能量守恒可知典型例题1. 图.1中三条曲线分别表示简谐振动中的位移x , 速度v ，加速度a ，下面哪个说法是正确的？(D)(A) 曲线3, 1, 2分别表示x , v , a 曲线 (B) 曲线2, 1, 3分别表示x , v , a 曲线(C) 曲线1, 3, 2分别表示x , v , a 曲线(D) 曲线1, 2, 3分别表示x , v , a 曲线2. 用余弦函数描述一简谐振子的振动,－时间(v －t )关系曲线如图2位为 (A)(A) π / 6 (B) π / 3 (C) π / 2 (D) 2π / 3 3. 一质点作简谐振动，振动方程为cos()x t ωϕ=+，当时间t =T / 2(T 为周期)时，质点的速度为 (B) (A)sin A ωϕ- (B)sin A ωϕ(C)cos A ωϕ- (D)co s A ωϕ4. 用余弦函数描述一简谐振动，已知振幅为A ，周期为T ，初位相/3ϕπ=-，则振动曲线为图3中哪一图？ (A)x ,v ,a图1－5. 用40N 的力拉一轻弹簧，可使其伸长20cm ，此弹簧下应挂 2.0 kg 的物体，才能使弹簧振子作简谐振动的周期 T =0.2πs 。
高一物理电磁感应现象练习题及答案
高一物理电磁感应现象练习题及答案练习题一：1. 一根导线以速度v穿过磁感应强度为B的均匀磁场，导线长度为L，角度θ为导线与磁场方向的夹角。
求导线在时间Δt内所受到的感应电动势。
答案：感应电动势E = B * v * L * sinθ2. 一根导线以速度v进入磁感应强度为B的均匀磁场，导线的长度为L。
当导线完全进入磁场后，突然停止不动。
求此过程中导线两端之间的电势差。
答案：电势差V = B * v * L3. 一个长度为L的导线以速度v匀速通过磁感应强度为B的均匀磁场，当导线通过时间Δt后，磁场方向突然发生改变。
求导线两端之间产生的感应电动势。
答案：感应电动势E = 2 * B * v * L4. 一根长度为L的导线以速度v与磁感应强度为B的均匀磁场垂直相交，导线所受到的感应电动势大小为E，如果将导线切成长度为L/2的两段导线，两段导线所受感应电动势的大小分别是多少？答案：每段导线所受感应电动势的大小都是E练习题二：1. 一台电动机的转子有60个磁极，额定转速为3000转/分钟。
求转子在额定转速下的转子导线所受的感应电动势大小。
答案：转子导线所受感应电动势的大小为ω * Magnetic Flux，其中ω为角速度，Magnetic Flux为磁通量。
转速为3000转/分钟，转速ω =2π * 3000 / 60。
由于转子有60个磁极，每转所经过的磁通量为60 * Magnetic Flux。
因此，转子导线所受感应电动势的大小为60 * 2π * 3000 / 60 * Magnetic Flux。
2. 一根长度为L的导线以角速度ω绕通过导线轴线的磁感应强度为B的磁场旋转。
求导线两端之间的电势差大小。
答案：电势差V = B * ω * L3. 一根输电线路的电阻为R，长度为L，电流为I。
如果在电力系统中，磁感应强度为B的磁场垂直于导线方向，求输电线路两端之间的感应电动势。
答案：感应电动势E = B * L * I4. 一块矩形线圈有N匝，每匝的边长为a和b，磁通量为Φ，求矩形线圈所受到的感应电动势。
电磁感应与动量、能量相关的计算题专题
电磁感应与动量、能量相关的计算题专题1.如图所示，两根光滑平行金属轨道MN、PQ固定在水平面内，导轨间距为L，电阻不计，两轨道间接一电容为C的电容器，磁感应强度为B的磁场垂直于轨道平面竖直向下。
导体棒ab垂直于MN、PQ放在轨道上，与轨道接触良好。
现给导体棒ab 一个向右的初速度v，求导体棒从开始运动到达到稳定状态时电容器带的电荷量。
2.电磁轨道炮利用电流和磁场的作用使炮弹获得超高速度，其原理可用来研制新武器和航天运载器。
电磁轨道炮示意如图所示，图中直流电动势为E，电容器的电容为C，两根固定于水平面内的光滑平行金属导轨间距为l，电阻不计。
炮弹可视为一质量为m、电阻为R的金属棒MN，垂直放在两导轨间处于静止状态，并与导轨良好接触。
首先开关S 接至1，使电容器完全充电。
然后将S接到2，导轨间存在垂直于导轨平面、磁感应强度大小为B的匀强磁场（图中未画出），MN开始向右加速运动。
当MN上的感应电动势与电容器两极板间的电压相等时，回路中电流为零，MN达到最大速度，之后离开导轨。
问：（1）磁场的方向；（2）MN刚开始运动时加速度a的大小；（3）MN离开导轨后电容器上剩余的电荷量Q是多少。
（4）安培力对“炮弹”所做的功。
【延伸题】3.（12分）如图所示，阻值为R、质量为m、边长为L的正方形金属框位于光滑绝缘的水平面上。
金属框的ab边与磁场边缘平行，并以初速度v进人磁场区域，运动方向与磁场边缘垂直。
竖直虚线之间有磁感应强度为B的匀强磁场，方向垂直水平面向下，在金属框运动方向上的长为3L。
已知金属框完全通过磁场后恰好静止，求：（1）金属框进入磁场的过程中通过ab边的电荷量；（2）从金属框完全进入磁场区域到金属框的ab边刚出磁场区域所经历的时间。
4.（14分）如图所示，有一足够大的匀强磁场区域，磁场的磁感应强度大小为1=B T，方向与水平放置的平行金属导轨所在的平面垂直，导轨光滑且足够长，宽度为2=L m，右端接有一电阻，其阻值Ω=3R。
初三电磁感应练习题及答案
初三电磁感应练习题及答案练习题1：1. 一个导线以2.0m/s的速度从一个均匀磁场中通过，磁感应强度为0.4T，导线长度为0.5m。
求导线所受的感应电动势大小。
2. 一个长度为3.0m的导线以10m/s的速度垂直通过一个磁感应强度为1.5T的磁场，求导线两端之间的感应电势差。
3. 一个矩形导线框架的长边长度为2.0m，短边长度为0.5m，框架的整体电阻为6.0Ω。
当磁感应强度为0.8T时，框架被拉动，导线切割磁力线的速度恒定为3.0m/s。
求在导线上出现的电动势大小。
答案：1. 感应电动势的大小与磁感应强度、导线长度和导线在磁场中的速度有关。
根据公式E = B*d*l*v，其中B为磁感应强度，d为导线长度，l为导线在磁场中的速度，v为导线长度。
将已知值代入计算，得到E = 0.4T * 0.5m * 2.0m/s = 0.4V。
故导线所受的感应电动势大小为0.4V。
2. 感应电势差的大小取决于磁感应强度、导线长度和导线在磁场中的速度之积。
根据公式∆V = B*l*v，其中B为磁感应强度，l为导线长度，v为导线在磁场中的速度。
将已知值代入计算，得到∆V = 1.5T * 3.0m * 10m/s = 45V。
导线两端之间的感应电势差为45V。
3. 在导线上出现的电动势大小取决于磁感应强度、导线长度、导线在磁场中的速度和导线的电阻之积。
根据公式E = B*d*l*v/R，其中B为磁感应强度，d为导线长度，l为导线在磁场中的速度，R为导线的电阻。
将已知值代入计算，得到E = 0.8T * 3.0m * 2.0m * 0.5m/s / 6.0Ω = 0.8V。
在导线上出现的电动势大小为0.8V。
练习题2：1. 一个磁感应强度为0.5T的磁场垂直于一个半径为0.2m的圆环，圆环的电阻为2.0Ω。
圆环以5rad/s的角速度绕垂直磁场线旋转，求圆环上出现的感应电动势大小。
2. 一个长度为4.0m的直导线绕过一个半径为2.0m的圆形电感线圈，电感线圈中有100个匝。
电磁感应习题含答案
临武一中电磁感应练习时间：75分钟 满分:100分 组题人:秦顺良一、单项选择题：（每题3分，共计18分）1、下列说法中正确的有： （ ） A 、只要闭合电路内有磁通量，闭合电路中就有感应电流产生B 、穿过螺线管的磁通量发生变化时，螺线管内部就一定有感应电流产生C 、线框不闭合时，若穿过线圈的磁通量发生变化，线圈中没有感应电流和感应电动势D 、线框不闭合时，若穿过线圈的磁通量发生变化，线圈中没有感应电流，但有感应电动势2、根据楞次定律可知感应电流的磁场一定是： （ ） A 、阻碍引起感应电流的磁通量； B 、与引起感应电流的磁场反向；C 、阻碍引起感应电流的磁通量的变化；D 、与引起感应电流的磁场方向相同。
3、穿过一个单匝闭合线圈的磁通量始终为每秒均匀增加2Wb,则 （ ） A.线圈中感应电动势每秒增加2V B.线圈中感应电动势每秒减少2VC.线圈中感应电动势始终为一个确定值，但由于线圈有电阻，电动势小于2VD.线圈中感应电动势始终为2V4、在竖直向上的匀强磁场中，水平放置一个不变形的单匝金属圆线圈，规定线圈中感应电流的正方向如图1所示，当磁场的磁感应强度B 随时间如图2变化时，图3中正确表示线圈中感应电动势E 变化的是 （ ）A ．B ．C ．D ．5、如图所示，竖直放置的螺线管与导线abcd 构成回路，导线所在区域内有一垂直纸面向里的变化的匀强磁场，螺线管下方水平桌面上有一导体圆环，导线abcd 所围区域内磁场的磁感强度按下列哪一图线所表示的方式随时间变化时，导体圆环将受到向上的磁场作用力 （ ）6.粗细均匀的电阻丝围成的正方形线框置于有界匀强磁场中，磁场方向垂直于线框平面，其2E E-E -2E2E E -E -2E E2E -E -2EE2E -E -2E 图1 /s 图2B边界与正方形线框的边平行，现使线框以同样大小的速度沿四个不同方向平移出磁场，如图所示，则在移动过程中线框的一边a 、b 两点间电势差绝对值最大的是 （ ）二、多项选择题：（每题4分，共计16分）7、如图所示，导线AB 可在平行导轨MN 上滑动，接触良好，轨道电阻不计 电流计中有如图所示方向感应电流通过时，AB 的运动情况是：（ ） A 、向右加速运动； B 、向右减速运动； C 、向右匀速运动； D 、向左减速运动。
初中电磁感应专题练习(含详细答案)
初中电磁感应专题练习(含详细答案)
一、选择题
1. 一个导线在磁场中匀速向右移动，感应电动势的方向如何？
A. 由左向右
B. 由右向左
C. 没有感应电动势
D. 无法确定
答案：B
2. 带电粒子在磁场中匀速运动，运动轨迹如何？
A. 直线运动
B. 圆形运动
C. 抛物线运动
D. 双曲线运动
答案：B
二、计算题
1. 一个弯曲的导线长为10cm，导线中有一个电流I=2A，若在
导线处有一个磁感应强度为B=3T的磁场，求电动势的大小为多少？
解答：
$\mathcal{E}=Blv=\frac{1}{2}Blv=\frac{1}{2}Blsin\theta=\frac{1}{2} \times 3 \times 0.1 \times 2=\frac{3}{20}$V。
三、简答题
1. 什么是电磁感应？
电磁感应是指导体中的电子受到磁场的作用从而在导体两端产
生的电动势。
2. 什么是法拉第电磁感应定律？
法拉第电磁感应定律指出，当导体中的磁力线发生变化时，沿
着导体的任意闭合回路中就会产生感应电动势，其大小与磁通量的
变化率成正比，方向满足楞次定律。
3. 什么是楞次定律？
楞次定律指出，当导体内有感应电流时，该电流所发出的磁场的方向是这样的，即它所引起的磁通量的变化总是阻碍引起这种变化的原因。
4. 什么情况下会产生感应电流？
当导体在磁场中发生运动或被磁场线穿过而发生变化时，就会在导体中产生感应电流。
《大学物理》电磁感应练习题及答案
《大学物理》电磁感应练习题及答案一、简答题1、简述电磁感应定律答：当穿过闭合回路所围面积的磁通量发生变化时，不论这种变化是什么原因引起的，回路中都会建立起感应电动势，且此感应电动势等于磁通量对时间变化率的负值，即dtd i φε-=。
2、简述动生电动势和感生电动势答：由于回路所围面积的变化或面积取向变化而引起的感应电动势称为动生电动势。
由于磁感强度变化而引起的感应电动势称为感生电动势。
3、简述自感和互感答：某回路的自感在数值上等于回路中的电流为一个单位时，穿过此回路所围成面积的磁通量，即LI LI =Φ=Φ。
两个线圈的互感M M 值在数值上等于其中一个线圈中的电流为一单位时，穿过另一个线圈所围成面积的磁通量，即212121MI MI ==φφ或。
4、简述位移电流与传导电流有什么异同答：共同点：都能产生磁场。
不同点：位移电流是变化电场产生的（不表示有电荷定向运动，只表示电场变化），不产生焦耳热；传导电流是电荷的宏观定向运动产生的，产生焦耳热。
5 简述感应电场与静电场的区别？答：感生电场和静电场的区别6、写出麦克斯韦电磁场方程的积分形式。
答：⎰⎰==⋅s v q dv ds D ρ dS tB l E s L ⋅∂∂-=⋅⎰⎰d 0d =⋅⎰S S B dS t D j l H s l ⋅⎪⎭⎫ ⎝⎛∂∂+=⋅⎰⎰d 7、简述产生动生电动势物理本质答：在磁场中导体作切割磁力线运动时，其自由电子受洛仑滋力的作用，从而在导体两端产生电势差8、 简述磁能密度, 并写出其表达式答：单位体积中的磁场能量,221H μ。
9、 简述何谓楞次定律答：闭合的导线回路中所出现的感应电流，总是使它自己所激发的磁场反抗任何引发电磁感应的原因（反抗相对运动、磁场变化或线圈变形等）.这个规律就叫做楞次定律。
10、全电流安培环路定理答：磁场强度沿任意闭合回路的积分等于穿过闭合回路围成的曲面的全电流 s d t D j l d H s e •⎪⎪⎭⎫ ⎝⎛∂∂+=•⎰⎰二、选择题1、有一圆形线圈在均匀磁场中做下列几种运动，那种情况在线圈中会产生感应电流( D )A 、线圈平面法线沿磁场方向平移B 、线圈平面法线沿垂直于磁场方向平移C 、线圈以自身的直径为轴转动，轴与磁场方向平行D 、线圈以自身的直径为轴转动，轴与磁场方向垂直2、有两个线圈，线圈1对线圈2的互感系数为21M ，而线圈2对线圈1的互感系数为12M .若它们分别流过1i 和2i 的变化电流且dt di dt di 21<，并设由2i 变化在线圈1中产生的互感电动势为12ε，由1i 变化在线圈1中产生的互感电动势为21ε，下述论断正确的是( D )A 、 12212112,εε==M MB 、 12212112,εε≠≠M MC 、 12212112,εε>=M MD 、 12212112,εε<=M M3、对于位移电流，下列四种说法中哪一种说法是正确的 ( A )A 、位移电流的实质是变化的电场B 、位移电流和传导电流一样是定向运动的电荷C 、位移电流服从传导电流遵循的所有规律D 、位移电流的磁效应不服从安培环路定理4、下列概念正确的是 ( B )。
电磁感应计算题及解答
电磁感应一、选择题1、如图所示，空间存在两个磁场，磁感应强度大小均为B，方向相反且垂直纸面，MN、PQ为其边界，OO’为其对称轴。
一导线折成变长为的正方形闭合回路abcd，回路在纸面内以恒定速度v o向右运动，当运动到关于OO’对称的位置时A.穿过回路的磁通量为零B.回路中感应电动势大小为C.回路中感应电流的方向为顺时针方向D.回路中ab边与cd边所受安培力方向相同2、如图8，在O点下方有一个具有理想边界的磁场，铜环在A点由静止释放向右摆至最高点B，不考虑空气阻力，则下列说法正确的是（）A.A、B两点在同一水平线B.A点高于B点C.A点低于B点D.铜环将做等幅摆动二、计算题3、如图所示，两根质量均为m=2kg的金属棒垂直地放在光滑的水平导轨上，左右两部分导轨间距之比为1∶2，导轨间有大小相等但左右两部分方向相反的匀强磁场，CD棒电阻为AB棒电阻的两倍，不计导轨电阻，今用250N的水平力F向右拉CD棒，在CD棒运动0.5m的过程中，两棒上产生的焦耳热共为45J，此时CD棒速率为8m/s，立即撤去拉力F，设导轨足够长且两棒始终在不同磁场中运动，求：（1）撤去拉力F瞬间AB棒速度v A；（2）两棒最终匀速运动的速度v A′和v C′。
4、如图所示，光滑矩形斜面ABCD的倾角为，在其上放置一矩形金属线框，的边长，的边长，线框的质量，电阻，线框通过细线绕过定滑轮与重物相连，细线与斜面平行且靠近。
重物质量，离地面的高度为。
斜面上区域是有界匀强磁场，方向垂直于斜面向上，已知AB到的距离为，到的距离为，到CD的距离为，取。
现让线框从静止开始运动（开始时刻与AB边重合），发现线框匀速穿过匀强磁场区域，求：（1）区域内匀强磁场的磁感应强度B（2）线框在通过磁场区域过程中产生的焦耳热Q（3）通过计算分析画出线框从开始运动到边与CD边重合过程中线框的图象5、如图所示，半径为r的圆形导线框内有一匀强磁场，磁场方向垂直于导线框所在平面，导线框的左端通过导线接一对水平放置的平行的金属板，两极间的距离为d，板长为L。
电磁感应计算题专项训练及答案
电磁感应计算题专项训练【注】该专项涉及规律：感应电动势、欧姆定律、牛顿定律、动能定理1、（2010重庆卷）法拉第曾提出一种利用河流发电的设想，并进行了实验研究。
实验装置的示意图如图所示，两块面积均为S 的矩形金属板，平行、正对、竖直地全部浸在河水中，间距为d 。
水流速度处处相同，大小为v ，方向水平。
金属板与水流方向平行。
地磁场磁感应强度的竖直分量为B ，水的电阻率为ρ，水面上方有一阻值为R 的电阻通过绝缘导线和电键K 连接到两金属板上。
忽略边缘效应，求：（1）该发电装置的电动势； （2）通过电阻R 的电流强度； （3）电阻R 消耗的电功率2、（2007天津）两根光滑的长直金属导轨MN 、M ´N ´平行置于同一水平面内，导轨间距为l ，电阻不计。
M 、M ´处接有如图所示的电路，电路中各电阻的阻值均为R ，电容器的电容为C 。
现有长度也为l ，电阻同为R 的金属棒ab 垂直于导轨放置，导轨处于磁感应强度为B 、方向竖直向下的匀强磁场中。
ab 在外力作用下向右匀速运动且与导轨保持良好接触，在ab 在运动距离为s 的过程中，整个回路中产生的焦耳热为Q 。
求：⑴ab 运动速度v 的大小；⑵电容器所带的电荷量q 。
3、（2010江苏卷）如图所示，两足够长的光滑金属导轨竖直放置，相距为L ，一理想电流表与两导轨相连，匀强磁场与导轨平面垂直。
一质量为m 、有效电阻为R 的导体棒在距磁场上边界h 处由静止释放。
导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为I 。
整个运动过程中，导体棒与导轨接触良好，且始终保持水平，不计导轨的电阻。
求：(1)磁感应强度的大小B ；(2)电流稳定后，导体棒运动速度的大小v ； (3)流经电流表电流的最大值I maNN ´4、（2008北京）均匀导线制成的单匝正方形闭合线框abcd ，每边长为L ，总电阻为R ，总质量为m ．将其置于磁感强度为B 的水平匀强磁场上方h 处，如图所示．线框由静止自由下落，线框平面保持在竖直平面内，且cd 边始终与水平的磁场边界平行．当cd 边刚进入磁场时，⑴求线框中产生的感应电动势大小； ⑵求cd 两点间的电势差大小；⑶若此时线框加速度恰好为零，求线框下落的高度h 所应满足的条件．5、（2010福建）如图所示，两条平行的光滑金属导轨固定在倾角为θ的绝缘斜面上，导轨上端连接一个定值电阻。
电磁感应典型题目(含答案)
电磁感应的典型计算1 如图所示，一与水平面夹角为θ=37°的倾斜平行金属导轨，两导轨足够长且相距L=0.2m，另外两根水平金属杆MN和PQ的质量均为m=0.01kg，可沿导轨无摩擦地滑动，MN杆和PQ杆的电阻均为R=0.2Ω(倾斜金属导轨电阻不计)，MN杆被两个垂直于导轨的绝缘立柱挡住，整个装置处于匀强磁场内，磁场方向垂直于导轨平面向上，磁感应强度B=1.0T．PQ杆在恒定拉力F作用下由静止开始向上加速运动，拉力F垂直PQ杆沿导轨平面向上，当运动位移x=0.1 m时PQ杆达到最大速度，此时MN杆对绝缘立柱的压力恰好为零(g取10m/s2，sin 37°=0.6 ，cos 37°=0.8)．求：(1) PQ杆的最大速度v m， (2)当PQ杆加速度时，MN杆对立柱的压力；(3)PQ杆由静止到最大速度过程中回路产生的焦耳热Q．解：（1）PQ达到最大速度时，关于电动势为：E m=BLv m，感应电流为：I m=REm2，根据MN杆受力分析可得：mg sinθ=BI m L，联立解得：v m=22sin2LBRmg=0.6m/s；（2）当PQ的加速度a=2 m/s2 时，对PQ根据牛顿第二定律可得：F－mg sinθ－BIL=ma，对MN根据共点力的平衡可得：BIL+F N－mg sinθ=0，PQ达到最大速度时，有：F－mg sinθ－BI m L=0，联立解得：F N=0.02N，根据牛顿第三定律可得对立柱的压力F N=0.02N；（3）PQ由静止到最大速度的过程中，根据功能关系可得：F x =221mmv+mgx sinθ+Q，解得：Q=4.2×10-3 J．答：（1）PQ杆的最大速度为0.6m/s；（2）当PQ杆加速度a=2m/s2时，MN杆对立柱的压力为0.02N （3）PQ杆由静止到最大速度回路产生的焦耳热为4.2×10-3 J．2 如图所示，平行金属导轨与水平面间夹角均为θ=37°，导轨间距为lm，电阻不计，导轨足够长．两根金属棒 ab 和a′b′的质量都是0.2kg，电阻都是1Ω，与导轨垂直放置且接触良好，金属棒a′b′和导轨之间的动摩擦因数为0.5，设金属棒a′b′受到的最大静摩擦力等于滑动摩擦力．金属棒ab和导轨无摩擦，导轨平面PMKO处存在着垂直轨道平面向上的匀强磁场，导轨平面PMNQ处存在着沿轨道平面向上的匀强磁场，磁感应强度B的大小相同．用外力让a′b′固定不动，将金属棒ab由静止释放，当ab下滑速度达到稳定时，整个回路消耗的电功率为18W．求：（1）ab 棒达到的最大速度；（2）ab棒下落了 30m 高度时，其下滑速度已经达到稳定，此过程中回路电流产生的焦耳热Q；（3）在ab棒下滑过程中某时刻将a′b′固定解除，为确保a′b′始终保持静止，则a′b′固定解除时ab棒的速度大小满足什么条件？（ g=10m/s2，sin37°=0.6，cos37°=0.8 ）解：（1）ab 棒达到最大速度时做匀速运动，其重力功率等于整个回路消耗的电功率，则有：mg sinθ•v m=P电，则得：ab棒的最大速度为：v m==m/s=15m/s；由P电==，得：B==T=0.4T（2）根据能量守恒得：mgh=Q+则得：Q=mgh-=0.2×10×30J-×0.2×152 =37.5 J（3）将a′b′固定解除，为确保a′b′始终保持静止，则对于a′b′垂直于斜面方向有：N=mg cos37°+BIL，平行于斜面方向有：mg sin37°≤f m=μN解得：I ≥2A对于ab棒：E=I•2R，E=BLv，则得：v=≥m/s=10m/s故ab的速度应满足的条件是：10m/s≤v≤15m/s答：（1）ab 棒达到的最大速度是15m/s；（2）ab棒下落了30m 高度时，其下滑速度已经达到稳定，此过程中回路电流产生的焦耳热Q是37.5J；（3）在ab棒下滑过程中某时刻将a′b′固定解除，为确保a′b′始终保持静止，则a′b′固定解除时ab棒的速度大小满足的条件是10m/s≤v≤15m/s3 如图所示，两电阻不计的足够长光滑平行金属导轨与水平面夹角为θ，导轨间距为L，所在平面的正方形区域abcd内存在有界匀强磁场，磁感应强度为B，方向垂直斜面向上．将甲乙两电阻阻值相同、质量均为m的相同金属杆如图放置在导轨上，甲金属杆处在磁场的上边界，甲乙相距L．静止释放两金属杆的同时，在甲金属杆上施加一个沿着导轨向下的外力F，使甲金属杆在运动过程中始终做沿导轨向下的匀加速直线运动，加速度大小g sinθ，乙金属杆刚进入磁场时，发现乙金属杆作匀速运动．（1）求乙刚进入磁场时的速度（2）甲乙的电阻R为多少；（3）乙刚释放时t=0，写出从开始释放到乙金属杆离开磁场，外力F随时间t的变化关系；（4 ）若从开始释放到乙金属杆离开磁场，乙金属杆中共产生热量Q，试求此过程中外力F对甲做的功．解：⑴在乙尚未进入磁场中的过程中，甲、乙的加速度相同，设乙刚进入磁场时的速度v乙刚进入磁场时，对乙由根据平衡条件得(2)设乙从释放到刚进入磁场过程中做匀加速直线运动所需要的时间为设乙从进入磁场过程至刚离开磁场的过程中做匀速直线运动所需要的时间为设乙离开磁场时，甲的速度设甲从开始释放至乙离开磁场的过程中的位移为x根据能量转化和守恒定律得：4 如图所示，倾斜角θ=30°的光滑倾斜导体轨道（足够长）与光滑水平导体轨道连接。
高考物理电磁感应练习题及答案
高考物理电磁感应练习题及答案1. 单选题：(1) 当穿过一根金属导线的电流方向改变时，导线中的电磁场磁感应强度的变化过程是：A. 逐渐增大，然后逐渐减小B. 逐渐减小C. 总是不变D. 逐渐增大答案：D(2) 一个圆形回路平面内以T/秒的速度向外运动，一匀强磁场的磁感应强度大小为B，方向垂直于回路平面。
圆形回路中的恒定磁通量的大小等于：A. BTB. BπT^2C. B/TD. B/T^2答案：B(3) 一根长度为l的匀强磁场中有一导线，导线以v的速度作匀速运动。
如果导线与磁感线的夹角为α，则磁感应强度大小的变化率为：A. l/vcosαB. vcosα/lC. v/lcosαD. v/(lcosα)答案：A2. 多选题：(1) 关于法拉第电磁感应定律的描述，下列说法中正确的是：A. 在一个闭合电路中，当磁通量发生变化时，电路中会产生感应电流B. 直流电流产生的磁感应强度可以通过法拉第电磁感应定律计算C. 在一个闭合电路中，当磁感应强度发生变化时，电路中会产生感应电流D. 电流在导体中流动会产生磁场，这是法拉第电磁感应定律的基础答案：A、B(2) 以下哪些现象可以用电磁感应来解释？A. 电动机的工作原理B. 发电机的工作原理C. 变压器的工作原理D. 电磁铁的吸铁石的原理答案：A、B、C3. 计算题：(1) 一根直导线的长度为0.2m，电流强度为2A。
将这根导线竖直放置在一个垂直于地面的匀强磁场中，磁感应强度为0.5T。
求导线上电流产生的磁场的磁感应强度大小。
解答：根据安培定律，导线产生的磁场的磁感应强度大小与电流强度和导线与磁感应强度之间的夹角有关。
在这个问题中，导线与磁场方向垂直，所以夹角为90°。
由于导线长度为0.2m，电流强度为2A，根据毕奥-萨伐尔定律，我们可以使用以下公式来计算导线上电流产生的磁场的磁感应强度大小：磁感应强度大小= (μ0/4π) * (I/l)其中，μ0是真空中的磁导率，其数值为4π * 10^-7 T·m/A，I是电流强度，l是导线长度。
高考复习超经典电磁感应计算难题-含答案
高考复习超经典电磁感应计算难题-含答案(总9页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面，使用请直接删除1、如图所示，半径为a的圆形区域内有匀强磁场，磁感应强度B＝0.2T，磁场方向垂直纸面向里，半径为b 的金属圆环与磁场同心地放置，磁场与环面垂直，其中a＝0.4m，b＝0.6m.金属环上分别接有灯L1、L2，两灯的电阻均为R0＝2Ω.一金属棒MN与金属环接触良好，棒与环的电阻均不计．(1)若棒以v0＝5m/s的速率在环上向右匀速滑动，求棒滑过圆环直径OO′的瞬时，MN中的感应电动势和流过灯L1的电流；(2)撤去中间的金属棒MN，将右面的半圆环OL2O′以OO′为轴向上翻转90°，若此时磁场强度随时间均匀变化，其变化率为＝T/s，求L1的功率．2、如图所示，两个端面半径同为R的圆柱形铁芯同轴水平放置，相对的端面之间有一缝隙，铁芯上绕导线并与电源连接，在缝隙中形成一匀强磁场.一铜质细直棒ab水平置于缝隙中，且与圆柱轴线等高、垂直.让铜棒从静止开始自由下落，铜棒下落距离为0.2R时铜棒中电动势大小为，下落距离为0.8R时电动势大小为，忽略涡流损耗和边缘效应.关于、的大小和铜棒离开磁场前两端的极性，下列判断正确的是A、>，a端为正B、>，b端为正C、<，a端为正D、<，b端为正3、如图所示，两平行的光滑金属导轨安装在一光滑绝缘斜面上，导轨间距为l、足够长且电阻忽略不计，导轨平面的倾角为，条形匀强磁场的宽度为d，磁感应强度大小为B、方向与导轨平面垂直。
长度为2d的绝缘杆将导体棒和正方形的单匝线框连接在一起组成“”型装置，总质量为m，置于导轨上。
导体棒中通以大小恒为I的电流（由外接恒流源产生，图中未图出）。
线框的边长为d（d < l），电阻为R，下边与磁场区域上边界重合。
将装置由静止释放，导体棒恰好运动到磁场区域下边界处返回，导体棒在整个运动过程中始终与导轨垂直。
(完整版)电磁感应练习题及答案
《电磁感应》练习题高二级_______班姓名______________ _______________号1．B 2. A 3. A4．B 5. BCD6．CD7. D8. C一.选择题1．下面说法正确的是（）A．自感电动势总是阻碍电路中原来电流增加B．自感电动势总是阻碍电路中原来电流变化. C．电路中的电流越大，自感电动势越大D．电路中的电流变化量越大，自感电动势越大2. 如图所示，一个矩形线圈与通有相同大小电流的平行直导线在同一平面，而且处在两导线的中央，则（ A ）A．两电流方向相同时，穿过线圈的磁通量为零B．两电流方向相反时，穿过线圈的磁通量为零C．两电流同向和反向时，穿过线圈的磁通量大小相等D．因两电流产生的磁场不均匀，因此不能判断穿过线圈的磁通量是否为零3. 一矩形线圈在匀强磁场中向右做加速运动如图所示, 设磁场足够大, 下面说法正确的是( A )A. 线圈中无感应电流, 有感应电动势B .线圈中有感应电流, 也有感应电动势C. 线圈中无感应电流, 无感应电动势D. 无法判断4．如图所示，AB为固定的通电直导线，闭合导线框P与AB在同一平面内。
当P远离AB做匀速运动时，它受到AB的作用力为（ B ）A．零B．引力，且逐步变小C．引力，且大小不变D．斥力，且逐步变小5. 长0.1m的直导线在B＝1T的匀强磁场中，以10m/s的速度运动，导线中产生的感应电动势：( )A．一定是1V B．可能是0.5V C．可能为零D．最大值为1V6．如图所示，在一根软铁棒上绕有一个线圈，a、b是线圈的两端，a、b分别与平行导轨M、N相连，有匀强磁场与导轨面垂直，一根导体棒横放在两导轨上，要使a点的电势均比b点的电势高，则导体棒在两根平行的导轨上应该（BCD ）A．向左加速滑动B．向左减速滑动C．向右加速滑动D．向右减速滑动7．关于感应电动势，下列说法正确的是（）A．穿过闭合电路的磁感强度越大，感应电动势就越大B．穿过闭合电路的磁通量越大，感应电动势就越大C．穿过闭合电路的磁通量的变化量越大，其感应电动势就越大D．穿过闭合电路的磁通量变化的越快，其感应电动势就越大4题5题8．恒定的匀强磁场中有一圆形的闭合导体线圈，线圈平面垂直于磁场方向，要使线圈中能产生感应电流，线圈在磁场中应做 （ ） A ．线圈沿自身所在的平面做匀速运动 B ．线圈沿自身所在的平面做匀加速运动 C ．线圈绕任意一条直径转动 D ．线圈沿磁场方向平动9．将一磁铁缓慢或迅速地插到闭和线圈中的同一位置，两次发生变化的物理量不同的是（ ）A 、磁通量的变化量B 、磁通量的变化率C 、感应电流的电流强度D 、消耗的机械功率10．如图所示，一长直导线在纸面内，导线一侧有一矩形线圈，且线圈一边M 与通电导线平行，要使线圈中产生感应电流，下列方法可行的是（ ） A 、保持M 边与导线平行线圈向左移动 B 、保持M 边与导线平行线圈向右移动C 、线圈不动，导线中电流减弱D 、线圈不动，导线中电流增强E 、线圈绕M 边转动 F11. 如图所示，将一线圈放在一匀强磁场中，线圈平面平行于磁感线，则线圈中有感应电流产生的是（ ）A 、当线圈做平行于磁感线的运动B 、当线圈做垂直于磁感线的平行运动C 、当线圈绕M 边转动D 、当线圈绕N 边转动12．如图所示，虚线所围的区域内有一匀强磁场，闭和线圈从静止开始运动，此时如果使磁场对线圈下边的磁场力方向向下，那么线圈应（ ） A 、向右平动 B 、向左平动 C 、以M 边为轴转动D 、以上都不对13．竖直放置的金属框架处于水平的匀强磁场中，如图所示，一长直金属棒AB 可沿框自由运动，当AB 由静止开始下滑一段时间后合上S ，则AB 将做（ ）A 、 匀速运动B 、加速运动C 、减速运动D 、无法判定14．如图所示，边长为h 的矩形线框从初始位置由静止开始下落，进入一水平的匀强磁场，且磁场方向与线框平面垂直。
(完整版)电磁感应习题带答案
电磁感应一、选择题(本题共10小题，每小题4分，在每小题给出的四个选项中，有多项符合题目要求的，全部选对的得4分，选对但不全的得2分，有选错的得0分)1．(2016届郑州联考)在电磁学发展过程中，许多科学家做出了贡献．下列说法正确的是()A．安培发现了电流磁效应；法拉第发现了电磁感应现象B．麦克斯韦预言了电磁波；楞次用实验证实了电磁波的存在C．库仑提出了电场线；密立根通过油滴实验测定了元电荷的数值D．感应电流遵从楞次定律所描述的方向，这是能量守恒定律的必然结果解析：奥斯特发现了电流磁效应，法拉第发现了电磁感应现象，A选项错误；麦克斯韦预言了电磁波，赫兹用实验证实了电磁波的存在，B选项错误；法拉第提出了电场线，C选项错误；楞次定律是能量守恒定律在电磁感应现象中的具体体现，D选项正确．答案：D2．(2016届浦东新区一模)如图所示，一根条形磁铁自左向右穿过一个闭合线圈，则流过灵敏电流计的感应电流方向是()A．先向左，再向右 B．先向右，再向左C．始终向右 D．始终向左解析：条形磁铁从左向右进入螺线管的过程中，闭合线圈向左的磁通量增加，根据楞次定律可知，感应电流的磁场向右，根据安培定则可知，感应电流从右向左通过电流计．磁铁从左向右离开螺线管的过程中，闭合线圈向左的磁通量减少，根据楞次定律可知，感应电流的磁场向左，根据安培定则可知，感应电流从左向右通过电流计，A选项正确．答案：A3．(2016届温州十校联考)等腰直角三角形OPQ区域内存在匀强磁场．另有一等腰直角三角形导线框ABC以恒定的速度沿如图所示方向穿过磁场．关于线框中的感应电流，以下说法中正确的是()A．开始进入磁场时感应电流沿顺时针方向B．开始进入磁场时感应电流一定最大C．开始穿出磁场时感应电流一定最大D．开始穿出磁场时感应电流一定最小解析：导线框开始进入磁场时，根据楞次定律可知，闭合回路向下的磁通量增加，感应电流方向沿逆时针方向，A选项错误；根据导体切割磁感线可知，E＝BLv，导线框刚进入磁场时有效切割长度最大，产生的感应电动势最大，感应电流最大，B选项正确；由于不知道两个三角形边长关系，故无法判断开始穿出磁场时有效切割长度的变化情况，C、D选项错误．答案：B4．(2016届南京模拟)有7个完全相同的金属框，表面涂有绝缘层．如图所示，A是一个框，B是两个框并列捆在一起，C是两个框上下叠放捆在一起，D是两个框前后叠放捆在一起．将他们同时从同一高度由静止释放，穿过水平向里的匀强磁场，最后落到水平地面．关于金属框的运动，以下说法正确的是()A．D最先落地 B．C最后落地C．A、B、D同时落地 D．B最后落地解析：设每一个金属框的质量为m，边长为L，电阻值为R，刚刚进入磁场时的速度为v，A图中，感应电动势为E＝BLv，感应电流为I＝，安培力为F＝BIL＝，根据牛顿第二定律得，aA＝＝g－；同理，B图中，安培力为2F＝，aB＝＝g－；C图中，安培力为是F＝，aC＝＝g－； D图中，安培力为2F＝，aD＝＝g－；A、B、D三个金属框在进入磁场的过程中的加速度相等，运动的情况是完全相同的，同时落地，C选项正确．答案：C5．(多选)(2016届广东省阳江市高三期中)矩形线圈abcd，长ab＝20 cm 宽bc＝10 cm，匝数n＝200匝，线圈回路总电阻R＝5 Ω，整个线圈平面内均有垂直于线圈平面的匀强磁场穿过．若匀强磁场的磁感应强度B随时间t的变化规律如图所示，则()A．线圈回路中感应电动势随时间均匀变化B．线圈回路中产生的感应电流为0.4 AC．当t＝0.3 s时，线圈的ab边所受的安培力大小为0.016 ND．在1 min内线圈回路产生的焦耳热为48 J解析：根据法拉第电磁感应定律可知，E＝n＝n·S＝2 V，感应电动势恒定不变，A选项错误；根据欧姆定律得，I＝＝0.4 A，B选项正确；分析图象可知，t＝0.3 s时，磁感应强度B＝0.2 T，安培力为F＝nBIL＝3.2 N，C选项错误；1 min内线圈回路产生的焦耳热为Q＝I2Rt＝48 J，D选项正确．答案：BD6．(多选)(2016届赣南州三校联考)如图所示，竖直光滑导轨上端接入一定值电阻R，C1和C2是半径都为a的两圆形磁场区域，其区域内的磁场方向都垂直于导轨平面向外，区域C1中磁场的磁感强度随时间按B1＝b＋kt(k>0)变化，C2中磁场的磁感强度恒为B2，一质量为m、电阻为r、长度为L的金属杆AB穿过区域C2的圆心C2垂直地跨放在两导轨上，且与导轨接触良好，并恰能保持静止．则()A．通过金属杆的电流大小为B．通过金属杆的电流方向为从B到AC．定值电阻的阻值为R＝－rD．整个电路中产生的热功率P＝解析：金属杆处于平衡状态，mg＝B2I·2a，解得I＝，A选项错误；安培力竖直向上，根据左手定则可知，电流方向从B到A，B选项正确；根据法拉第电磁感应定律得，E＝＝·πa2＝kπa2，根据闭合电路欧姆定律得，R＝－r，C选项正确；整个电路中产生的热功率P＝IE＝，D选项正确．答案：BCD7．(2016届河北“五个一联盟”质检 )如图，闭合铜环由高处从静止开始下落，穿过一根竖直悬挂的条形磁铁，铜环的中心轴线与条形磁铁的中轴线始终保持重合．若取磁铁中心O为坐标原点，建立竖直向下为正方向的x轴，则下图中最能正确反映环中感应电流i随环心位置坐标x变化的关系图象是()解析：闭合铜环穿过磁铁的过程中，环中磁通量变化不均匀，产生的感应电流不是线性变化，A选项错误；铜环在下落过程中，下落到磁铁顶端的速度小于底端的速度，故铜环下落到磁铁顶端产生的感应电流小于底端的感应电流，C选项错误；根据楞次定律可知，圆环靠近磁体的过程中向上的磁通量最大，而离开磁体的过程中向上的磁通量减小，磁通量的变化相反，感应电流的方向相反，D选项错误，B选项正确．答案：B8.(多选)(2016届长宁区一模)如图所示，有五根完全相同的金属杆，其中四根连在一起构成正方形闭合框架，固定在绝缘水平桌面上，另一根金属杆ab搁在其上且始终接触良好．匀强磁场垂直穿过桌面，不计ab杆与框架的摩擦，当ab杆在外力F作用下匀速沿框架从最左端向最右端运动过程中()A．外力F先减小后增大B．桌面对框架的水平作用力保持不变C．ab杆的发热功率先减小后增大D．正方形框架的发热功率总是小于ab杆的发热功率解析：ab杆匀速切割磁感线，产生恒定的感应电动势，闭合框架的左右部分并联，当ab杆运动到中央位置时，外电阻最大，根据欧姆定律可知，此时感应电流最小，故感应电流先减小再增大，外力和安培力平衡，故外力先减小再增大，A选项正确；电流流过框架，框架受到安培力作用，水平作用力和安培力平衡，安培力先减小再增大，故水平作用力先减小再增大，B选项错误；ab杆的发热功率Pr＝I2r，先减小后增大，C选项正确；当ab在框架的中央时，内、外电阻相等，正方形框架的发热功率等于ab杆的发热功率，D选项错误．答案：AC9．(2016届河北联考)如图所示，在平面直角坐标系的第一象限分布着非匀强磁场，磁场方向垂直纸面向里，沿y轴方向磁场分布是不变的，沿x轴方向磁感应强度与x满足关系B＝kx，其中k是一恒定的正数，正方形线框ADCB边长为a，A处有一极小开口AE，由粗细均匀的同种规格导线制成，整个线框放在磁场中，且AD边与y轴平行，AD边与y轴距离为a，线框AE两点与一电源相连，稳定时流入线框的电流为I，关于线框受到的安培力情况，下列说法正确的是()A．整个线框受到的合力方向与BD连线垂直B．整个线框沿y轴方向所受合力为0C．整个线框在x轴方向所受合力为ka2I，沿x轴正向D．整个线框在x轴方向所受合力为ka2I，沿x轴正向解析：分析题意可知，AD边所在位置的磁感应强度B1＝ka，AD边受到的安培力大小为FAD＝B1IL＝ka2I，根据左手定则知，方向沿x轴负方向；BC边所在位置的磁感应强度B2＝2ka，BC边受到的安培力大小为FBC＝B2IL＝2ka2I，根据左手定则知，方向沿x轴正方向；沿y轴方向磁场分布是不变的，故AB和CD边受到的安培力等大反向，相互抵消，整个线框受到的合力为FBC－FAD＝ka2I，方向沿x轴正方向，B选项正确．答案：B10．(2016届本溪市二模)如图所示，灯泡A、B与固定电阻的阻值均为R，L是带铁芯的理想线圈，电源的内阻不计．开关S1、S2均闭合且电路达到稳定．已知电路中的各种元件均在安全范围之内．下列判断中正确的是()A．灯泡A中有电流通过，方向为a→bB．将S1断开的瞬间，灯泡A、B同时熄灭C．将S1断开的瞬间，通过灯泡A的电流最大值要比原来通过灯泡B的电流大D．将S2断开，电路达到稳定，灯泡A、B的亮度相同解析：理想线圈的电阻为零，电路稳定后，灯泡A被短路，没有电流流过，A选项错误；将S1断开的瞬间，线圈L发生自感现象，相当于电源，电流流过灯泡A，灯泡B被短路，B选项错误；根据自感现象的规律可知，流过L的电流是流过灯泡B与电阻R上电流之和，故通过灯泡A的电流最大值要比原来通过灯泡B的电流大，C选项正确；将S2断开，电路达到稳定，灯泡A的亮度低于灯泡B的亮度，D选项错误．答案：C第Ⅱ卷(非选择题，共60分)二、实验题(本题共1小题，共8分)11．(8分)(2016届新级模拟)某实验小组设计了如图(a)的实验电路，通过调节电源可在原线圈中产生变化的电流，用磁传感器可记录原线圈中产生的磁场B的变化情况，用电压传感器可记录副线圈中感应电动势E的变化情况，二者的变化情况可同时显示在计算机显示屏上．某次实验中得到的B-t、E-t图象如图(b)所示．(1)试观察比较这两组图象，可得出的定性结论是(请写出两个结论)：________________________________________________________________________；________________________________________________________________________.(2)该实验小组利用两组图象求出六组磁感应强度变化率和对应的感应电动势E的数据，并建立坐标系，描出的六个点如图(c)所示．请在图(c)中绘出E-的图线．(3)在该实验中，若使用的副线圈的匝数为100匝，则由图线可求得该副线圈的横截面积为________cm2.(保留3位有效数字)解析：(1)分析图(b)可知，当磁感应强度B恒定时，感应电动势E为零，而磁感应强度B均匀变化，产生恒定的感应电动势E，并且磁感应强度B的变化率越大，产生的感应电动势E 越大．(2)连线如图所示：(3)根据法拉第电磁感应定律得，E＝n＝n·S，当线圈面积S和匝数n一定时，电动势与磁场的变化率成正比，E∝.分析图象可知，E-图象的斜率大小表示匝数n与线圈横截面积S的乘积，S＝2.77(2.75～2.82)cm2.答案：(1)当磁感应强度B恒定时，感应电动势E为零，而磁感应强度B均匀变化，产生恒定的感应电动势E；磁感应强度B的变化率越大，产生的感应电动势E越大(2)见解析(3)2.77(2.75～2.82)三、计算题(本题共4小题，共52分)12．(12分)(2016届广东模拟)如图甲所示，半径为r、匝数为n的线圈，其两极分别与固定水平放置的平行金属板A、B连接，线圈处在匀强磁场中，磁场方向垂直线圈平面，磁感应强度随时间变化规律如图乙所示．在t＝0时刻，将一质量为m、带电荷量为＋q、重力不计的粒子从平行金属板中心位置由静止释放，发现在第一个周期内粒子未与金属板相撞．求：(1)平行金属板间的距离d应满足的条件；(2)在满足(1)的前提下，在T时间内粒子的最大动能为多大？解析：(1)前半个周期内，根据法拉第电磁感应定律得感应电动势U＝n＝n·πr2，金属板A、B 间产生匀强电场，场强E＝，粒子在电场力作用下，加速运动；后半个周期内，感应电动势反向，粒子减速运动，在第一个周期内粒子未与金属板相撞，则≥2×·2 解得d≥ .(2)当平行板间距刚好等于d，且粒子运动时间为时，粒子的速度达到最大，则动能也最大，根据动能定理得，q＝Ekm－0，解得，Ekm＝.答案：(1)d≥ (2)13．(14分)(2016届开封高三联考)如图1，abcd为质量M的导轨，放在光滑绝缘的水平面上，另有一根质量为m的金属棒PQ平行bc放在水平导轨上，PQ棒左边靠着绝缘固定的竖直立柱e、f，导轨处于匀强磁场中，磁场以OO′为界，左侧的磁场方向竖直向上，右侧的磁场方向水平向右，磁感应强度均为B.导轨bc段长l，其电阻为r，金属棒电阻为R，其余电阻均可不计，金属棒与导轨间的动摩擦因数μ.若在导轨上作用一个方向向左、大小恒为F的水平拉力，设导轨足够长，PQ棒始终与导轨接触．试求：(1)导轨运动的最大加速度amax；(2)流过导轨的最大感应电流Imax；(3)在如图2中定性画出回路中感应电流I随时间t变化的图象，并写出分析过程．解析：(1)导轨刚开始运动时，加速度最大，根据牛顿第二定律得，F－μmg＝Mamax，解得amax＝.(2)随着导轨速度增加，bc边切割磁感线，感应电流增大，当加速度为零时，速度最大，感应电流最大，F－BImaxl－μ(mg－BImaxl)＝0，联立解得Imax＝.(3)画出图象如下：从刚拉动开始计时，t＝0时，v＝0，I＝0；t＝t1时，a＝0，v最大，I＝Im；0～t1之间，导轨做加速度减小的加速运动，a＝0时，v保持不变，I保持不变．答案：(1)(2)(3)见解析。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
电磁感应计算题专项训练【注】该专项涉及规律：感应电动势、欧姆定律、牛顿定律、动能定理1、( 2010重庆卷)法拉第曾提出一种利用河流发电的设想，并进行了实验研究。
实验装置 的示意图如图所示，两块面积均为S 的矩形金属板，平行、正对、竖直地全部浸在河水中,间距为d 。
水流速度处处相同，大小为 v ,方向水平。
金属板与水流方向平行。
地磁场磁感应强度的竖直分量为 B,水的电阻率为 p 键K 连接到两金属板上。
忽略边缘效应，求:(1) 该发电装置的电动势； (2) 通过电阻R 的电流强度； (3) 电阻R 消耗的电功率水面上方有一阻值为 R 的电阻通过绝缘导线和电2、(2007天津)两根光滑的长直金属导轨 MN MN'平行置于同一水平面内，导轨间距为I ,电阻不计。
M M 处接有如图所示的电路，电路中各电阻的阻值均为R,电容器的电容为 C 。
现有长度也为I ,电阻同为R 的金属棒ab 垂直于导轨放置，导轨处于磁感应强度为 B 方向 竖直向下的匀强磁场中。
ab 在外力作用下向右匀速运动且与导轨保持良好接触，在ab 在运动距离为s 的过程中，整个回路中产生的焦耳热为 Q 求：⑴ab 运动速度v 的大小；⑵电容3、( 2010江苏卷)如图所示，两足够长的光滑金属导轨竖直放置，相距为 L , 一理想电流表与两导轨相连，匀强磁场与导轨平面垂直。
一质量为m 有效电阻为R 的导体棒在距磁场上边界h 处由静止释放。
导体棒进入磁场后，流经电流表的电流逐渐减小，最终稳定为 I 。
整个运动过程中，导体棒与导轨接触良好，且始终保持水平，不计导轨的电阻。
求：⑴磁感应强度的大小 B;⑵ 电流稳定后，导体棒运动速度的大小 v ；⑶ 流经电流表电流的最大值 Im器所带的电荷量q 。
4、( 2008北京)均匀导线制成的单匝正方形闭合线框abed，每边长为L,总电阻为R总质量为m将其置于磁感强度为B的水平匀强磁场上方h处，如图所示.线框由静止自由下落，线框平面保持在竖直平面内，且ed边始终与水平的磁场边界平行•当ed边刚进入磁场时,⑴求线框中产生的感应电动势大小；⑵求ed两点间的电势差大小；⑶若此时线框加速度恰好为零，求线框下落的高度X X X XX X X XX BXX X5、(2010福建)如图所示，两条平行的光滑金属导轨固定在倾角为e的绝缘斜面上，导轨上端连接一个定值电阻。
导体棒a和b放在导轨上，与导轨垂直并良好接触。
斜面上水平虚线PQ 以下区域内，存在着垂直穿过斜面向上的匀强磁场。
现对a棒施以平行导轨斜向上的拉力，使它沿导轨匀速向上运动，此时放在导轨下端的b棒恰好静止。
当a棒运动到磁场的上边界PQ处时，撤去拉力，a棒将继续沿导轨向上运动一小段距离后再向下滑动，此时 b 棒已滑离导轨。
当a棒再次滑回到磁场上边界PQ处时，又恰能沿导轨匀速向下运动。
已知a棒、b 棒和定值电阻的阻值均为R b棒的质量为m重力加速度为g,导轨电阻不计。
求：(1)a棒在磁场中沿导轨向上运动的过程中，a 棒中的电流强度I a与定值电阻中的电流强度I b之比；(2)a棒质量n a;(3)a棒在磁场中沿导轨向上运动时所受的拉力F。
6> (2005上海)如图所示，处于匀强磁场中的两根足够长、电阻不计的平行金属导轨相距1mh所应满足的条件.导轨平面与水平面成 e =37°角，下端连接阻值为 R 的电阻.匀强磁场方向与导轨平面垂直， 质量为、电阻不计的金属棒放在两导轨上， 棒与导轨垂直并保持良好接触， 它们之间的动摩擦因数为.(1 )求金属棒沿导轨由静止开始下滑时的加速度大小； (2)当金属棒下滑速度达到稳定时，电阻 R 消耗的功率为8W 求该速度的大小；(3) 在上问中，若 R=2Q ，金属棒中的电流方向由a 到b ,求磁感应强度的大小与方向.(g =10m/s 2, si n37 ° =, cos37° =)7、( 2005天津)图中MN 和PQ 为竖直方向的两平行长直金属导轨，间距 I 为，电阻不计，导轨所在平面与磁感应强度B 为的匀强磁场垂直。
质量 m 为x l0-3kg 、电阻为 Q 的金属杆ab 始终垂直于导轨，并与其保持光滑接触。
导轨两端分别接有滑动变阻器和阻值为Q 的电阻R 。
当杆ab 达到稳定状态时以速率 v 匀速下滑，整个电路消耗的电功率P 为，重力加速度取10m/s 2,试求速率v 和滑动变阻器接入电路部分的阻值R 。
R1 —II —x x x8、( 2010天津卷)如图所示，质量m =、电阻R =Q 、长度I =0.4m 的导体棒ab 横放在U 型金属框架上。
框架质量 m =0.2kg ，放在绝缘水平面上，与水平面间的动摩擦因数 口 =，相距0.4m 的MM '、NN '相互平行，电阻不计且足够长。
电阻 F 2=Q 的MN 垂直于MM '。
整个装置处于竖直向上的匀强磁场中，磁感应强度B =。
垂直于ab 施加F =2N 的水平恒力，ab 从静止开始无摩擦地运动，始终与 MM 、NN '保持良好接触，当 ab 运动到某处时，框架开 始运动。
设框M x axx x vxxx x BxxxP xb x x Q架与水平面间最大静摩擦力等于滑动摩擦力，g取10m/s2.(1)求框架开始运动时ab速度v的大小；(2)从ab开始运动到框架开始运动的过程中，MN上产生的热量Q=,求该过程ab位移x 的大小。
9、(2009全国n )如图，匀强磁场的磁感应强度方向垂直于纸面向里，大小随时间的变化率P 、横截面积为s 的硬导线做成一边长为I 的方框，将方框固定于纸面内，其右侧一半位于磁场区域中，求(1) 导线中感应电流的大小；(2) 磁场对方框作用力的大小随时间的变化率10、( 2008天津)磁悬浮列车是一种高速低耗的新型交通工具。
它的驱动系统简化为如下 模型，固定在列车下端的动力绕组可视为一个矩形纯电阻金属框，电阻为R 金属框置于xOy平面内，长边 MN 长为I ，平行于y 轴，宽为d 的NP 边平行于x 轴，如图1所示。
列车轨道 沿Ox 方向，轨道区域内存在垂直于金属框平面的磁场，磁感应强度B 沿Ox 方向按正弦规律分布，其空间周期为 入，最大值为B 0,如图2所示，金属框同一长边上各处的磁感应强度 相同，整个磁场以速度 V 0沿Ox 方向匀速平移。
设在短暂时间内， MN PQ 边所在位置的磁感 应强度随时间的变化可以忽略，并忽略一切阻力。
列车在驱动系统作用下沿 Ox 方向加速行驶，某时刻速度为 V (V <V 0)。
(1) 简要叙述列车运行中获得驱动力的原理；(2) 为使列车获得最大驱动力， 写出MN PQ &应处于磁场中的什么位置及 入与d 之间应满足的关系式：(3) 计算在满足第(2)问的条件下列车速度为 v 时驱动力的大小。
答案:1、解: (1)由法拉第电磁感应定律，有E = Bdvk ，k 为常量。
用电阻率为 XX冥X Xx x XXX XX XX X X Xpl(2)两板间河水的电阻r=-S由闭合电路欧姆定律，有E BdvS r R d SR(3)由电功率公式，P =|2R得 P =BdvSd SRc 小 4RQ 2、⑴v 尹⑵qB l s解析：⑴ 设ab 上产生的感应电动势为 t ,则有 E BlvE 4R s2I 2(4R)tCQRE ，回路中电流为I ，ab 运动距离s 所用时间为由上述方程得4QR B 2|2S(2)设电容器两极板间的电势差为U 则有U IR解得电容器所带电荷量为 q CU CQR Bls3、( 1)电流稳定后，导体棒做匀速运动BIL = mg解得B =mgIL(2)感应电动势感应电流 1=-RE = BLv①②③ ④由②③④式解得mg(3)由题意知，导体棒刚进入磁场时的速度最大，设为v m1 2机械能守恒mv m = mgh2感应电动势的最大值 VLV 感应电流的最大值I m =E m解得I m=贬辿IR4、⑴cd边刚进入磁场时，线框速度v= . 2gh , BL.. 2gh⑵此时线框中电流I = ER3 3 , ___cd两点间的电势差U= I ( R) = BL 2gh4 4 'B L 2gh⑶安培力：F= BIL =R根据牛顿第二定律得：mg- F= ma由a= 02 2解得下落高度满足；h= 兰餐2B L5、( 1)棒沿导轨向上运动时，棒、棒及电阻中放入电流分别为，有解得：* 2 。
I b(2)由于棒在上方滑动过程中机械能守恒，因而棒在磁场中向上滑动的速度大小与在磁场中向下滑动的速度大小相等，即，设磁场的磁感应强度为，导体棒长为，在磁场中运动时产生的感应电动势为当棒沿斜面向上运动时，向上匀速运动时，棒中的电流为，则由以上各式联立解得：。
(3)由题可知导体棒沿斜面向上运动时，所受拉力6、( 1)金属棒开始下滑的初速为零，根据牛顿第二定律mgsin 0 — ^ mgcos B =ma ①由①式解得a=10 x(—x) m/s =4m/s ②(2)设金属棒运动达到稳定时，速度为v,所受安培力为F,棒在沿导轨方向受力平衡mgsin 0 —口mgcos0—F=0 ③此时金属棒克服安培力做功的功率等于电路中电阻 R 消耗的电功率Fv=P④由③、④两式解得磁场方向垂直导轨平面向上. 7、解：由能量守恒，有 mgv=P 代入数据解得 v=s 又 E=BLv设电阻R i 与F 2的并联电阻为 R 并，ab 棒的电阻为r ，有 1 1 1 + —= - R R ? R 并代入数据解得 R>= Q8、（ 1） ab 对框架的压力框架受水平面的支持力F N m ? g F 1依题意，最大静摩擦力等于滑动摩擦力，则框架受到最大静摩擦力ab 中的感应电动势E Blv MN 中电流E R 1 R 2MN 受到的安培力F 安 IlB框架开始运动时由上述各式代入数据解得__E_=F 并 +rP=IEp 8vm/s 10m/s⑤F 0.2 10 (0.60.25 0.8)(3) 设电路中电流为1 , 两导轨间金属棒的长为 1 ，磁场的磁感应强度为 BI vBl⑥RP I 2R⑦由⑥、 ⑦两式解得B、PR.8 20 4T ⑧vl10 1v 6m/s ⑧(2)闭合回路中产生的总热量Q总虫卫Q ⑨R Q.由能量守恒定律，得Fx - gv2Q 总2 ⑩代入数据解得x 1.1m (11)9、答案(1) I kls82 2(2)k 1 S8【解析】本题考查电磁感应现象.(1)线框中产生的感应电动势/ t Bs 1.2.1 kt 2……①在线框产生的感应电流41I ,……②R 41,……'R s③联立①②③得I kls8(2)导线框所受磁场力的大小为 F BI1 ,它随时间的变化率为F Il B, t t由以上式联立可得10、解析：(1)由于列车速度与磁场平移速度不同，导致穿过金属框的磁通量发生变化，由于电磁感应，金属框中会产生感应电流，该电流受到的安培力即为驱动力。