第三章稳恒电流
稳恒电流(Steady

第三章稳恒电流(Steady Current)[基本要求]1、理解电流密度概念及其与电流强度的关系。
2、理解稳恒电流及稳恒电场的意义和它们的基本性质。
3、掌握电动势的概念。
4、掌握欧姆定律的微分形式,学会用场的观点去阐述电路的原理。
5、理解基尔霍夫方程组,学会用基尔霍夫定律解题。
6、了解温差电现象、电子发射与气体导电。
[重点难点]1、理解稳恒电场的概念及与静电场的异同,明确稳恒电流的条件,理解其数学表达式的物理意义。
2、电流密度矢量和电动势是本章的两个基本概念,要着重理解它们的物理意义。
3、欧姆定律的微分形式(不含源电路,含源电路),学会用场的观点去阐述电路的原理。
[教学内容]§1 电流的稳恒条件和导电规律一.电流强度,电流密度矢量1.电流·电流—带电粒子的定向运动。
·载流子—形成电流的带电粒子。
例:电子、质子、离子、空穴。
·电流形成条件(导体内):(1)导体内有可以自由运动的电荷;(2)导体内要维持一个电场。
(导体内有电荷运动说明导体内肯定有电场,这和静电平衡时导体内场强为零情况不同。
) 2.电流强度·大小:单位时间内通过导体某一横截面的电量。
·方向:正电荷运动的方向 ·单位:安培(A )3.电流密度(Current density) ·电流强度对电流的描述比较粗糙:况。
·引入电流密度矢量—描写空间各点电流大小和方向的物理量。
·某点的电流密度:是一个矢量。
方向:该点正电荷定向运动的方向。
大小:通过垂直于该点正电荷运动方向的单位面积上的电流强度。
单位:安培/米 2·电流场:导体内每一点都有自己的j, ),,(z y x j jdtdqt q IlimdS dI j即导体内存在一个j场---称电流场。
·电流线:类似电力线,在电流场中可画电流线。
3.电流密度和电流强度的关系 (1)通过面元d S 的电流强度d I = j d S = j d S cos(2)通过电流场中任一面积S 的电流强度s d j I电流强度是通过某一面积的电流密度的通量。
第三章 静电场和稳恒磁场1

y
r′
q′
r
q x
( x, y , z ) x = 0 = 0
(1)
ε
z
q
2
O v n 1 2 ε
q
4πε ( x a ) + y 2 + z 2 4πε r 由对称性:a, 0, 0 ) , q ( a, 0, 0 ) , q′ = q : (
r = 3ε 0 E 0 c o s θ
r=a
由真空中电偶极矩 v 在真空中产生的电势
P
v v P r = 4π ε 0 r 3
P P cos θ = 4π ε 0 r 2
v P = 4π ε 0 E 0 a 3
例2.
P75
解:电势是球对称,则 b1 1 = a1 + (R > R3 ) R b2 2 = a2 + ( R 2 > R > R1 ) R 条件:
v δ (x) = 0
v
∫ δ ( x )dV = 1
v x≠0 v x = 0 ∈V
v v x δ x x′ 表示 ( ) v 与 x = 0 的 δ 函数定义相较,则有
v v δ ( x x′) = 0
v v
v 处于 x′点上的单位点电荷密度用函数
∫ δ ( x x′)dV = 1
v v x ≠ x′ v x′ ∈V
1) 2 3) σ ∴
R = R1
R3
2
R2 R1 1
= 1
R→ ∞
= 0, 2 ) 2 ,σ
R = R3 2
R = R2
= 1
R = R3
1
= ε0
1 R
= ε0
2 R
大物电磁学课后答案3经典.ppt
(1)电流强度在10秒内均匀的有零增加到3安培; (2)电流强度从18安培起,每过0.01秒减少一半,直到零。
解:(1)I 3 t 10
q
I dt
010
t 10
dt
15(库 仑)
(2)q I0k
1 2
I
0k
1 4
I0k
I0k(1 1 / 2 1 / 4 ) 180.011/(11/ 2)0.36(库 仑)
安培起,每过0.01秒减少一半,直到零。求导线产生的热量。
解:
3
2
(1) I 10 t dQ I rdt
| Q
t
(
3
t)2 Rdt
3
Rt3
10
180(焦)
0 10
10 0
2
2
2
(2) Q Q1 Q 2 Q 3 I1 Rt I 2Rt I 3Rt
Rt[I02
(
I0
/
2)2
电势差为4.25伏特,当该电池放电时,通过的电流为4安培两极
间的电势差为3.90伏特,求该电池的电动势和电阻。
解:
I1r 4.25 I 2r 3.90
精品文档
r
0.05(欧 4.10(伏
姆) 特)
6
3-10 设在图中所示的电路中,三个电容开始时均不带电,求将 它们与A、B、C点联结后,各极板上的电量。
7
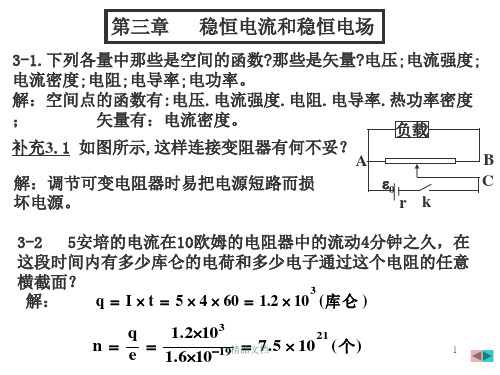
补 Rr;3(2==充330)..3a06.,欧欧4d一姆姆两电,,点R路4求电=如1:势.(图01差欧),通其;姆(过中4,)每bb1点,=个c6接.电两0地伏阻点,,的电rR1电1势==01流差.04.;(00(5欧欧2))a姆姆每,b,,个,c2R电=,28d=源.各20.的伏点5欧端特电姆电势,压。
高等电磁理论第三章答案3

第三章 稳恒电流场的边值问题3-1 在电导率为σ的均匀半空间表面布以相距2L 的电极A 和B ,并分别以I +和I -向媒质中供电。
试根据电场的叠加原理,求出A 和B 两个点电流源在表面上M 点形成的电位。
解:易知点电流源A 在介质中任意一点产生的电位为2A I RΦπσ=,同理可得点电流源B 在介质中任意一点产生的电位为2B IRΦπσ=-,则叠加后介质中任意一点的总电位为22A BI IR R Φπσπσ=-对于表面上一点M (设其坐标为(0)x ,)而言,||A R x L =+,||B R x L =-,则有22||||2||2||2||I I I x L x L x L x L x L Φπσπσπσ--+=-=+--3-2 当地表水平、地下为均匀各向同性岩石时,在地层表面布以相距2L 的电极A 和B ,并分别以电流强度I +和I -向地下供电,在地下建立稳定电流场。
试解答如下问题:(1)求A 和B 连线中垂线上h 处电流密度h j 的表达式;(2)计算并绘图说明深度为h 处的电流密度h j 随AB 的变化规律;(3)确定使h j 为最大时,供电电极距AB 与h 的关系式。
解:(1)易知点电流源A 在介质中任意一点产生的电位为2A IRΦπσ=,则31()()()=22A I I E R RσσΦσπσπ==⋅-∇=⋅-⋅∇Rj 同理可得点电流源B 在介质中任意一点产生的电流密度为32B I Rπ=-Rj ,叠加后得介质中任意一点的电流密度为3322A BA BI I R R ππ=-R R j 在A 、B 连线的中垂线上,A B R =R ,A B =2L ρ-R R e ,则有3322222()I I L L R L h ρρππ=⋅=⋅+j e e (2)(3)设3222()()f L L L h -=⋅+,对其求导可得35'2222222()()3()f L L h L L h --=+-+令其等于0,得22230L h L +-=,解得L = 故h j 为最大时电极距AB 与h 的关系为22AB L ===3-3 在习题3-2中,电极距AB 时,均匀各向同性半空间中h 深度处的电流密度最大。
《电磁学》赵凯华陈熙谋No3chapter答案

第三章 稳 恒 电 流§3.1 电流的稳恒条件和导电规律思考题:1、 电流是电荷的流动,在电流密度j ≠0的地方,电荷的体密度ρ是否可能等于0? 答:可能。
在导体中,电流密度j ≠0的地方虽然有电荷流动,但只要能保证该处单位体积内的正、负电荷数值相等(即无净余电荷),就保证了电荷的体密度ρ=0。
在稳恒电流情况下,可以做到这一点,条件是导体要均匀,即电导率为一恒量。
2、 关系式U=IR 是否适用于非线性电阻?答:对于非线性电阻,当加在它两端的电位差U改变时,它的电阻R要随着U的改变而变化,不是一个常量,其U-I曲线不是直线,欧姆定律不适用。
但是仍可以定义导体的电阻为R=U/I。
由此,对非线性电阻来说,仍可得到U=IR的关系,这里R不是常量,所以它不是欧姆定律表达式的形式的变换。
对于非线性电阻,U、I、R三个量是瞬时对应关系。
3、 焦耳定律可写成P=I 2R 和P=U 2/R 两种形式,从前者看热功率P 正比于R ,从后式看热功率反比于R ,究竟哪种说法对?答:两种说法都对,只是各自的条件不同。
前式是在I一定的条件下成立,如串联电路中各电阻上的热功率与阻值R成正比;后式是在电压U一定的条件下成立,如并联电路中各电阻上的热功率与R成反比。
因此两式并不矛盾。
4、 两个电炉,其标称功率分别为W 1、W 2,已知W 1>W 2,哪个电炉的电阻大? 答:设电炉的额定电压相同,在U一定时,W与R成反比。
已知W 1>W 2,所以R1<R 2,5、 电流从铜球顶上一点流进去,从相对的一点流出来,铜球各部分产生的焦耳热的情况是否相同?答:沿电流方向,铜球的截面积不同,因此铜球内电流分布是不均匀的。
各点的热功率密度p=j 2/σ不相等。
6、 在电学实验室中为了避免通过某仪器的电流过大,常在电路中串接一个限流的保护电阻。
附图中保护电阻的接法是否正确?是否应把仪器和保护电阻的位置对调? 答:可以用图示的方法联接。
稳恒电流知识介绍

非静电力场强 二.电动势
EK
FK q
把单位正电荷经电源内部由负极移向正极
过程中 非静电力所作的功
EK dl EK dl
L
第三章 稳恒电流 steady current(自学)
从场的角度认识 内容要点 §1 电流和电流密度 一.电流强度 大小:单位时间内通过导体某一横截面的电量
I dq dt
方向:正电荷运动的方向 单位:安培
二.电流密度 current density
1.电流密度 J dI dS
dI
ds
ds
导体中某点的电流密度,数值上等于和该点正电荷定 性移动方向垂直的单位面积上的电流强度。
稳恒电场对运动电荷作功 稳恒电场的存在 总伴随着能量的转移
§3 欧姆定律的微分形式
导体中任一点电流密度的方向(正电荷运动的
方向)和该点场强方向相同
有关系式
J E
§4 电动势 electromotive force (emf)
一.电源及电源的作用 source of emf
非静电力 non-electrostatic force
对于稳恒电路 导体内存在电场 稳恒电场 由不随时间改变的电荷分布产生
2.和静电场比较
相同之处
电场不随时间改变
满足高斯定理 满足环路定理 是保守场
可引入电势概念
LE dl 0
回路电压定律(基尔霍夫第二定律)
在稳恒电路中 沿任何闭合回路一周的电势 降落的代数和等于零
不同之处
产生稳恒电流的电荷是运动的电荷 电荷 分布不随时间改变
方向:该点正电荷定向移动的方向。
2.电流密度和电流强度的关系
I SJ ds
dI Jds J ds
电磁学练习题积累(含部分答案)

一.选择题(本大题15小题,每题2分)第一章、第二章1.在静电场中,下列说法中哪一个是正确的 [ ](A)带正电荷的导体,其电位一定是正值(B)等位面上各点的场强一定相等(C)场强为零处,电位也一定为零(D)场强相等处,电位梯度矢量一定相等2.在真空中的静电场中,作一封闭的曲面,则下列结论中正确的是[](A)通过封闭曲面的电通量仅是面内电荷提供的(B) 封闭曲面上各点的场强是面内电荷激发的(C) 应用高斯定理求得的场强仅是由面内电荷所激发的(D) 应用高斯定理求得的场强仅是由面外电荷所激发的3.关于静电场下列说法中正确的是 [ ](A)电场和试探电荷同时存在和消失(B)由E=F/q知道,电场强度与试探电荷成反比(C)电场强度的存在与试探电荷无关(D)电场是试探电荷和场源电荷共同产生的4.下列几个说法中正确的是: [ ](A)电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向(B)在以点电荷为中心的球面上,由该点电荷所产生的场强处处相同(C)场强方向可由E=F/q定出,其中q为试验电荷的电量,q可正、可负,F为试验电荷所受的电场力(D)以上说法全不对。
5.一平行板电容器中充满相对介电常数为的各向同性均匀电介质。
已知介质两表面上极化电荷面密度为,则极化电荷在电容器中产生的电场强度的大小为 [ ](A)0εσ' (B) 02εσ' (C) 0εεσ' (D) εσ'6. 在平板电容器中充满各向同性的均匀电介质,当电容器充电后,介质中 D 、E 、P 三矢量的方向将是 [ ] (A) D 与E 方向一致,与P 方向相反 (B) D 与E 方向相反,与P 方向一致 (C) D 、E 、P 三者方向相同(D) E 与P 方向一致,与D 方向相反7. 在一不带电荷的导体球壳的球心处放一点电荷,并测量球壳内外的场强分布,如果将此点电荷从球心移到球壳内其它位置,重新测量球壳内外的场强分布,则将发现: [ ] (A) 球壳内、外场强分布均无变化 (B) 球壳内场强分布改变,球壳外的不变 (C) 球壳外场强分布改变,球壳内的不变 (D) 球壳内、外场强分布均改变8. 一电场强度为E 的均匀电场,E 的方向与x 轴正向平行,如图所示,则通过图中一半径为R 的半球面的电场强度通量为 [ ](A) 2R E π;(B) 212R E π;(C) 22R E π;(D ) 0。
静磁场Staticmagneticfield

Ay
0I 4
2 0
a cosd
R2 a2 2Ra cos
又∵ 园电流环在xy平面上,故 ,于是得到
2
cos cos cos sin sin cos( )
sin cos 因此得到:
(其中 , 0)
2
Ax
0I 4
2 0
a sind
R2
a2
2Rasin
c os
1 2
0I
I 2R
e
结果与电磁学求解一致。
[例2]半径为a的导线园环载电流为I,求空间的矢势和 磁感应强度。
Solution:
首先求解矢势
A
P(r,θ,φ)
z
R
r
A
0
r j
(
xr)
dV
4 V
r r
0 4
Ñ Idrl
x
r
θ
o
y
φ' a
Idl
(a,φ',o)
由于问题具有轴对称性,可以把观察点选在xz平面上,
这样的好处是φ'=0,故 只与r,θ有关。
Q r2 a2 R2 2Ra cos ( R·r , ar )
rr r
dl idlx jdly
其中
lx cosa dlx a sin d ly sin a dly a cosd
即得
Ax
0I 4
2 0
a sin d
R2 a2 2Ra cos
,dS可r 得0到
乙S Br
r dS
(
rr A) dS
?L
rr A dl
S
S
由此可看到矢势 A的物理意义是:
矢势 沿A任一闭合回路的环量代表通过以该回路为
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Ua Ub
RI Ri I (放电) RI Ri I (充电)
上式即为一段含源电路的欧姆定律.
若R=0,则有
Ua Ub
IRi (放电) IRi (充电)
此时是电源正、负极间的电势差,称为电源的端电压. 21
电源的电动势与端电压的区别:
电动势:非静电力做功,仅取决于电源本身的性质,与外电 路性质及是否接通无关;
j
K
dl
j
E
dl
j
dl dl dl
利用欧姆定律,得
外 j
dl
外
j
内
E dl
外
U1
IR
内
dl
E dl
内
U2 Ir
而
K dl E dl K dl
I R r 全电路欧姆定律
19
三、一段含源电路的欧姆定律
a , Ri c
R
I
i
j
0
j
i 1,2,, n
汇于节点各支路电流强度的代数和为0.
基尔霍夫第二定律
把关于一段含源电路欧姆定律应用到闭合回路上,这时
Uab 0 ,可得
( Ii Ri ) j 0
i
j
沿任一闭合回路中电动势的代数和等于回路中电阻上电势 降落的代数和。
26
应用基尔霍夫定律列方程组应注意:
名词: ①支路:由电阻、电源串联而成的电流通路.
②节点:3条以上支路的连接点.
③回路:由几条支路组成的闭合电流通路.
基尔霍夫第一定律:
如图,在节点处,根据电流的恒定条件
s
j
dS
0
I1
j dS j dS j dS 0
S1
S2
S3
I3 I2
25
I1 I2 I3 0
基尔霍夫第一定律一般形式
Uef 3
Uaf I1R1 I2R2 3 1 2
23
例题. 3-2-2 试求电源向负载输出功率最大的条件.
解: 设一闭合回路,电源电动势为 ,
内电阻为r,负载电阻为R,则
R
I
Rr
r
电源向负载输出的功率为
P
I
2R
2
R r2
R
根据求极值的方法
dP dR
2
rR
R r3
0
由此得到向负载输出功率最大的条件是: R= r
① 在给定电路上标定各支路上电流的参考方向.
② 方程组中各项之前的正负号约定: 对于节点方程,流出节点的电流I之前取正号,流入取负
号.对回路方程,首先标定回路绕行方向.若电阻中电流方向 与绕行方向一致,电位降落,IR之前加正号,反之加负号.
若电动势与绕行方向一致,电位升高, 之前加正号,反之
加负号.
当 dq 0时,有
j dS 0,则流入S面内电荷量多于流出量。
dt
当 dq
0时,有
S
j dS
0,则流出S面内电荷量多于流入量。
dt
S
5
利用数学上的高斯定理
j dS j dV
s
v
dq dt
v
t
dV
得
j
0
t
电流连续方程微分形式
2. 电流的恒定条件
0
t
j 0
S j dS 0
上式计算出的电导率与实际相差甚远.这些困难需要量子理论
来解决.
12
例题3-1-1 两同轴铜质圆形套管,长为L,内圆柱的
半径a,外圆柱的半径为b,两圆柱间充以电阻率为
的石墨.若以内、外圆柱分别为一个电极,求石墨的 电阻.
解:两根铜管分别作为一个等势面,电流
沿着径向由一个圆筒流向另一个圆筒, b
根据对称性
上式称为匹配条件.应当注意,对于一般化学电源,内阻都很小
当满足匹配条件时,总电阻很小,会使电流超过额定值,故一般
条件不能在匹配条件下使用化学电源.但在电子技术中的某些电
源,其内阻很大,考虑匹配是很重要的.
24
㈢ 复杂电路与基尔霍夫定律
在实际直流电路中,往往碰到多电源多回路的复杂电路。 处理复杂电路的基本方法是根据基尔霍夫定律列出一组电路 的线性方程,通过解线性方程组解决复杂电路问题。
场E的方向附加一个定向加速度
a
e
E
me
11
自由电子同原子实碰撞,只能在连续两次碰撞的时间间隔内 得以定向加速,从统计角度考虑,平均定向运动速度为
u
1
e
E
1
e
E
2 me
2 me v
若导体内自由电子(载流子)密度为n,则
j
n e
u
ne2
E
E
2mev
ne2
2mev
由经典电子论导出的结果只能定性说明金属导电的规律由
Rab
R
Rr r
R r r
Rr Rr
r
借助偏导 同样可得 此结论
Rr rR
rRr
r R2
r
R 2 r R
15
设r不变,R改变 R时,则 Rab 的改变为
Rab
r
rR rR
rRR
r R2
r
r
2
R
R
两者之比为
Rab
R
Rab
r
R 2
r
r R
当 R r 时,便有
因R>>r,故得
⑵ 若电动势的指向与积分路径的方向相同,该电动势前 取“+”号,相反则取“-”号.
例题3-2-1 如图所示,求电路a、f间电势差.
a R1 b
d R2 e
f
I1 1 c 2
I2 3
解 各支电路设置的电流方向如图所示,则对电阻有
Uab I1R1
Ude I2R2
对电源有 Ubc 1
Ucd 2
3
2. 电流密度矢量 j
定义
j
dI
n
dI
n
dS dS cos
S0
S
S
n
j
电流密度是一个矢量,其方向和该点正电荷运动的方向 一致,数值上等于通过该点单位垂直截面的电流强度.
电流密度矢量构成的矢量场称之为电流场。
3. 电流线:用电流线描述电流场 曲线方向:该点电流密度方向; 曲线密度:与该点电流密度的大小成正比。
注意:此处的dS是垂直电流方向的截面面积。
8
五、焦耳-楞次定律
电流通过一段电路时,电场力要对移动电荷做功
A IUt Q A I 2Rt U 2 t
R
在一段纯电阻电路中,电功等于电热。但在非纯电阻电路 中(如含有电动机等输出设备)电功和电热两者不相等。
电功率则为
P A IU I 2R U 2
10
六、经典金属电子论
金属导体的微观电结构图像(自由电子模型): • 金属具有晶格点阵结构; • 电场力作用下电子的无规热运动附加了定向运动; • 大量电子不断地与晶格碰撞。
自由电子的定向运动是一段一段加速运动的衔接,各段 加速运动都从定向速度为0开始。
欧姆定律的经典解释
金属内自由电子在电场E作用下,会在热运动的同时逆电
第三章 稳恒电流
目录
1、电流 电流密度 2、电源 电动势 3、复杂电路与基尔霍夫定律
1
经过多年的研究,1800年春,意大利的伏打(Count Alessa -Ndro Volta,1745-1827)制成了伏打电池,从而获得持续 的电流。有了稳定的电源,就为人类从研究静电现象过渡到研 究动电现象提供了坚实的技术基础。
a
I s jr dS jr 2rL
l
通过各柱面的I是相等的,故
j I 1
2L r
E j
I
1
2L r
13
两极间的电势差为
U1 U2
E dl
b I
dr
I ln b
a 2L r 2L a
R U1 U2 ln b I 2L a
例题3-1-2 图中所示是电学仪器中调节电阻的装置,其
I
不同类型电源中,非静电力不同:
A
•发电机:电机作用将机械能转化为电能; •化学电池:化学作用将化学能转化为电能; •温差电源:扩散作用将热能转化为电能; •太阳能电池:直接将光能转化为电能; •核能电池:直接将核能转换为电能。
B 17
二、电源的电动势
设K表示作用在单位正电荷上的非静电力,其方向在电源 内与电场E的方向相反,量纲、单位相同。在有电场E和非电 场力K同时存在的电路中(如电源内),应把欧姆定律推广为
注意:欧姆定律在某些情况下会失效,其主要表现是I与U 的比例关系遭到破坏,而代之以非线性关系。
7
2.欧姆定律的微分形式
将欧姆定律应用于微圆柱体,有
dI dU , R dl ,
ds
R
dS
j E dl
j dI , dU Edl dS
得 j E
j
E
E
上式适用于恒定及非恒定情况,是实验定律的总结。描述 了导体中电场和电流分布之间细节关系。
二、电流强度 与电流密度
1. 电流强度:单位时间内通过导体任一横截面的电量.
取 t 0,则得
I q t
I lim q dq t0 t dt
单位: 1A 103 mA 106 A
电流强度是标量,它只能描述导体中通过某一截面的整体特征. 为反映导体中各处电荷定向运动的情况,需引入电流密度概念.
b
I
⑴ 放电
a , Ri c R
I
⑵ 充电
如图所示,在一段含源的电路中
j
K
E
E
j
K
