2malthus和logistic模型
ode建模初步

这就是t时刻空气中含CO2的百分比。 通常 Km r x 0 否则含CO 的量只会增加。 2 K
令t
得
Km r lim x(t ) % t K
这表明车间空气中含CO2的量最多只能降到
Km r % K
讨论:如果设V=10000立方米,r=0.3立方米/分钟, K=1500立方米/分钟,m=0.04%,x0=0.12%。试问: (1)需多少分钟后,车间空气中含CO2的百分比低于 0.08%? (2)车间空气中含CO2的百分比最多只能降到多少?
量很大时,会对自身增大产生抑制性,故一次项又被称为竞争项。
从而有: dN r ( N ) N (1) (3)式还有另一解释,由于空间和资源都是有限的,不可能供养无限
对(3)分离变量: 两边积分并整理得:
令N(0)=N0,求得:
1 1 dN kKdt N KN K N 1 Ce kKt K N0 C N0
令种群数量翻一番所需的时间为T,则有:
2 N0 N0 e
故
ln 2 T r
rT
模型预测 模型检验 假如人口数真能保持每34.6年增加一倍,那么人口数将 比较历年的人口统计资料,可发现人口增长的实际情况 以几何级数的方式增长。例如,到2510年,人口达2×1014个, 与马尔萨斯模型的预报结果基本相符,例如,1961年世界人 即使海洋全部变成陆地,每人也只有9.3平方英尺的活动范围, 口数为30.6 (即3.06×109),人口增长率约为2%,人口数 Malthus模型实际上只有在群体总数 而到2670年,人口达36×1015个,只好一个人站在另一人的 大约每35年增加一倍。检查1700年至1961的260年人口实际 不太大时才合理,到总数增大时, 肩上排成二层了。 故马尔萨斯模型是不完善的。 数量,发现两者几乎完全一致,且按马氏模型计算,人口数 所以Malthus模型假设的人口净 生物群体的各成员之间由于有限的 量每34.6年增加一倍,两者也几乎相同。 增长率不可能始终保持常数, 生存空间,有限的自然资源及食物 它应当与人口数量有关。 等原因,就可能发生生存竞争等现
生物增长模型

生物增长模型生物增长模型是一种数学模型,用于描述生物种群增长过程中生物个体数量的变化规律。
生物增长模型具有很高的应用价值,可以用来预测生物种群数量的变化趋势以及控制生物种群数量的增长规律,对于生态保护、农业生产、环境监测等领域都具有重要意义。
本文将分为以下几个方面详细介绍生物增长模型的相关知识:一、生物增长模型的种类生物增长模型通常分为离散型模型和连续型模型两种。
离散型模型采用基于时间的离散点来描述生物个体数量的增长过程,常见的离散型模型有Malthus模型、Logistic模型等。
连续型模型则是采用微积分的方法来描述生物个体数量的增长过程,常见的连续型模型有Verhulst模型、Lotka-Volterra模型等。
二、Malthus模型Malthus模型是一个简单的生长模型,其基本假设是生物个体数量的增长速率与个体数量成正比。
数学表达式为:Nt+1 = Nt*e^(rt)。
其中Nt表示t时刻的生物个体数量,r表示生物个体数量的增长速率。
Malthus模型的缺点是忽略了环境和资源的限制,因此实际应用较为有限。
三、Logistic模型Logistic模型是目前最为广泛使用的生物增长模型之一,其基本假设是生物个体数量的增长速率随着数量的增加而逐渐减缓,最终趋向于一个稳定值。
数学表达式为:dN/dt = rN(1-N/K)。
其中Nt表示t时刻的生物个体数量,r表示生物个体数量的增长速率,K表示生物种群的承载力。
Logistic模型具有较强的实用价值,广泛应用于生态系统建模、渔业资源管理、疾病传播动力学等领域。
四、Verhulst模型Verhulst模型是Logistic模型的改进版本,相较于Logistic模型增加了一项小的基本死亡率,从而更好地符合实际情况。
Verhulst模型的数学表达式为:dN/dt = rN - (r/k)N^2。
其中Nt表示t时刻的生物个体数量,r表示生物个体数量的增长速率,K表示生物种群的承载力。
Malthus和Logistic模型及其医学应用

不会导致死 亡也 不会康 复 , Ma h s 用 l u 模型 来描 述在 医学 上 t
有 一定 的参 考价值 , 随着 时间的推移 , 但 它将越来越 偏离 实际
情况 。
8 Da i ,CS, e 1 Cae o ia t ayssU sn heS vs ta. tg rc lDa a An l i ig t AS ys S —
乌鲁木 齐 8 05 ) 304
要 : Ma h s l u 模型和 L g t 模 型是种群生态学 的核心理论之一 , t oii sc 它们在医学中的应用涉及传染病模型 、 肿瘤 生长 、 肿瘤治
太大时 , l u 模 型能够很好的说明人 口总数 的增长情况 。 Ma h s t
1 Matu 模 型 l s h
ln ,2 0 . i a 0 0
T e a T xct rdcino h n l i t i Q T h l o i yP e it f e os nRa a S R Or i o P v
S n Ye h , ta u z ie l
( c ol f Ph r c C iaM e i l ies y, h n a g 1 O 0 ) S h o a ma y, h n d c vri S ey n 1 O 1 o a Un t
f r r e r s . ec efce tc rea in wh c s0 9 4 sds u s d wih t e r lto s i so o wa d r g e s Th o fiin o r lt ih i . 7 9 i ic s e t h eain h p fLDs a d o 0 n
c e sr aa tr r p e osaec l ltd T eQS f 2p e osi st p whc o ie t h mi yp rmeesf 9 h n l r ac ae . h TR o h n l s e i cmbn dwi t o 3 u 2 u h h
Malthus 模型和Logistic 模型

Malthus 模型和Logistic 模型随着社会的发展,人口问题与经济、资源、环境、社会的冲突日益成为制约国家发展的瓶颈,了解了人口增长函数,也就掌握了人口的发展动态和发展规律,这对国家的发展有重要意义。
1798年.英国人口学家和政治经济学家马尔萨斯以两个假设为前提:第一,食物为人类生存所必须;第二,人的性本能几乎无法限制,提出了闻名于世的人口指数增长模型,即Malthus 人口模型:人口总数为)(t p ,人口的出生率为b ,死亡率为d 。
任取时段【t ,t +dt 】,在此时段中的出生人数为b )(t p dt ,死亡人数为d )(t p dt 。
假设出生数及死亡数与)(t p 及dt 均成正比,而且以矩形取代了曲边梯形的面积。
在时段【t ,t +dt 】中,人口增加量为)(dt t p +-)(t p ≈d )(t p ,它应等于此时段中的出生人数与死亡人数之差,即d )(t p =b )(t p dt -d )(t p dt =a )(t p dt ,其中a =b -d 称为人口的净增长率。
于是)(t p 满足微分方程dtt dp )(=a )(t p . (1) 若已知初始时刻t =t 0时的人口总数为p 0,那么)(t p 还满足初始条件t =t 0时,)(t p =p 0. (2)可以求得微分方程(1)满足初始条件(2)的解为(设a 是常数))(t p =p 0e )0(t t a -, (3)即人口总数按指数增长。
模型参数的意义和作用:t 0为初始时刻(初始年度),p 0为初始年度t 0的人口总数,a 为每年的人口净增长率,b 为人口出生率,d为人口死亡率。
Malthus人口模型所说的人口并不一定限于人,可以是认可一个生物群体,只要满足类似的性质即可。
现在讨论模型的应用和正确性。
例如,根据统计数据知在1961年全世界人口为30.6亿,1951年-1961年十年每年人口净增长率约为0.02。
种群增长和竞争的数学模型

种群增长和竞争的数学模型摘 要:本文首先简要介绍Malthus 和Logistic 两种单种群增长模型,然后详细介绍双种群竞争的Volterra 模型,最后介绍了多种群的Gause-Lotka-Volterra 和三种群的RPS 博弈模型,对其做了比较和分析,得出了一些有益的启示。
为了保持自然资料的合理开发与利用,人类必须保持并控制生态平衡,甚至必须控制人类自身的增长。
本文首先简要介绍Malthus 和Logistic 两种单种群增长模型,然后详细介绍双种群竞争的V olterra 模型,最后介绍了三种群的Gause-Lotka-V olterra 和RPS 博弈模型。
一般生态系统的分析可以通过一些简单模型的复合来研究,根据生态系统的特征建立相应的模型。
种群的数量本应取离散值,但由于种群数量一般较大,为建立微分方程模型,可将种群数量看作连续变量,甚至允许它为可微变量,由此引起的误差将是十分微小的。
1.1 马尔萨斯(Malthus )模型马尔萨斯在分析人口出生与死亡情况的资料后发现,人口净增长率r 基本上是一常数,(r =b -d , b 为出生率,d 为死亡率),既: 1dN r N dt = 或 dNrN dt= (1)其解为0()0()r t t N t N e -=(2)其中N 0=N (t 0)为初始时刻t 0时的种群数。
马尔萨斯模型的一个显著特点:种群数量翻一番所需的时间是固定的。
令种群数量翻一番所需的时间为T ,则有: 002rT N N e =(3)ln 2T r=(4)人口统计数据与Malthus 模型计算数据对比:表1 世界人口数量统计数据表2 中国人口数量统计数据比较历年的人口统计资料,可发现人口增长的实际情况与马尔萨斯模型的预报结果基本相符,例如,1961年世界人口数为30.6亿(即3.06×1010),人口增长率约为2%,人口数大约每35年增加一倍。
查1700年至1961年共260年的人口实际数量,发现两者几乎完全一致,且按马氏模型计算,人口数量每34.6年增加一倍,两者也几乎相同。
人口指数增长模型和Logistic模型
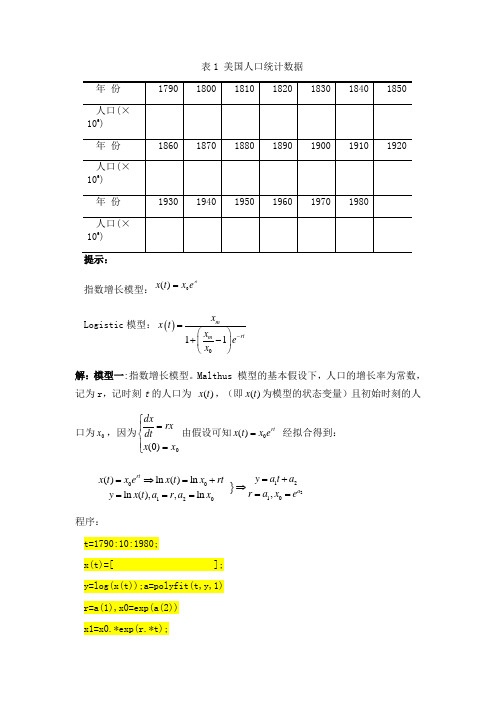
表1 美国人口统计数据指数增长模型:rt e x t x 0)(=Logistic 模型:()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭解:模型一:指数增长模型。
Malthus 模型的基本假设下,人口的增长率为常数,记为r ,记时刻t 的人口为 )(t x ,(即)(t x 为模型的状态变量)且初始时刻的人口为0x ,因为⎪⎩⎪⎨⎧==0)0(x x rxdt dx由假设可知0()rt x t x e = 经拟合得到:}2120010120()ln ()ln ,ln (),,ln rt a y a t a x t x e x t x rt r a x ey x t a r a x =+=⇒=+⇒=====程序:t=1790:10:1980;x(t)=[ ]; y=log(x(t));a=polyfit(t,y,1) r=a(1),x0=exp(a(2)) x1=x0.*exp(r.*t);plot(t,x(t),'r',t,x1,'b') 结果:a =r= x0=所以得到人口关于时间的函数为:0.02140()t x t x e =,其中x0 = , 输入:t=2010;x0 = ;x(t)=x0*exp*t)得到x(t)= 。
即在此模型下到2010年人口大约为 610⨯。
模型二:阻滞增长模型(或 Logistic 模型) 由于资源、环境等因素对人口增长的阻滞作用,人口增长到一定数量后,增长率会下降,假设人口的增长率为 x 的减函数,如设)/1()(m x x r x r -=,其中 r 为固有增长率 (x 很小时 ) ,m x 为人口容量(资源、环境能容纳的最大数量), 于是得到如下微分方程:⎪⎩⎪⎨⎧=-=0)0()1(xx x x rx dt dxm 建立函数文件function f=curvefit_fun2 (a,t)f=a(1)./(1+(a(1)/*exp(-a(2)*(t-1790))); 在命令文件中调用函数文件 % 定义向量(数组) x=1790:10:1990; y=[ 76 ... 92 204 ];plot(x,y,'*',x,y); % 画点,并且画一直线把各点连起来 hold on;a0=[,1]; % 初值% 最重要的函数,第1个参数是函数名(一个同名的m 文件定义),第2个参数是初值,第3、4个参数是已知数据点 a=lsqcurvefit('curvefit_fun2',a0,x,y); disp(['a=' num2str(a)]); % 显示结果 % 画图检验结果 xi=1790:5:2020; yi=curvefit_fun2(a,xi); plot(xi,yi,'r'); % 预测2010年的数据 x1=2010;y1=curvefit_fun2(a,x1) hold off 运行结果: a= y1 =其中a(1)、a(2)分别表示()011mrtm x x t x e x -=⎛⎫+- ⎪⎝⎭中的m x 和r ,y1则是对美国美国2010年的人口的估计。
7.2.2-Logistic人口增长模型
Logistic人口增长模型实验目的●熟悉MATLAB解微分方程数值解的函数ode23的使用方法●了解Logistic人口增长模型比利时数学家Verhulst 在1844-1845年研究人口增长时指出:受自然资源,环境条件等因素限制,人口数量在初始阶段接近指数增长,当逐渐变得饱和时增速变缓,最终达到稳定后增长停止。
()r d N dt N N =r(N)表示人口数量为N 时的增长率(1)m d r N N N d N t =-N m 表示环境能供养的人口总量的上界,r 为常数变化率。
Logistic 方程:Logistic 人口增长模型微分方程表示:r(N)是减函数比较Malthus 模型:dN N dt r r 为常数增长率Logistic 模型中,r(N)是N 的线性减函数。
应用:Logistic 方程广泛应用于化学,统计学,经济学和神经网络等。
某国2000年总人口为12.674亿,假设受环境限制人口上限为20亿,人口变化率为0.0173。
根据Logistic 人口增长模型,总人口数满足微分方程:(1)(2000)12.670.0174320dN N N dt N ⎧=-⎪⎨⎪=⎩程序文件求解:plot(t,N)function logistic [t, N]=ode23(@fun,[2000,2050],12.674);function vfun=fun(t,N)vfun=0.0173*(1-N/20).*N;(1)md r N N N d N t =-Logistic 方程:示例:图1Logistic人口增长模型图2Malthus模型和Logistic人口增长模型题目中有关Logistic 人口增长模型的参数都是给定的。
如果已有一组人口数据,能否根据这些数据估计r 和N m ?思考:(1)m d r N N N d N t =-。
人口模型(马尔萨斯__vs__logistic)
表示: y 0.2743t 1.4323
ln x0 1.4323 x0 4.1884 x(t ) 4.1884e0.2743t
模型预测
假如人口数真能保持每34.6年增加一倍,那么人口数将
以几何级数的方式增长。例如,到2510年,人口达2×1014个,
(4.2)
x(t ) x0ert
(4.2)
当r>0时,表明人口将按指数规律无限增长,因此又称为人 口指数模型。
马尔萨斯模型的一个显著特点:种群数量翻一番所需的时 间是固定的。
令种群数量翻一番所需的时间为T,则有:2 x0 x0erT 故 T ln 2
r
模型检验
x(t ) x0ert
(4.2)
(4.4)
x(0) x0
增长对的(马4.种6尔)群式萨个还斯体有,模另当一型种解引群释入数,一量由过次于多空项时间(,和竞由资争于源人项都均是)资有,源限令占的有,r(率不x)的可=r下能-a降供x及养环无境限
恶化此、时疾得病到增微多等分原方因程,:出生率将降低而死亡率却会提高。设环境能供养
的x积被m(成 称种-(x4恰正为群4..为55数比统))环量,计被可境的正筹称还d改上d好算为xtdd能L界符律xt写o供为合的gx成rim(养sx统原rt(m:ix的c计 因(rm得马(模ax就种规 。近x据r)到 尔型为 模 程 实 是)最(是x群xx律似实或)的 萨拟了 型 师 采际)简x引数是,地际生就 斯合得 , 原 用问单或进量未得将物背是 模方题出 我 则 尽的一,总知到x景马 型法dm的一 们 。 可d形次数(函x了看t,尔 的来个 不 工 能数式增项4数实成它萨 最.求有 妨 程 简学(是6长r(,验常无)(斯 简14的实 采 师 单模常。竞.但结数法指6模 单统际 用 们 的型数)争x根果)用出x型 的计m时意 一 在 方,项的),,筹。 改x,义 下 建 法此)支x种算对 进的工立。表总时持律(群示,4,增.当5是这)长前由就率的荷是与兰种(两数群4者学.数6的生)量乘也,
4-微分方程建模实例——Malthus模型与Logistic模型-课件PPT
23
于是,
N0 N (t)e (tt0 ) r[e (tt0 ) 1].
若此画是真品,t - t0 ≈ 300 (年) . 从而可求出 λN0 的 近似值. 对油画《在埃牟斯的门徒》具体计算如下:
N0 N (t)e300 r[e300 1]
由于半衰期: T ln 2 ,
于是, ln 2 .
4.1. 人口增长模型 4.2. 赝品的鉴定 4.3. 耐用新产品的销售速度问题 4.4. 传染病模型
1
4.1 人口增长模型
世界人口增长概况
年
1625 1830 1930 1960 1974 1987 1999
人口(亿) 5 10 20 30 40 50 60
中国人口增长概况
年 1908 1933 1953 1964 1982 1990 1995 2000 人口(亿) 3.0 4.7 6.0 7.2 10.3 11.3 12.0 13.0
马尔萨斯(1766~1834) Malthus,Thomas Robert
4
模型假设: • 人口增长率 r 是常数. • 人口的数量本应取离散
值,但由于人口数量一 般较大,为建立微分方 程模型,可以将人口数 量看作连续变量,甚至 允许它为可微变量,由 此引起的误差将是十分 微小的.
5
模型构成:
设 x(t) 表示 t 时刻的人口,有
16
• 六十年后,美国记者、专栏作家乔 纳森·洛佩兹(Jonathan Lopez)出 版了《制造维米尔的人》(The man who made Vermeers) 一书. 在书中,洛佩兹表达了对那个时代 荷兰人民的体谅:“荷兰人对米格 伦的态度并非不可理解. 在二战中, 这个国家遭遇了残酷的羞辱,光复 也是在盟国的帮助下完成. 米格伦 给了未能主宰自身命运的荷兰人内 心深处想要得到的东西. 而对于 ‘欺骗’这种事情,他又是太熟谙 了.”
数学建模 微分方程模型讲解
量在初始阶段的增长情况比较相符。
(2)由(3—19)式推得,t=0 时显然 x=0,这一结果自然与
事实不符。产生这一错误结果的原因在于我们假设产品是自然推
销的,然而,在最初产品还没卖出之时,按照自然推销的方式,
便不可能进行任何推销。事实上,厂家在产品销售之初,往往是
通过广告、宣传等各种方式来推销其产品的。
? 1. 新产品推销模型 ? 一种新产品问世,经营者自然要关心产
品的卖出情况。下面我们根据两种不同 的假设建立两种推销速度的模型。
模型 A 假设产品是以自然推销的方式卖出,换句话说,被卖出的产品
实际上起着宣传的作用, 吸引着未来购买的消费者。 设产品总数与时刻 t 的关
系为 x(t), 再假设每一产品在单位时间内平均吸引 k 个顾客,则 x(t) 满足微
样,从根本上解决了模型 A 的不足。 由(3—20)式易看出, dx ? 0 ,即 x(t) 是关于时刻 t 的单调增
dt
加函数,实际情况自然如此,产品的卖出量不可能越卖越少。另外,
对(3—20)式两端求导,得
d 2x dt 2
?
k(M
?
2 x)
dx dt
故令 d 2x
dt 2
?
0 ,得到 x(t0 ) ?
Nm N0
)e? n
易看出,当t→? 时,当N(t) →Nm。这个模型称为Logistic 模型,其结果 经过计算发现与实际情况比较吻合。上面所画的是 Logistic 模型的的图形。
你也可从这个图形中,观察到微分方程解的某些性态。
捕鱼问题
在鱼场中捕鱼,捕的鱼越多,所获得的经济效益越大。但捕捞的鱼过多,
根据上面的假设,我们建立模型
dS ? P ? A(t) ? ??1 ? S (t) ?? ? ? S(t )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
为了保持自然资料的合理开发与利用,人类必须保持并控制生态平衡,甚至必须控制人类自身的增长。
本节将建立几个简单的单种群增长模型,以简略分析一下这方面的问题。
一般生态系统的分析可以通过一些简单模型的复合来研究,大家若有兴趣可以根据生态系统的特征自行建立相应的模型。
美丽的大自然种群的数量本应取离散值,但由于种群数量一般较大,为建立微分方程模型,可将种群数量看作连续变量,甚至允许它为可微变量,由此引起的误差将是十分微小的。
离散化为连续,方便研究§3.2Malthus 模型与Logistic 模型模型1马尔萨斯(Malthus )模型马尔萨斯在分析人口出生与死亡情况的资料后发现,人口净增长率r 基本上是一常数,(r =b -d ,b 为出生率,d 为死亡率),既:1dN r N dt =dN rN dt =或(3.5)0()0()r t t N t N e -=(3.6)(3.1)的解为:其中N 0=N (t 0)为初始时刻t 0时的种群数。
马尔萨斯模型的一个显著特点:种群数量翻一番所需的时间是固定的。
令种群数量翻一番所需的时间为T ,则有:002rTN N e =ln 2T r =故模型检验比较历年的人口统计资料,可发现人口增长的实际情况与马尔萨斯模型的预报结果基本相符,例如,1961年世界人口数为30.6 (即3.06×109),人口增长率约为2%,人口数大约每35年增加一倍。
检查1700年至1961的260年人口实际数量,发现两者几乎完全一致,且按马氏模型计算,人口数量每34.6年增加一倍,两者也几乎相同。
19502000205021002150220000.511.522.533.5x 1011t/年N /人马尔萨斯模型人口预测模型预测假如人口数真能保持每34.6年增加一倍,那么人口数将以几何级数的方式增长。
例如,到2510年,人口达2×1014个,即使海洋全部变成陆地,每人也只有9.3平方英尺的活动范围,而到2670年,人口达36×1015个,只好一个人站在另一人的肩上排成二层了。
故马尔萨斯模型是不完善的。
几何级数的增长Malthus 模型实际上只有在群体总数不太大时才合理,到总数增大时,生物群体的各成员之间由于有限的生存空间,有限的自然资源及食物等原因,就可能发生生存竞争等现象。
所以Malthus 模型假设的人口净增长率不可能始终保持常数,它应当与人口数量有关。
模型2 Logistic 模型人口净增长率应当与人口数量有关,即:r =r (N )从而有:()dN r N N dt=(3.7)r (N )是未知函数,但根据实际背景,它无法用拟合方法来求。
为了得出一个有实际意义的模型,我们不妨采用一下工程师原则。
工程师们在建立实际问题的数学模型时,总是采用尽可能简单的方法。
r (N )最简单的形式是常数,此时得到的就是马尔萨斯模型。
对马尔萨斯模型的最简单的改进就是引进一次项(竞争项)对马尔萨斯模型引入一次项(竞争项),令r (N )=r -aN 此时得到微分方程:()dN r aN N dt =-(1)dN N r N dt K =-或(3.8)(3.8)被称为Logistic 模型或生物总数增长的统计筹算律,是由荷兰数学生物学家弗赫斯特(Verhulst )首先提出的。
一次项系数是负的,因为当种群数量很大时,会对自身增大产生抑制性,故一次项又被称为竞争项。
(3.8)可改写成:()dN k K N N dt =-(3.9)(3.9)式还有另一解释,由于空间和资源都是有限的,不可能供养无限增长的种群个体,当种群数量过多时,由于人均资源占有率的下降及环境恶化、疾病增多等原因,出生率将降低而死亡率却会提高。
设环境能供养的种群数量的上界为K (近似地将K 看成常数),N 表示当前的种群数量,K -N 恰为环境还能供养的种群数量,(3.9)指出,种群增长率与两者的乘积成正比,正好符合统计规律,得到了实验结果的支持,这就是(3.9)也被称为统计筹算律的原因。
图3-5对(3.9)分离变量:11dN kKdt N K N ⎛⎫+= ⎪-⎝⎭两边积分并整理得:1kKt K N Ce -=+令N (0)=N 0,求得:00K N C N -=故(3.9)的满足初始条件N (0)=N 0的解为:000()()kKt N K N t N K N e -=+-(3.10)易见:N (0)=N 0,lim ()t N t K →+∞=N (t )的图形请看图3.5模型检验用Logistic 模型来描述种群增长的规律效果如何呢?1945年克朗皮克(Crombic )做了一个人工饲养小谷虫的实验,数学生物学家高斯(E ·F ·Gauss )也做了一个原生物草履虫实验,实验结果都和Logistic 曲线十分吻合。
大量实验资料表明用Logistic 模型来描述种群的增长,效果还是相当不错的。
例如,高斯把5只草履虫放进一个盛有0.5cm 3营养液的小试管,他发现,开始时草履虫以每天230.9%的速率增长,此后增长速度不断减慢,到第五天达到最大量375个,实验数据与r =2.309,a =0.006157,N (0)=5的Logistic 曲线:几乎完全吻合,见图 3.6。
2.309375()174t N t e-=+图3-6Malthus模型和Logistic模型的总结Malthus模型和Logistic模型均为对微分方程(3.7)所作的模拟近似方程。
前一模型假设了种群增长率r为一常数,(r被称为该种群的内禀增长率)。
后一模型则假设环境只能供养一定数量的种群,从而引入了一个竞争项。
用模拟近似法建立微分方程来研究实际问题时必须对求得的解进行检验,看其是否与实际情况相符或基本相符。
相符性越好则模拟得越好,否则就得找出不相符的主要原因,对模型进行修改。
Malthus模型与Logistic模型虽然都是为了研究种群数量的增长情况而建立的,但它们也可用来研究其他实际问题,只要这些实际问题的数学模型有相同的微分方程即可,下面我们来看两个较为有趣的实例。
历史背景:例5赝品的鉴定在第二次世界大战比利时解放以后,荷兰野战军保安机关开始搜捕纳粹同谋犯。
他们从一家曾向纳粹德国出卖过艺术品的公司中发现线索,于1945年5月29日以通敌罪逮捕了三流画家范·梅格伦(H ·A ·Vanmeegren ),此人曾将17世纪荷兰名画家扬·弗米尔(Jan Veermeer )的油画“捉奸”等卖给纳粹德国戈林的中间人。
可是,范·梅格伦在同年7月12日在牢里宣称:他从未把“捉奸”卖给戈林,而且他还说,这一幅画和众所周知的油画“在埃牟斯的门徒”以及其他四幅冒充弗米尔的油画和两幅德胡斯(17世纪荷兰画家)的油画,都是他自己的作品,这件事在当时震惊了全世界,为了证明自己是一个伪造者,他在监狱里开始伪造弗米尔的油画“耶稣在门徒们中间”,当这项工作接近完成时,范·梅格伦获悉自己的通敌罪已被改为伪造罪,因此他拒绝将这幅画变陈,以免留下罪证。
为了审理这一案件,法庭组织了一个由著名化学家、物理学家和艺术史学家组成的国际专门小组查究这一事件。
他们用X 射线检验画布上是否曾经有过别的画。
此外,他们分析了油彩中的拌料(色粉),检验油画中有没有历经岁月的迹象。
科学家们终于在其中的几幅画中发现了现代颜料钴兰的痕迹,还在几幅画中检验出了20世纪初才发明的酚醛类人工树脂。
根据这些证据,范·梅格伦于1947年10月12日被宣告犯有伪造罪,被判刑一年。
可是他在监狱中只待了两个多月就因心脏病发作,于1947年12月30日死去。
然而,事情到此并未结束,许多人还是不肯相信著名的“在埃牟斯的门徒”是范·梅格伦伪造的。
事实上,在此之前这幅画已经被文物鉴定家认定为真迹,并以17万美元的高价被伦布兰特学会买下。
专家小组对于怀疑者的回答是:由于范·梅格伦曾因他在艺术界中没有地位而十分懊恼,他下决心绘制“在埃牟斯的门徒”,来证明他高于三流画家。
当创造出这样的杰作后,他的志气消退了。
而且,当他看到这幅“在埃牟斯的门徒”多么容易卖掉以后,他在炮制后来的伪制品时就不太用心了。
这种解释不能使怀疑者感到满意,他们要求完全科学地、确定地证明“在埃牟斯的门徒”的确是一个伪造品。
这一问题一直拖了20年,直到1967年,才被卡内基·梅伦(Carnegie-Mellon )大学的科学家们基本上解决。
原理与模型测定油画和其他岩石类材料的年龄的关键是本世纪初发现的放射性现象。
放射性现象:著名物理学家卢瑟夫在本世纪初发现,某些“放射性”元素的原子是不稳定的,并且在已知的一段时间内,有一定比例的原子自然蜕变而形成新元素的原子,且物质的放射性与所存在的物质的原子数成正比。
用N (t )表示时间t 时存在的原子数,则:dN N dt λ=-常数λ是正的,称为该物质的衰变常数用λ来计算半衰期T :00()dN N dt N t N λ⎧=-=⎪⎨⎪⎩与负增长的Malthus 模型完全一样其解为: 0()0()t t N t N e λ--=012N N =令0ln 2T t t λ=-=则有:许多物质的半衰期已被测定,如碳14,其T =5568;轴238,其T =45亿年。
与本问题相关的其他知识:(1)艺术家们应用白铅作为颜料之一,已达两千年以上。
白铅中含有微量的放射铅210,白铅是从铅矿中提炼出来的,而铅又属于铀系,其演变简图如下(删去了许多中间环节)(2)地壳里几乎所有的岩石中均含有微量的铀。
一方面,铀系中的各种放射性物质均在不断衰减,而另一方面,铀又不断地衰减,补充着其后继元素。
从而,各种放射性物质(除铀以外)在岩石中处于放射性平衡中。
根据世界各地抽样测量的资料,地壳中的铀在铀系中所占平均重量比约为百万分之2.7(一般含量极微)。
各地采集的岩石中铀的含量差异很大,但从未发现含量高于2—3%的。
(3)从铅矿中提炼铅时,铅210与铅206一起被作为铅留下,而其余物质则有90—95%被留在矿渣里,因而打破了原有的放射性平衡。
(注:这些有关物理、地质方面的知识在建模时可向相应的专家请教。
)简化假定:本问题建模是为了鉴定几幅不超过300年的古画,为了使模型尽可能简单,可作如下假设:(1)由于镭的半衰期为1600年,经过300年左右,应用微分方程方法不难计算出白铅中的镭至少还有原量的90%,故可以假定,每克白铅中的镭在每分钟里的分解数是一个常数。
(2)铅210的衰变为:铅210T=22年钋210铅206T=138天若画为真品,颜料应有300年左右或300年以上的历史,容易证明:每克白铅中钋210的分解数等于铅210的分解数(相差极微,已无法区别)。
