OFDM调制解调仿真
实验三-基带OFDM系统及其仿真
实验三基带OFDM系统及其仿真一、实验原理正交频分复用(OFDM)系统是一种特殊的多载波传输方案,它可以被看作是一种调制技术,也可以被当作一种复用技术。
多载波传输把数据流分解成若干个子比特流,这样每个子数据流将具有低得多的比特速率,用这样的低比特率形成的低速率多状态符号再去调制相应的子载波,就构成多个低速率符号并行发送的传输系统。
正交频分复用是对多载波调制(MCM)的一种改进。
它的特点是各子载波相互正交,所以扩频调制后的频谱可以相互重叠,不但减小了子载波间的相互干扰,还大大提高了频谱利用率。
选择OFDM的一个主要原因在于该系统能够很好地对抗频率选择性衰落和窄带干扰。
在单载波系统中,一次衰落或者干扰就可以导致整个链路失效,但是在多载波系统中,某一时刻只会有少部分的子信道会受到深衰落的影响。
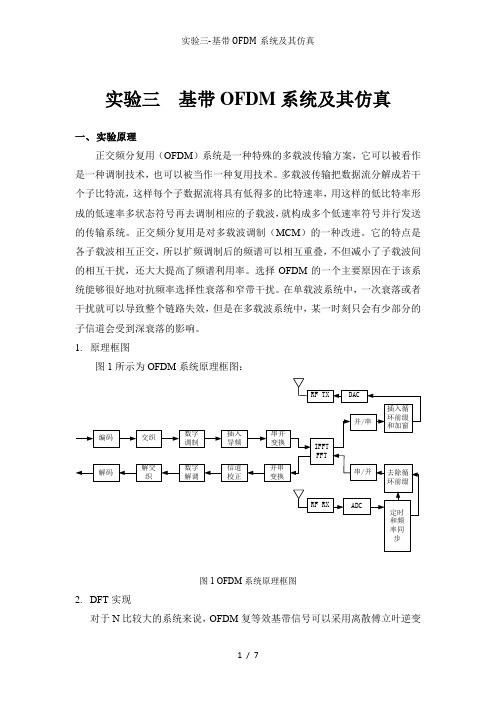
1.原理框图图1所示为OFDM系统原理框图:图1 OFDM系统原理框图2.DFT实现对于N比较大的系统来说,OFDM复等效基带信号可以采用离散傅立叶逆变换(IDFT )方法来实现。
对信号)(t s 以N T 的速率进行抽样,即令N kT t =)1,,1,0(-⋅⋅⋅=N k ,则得到:210(/),01ik N j N k i i s s kT N d e k N π-===≤≤-∑ 可以看到k s 等效为对i d 进行IDFT 运算。
同样在接收端,为了恢复出原始的数据符号i d ,可以对k s 进行逆变换 ,即DFT 得到:210,01ikN j Ni k k d s e i N π--==≤≤-∑OFDM 系统的调制和解调可以分别由IDFT 和DFT 来代替。
通过N 点的IDFT 运算,把频域数据符号i d 变换为时域数据符号k s ,经过射频载波调制之后,发送到无线信道中。
其中每个IDFT 输出的数据符号k s 都是由所有子载波信号经过叠加而生成的,即对连续的多个经过调制的子载波的叠加信号进行抽样得到的。
OFDM基带系统仿真及频谱特性分析

白噪声下OFDM调制解调基带系统仿真一、实验要求1、信噪比 2~14dB,步进2dB2、误码率性能<10-43、仿真分析OFDM信号的功率谱特性二、实验程序流程图和程序本实验中只进行了OFDM基带的系统设计仿真,分别采用了16QAM和QPSK两种方式进行映射和逆映射,OFDM基带系统程序流程图如图1所示:图1 OFDM基带系统程序流程图实验程序:1、QPSK映射程序function [out_message]=QPSK(Sig)[a1,b1]=find(Sig(:,1)==0&Sig(:,2)==0); out_message(a1)=-1-j;[a2,b2]=find(Sig(:,1)==0&Sig(:,2)==1);out_message(a2)=-1+j;[a3,b3]=find(Sig(:,1)==1&Sig(:,2)==0);out_message(a3)=1-j;[a4,b4]=find(Sig(:,1)==1&Sig(:,2)==1);out_message(a4)=1+j;end2、QPSK逆映射程序function [out_symbol,out_bit]=DeQPSK(Sig_noise)m1=find(angle(Sig_noise)<=pi/2&angle(Sig_noise)>0);out_symbol(1,m1)=1+j; out_bit(m1,1)=1; out_bit(m1,2)=1;m2=find(angle(Sig_noise)>pi/2&angle(Sig_noise)<=pi);out_symbol(1,m2)=-1+j; out_bit(m2,1)=0; out_bit(m2,2)=1;m3=find(angle(Sig_noise)>-pi&angle(Sig_noise)<=-pi/2);out_symbol(1,m3)=-1-j; out_bit(m3,1)=0; out_bit(m3,2)=0;m4=find(angle(Sig_noise)>-pi/2&angle(Sig_noise)<=0);out_symbol(1,m4)=1-j; out_bit(m4,1)=1; out_bit(m4,2)=0;end3、复高斯白噪声程序function [sig_noise,snr_dB] = fu_awgn (Sig,SNR,Num_signal)L_SNR = 10.^(SNR/10); % 转换为线性信噪比Eb = sum(abs(Sig).^2)/Num_signal; % 每比特的能量N0 = Eb/L_SNR; % 噪声功率谱密度noise_R1 = randn(1,length(Sig)); % 实际产生均值为0,方差为1的随机高斯序列,功率谱密度是1noise_R2 = noise_R1-mean(noise_R1); % 让均值再更接近0noise_R3 = noise_R2./std(noise_R2); % 标准差归一化让均值等于0 noise_R = noise_R3*sqrt(N0/2); % 使得功率谱密度是N0/2noise_I1 = randn(1,length(Sig)); % 实际产生均值为0,方差为1的随机高斯序列,功率谱密度是1noise_I2 = noise_I1-mean(noise_I1); % 让均值再更接近0noise_I3 = noise_I2./std(noise_I2); % 标准差归一化让均值等于0 noise_I = noise_I3*sqrt(N0/2); % 使得功率谱密度是N0/2x = noise_R + j*noise_I; % 生成复噪声sig_noise = Sig+x; % 此时加入的就是Eb/N0snr=sum(abs(Sig).^2)/sum(abs(x).^2);snr_dB=10*log10(snr); % 实际加入的信噪比SNRend4、主程序(求误比特率曲线)%% OFDM基带系统clear all;close all;clc%% 参数设置N = 256; % fft点数Num_carriers = 256; % 载波数length_symbol =10000; % 符号长度bit_num = Num_carriers*length_symbol*M; % 数据个数Pe_check = [];for SNR = 2:2:14 % 输入信噪比%% 产生基带数据信号Sig= randi([0 1],1,bit_num);%% QPSK调制Sig =reshape(Sig,2,bit_num/2)'; %QPSK映射[out_message]=QPSK(Sig);%% 串并转换Sig__modulation = reshape(out_message,Num_carriers,length_symbol);%% 插值interp_Sig_modulation = [Sig__modulation(1:Num_carriers/2,:);zeros(N-Num_carriers,length_symbol);Sig__modulation(Num_carriers/2+1:Num_carriers,:)]; %% ifftifft_message = ifft(interp_Sig_modulation,N);% 求PSDfft_ps_ifft_message = fftshift(fft(ifft_message,1024));PSD_message =10*log10(abs(fft_ps_ifft_message).^2/max(abs(fft_ps_ifft_message).^2));f1 = (0:length(PSD_message)-1)/length(PSD_message);figure(1)plot(f1,PSD_message);hold on ;plot(0:1/N:1, 0, 'r*');axis([0 1 -400]);xlabel('归一化频率');ylabel('归一化功率');title('OFDM信号功率谱')%% 加入复高斯白噪声Re_message = reshape(ifft_message,1,N*length_symbol);[sig_noise,snr_dB] = fu_awgn (Re_message,SNR,length(Re_message));%% 并串转换ps_sig_noise = reshape(sig_noise,N,length_symbol);fft_Re_message = fft(ps_sig_noise,N);%% 抽值samp_fft_Re_message =[fft_Re_message(1:Num_carriers/2,:);fft_Re_message(Num_carriers/2+1:Num_carriers,:) %% QPSK解调samp_fft_Re_message =reshape(samp_fft_Re_message,1,Num_carriers*length_symbol);[out_symbol,out_bit]=DeQPSK(samp_fft_Re_message); % QPSK逆映射[resum,ratio1]=symerr(Sig,out_bit);Pe = ratio1;Pe_check = [Pe_check,Pe];endSNR = 2:2:14;figuresemilogy(SNR,Pe_check,'-kd');xlabel('信噪比/dB');ylabel('误比特率');axis([2 14 1e-6 1]);5、主程序(绘制功率谱和频谱)%% OFDM基带系统clear all;close all;clc%% 参数设置N = 64; % fft点数Num_carriers = 32; % 载波数length_symbol =100; % 符号长度M = 2;bit_num = Num_carriers*length_symbol*M; % 数据个数%% 产生基带数据信号Sig= randi([0 1],1,bit_num);%% QPSK调制Sig =reshape(Sig,2,bit_num/2)'; %QPSK映射[Sig_modulation]=QPSK(Sig);%% 串并转换Sig_modulation = reshape(Sig_modulation,Num_carriers,length_symbol);%% 插值interp_Sig_modulation_psd = [Sig_modulation(1:Num_carriers/2,:);zeros(N-Num_carriers,length_symbol);Sig_modulation(Num_carriers/2+1:Num_carriers,:)]; %求功率谱插值Sig_modulation = [Sig_modulation';zeros(length_symbol,Num_carriers)];%每隔一个信道插值一个符号长度的0;此时得到的频谱不正交interp_Sig_modulation =reshape(Sig_modulation,length_symbol,2*Num_carriers)';%% ifftifft_message = ifft(interp_Sig_modulation_psd,N);% 求PSDfft_ps_ifft_message = fftshift(fft(ifft_message,1024));PSD_message =10*log10(abs(fft_ps_ifft_message).^2/max(abs(fft_ps_ifft_message).^2));f1 = (0:length(PSD_message)-1)/length(PSD_message);figure(1)plot(f1,PSD_message)hold onplot(0:1/N:1, 0, 'r*')axis([0 1 -40 0]);xlabel('归一化频率');ylabel('归一化功率谱');title('OFDM符号功率谱')%求频谱fft_ps_ifft_message1 = fftshift(interp_Sig_modulation(:,1),2048); %进行了插值fft_ps_ifft_message2 = fftshift(Sig_modulation(:,1),2048); %未进行插值f1 = (0:length(fft_ps_ifft_message1)-1)/length(fft_ps_ifft_message1);f2 = (0:length(fft_ps_ifft_message2)-1)/length(fft_ps_ifft_message2);figure(2)subplot(211)plot(f1,abs(fft_ps_ifft_message1)/max(abs(fft_ps_ifft_message1)));axis([0 1 0 1.2]);xlabel('归一化频率');ylabel('归一化频谱');title('一倍插值后的OFDM符号频谱')subplot(212)plot(f2,abs(fft_ps_ifft_message2)/max(abs(fft_ps_ifft_message2)));axis([0 1 0 1.2]);xlabel('归一化频率');ylabel('归一化频谱');title('未插值的OFDM符号频谱')三、实验结果1、OFDM基带系统误比特曲线Image图2 采用QPSK映射时OFDM基带系统的误比特曲线2、OFDM信号功率谱Image图3 OFDM信号功率谱(64点fft)3、OFDM信号频谱Image图4 OFDM符号的频谱四、总结本实验只进行了OFDM基带调制解调系统的设计仿真,数字信号的映射和逆映射采用的是QPSK调制方式,得到了OFDM基带系统的误比特性能曲线以及OFDM信号的功率谱和OFDM符号的频谱,从得到的仿真结果来看,在信噪比等于14dB的时候系统的误比特率小于10-4 ,符合设计要求。
(2015届通信工程毕设)OFDM调制解调系统仿真与结果分析

4 系统仿真与性能分析4.1 仿真参数设置结合OFDM调制解调系统原理图与仿真流程图,基于MATLAB软件平台,设置系统仿真参数,如表4-1所示:由OFDM系统原理和仿真流程可知,由信源产生一个待传输的二进制随机信号。
此处,我们以QPSK调制为例,根据表4-1设置的系统默认仿真参数,子载波数目1024个,每个子载波中OFDM符号数为50个,每OFDM符号数所含的比特数为2 bit,信噪比(SNR)为2 dB,经过运算、取整等操作,可产生一组包含20000(子载波数⨯符号数/载波⨯位数/符号)个由0和1构成的一维随机二进制数组,即待传信号,截取待传信号的前101(0—100)个码元,其对应的波形与经过OFDM系统传输、解调还原后所得到的信号波形,如图4-1所示:图4-1 待传输信号与解调还原信号对比图由图4-1可知,经过系统发送、传输、解调过后的信号经过并串变换后,还原后所得到的信号与原信号相比,存在数据出错的情况,即产生误码,此时的误码率如图4-3所示:图4-2 默认参数下QPSK调制的系统误码率误码率(SER)是衡量数据在规定时间内数据传输精确性的指标。
即,数据经过通信信道传输以后,接收端所接收到的数据与发送端发送的原始数据相比,发生错误的码元个数占发送端发送的原始数据的总码元个数之比,误码率的计算公式如下所示:误码率=错误码元数/传输总码元数一个通信系统在进行数据传输时的误码率越小,则说明该通信系统的传输精确度越高。
4.2 OFDM系统仿真实现以QPSK调制为例,系统的仿真参数为默认值。
即,子载波数目1024个,每个子载波中OFDM符号数为50个,每OFDM符号数所含的比特数为2 bit,信噪比(SNR)为2 dB。
4.2.1 待传信号与还原信号图4-3 待传信号与还原信号码元波形由仿真参数默认值及仿真程序,信源产生的随机序列的长度为20000(子载波数⨯符号数/载波⨯位数/符号),大小介于0到 1之间,经过取整后即得到长度为20000,大小为0或1的待发送的一维随机二进制数组。
基于MATLAB的OFDM系统仿真及分析

基于MATLAB的OFDM系统仿真及分析OFDM(正交频分复用)是一种广泛应用于无线通信系统中的多载波调制技术。
在OFDM系统中,信号被分为多个独立的子载波,并且每个子载波之间正交。
这种正交的特性使得OFDM系统具有抗频率选择性衰落和多径干扰的能力。
本文将基于MATLAB对OFDM系统进行仿真及分析。
首先,我们需要确定OFDM系统的参数。
假设我们使用256个子载波,其中包括8个导频符号用于信道估计,每个OFDM符号的时域长度为128个采样点。
接下来,我们需要生成调制信号。
假设我们使用16QAM调制方式,每个子载波可以传输4个比特。
在MATLAB中,我们可以使用randi函数生成随机的比特序列,然后将比特序列映射为16QAM符号。
生成的符号序列可以通过IFFT(Inverse Fast Fourier Transform)将其转换为时域信号。
OFDM系统的发射端包括窗函数、导频符号插入、IFFT和并行到串行转换等模块。
窗函数用于增加OFDM符号之间的过渡带,导频符号用于信道估计和符号同步。
通过将符号序列与导频图案插入到OFDM符号序列中,然后进行IFFT变换,再进行并行到串行转换即可得到OFDM信号的时域波形。
接下来,我们需要模拟OFDM信号在信道中传输和接收。
假设信道是Additive White Gaussian Noise(AWGN)信道。
在接收端,OFDM信号的时域波形通过串行到并行转换,然后进行FFT(Fast Fourier Transform)变换得到频域信号。
通过在频域上对导频符号和OFDM信号进行正交插值,可以进行信道估计和等化。
最后将频域信号进行解调,得到接收后的比特序列。
通过比较发送前和接收后的比特序列,我们可以计算比特误码率(BER)来评估OFDM系统的性能。
比特误码率是接收到错误比特的比特数与总传输比特数之比。
通过改变信噪比(SNR)值,我们可以评估OFDM系统在不同信道条件下的性能。
OFDM系统仿真实验报告

无线通信——OFDM系统仿真一、实验目的1、了解OFDM 技术的实现原理2、利用MATLAB 软件对OFDM 的传输性能进行仿真并对结论进行分析。
二、实验原理与方法1 OFDM 调制基本原理正交频分复用(OFDM)是多载波调制(MCM)技术的一种。
MCM 的基本思想是把数据流串并变换为N 路速率较低的子数据流,用它们分别去调制N 路子载波后再并行传输。
因子数据流的速率是原来的1/N ,即符号周期扩大为原来的N 倍,远大于信道的最大延迟扩展,这样MCM 就把一个宽带频率选择性信道划分成N 个窄带平坦衰落信道,从而“先天”具有很强的抗多径衰落和抗脉冲干扰的能力,特别适合于高速无线数据传输。
OFDM 是一种子载波相互混叠的MCM ,因此它除了具有上述毗M 的优势外,还具有更高的频谱利用率。
OFDM 选择时域相互正交的子载波,创门虽然在频域相互混叠,却仍能在接收端被分离出来。
2 OFDM 系统的实现模型利用离散反傅里叶变换( IDFT) 或快速反傅里叶变换( IFFT) 实现的OFDM 系统如图1 所示。
输入已经过调制(符号匹配) 的复信号经过串P 并变换后,进行IDFT 或IFFT 和并/串变换,然后插入保护间隔,再经过数/模变换后形成OFDM 调制后的信号s (t ) 。
该信号经过信道后,接收到的信号r ( t ) 经过模P 数变换,去掉保护间隔以恢复子载波之间的正交性,再经过串/并变换和DFT 或FFT 后,恢复出OFDM 的调制信号,再经过并P 串变换后还原出输入的符号。
图1 OFDM 系统的实现框图从OFDM 系统的基本结构可看出, 一对离散傅里叶变换是它的核心,它使各子载波相互正交。
设OFDM 信号发射周期为[0,T],在这个周期内并行传输的N 个符号为001010(,...,)N C C C -,,其中ni C 为一般复数, 并对应调制星座图中的某一矢量。
比如00(0)(0),(0)(0)C a j b a b =+⋅和分别为所要传输的并行信号, 若将其合为一个复数信号, 很多个这样的复数信号采用快速傅里叶变换, 同时也实现对正交载波的调制, 这就大大加快了信号的处理调制速度(在接收端解调也同样) 。
实验四 OFDM调制解调仿真

实验四 OFDM调制解调仿真一、实验目的1.了解OFDM调制解调的原理。
2.学会用星座图分析系统性能。
二、实验内容1.编写MATLAB程序,实现OFDM系统调制解调。
2.绘制各步骤图形并分析系统特性。
三、实验代码1)程序主代码clear all;close all;N=input('请输入码元数');SNR=input('请输入信噪比');xx=randint(1,4*N);figure(1),stem(xx,'.k');title('原序列');B=0;for m=1:4:4*NA=xx(m)*8+xx(m+1)*4+xx(m+2)*2+xx(m+3);B=B+1;ee(B)=A;endfigure(2),stem(ee,'.b');title('化为0~15的码元');yy=star(ee,N);figure(3),plot(yy,'.r');title('映射后的星座图');ff=ifft(yy,N);N1=floor(N*1/4);N3=floor(N*3/4);N5=floor(N*5/4);figure(4),stem(ff,'.m');title('傅里叶反变换后');for j=1:N1ss(j)=ff(N3+j);for j=1:Nss(N1+j)=ff(j);endfigure(5),stem(ss,'.k');title('加N/4循环前后缀');%ss=wgn(1,N5,0,10,'dBW','complex');ss=awgn(ss,SNR);figure(6),stem(ss,'.m');title('加入噪声后');zz=fft(ss((N1+1):N5),N);figure(7),plot(zz,'.b');title('傅里叶变换后');rr=istar(zz,N);figure(8),plot(rr,'.r');title('纠错后的星座图');dd=decode(rr,N);figure(9),stem(dd,'.m');title('星座图纠错并解码后');%bb=d2b(dd,N);bb=d2bb(dd,N);figure(10),stem(bb,'.b');title('转化为0/1比特流后');2)十进制转二进制函数%十进制转二进制function bb=d2b(dd,N)for j=1:N*4bb(j)=0;endfor j=1:4:N*4bb1=dec2bin(dd(floor(j/4)+1),4); for k=1:4bb(4*(j-1)+k)=bb1(k);endend3)十进制转化为01比特流函数%十进制转化为01比特流function bb=d2bb(dd,N)for j=1:N*4bb(j)=1;endwhile(j<=N*4)N1=ceil(j/4)a4=mod(dd(N1),2);dd(N1)=floor(dd(N1)/2); a3=mod(dd(N1),2);dd(N1)=floor(dd(N1)/2); a2=mod(dd(N1),2);dd(N1)=floor(dd(N1)/2); a1=mod(dd(N1),2);bb(j)=a1;j=j+1;bb(j)=a2;j=j+1;bb(j)=a3;j=j+1;bb(j)=a4;j=j+1;end4)星座图逆映射函数%星座图逆映射function yy=decode(rr,N)for j=1:Nswitch(rr(j))case -3-3*i yy(j)=0;case -3-iyy(j)=1;case -1-3*i yy(j)=2;case -1-iyy(j)=3;case -3+3*iyy(j)=4;case -3+iyy(j)=5;case -1+3*i yy(j)=6;case -1+iyy(j)=7;case 3-3*i yy(j)=8;case 3-iyy(j)=9;case 1-3*iyy(j)=10;case 1-iyy(j)=11;case 3+3*iyy(j)=12;case 3+iyy(j)=13;case 1+3*iyy(j)=14;case 1+iyy(j)=15;otherwise break;endend5)星座图逆映射函数%星座图逆映射function rr=istar(zz,N)for j=1:Nif(mod((floor(real(zz(j)))),2)==0)zz1(j)=ceil(real(zz(j)));else zz1(j)=floor(real(zz(j)));endif(mod((floor(imag(zz(j)))),2)==0)zz1(j)=zz1(j)+ceil(imag(zz(j)))*i;else zz1(j)=zz1(j)+floor(imag(zz(j)))*i;endrr(j)=zz1(j);end6)星座图映射函数%星座图映射function yy=star(xx,N)B=[-3-3*i,-3-i,-1-3*i,-1-i,-3+3*i,-3+i,-1+3*i,-1+i,3-3*i,3-i,1-3*i,1-i,3+3*i,3+i,1+3*i,1+i];for j=1:Nyy(j)=B(xx(j)+1);end四、实验结果五、实验结论OFDM技术可以有效地对抗信号波形间的干扰,适用于多径环境和衰落信道中的高速数据传输。
毕业设计(论文)OFDM系统原理及仿真实现

目录摘要 (2)ABSTRACT (3)第一章绪论 (4)第二章OFDM系统的基本介绍 (5)2.1OFDM的基本原理 (5)2.1.1 OFDM的产生和发展 (6)2.1.2 DFT的实现 (7)2.1.3 保护间隔、循环前缀和子载波数的选择 (8)2.1.4 子载波调制与解调 (10)2.2OFDM系统的优缺点 (11)2.3OFDM系统的关键技术 (11)第三章OFDM系统仿真实现 (13)3.1OFDM信号的时域及频域波形 (13)3.2带外功率辐射以及加窗技术 (15)3.3在不同信道环境和系统不同实现方式下的仿真 (18)3.3.1 调制与解调 (18)3.3.2 不同信道环境下的系统仿真实现 (20)3.3.3 系统不同实现方式的仿真实现 (22)第四章OFDM系统的仿真结果及性能分析 (23)4.1不同信道环境下的误码特性 (23)4.2不同系统实现方式下的误码特性 (28)第五章总结 (30)摘要本论文以OFDM系统为基础,介绍了OFDM系统的基本原理,以及使用OFDM技术的优势所在,并且展望了今后的无线移动技术的发展前景。
在简单介绍OFDM原理的同时,着重阐述了OFDM系统在不同信道环境和不同实现方式下的误码性能。
主要包括了OFDM系统在加性白高斯信道,在加性白高斯信道和多径干扰两种不同信道环境下系统的误码性能,其中后者还研究了系统在有保护间隔与无保护间隔的误码性能比较。
在理论分析的基础上,用MATLAB进行仿真,最后做出误码性能的分析和比较。
关键字: 正交频分复用(OFDM),离散傅立叶变换,AWGN,,多径干扰,保护间隔。
ABSTRACTThis paper presents you the basic priciple of OFDM(Orthogonal Frequency Division Multiplexing)and where it excels based on OFDM system , following with the prospective of wireless mobile communication. After a brief introduction to OFDM principle , it mainly focuses on the effect of OFDM system under different channels and with different system realizations on the Binary Error Rate (BER). It mainly includes two kinds of channels: the AWGN channel and the AWGN channel with Rayleigh fading. In the latter, we compare the BER with two different system realizations: one with Guarded Intervals(GI), and the other without (GI).Key Words : OFDM, DFT, AWGN, Rayleigh fading ,GI第一章绪论现代移动通信是一门复杂的高新技术,不但集中了无线通信和有线通信的最新技术成就,而且集中了网络接收和计算机技术的许多成果。
基于matlab的OFDM调制与解调性能仿真与分析

1 OF DM 原 理
OD F M的主要思想是将串行 的数据流串并转换成 比特速率较低的 J 个并行支路码流 ,每个 支路码 7 v 流再调制在一个子载波上 , 最后将每个子载波合成输出。由于这些子载波信号相互正交, 使得各子载波 的 频谱可以重叠 , 大大提高了频谱效率 。 OD F M系统作为一种特殊的多载波系统 , 每个数据周期 为 , 设 数据流被串并转换为 Ⅳ路并行低速
调 的基 本原 理 框 图如 图 1 所示 。
审 — ■ 州 l 并 直 —. _■ - F — 并 .
这 样用 In1F F / T模块 就可 实现 O D 系统 的调制解 调 过程 , 大简化 了系统 的硬 件构 成 。 F M调 制解 F FM 大 OD
转. 并- ■ 叵 并-F—串 1 串 -F 转 4 * 转-T_ t ■ . I 转 ,
被 无 线 局域 网标 准 IE 821aIE 821g IE 821 , iel / Hg e omac A p ) E E 0 .l , E 0 .l , E 0 . Hpr n2(i Pr r neL Nt e 以及 E E 6 a h f y 2
数字音频广播(A ) D B、 数字用户环( S )地面数字 电视系统(V _ , D ) 4 x L, D D B T I B 、 代移动通信( ) S 第 4 等技术方 G
据 符号 d, 以对 s进行 逆变 换 , F 得到 可 即 兀’
( 2 )
( 3 )
可 以看到时域数据信号 s等效对频域数据信号 d进行 I丌 运算 。同样在接收端 , F 为了恢复 出原始的数
d∑spjr = 唧 , ≤≤ _ , F k (2告) e -r 导 x 0 Ⅳ1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
O F D M调制解调仿真
------------------------------------------作者xxxx
------------------------------------------日期xxxx
实验四 OFDM调制解调仿真
一、实验目的
(1)了解OFDM调制解调的原理。
(2)学会用星座图分析系统性能。
二、实验内容
(1)编写MATLAB程序,实现OFDM系统调制解调。
(2)绘制各步骤图形并分析系统特性。
三、实验代码
1、主代码如下:
clear all;
close all;
N=input('请输入码元数');
SNR=input('请输入信噪比');
xx=randint(1,4*N); %原序列
figure(1),stem(xx,'.k'); %原序列图形
title('原序列');
B=0;
for m=1:4:4*N
A=xx(m)*8+xx(m+1)*4+xx(m+2)*2+xx(m+3);
B=B+1;
ee(B)=A;
end
figure(2),stem(ee,'.b');
title('化为0~15的码元');
yy=star(ee,N);
figure(3),plot(yy,'.r'); %映射后的星座图
title('映射后的星座图');
ff=ifft(yy,N); %傅里叶反变换
N1=floor(N*1/4);
N3=floor(N*3/4);
N5=floor(N*5/4);
figure(4),stem(ff,'.m');
title('傅里叶反变换后');
for j=1:N1 %加循环前缀
ss(j)=ff(N3+j);
end
for j=1:N %变成长度为N*5/4的序列 ss(N1+j)=ff(j);
end
figure(5),stem(ss,'.k'); %画出图形
title('加N/4循环前后缀');
%ss=wgn(1,N5,0,10,'dBW','complex');
ss=awgn(ss,SNR); %加入噪声
figure(6),stem(ss,'.m'); %加入噪声后的图形title('加入噪声后');
zz=fft(ss((N1+1):N5),N); %傅里叶变换figure(7),plot(zz,'.b'); %画图
title('傅里叶变换后');
rr=istar(zz,N); %星座图纠错
figure(8),plot(rr,'.r'); %画图
title('纠错后的星座图');
dd=decode(rr,N); %解码
figure(9),stem(dd,'.m'); %画图
title('星座图纠错并解码后');
%bb=d2b(dd,N);
bb=d2bb(dd,N); %转化为0/1比特流figure(10),stem(bb,'.b');
title('转化为0/1比特流后');
2、调用的函数:
(1)星座图映射
%星座图映射
function yy=star(xx,N)
B=[-3-3*i,-3-i,-1-3*i,-1-i,-3+3*i,-3+i,-1+3*i,-1+i,3-3*i,3-i,1-3*i,1-i,3+3*i,3+i,1+3*i,1+i];
for j=1:N
yy(j)=B(xx(j)+1);
end
(2)星座图逆映射
%星座图逆映射
function rr=istar(zz,N)
for j=1:N
if(mod((floor(real(zz(j)))),2)==0)
zz1(j)=ceil(real(zz(j)));
else zz1(j)=floor(real(zz(j)));
end
if(mod((floor(imag(zz(j)))),2)==0)
zz1(j)=zz1(j)+ceil(imag(zz(j)))*i;
else zz1(j)=zz1(j)+floor(imag(zz(j)))*i;
end
rr(j)=zz1(j);
end
(3)十进制转二进制
function bb=d2b(dd,N)
%十进制转二进制
for j=1:N*4
bb(j)=;
end
for j=1:4:N*4
bb1=dec2bin(dd(floor(j/4)+1),4);
for k=1:4
bb(4*(j-1)+k)=bb1(k);
end
end
(4)十进制转化为01比特流
%十进制转化为01比特流
function bb=d2bb(dd,N)
for j=1:N*4
bb(j)=1;
end
j=1;
while(j<=N*4)
N1=ceil(j/4)
a4=mod(dd(N1),2);
dd(N1)=floor(dd(N1)/2);
a3=mod(dd(N1),2);
dd(N1)=floor(dd(N1)/2);
a2=mod(dd(N1),2);
dd(N1)=floor(dd(N1)/2);
a1=mod(dd(N1),2);
bb(j)=a1;
j=j+1;
bb(j)=a2;
j=j+1;
bb(j)=a3;
j=j+1;
bb(j)=a4;
j=j+1;
end
(5)星座图逆映射
function yy=decode(rr,N)
for j=1:N
switch(rr(j))%星座图逆映射
case -3-3*i
yy(j)=0;
case -3-i
yy(j)=1;
case -1-3*i
yy(j)=2;
case -1-i
yy(j)=3;
case -3+3*i
yy(j)=4;
case -3+i
yy(j)=5;
case -1+3*i
yy(j)=6;
case -1+i
yy(j)=7;
case 3-3*i
yy(j)=8;
case 3-i
yy(j)=9;
case 1-3*i
yy(j)=10;
case 1-i
yy(j)=11;
case 3+3*i
yy(j)=12;
case 3+i
yy(j)=13;
case 1+3*i
yy(j)=14;
case 1+i
yy(j)=15;
otherwise break;
end
end
四、
五、实验结果
【精品文档】【精品文档】。
