三角函数图像平移变换及图像解析式
三角函数的变换与性质
三角函数的变换与性质三角函数在数学中起着重要的作用，它们与三角学和几何学密切相关。
本文将探讨三角函数的变换与性质，包括平移、缩放和反射等变换，以及周期性、奇偶性和对称性等性质。
1. 平移变换三角函数的平移变换指的是在横轴或纵轴方向上对函数图像进行平移操作。
对于y = sin(x)来说，平移变换可以表示为y = sin(x - a)或y = sin(x + a)，其中a表示平移的量。
当a大于0时，图像向右平移；当a小于0时，图像向左平移。
同样地，对于y = cos(x)和y = tan(x)等函数，也可以用相似的方式进行平移变换。
平移变换可以帮助我们理解函数图像的移动规律，对解决实际问题中的几何和物理相关问题具有重要意义。
2. 缩放变换三角函数的缩放变换是指改变函数图像在横轴或纵轴方向上的尺度。
对于y = sin(x)来说，缩放变换可以表示为y = a*sin(x)或y = sin(ax)，其中a表示缩放的比例。
当a大于1时，函数的振幅增大，图像变窄；当a小于1时，函数的振幅减小，图像变宽。
类似地，对于y = cos(x)和y = tan(x)等函数，缩放变换也可以用类似的方式进行。
缩放变换可以帮助我们研究函数图像的形状和变化，对数学建模和图像处理等领域有着广泛应用。
3. 反射变换三角函数的反射变换是指改变函数图像关于横轴或纵轴的对称性。
对于y = sin(x)来说，反射变换可以表示为y = -sin(x)或y = sin(-x)，其中负号表示对称性的改变。
经过纵轴反射后，图像关于纵轴对称；经过横轴反射后，图像关于横轴对称。
对于y = cos(x)和y = tan(x)等函数，也可以通过反射变换来改变图像的对称性。
反射变换有助于我们研究三角函数图像的特征和性质，对对称几何和信号处理等领域有一定的应用价值。
4. 周期性三角函数具有明显的周期性特征，即函数在一定区间内的值重复出现。
对于y = sin(x)来说，它的周期为2π，即在每个2π的区间内，函数的值会重复。
三角函数中的平移与伸缩变换
三角函数中的平移与伸缩变换三角函数是数学中的重要概念之一，通过平移和伸缩变换可以对三角函数图像进行调整和变化。
本文将探讨三角函数中的平移与伸缩变换，并说明它们对函数图像的影响。
一、平移变换平移变换是指将函数图像沿着坐标轴平行移动的过程。
在三角函数中，平移变换会改变函数的水平位置。
具体而言，对于三角函数y = f(x)，平移变换可以表示为y = f(x ± b)，其中b为平移量。
1. 正弦函数的平移变换正弦函数y = sin(x)在平移变换下，可以写作y = sin(x ± b)。
当b为正值时，图像向左平移；当b为负值时，图像向右平移。
平移量b的绝对值越大，图像平移的距离越远。
2. 余弦函数的平移变换余弦函数y = cos(x)的平移变换形式为y = cos(x ± b)。
与正弦函数类似，当b为正值时，图像向左平移；当b为负值时，图像向右平移。
平移量b的绝对值越大，图像平移的距离越远。
3. 正切函数的平移变换正切函数y = tan(x)在平移变换下，可以写作y = tan(x ± b)。
与正弦函数和余弦函数不同，正切函数的平移变换会导致图像的水平拉伸与压缩。
当b为正值时，图像向左平移；当b为负值时，图像向右平移。
平移量b的绝对值越大，图像平移的距离越远。
二、伸缩变换伸缩变换是指将函数图像在x轴或y轴上进行拉伸或压缩的过程。
在三角函数中，伸缩变换会改变函数图像的形状和振幅。
具体而言，对于三角函数y = f(x)，伸缩变换可以表示为y = af(bx)，其中a为纵向伸缩因子，b为横向伸缩因子。
1. 正弦函数的伸缩变换正弦函数y = sin(x)在伸缩变换下，可以写作y = a sin(bx)。
纵向伸缩因子a决定了函数图像的振幅，a越大，则振幅越大；a越小，则振幅越小。
横向伸缩因子b决定了函数图像的周期，b越大，则周期越短；b越小，则周期越长。
2. 余弦函数的伸缩变换余弦函数y = cos(x)的伸缩变换形式为y = a cos(bx)。
三角函数图像平移变换及图像解析式
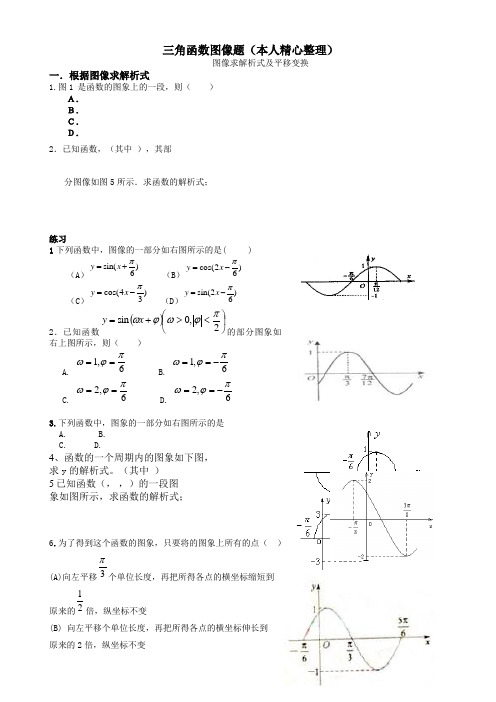
三角函数图像题（本人精心整理）-------图像求解析式及平移变换一．根据图像求解析式1.图1 是函数的图象上的一段，则（ ）Ａ． Ｂ． Ｃ． Ｄ． 2．已知函数，（其中 ），其部分图像如图5所示．求函数的解析式；练习1下列函数中，图像的一部分如右图所示的是( )（A ）（B ） （C ）（D ） 2．已知函数的部分图象如右上图所示，则（）A.B.C.D.3.下列函数中，图象的一部分如右图所示的是 A. B. C. D.4、函数的一个周期内的图象如下图， 求y 的解析式。
（其中 ） 5已知函数（， ，）的一段图 象如图所示，求函数的解析式；6.为了得到这个函数的图象，只要将的图象上所有的点（ ）(A)向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变(B) 向左平移个单位长度，再把所得各点的横坐标伸长到 原来的2倍，纵坐标不变sin()6y x π=+cos(2)6y x π=-cos(4)3y x π=-sin(2)6y x π=-()⎪⎭⎫ ⎝⎛<>+=2,0sin πϕωϕωx y 6,1πϕω==6,1πϕω-==6,2πϕω==6,2πϕω-==3π12(C) 向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍，纵坐标不变 (D) 向左平移个单位长度，再把所得各点的横坐标伸长到原来的2倍，纵坐标不变二．图像平移变换问题相位变换：① 将图像沿轴向左平移个单位 ② 将图像沿轴向右平移个单位周期变换： ① 将图像上所有点的纵坐标不变，横坐标伸长为原来的倍②将图像上所有点的纵坐标不变，横坐标缩短为原来的倍 振幅变换：①将图像上所有点的横坐标不变，纵坐标缩短为原来的倍 ②将图像上所有点的横坐标不变，纵坐标伸长为原来的倍 【特别提醒】由y ＝sin x 的图象变换出y ＝Asin(＋)的图象一般有两个途径，只有区别开这两个途径，才能灵活进行图象变换。
利用图象的变换作图象时，提倡先平移后伸缩，但先伸缩后平移也经常出现/wxc/途径一：先平移变换再周期变换(伸缩变换)先将y ＝sin x 的图象向左(＞0)或向右（）平移｜｜个单位，再将图象上各点的横坐标变为原来的倍(＞0)，便得y ＝sin(ωx ＋)的图象途径二：先周期变换(伸缩变换)再平移变换先将y ＝sin x 的图象上各点的横坐标变为原来的倍(＞0)，再沿x 轴向左(＞0)或向右平移个单位，便得y ＝sin(＋)的图象【特别提醒】若由得到的图象，则向左或向右平移应平移个单位1.为了得到函数的图像，只需把函数的图像（ ） （A ）向左平移个长度单位 （B ）向右平移个长度单位 （C ）向左平移个长度单位 （D ）向右平移个长度单位2.函数f (x )=2sin x cos x 是（ ）(A)最小正周期为2π的奇函数 （B ）最小正周期为2π的偶函数 (C)最小正周期为π的奇函数（D ）最小正周期为π的偶函数3.设,函数的图像向右平移个单位后与原图像重合，则的最小值是（ ）（A ） （B ） （C ） （D ） 3 4.下列函数中，周期为，且在上为减函数的是（ ）sin y x =w 1sin y x =sin y x =A x ωϕϕϕω1ωϕϕϕsin(2)3y x π=-sin(2)6y x π=+4π4π2π2π振幅 变换 相位 变换 周期 变换y ＝sin x（A ） （B ） （C ） （D ）5.将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是（ ） （A ） （B ） （C ） （D ）6、要得到函数的图象，只需将函数的图象（ ）（A ）向左平移个单位 （B ）向右平移个单位 （C ）向左平移个单位 （D ）向右平移个单位7、将函数y=sin3x 的图象作下列平移可得y=sin(3x+)的图象（A) 向右平移 个单位 (B) 向左平移 个单位（C ）向右平移 个单位 （D ）向左平移 个单位8．将函数的图象上每点的横坐标缩小为原来的（纵坐标不变），再把所得图象向左平移个单位，得到的函数解析式为（ ）9、把函数的图象上所有的点的横坐标缩小到原来的一半，纵坐标保持不变，然后把图象向左平移个单位长度，得到新的函数图象，那么这个新函数的解析式为 （A ） （B ） （C ） （D ）11．要得到函数的图象，只需将函数的图象上所有的点的（ ）(A)横坐标缩短到原来的倍（纵坐标不变）,再向左平行移动个单位长度(B)横坐标缩短到原来的倍（纵坐标不变），再向右平行移动个单位长度 (C)横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动个单位长度 (D)横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动个单位长度12 将函数的图象上各点的横坐标扩大为原来的2倍（纵坐标不变），再将整个图形沿轴正向平移，得到的新曲线与函数的图象重合，则（ ） A. B. C. D.5为了得到函数的图象,可以将函数的图象( ) A ．向右平移个单位长度 B ．向右平移个单位长度C ．向左平移个单位长度D ．向左平移个单位长度13.将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是（ ）6π6π218π4π)62sin(π-=x y x y 2cos =6π3π6π3π（A ） （B ） （C ） （D ）14.函数f(x)= 的最小正周期为（ ） A.B.xC.2D.415.为得到函数的图像，只需将函数的图像（ ）A ．向左平移个长度单位B ．向右平移个长度单位C ．向左平移个长度单位D ．向右平移个长度单位 17.要得到函数的图象，只需将函数的图象（ ） A ．向右平移个单位 B ．向右平移个单位 C ．向左平移个单位 D ．向左平移个单位 18.为了得到函数的图象，可以将函数的图象（ ）(A)向右平移个单位长度 (B)向右平移个单位长度(C)向左平移个单位长度 (D)向左平移个单位长度19.把函数（）的图象上所有点向左平行移动个单位长度，再把所得图象上所有点的横坐标缩短到原来的倍（纵坐标不变），得到的图象所表示的函数是A ，B ，C ，D ，20.为了得到函数的图像，只需把函数的图像（A ）向左平移个长度单位 （B ）向右平移个长度单位 （C ）向左平移个长度单位 （D ）向右平移个长度单位21.已知函数的最小正周期为，为了得到函数 的图象，只要将的图象A 向左平移个单位长度B 向右平移个单位长度C 向左平移个单位长度D 向右平移个单位长度22.函数的图象按向量平移到,的函数解析式为当为奇函数时，向量可以等于B23.将函数y=sinx 的图象向左平移0 ＜2的单位后，得到函数y=sin 的图象，则等于A ．B ． C. D.24.若将函数的图像向右平移个单位长度后，与函数的图像重合，则的最小值为D A ． B. C. D.25.设函数，将的图像向右平移个单位长度后，所得的图像与原图像重合，则的最小值等于C （A ） （B ） （C ） （D ）26.将函数的图象按向量平移后所得的图象关于点中心对称，则向量的坐标可能为（ C ）A ．B ．C ．D ．27.将函数的图象F 按向量平移得到图象,若的一条对称轴是直线,则的一个可能取值是AA. B. C. D.28.将函数y=3sin （x -θ）的图象F 按向量（，3）平移得到图象F ′,若F ′的一条对称轴是直线x=,则θ的一5π126π3πx R ∈x R ∈x R ∈x R ∈4π2πϕϕsin(2)3y x π=+α(,0)12π-α(,0)12π-(,0)6π-(,0)12π(,0)6πF 'π125π125-π1211个可能取值是A. B. C. D. A29．将函数的图象按向量平移后所得的图象关于点中心对称，则向量的坐标可能为（ ）A ．B ．C ．D ． C 29为了得到函数的图像，只需把函数的图像上所有的点（A ）向左平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变）（B ）向右平移个单位长度，再把所得各点的横坐标缩短到原来的倍（纵坐标不变） （C ）向左平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变） （D ）向右平移个单位长度，再把所得各点的横坐标伸长到原来的3倍（纵坐标不变）综合1.(2004全国Ⅰ卷文、理)为了得到函数的图象,可以将函数的图象( ) A ．向右平移个单位长度 B ．向右平移个单位长度C ．向左平移个单位长度D ．向左平移个单位长度 2（2006四川文、理）下列函数中，图像的一部分如右图所示的是( )（A ） （B ） （C ） （D ）二.填空题: （每小题5分，计20分） 3. (2008辽宁理)已知，且在区间有最小值，无最大值，则＝__________． 4．(2008陕西理)已知函数．（Ⅰ）求函数的最小正周期及最值；（Ⅱ）令，判断函数的奇偶性，并说明理由． 5.（2008安徽文、理）已知函数 （Ⅰ）求函数的最小正周期和图象的对称轴方程（Ⅱ）求函数在区间上的值域6.(2005全国Ⅰ文)设函数图像的一条对称轴是直线. (Ⅰ)求； (Ⅱ)求函数的单调增区间；7.（四川卷理）将函数的图像上所有的点向右平行移动个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是( ) A. B. C. D.8．（重庆卷理）已知函数的部分图象如右上图所示，则（ ） A. B. C. D.9．（天津卷理）已知函数（Ⅰ）求函数的最小正周期及在区间上的最大值和最小值； （Ⅱ）若，求的值。
三角函数的图像变换
cosθ = 邻边/斜边，在单位圆中表示为x坐标。
正切函数（tangent）
三角函数的周期性
tanθ = 对边/邻边，表示为正弦与余弦之比。
正弦、余弦函数周期为2π，正切函数周期为 π。
三角函数在各象限表现
第一象限
所有三角函数值均为正。
第三象限
正弦、余弦函数值为负，正切函数值为正。
第二象限
正弦函数值为正，余弦、正切函数值为负。
伸缩变换对正弦函数影响
横向伸缩
改变正弦函数图像的周期长度。缩小周期使得函数图像更加紧密，扩大周期则 使得函数图像更加稀疏。
纵向伸缩
改变正弦函数图像的振幅大小。增大振幅使得函数图像波动范围更大，减小振 幅则使得函数图像波动范围更小。
周期性与相位调整方法
周期性调整
通过改变正弦函数的周期来调整图像的疏密程度。可以通过调整函数中的系数来 实现周期的变化。
相位调整
通过改变正弦函数的相位来调整图像出现的位置。可以通过在函数中添加常数项 来实现相位的调整。同时，利用三角函数的和差化积公式，也可以实现相位的调 整。
03 余弦函数图像变换分析
余弦函数基本图像特征
波形图像
余弦函数图像呈现周期性波动，具有典型的波形 特征。
振幅和周期
余弦函数的振幅和周期是确定其图像形状和尺寸 的关键参数。
拓展：其他类型周期函数图像变换
锯齿波和方波
除了正弦波和余弦波外，还有其 他类型的周期函数如锯齿波和方 波等，它们的图像变换同样具有 实际应用价值。
周期函数的合成与分解
通过三角函数的线性组合可以合 成其他类型的周期函数；反之， 其他类型的周期函数也可以通过 傅里叶级数展开成三角函数的线 性组合。
三角函数图像的变换与特征
三角函数图像的变换与特征三角函数图像的变换是数学中一个重要的概念，它描述了三角函数图像相对于原始函数图像的位置、形状和特征的变化。
在本文中，我们将探讨三角函数的变换和它们的特征。
一、平移变换平移是指将函数图像沿着横轴或纵轴方向移动的操作。
对于三角函数而言，平移的规律如下：1. 正弦函数（Sine Function）的平移：a. 沿横轴平移：f(x) = sin(x - a)，其中a为平移的距离，若a > 0，则向右平移；若a < 0，则向左平移。
b. 沿纵轴平移：f(x) = a + sin(x)，其中a为平移的距离，若a > 0，则向上平移；若a < 0，则向下平移。
2. 余弦函数（Cosine Function）的平移：a. 沿横轴平移：f(x) = cos(x - a)，其中a为平移的距离，若a > 0，则向右平移；若a < 0，则向左平移。
b. 沿纵轴平移：f(x) = a + cos(x)，其中a为平移的距离，若a > 0，则向上平移；若a < 0，则向下平移。
二、伸缩变换伸缩是指对函数图像进行拉伸或压缩的操作。
对于三角函数而言，伸缩的规律如下：1. 正弦函数的伸缩：a. 沿横轴伸缩：f(x) = sin(kx)，其中k为伸缩的系数，若k > 1，则图像水平方向收缩；若0 < k < 1，则图像水平方向拉伸。
b. 沿纵轴伸缩：f(x) = a * sin(x)，其中a为伸缩的系数，若a > 1，则图像垂直方向收缩；若0 < a < 1，则图像垂直方向拉伸。
2. 余弦函数的伸缩：a. 沿横轴伸缩：f(x) = cos(kx)，其中k为伸缩的系数，若k > 1，则图像水平方向收缩；若0 < k < 1，则图像水平方向拉伸。
b. 沿纵轴伸缩：f(x) = a * cos(x)，其中a为伸缩的系数，若a > 1，则图像垂直方向收缩；若0 < a < 1，则图像垂直方向拉伸。
高考数学《图像变换在三角函数中的应用》基础知识与典型例题分析
高考数学《图像变换在三角函数中的应用》基础知识与典型例题分析在高考中涉及到的三角函数图像变换主要指的是形如()sin y A x ωϕ=+的函数，通过横纵坐标的平移与放缩，得到另一个三角函数解析式的过程。
要求学生熟练掌握函数图像变换，尤其是多次变换时，图像变化与解析式变化之间的对应联系。
一、基础知识：（一）图像变换规律：设函数为()y f x =（所涉及参数均为正数） 1、函数图像的平移变换：（1）()f x a +：()f x 的图像向左平移a 个单位 （2）()f x a −：()f x 的图像向右平移a 个单位 （3）()f x b +：()f x 的图像向上平移b 个单位 （4）()f x b −：()f x 的图像向下平移b 个单位 2、函数图像的放缩变换：（1）()f kx ：()f x 的图像横坐标变为原来的1k（图像表现为横向的伸缩） （2）()kf x ：()f x 的图像纵坐标变为原来的k 倍（图像表现为纵向的伸缩） 3、函数图象的翻折变换： （1）()fx ：()f x 在x 轴正半轴的图像不变，负半轴的图像替换为与正半轴图像关于y 轴对称的图像（2）()f x ：()f x 在x 轴上方的图像不变，x 轴下方的部分沿x 轴向上翻折即可（与原x 轴下方图像关于x 轴对称）（二）图像变换中要注意的几点：1、如何判定是纵坐标变换还是横坐标变换？在寻找到联系后可根据函数的形式了解变换所需要的步骤，其规律如下： ① 若变换发生在“括号”内部，则属于横坐标的变换 ② 若变换发生在“括号”外部，则属于纵坐标的变换例如：()31y f x =+：可判断出属于横坐标的变换：有放缩与平移两个步骤()2y f x =−+：可判断出横纵坐标均需变换，其中横坐标的为对称变换，纵坐标的为平移变换2、解析式变化与图像变换之间存在怎样的对应？由前面总结的规律不难发现： （1）加“常数”⇔ 平移变换（2）添“系数”⇔放缩变换 （3）加“绝对值”⇔翻折变换3、多个步骤的顺序问题：在判断了需要几步变换以及属于横坐标还是纵坐标的变换后，在安排顺序时注意以下原则：① 横坐标的变换与纵坐标的变换互不影响，无先后要求 ② 横坐标的多次变换中，每次变换只有x 发生相应变化 例如：()()21y f x y f x =→=+可有两种方案方案一：先平移（向左平移1个单位），此时()()1f x f x →+。
初中数学知识归纳三角函数的解析式和像的平移
初中数学知识归纳三角函数的解析式和像的平移三角函数作为数学中重要的概念之一，在初中数学中也是必须学习和掌握的内容。
本文将对初中数学中关于三角函数的解析式和像的平移进行归纳和总结。
首先，我们将介绍三角函数的定义和解析式，然后详细讨论三角函数图像的平移。
一、三角函数的解析式三角函数包括正弦函数sin(x)、余弦函数cos(x)和正切函数tan(x)。
在解析式中，x代表角度，而不是弧度。
具体的解析式如下：1. 正弦函数 sin(x)：解析式：sin(x) = 对边/斜边反函数：arcsin(x) = sin^-1(x)2. 余弦函数 cos(x)：解析式：cos(x) = 临边/斜边反函数：arccos(x) = cos^-1(x)3. 正切函数 tan(x)：解析式：tan(x) = 对边/临边反函数：arctan(x) = tan^-1(x)需要注意的是，反函数的定义域和值域与原函数相反。
二、三角函数图像的平移三角函数图像的平移是指通过某种变换将函数图像沿着水平和垂直方向进行移动。
对于三角函数图像的平移，可以分为水平平移和垂直平移两种情况。
1. 水平平移水平平移是指将函数图像沿着x轴的方向移动。
对于正弦函数和余弦函数，平移的规律如下：- 正弦函数sin(x)：f(x) = sin(x ± a)- 余弦函数cos(x)：f(x) = cos(x ± a)其中，当a>0时，图像向左移动a个单位；当a<0时，图像向右移动|a|个单位。
这里的正负号表示方向。
2. 垂直平移垂直平移是指将函数图像沿着y轴的方向移动。
对于正弦函数和余弦函数，平移的规律如下：- 正弦函数sin(x)：f(x) = a + sin(x)- 余弦函数cos(x)：f(x) = a + cos(x)其中，当a>0时，图像向上移动a个单位；当a<0时，图像向下移动|a|个单位。
这里的正负号表示方向。
三角函数左右平移规律
三角函数左右平移规律
三角函数左右平移规律是指，在三角函数函数图像的横轴上做一定的移动，函
数图像也能实现左右平移的效果。
这种方式要求首先要理解三角函数的基本特征，以及相关定义域、值域等概念，并根据定义原理建立函数图像，然后再根据它规定的规律把它向左右移动。
三角函数左右平移规律可以总结为如下几条：
（1）正弦函数向右平移A，它的函数图像就会右移A，函数表达式也会相应地变
换为sin（x+A）。
（2）余弦函数向右平移A，它的函数图像就会右移A，函数表达式也会相应地变
换为cos（x+A）。
（3）正切函数向右平移A，它的函数图像就会右移A，函数表达式也会相应地变
换为tan（x+A）。
三角函数左右平移规律是理解和应用复杂函数的基础，对于理解复杂函数的定
义区间、值域等概念、掌握其图象的变幻规律性，乃至改变函数的一定性质均非常有帮助。
掌握三角函数的左右平移规律，并能够巧妙运用于实际应用尤为重要。
因此，研究三角函数的左右平移规律，既让我们能够熟练掌握三角函数的知识，对我们日常所学理论或应用中三角函数的使用也会变得更加熟练。
同时，三角函数还以它独特的规律性，与许多其他函数组合，为我们提供了十分有用的函数数学工具，能够清楚理解多边形、椭圆、曲线、几何体等各种实体，且特别是研究计算机图形学和机器人尤为重要。
总之，三角函数的左右平移规律是一种重要的数学知识，理解它的基本特征以
及平移的规律，有助于我们掌握更多的函数知识，并且运用三角函数的定义与规律，使得数学运算也变得更加简单。
高中数学中的三角函数的基本变换规律
高中数学中的三角函数的基本变换规律在高中数学的学习过程中，三角函数是一个重要的内容。
它们在解决几何问题、物理问题以及工程问题中发挥着重要的作用。
而要理解三角函数的性质和应用，我们首先需要掌握它们的基本变换规律。
一、平移变换规律平移是指将函数图像沿着横坐标或纵坐标方向进行平移。
对于三角函数而言，平移变换规律可以用以下形式表示：1. 正弦函数的平移变换规律：y = a*sin(b(x-c)) + d其中，a表示振幅的变化，b表示周期的变化，c表示横坐标方向的平移量，d表示纵坐标方向的平移量。
2. 余弦函数的平移变换规律：y = a*cos(b(x-c)) + d同样地，a、b、c、d分别表示振幅、周期、横坐标方向平移量和纵坐标方向平移量。
通过平移变换规律，我们可以将函数图像在平面上进行移动，从而观察到函数图像的变化。
二、伸缩变换规律伸缩是指将函数图像沿着横坐标或纵坐标方向进行拉伸或压缩。
对于三角函数而言，伸缩变换规律可以用以下形式表示：1. 正弦函数的伸缩变换规律：y = a*sin(b(x-c)) + d其中，a表示纵坐标方向的伸缩倍数，b表示横坐标方向的伸缩倍数，c表示横坐标方向的平移量，d表示纵坐标方向的平移量。
2. 余弦函数的伸缩变换规律：y = a*cos(b(x-c)) + d同样地，a、b、c、d分别表示纵坐标方向的伸缩倍数、横坐标方向的伸缩倍数、横坐标方向平移量和纵坐标方向平移量。
通过伸缩变换规律，我们可以观察到函数图像在平面上的形状发生变化，从而更好地理解函数的性质。
三、反射变换规律反射是指将函数图像沿着横坐标或纵坐标方向进行镜像。
对于三角函数而言，反射变换规律可以用以下形式表示：1. 正弦函数的反射变换规律：y = -a*sin(b(x-c)) + d其中，a表示振幅的变化，b表示周期的变化，c表示横坐标方向的平移量，d表示纵坐标方向的平移量。
2. 余弦函数的反射变换规律：y = -a*cos(b(x-c)) + d同样地，a、b、c、d分别表示振幅、周期、横坐标方向平移量和纵坐标方向平移量。
三角函数平移变换及求解析式
三角函数平移变换及解析式的求法类型一：平移变换1. y ＝2sin(2x －π6)＋1的图像是由y ＝sin x 的图像怎样变换而来的？解 方法一 先伸缩后平移y ＝sin x ――――――――――――――→各点的横坐标缩小为原来的12倍纵坐标不变y ＝sin 2x ――――――――――――→向右平移π12个单位y ＝sin(2x －π6)―――――――――――――――→各点的纵坐标伸长为原来的2倍横坐标不变y ＝2sin(2x －π6)――――――――――――→向上平移1个单位y ＝2sin(2x －π6)＋1.方法二 先平移后伸缩y ＝sin x ――――――――――→向右平移π6个单位y ＝sin(x －π6)――――――――――――――→各点的横坐标缩短为原来的12纵坐标不变y ＝sin(2x －π6)――――――――――→各点纵坐标伸长为原来的2倍横坐标不变y ＝2sin(2x －π6)――――――――――→向上平移1个单位y ＝2sin(2x －π6)＋1.2.试述如何由y ＝13sin(2x ＋π3)的图像得到y ＝sin x 的图像.解 方法一 y ＝13sin(2x ＋π3)――――――――――――――→横坐标扩大为原来的2倍纵坐标不变y ＝13sin(x ＋π3)――――――――――――――→图像向右平移π3个单位纵坐标不变y ＝13sin x――――――――――――――→纵坐标扩大到原来的3倍横坐标不变y ＝sin x .方法二 (1)先将y ＝13sin(2x ＋π3)的图像向右平移π6个单位长度，得y ＝13sin 2x 的图像；(2)再将y ＝13sin 2x 图像上各点的横坐标扩大为原来的2倍(纵坐标不变)，得y ＝13sin x 的图像；(3)最后将y ＝13sin x 的图像上各点的纵坐标扩大为原来的3倍(横坐标不变)得到y ＝sin x 的图像.3.将函数x y sin =的图象上所有的点向右平行移动10π个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图象的函数解析式是() A ．)102sin(π-=x y B ．)102sin(π+=x yC ．)1021sin(π-=x yD ．)1021sin(π+=x y解：将函数sin y =x 的图象上所有的点向右平行移动10π个单位长度，得到函数sin()10y x π=-，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），得到函数1sin()210y x π=-的图象，故选：C ． 4.把函数)42sin(π+=x y 的图象向左平移8π个单位长度，再将横坐标压缩到原来的21，所得函数的解析式为（ ）A. x y 4sin =B. x y 4cos =C. )84sin(π+=x yD.)324sin(π+=x y解：选B5.要得到)42cos(π-=x y 的图象，只需将x y 2sin =图象()A ．向左平移4π个单位 B ．向右平移4π个单位 C ．向左平移8π个单位D ．向右平移8π个单位解：将sin y = 2x 的图象向右平移8π个单位，可得sin(2)4y x π=-的图象， 故选：D ．6.要得到函数x y cos 2=的图象，将函数)42sin(2π+=x y 的图象上所有的点的( )A ．横坐标缩短到原来的21倍（纵坐标不变），再向左平行移动8π个单位长度B ．横坐标缩短到原来的21倍（纵坐标不变），再向右平行移动4π个单位长度 C ．横坐标伸长到原来的2倍（纵坐标不变），再向左平行移动4π个单位长度D ．横坐标伸长到原来的2倍（纵坐标不变），再向右平行移动8π个单位长度解：2sin(2)cos(2)cos(2))42444y x x x x πππππ=+=--=-=- 答案为C 故选：C ．7.已知函数)4sin()(πω+=x x f R x ∈(，)0>ω的最小正周期为π，为了得到函数xx g ωcos )(=的图象，只要将)(x f y =的图象()A ．向左平移8π个单位长度 B ．向右平移8π个单位长度 C ．向左平移4π个单位长度D ．向右平移4π个单位长度解：由题知2ω=，所以()sin(2)cos[(2)]cos(2)cos2()42448f x x x x x πππππ=+=-+=-=-，故选：A ．类型二：求函数y ＝A sin(ωx ＋φ)＋b 的解析式1.已知函数)sin(ϕω+=x A y 0(>A ，0>ω，)0πϕ<<的一段图象如图所示，则此函数解析式为__________.（例10）解：)33sin(2π+=x y2.下图是函数)sin(ϕω+=x A y 0(>A ，0>ω，)20πϕ<<的图象的一部分，试求此函数解析式.解：)438sin(2ππ-=x y3.已知函数)sin(ϕω+=x A y ，在同一周期内，当9π=x 时函数取得最大值2，当94π=x 时取得最小值2-，则该函数的解析式为( )A ．⎪⎭⎫ ⎝⎛-=63sin 2πx yB ．⎪⎭⎫ ⎝⎛+=63sin 2πx yC ．⎪⎭⎫ ⎝⎛+=631sin 2πx yD ．⎪⎭⎫ ⎝⎛-=631sin 2πx y解：由题意可知42993T πππ=-=，223T ππω∴==，解得3ω=， 函数的最大值为2，最小值为2-，2A ∴=， 9x π=时函数取得最大值2，2sin(3)29πϕ∴⨯+=，解得6πϕ=．∴函数解析式为2sin(3)6y x π=+．故选：B ．4.若函数f (x )＝A sin(ωx ＋φ)＋b (其中A >0，ω>0，|φ|<π2)的图像如图所示.(1)求函数f (x )的解析式；(2)求S ＝f (0)＋f (1)＋f (2)＋f (3)＋…＋f (2 012)的值.解 (1)由图像知A ＝32－122＝12，b ＝32＋122＝1，ω＝2πT ＝2π4＝π2.∴f (x )＝12sin(π2x ＋φ)＋1.又∵点(0,1)在函数图像上，∴f (0)＝1即1＝12sin φ＋1，∴sin φ＝0.又|φ|<π2，故φ＝0，∴f (x )＝12sin π2x ＋1.(2)由(1)知函数f (x )＝12sin π2x ＋1，周期T ＝2ππ2＝4.∴S ＝f (0)＋f (1)＋f (2)＋f (3)＋…＋f (2 012) ＝f (0)＋[f (1)＋f (2)＋f (3)＋f (4)]×503.又∵f (0)＝1，f (1)＝32，f (2)＝1，f (3)＝12，f (4)＝1，∴S ＝1＋(32＋1＋12＋1)×503＝2 013.反思与感悟 要求y ＝A sin(ωx ＋φ)＋b (A >0，ω>0)的解析式，其关键是求参数A 、φ、ω、b 的值.求A 、ω、b 三参数相对容易，设函数的最大值为m ，最小值为n ，则⎩⎨⎧A ＝m －n2，b ＝m ＋n2.已知函数周期为T ，则由T ＝2πω可求出参数ω的值.5.已知函数f (x )＝A sin(ωx ＋φ)在一个周期内的图像如图所示，(1)求f (x )的解析式；(2)求f (π4)＋f (2π4)＋f (3π4)＋…＋f (2 015π4)的值.解 (1)由图像可知A ＝2， 周期T ＝2(7π12－π12)＝π，所以ω＝2πT ＝2ππ＝2，则f (x )＝2sin(2x ＋φ)， 由图像过点(π12，2)，得2sin(2×π12＋φ)＝2，即sin(π6＋φ)＝1，取π6＋φ＝π2得φ＝π3， 故f (x )＝2sin(2x ＋π3).(2)由(1)可知f (x )的周期为π，因为f (π4)＋f (2π4)＋f (3π4)＋f (4π4)＝1－3－1＋3＝0，所以f (π4)＋f (2π4)＋f (3π4)＋…＋f (2 015π4)＝0×503＋f (2 013π4)＋f (2 014π4)＋f (2 015π4)＝f (π4)＋f (2π4)＋f (3π4)＝1－3－1＝－ 3.6.将函数y ＝sin ωx (ω>0)的图像向左平移π6个单位，平移后的图像如图所示，则平移后的图像所对应函数的解析式是________.答案 y ＝sin(2x ＋π3)解析 函数y ＝sin ωx (ω>0)的图像向左平移π6个单位得到y ＝sin(ωx ＋ωπ6)，则712πω＋ωπ6＝3π2，解得ω＝2， 故平移后的图像的解析式为y ＝sin(2x ＋π3).7.已知函数)cos(ϕω+=x A y 的图象如图所示，32)2(-=πf ,则=)0(f ( )(例13)A ．32-B ．21-C ．32 D ．21 解：由题意可知，此函数的周期11722()12123T πππ=-=，故223ππω=，3ω∴=，()cos(3)f x A x ϕ=+． 32()cos()sin 223f A A ππϕϕ=+==-． 又由题图可知771()cos(3)cos()12124f A A ππϕϕπ=⨯+=-cos sin )02A A ϕϕ=+=， 2(0)cos 3f A ϕ∴==．故选：C ．。
高中数学三角函数图像的性质及变换规律
高中数学三角函数图像的性质及变换规律三角函数是高中数学中重要的内容之一，它们的图像性质及变换规律是我们学习和应用三角函数的基础。
在本文中，我将详细介绍正弦函数、余弦函数和正切函数的图像性质，并讨论它们的平移、伸缩和翻转变换规律。
一、正弦函数的图像性质及变换规律正弦函数的图像是一条连续的波浪线，它的周期是2π，振幅为1。
正弦函数的图像在原点处有一个特殊点，即(0, 0)，称为正弦函数的零点。
正弦函数的图像在每个周期内呈现对称性，即关于y轴对称。
下面我们来看一个具体的例子：求解方程sin(x) = 0.5在区间[0, 2π]内的解。
首先，我们可以通过观察正弦函数的图像，知道sin(x) = 0.5有两个解，一个在第一象限，一个在第二象限。
我们可以通过求解sin(x) = 0.5的解析解来验证这一点。
sin(x) = 0.5的解析解为x = π/6 + 2πn和x = 5π/6 + 2πn，其中n为整数。
在区间[0, 2π]内，满足sin(x) = 0.5的解为x = π/6和x = 5π/6。
这个例子说明了正弦函数的图像性质，以及如何通过观察图像来快速得到方程的解。
二、余弦函数的图像性质及变换规律余弦函数的图像也是一条连续的波浪线，它的周期也是2π，振幅为1。
余弦函数的图像在原点处有一个特殊点，即(0, 1)，称为余弦函数的最大值点。
余弦函数的图像在每个周期内呈现对称性，即关于y轴对称。
下面我们来看一个具体的例子：求解方程cos(x) = -0.5在区间[0, 2π]内的解。
根据余弦函数的图像性质，我们可以知道cos(x) = -0.5有两个解，一个在第二象限，一个在第三象限。
我们可以通过求解cos(x) = -0.5的解析解来验证这一点。
cos(x) = -0.5的解析解为x = 2π/3 + 2πn和x = 4π/3 + 2πn，其中n为整数。
在区间[0, 2π]内，满足cos(x) = -0.5的解为x = 2π/3和x = 4π/3。
三角函数的平移与伸缩
三角函数的平移与伸缩三角函数在数学中占据着重要的地位，其在几何、物理、工程等各个领域都有广泛的应用。
而三角函数的平移与伸缩是对原本的函数图像进行操作，使其在坐标系中发生移动和变形。
本文将探讨三角函数的平移与伸缩，以及其对函数图像的影响。
1. 平移变换平移是指将函数图像沿着坐标系的横轴或纵轴方向进行移动。
对于正弦函数y = sin(x)和余弦函数y = cos(x)，平移操作可以通过改变自变量x发生。
如果横轴上的平移量为a，那么正弦函数的平移变换可以表示为y = sin(x - a)，余弦函数的平移变换可以表示为y = cos(x - a)。
这样，原本位于x轴上的函数图像将平移至新的位置。
2. 伸缩变换伸缩是指通过改变函数图像在坐标系中的大小和形状来实现。
伸缩操作可以通过改变函数的自变量或因变量进行。
对于正弦函数和余弦函数，分别称为sine函数和cosine函数，它们的伸缩变换形式可以表示为y = A*sin(Bx)和y = A*cos(Bx)。
其中，A和B分别代表着振幅和周期。
振幅A决定了函数图像在纵向上的幅度，而周期B则决定了函数图像在横向上的重复性。
当A增大时，函数图像的“峰”和“谷”之间的距离增大，振幅变大；反之，当A 减小时，振幅变小。
当B增大时，函数图像在横轴方向上的周期变长，每个周期内包含更多的“峰”和“谷”；反之，当B减小时，周期变短，每个周期内的“峰”和“谷”减少。
综合平移和伸缩，我们可以得到更加复杂的三角函数的变换。
例如对于正弦函数y = sin(x)进行平移和伸缩的组合操作，可以表示为y =A*sin(B(x - C)) + D。
其中C为平移量，A为伸缩因子，D为上下方向的平移量。
同样地，对于余弦函数也可以进行类似的操作。
三角函数的平移与伸缩在实际应用中起到了重要的作用。
它们能够改变函数图像在坐标系中的位置和形状，进而影响到相关问题的解决。
例如在物理学中，正弦函数和余弦函数可以用来描述周期性现象，如电磁波的传播及机械振动等。
高中数学三角函数的变换与图像分析
高中数学三角函数的变换与图像分析一、引言三角函数是高中数学中的重要内容之一，它们的变换与图像分析是解决三角函数相关问题的关键。
本文将从正弦函数、余弦函数和正切函数三个方面进行讲解，并通过具体题目的举例，分析其考点和解题技巧，帮助高中学生和家长更好地理解和应用三角函数的变换与图像分析。
二、正弦函数的变换与图像分析正弦函数的一般式为y = A sin(Bx + C) + D，其中A、B、C、D分别为常数，控制函数的振幅、周期、相位和纵坐标平移。
1. 振幅的变换振幅A决定了正弦函数图像的最大值和最小值，当A>1时，图像的振幅增大；当0<A<1时，图像的振幅减小。
例如，考虑函数y = 2sinx和y = 0.5sinx，它们的图像如下所示：（插入图像：y = 2sinx和y = 0.5sinx的图像）2. 周期的变换周期T决定了正弦函数图像的重复性，周期越大，图像的波动越缓慢。
周期T与常数B的关系为T = 2π/|B|。
例如，考虑函数y = sin2x和y = sin0.5x，它们的图像如下所示：（插入图像：y = sin2x和y = sin0.5x的图像）3. 相位的变换相位C决定了正弦函数图像的左右平移，相位为正时图像向左平移，相位为负时图像向右平移。
例如，考虑函数y = sin(x + π/2)和y = sin(x - π/2)，它们的图像如下所示：（插入图像：y = sin(x + π/2)和y = sin(x - π/2)的图像）4. 纵坐标平移的变换纵坐标平移D决定了正弦函数图像的上下平移，纵坐标平移为正时图像向上平移，纵坐标平移为负时图像向下平移。
例如，考虑函数y = sinx + 2和y = sinx - 2，它们的图像如下所示：（插入图像：y = sinx + 2和y = sinx - 2的图像）三、余弦函数的变换与图像分析余弦函数的一般式为y = A cos(Bx + C) + D，其中A、B、C、D分别为常数，控制函数的振幅、周期、相位和纵坐标平移。
三角函数(正弦函数与余弦函数)图像的变换及三角函数解析式的求法
1、（安徽卷文8）函数sin(2)3y x π=+图像的对称轴方程可能是（ ）A ．6x π=-B ．12x π=-C ．6x π=D ．12x π=2、（广东卷文5）已知函数2()(1cos 2)sin ,f x x x x R =+∈，则()f x 是（ ） A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 3、（全国Ⅰ卷文6）2(sin cos )1y x x =--是（ ） A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数4、（湖南卷理6）函数2()sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( )A.1C. 325、（天津卷文6）把函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是（ ）A ．sin 23y x x π⎛⎫=-∈ ⎪⎝⎭R ，B ．sin 26x y x π⎛⎫=+∈ ⎪⎝⎭R ，C ．sin 23y x x π⎛⎫=+∈ ⎪⎝⎭R ，D ．sin 23y x x 2π⎛⎫=+∈ ⎪⎝⎭R ，6、（全国Ⅰ卷文9）为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin y x =的图像（ ）A ．向左平移π6个长度单位B ．向右平移π6个长度单位 C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位7、（全国Ⅰ卷理8）为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像（ ）A ．向左平移5π12个长度单位 B ．向右平移5π12个长度单位 C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位1.（安徽卷文8）函数sin(2)3y x π=+图像的对称轴方程可能是（ ）A ．6x π=-B ．12x π=-C ．6x π=D ．12x π=解：sin(2)3y x π=+的对称轴方程为232x k πππ+=+，即212k x ππ=+，0,12k x π==2.（广东卷文5）已知函数2()(1cos 2)sin ,f x x x x R =+∈，则()f x 是（ ） A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 【解析】222211cos 4()(1cos 2)sin 2cos sin sin 224xf x x x x x x -=+===,选D.9.（全国Ⅰ卷文6）2(sin cos )1y x x =--是（ ） A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数sinx cosx,2sinxcosx 2y=1sin 2x 1=sin 2x T D2ππ±解析:本题主要考查了三角函数的化简，主要应用了与的关系，同时还考查了二倍角公式和函数的奇偶性和利用公式法求周期。
三角函数图像变换总结
三角函数图像变换总结三角函数是高中数学中非常重要的一个概念，它在几何、物理、工程等领域中有着广泛的应用。
在学习三角函数时，我们经常会接触到三角函数的图像变换。
图像变换是指通过对原始函数的一系列操作，得到一个新的函数的过程。
一、平移变换平移变换是指将函数的图像沿着横轴或纵轴方向平移一定的距离。
当我们将函数沿着横轴平移时，可以通过将自变量加上一个常数来实现。
例如，若将函数f(x)沿着横轴向右平移a个单位，则新函数为f(x-a)。
同样，当我们将函数沿着纵轴平移时，可以通过将因变量加上一个常数来实现。
二、伸缩变换伸缩变换是指通过改变函数的自变量或因变量的取值范围来改变函数的图像形状。
当我们将函数的自变量进行伸缩时，可以通过改变自变量的比例系数来实现。
例如，若将函数f(x)的自变量x进行伸缩，新函数为f(kx)，其中k是一个正常数。
当k 大于1时，函数图像会水平压缩；当0<k<1时，函数图像会水平拉伸。
同样，我们可以将函数的因变量进行伸缩，通过改变因变量的比例系数来实现。
三、翻折变换翻折变换是指通过改变函数的自变量或因变量的正负号来改变函数的图像形状。
当我们将函数的自变量进行翻折时，可以通过将自变量取相反数来实现。
例如，若将函数f(x)的自变量进行翻折，新函数为f(-x)。
同样，我们可以将函数的因变量进行翻折，通过将因变量取相反数来实现。
四、迭加变换迭加变换是指将多个变换效果叠加在一起，从而得到一个新的函数的图像。
例如，我们可以将平移、伸缩和翻折等变换操作应用于原始函数，得到一个经过多次变换的新函数的图像。
通过迭加变换，我们可以获得更加丰富多样的函数图像。
总结起来，三角函数的图像变换是通过对函数的自变量和因变量进行平移、伸缩、翻折等操作来改变函数的图像形状。
通过合理地应用这些图像变换，我们可以更好地理解和应用三角函数，并在解决实际问题时提供便利。
因此，掌握三角函数的图像变换是非常重要的数学技能之一，也是我们在数学学习中需要重点关注和掌握的内容之一。
三角函数图像的变换
三角函数图像的变换三角函数是一类重要的基础函数，包括正弦函数、余弦函数、正切函数等。
在数学中，我们经常遇到需要对三角函数进行图像变换的情况，比如平移、伸缩、翻转等。
本文将介绍三角函数图像的常见变换以及它们对函数图像的影响。
一、平移变换平移是指将函数图像沿着横轴或纵轴方向移动一段距离。
以正弦函数为例，设原函数为y=sin(x)，将它沿横轴向右平移a个单位，新函数为y=sin(x-a)。
当a取正值时，函数图像向右平移；当a取负值时，函数图像向左平移。
平移变换后的图像与原图像形状相同，只是位置不同。
二、伸缩变换伸缩是指将函数图像进行横向或纵向的比例拉伸或压缩。
以正弦函数为例，设原函数为y=sin(x)，将它沿横轴方向进行压缩b倍，新函数为y=sin(bx)。
当b大于1时，函数图像横向压缩；当0<b<1时，函数图像横向拉伸。
同样，沿纵轴方向进行伸缩也可得到相应的函数图像变换。
三、翻转变换翻转是指将函数图像沿着横轴或纵轴进行翻转，也称为镜像变换。
以正弦函数为例，设原函数为y=sin(x)，将它沿横轴进行翻转，新函数为y=-sin(x)。
同样地，纵向翻转可得到相应的函数图像变换。
四、混合变换除了单一的平移、伸缩和翻转变换，我们还可以通过组合这些变换来得到更复杂的函数图像变换。
比如，可以将平移、伸缩和翻转变换相结合，得到更丰富多样的变换效果。
以上是对三角函数图像常见变换的简要介绍，下面我们将进一步讨论这些变换对函数图像的具体影响。
1.平移变换的影响：平移变换只改变了函数图像的位置，不改变其形状。
假设原函数图像位于坐标系上方，若平移后函数图像向右移动，则新函数图像将出现在原来的右侧；若平移后函数图像向左移动，则新函数图像将出现在原来的左侧。
平移变换对函数图像的垂直位置没有影响。
2.伸缩变换的影响：横向伸缩会拉伸或压缩函数图像。
当b大于1时，函数图像在x轴方向上被压缩，变得更加陡峭；当0<b<1时，函数图像在x轴方向上被拉伸，变得更加平缓。
三角函数的像变换规律总结
三角函数的像变换规律总结三角函数是数学中的重要概念，它们在数学和物理等领域中有广泛的应用。
像变换规律是描述三角函数在图像上的移动、拉伸和反转等变化规律。
在本文中，我们将总结常见的三角函数的像变换规律。
一、正弦函数的像变换规律正弦函数是最常见的三角函数之一，其一般式为y =A*sin(Bx+C)+D，其中A、B、C、D为常数参数。
1. 水平方向平移：当C改变时，函数图像在水平方向上发生平移。
当C>0时，向左平移；当C<0时，向右平移。
平移的距离等于C的绝对值除以B。
2. 垂直方向平移：当D改变时，函数图像在垂直方向上发生平移。
当D>0时，向上平移；当D<0时，向下平移。
平移的距离等于D。
3. 垂直方向拉伸或压缩：当A改变时，函数图像在垂直方向上发生拉伸或压缩。
当|A|>1时，发生纵向拉伸；当|A|<1时，发生纵向压缩。
拉伸或压缩的程度与|A|的大小有关。
二、余弦函数的像变换规律余弦函数也是常见的三角函数之一，其一般式为y =A*cos(Bx+C)+D，其中A、B、C、D为常数参数。
1. 水平方向平移：与正弦函数类似，余弦函数在改变C时在水平方向上发生平移。
当C>0时，向左平移；当C<0时，向右平移。
平移的距离等于C的绝对值除以B。
2. 垂直方向平移：与正弦函数类似，余弦函数在改变D时在垂直方向上发生平移。
当D>0时，向上平移；当D<0时，向下平移。
平移的距离等于D。
3. 垂直方向拉伸或压缩：与正弦函数类似，余弦函数在改变A时在垂直方向上发生拉伸或压缩。
当|A|>1时，发生纵向拉伸；当|A|<1时，发生纵向压缩。
拉伸或压缩的程度与|A|的大小有关。
三、正切函数的像变换规律正切函数是另一个常见的三角函数，其一般式为y =A*tan(Bx+C)+D，其中A、B、C、D为常数参数。
由于正切函数在某些点上无定义，因此在图像上会有一些特殊的性质。
三角函数的解析式与像变换
三角函数的解析式与像变换在数学中，三角函数是研究角度和对应直角三角形边之间关系的一种函数形式。
三角函数有很多种，其中最常见的是正弦函数、余弦函数和正切函数，它们的解析式可以用来描述函数的性质和特点。
一、正弦函数正弦函数是三角函数中最基本的一种，通常用sin(x)或者sinθ表示。
正弦函数的解析式为：sin(x) = opposite / hypotenuse其中opposite表示直角三角形中与角度x对应的边长，hypotenuse表示直角三角形的斜边。
正弦函数具有以下性质：1. 定义域为实数集。
即对于任意实数x，都可以计算出sin(x)的值。
2. 值域为[-1, 1]。
正弦函数的值在[-1, 1]之间变化。
3. 周期性。
正弦函数的图像在横轴方向上以2π为周期重复。
4. 对称性。
正弦函数关于原点对称，即sin(-x) = -sin(x)。
二、余弦函数余弦函数是三角函数中另一种常见的函数形式，通常用cos(x)或者cosθ表示。
余弦函数的解析式为：cos(x) = adjacent / hypotenuse其中adjacent表示直角三角形中与角度x相邻的边长，hypotenuse 表示直角三角形的斜边。
余弦函数的性质包括：1. 定义域为实数集。
与正弦函数类似，余弦函数对于任意实数x都有定义。
2. 值域为[-1, 1]。
余弦函数的取值范围也在[-1, 1]之间，但与正弦函数的值略有不同。
3. 周期性。
余弦函数的周期为2π，即在横轴方向上以2π为周期重复。
4. 对称性。
余弦函数关于y轴对称，即cos(-x) = cos(x)。
三、正切函数正切函数是三角函数中第三种常见的函数形式，通常用tan(x)或者tanθ表示。
正切函数的解析式为：tan(x) = opposite / adjacent其中opposite表示直角三角形中与角度x对应的边长，adjacent表示直角三角形中与角度x相邻的边长。
正切函数具有以下性质：1. 定义域为实数集，但除去一些特殊点。
三角函数第七课(三角函数图像变换)讲义高一上学期数学人教A版
三角函数第七课 §三角函数图像变换复习：指出y = sin x 的图像变换为)32sin(π+=x y 的图像的两种方法平移法过程：两种方法殊途同归(1) y=sinx相位变换y=sin(x+φ)周期变换y=sin(ωx+φ)振幅变换 )sin(ϕ+ω=x A y (2)y=sinx 周期变换y=sin ωx 相位变换y=sin(ωx+φ)振幅变换)sin(ϕ+ω=x A y三种变换： 1. 平移变换①对“x ”左加右减; ②对“y ”上加下减。
2. 翻折变换 ①关于x 轴翻折 ②关于y 轴翻折 ③关于原点翻折 ④对“x ”加绝对值 ⑤对“y ”加绝对值 3. 伸缩变换②周期变换巧求初相角，最高点法例题如图，它是函数y ＝A sin(ωx ＋ϕ)(A ＞0，ω＞0)，｜ϕ｜＜π的图象，由图中条件，写出该函数解析式.练习：1.(1)y ＝sin(x ＋4π)是由y ＝sin x 向 平移 个单位得到的. (2)y ＝sin(x －4π)是由y ＝sin x 向 平移 个单位得到的. (3)y ＝sin(x －4π)是由y ＝sin(x ＋4π)向 平移 个单位得到的.2.要得到函数y ＝sin(2x －3π)的图象，只须将函数y ＝sin2x 的图象 A.向左平移3πB.向右平移3πC.向左平移6πD.向右平移6π3.若将某函数的图象向右平移2π以后所得到的图象的函数式是y ＝sin(x ＋4π)，则原来的函数表达式为( )A.y ＝sin(x ＋43π) B.y ＝sin(x ＋2π) C.y ＝sin(x －4π) D.y ＝sin(x ＋4π)－4π4.将函数y ＝f (x )的图象沿x 轴向右平移3π，再保持图象上的纵坐标不变，而横坐标变为原来的2倍，得到的曲线与y ＝sin x 的图象相同，则y ＝f (x )是( )A.y ＝sin(2x ＋3π)B.y ＝sin(2x －3π)C.y ＝sin(2x ＋32π)D.y ＝sin(2x －32π)5. 函数y ＝cos(432ππ+x )的最小正周期是__________. 6.要得到函数y ＝cos(2x －4π)的图象，只需将函数y ＝sin2x 的图象A.向左平移8π个单位B.向右平移8π个单位 C.向左平移4π个单位 D.向右平移4π个单位7.把函数y ＝cos(3x ＋4π)的图象适当变动就可以得到y ＝sin(－3x )的图象，这种变动可以是( ) A.向右平移4π B.向左平移4π C.向右平移12π D.向左平移12π8.如图b 是函数y ＝A sin(ωx ＋φ）＋2的图象的一部分，它的振幅、周期、初相各是( )A.A ＝3，Ｔ＝34π，φ＝－6πB.A ＝1，Ｔ＝34π，φ＝－43πC.A ＝1，Ｔ＝32π，φ＝－43πD.A ＝1，Ｔ＝34π，φ＝－6π9.如图c 是函数y ＝A sin （ωx ＋φ）的图象的一段，它的解析式为( )A.)32sin(32π+=x yB.)42sin(32π+=x yC.)3sin(32π-=x yD.)322sin(32π+=x y10.函数y ＝A sin （ωx ＋φ）（A ＞0，ω＞0）在同一周期内，当x ＝3π时，有y ｍa x ＝2，当x ＝0时，有y min ＝－2，则函数表达式是 .11.如图d 是f （x ）＝A sin （ωx ＋φ），A ＞0，｜φ｜＜2π的一段图象，则函数f （x ）的表达式为 .12.如图e ，是f （x ）＝A sin （ωx ＋φ），A ＞0，｜φ｜＜2π的一段图象，则f （x ）的表达式为 .13.如图f 所示的曲线是y ＝A sin （ωx ＋φ）（A ＞0，ω＞0）的图象的一部分，求这个函数的解析式.图c图d图e图f14.函数y ＝A sin （ωx ＋φ）＋ｋ（A ＞0，ω＞0）在同一周期内，当x ＝35π时，y 有最大值为37π，当x ＝311π时，y 有最小值－32，求此函数的解析式.15．由图g 所示函数图象，求y ＝A sin （ωx ＋φ）（｜φ｜＜π）的表达式.16．函数y ＝Asin(ωx ＋φ）（｜φ｜＜π）的图象如图h ，求函数的表达式.图g图h。
三角函数(正弦函数与余弦函数)图像的变换及三角函数解析式的求法
1、（安徽卷文8）函数sin(2)3y x π=+图像的对称轴方程可能是（ ）A ．6x π=-B ．12x π=-C ．6x π=D ．12x π=2、（广东卷文5）已知函数2()(1cos 2)sin ,f x x x x R =+∈，则()f x 是（ ） A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 3、（全国Ⅰ卷文6）2(sin cos )1y x x =--是（ ） A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数4、（湖南卷理6）函数2()sin cos f x x x x =+在区间,42ππ⎡⎤⎢⎥⎣⎦上的最大值是( )A.1C. 325、（天津卷文6）把函数sin ()y x x =∈R 的图象上所有的点向左平行移动3π个单位长度，再把所得图象上所有点的横坐标缩短到原来的12倍（纵坐标不变），得到的图象所表示的函数是（ ）A ．sin 23y x x π⎛⎫=-∈ ⎪⎝⎭R ，B ．sin 26x y x π⎛⎫=+∈ ⎪⎝⎭R ，C ．sin 23y x x π⎛⎫=+∈ ⎪⎝⎭R ，D ．sin 23y x x 2π⎛⎫=+∈ ⎪⎝⎭R ，6、（全国Ⅰ卷文9）为得到函数πcos 3y x ⎛⎫=+ ⎪⎝⎭的图象，只需将函数sin y x =的图像（ ）A ．向左平移π6个长度单位B ．向右平移π6个长度单位 C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位7、（全国Ⅰ卷理8）为得到函数πcos 23y x ⎛⎫=+ ⎪⎝⎭的图像，只需将函数sin 2y x =的图像（ ）A ．向左平移5π12个长度单位 B ．向右平移5π12个长度单位 C ．向左平移5π6个长度单位D ．向右平移5π6个长度单位1.（安徽卷文8）函数sin(2)3y x π=+图像的对称轴方程可能是（ ）A ．6x π=-B ．12x π=-C ．6x π=D ．12x π=解：sin(2)3y x π=+的对称轴方程为232x k πππ+=+，即212k x ππ=+，0,12k x π==2.（广东卷文5）已知函数2()(1cos 2)sin ,f x x x x R =+∈，则()f x 是（ ） A 、最小正周期为π的奇函数 B 、最小正周期为2π的奇函数 C 、最小正周期为π的偶函数 D 、最小正周期为2π的偶函数 【解析】222211cos 4()(1cos 2)sin 2cos sin sin 224xf x x x x x x -=+===,选D.9.（全国Ⅰ卷文6）2(sin cos )1y x x =--是（ ） A ．最小正周期为2π的偶函数B ．最小正周期为2π的奇函数C ．最小正周期为π的偶函数D ．最小正周期为π的奇函数sinx cosx,2sinxcosx 2y=1sin 2x 1=sin 2x T D2ππ±解析:本题主要考查了三角函数的化简，主要应用了与的关系，同时还考查了二倍角公式和函数的奇偶性和利用公式法求周期。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
三角函数图像题
---图像求解析式及平移变换 一．根据图像求解析式
1.图 1 是函数π2sin()2y x ωϕϕ⎛
⎫=+< ⎪⎝⎭的图象上的一段，则（ ）
A.10π116ωϕ=
=， B.10π116ωϕ==-， C.π
26ωϕ==， D.π
26
ωϕ==-，
2．已知函数()sin()f x A x ωϕ=+，x ∈R （其中2
2
,0,0π
π
ω<
<->>x A ），其部
分图像如图5所示．求函数()f x 的解析式；
3.下列函数中，图像的一部分如右图所示的是( )
A.sin()6y x π=+
B.cos(2)6y x π=-
C.cos(4)3y x π=-
D.sin(2)6y x π=- 4.已知函数()⎪⎭
⎫
⎝
⎛
<>+=2,0sin πϕωϕωx y 的部分图象如右图所示，则（ ） A. 6
,1π
ϕω=
= B. 6
,1π
ϕω-
== C. 6
,2π
ϕω=
= D. 6
,2π
ϕω-
==
5.下列函数中，图象的一部分如右图所示的是 A.sin 6y x π⎛⎫
=+
⎪⎝
⎭
B.sin 26y x π⎛⎫
=-
⎪⎝
⎭
C.cos 43y x π⎛⎫
=-
⎪⎝
⎭
D.cos 26y x π⎛⎫
=-
⎪⎝
⎭
6.函数()ϕω+=x A y sin 的一个周期内的图象如下图，求y 的解析式。
（其中
πϕπω<<->>,0,0A ）
7.已知函数)sin(ϕω+=x A y （0>A ， 0ω>，πϕ<||）的一段图象如图所示，求函数的解析式；
二．图像平移变换问题 1.为了得到函数sin(2)3y x π=-
的图像，只需把函数sin(2)6
y x π
=+的图像（ ） A.向左平移4π B.向右平移4π C.向左平移2π D.向右平移2
π
图5
y
x
2
-1-0
1
-1
1
2345
6
2.将函数sin y x =的图像上所有的点向右平行移动10
π
个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是（ ）
A.sin(2)10y x π
=-
B.sin(2)5y x π=-
C.1sin()210y x π=-
D.1sin()220y x π
=-
3.将函数sin y x =的图象上每点的横坐标缩小为原来的12（纵坐标不变），再把所得图象向左平移6
π
个单位，得到的
函数解析式为（ ）
()sin 26A y x π⎛⎫=+ ⎪⎝⎭ ()sin 23B y x π⎛⎫=+ ⎪⎝⎭ ()sin 26x C y π⎛⎫=+ ⎪⎝⎭ ()sin 212x D y π⎛⎫=+ ⎪
⎝⎭
4.把函数x y cos =的图象上的点的横坐标缩小到原来的一半，纵坐标保持不变，然后把图象向左平移4
π
个单位长度，得到新的函数图象，那么这个新函数的解析式为 （A ）⎪⎭⎫
⎝
⎛+
=42cos πx y （B ）⎪⎭
⎫
⎝⎛+=42cos πx y （C ）x y 2sin = （D ）x y 2sin -= 5.将函数sin y x =的图像上所有的点向右平行移动10
π
个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是（ ）
A.sin(2)10y x π
=-
B.y =sin(2)5x π-
C.y =1sin()210x π-
D.1sin()220
y x π
=- 6.要得到函数)4
2sin(3π
+=x y 的图象，只需将函数x y 2sin 3=的图象（ ） A.向左平移
4π B.向右平移4π C.左平移8π D.向右平移8
π 7.将函数y=sin3x 的图象作下列平移可得y=sin(3x+6
π
)的图象 A.向右平移 6π B.向左平移6π C.向右平移18π D.向左平移18
π
8.为了得到函数)6
2sin(π
-=x y 的图象,可以将函数x y 2cos =的图象( )
A 向右平移6π
B 向右平移3π
C 向左平移6π
D 向左平移3
π
9.为得到函数πcos 23y x ⎛
⎫
=+ ⎪⎝
⎭
的图像，只需将函数sin 2y x =的图像（ ） A 向左平移
5π12 B 向右平移5π12 C 向左平移5π6 D 向右平移5π6
10.为了得到函数)6
2sin(π
-=x y 的图象，可以将函数x y 2cos =的图象（ ）
A 向右平移6π
B 向右平移3π
C 向左平移6π
D 向左平移3
π
11.设函数()cos (0)f x x ωω=＞，将()y f x =的图像向右平移3
π
后，所得的图像与原图像重合，则ω的最小值等于
（A ）1
3
（B ）3 （C ）6 （D ）9
综合
1.(2004全国Ⅰ卷文、理)为了得到函数)6
2sin(π
-=x y 的图象,可以将函数x y 2cos =的图象( )
A ．向右平移
6π个单位长度B ．向右平移3π个单位长度C ．向左平移6π个单位长度D ．向左平移3
π
个单位长度 2（2006四川文、理）下列函数中，图像的一部分如右图所示的是( )
A.sin()6y x π=+
B.cos(2)6y x π=-
C.cos(4)3y x π=-
D.sin(2)6
y x π=-
二.填空题: （每小题5分，计20分） 3.已知函数2()2sin
cos 23sin 3444
x x x
f x =-+． （Ⅰ）求函数()f x 的最小正周期及最值； （Ⅱ）令π()3
g x f x ⎛
⎫
=+ ⎪⎝
⎭
，判断函数()g x 的奇偶性，并说明理由．
4.已知函数()cos(2)2sin()sin()344
f x x x x π
ππ
=-
+-+ （Ⅰ）求函数()f x 的最小正周期和图象的对称轴方程（Ⅱ）求函数()f x 在区间[,]122
ππ
-上的值域
5.设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8
π
=x .
(Ⅰ)求ϕ； (Ⅱ)求函数)(x f y =的单调增区间；
6.将函数x y sin =的图像上所有的点向右平行移动10
π
个单位长度，再把所得各点的横坐标伸长到原来的2倍（纵坐标不变），所得图像的函数解析式是( )
A.⎪⎭⎫
⎝
⎛-
=102sin πx y B. ⎪⎭⎫ ⎝⎛-=52sin πx y C. ⎪⎭⎫ ⎝⎛-=1021sin πx y D. ⎪⎭⎫ ⎝⎛-=202
1
sin πx y 7.已知函数()⎪⎭
⎫
⎝
⎛
<>+=2,0sin πϕωϕωx y 的部分图象如右上图所示，则（ ） A. 6
,1π
ϕω=
= B. 6
,1π
ϕω-
== C. 6
,2π
ϕω=
= D. 6
,2π
ϕω-
==
8.已知函数()()R x x x x x f ∈-+=1cos 2cos sin 322
①求函数()x f 的最小正周期及在区间⎥⎦⎤⎢⎣⎡2,0π上的最大值和最小值；②若()⎥⎦
⎤⎢⎣⎡∈=2,4,5600ππx x f ，求02cos x 的值。
9.已知函数2ππ()sin sin 2cos 662x f x x x x ωωω⎛
⎫⎛⎫=+
+--∈ ⎪ ⎪⎝
⎭⎝⎭
R ，（其中0ω>）,（I ）求函数()f x 的值域； （II ）若函数()y f x =的图象与直线1y =-的两个相邻交点间的距离为π
2
，求函数()y f x =的单调增区间．
10.设函数)(),0( )2sin()(x f y x x f =<<-+=ϕπϕ图像的一条对称轴是直线8
π
=x 。
（Ⅰ）求ϕ；（Ⅱ）求函数)(x f y =的单调增区间；
11.已知2
()2cos 32f x x x a =++（a R ∈是常数)
（1）若()f x 的定义域为R ，求()f x 的单调增区间；（2）若[0,]2
x π
∈时，()f x 的最大值为4，求a 的值。
12.已知函数sin()(0,0,||)2
y A x B A π
ωϕωϕ=++>><在同一个周期上的最高点为(2,2)，最低点为(8,4)-。
求函
数解析式。
13.（2006年福建卷）已知函数22
()sin 3cos 2cos ,.f x x x x x x R =++∈
①求函数()f x 的最小正周期和单调增区间； ②函数()f x 的图象可以由函数sin 2()y x x R =∈的图象经过怎样的变换得到？。