试验设计与数据处理(第二版)课后习题答案
最新试验设计与数据处理课后答案

试验设计与数据处理》第三章:统计推断3- 13解:取假设HO : u1-u2w 0和假设H1: u1-u2 > 0用sas 分析结果如下:Sample StatisticsGroupNMeanStd. Dev.Std. Errorx8 0.231875 0.0146 0.0051 y100.20970.00970.0031Hypothesis TestNull hypothesis:Mean 1 - Mean 2 = 0Alternative:Mean 1 - Mean 2 A= 0If Varianees Aret statistie DfPr > tEqual3.878 16 0.0013 Not Equal3.70411.670.0032由此可见p 值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中 由 3 个字母组成的词的比例均值差异显著。
3-14解:用sas 分析如下: Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1 Alternative:Varia nee 1 / Varia nee 2 A = 1- Degrees of Freedom -FNumer. Denom.Pr > F第四章:方差分析和协方差分析4- 1 解:Sas 分析结果如下:Dependent Variable: ySum ofSouree DF Squares Mean Square F Value Pr > F Model 41480.823000370.20575040.88<.00012.27 7 由p 值为0.2501 > 0.05 (显著性水平) 9 0.2501,所以接受原假设, 两方差无显著差异Source DF Type I SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n627.000000004.500000000.830.5684Source DF Type III SS Mean Square F ValuePr > F m 2 44.33333333 22.16666667 4.09 0.0442 n 3 11.50000000 3.83333333 0.71 0.5657 m*n 627.000000004.500000000.830.5684由结果可知, 在不同浓度下得率有显著差异, 在不同温度下得率差异不明显, 交 互作用的效应不显著。
实验设计与数据处理课后答案

《试验设计与数据处理》专业:机械工程班级:机械11级专硕学号:S110805035 姓名:赵龙第三章:统计推断3-13 解:取假设H0:u1-u2≤0和假设H1:u1-u2>0用sas分析结果如下:Sample StatisticsGroup N Mean Std. Dev. Std. Error----------------------------------------------------x 8 0.231875 0.0146 0.0051y 10 0.2097 0.0097 0.0031Hypothesis TestNull hypothesis: Mean 1 - Mean 2 = 0Alternative: Mean 1 - Mean 2 ^= 0If Variances Are t statistic Df Pr > t----------------------------------------------------Equal 3.878 16 0.0013Not Equal 3.704 11.67 0.0032由此可见p值远小于0.05,可认为拒绝原假设,即认为2个作家所写的小品文中由3个字母组成的词的比例均值差异显著。
3-14 解:用sas分析如下:Hypothesis TestNull hypothesis: Variance 1 / Variance 2 = 1Alternative: Variance 1 / Variance 2 ^= 1- Degrees of Freedom -F Numer. Denom. Pr > F----------------------------------------------2.27 7 9 0.2501由p值为0.2501>0.05(显著性水平),所以接受原假设,两方差无显著差异第四章:方差分析和协方差分析4-1 解:Sas分析结果如下:Dependent Variable: ySum ofSource DF Squares Mean Square F Value Pr > FModel 4 1480.823000 370.205750 40.88 <.0001Error 15 135.822500 9.054833Corrected Total 19 1616.645500R-Square Coeff Var Root MSE y Mean0.915985 13.12023 3.009125 22.93500Source DF Anova SS Mean Square F Value Pr > Fc 4 1480.823000 370.205750 40.88 <.0001由结果可知,p值小于0.001,故可认为在水平a=0.05下,这些百分比的均值有显著差异。
实验设计与数据处理(第二版部分答案)

试验设计与数据处理学院班级学号学生指导老师第一章 4、 相故100g 中维生素C 的质量围为:。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则2)、1mm 的汞柱代表的大气压为0.133KPa , 所以3)、1mm 则:6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 20.002136667总体方差σ20.001780556|||69.947|7.747 6.06d x =-=>算术平均误差△0.038333333极差R 0.117、S₁²=3.733,S₂²=2.303F=S₁²/S₂²=3.733/2.303=1.62123而F 0.975(9.9)=0.248386,F0.025(9.9)=4.025994所以F 0.975(9.9)< F <F0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
分析人员A 分析人员B8 7.5 样本方差1 3.7333338 7.5 样本方差2 2.30277810 4.5 Fa值0.248386 4.02599410 4 F值 1.621236 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量1 变量2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量1 变量2平均0.025684615 2.291111111方差0.000005861 0.031611111观测值13 9df 12 8F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349.检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
实验设计与数据处理第六章例题及课后习题答案
15.2
14.6 12.3 14.1
K2
15.5
14.7 12.8 12.6
K3
9.6
11 15.2 13.6
k1
5.066667 4.866666667
4.1
4.7
k2
5.166667
4.9 4.266667
4.2
k3
3.2 3.666666667 5.066667 4.533333
极差R
1.966667 1.233333333 0.966667
70
82
22
C
1
1
2
2
3
3
1
2
2
3
3
1
1
3
2
1
3
2
210
195
225
237
201
204
70
65
75
79
67
68
8
14
y
1
51
2
71
3
58
3
82
1
69
2
59
2
77
3
85
1
84
204
207
225
68
69
75
7
60
70
85
82
80
75
75
收率/%
67 70
70
65
65
79
60
68
55
50 80 85 90
1.0425 0.915 0.9825 0.875 0.915
0.7875
0.8775 1.005 0.9375 1.045 1.005
实验设计与数据处理(第二版部分答案)教学内容

实验设计与数据处理(第二版部分答案)试验设计与数据处理学院班级学号学生姓名指导老师第一章4、相对误差18.20.1%0.0182x mg mg ∆=⨯=故100g 中维生素C 的质量范围为:18.2±0.0182mg 。
5、1)、压力表的精度为1.5级,量程为0.2MPa ,则 max 0.2 1.5%0.003330.3758R x MPa KPax E x ∆=⨯==∆=== 2)、1mm 的汞柱代表的大气压为0.133KPa , 所以max 20.1330.1331.6625108R x KPax E x -∆=∆===⨯ 3)、1mm 水柱代表的大气压为gh ρ,其中29.8/g m s = 则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯ 6.样本测定值3.48 算数平均值 3.421666667 3.37 几何平均值 3.421406894 3.47 调和平均值 3.421147559 3.38 标准差s 0.046224092 3.4 标准差σ 0.04219663 3.43 样本方差S 2 0.002136667总体方差σ20.001780556算术平均误差△ 0.038333333 极差R 0.117、S ₁²=3.733,S ₂²=2.303F =S ₁²/ S ₂²=3.733/2.303=1.62123而F 0.975 (9.9)=0.248386,F 0.025(9.9)=4.025994 所以F 0.975 (9.9)< F <F 0.025(9.9)两个人测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
分析人员A分析人员B8 7.5 样本方差1 3.733333 8 7.5 样本方差2 2.302778 10 4.5 Fa 值 0.248386 4.025994104F 值1.62123|||69.947|7.747 6.06p pd x =-=>6 5.56 84 7056 7.56 5.58 88.旧工艺新工艺2.69% 2.62%2.28% 2.25%2.57% 2.06%2.30% 2.35%2.23% 2.43%2.42% 2.19%2.61% 2.06%2.64% 2.32%2.72% 2.34%3.02%2.45%2.95%2.51%t-检验: 双样本异方差假设变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 假设平均差0df 8t Stat -38.22288611P(T<=t) 单尾0t 单尾临界 1.859548033P(T<=t) 双尾0t 双尾临界 2.306004133F-检验双样本方差分析变量 1 变量 2平均0.025684615 2.291111111 方差0.000005861 0.031611111 观测值13 9 df 12 8 F 0.000185422P(F<=f) 单尾0F 单尾临界0.3510539349. 检验新方法是否可行,即检验新方法是否有系统误差,这里采用秩和检验。
实验设计与数据处理习题答案完整版

部分习题答案习题三1、62621086.6S 104.1ˆ002.74ˆ--⨯=⨯=σ=μ2、λ的极大似然估计和矩估计量均为x =λˆ 3、5、 6、(1)(5.608, 6.392) (2)(5.558, 6.442) 7、(1)(6.675, 6.681), (6.8×10-6, 6.8×10-5) (2)(6.61, 6.667), (3.8×10-6, 5.06×10-5) 8、σ已知6.239;σ未知6.356 9、4.052610、接受H O 11、认为不合格 12、认为显著大于10 13、拒绝H O 19、接受H O习题四1、差异显著;2、只有浓度的影响是显著的.习题五1、 填料A 用量范围可能选低了.2、培烧温度与三氧化铝两个因素用量范围可能偏低.习题六1、(2)xy5503.129584.13ˆ+= (4)(11.82,13.28)(5)(19.66,20.18) 2、xy05886.06287.24ˆ+= 3、(2))17.14,29.13)(3(,988.0104.0ˆx y+-=4、x0867318.0e 4556.32y ˆ-=5、2020381.00086.10333.19ˆx x y-+= 6、(1)31321x15.1x 575.09.9yˆ)2(x 15.1x 55.0x 575.09.9yˆ++=+++=习题七1、218.079.1419.300ˆz z y+-= 2、)1(21-=n c 212211,n n n b n n n a +=+=⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-+-⎪⎭⎫⎝⎛-+⨯+⎥⎥⎦⎤⎢⎢⎣⎡-⎪⎭⎫⎝⎛++⎪⎭⎫⎝⎛-++=-625.1589625.1102879.11025.105613.0625.160073.0263.2ˆ332z z z z y3、 4、 5、 6、 最优工艺条件 7、 最优凝固条件 即 8、.078.1=γ习题八习题九(1) E(5, , 0) (2)(i)扩大反射)1(>α;(ii)内收缩)0(<α;(iii )反射收缩)10(<α<;(3)B(2,4,3),A '(1.5,3,3.5),D '(2.5,2.5,2.5),C '(3,3.5,2)习题十1、 A 3B 3C 32、A 2B 3CD3、最优工艺条件x 1=-0.076,x 2=-0.118,即z 1=3. 848,z 2=0. 753,9.37ˆ=y4、 最优适宜条件 x 1=-0.0135, x 2=0.2557,x 3=-0.3364, 即z 1=6.4865, z 2=112.7865,z 3=0.3318.习题十一1、3.3962、3.54, 3.463、 5、6、 7、有系统误差2221212122212121z 9.21z 676.0z z 469.4z 465.50z 566.8572.2x504.3x 704.2xx 575.3x 1.1x 833.0838.37yˆ---++=-----=323121232221321x x 3.5x x 35.2x x 78.2x 38.3x 8.2x 1.3x 95.0x 388.0x 163.04.37y ˆ---------=.nσ.T2l g⎪⎭⎫⎝⎛σ+⎪⎭⎫⎝⎛σ≈σ.VMVV,VW W M σ+σ+σ≈σ-=.z 0019.0z 0148.0z 1388.0z 1269.06250.47yˆ4321--++=.z z 2.2z 15.058.125y ˆ321+++-=.z 0201.0z 00225.0z 00184.0z 000885.0114.0y ˆ4321-+--=,x 041.0x 023.0.x x 002.0x 052.0x 017.0351.0yˆ22212121--+++=.371.0yˆ,576.8z ,9.119z ,644.0x ,398.0x 2121=====即xx 02.0xx 025.0x025.0x475.0x 400.0218.89yˆ-+-++=,x 896.0x947.0x 399.0x x 375.023222132---+,0735.0x ,261.0x,483.0x 321===.38.89yˆ,02.6z ,13.4z ,42.17z 321====3108、无系统误差 9、是异常数据.习题十二1、543.02、(1)0.695 (2) (3)0.4253、(1)(2)2.98; (3) 0.898;4、(-1.28, -0.255, 0.675, 1.645)习题十四(1)一般; 2.5888(介于良与一般之间);(2)68.2245分.习题十五1、{}{}6,5,4,3,2,12、{}{}6,5,4,3,2,1习题十六2、ρ︒复相关系数上的投影在是其中与;),,,(L ˆ,)ˆ(*p *2*1***o*x x x y y y y⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=16.0431.06.0165.0431.065.01R )10.1,10.1,27.0,55.0,37.1,55.0(x)28.1,91.0,18.0,18.0,91.0,28.1(x ---=---=参考文献[1] Andenson T W. An Introduction to Multivariate StatisticalAnalysis. znd ed . New york: Wiley, 1984[2] 费荣昌试验设计与数据处理,4(1997)[3] 方开泰实用多元统计分析,上海:华东师范大学出版社,1989[4] 盛骤等概率论与数理统计,北京:高等教育出版社,1989[5] 朱道元等多元统计分析与软件SAS,南京:东南大学出版社,1999[6] 彭昭英SAS系统应用开发指南,北京:北京希望电子出版社,2000[7] 邓勃分析测试数据的统计处理方法,北京:清华大学出版社,1995[8] 中国现场统计会三次设计组,正交法和三次设计,北京:科学出版社,1985[9] 张尧庭、方开泰多元统计分析引论,北京:科学出版社,1983[10] 上海师范大学数学系回归分析及其试验设计,上海:上海教育出版社,1978[11] 韦博成、鲁国斌统计诊断引论,南京:东南大学出版社,1991[12] 张明淳工程矩阵理论,南京:东南大学出版社,1995[13] 赵德齐模糊数学,北京:中央民族大学出版社,1995[14] 胡永宏、贺思辉综合评价方法,北京:科学出版社,2000[15] 张崇甫等统计分析方法及其应用,重庆:重庆大学出版社,1995[16] 蒋尔雄等线性代数,北京:人民教育出版社,1978[17]王松桂线性模型的理论及其应用,合肥:安徽教育出版社,1987。
实验与数据处理习题及解答.docx
1.在^xcel中用AVERAGE函数计算平均值,用STEDV函数计算标准偏差,得到结果如表1所示。
表1该污水厂进、出水水质标准偏差及平均值COD SS 氨氮进水出水进水出水进水出水标准偏差102.70497 5.6417987 40.44311 2.2590321 7.7226061 1.1480863 平均值368.39 42.05 243.39 16.65 33.77 1.85图1该污水厂进、出水水质示意图2.在excel中作图如下:(1)加药量(mg/L)加药量(mg/L)图6加药量与浊度去除率、总磷去除率、总氮去除率、COD 去除率的关系图3. (1)图2总磷随加药质的变化关系图 图3余浊随加药质的变化关系图5075 100125150加药量(mg/L)5075100125150加药量(mg/L)图4总氮随加药■的变化关系图 图5 COD 随加药■的变化关系图(8)瓣泰2 0164 2108 6 4 (T/SUONH50 49 485756554 3 2 155 5 5 (q/SUIQooo o Oo o o o O图7进水量Q 与SVI 关系图10.015.020.025.030.035.0水温(笆)图8水温与SVI 关系图0.0010.00 20.00 30.00 40.00 50.00 60.00 70.00SV30 (%)图9 SV30与SVI 关系图0.00 20.0025.00 45.00 2(10(1HUM Hloo O oo O O.O.O. 8 6 430.0035.00 40.00 进水流量Q (万m3/d)50.00II)2((T /SUI0.002.004.006.00 8.0010.0012.00MLSS (g/L)图10 MLSS 与SVI 关系图(2) 用excel 中correl 函数求出相关系数r,再根据0V|rl<l,存在一定线性关系:①0 VlrlVO.3,微弱相关;②0.3VIHV0.5,低度相关;③0.5<lrl<0.8,显著相关;④0.8 <lrlVl,高度相关。
试验设计与数据处理 第二版 第6章 正交试验设计
按照规定的方案完成每一号试验 试验次序可随机决定 试验条件要严格控制
(5)计算极差,确定因素的主次顺序
三个符号: Ki:表示任一列上水平号为 i 时,所对应的试验结果之和。 ki :ki= Ki/s,其中s为任一列上各水平出现的次数 R(极差):在任一列上
R=max{K1 ,K2 ,K3}-min{K1 ,K2 ,K3},
上一张 下一张 主 页 退 出
图6-3
上一张 下一张 主 页
退 出
正交设计就是从选优区全面试验点(水 平组合)中挑选出有代表性的部分试验点(水
平组合)来进行试验。图6-3中标有试验号的九
个“(·)”,就是利用正交表 L9(34) 从 27 个试
验点中挑选出来的9个试验点。即:
(1)A1B1C1 (2)A2B1C2 (3)A3B1C3
图6-3
3 因 素 3 水 平 的 全 面试验水平组合数为 33=27,4 因素3水平的全面试验水平组合数为34=81 , 5因素3水平的全面试验水平组合数为35=243,这在科 学试验中是有可能做不到的。
上一张 下一张 主 页 退 出
表10-1
上一张 下一张 主 页
退 出
图6-1 全面实验 实验点分布
试验目的与要求
试验方案设计:
试验指标
选因素、定水平 因素、水平确定 选择合适正交表 表头设计 列试验方案 试验结果分析
验证试验
试验结果分析:
进行试验,记录试验结果
试验结果极差分析
试验结果方差分析
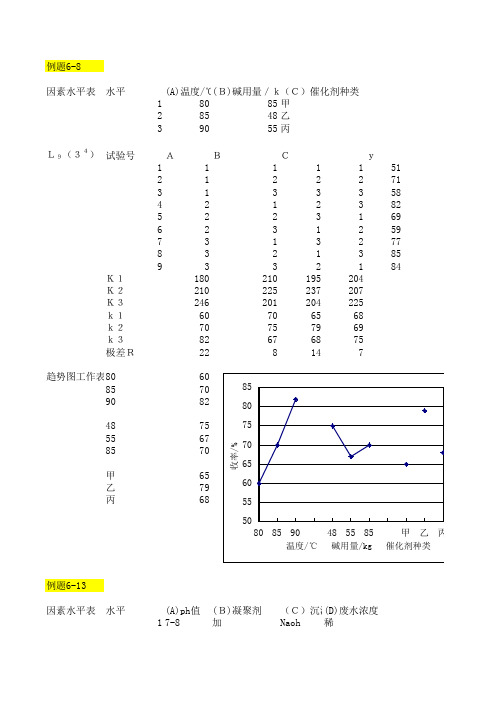
绘 制 因 素 指 标 趋 势 图
计 算 K 值
计 算 k 值
计 算 极 差 R
计算各列偏差平方和、 自由度 列方差分析表, 进行F 检验 分析检验结果, 写出结论
实验设计与数据处理第六章例题及课后习题答案
实验设计与数据处理第六章例题及课后习题答案例题6-8(C)催化剂种类因素⽔平表⽔平(A)温度/℃(B)碱⽤量/kg18085甲28548⼄39055丙L9(34)试验号ABCy111115121222713133358421238252231696231259731327783213859332184K1180210195204K2210225237207K3246201204225k160706568k270757969k382676875极差R228147趋势图⼯作表8060 Array 85709082487555678570甲65⼄79丙68例题6-13(D)废⽔浓度28-9不加Na2CO3浓39-10410-11L8(41×24)试验号A B C D空列得分yi 11111145212222703211225542221165531212856321219574122190842112100 K1115275295295295K2120330310310310K3180K4190k157.568.873.873.873.8k260.082.577.577.577.5k390.0k495.0极差R37.513.8 3.8 3.8 3.8SS2309.375378.12528.12528.12528.125总和T605P=T2/n45753.13⽅差分析表差异源SS df MS F显著性A2309.3753769.79227.3704*B378.1251378.12513.4444*C28.125128.125D28.125128.125误差e28.125128.125误差eΔ84.375328.125F0.05(3,3)9.277F0.01(3,3)29.457F0.05(1,3)10.128F0.01(1,3)34.116280160231001801L9(34)试验号ABCy11111 5.321222531333 4.942123 5.452231 6.462312 3.773132 3.983213 3.393321 2.4K115.214.612.314.1K215.514.712.812.6K39.61115.213.6k15.066667 4.866666667 4.1 4.7k25.166667 4.9 4.26667 4.2k33.2 3.666666667 5.066674.53333极差R1.966667 1.2333333330.966670.5因素主→次优⽅案趋势图⼯作表605.066667804.8666671604.91803.66666715.06666724.2666673 4.1习题6.2⽔平(A)反应温度(B)CU2+与氨⽔质?CuSO4溶液浓度/(g/ml)17001:00.00.12528001:00.50.539001:00.51L9(34)试验号ABC转换率1111140.262122240.463133361.79ABC A2B2C24212360.155223173.976231291.317313273.528321387.199332197.26K1142.51173.93218.76211.49K2225.43201.62197.87205.29K3257.97250.36209.28209.13k147.5033333357.976772.9270.497k275.1433333367.206765.956768.43k385.9983.453369.7669.71极差R38.4866666725.4767 6.96333 2.0667因素主→次优⽅案K1 4.474.8465.898 5.445K2 5.6843.421 3.813 5.01K34.4816.368 4.924 4.18k1 1.491.61533 1.966 1.815k2 1.8946666671.14033 1.271 1.67k3 1.4936666672.12267 1.64133 1.3933极差R0.404666667最终优⽅案A3B2C2习题6.3L9(34)试验号ABC包合率包合物收率1111112.0161.82122215.8684.313133316.9580.15421238.667.235223113.7177.26623127.2276.5373132 6.5458.61832137.7878.1293321 5.4377.6K12.270840.74943823 1.19055 1.40944K21.392932.090804961 1.53806 1.37318K30.77943 1.602956793 1.71459 1.66057k10.7569470.2498127430.396850.46981k20.464310.6969349870.512690.45773k30.259810.5343189310.571530.55352极差R0.4971370.4471222440.174680.0958因素主→次优⽅案ABC A3B3C1BCA B2C2A1转换率铜粉松密度ABC A1B2C3习题6.4L8(27)试验号A B A×B C空列空列11111112111222312211241222215212121621221272211228221211 K1283282268268276275k26868.2571.7571.7569.7570极差R119191935A*B C A B D因素主→次因素A*B⽔平搭配表A1A2B169.571.5B27264.5习题6-5L8(41×24)试验号A B C D空列得分yi 111111195212222205321122220422211225531212210632121215741221185842112190 K1400810820820820K2445835825825825K3425K4375k1200.0202.5205.0205.0205.0k2222.5208.8206.3206.3206.3k3212.5k4187.5极差R35.0 6.3 1.3 1.3 1.3因素主→次优⽅案习题6-6L 9(34)实验号C C(虚拟)B AD 酸洗时间/min 11111136222123225222313462231221723132168232131992332137K1887476107K2149859169K3787061k129.3333324.666725.333335.667k224.8333328.333330.333323k32623.333320.333极差R-4.5 3.77.015.3因素主→次优⽅案习题6-7L 8(27)试验号A B A×B C A×C B×C 11111112111222312211241222215212121621221272211228221211K14.53 4.17 3.66 3.93 3.5 3.66K23.15 3.514.02 3.75 4.18 4.02k11.1325 1.04250.9150.98250.8750.915k20.78750.8775 1.0050.9375 1.045 1.005极差R1.380.660.36-0.180.680.36因素主→次A BCD或者ABDC A 2B2C2D2或A2B2D2C2DABC D3A3B1C2A A×CB D A×B B×C C 或 A A×C BA1A2C1 1.070.895C2 1.1950.68因素B×C⽔平搭配表B1B2C1 1.020.945C2 1.0650.81习题6-8123456试验号L27(313)A B(A×B)1(A×B)2C(A×C)1 111111121111223111133412221151222226122233713331181333229133333102123121121232312212331132231121422312315223131162312121723122318231231193132132031322121313232223213132332132127332132 K1879800795807796800K2785790807790802792K3732806794799798804极差R147161317612SS1231.6314.5185185211.629616.0741 2.07418.2963总和T2396P=T2/n212622.8⽅差分析表差异源SS df MS F显著性A1231.632615.815218.776**B14.5185227.25926 2.57895AB27.70374 6.92593 2.46053C 2.0740742 1.037040.36842AC28.1481547.03704 2.5D312.51852156.25955.5132**BC56.59259414.1481 5.02632*E107.1852253.592619.0395*F 3.629632 1.814810.64474误差e11.185192 5.59259误差eΔ16.888896 2.81481F0.05(2,6) 5.14F0.01(2,6)10.52F0.05(4,6) 4.53F0.01(4,6)9.15⽔平搭配表B1B2B3C1868891.33333333C29088.6666788.66666667C390.666666786.6666788.66666667A1D1E1B3C1优⽅案习题6-9L9(34)试验号ABCy11111 5.321222562312 3.773132 3.983213 3.393321 2.4K115.214.612.314.1K215.514.712.812.6K39.61115.213.6极差R 5.9 3.7 2.9 1.5SS7.362222 2.962222222 1.602220.38889SST=总和T40.3P=T2/n180.4544⽅差分析表差异源SS df MS F显著性A7.3622222 3.6811118.9314B 2.9622222 1.481117.61714C 1.60222220.80111 4.12误差e0.38888920.19444误差eΔ0.38888920.19444F0.05(2,2)19习题6-10L8(41×24)试验号A B C D空列得分yi 111111195212222205321122220422211225531212210632121215741221185842112190 K1400810820820820K2445835825825825K3425K4375总和T1645P=T2/n338253.1⽅差分析表差异源SS df MS F显著性A1384.3753461.458147.667**B78.125178.12525*C 3.1251 3.1251D 3.1251 3.1251误差e 3.1251 3.125误差eΔ9.3753 3.125F0.05(1,3)10.13F0.01(1,3)34.12F0.05(3,3)9.28F0.01(3,3)29.46习题6-11L9(34)实验号C C(虚拟)B A D酸洗时间/min 111111362112223231133320422123225222313462231221723132168232131992332137 K1887476107K2149859169K3787061SS40.520.666778402.67SST=总和T237P=T2/n6241⽅差分析表差异源SS df MS F显著性A7823918.72B20.66667210.3333 4.96C40.5140.519.44*D402.66672201.33396.64**误差e 4.1666672 2.08333误差eΔ 4.1666672 2.08333F0.05(2,2)19F0.01(2,2)39F0.05(1,2)18.51F0.01(1,2)38.51铜粉松密度2.0080.6931.7691.2961.6132.7751.5421.1151.824包合物收率综合分包合率⾪属0.571180.124120.392 0.9053810.94310.838130.935 0.275170.335410.299 0.718750.725680.722 0.155380.697280.372 0.0963500.058 0.203990.759140.426 00.738910.296D得率/%16527427117327017316226727328268.2570.59时间/minD提取量/mL1 1.012 1.332 1.131 1.062 1.0310.810.7620.563.634.050.90751.01250.42A×B C78910111213(A×C)2(B×C)1D(B×C)2E F抗压强度/kg.cm-2 1111111100 2222222983333333971222333952333111963111222991333222942111333993222111101312312385123123182231231298323131285131212390212323185331223191112331289223112380213213273321321390132132177221332184332113280113221376232121389313232178121313285 788784836791790824794 802800799800804785801 806812761805802787801182875141439719.851943.8519312.511.1912.7407107.2 3.63SST=1795.185 12.3156 1471.88。
实验设计与数据处理第一章例题及课后习题(附答案)
1、 根据三组数据的绝对误差计算权重:12322211110000,25,400000.010.20.005w w w ====== 因为123::400:1:1600w w w = 所以1.54400 1.71 1.53716001.53840011600pH ⨯+⨯+⨯==++2、 因为量程较大的分度值也较大,用量程大的测量数值较小的物理量会造成很大的系统误差。
3.、含量的相对误差为0.2g ,所以相对误差为:0.20.99790525.3Rx E x ∆===。
4、 相对误差18.20.1%0.0182x mg mg ∆=⨯= 故100g 中维生素C 的质量范围为:18.2±0.0182。
5、1)、压力表的精度为1.5级,量程为0.2,则max 0.2 1.5%0.003330.3758R x MPa KPa x E x ∆=⨯==∆===2)、1的汞柱代表的大气压为0.133,所以max 20.1330.133 1.6625108R x KPax E x -∆=∆===⨯ 3)、1水柱代表的大气压为gh ρ,其中29.8/g m s =则:3max 339.8109.810 1.225108R x KPax E x ---∆=⨯∆⨯===⨯6、样本测定值算术平均值 3.421666667 3.48 几何平均值 3.421406894 3.37 调和平均值 3.421147559 3.47 标准差s 0.046224092 3.38 标准差 0.04219663 3.4 样本方差 0.002136667 3.43 总体方差0.001780556 算住平均误差 0.038333333极差 0.117、依题意,检测两个分析人员测定铁的精密度是否有显著性差异,用F双侧检验。
根据试验值计算出两个人的方差及F值:221221223.733, 2.3033.7331.621232.303s s s F s ===== 而0.9750.025(9,9)0.248386,(9,9) 4.025994F F ==, 所以0.9750.025(9,9)(9,9)F F F <<两个人的测量值没有显著性差异,即两个人的测量方法的精密度没有显著性差异。
