西工大大学物理 大作业参考答案-真空中的静电场2009
大学物理第九章习题答案
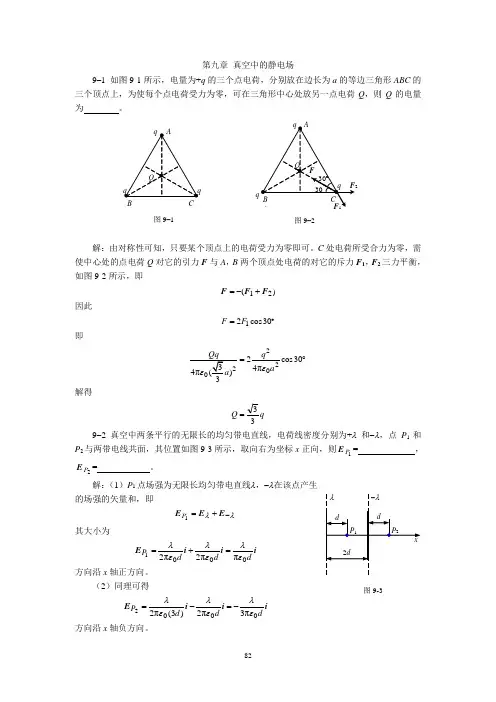
第九章 真空中的静电场9–1 如图9-1所示,电量为+q 的三个点电荷,分别放在边长为a 的等边三角形ABC 的三个顶点上,为使每个点电荷受力为零,可在三角形中心处放另一点电荷Q ,则Q 的电量为 。
解:由对称性可知,只要某个顶点上的电荷受力为零即可。
C 处电荷所受合力为零,需使中心处的点电荷Q 对它的引力F 与A ,B 两个顶点处电荷的对它的斥力F 1,F 2三力平衡,如图9-2所示,即)21(F F F +-=因此12cos30F F ︒=即2202cos304πq aε=︒解得q Q 33=9-2 真空中两条平行的无限长的均匀带电直线,电荷线密度分别为+λ 和-λ,点P 1和P 2与两带电线共面,其位置如图9-3所示,取向右为坐标x 正向,则1P E = ,2P E = 。
解:(1)P 1点场强为无限长均匀带电直线λ,-λ在该点产生的场强的矢量和,即λλ-+=E E E 1P其大小为i i i E dd d P 000ππ2π21ελελελ=+=方向沿x 轴正方向。
(2)同理可得i i i E dd d P 000π3π2)3(π22ελελελ-=-=方向沿x 轴负方向。
图9–2图9-3C B图9–19-3 一个点电荷+q 位于一边长为L 的立方体的中心,如图9-4所示,则通过立方体一面的电通量为 。
如果该电荷移到立方体的一个顶角上,那么通过立方体每一面的电通量是 。
解:(1)点电荷+q 位于立方体的中心,则通过立方体的每一面的电通量相等,所以通过每一面的通量为总通量的1/6,根据高斯定理1d in Sq ε⋅=∑⎰⎰E S ,其中S 为立方体的各面所形成的闭合高斯面,所以,通过任一面的电通量为0d 6Sqε⋅=⎰⎰E S 。
(2)当电荷+q 移至立方体的一个顶角上,与+q 相连的三个侧面ABCD 、ABFE 、BCHF 上各点的E 均平行于各自的平面,故通过这三个平面的电通量为零,为了求另三个面上的电通量,可以以+q 为中心,补作另外7个大小相同的立方体,形成边长为2L 且与原边平行的大立方体,如图9–5所示,这个大立方体的每一个面的电通电都相等,且均等于6εq ,对原立方体而言,每个面的面积为大立方体一个面的面积的1/4,则每个面的电通量也为大立方体一个面的电通量的1/4,即此时通过立方体每一面的电通量为0111d 4624Sqε⋅⋅=⎰⎰E S 。
静电场(答案)

一. 选择题[B]1图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+?(x <0)和-?(x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A)0.(B)i a02ελπ. (C)i4λ.(D)()j i +λ. E +E 合[B 距离r 柱面r ≤20r 2rL=LE ρππε,即:r r >2R 2rL=LE ρππε,即:2R r[C 如图所示,一个电荷为q 的点于立方体的A 角上,则通过侧面abcd (A)06εq (C)024ε048ε【提示】:添加7个与如图相同的小立方体构成一个大立方体,使A 处于大立方体的中心。
则大立方体外围的六个正方形构成一个闭合的高斯面。
由Gauss 定理知,通过该高斯面的电通量为qε。
再据对称性可知,通过侧面abcd 的电场强度通量等于24εq。
[D ]4在点电荷+q 的电场中,若取图中P 点处为电势零点,则M 点的电势为(A)a q 04επ.(B)aq 08επ.(C)a q 04επ-.(D)aq08επ-. 【提示】:220048PaM Maq q V E dl dr raπεπε-===⎰⎰[C ]5已知某电场的电场线分布情况如图所示.现观察到一负电荷从M 点移到N 点.有人根据这个图作出下列几点结论,其中哪点是正确的? (A)电场强度E M <E N . (B)电势U M <U N .(C)电势能W M <W N . (D)电场力的功A >0. 【提示】:静电力做负功,电势能增加。
1232E dS R E π=4“无限大”均匀带电平面,A 、B 、C 三个区域的电场强度分别为:E A =5R ,则b 【提示】:设无穷远处为电势零点,则点电荷在空间任一点产生的电势为:04P PV r πε=,P r 为点电荷q 到场点P 的距离。
题中b 点的电势为123q q q 、、在该点独自产生电势的代数和。
6真空中电荷分别为q 1和q 2的两个点电荷,当它们相距为r 时,该电荷系统的相互作用电势能W =1204q qr πε.(设当两个点电荷相距无穷远时电势能为零)【提示】:电荷系统的相互作用电势能,即建立该电荷系统,外力所作的功。
大学物理第9章习题解答

第9章 真空中的静电场 习题解答9-1 精密的实验已表明,一个电子与一个质子的电量在实验误差为e 2110-±的范围内是相等的,而中子的电量在e 2110-±的范围内为零。
考虑这些误差综合的最坏情况,问一个氧原子(含8个电子、8个质子、8个中子)所带的最大可能净电荷是多少?若将原子看成质点,试比较两个氧原子间的电力和万有引力的大小,其净力是引力还是斥力?解:(1)一个氧原子所带的最大可能净电荷为 e q 21max 1024-⨯±= (2)两个氧原子间的电力和万有引力的大小之比为6222711221921122222max 0108.2)1067.116(1067.6)106.11024(1085.84141------⨯≈⨯⨯⨯⨯⨯⨯⨯⋅⨯⨯=≤r r rm G r q f f G e ππε氧 其净力是引力。
9-2 如习题9-2图所示,在直角三角形ABC 的A 点处,有点电荷q 1 = 1.8×10-9C ,B 点处有点电荷q 2 = -4.8×10-9C ,AC = 3cm ,BC = 4cm ,试求C 点的场强。
解:根据点电荷场强大小的公式22014q qE kr r==πε, 点电荷q 1在C 点产生的场强大小为112014q E AC =πε 994-1221.810910 1.810(N C )(310)--⨯=⨯⨯=⨯⋅⨯ 方向向下。
点电荷q 2在C 点产生的场强大小为2220||14q E BC =πε994-1224.810910 2.710(N C )(410)--⨯=⨯⨯=⨯⋅⨯, 方向向右。
C 处的总场强大小为E =44-110 3.24510(N C )==⨯⋅,总场强与分场强E 2的夹角为12arctan33.69E E ==︒θ.9-3 半径为R 的一段圆弧,圆心角为60°,一半均匀带正电,另一半均匀带负电,其电荷线密度分别为+λ和-λ,求圆心处的场强。
大作业参考答案-真空中的静电场

第九章 真空中的静电场一、选择题⒈ C ; ⒉B ;⒊ C ; ⒋ B ; ⒌ B ; 6.C ; 7.E ; 8.A,D ; 9.B ;10. B,D 二、填空题 ⒈2308qb Rπε,缺口。
⒉ 0qε,< ;⒊ 半径为R 的均匀带电球面(或带电导体球); ⒋ 1221E E h h ε--; 2.21⨯10-12C/m 3; ⒌ 100N/C ;-8.85×10-9C/m 2 ; ⒍ -135V ; 45V ; ⒎006q Q R πε;0;006q Q Rπε- ;006q QR πε ; ⒏ 122204()q x R πε+;322204()qx x R πε+;2R ;432.5 V/m ; 9.有源场;无旋场 (注意不能答作“保守场”,保守场是针对保守力做功讲的)。
三、 问答题1. 答: 电场强度0E F q =是从力的角度对电场分布进行的描述,它给出了一个矢量场分布的图像;而电势V =W /q 是从能量和功的角度对电场分布进行的描述,它给出了一个标量场分布的图像。
空间任意一点的电场强度和该点的电势之间并没有一对一的关系。
二者的关系是:"0"p d grad ,d d PVE V V E l n =-=-=⋅⎰ 。
即空间任一点的场强和该点附近电势的空间变化率相联系;空间任一点的电势和该点到电势零点的整个空间的场强分布相联系。
由于电场强度是矢量,利用场叠加原理计算时,应先将各电荷元产生的电场按方向进行分解,最后再合成,即:d d d d ;x y z E E i E j E k =++, d ,d ,d x x y y z zE E E E E E ===⎰⎰⎰ 而电势是标量可以直接叠加,即:V dV =⎰。
但用这种方法求电势时,应注意电势零点的选择。
四、计算与证明题1. 证:①根据对称性分析,两段带电直线各自在O 点的电场强度大小相等,方向相反,相互抵消,所以只计算带电细线半圆形部分的电场。
大学物理第7章真空中的静电场答案

Q 与坐标原点0的距离为ydE方向沿轴正向。
4二;0x (x _ L )(2)如图7— 2图b ,设通过棒的端点与棒垂直上任一点• dx2 4二;°r第七章 真空中的静电场7- 1在边长为a 的正方形的四角,依次放置点电荷 q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为 一^甘4)= 4二;。
(2 a ) 5q 2,方向由q 指向-4q 。
2二;°a 7 — 2如图,均匀带电细棒,长为 L ,电荷线密度为 入。
(1) 求棒的延长线上任一点 P 的场强;(2)求通过棒的端点与棒垂直上 任一点Q 的场强。
解:(1)如图7 — 2图a ,在细棒上任取电荷元 dq ,建立如图坐标, P 与坐标原点0的距离为x ,贝U dq = ■ d ■,设棒的延长线上任一点 dE4二;0(x _ )2 4二;0(x _ )2 则整根细棒在 P 点产生的电场强度的大小为 dq 0 n_(」L 一丄x - L x习题7—2图adE y■ dx 2 4二;0rdE x 亠si n ,4 二;°r因x 二ytg pdxcos2 -习题7—2图b代入上式,则E x 二-dE xPL QE「dE「石石。
込还R S Z= 4jy y2L27— 3 一细棒弯成半径为R的半圆形,均匀分布有电荷q,求半圆中心0处的场强。
解:如图,在半环上任取dl=Rdr的线元,其上所带的电荷为dq=,Rd=对称分析E y=o。
dE x■ Rd v24二0RE = dE x sin -4二0R 02 0Rq2 二2;0R2,如图,方向沿x轴正向。
7 —4如图线电荷密度为入1的无限长均匀带电直线与另一长度为I、线电荷密度为 & 的均匀带电直线在同一平面内,二者互相垂直,求它们间的相互作用力。
西工大 大学物理学习题册答案

第一章 真空中的静电场一、选择题 1.C ;2.B ;3.C ;4.B ;5.B ;6.C ;7.E ;8.AD ; 9.B ;10.BD 二、填空题 1.30281R qb επ;由圆心指向缺口。
2. 0εq;21Φ<Φ。
3. 均匀带电薄球壳。
4. 12210h h E E --ε;312C/m 1021.2-⨯。
5. N/C 100;2-9C/m 10.858⨯。
6. V 135-;V 45。
7.R Q q U q E 0006πε=;00=∞C U q ;R Q q U q CE 0006πε-=;RQq U q E 0006πε=∞。
8.41220R x q+πε; 2322)(41R x qx πε+; R22; N/C 4333620=Rπεq 。
9. 有源场;无旋场(或保守场)。
三、问答题答:E 电场强度从力的角度描述电场的性质,矢量场分布;U 从能和功的角度描述电场的性质,标量场。
E 与U 的关系为: U E grad -= ,⎰∞⋅=ad l E U a使用叠加原理计算电场强度,注意先将各个场源产生的电场强度分解到各坐标轴,然后再叠加。
使用叠加原理计算电势,要注意电势零点的选择。
四、计算与证明题:1.证:(1) CD BC AB E E E E++=根据对称性分布,两段直导线AB 和CD 在O 点产生的电场强度大小相等,方向相反,则0=+CD AB E E。
在半圆形BC 上取电荷元d l ,则l q d d λ=,相应的在O 点产生d E 为 204d d alE πελ=由于对称分布分析可知0=x E ,设d E 和y 轴夹角为θ,且有θd d a l =θθελθελd cos 4πcos 4πd d 020y aa l E ==a a E y 02202πd cos 4πελθθελππ==⎰- j a εE 02πλ=∴ 得证(2)半圆形BC 在O 点产生的电势为:aεlU 014πd d λ=, ⎰==aεl a εU π0014πd 4πλπλ带电导线AB 或CD 在O 点产生的电势为:l l 024πd dU ελ=, ⎰==aal dl U 2022ln 44ππελελ总电势:)2ln 2π(4π2021+=+=ελU U U 得证 2.解:①取高斯面为同心球面,由高斯定理:∑⎰⎰===⋅q r E dS E S d E SS214επ ,得当r ≤R 时,)( 4πππ34π3430133333R r RQrE QR r r R Q r q <=⇒===∑ερ 当r >R 时 )( 4π1π4202022R r rQE Q r E Q q >=⇒=⇒=∑εε ② 选无穷远为势能零点。
真空中的静电场答案
对各分量分别求和
E x
0 4 0 R
sin cos d
0
E y
0 4 0 R
sin 2 d 0
0
8 0 R
所以
E
Exi
Ey
j
0 8 0 R
j
3.(1059)
图中虚线所示为一立方形的高斯面,已知空间的场强分布为:Ex=bx, Ey=0, Ez=0.
高斯面边长a=0.1 m,常量b=1000 N/(C·m).试求该闭合面中包含的净电荷.(真空介电
试验电荷从A点分别移动到B、C、D各点,则
(A) 从A到B,电场力作功最大.
(B) 从A到C,电场力作功最大.
(C) 从A到D,电场力作功最大. (D) 从A到各点,电场力作功相等.
[D ]
A
-q O
B
C D
二、填空题 1.(1042) A、B为真空中两个平行的“无限大”均匀带电平面,已知两平 面间的电场强度大小为E0,两平面外侧电场强度大小都为E0/3, 方向如图.则A、B两平面上的电荷面密度分别为δA=
解:选杆的左端为坐标原点,x轴沿杆的方向 .在x处取
q0
一电荷元λdx,它在点电荷所在处产生场强为:
d
E
d
4 0 d
x
x 2
d
l
d
l
整个杆上电荷在该点的场强为:
dx
q0
O
x
x
E
4 0
l dx
0d x2
l
40d d
l
d+ x
点电荷q0所受的电场力为:
F
q0l
40d d
l
=0.90
N
09真空中的静电场
真空中的静电场一、单选题:1、(0388A10) 在坐标原点放一正电荷Q ,它在P 点(x =+1,y =0)产生的电场强度为E .现在,另外有一个负电荷-2Q ,试问应将它放在什么位置才能使P 点的电场强度等于零? (A) x 轴上x >1. (B) x 轴上0<x <1.(C) x 轴上x <0.(D) y 轴上y >0.(E) y 轴上y <0.[ ]2、(1001A10)一均匀带电球面,电荷面密度为σ,球面内电场强度处处为零,球面上面元d S 带有σ d S 的电荷,该电荷在球面内各点产生的电场强度(A) 处处为零. (B) 不一定都为零.(C) 处处不为零. (D) 无法判定 . [ ]3、(1003B30)下列几个说法中哪一个是正确的?(A) 电场中某点场强的方向,就是将点电荷放在该点所受电场力的方向.(B) 在以点电荷为中心的球面上, 由该点电荷所产生的场强处处相同. (C) 场强可由q F E / =定出,其中q 为试验电荷,q 可正、可负,F 为试验电荷所受的电场力.(D) 以上说法都不正确. [ ]4、(1366B30) 如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P 点是x 轴上的一点,坐标为(x ,0).当x >>a 时,该点场强的大小为: (A) x q 04επ. (B) 30x qa επ. (C) 302x qa επ. (D) 204x q επ. [ ] 5、(1367B30)如图所示,在坐标(a ,0)处放置一点电荷+q ,在坐标(-a ,0)处放置另一点电荷-q .P 点是y 轴上的一点,坐标为(0,y ).当y >>a 时,该点场强的大小为: (A) 204y q επ. (B) 202y q επ. (C) 302y qa επ. (D) 304yqa επ. [ ]6、(1402A10)在边长为a 的正方体中心处放置一电荷为Q 的点电荷,则正方体顶角处的电场强度的大小为:(A) 2012a Q επ. (B) 206aQ επ. (C) 203a Q επ. (D) 20aQ επ. [ ] 7、(1403A20)电荷面密度分别为+σ和-σ的两块“无限大”均匀带电的平行平板,如图放置,则其周围空间各点电场强度 随位置坐标x 变化的关系曲线为:(设场强方向向右为正、向左为负) [ ]8、(1404B25)电荷面密度均为+σ的两块“无限大”均匀带电的平行平板如图放置,其周围空间各点电场强度E 随位置坐标x 变化的关系曲线为:(设场强方向向右为正、向左为负) [ ]9、(1405A15) 设有一“无限大”均匀带正电荷的平面.取x 轴垂直带电平面,坐标原点在带电平面上,则其周围空间各点的电场强度E 随距离平面的位置坐标x 变化的关系曲线为(规定场强方向沿x 轴正向为正、反之为负): [ ]10、(1406A15)(B)σ(D)002εxx设有一“无限大”均匀带负电荷的平面.取x 轴垂直带电平面,坐标原点位于带电平面上,则其周围空间各点的电场强度E 随距离平面的位置坐标x 变化的关系曲线为(规定场强方向沿x轴正向为正、反之为负):[ ]11、(1033A10) 一电场强度为E 的均匀电场,E 的方向与沿x 轴正向,如图所示.则通过图中一半径为R 的半球面的电场强度通量为 (A) πR 2E . (B) πR 2E / 2. (C) 2πR 2E . (D) 0. [ ]12、(1034B25)有两个电荷都是+q 的点电荷,相距为2a .今以左边的点电荷所在处为球心,以a 为半径作一球形高斯面 . 在球面上取两块相等的小面积S 1和S 2,其位置如图所示. 设通过S 1和S 2的电场强度通量分别为Φ1和Φ2,通过整个球面的电场强度通量为ΦS ,则(A) Φ1>Φ2,ΦS =q /ε0.(B) Φ1<Φ2,ΦS =2q /ε0.(C) Φ1=Φ2,ΦS =q /ε0.(D) Φ1<Φ2,ΦS =q /ε0. [ ]13、(1035B30) 有一边长为a 的正方形平面,在其中垂线上距中心O 点a /2处,有一电荷为q 的正点电荷,如图所示,则通过该平面的电场强度通量为(A) 03εq . (B) 04επq(C) 03επq . (D) 06εq [ ] 14、(1054A10)已知一高斯面所包围的体积内电荷代数和∑q =0,则可肯定:(A) 高斯面上各点场强均为零.(B) 穿过高斯面上每一面元的电场强度通量均为零.(C) 穿过整个高斯面的电场强度通量为零.(D) 以上说法都不对. [ ]15、(1055A05)一点电荷,放在球形高斯面的中心处.下列哪一种情况,通过高斯面的电场强度通量发生变化:q(A) 将另一点电荷放在高斯面外.(B) 将另一点电荷放进高斯面内.(C) 将球心处的点电荷移开,但仍在高斯面内.(D) 将高斯面半径缩小.]16、(1056A10)点电荷Q 被曲面S 所包围 , 从无穷远处引入另一点电荷q 至曲面外一点,如图所示,则引入前后:(A) 曲面S 的电场强度通量不变,曲面上各点场强不变.(B) 曲面S 的电场强度通量变化,曲面上各点场强不变. (C) 曲面S 的电场强度通量变化,曲面上各点场强变化.(D) 曲面S 的电场强度通量不变,曲面上各点场强变化. []17、(1251A20) 半径为R 的均匀带电球面的静电场中各点的电场强度的大小E 与距球心的距离r 之间的关系曲线为: [ ]18、(1252A20) 半径为R 的“无限长”均匀带电圆柱面的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为: [ ]19、(1253A20) 半径为R 的均匀带电球体的静电场中各点的电场强度的大小E 与距球心的距离r 的关系曲线为: [ ]20、(1254A20)半径为R 的“无限长”均匀带电圆柱体的静电场中各点的电场强度的大小E 与距轴线的距离r 的关系曲线为:[ ]E O r (D) E ∝1/r 2 E O r (A)E ∝1/r21、(1255B30) 图示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的.(A) 半径为R 的均匀带电球面.(B) 半径为R 的均匀带电球体. (C) 半径为R 的、电荷体密度为ρ=A r (A 为常数)的非均匀带电球体.(D) 半径为R 的、电荷体密度为ρ=A/r (A 为常数)的非均匀带电球体.[ ]22、(1256A10)两个同心均匀带电球面,半径分别为R a 和R b (R a <R b ), 所带电荷分别为Q a 和Q b .设某点与球心相距r ,当R a <r <R b 时,该点的电场强度的大小为:(A) 2041r Q Q b a +⋅πε. (B) 2041rQ Q b a -⋅πε. (C) ⎪⎪⎭⎫ ⎝⎛+⋅π22041b b a R Q r Q ε. (D) 2041r Q a ⋅πε. 23、(1257C45) 图示为一具有球对称性分布的静电场的E ~r 关系曲线.请指出该静电场是由下列哪种带电体产生的.(A) 半径为R 的均匀带电球面.(B) 半径为R 的均匀带电球体.(C) 半径为R 、电荷体密度ρ=Ar (A 为常 数)的非均匀带电球体.(D) 半径为R 、电荷体密度ρ=A/r (A 为常数)的非均匀带电球体.[ ]24、(1282B35) 如图所示,一个电荷为q 的点电荷位于立方体的A 角上,则通过侧面abcd 的电场强度通量等于: (A) 06εq . (B) 012εq . (C) 024εq . (D) 048εq . [ ] 25、(1370A20)半径为R 的均匀带电球面,若其电荷面密度为σ,则在距离球面R 处的电场强度大小为:(A) 0εσ. (B) 02εσ. (C) 04εσ. (D) 08εσ. [ ] 26、(1432A10) 高斯定理 ⎰⎰⋅=VS V S E 0/d d ερ E E(A) 适用于任何静电场.(B) 只适用于真空中的静电场.(C) 只适用于具有球对称性、轴对称性和平面对称性的静电场.(D) 只适用于虽然不具有(C)中所述的对称性、但可以找到合适的高斯面的静电场.27、(1433A10) 根据高斯定理的数学表达式⎰∑⋅=Sq S E 0/d ε 可知下述各种说法中,正确的是: (A) 闭合面内的电荷代数和为零时,闭合面上各点场强一定为零.(B) 闭合面内的电荷代数和不为零时,闭合面上各点场强一定处处不为零.(C) 闭合面内的电荷代数和为零时,闭合面上各点场强不一定处处为零.(D) 闭合面上各点场强均为零时,闭合面内一定处处无电荷. [ ]28、(1434A10)关于高斯定理的理解有下面几种说法,其中正确的是: (A) 如果高斯面上E 处处为零,则该面内必无电荷. (B) 如果高斯面内无电荷,则高斯面上E 处处为零. (C) 如果高斯面上E 处处不为零,则高斯面内必有电荷.(D) 如果高斯面内有净电荷,则通过高斯面的电场强度通量必不为零.[ ]29、(1490B25)如图所示,两个同心的均匀带电球面,内球面半径为R 1、带有电荷1Q , 外球面半径为R 2、带有电荷Q 2,则在内球面里面、距离球心为r 处的P 点的场强大小E 为:(A) 20214r Q Q επ+. (B) 2202210144R Q R Q εεπ+π (C) 2014r Q επ. (D) 0.[ ]30、(1016A05)静电场中某点电势的数值等于(A)试验电荷q 0置于该点时具有的电势能.(B)单位试验电荷置于该点时具有的电势能.(C)单位正电荷置于该点时具有的电势能.(D)把单位正电荷从该点移到电势零点外力所作的功. [ ]31、(1017B30) 半径为R 的均匀带电球面,总电荷为Q .设无穷远处电势为零,则该带电体所产生的电场的电势U ,随离球心的距离r 变化的分布曲线为 [ ]32、(1019B30) (A) (B)(C)2 (D) 2 (E)在点电荷+q 的电场中,若取图中P 点处为电势零点 , 则M 点的电势为 (A) a q 04επ. (B) aq 08επ. (C) a q 04επ-. (D) aq 08επ-. [ ] 33、(1020B30) 电荷面密度为+σ和-σ的两块“无限大”均匀带电的平行平板,放在与平面相垂直的x 轴上的+a和-a 位置上,如图所示.设坐标原点O 处电势为零,则在-a <x <+a 区域的电势分布曲线为 [ ]34、(1021B35)如图,在点电荷q 的电场中,选取以q 为中心、R 为半径的球面上一点P 处作电势零点,则与点电荷q 距离为r 的P'点的电势为 (A)r q04επ (B) ⎪⎭⎫ ⎝⎛-πR r q 1140ε (C) ()R r q-π04ε (D) ⎪⎭⎫ ⎝⎛-πr R q 1140ε [ ]35、(1046A15)如图所示,边长为l 的正方形,在其四个顶点上各放有等量的点电荷.若正方形中心O 处的场强值和电势值都等于零,则: (A) 顶点a 、b 、c 、d 处都是正电荷.(B) 顶点a 、b 处是正电荷,c 、d 处是负电荷. (C) 顶点a 、c 处是正电荷,b 、d 处是负电荷.(D) 顶点a 、b 、c 、d 处都是负电荷. [ ]36、(1047A20)如图所示,边长为 0.3 m 的正三角形abc ,在顶点a 处有一电荷为10-8 C 的正点电荷,顶点b 处有一电荷为-10-8 C 的负点电荷,则顶点c 处的电场强度的大小E 和电势U 为: (041επ=9³10-9 N m /C 2) (A) E =0,U =0.(B) E =1000 V/m ,U =0.(C) E =1000 V/m ,U =600 V .(D) E =2000 V/m ,U =600 V . [ ]37、(1087A20)(A)(B)(C) (D)ba如图所示,半径为R 的均匀带电球面,总电荷为Q ,设无穷远处的电势为零,则球内距离球心为r 的P 点处的电场强度的大小和电势为: (A) E =0,r Q U 04επ=. (B) E =0,RQ U 04επ=. (C) 204r Q E επ=,rQ U 04επ= . (D) 204r Q E επ=,RQ U 04επ=. [ ] 38、(1172B25) 有N 个电荷均为q 的点电荷,以两种方式分布在相同半径的圆周上:一种是无规则地分布,另一种是均匀分布.比较这两种情况下在过圆心O 并垂直于圆平面的z 轴上任一点P (如图所示)的场强与电势,则有 (A) 场强相等,电势相等.(B) 场强不等,电势不等. (C) 场强分量E z 相等,电势相等.(D) 场强分量E z 相等,电势不等.[]39、(1267A20)关于静电场中某点电势值的正负,下列说法中正确的是:(A) 电势值的正负取决于置于该点的试验电荷的正负.(B)电势值的正负取决于电场力对试验电荷作功的正负.(C) 电势值的正负取决于电势零点的选取.(D) 电势值的正负取决于产生电场的电荷的正负. [ ]40、(1414A15)在边长为a 的正方体中心处放置一点电荷Q ,设无穷远处为电势零点,则在正方体顶角处的电势为:(A) aQ 034επ . (B) a Q 032επ. (C) a Q 06επ. (D) aQ 012επ . [ ] 41、(1415B25) 一“无限大”带负电荷的平面,若设平面所在处为电势零点,取x 轴垂直电平面,原点在带电平面处,则其周围空间各点电势U 随距离平面的位置坐标x 变化的关系曲线为:[ ]42、(1416B25) 有一“无限大”带正电荷的平面,若设平面所在处为电势零点,取x 轴垂直带电平面,原点在带电平面上,则其周围空间各点电势U随距离平面的位置坐标x 变化的关系曲线为: [ ]43、(1417C60) 设无穷远处电势为零,则半径为R 的均匀带电球体产生的电场的电势分布规律为(图中的U 0和b 皆为常量): [ ]44、(1482B40)如图所示,两个同心球壳.内球壳半径为R 1,均匀带有电荷Q ;外球壳半径为R 2,壳的厚度忽略,原先不带电,但与地相连接.设地为电势零点,则在内球壳里面,距离球心为r 处的P 点的场强大小及电势分别为: (A) E =0,U =104R Q επ. (B) E =0,U =⎪⎪⎭⎫ ⎝⎛-π21114R R Q ε.(C) E =204r Q επ,U =rQ 04επ. (D) E =204r Q επ, U =104R Q επ. [ ] 45、(1483B40)如图所示,两个同心球壳.内球壳半径为R 1,均匀带有电荷Q ;外球壳半径为R 2,壳的厚度忽略,原先不带电,但与地相连接.设地为电势零点,则在两球之间、距离球心为r 的P 点处电场强度的大小与电势分别为:(A) E =204r Q επ,U =r Q 04επ. (B) E =204r Q επ,U =⎪⎪⎭⎫ ⎝⎛-πr R Q 11410ε. (C) E =204r Q επ,U =⎪⎪⎭⎫ ⎝⎛-π20114R r Q ε.(D) E =0,U =204R Qεπ. [ ](A)(C)(B)(D)46、(1484B40)如图所示,一半径为a 的“无限长”圆柱面上均匀带电,其电荷线密度为λ.在它外面同轴地套一半径为b 的薄金属圆筒,圆筒原先不带电,但与地连接.设地的电势为零,则在内圆柱面里面、距离轴线为r 的P 点的场强大小和电势分别为:(A) E =0,U =raln 20ελπ.(B) E =0,U =ab ln 20ελπ. (C) E =r 02ελπ,U =rb ln 20ελπ. (D) E =r 02ελπ,U =ab ln 20ελπ. [ ] 47、(1075A10)真空中有一点电荷Q ,在与它相距为r 的a 点处有一试验电荷q .现使试验电荷q 从a 点沿半圆弧轨道运动到b 点,如图所示.则电场力对q 作功为(A)24220r r Qq π⋅πε. (B) r r Qq 2420επ. (C) r rQq ππ204ε. (D) 0. [ ] 48、(1076A10)点电荷-q 位于圆心O 处,A 、B 、C 、D 为同一圆周上的四点,如图所示.现将一试验电荷从A 点分别移动到B 、C 、D 各点,则 (A) 从A 到B ,电场力作功最大. (B) 从A 到C ,电场力作功最大.(C) 从A 到D ,电场力作功最大.(D) 从A 到各点,电场力作功相等. [ ]49、(1192B30) 两块面积均为S 的金属平板A 和B 彼此平行放置,板间距离为d (d 远小于板的线度),设A 板带有电荷q 1,B 板带有电荷q 2,则AB两板间的电势差U AB 为(A) d S q q 0212ε+. (B) d S q q 0214ε+. (C) d S q q 0212ε-. (D) d S q q 0214ε-. [ ] A A S q 1q 250、(1198B25)如图所示,CDEF 为一矩形,边长分别为l 和2l .在DC 延长线上CA =l 处的A 点有点电荷+q ,在CF 的中点B 点有点电荷-q ,若使单位正电荷从C 点沿CDEF 路径运动到F 点,则电场力所作的功等于: (A)l l q --⋅π51540ε . (B) 55140-⋅πl q ε(C)31340-⋅πl q ε . (D) 51540-⋅πl q ε. [] 51、(1199A20) 如图所示,边长为a 的等边三角形的三个顶点上,分别放置着三个正的点电荷q 、2q 、3q .若将另一正点电荷Q从无穷远处移到三角形的中心O 处,外力所作的功为: (A) a qQ 023επ . (B) aqQ 03επ. (C) a qQ 0233επ. (D) aqQ032επ. [ ]52、(1266A20)在已知静电场分布的条件下,任意两点P 1和P 2之间的电势差决定于 (A) P 1和P 2两点的位置.(B) P 1和P 2两点处的电场强度的大小和方向. (C) 试验电荷所带电荷的正负.(D) 试验电荷的电荷大小. [ ] 53、(1268B25) 半径为r 的均匀带电球面1,带有电荷q ,其外有一同心的半径为R 的均匀带电球面2,带有电荷Q ,则此两球面之间的电势差U 1-U 2为:(A) ⎪⎭⎫ ⎝⎛-πR r q 1140ε . (B) ⎪⎭⎫⎝⎛-πr R Q 1140ε .(C) ⎪⎭⎫ ⎝⎛-πR Q r q 041ε . (D)r q04επ . [ ] 54、(1085A10)图中实线为某电场中的电场线,虚线表示等势(位)面,由图可看出:(A) E A >E B >E C ,U A >U B >U C .(B) E A <E B <E C ,U A <U B <U C . (C) E A >E B >E C ,U A <U B <U C .(D) E A <E B <E C ,U A >U B >U C . [ ] 55、(1069B35)面积为S 的空气平行板电容器,极板上分别带电量±q ,若不考虑边缘效应,则两极板间的相互作用力为(A)Sq 02ε. (B) S q 022ε.A E FC D l lq2q(C) 2022S q ε. (D) 202Sq ε. [ ] 56、(1088C50)充了电的平行板电容器两极板(看作很大的平板)间的静电作用力F 与两极板间的电压U 的关系是:(A) F ∝U . (B) F ∝1/U .(C) F ∝1/U 2. (D) F ∝U 2. [ ]57、(1240B25)如图所示,在真空中半径分别为R 和2R 的两个同心球面,其上分别均匀地带有电荷+q 和-3q .今将一电荷为+Q的带电粒子从内球面处由静止释放,则该粒子到达外球面时的动能为:(A) R Qq 04επ. (B) R Qq 02επ.(C) R Qq 08επ. (D) RQq083επ. [ ]58、(1299B40)在一个带有负电荷的均匀带电球外,放置一电偶极子,其电矩p的方向如图所示.当电偶极子被释放后,该电偶极子将(A) 沿逆时针方向旋转直到电矩p沿径向指向 球面而停止. (B) 沿逆时针方向旋转至p沿径向指向球面,同时沿电场线方向向着球面移 动.(C) 沿逆时针方向旋转至p沿径向指向球面,同时逆电场线方向远离球面移 动.(D) 沿顺时针方向旋转至p沿径向朝外,同时沿电场线方向向着球面移动. [ ]59、(1300B40)在一个带有正电荷的均匀带电球面外,放置一个电偶极子,其电矩p 的方向如图所示.当释放后,该电偶极子的运动主要是(A) 沿逆时针方向旋转,直至电矩p沿径向指向球面而停止.(B) 沿顺时针方向旋转,直至电矩p沿径向朝外而停止.(C) 沿顺时针方向旋转至电矩p沿径向朝外,同时沿电场线远离球面移动.(D) 沿顺时针方向旋转至电矩p沿径向朝外,同时逆电场线方向向着球面移动. [ ] 60、(1303A15)电子的质量为m e ,电荷为-e ,绕静止的氢原子核(即质子)作半径为r 的匀速率圆周运动,则电子的速率为(A) kr m ee . (B) r m ke e .(C) r m k ee 2. (D) rm ke e 2. (式中k =1 / (4πε0) ) [ ]61、(1304A20) 质量均为m ,相距为r 1的两个电子,由静止开始在电力作用下(忽略重力作用)运动至相距为r 2,此时每一个电子的速率为 (A)⎪⎪⎭⎫⎝⎛-21112r r m ke . (B) ⎪⎪⎭⎫⎝⎛-21112r r m ke . (C) ⎪⎪⎭⎫ ⎝⎛-21112r r m k e. (D) ⎪⎪⎭⎫⎝⎛-2111r r m k e (式中k =1 / (4πε0) ) [ ] 62、(1316A20)相距为r 1的两个电子,在重力可忽略的情况下由静止开始运动到相距为r 2,从相距r 1到相距r 2期间,两电子系统的下列哪一个量是不变的? (A) 动能总和; (B) 电势能总和;(C) 动量总和; (D) 电相互作用力. [ ] 63、(1393B35)密立根油滴实验,是利用作用在油滴上的电场力和重力平衡而测量电荷的,其电场由两块带电平行板产生.实验中,半径为r 、带有两个电子电荷的油滴保持静止时,其所在电场的两块极板的电势差为U 12.当电势差增加到4U 12时,半径为2r 的油滴保持静止,则该油滴所带的电荷为: (A) 2e (B) 4e(C) 8e (D) 16e [ ] 64、(1394B25)一个静止的氢离子(H +)在电场中被加速而获得的速率为一静止的氧离子(O +2)在同一电场中且通过相同的路径被加速所获速率的: (A) 2倍. (B) 22倍.(C) 4倍. (D) 42倍. [ ] 65、(1395B35)一平行板电容器,板间距离为d ,两板间电势差为U 12,一个质量为m 、电荷为-e 的电子,从负极板由静止开始飞向正极板.它飞行的时间是:(A) 122eU m d . (B) 122eU m d .(C) 122eU md(D) meU d 212 [ ] 66、(1439A10)一电偶极子放在均匀电场中,当电偶极矩的方向与场强方向不一致时,其所受的合力F 和合力矩M为:(A) F =0,M = 0. (B) F = 0,M≠0.(C) F ≠0,M =0. (D) F ≠0,M≠0. [ ] 67、(1440A10)真空中有两个点电荷M 、N ,相互间作用力为F,当另一点电荷Q 移近这两个点电荷时,M 、N 两点电荷之间的作用力 (A) 大小不变,方向改变. (B) 大小改变,方向不变.(C) 大小和方向都不变. (D) 大小和方向都改. [ ] 68、(1441A10) 设有一带电油滴,处在带电的水平放置的大平行金属板之间保持稳定,如图所示.若油滴获得了附加的负电荷,为了继续使油滴保持稳定,应采取下面哪个措施?(A) 使两金属板相互靠近些.(B) 改变两极板上电荷的正负极性. (C) 使油滴离正极板远一些.(D) 减小两板间的电势差. [ ]69、(1442B30) 一个带正电荷的质点,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示.已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示中正确的是:[ ]70、(1443B30) 一个带正电荷的质点,在电场力作用下从A 点出发经C 点运动到B 点,其运动轨迹如图所示.已知质点运动的速率是递减的,下面关于C点场强方向的四个图示中正确的是:[]71、(1444B30) 一个带负电荷的质点,在电场力作用下从A 点出发经C 点运动到B点,其运动轨迹如图所示.已知质点运动的速率是递增的,下面关于C 点场强方向的四个图示中正确的是:[ ] 72、(1445B30)-+ E(C)EE(C)(A)一个带负电荷的质点,在电场力作用下从A 点经C 点运动到B 点,其运动轨迹如图所示.已知质点运动的速率是递减的,下面关于C 点场强方向的四个图示中正确的是: [ ]73、(1551A10) 关于电场强度定义式0/q F E=,下列说法中哪个是正确的?(A) 场强E的大小与试探电荷q 0的大小成反比.(B) 对场中某点,试探电荷受力F与q 0的比值不因q 0而变.(C) 试探电荷受力F 的方向就是场强E的方向.(D) 若场中某点不放试探电荷q 0,则F =0,从而E=0. [ ]74、(1555A20)将一个试验电荷q 0 (正电荷)放在带有负电荷的大导体附近P 点处(如图),测得它所受的力为F .若考虑到电荷q 0不是足够小,则(A) F / q 0比P 点处原先的场强数值大. (B) F / q 0比P 点处原先的场强数值小. (C) F / q 0等于P 点处原先场强的数值.(D) F / q 0与P 点处原先场强的数值哪个大无法确定. [ ] 75、(1558A20)下面列出的真空中静电场的场强公式,其中哪个是正确的?(A) 点电荷q 的电场:204rqE επ= .(r 为点电荷到场点的距离) (B) “无限长”均匀带电直线(电荷线密度λ)的电场:r r E302ελπ=(r为带电直线到场点的垂直于直线的矢量)(C) “无限大”均匀带电平面(电荷面密度σ)的电场:02εσ=E(D) 半径为R 的均匀带电球面(电荷面密度σ)外的电场:r rR E302εσ= (r为球心到场点的矢量) [ ] 76、(1559B30) 图中所示为一沿x 轴放置的“无限长”分段均匀带电直线,电荷线密度分别为+λ(x <0)和-λ (x >0),则Oxy 坐标平面上点(0,a )处的场强E为(A) 0. (B)i a02ελπ. (C) i a 04ελπ. (D)()j i a+π04ελ. [ ] E(C)(A) P77、(1633B25)图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系,请指出该曲线可描述下列哪方面内容(E 为电场强度的大小,U 为电势):(A) 半径为R 的无限长均匀带电圆柱体电场的E ~r 关 系.(B) 半径为R 的无限长均匀带电圆柱面电场的E ~r 关系.(C) 半径为R 的均匀带正电球体电场的U ~r 关系.(D) 半径为R 的均匀带正电球面电场的U ~r 关系. [ ]78、(1635B25)图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系,请指出该曲线可描述下列哪方面内容(E 为电场强度的大小,U 为电势):(A) 半径为R 的无限长均匀带电圆柱体电场的E~r 关 系. (B) 半径为R 的无限长均匀带电圆柱面电场的E~r 关系.(C) 半径为R 的均匀带正电球体电场的U~r 关系.(D) 半径为R 的均匀带正电球面电场的U~r 关系. [ ]79、(1491A15)如图所示,两个同心均匀带电球面,内球面半径为R 1、带有电荷Q 1,外球面半径为R 2、带有电荷Q 2,则在外球面外面、距离球心为r 处的P 点的场强大小E 为:(A) 20214r Q Q επ+.(B)()()2202210144R r Q R r Q -π+-πεε. (C) ()2120214R R Q Q -π+ε. (D) 2024rQ επ. [ ] 80、(1492B25) 如图所示,两个同心的均匀带电球面,内球面带电荷Q 1,外球面带电荷Q 2,则在两球面之间、距离球心为r 处的P 点的场强大小E 为:(A) 2014r Q επ. (B) 20214r Q Q επ+. (C) 2024r Q επ. (D) 20124rQ Q επ-. [ ]81、(1493B25)如图所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面均匀带电,沿轴线方向单位长度上所带电荷分别为λ1和λ2,则在内圆柱面里面、距离轴线为r 处的P 点的电场强度大小E 为:(A) r0212ελλπ+. (B) 20210122R R ελελπ+π(C)1012R ελπ. (D) 0.] 82、(1494A20)如图所示,两个“无限长”的、半径分别为R 1和R 2的共轴圆柱面,均匀带电,沿轴线方向单位长度上的所带电荷分别为λ1和λ2,则在外圆柱面外面、距离轴线为r处的P 点的电场强度大小E 为:(A) r 0212ελλπ+.(B)()()20210122R r R r -π+-πελελ.(C) ()20212R r -π+ελλ.(D)20210122R R ελελπ+π. [ ] 83、(1495B25)如图所示,两个“无限长”的共轴圆柱面,半径分别为R 1和R 2,其上均匀带电,沿轴线方向单位长度上所带电荷分别为λ1和λ2,则在两圆柱面之间、距离轴线为r 的P 点处的场强大小E 为:(A) r012ελπ. (B) r 0212ελλπ+.(C)()r R -π2022ελ. (D)()1012R r -πελ.[ ] 84、(1561B25)图中所示为一球对称性静电场的E ~r 曲线,请指出该电场是由下列哪一种带电体产生的(E 表示电场强度的大小,r 表示离对称中心的距离).(A) 均匀带电球面; (B) 均匀带电球体; (C) 点电荷; (D) 不均匀带电球面.[ ]E85、(1562B25) 图中所示曲线表示某种球对称性静电场的场强大小E随径向距离r 变化的关系,请指出该电场是由下列哪一种带电体产生的.(A) 半径为R 的均匀带电球面;(B) 半径为R 的均匀带电球体;(C) 点电荷;(D) 外半径为R ,内半径为R / 2的均匀带电球壳体. [ ] 86、(1563B25) 图中所示为轴对称性静电场的E ~r 曲线,请指出该电场是由下列哪一种带电体产生的(E 表示电场强度的大小,r 表示离对称轴的距离).(A) “无限长”均匀带电圆柱面; (B) “无限长”均匀带电圆柱体; (C) “无限长”均匀带电直线;(D) “有限长”均匀带电直线. [ ] 87、(1564B25) 图示为一轴对称性静电场的E ~r 关系曲线,请指出该电场是由哪种带电体产生的(E 表示电场强度的大小,r 表示离对称轴的距离).(A) “无限长”均匀带电直线; (B) “无限长”均匀带电圆柱体(半径为R );(C) “无限长”均匀带电圆柱面(半径为R );(D) 有限长均匀带电圆柱面(半径为R ). [ ]88、(5083B25)若匀强电场的场强为E ,其方向平行于半径为R 的半球面的轴,如图所示.则通过此半球面的电场强度通量Φe为(A) E R 2π (B) E R 22π(C) E R 221π (D) E R 22π(E) 2/2E R π [ ] 89、(5084A20) A 和B 为两个均匀带电球体,A 带电荷+q ,B带电荷-q ,作一与A 同心的球面S 为高斯面,如图所示.则 (A) 通过S 面的电场强度通量为零,S 面上 各点的场强为零.(B) 通过S 面的电场强度通量为q / ε0,S 面上场强的大小为20π4r qE ε=.(C) 通过S 面的电场强度通量为(- q ) / ε0,S 面上场强的大小为20π4rqE ε=. (D) 通过S 面的电场强度通量为q / ε0,但S 面上各点的场强不能直接由高斯定理求出. [ ]E EE90、(5272A15)在空间有一非均匀电场,其电场线分布如图所示.在电场中作一半径为R 的闭合球面S ,已知通过球面上某一面元∆S 的电场强度通量为∆Φe ,则通过该球面其余部分的电场强度通量为 (A) - ∆Φe . (B)e SR Φ∆∆π24. (C)e SS R Φ∆∆∆-π24. (D) 0. [ ] 91、(1514B25)如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带有电荷Q 2.设无穷远处为电势零点,则在内球面之内、距离球心为r 处的P 点的电势U 为: (A) rQ Q 0214επ+. (B) 20210144R Q R Q εεπ+π. (C) 0. (D) 1014R Q επ.[ ]92、(1515B25)如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带电荷Q 2 .设无穷远处为电势零点,则在外球面之外距离球心为r 处的P 点的电势U 为:(A) r Q Q 0214επ+ (B) 20214R Q Q επ+(C) 20210144R Q R Q εεπ+π (D) rQ 024επ [ ]93、(1516B25) 如图所示,两个同心的均匀带电球面,内球面半径为R 1、带电荷Q 1,外球面半径为R 2、带电荷Q 2 .设无穷远处为电势零点,则在两个球面之间、距离球心为r 处的P 点的电势U 为:(B) rQ Q 0214επ+ (B)20210144R Q R Q εεπ+π (C)2020144R Q r Q εεπ+π (D) rQ R Q 0210144εεπ+π [ ] 94、(1581A20) 图中所示为一球对称性静电场的电势分布曲线,r 表示离对称中心的距离.请指出该电场是由下列哪一种带电体产生的.(A) 半径为R 的均匀带正电球面.(B) 半径为R的均匀带正电球体.(C) 正点电荷.(D) 负点电荷. [ ] 95、(1582A20) 图中所示为一球对称性静电场的电势分布曲线,r 表示离对称中心的距离.请指出该电场是由下列哪一种带电体产生的. (A) 半径为R 的均匀带负电球面. (B) 半径为R 的均匀带负电球体. (C) 正点电荷.(D) 负点电荷. [ ] 96、(1584A20)一半径为R 的均匀带电球面,带有电荷Q .若规定该球面上的电势值为零,则无限远处的电势将等于(A) R Q0π4ε. (B) 0.(C) RQ0π4ε-. (D) ∞. [ ]97、(1634B25)图中所示曲线表示球对称或轴对称静电场的某一物理量随径向距离r 变化的关系,该曲线所描述的是(E 为电场强度的大小,U 为电势)(A) 半径为R 的无限长均匀带电圆柱体电场的E~r 关 系. (B) 半径为R 的无限长均匀带电圆柱面电场的E~r 关系.(C) 半径为R 的均匀带正电球面电场的U~r 关系.(D) 半径为R 的均匀带正电球体电场的U~r 关系.] 98、(1635B25)真空中一半径为R 的球面均匀带电Q ,在球心O 处有一电荷为q 的点电荷,如图所示.设无穷远处为电势零点,则在球内离球心O 距离为r 的P 点处的电势为(A) r q04επ (B) ⎪⎭⎫ ⎝⎛+πR Q r q 041ε.(C) r Qq 04επ+ (D) ⎪⎭⎫ ⎝⎛-+πR q Q r q 041ε. [ ]99、(1505A10) 如图所示,直线MN 长为2l ,弧OCD 是以N点为中心,l 为半径的半圆弧,N 点有正电荷+q ,M 点有负电荷-q .今将一试验电荷+q 0从O 点出发沿路径OCDP 移到无穷远处,设无穷远处电势为零,则电场力作功(A) A <0 , 且为有限常量. (B) A >0 ,且为有限常量.(C) A =∞. (D) A =0. [ ]-。
7.真空中的静电场 大学物理习题答案
l
xd x
2
k l a ( ln ) 4 0 a la
方向沿 x 轴正向。
7-4 一半径为 R 的绝缘半圆形细棒,其上半段均匀带电量+q,下半段均匀带电量-q,如图 7-4 所示,求半 圆中心处电场强度。 解:建立如图所示的坐标系,由对称性可知,+q 和-q 在 O 点电场强度沿 x 轴的分量之和为零。取长为 dl 的线元,其上所带电量为
大学物理练习册—真空中的静电场
库仑定律 7-1 把总电荷电量为 Q 的同一种电荷分成两部分, 一部分均匀分布在地球上, 另一部分均匀分布在月球上, 24 使它们之间的库仑力正好抵消万有引力, 已知地球的质量 M=5.98l0 kg, 月球的质量 m=7.34l022kg。 (1)求 Q 的最小值; (2)如果电荷分配与质量成正比,求 Q 的值。 解: (1)设 Q 分成 q1、q2 两部分,根据题意有 k
x
d 时 2
1 E d S 2 E1S 2 xS , E1 x 1 S 0 0
28
大学物理练习册—真空中的静电场
x
d 时 2
1 d d E d S S 2 2 E 2 S 0 2 2 S , E 2 0
r R sin , x R cos
x
d E
sin cos d 2 0
因为球面上所有环带在 O 处产生的电场强度方向相同, E 2 0
2 0
sin cos d i i 4 0
7-6 一无限大均匀带电薄平板,面电荷密度为 ,平板中部有一半径为 R 的圆孔, 如图 7-6 所示。求圆孔 中心轴线上的场强分布。 (提示:利用无穷大板和圆盘的电场及场强叠加原理) 解:利用补偿法,将圆孔看作由等量的正、负电荷重叠而成,即等效为一个 完整的带电无穷大平板和一个电荷面密度相反的圆盘叠加而成。 R 无穷大平板的电场为
大学物理第7章真空中的静电场答案解析
第七章 真空中的静电场7-1 在边长为a 的正方形的四角,依次放置点电荷q,2q,-4q 和2q ,它的几何中心放置一个单位正电荷,求这个电荷受力的大小和方向。
解:如图可看出两2q 的电荷对单位正电荷的在作用力 将相互抵消,单位正电荷所受的力为)41()22(420+=a q F πε=,2520aqπε方向由q 指向-4q 。
7-2 如图,均匀带电细棒,长为L ,电荷线密度为λ。
(1)求棒的延长线上任一点P 的场强;(2)求通过棒的端点与棒垂直上任一点Q 的场强。
解:(1)如图7-2 图a ,在细棒上任取电荷元dq ,建立如图坐标,dq =λd ξ,设棒的延长线上任一点P 与坐标原点0的距离为x ,则2020)(4)(4ξπεξλξπεξλ-=-=x d x d dE则整根细棒在P 点产生的电场强度的大小为)11(4)(40020xL x x d E L--=-=⎰πελξξπελ=)(40L x x L-πελ方向沿ξ轴正向。
(2)如图7-2 图b ,设通过棒的端点与棒垂直上任一点Q 与坐标原点0的距离为y习题7-1图0 dqξd ξ习题7-2 图a204r dxdE πελ=θπελcos 420rdxdE y =, θπελsin 420r dxdE x =因θθθθcos ,cos ,2yr d y dx ytg x ===, 代入上式,则)cos 1(400θπελ--=y =)11(4220Ly y+--πελ,方向沿x 轴负向。
θθπελθd ydE E y y ⎰⎰==000cos 4 00sin 4θπελy ==2204Ly y L+πελ7-3 一细棒弯成半径为R 的半圆形,均匀分布有电荷q ,求半圆中心O 处的场强。
解:如图,在半环上任取d l =Rd θ的线元,其上所带的电荷为dq=λRd θ。
对称分析E y =0。
θπεθλsin 420RRd dE x =⎰⎰==πθπελ00sin 4RdE E x R02πελ= θθπελθd y dE E x x ⎰⎰-=-=0sin 4xdx习题7-2 图byx习题7-3图2022R q επ=,如图,方向沿x 轴正向。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第九章 真空中的静电场
一、选择题
⒈ C ; ⒉B ;⒊ C ; ⒋ B ; ⒌ B ; 6.C ; 7.E ; 8.A,D ; 9.B ;10. B,D 二、填空题 ⒈
2
3
08qb R
πε,缺口。
⒉ 0
q
ε,< ;
⒊ 半径为R 的均匀带电球面(或带电导体球); ⒋ 12
21
E E h h ε--; 2.21⨯10-12C/m 3; ⒌ 100N/C ;-8.85×10-9C/m 2 ; ⒍ -135V ; 45V ; ⒎
006q Q R πε;0;006q Q R πε- ;006q Q
R
πε ; ⒏ 1
2
22
04()
q x R πε+;
32
22
04()
qx x R πε+
;
2
R ;432.5 V/m ; 9.有源场;无旋场 (注意不能答作“保守场”,保守场是针对保守力做功讲的)。
三、 问答题
1. 答: 电场强度0E F q =r r
是从力的角度对电场分布进行的描述,它给出了一个矢量场分布的图像;而电势V =W /q 是从能量和功的角度对电场分布进行的描述,它给出了一个标量场分布的图像。
空间任意一点的电场强度和该点的电势之间并没有一对一的关系。
二者的关系是:
"0"p d grad ,d d P
V
E V V E l n =-=-=⋅⎰r r r 。
即空间任一点的场强和该点附近电势的空间变化率相联
系;空间任一点的电势和该点到电势零点的整个空间的场强分布相联系。
由于电场强度是矢量,利用场叠加原理计算时,应先将各电荷元产生的电场按方向进行分解,最后再合成,即:
d d d d ;x y z E E i E j E k =++r r r r
, d ,d ,d x x y y z z E E E E E E ===⎰⎰⎰
而电势是标量可以直接叠加,即:V dV =⎰。
但用这种方法求电势时,应注意电势零点的选择。
四、计算与证明题
1. 证:①根据对称性分析,两段带电直线各自在O 点的电场强度大小相等,方向相反,相互抵消,所以只计算带电细线半圆形部分的电场。
取电荷元d q =λd l ,设d E 和y 轴夹角为θ,其大小为:
d E =
根据其对称性有:E x =0;θπελ
θπελd cos 4cos 4d d 020a
a l E y ==
(如果设d E 和x 轴夹角为θ,那么上面表达式中的cos θ1要变成sin θ)
a a E y 0/2/202d cos 4πελθθπελππ==⎰-, j a
E ϖ
ϖ02πελ=
②设带电直线上电荷元d q =λd l 到O 点的距离为l ,则其在O 点的电势为:
l l U 014d d πελ=, 2ln 4d 40
201πελπελ==
⎰a a l l U 半圆形带电细线上任一电荷元在O 点的电势为:
a l U 024d d πελ=,0
0014d 4πελππελπ==⎰a l a U
两段带电直线在O 点的电势相同,故O 点电势为: )2ln 2(40
21ππελ
+=+=U U U 得证。
2. 解:①根据对称性,选半径为r 的同心球面为高斯面,则由高斯定理有:
2S
4d d επ∑⎰⎰⎰⎰=
==⋅q Er s E S E ϖ
ϖ,
当r <R: ∑==Q R
r r q 33334πρ, 于是:304R Qr
E πε=内
当r >R:
∑=Q q , 于是:2
04r Q E πε=
外
②选无穷远点位电势零点。
则球内任一点电势为:
⎰⎰⎰∞
∞⋅+⋅=⋅=R
r
r
d d d r E r E r E U R 外内内ϖϖ
R
Q r R R Q r r Q r r R Qr R
r
R r 02
23020
304)(8d 4d 4πεπεπεπε+-=+
=
⎰
⎰ r
E
R
球外一点电势:r Q r r Q r E r E U r r 0
2
r
4d d d πε=⋅=⋅=⋅=⎰⎰⎰
∞∞∞
外外ϖϖ
图:
③同样根据对称性,选半径为r 的同心球面为高斯面,则由高斯定理有:
2
S
4d d επ∑⎰⎰
⎰⎰===⋅q Er s E S E ϖϖ,
当r <R ,在高斯面内作一半径r '厚度dr '的同心薄球壳,薄球壳带电量为
r r r R Q r q '''
='=d 41
2d )(d 22
ππυρ, 高斯面内总电量2202d 2d )(r R
Q
r r R Q V r q r V =''='=⎰∑⎰ρ
于是:2
04R
Q E πε=内
得证。
3. 解:①两个球面将空间分为三个区域,据高斯定理, 在Ⅰ区:0<r <R 1,10E =;在Ⅱ区:R 1<r <R 2,22
04q E r πε=
;
在Ⅲ区: r >R 2,32
04Q q
E r
πε+=
;则所求电势分别为: 3304r
Q q
V E dr r
πε∞
+==
⎰,024Q q V R πε+==外;
② 2
2
223002
44R r
R q Q V E dr E dr r R πεπε∞
=
+=
+
⎰⎰,020144q q V V
R R πεπε∆=-
;
③ 2
1
2
12301
02
44R R R q
Q V E dr E dr R R πεπε∞
=
+=
+
⎰⎰,0102
44q
Q
V R R πεπε=
+
内
r
R
④ 2
01
02
1
044R q Q V Q q R R R πεπε=+
==-
内由,得 。
五、附加题
1. 解:在半球的下部再对称地补充一个半球,根据高斯定理, 球内电场强度为零。
如果圆形底面上一点电场强度不垂直于底面, 那么如图,上下半球面电场强度叠加将不为零,与前述结论矛盾。
故,半球底面上任何一点电场强度垂直于底面。
2. 解:在细杆上取电荷元 d q=λd x (1)球面电荷在线单元d x 处的电场:
2
0π4x q E ε=
电荷元受到的电场力为
2
0π4d d x x q F ελ=
整根线受到的力:
)11(π4d π4d 020
l
a a q x x q F F l
a a
+-===⎰
⎰+ελελ 力的方向沿x 轴正方向。
(2)电荷元在球面电荷电场中的电势能为:
x x
q
W e d π4d 0λε=
整根线在该场中的总电势能为:
a
l a q x x q W W l
a a
e e +==
=⎰
⎰+ln π4d π4d 00
ελελ。
