初中数学专题复习——求阴影面积的常用方法
初中数学专题辅导：阴影面积求法9种方法(不规则图形)
阴影面积求法阴影部分的图形一般是不规则图形或没有可直接利用的公式，因此，同学们常感到困难。
本文指出：求解这类问题的关键是将阴影部分图形转化为可求解的规则图形的组合。
如何转化呢?这里给出常用的9种转化方法。
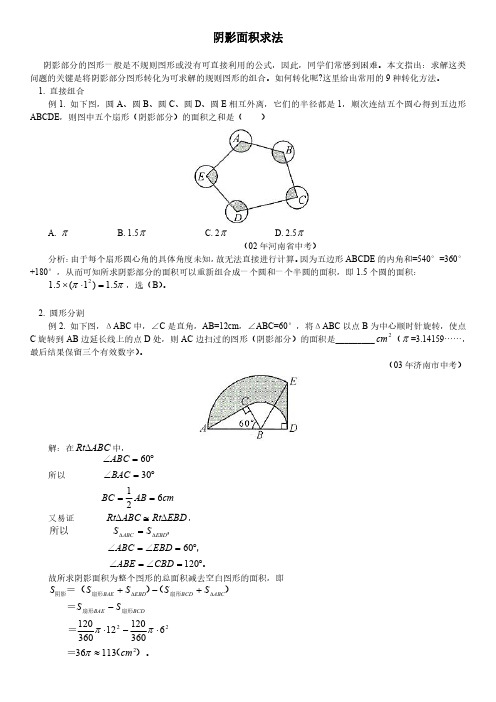
1.直接组合例1.如下图，圆A 、圆B 、圆C 、圆D 、圆E 相互外离，它们的半径都是1，顺次连结五个圆心得到五边形ABCDE ，则图中五个扇形（阴影部分）的面积之和是（）A.π B.1.5π C.2πD.2.5π（02年河南省中考）分析：由于每个扇形圆心角的具体角度未知，故无法直接进行计算。
因为五边形ABCDE 的内角和=540°=360°+180°，从而可知所求阴影部分的面积可以重新组合成一个圆和一个半圆的面积，即1.5个圆的面积：ππ5.1)1(5.12=⋅⨯，选（B ）。
2.圆形分割例2.如下图，ΔABC 中，∠C 是直角，AB=12cm ，∠ABC=60°，将ΔABC 以点B 为中心顺时针旋转，使点C 旋转到AB 边延长线上的点D 处，则AC 边扫过的图形（阴影部分）的面积是_________2cm （π=3.14159……，最后结果保留三个有效数字）。
（03年济南市中考）解：在ABC Rt ∆中，所以cm AB BC BAC ABC 6213060==︒=∠︒=∠又易证EBD Rt ABC Rt ∆≅∆，。
，，所以︒=∠=∠︒=∠=∠=∆∆12060CBD ABE EBD ABC S S EBD ABC 故所求阴影面积为整个图形的总面积减去空白图形的面积，即）。
（＝＝＝）（）＝（扇形扇形扇形扇形阴影22211336636012012360120cm S S S S S S S BCDBAE ABC BCD EBD BAE ≈⋅-⋅-+-+∆∆πππ3.平移例3.如下图，矩形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为________________。
求阴影部分面积的几种常用方法
求阴影部分面积的几种常用方法阴影部分面积的计算是许多科学，工程和设计领域中常见的问题。
以下是几种常用的方法：1.基于几何模型的计算：这种方法适用于简单的阴影形状和物体表面。
可以通过几何关系和公式来计算阴影部分的面积。
例如，如果阴影形状是矩形或圆形，可以计算出其面积并减去被遮挡的部分。
对于其他形状，可以尝试将其近似为几何图形，然后计算阴影部分的面积。
2.基于光线投射的计算：这种方法基于光的直线传播特性。
通过确定光源的位置和阴影对象的形状，并追踪光线的路径，可以计算出阴影部分的面积。
这可以通过数值方法，如光线追踪算法，来实现。
光线追踪算法通过逐个追踪光线，计算出光线与物体的交点，并对光照强度进行积分来生成图像。
通过分析生成的图像，可以确定阴影部分的面积。
3.基于遮挡关系的计算：这种方法基于阴影对象和背景之间的遮挡关系。
可以使用二维图像处理算法，如阈值分割和连通区域分析，来分析图像中的遮挡关系。
首先，需要在图像中分割出阴影对象和背景，并标记出遮挡的区域。
然后，通过计算遮挡区域的像素数或像素面积，就可以得到阴影部分的面积。
这种方法适用于基于摄像机或传感器捕获的实时图像数据。
4.基于数值积分的计算：这种方法使用数值积分技术来计算阴影部分的面积。
数值积分是一种数值近似方法，用于计算曲线下的面积或曲线之间的面积。
可以将阴影形状建模为二维或三维曲线，然后使用数值积分算法，如拉格朗日插值法或梯形法则，来计算阴影部分的面积。
这种方法在精确模型或复杂阴影场景的计算中比较有效。
总之，根据具体情况和问题，可以选择不同的方法来计算阴影部分的面积。
这些方法可以根据问题的复杂性、可用数据和计算资源的限制来选择。
对于简单的几何形状和光线传播特性明确的场景，基于几何模型或光线投射的方法可能更为适用。
对于实时图像数据或复杂阴影场景，基于遮挡关系或数值积分的方法可能更为合适。
(完整版)求阴影部分面积的几种常用方法
总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有：一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，下图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，下图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它就是一个底是2、高是4的三角形，其面积直接可求为|：四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求下图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了.五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如下图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便.六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如下图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如，如下图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。
八、旋转法：这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如，欲求下图（1）中阴影部分的面积，可将左半图形绕B 点逆时针方向旋转180°，使A与C 重合，从而构成如右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如，欲求下图中阴影部分的面积，沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
阴影部分面积的求法
阴影部分面积的求法
1.矩形法：当阴影部分与原图形为矩形相交时，可通过计算阴影矩形的面积来求得阴影部分面积。
2. 几何图形分解法：当阴影部分与原图形为多边形相交时，可将其分解为若干个几何图形，再对各个图形进行面积计算后相加得到阴影部分的面积。
3. 分割法：当阴影部分与原图形为曲线相交时，可通过将原图形分割为若干小块，再对每个小块内的阴影部分进行面积计算后相加得到阴影部分的面积。
4. 积分法：当阴影部分为较为复杂的形状时，可通过积分计算得到其面积。
这种方法需要一定的数学基础和计算能力。
需要注意的是，在进行阴影部分面积的求解时，需要注意精度问题，特别是在使用积分法时更为重要。
同时，在进行计算时也要注意单位的一致性，以避免出现计算错误。
- 1 -。
(完整版)求阴影部分面积的几种常用方法
总结：对于不规则图形面积的计算问题一般将它转化为若干基本规则图形的组合，分析整体与部分的和、差关系，问题便得到解决.常用的基本方法有：一、相加法：这种方法是将不规则图形分解转化成几个基本规则图形，分别计算它们的面积，然后相加求出整个图形的面积.例如，下图中，要求整个图形的面积，只要先求出上面半圆的面积，再求出下面正方形的面积，然后把它们相加就可以了.二、相减法：这种方法是将所求的不规则图形的面积看成是若干个基本规则图形的面积之差.例如，下图，若求阴影部分的面积，只需先求出正方形面积再减去里面圆的面积即可.三、直接求法：这种方法是根据已知条件，从整体出发直接求出不规则图形面积.如下页右上图，欲求阴影部分的面积，通过分析发现它就是一个底是2、高是4的三角形，其面积直接可求为|：四、重新组合法：这种方法是将不规则图形拆开，根据具体情况和计算上的需要，重新组合成一个新的图形，设法求出这个新图形面积即可.例如，欲求下图中阴影部分面积，可以把它拆开使阴影部分分布在正方形的4个角处，这时采用相减法就可求出其面积了.五、辅助线法：这种方法是根据具体情况在图形中添一条或若干条辅助线，使不规则图形转化成若干个基本规则图形，然后再采用相加、相减法解决即可.如下图，求两个正方形中阴影部分的面积.此题虽然可以用相减法解决，但不如添加一条辅助线后用直接法作更简便.六、割补法：这种方法是把原图形的一部分切割下来补在图形中的另一部分使之成为基本规则图形，从而使问题得到解决.例如，如下图，欲求阴影部分的面积，只需把右边弓形切割下来补在左边，这样整个阴影部分面积恰是正方形面积的一半.七、平移法：这种方法是将图形中某一部分切割下来平行移动到一恰当位置，使之组合成一个新的基本规则图形，便于求出面积.例如，如下图，欲求阴影部分面积，可先沿中间切开把左边正方形内的阴影部分平行移到右边正方形内，这样整个阴影部分恰是一个正方形。
八、旋转法：这种方法是将图形中某一部分切割下来之后，使之沿某一点或某一轴旋转一定角度贴补在另一图形的一侧，从而组合成一个新的基本规则的图形，便于求出面积.例如，欲求下图（1）中阴影部分的面积，可将左半图形绕B 点逆时针方向旋转180°，使A与C 重合，从而构成如右图（2）的样子，此时阴影部分的面积可以看成半圆面积减去中间等腰直角三角形的面积.九、对称添补法：这种方法是作出原图形的对称图形，从而得到一个新的基本规则图形.原来图形面积就是这个新图形面积的一半.例如，欲求下图中阴影部分的面积，沿AB在原图下方作关于AB为对称轴的对称扇形ABD.弓形CBD的面积的一半就是所求阴影部分的面积。
初中数学学法指导：求阴影部分面积的三种方法(由圆、扇形、三角形、四边形等组成的图形面积)
初中数学学法指导：求阴影部分面积的三种方法求阴影部分的面积，在近几年中考题中，形成一个新的热点，在计算由圆、扇形、三角形、四边形等组成的图形面积时，要注意观察和分析图形，学会分解和组合图形，明确要计算图形的面积，可以通过哪些图形的和或差得到，切勿盲目计算。
现举例谈谈三种主要的方法：一. 和差法和差法是指不改变图形的位置，而将它的面积用规则图形的面积的和或差表示，经过计算后即得所求图形面积。
例1. 如图1所示，半径OA=2cm ，圆心角为90°的扇形AOB 中，C 为AB 的中点，D 为OB 的中点，求阴影部分的面积。
解：连结OC ，过点C 作CE ⊥OB 于E 。
因为C 为AB 的中点，所以 ∠BOC=︒=∠45AOB 21，所以CE=OC ·sin45°=cm 2。
所以22COB cm 2360245S ππ=⨯=扇形 2COD cm 22222121CE OD 21S =⨯⨯⨯=⨯=∆ 所以))(cm 222(S S S 2COD COB -=-=∆π扇形阴影点拨：不要将图形CBD 当作扇形计算，对于不规则图形的面积的计算问题，通常是经过适当的几何变换，把不规则的图形面积求解问题转化为规则图形面积的求解。
二. 移动法移动法是指将图形的位置进行移动，以便为使用和差法提供条件。
具体方法有：平移、旋转、割补、等积变换等。
例2. 如图2所示，AB 是半圆的直径，AB=2R ，C 、D 为半圆的三等分点，求阴影部分的面积。
解：连结OC 、OD 。
因为AC=BD ，所以∠CDA=∠DAB ，所以CD//AB所以COD S S 扇形阴影= 又因为∠COD=︒=∠60AOB 31所以222COD R 61360R 60360R n S S πππ====扇形阴影点拨：此阴影部分为不规则图形，可应用等积方法，转化为规则图形——扇形COD 。
例3. 某种商品的商标图案如图3所示（阴影部分），已知菱形ABCD 的边长为4，︒=∠60A ，BD 是以A 为圆心，AB 长为半径的弧，CD 是以B 为圆心，BC 长为半径的弧，求商标图案的面积。
初中数学求几何阴影面积解法
初中数学求几何阴影面积解法一、公式法这属于最简单的方法，阴影面积是一个常规的几何图形，例如三角形、正方形等等。
简单举出2个例子：二、和差法攻略一直接和差法这类题目也比较简单，属于一目了然的题目。
只需学生用两个或多个常见的几何图形面积进行加减。
攻略二构造和差法从这里开始，学生就要构建自己的数学图形转化思维了，学会通过添加辅助线进行求解。
三、割补法割补法，是学生拥有比较强的转化能力后才能轻松运用的，否则学生看到这样的题目还是会无从下手。
尤其适用于直接求面积较复杂或无法计算时，通过对图形的平移、旋转、割补等，为利用公式法或和差法求解创造条件。
攻略一全等法训练题：1.如图所示：在正方形ABCD中，红色、绿色正方形的面积分别为52和12，且红绿两个正方形有一个顶点重合。
黄色正方形的一个顶点位于红色正方形两条对角线的交点，另一个顶点位于绿色正方形两条对角线的交点。
求黄色正方形的面积。
2.如图是一个大正方形和一个小正方形拼成的图形，已知小正方形的边长是6厘米，阴影部分的面积是66平方厘米，则空白部分的面积是多少？3.一个长方形被两条直线分成四个长方形，其中三个的面积分别是12平方厘米，8平方厘米，20平方厘米，求整个长方形的面积。
4.大正六边形的面积是720平方厘米，阴影部分是一个小正六边形，它的面积是____平方厘米。
（A）360（B）240（C）180（D）1205.如图，在两个半圆中，大圆的弦MN与小圆相切于点D，MN∥AB，MN＝a，ON、CD分别是两圆的半径，求阴影部分的面积。
6.如图，A是半径为2的⊙O外一点，OA＝4，AB是⊙O的切线，点B是切点，弦BC∥OA，连结AC，求图中阴影部分的面积。
初中数学阴影面积计算方法讲解
初中数学阴影面积计算方法讲解阴影面积是指在光照、光线等因素影响下，物体表面未被直接照射到的面积部分。
在初中数学中，我们可以通过一些基本的几何知识和方法计算阴影面积。
下面就介绍一下初中数学中常见的几种阴影面积计算方法。
一、计算矩形阴影面积：```A，—BC，—D```在光线OA和OC照射下，阴影面积为ADCB区域。
矩形的阴影面积计算方法为：阴影面积=矩形面积-三角形面积其中，矩形面积为AB * BC，三角形面积可通过以下公式计算：三角形面积 = 1/2 * BC * heightheight为光线OC到AB的距离，可以通过相似三角形的比例关系计算得到：height = (OC / OA) * BC将得到的height代入三角形面积公式，即可计算出阴影面积。
二、计算三角形阴影面积：```A\C，—B```在光线OA和OC照射下，阴影面积为ACB区域。
三角形的阴影面积计算方法为：阴影面积=三角形面积-三个小三角形面积之和其中，三角形面积可以通过以下公式计算：三角形面积=1/2*AC*BC 小三角形面积为：1/2 * AC * height_ACO + 1/2 * BC *height_BCO + 1/2 * AB * height_ABOheight_ACO、height_BCO和height_ABO分别为光线OC到AC、BC、AB的距离，可以通过相似三角形的比例关系计算得到。
将得到的三角形面积和小三角形面积相减，即可计算出阴影面积。
三、计算圆形阴影面积：```O/\/\A，—C\/\/在光线OA和OC照射下，阴影面积为ACO区域。
圆形的阴影面积计算方法为：阴影面积=圆形面积-扇形面积其中，圆形面积为π*r*r，扇形面积可通过以下公式计算：扇形面积=1/2*扇形的弧长*r扇形的弧长可以通过扇形角的度数和圆的周长计算得到：扇形的弧长=(扇形角的度数/360)*2*π*r将得到的扇形的弧长代入扇形面积公式，即可计算出阴影面积。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
初中数学专题复习——求阴影面积的常用方法
计算平面图形的面积问题是常见题型，求平面阴影部分的面积是这类问题的难点。
不规则阴影面积常常由三角形、四边形、弓形、扇形和圆、圆弧等基本图形组合而成的，在解此类问题时，要注意观察和分析图形，会分解和组合图形。
介绍几种常用的方法。
1.转化法
此法就是通过等积变换、平移、旋转、割补等方法将不规则的图形转化成面积相等的规则图形，再利用规则图形的面积公式，计算出所求的不规则图形的面积。
例1. 如图1，点C、D是以AB为直径的半圆O上的三等分点，AB=12，则图
中由弦AC、AD和围成的阴影部分图形的面积为_________。
2.和差法
有一些图形结构复杂，通过观察，分析出不规则图形的面积是由哪些规则图形组合而成的，再利用这些规则图形的面积的和或差来求，从而达到化繁为简的目的。
例2. 如图3是一个商标的设计图案，AB=2BC=8，为圆，求阴影部分面积。
3.重叠法
就是把所求阴影部分的面积问题转化为可求面积的规则图形的重叠部分的方法。
这类题阴影一般是由几个图形叠加而成。
要准确认清其结构，理顺图形间的大小关系。
例3. 如图4，正方形的边长为a，以各边为直径在正方形内作半圆，求所围成阴影部分图形的面积。
4.补形法
将不规则图形补成特殊图形，利用特殊图形的面积求出原不规则图形的面积。
例4. 如图5，在四边形ABCD中，AB=2，CD=1，，求四边形ABCD所在阴影部分的面积。
5.拼接法
例5. 如图6，在一块长为a、宽为b的矩形草地上，有一条弯曲的柏油小路（小路任何地方的水平宽都是c个单位），求阴影部分草地的面积。
6.特殊位置法
例6. 如图8，已知两个半圆中长为4的弦AB与直径CD平行，且与小半圆相切，那么图中阴影部分的面积等于__________。
7.代数法
将图形按形状、大小分类，并设其面积为未知数，通过
建立方程或方程组来解出阴影部分面积的方法。
例7. 如图10，正方形的边长为a，分别以两个对角顶点为圆心、以a为半径画弧，求图中阴影部分的面积。
需要说明的是，在求阴影部分图形的面积问题时，要具体问题具体分析，从而选取一种合理、简捷的方法。
跟踪练习：
1.如图11，正方形的边长为1，以CD为直径在正方形内画半圆，再以点C 为圆心、1为半径画弧BD，则图中阴影部分的面积为___________。
2.如图，A、B、C、D是圆周上的四点，且AB＋CD＝AD＋BC，如果弦AB的长为8，弦CD的长为4，那么图中两个弓形(阴影部分)的面积和是。
(π取3)
3.如图，在两个同心圆中，P是大圆上任一点，PA切小圆于点A，设PA＝4，则图中阴影部分面积是。
4.如图，在矩形ABCD中，AB＝1，AD＝，以BC的中点E为圆心的MPN与AD
相切于P，则图中阴影部分的面积为( )(A)
3
2π(B)
3π (C)
4
3π (D)
3
π
5.如图，四个正方形的边长都相等，其中阴影部分面积相等的图形个数是( )
（A）0；（B）2；（C）3；（D）
4。
6.如图，设计一个商标图案(如图阴影部分
2BC，且AB＝8cm，以点为圆心，AD2.
D
C D
A
C
B E
M N
7.如图，⊙O 半径为2cm ，直径AB 垂直于直径CD ，以B 为圆
心，BC 的长为半径作CED ，则CED 与CAD 所围成的阴影部分的面积是 ；
8.矩形ABCD 的长、宽分别为5和3，将顶点C 折过来，使它落在AB 上的C /点(DE 为折痕)，那么阴影部分的面积是 ；
9.如图，将边长为1的正方形ABCD 绕A 点按逆时针方向旋转600，得正方形A /B /C /D /，则旋转前后两个正方形重叠部分的面积是 。
B
D
C
B
D
E。