2019安徽中考数学专题训练——规律探索题
2019安徽中考数学专题训练——规律探索题 初高中知识衔接
初高中知识衔接1. 我们根据指数运算，得出了一种新的运算，下表是两种运算对应关系的一组实例：根据上表规律，某同学写出了三个式子：①log 216＝4，②log 525＝5，③log 212＝－1.其中正确的是( )A . ①②B . ①③C . ②③ D. ①②③B 【解析】①∵24＝16，∴log 216＝4，故①正确；②∵52＝25，∴log 525＝2≠5，故②不正确；③∵2－1＝12，∴log 212＝－1，故③正确；应选B .2.阅读理解：如图①，在平面内选一定点O ，引一条有方向的射线Ox ，再选定一个单位长度，那么平面上任一点M 的位置可由MOx 的度数θ与OM 的长度m 确定，有序数对（θ，m ）称为M 点的“极坐标”，这样建立的坐标系称为“极坐标系”.应用：在图②的极坐标系下，如果正六边形的边长为2，有一边OA 在射线Ox上，则正六边形的顶点C的极坐标应记为（ ） A .（60°，4） B .（45°，4） C .（60°，22） D .（50°，22）图① 图②第2题图A 【解析】如解图，连接AC ，∵正六边形的每个内角为120°，∴∠AOC =60°，AC ⊥OA ，∴∠ACO =30°，根据直角三角形中，30°角所对的直角边等于斜边的一半得：OC =2OA =4，∴六边形的顶点C 的极坐标应记为（60°，4），故应选A .第2题解图3.阅读理解题：定义：如果一个数的平方等于-1，记为i 2=-1①，这个数i 叫做虚数单位，那么和我们所学的实数对应起来就叫做复数，表示为a +b i （a ,b 为实数），a 叫这个复数的实部，b 叫做这个复数的虚部.如果只把i 当成代数，则i 将符合一切实数运算规则，但要根据①式变通来简便运算.（不要把复数当成高等数学，它只是一个小学就学过的代数而已！它的加、减、乘法运算与整式的加、减、乘法运算类似.） 例题1：i i i ⋅=23=i i -=⋅-1；1)1(34=--=⋅-=⋅=i i i i i ； 例题2 ：（2+i ）+（3-4i ）=（2+3）+（1-4）i =5-3i ;()()2432015435i i i i i -+-=-⨯+i i 171941715-=+-=;同样我们也可以化简i i 22)1(4422=⨯=-⨯=-，也可以解方程x 2=-1，解为x 1=i ，x 2=-i .读完这段文字，请你解答以下问题：（1）填空：i 5= ,i 6= ; （2）计算：（2+i ）2；（3）在复数范围内解方程：x 2-x +1=0. 解：（1）i ，-1;【解法提示】i 5=（i 2）2·i =i ，i 6=（i 2）3=-1. （2）原式=4+4i +i 2=4i +4-1=3+4i ; （3）x 2-x +1=0，12114)1()1(2⨯⨯⨯--±--=x 2312312ii ±=±=， 解得2311i x +=，2312ix -=.4. 阅读下面的材料：如果函数y ＝f (x )满足：对于自变量x 的取值范围内的任意x 1，x 2. (1)若x 1＜x 2，都有f (x 1)＜f (x 2)，则称f (x )是增函数： (2)若x 1＜x 2，都有f (x 1)＞f (x 2)，则称f (x )是减函数． 例题：证明函数f (x )＝2x (x ＞0)是减函数． 证明：假设x 1＜x 2，x 1＞0，x 2＞0，f (x 1)－f (x 2)＝2x 1－2x 2＝2x 2－2x 1x 1x 2＝2（x 2－x 1）x 1x 2，∵x 1＜x 2，且x 1＞0，x 2＞0， ∴x 2－x 1＞0，x 1x 2＞0，∴2（x 2－x 1）x 1x 2＞0，即f (x 1)－f (x 2)＞0，∴f (x 1)＞f (x 2)，∴函数f (x )＝2x (x ＞0)是减函数． 根据以上材料，解答下面的问题：(1)函数f (x )＝1x 2(x ＞0), f (1)＝112＝1, f (2)＝122＝14.计算， f (3)＝________，f (4)＝________，猜想f (x )＝1x 2(x ＞0)是________函数(填“增”或“减”)；(2)请仿照材料中的例题证明你的猜想． (1)解：19，116，减；【解法提示】∵f (x )＝1x 2(x ＞0)，f (1)＝211＝1，f (2)＝122＝14，∴f (3)＝132＝19，f (4)＝142＝116，∵19＞116， ∴猜想f (x )＝1x 2(x ＞0)是减函数.(2)证明：假设x 1＜x 2，且x 1＞0，x 2＞0，f (x 1)－f (x 2)＝1x 21－1x 22＝x 22－x 21x 21x 22＝()x 2－x 1()x 2＋x 1x 21x 22， ∵x 1＜x 2，且x 1＞0，x 2＞0，∴x 2－x 1＞0，x 2＋x 1＞0，x 21·x 22＞0，∴()x 2－x 1()x 2＋x 1x 21x 22＞0，即f (x 1)－f (x 2)＞0， ∴f (x 1)＞f (x 2)，∴f (x )＝1x 2(x ＞0)是减函数．5.阅读材料：各类方程的解法.（1）问题：方程0223=-+x x x 的解是01=x ，2x = ，3x = ； （2）拓展：用“转化”思想求方程x x =+32的解；（3）应用：如图，已知矩形草坪ABCD 的长AD =8 m ，宽AB =3 m ,小华把一根长为10 m 的绳子固定在点B ，沿草坪边沿BA 、AD 走到点P 处，把长绳PB 段拉直并固定在点P ，然后沿草坪边沿PD 、DC 走到点C 处，把长绳剩下的一段拉直，长绳的另一端恰好落在点C ，求AP 的长.第5题图解：（1）1，-2； （2） x x =+32， 两边平方，得232x x =+， 移项，得0322=--x x ，解此方程，得1,321-==x x ， ∵032≥+x ，∴23-≥x ， 当1-=x 时，1132-≠=+x ， 当3=x 时，3932==+x ， ∴原方程的根为3=x ；（3）设AP =x m ，∵AD =8 m ，∴PD =（8-x ）m ， 在Rt △ABP 中，PB = 22AB AP +=223+x =92+x m ， 在Rt △PCD 中，PC =22CD PD +=()2238+-x =73162+-x x m ， ∵PB =10-PC ，∴92+x =10-73162+-x x ，两边平方，化简得573162+-x x =41-4x ，再次两边平方，整理得到01682=+-x x ，即()042=-x ， 解得4=x ，经检验，4=x 满足题意. ∴AP 的长为4 m .6.请阅读以下材料：已知向量()11,y x a =，()22,y x b = 满足下列条件：①2121y x a += ，2222y x b += ；②b a ⊗=αcos b a ⨯（角α的取值范围是︒︒900＜α＜）；③b a⊗=2121y y x x +. 利用上述所给条件解答问题：如：已知()3,1=a，()3,3-=b ，求角α的大小.解：∵2121y x a +==()2231+=2，2222y x b += =()2233+-=23，∴b a ⊗=αcos b a⨯=2×23αcos =43αcos ， 又∵b a⊗=2121y y x x +=1×（-3）+3×3=23，∴32cos 34=α，∴21cos =α，∴α=60°， ∴角α的值为60°.请仿照以上解答过程，完成下列问题：已知()0,1=a，()1,1-=b ，求角α的大小. 解：∵()0,1=a，()1,1-=b ，∴2121y x a += =2201+=1，2222y x b += =()2211-+=2，∴b a ⊗=αcos b a⨯=1×2αcos =2αcos ， 又∵b a⊗=2121y y x x +=1×1+0×（-1）=1，∴1cos 2=α， ∴22cos =α，∴α=45°， ∴角α的值为45°.7.阅读材料：基本不等式2ba ab +≤（a ＞0，b ＞0），当且仅当a =b 时，等号成立.其中我们把2ba +叫做正数a 、b 的算术平均数，ab 叫做正数a 、b 的几何平均数，它是解决最大（小）值问题的有力工具.例如：在x ＞0的条件下，当x 为何值时，xx 1+有最小值，最小值是多少？ 解：∵x ＞0，x1＞0，∴xx x x 121⋅≥+，即x x 1+x x 12⋅≥， ∴xx 1+≥2，当且仅当x =x 1，即x =1时，x x 1+有最小值，最小值为2.请根据阅读材料解答下列问题：（1）若x ＞0，函数xx y 12+=，当x 为何值时，函数有最值，并求出其最值； （2）当x ＞0时，式子211122≥+++x x 成立吗？ 解：（1）∵x ＞0， ∴2x ＞0，x1＞0，∴xx x x 12212⋅≥+， 即2x +x1≥2 xx 12⋅，∴2x +x1≥22，当且仅当2x =x1，即x =22时，2x +x1有最小值，最小值为22； （2）不成立， 当且仅当11122+=+x x ，即x =0时等号才成立. ∵x ＞0， ∴不等式不成立.8. 在平面直角坐标系中，借助直角三角板可以找到一元二次方程的实数根．比如对于方程x 2－5x ＋2＝0，操作步骤是：第一步：根据方程的系数特征，确定一对固定点A (0，1)，B (5，2)；第二步：在坐标平面中移动一个直角三角板，使一条直角边恒过点A ，另一条直角边恒过点B ；第三步：在移动过程中，当三角板的直角顶点落在x 轴上点C 处时，点C 的横坐标m 即为该方程的一个实数根(如图①)；第四步：调整三角板直角顶点的位置，当它落在x 轴上另一点D 处时，点D 的横坐标n 即为该方程的另一个实数根．(1)在图②中，按照“第四步”的操作方法作出点D (请保留作出点D 时直角三角板两条直角边的痕迹)；(2)结合图①，请证明“第三步”操作得到的m 就是方程x 2－5x ＋2＝0的一个实数根；(3)上述操作的关键是确定两个固定点的位置．若要以此方法找到一元二次方程ax 2＋bx ＋c ＝0(a ≠0，b 2－4ac ≥0)的实数根，请你直接写出一对固定点的坐标；(4)实际上，(3)中的固定点有无数对，一般地，当m 1，n 1，m 2，n 2与a ，b ，c 之间满足怎样的关系时，点P (m 1，n 1)，Q (m 2，n 2)就是符合要求的一对固定点？第8题图解：(1)作图如解图①，第8题解图①【作法提示】先作出AB 的中点O 1，以O 1为圆心，12AB 长为半径画圆．x轴上另外一个交点即为D 点.（2）证明：如解图①，过点B 作x 轴的垂线交x 轴于点E ， ∵∠ACB ＝90°， ∴∠ACO ＋∠BCE ＝90°， ∵∠OAC ＋∠ACO ＝90°， ∴∠OAC ＝∠BCE ， ∵∠AOC ＝∠CEB ＝90°， ∴△AOC ∽△CEB ， ∴AO CE ＝OC EB ，即15－m ＝m2，∴m 2－5m ＋2＝0，∴m 是x 2－5x ＋2＝0的一个实数根； （3）(0，1)、(－b a ，ca )(答案不唯一)；【解法提示】∵方程ax 2＋bx ＋c ＝0可化为02=++ac x abx ，⎪⎭⎫⎝⎛--=--=x a b x x x a b a c 2，∴xa b a c x -=1，∴固定点坐标可以为（0,1），(－b a ，c a ). （4）如解图②，点P 在AD 上，Q 在BD 上，过P ，Q 分别作x 轴的垂线交x 轴于M ，N ，第8题解图②易得△PMD ∽△DNQ ， ∴PM DN ＝MDNQ ，即n 1m 2－x ＝x －m 1n 2，∴x 2－(m 1＋m 2)x ＋m 1m 2＋n 1n 2＝0与ax 2＋bx ＋c ＝0有相同解， ∴－b a ＝m 1＋m 2，ca ＝m 1m 2＋n 1n 2.。
安徽省中考数学专题复习课件——专题3规律探究问题
1．[2018·德阳]如下表，从左到右在每个小格子中都填入一个整 数，使得其中任意三个相邻格子中所填整数之和都相等，则第2018 个格子的数为 －1 ．
3 a b c -1 2 …
解题要领►对于数字规律题，解题的关键是根据已知的数得出前 后数之间的变化关系或数与序数之间的关系，当求第n个数时直 接套用关系式即可． 解答数的规律探索题的方法： 第一步：标序数； 第二步：找规律，分别比较数中各部分与序数(1，2，3，4，… ，n)之间的关系，把其蕴含的规律用含序数的式子表示出来； 第三步：根据找出的规律得出第n个数． 我们需要熟记的数字规律有： (1)自然数列规律：0，1，2，3，…，n(n≥0)； (2)正整数列规律：1，2，3，…，n－1，n(n≥1)； (3)奇数列规律：1，3，5，7，9，…，2n－1(n≥1)； (4)偶数列规律：2，4，6，8，…，2n(n≥1)； n(n 1) (5)正整数和：1＋2＋3＋4＋…＋n＝ 2 ； (6)正整数平方：1，4，9，16，…，n2(n≥1)； (7)正整数平方加1：2，5，10，17，…，n2＋1(n≥1)； (8)正整数平方减1：0，3，8，15，…，n2－1(n≥1)．
2．[2018·梧州]按一定规律排列的一列数依次为：2，3，10，15， 26，35，…，按此规律排列下去，则这列数中的第100个数是( A ) A．9999 B．10000 C．10001 D．10002
3．[2018·湖州三模]把所有正偶数从小到大排列，并按如下规律 分组：(2)，(4，6，8)，(10，12，14，16，18)，(20，22，24， 26，28，30，32)，…，现用等式 AM＝(i，j)表示正偶数M是第i 组 第j个数(从左往右数)，如 A8＝(2，3)，则 A2018＝ ( B )
安徽中考数学大题题型汇总之规律题
安徽中考数学大题题型汇总之规律题1．[2019安徽省淮南市潘集区第5次联考]观察以下等式:第1个等式:1111 1122-+=⨯，第2个等式:1121 2233-+=⨯，第3个等式:1131 3344-+=⨯，第4个等式:1141 4455-+=⨯，……按照以上规律,解决下列问题：（1）写出第5个等式：；（2）写出你猜想的第n(n为正整数)个等式： (用含n的等式表示)，并证明.2．[安徽省合肥市瑶海区一模]下列每一幅图都是由白色小正方形和和黑色小正方形组成．（1）第10幅图中有个白色正方形，个黑色正方形；（2）第n个图形中白色小正方形和黑色小正方形的个数总和等于．（用n表示，n是正整数）3．（2020·安徽初三学业考试）观察以下一系列等式：①22﹣21＝4﹣2＝21；②23﹣22＝8﹣4＝22；③24﹣23＝16﹣8＝23；④；…（1）请按这个顺序仿照前面的等式写出第④个等式：；（2）根据你上面所发现的规律，用含字母n的式子表示第n个等式：，并说明这个规律的正确性；（3）请利用上述规律计算：21+22+23+ (2100)4．如图，认真观察下面这些算式，并结合你发现的规律，完成下列问题：①32﹣12=（3+1）（3﹣1）=8=8×1，②52﹣32=（5+3）（5﹣3）=16=8×2，③72﹣52=（7+5）（7﹣5）=24=8×3，④92﹣72=（9+7）（9﹣7）=32=8×4．…（1）请写出：算式⑤；算式⑥；（2）上述算式的规律可以用文字概括为：“两个连续奇数的平方差能被8整除”，如果设两个连续奇数分别为2n﹣1和2m+1（n为整数），请说明这个规律是成立的；（3）你认为“两个连续偶数的平方差能被8整除”这个说法是否也成立呢？请说明理由．5.从2开始，连续的偶数相加，它们和的情况如下表：(1)若n=8时，则S的值为__________．(2)根据表中的规律猜想：用n的式子表示S的公式为：S=2+4+6+8+…+2n=__________．(3)根据上题的规律求102+104+106+108+…+200的值(要有过程)6．已知a是不为1的有理数，我们把11a-称为a的差倒数，如：2的差倒数是112-=-1.（1）求－3的差倒数；（2）－13的差倒数是，34的差倒数是，4的差倒数是；（3）已知1α=－13，2α是1α的差倒数，3α是2α的差倒数，4α是3α的差倒数，…，以此类推，则2017a = .7．观察下列等式：13218+⨯+=，163827+⨯+=，1942764+⨯+=，…按照以上规律，解决下列问题：（1）写出第4个等式：________；（2）写出你猜想的第n 个等式：________（用含n 的式子表示），并证明.8.发现 任意五个连续整数的平方和是5的倍数．验证 (1)22222(1)0123-++++的结果是5的几倍？(2)设五个连续整数的中间一个为n ，写出它们的平方和，并说明是5的倍数． 延伸 任意三个连续整数的平方和被3整除余数是几呢？请写出理由.9．如图，由两个长为2，宽为1的长方形组成“7”字图形（1）将一个“7”字图形按如图摆放在平面直角坐标系中，记为“7”字图形ABCDEF，其中顶点A位于x轴上，顶点B，D位于y轴上，O为坐标原点，则OBOA的值为__________．（2）在（1）的基础上，继续摆放第二个“7”字图形得顶点F1，摆放第三个“7”字图形得顶点F2，依此类推，…，摆放第n个“7”字图形得顶点F n-1，…，则顶点F2019的坐标为__________．10．（2019•随州）若一个两位数十位、个位上的数字分别为m，n，我们可将这个两位数记为mn，易知mn=10m+n；同理，一个三位数、四位数等均可以用此记法，如abc =100a+10b+c．【基础训练】（1）解方程填空：①若2x+3x=45，则x=__________；②若7y–8y=26，则y=__________；③若93t+58t=131t，则t=__________；【能力提升】（2）交换任意一个两位数mn的个位数字与十位数字，可得到一个新数nm，则mn+nm 一定能被__________整除，mn–nm一定能被__________整除，mn•nm–mn一定能被__________整除；（请从大于5的整数中选择合适的数填空）【探索发现】（3）北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚．数学中也存在有趣的黑洞现象：任选一个三位数，要求个、十、百位的数字各不相同，把这个三位数的三个数字按大小重新排列，得出一个最大的数和一个最小的数，用得出的最大的数减去最小的数得到一个新数（例如若选的数为325，则用532–235=297），再将这个新数按上述方式重新排列，再相减，像这样运算若干次后一定会得到同一个重复出现的数，这个数称为“卡普雷卡尔黑洞数”．①该“卡普雷卡尔黑洞数”为__________；②设任选的三位数为abc（不妨设a＞b＞c），试说明其均可产生该黑洞数．11．（2019·甘肃天水）如图1，对角线互相垂直的四边形叫做垂美四边形．（1）概念理解：如图2，在四边形ABCD中，AB=AD，CB=CD，问四边形ABCD是垂美四边形吗？请说明理由；（2）性质探究：如图1，四边形ABCD的对角线AC、BD交于点O，AC⊥B D．试证明：AB2+CD2=AD2+BC2；（3）解决问题：如图3，分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG 和正方形ABDE，连结CE、BG、GE．已知AC=4，AB=5，求GE的长．。
安徽中考数学复习(四)规律探索题(PPT)PPT优质公开课
根据表所中规以律图猜想n，中图由n(nn≥个2)中大特征的图特形的征个图数为形__，__[_1__＋_(用3×含n(的n式－子2表)]示个)；小的特征图形组成，特征图形的
(5)分析对比所得的结果，从结果与序数或结果与所给数式中数字的构成个数两方面进行对比，寻找不变的量及变化的量之间的变化关
系根，据从 表个而中得规数到律是结猜果想n与，＋各图1个n＋(n等≥32式)×中或特式(n征子－图之形2间)的满＝个足4数的n为关－_系_5式__.，__求__第(用n个含数n的式式时子直表接示套)；用关系式即可．
根(1)据分表别有中写规出20律第2猜40个想个和，大第图5n的个(n等≥特2式)中征；特图征图形形，的个4数×为2_0__2_0_－___5(用－含2n0的2式0子＝表6示0)5；5个小的特征图形，其面积和为
图3中由203个20大×的特4＋征图6形05，51×＋31＝＝4个1小41的3特5征. 图
类型一 数式规律探索
（2019、2018.18，2015.13，2014.16，2010.9）
例1 已知一组等式：
1
1
2 ;
123 2 3
1 1 3; 234 3 8
1 1 4 ; 345 4 15 …
根据上述等式反映的规律，解答下列问题：
(1)分别写出第4个和第5个等式； (2)猜想第n个等式(用含n的式子表示)，并证明你的猜想．
解：(1)观察发现，第1个等式为：1111 121 111 11 1 21;
1
1 21
第2个等式为：22122212121;
1
1 31
第3个等式为：33132313121;
∴第4个等式为：441 1 424 114 41 1 21，即
2019版中考专题(1)规律探索问题(含答案).docx
第二篇专题能力突破 专题一规律探索问题—年创新导向一、选择题1. (原创题)观察下列图形，它们是按一定的规律排列的，依照此规律，第20个图形中的“★”有()★★ ★ ★★★ ★ ★ ★ ★ ★ ★ ★ ★ ★ ★★ ★★ ★ ★★ ★ ★ ★★ ★ ★ ★ ★第1个图形 第2个图形第3个图形 第4个图形A. 57 个B. 60 个C.63个 D. 85 个解析 第1个图形有3个“★”，第2个图形有6=2X3个“★” ,第3个图形有9=3X3个“★” , 第4个图形有12=4X3个“★ ”，…，第20个图形有20X3=60个.故选B.答案B2. (原创题)如图，在一个三角点阵中，从上向下数有无数多行，其中各行点数依次为2, 4, 6,…，2n,…, 请你探究出前n行的点数和所满足的规律.若前n 行点数和为930,则n=()• • • • A 2• • • • • «A 3A. 29B. 30C. 31D. 32解析 前n 行的点数和可以表示成2+4+6+・・・+2n=2(l+2+3 + ・・・+n) =2X —=n(n+1), 从而得到一元二次方程n(n+1) =930,可以求出n=30・故选B.答案B3. (原创题)符号“f”表示一种运算，它对一些数的运算结果如下：(l)f(l)=2, f ⑵=4, f ⑶=6,…;(2)f 閤=2, -(為)等于()A. 2 013B. 2 014c -----2 013答案B4. (原创题)观察下列一组图形中点的个数，其中第一个图形中共有4个点，第2个图形中共有10个点,f(J)=3, f(f|=4,…利用以上规律计算：f(2 014) 解析根据题意，得f (2 014)—=2 014X2-2 014=2 014.故选B.第3个图形中共有19个点，…按此规律第6个图形中共有点的个数是解析第1个图形中共有4个点，第2个图形中共有10个点，比第1个图形中多了6个点；第3个图形中共有19个点，比第2个图形中多了9个点；…，按此规律可知，第4个图形比第3个图形中多12个点，所以第4个图形中共有12+19=31个点，第5个图形比第4个图形中多15个点，所以第5个图形中共有31 + 15=46个点，第6个图形比第5个图形中多18个点，所以第6个图形中共有46+18=64个点，故选D. 答案D二、填空题5.(原创题)图中各正三角形中的四个数之间都有相同的规律，据此规律，第n个正三角形中，四个数的解析观察图形发现：1><2—3 = — 1, 2X3-4=2, 3X4—5 = 7,故第n个正三角形中的外围的三个数分别是n, n+1, n+2,中间的数为n(n+l) — (n+2) =n2—2,所以这四个数的和为n+n+l+n+2 +n2—2=n2+3n+l.答案n+3n+l6.(原创题)如图，ZA0B=45° ,过射线0A上到点03,5, 7, 9, 11,…的点作OA的垂线与OB相交，黑色梯形，它们的面积分别为S“ S2, S3, S4…….律，则第2 015个黑色梯形的面积S2O15= __________ •(1 -LOA X 9 解析根据题意可得：S尸一=4=1X8的距离分别为h 得到并描出一组观察图中的规—4 , S2 —空严=12=2X8-42 (9+11)><2=20=3X8-4,2 S2 015=2 015X8-4=16 116.答案16 116 (13 + 15)=28=4X8-4，…，2019-2020学年数学中考模拟试卷一、选择题1.小明总结了以下结论：①a(b+c) =ab+ac ；②a(b - c) =ab - ac ； (3)(b - c) -ra=b4-a - c4-a(a^0)；④ a4- (b+c) =a-rb+a4-c(a^0)；其中一定成立的个数是() A. 1B ・2C ・3D ・424.如图，在反比例函数y=-—的图象上有一动点A,连结A0并延长交图象的另一支于点B,在第一象限x内有一点C,满足AC=BC,当点A 运动时，点C 始终在函数y=£的图象上运动，若tanZCAB=3,则kA. -B. 6C. 8D. 1835.甲、乙两人沿相同的路线由A 地到B 地匀速前进，A 、B 两地间的路程为20km.他们前进的路程为s (km), 甲出发后的时间为t(h),甲、乙前进的路程与时间的函数图象如图所示.根据图象信息，下列说法正确 的是()A. x< - 3B. x> - 33.下列运算正确的是( )A. a 6 -a 2 =a 4B. (a 2)3 = a 5C. x< - 6 C. a 2-a 3=a 5D. x> - 6D. a 6 4-a 2 = a 3A.甲的速度是4km/h C.乙比甲晚出发lhB. 乙的速度是10km/h D.甲比乙晚到B 地3h6.如图，AB/7CD,直线L 交AB 于点E,交CD 于点F,若Z2=75° ,则Z1等于（ ）7.如图，幼儿园计划用30m 的围栏靠墙围成一个面积为lOfW 的矩形小花园（墙长为15m ）,则与墙垂直的边x 为（）A. 10m 或 5m B ・ 5m 或 8m C ・ 10m D ・ 5m8. 下列运算正确的是（） A. J （-5）2 = - 5 B. （x 3）2=x 5 C. X 64-X 3=X 2D. （- -）_2=1649. 如图，一个游戏转盘分成红、黄、蓝三个扇形，其中红、黄两个扇形的圆心角度数分别为90° , 120° •让转盘自由转动，停止后，指针落在蓝色区域的概率是（）10. 某企业2018年初获利润300万元，到2020年初计划利润达到507万元，求这两年的年利润的平均增长率，设企业这两年的年利润平均增长率为X,则可列方程为（）A. 300 （1+x ） 2=507B. 300 （1 -x ） 2=507x+5 > 211•不等式组4_心的最小整数解是（）、填空题C. 125°D. 75°a5J11 5A ・ 一氏一 c.— 43 12 D.无法确定 C. 300 (l+2x) =507D. 300 (1+x 2) =507B.115°A. -3B. - 2C. 0D. 1A. AABC^ADCBB. AAOD^ACOBC. AABO^ADCOD. AADB^ADAC13.问题背景：如图，将AABC绕点A逆时针旋转60°得到AADE, DE与BC交于点P,可推出结论: PA+PC = PE问题解决：如图，在AM2VG中，MN = 6, ZM=75°, MG = 4近.点O是AWG内一点，则点O到AMNG三个顶点的距离和的最小值是_________________16.如果(2 +血)2=a+b逅(a, b为有理数)，那么a+b等于 ________________ .3 1 1 3 17.如图，点A (1, a)是反比例函数y= 的图象上一点，直线y= ------------------------- x+ —与反比例函数y= ---------- 的x 2 2 x图象在第四象限的交点为点B,动点P (x, 0)在x轴的正半轴上运动，当线段PA与线段PB之差达到最大时，则点P的坐标是 _________________________ .18.若矩形两条对角线的夹角是60° ,且较短的边长为3,则这个矩形的面积为—•三、解答题19.在箱子中有10张卡片，分别写有1到10的十个整数，从箱子中任取一张卡片，记下它的读数x,然后再放回箱子中，第二次再从箱子中任取一张卡片，记下它的读数y,试求x+y是10的倍数的概率.有意义的x的取值范围是___________20. 如图，在平面直角坐标系xOy 中，将直线y=x 向右平移2个单位后与双曲线y=3 (x>0)有唯一 公共点A,交另一双曲线y=' (x>0)于B.x(1) 求直线AB 的解析式和a 的值; (2) 若x 轴平分AAOB 的面积，求k 的值.x-1 > 01 1(3) 已知x“ X2是方程x 2- 3x - 1 =0的两不等实数根，求一+ —的值 X] x 223. 观察下列等式：©32-31=2X31；②3—32=2X3〈③3"-33=2XT ；④36 - 34=2X34…根据等式所反映的规律，解答下列问题：(1) 直接写出：第⑤个等式为 __________ ;(2) 猜想：第n 个等式为 _________ (用含n 的代数式表示)，并证明. 24. 已知二次函数y=x2—2(m+l)x+加+1 (m 为常数)，函数图像的顶点为C. (1) 若该函数的图像恰好经过坐标原点，求点C 的坐标；(2)该函数的图像与x 轴分别交于点A 、B,若以A 、B 、C 为顶点的三角形是直角三角形，求m 的值.25. 如图，AP 平分ZBAC, ZADP 和ZAEP 互补.⑴作P 到角两边AB, AC 的垂线段PM, PN.(2)求证:PD=PE.【参考答案】*** 一、选择题13. 2A /29 14. xH_315.22. (1)计算：| 2—舲 |+(血+ 1)°—3 tan 30°+(—1)258(2)解不等式组:1 x221.计算:15.1016.(4, 0)17.运.三、解答题18. 1【解析】【分析】本题是一个等可能事件的概率，试验发生包含的事件是先后取两次卡片，每次都有1〜10这10个结果，满足条件的事件x+y是10的倍数的数对可以列举出结果数，根据等可能事件的概率公式得到结果.【详解】解：由题意知本题是一个等可能事件的概率，试验发生包含的事件是先后取两次卡片，每次都有1~10这10个结果，故形成的数对(x, y)共有100个.满足条件的事件x+y是10的倍数的数对包括以下10个：(1, 9), (9, 1), (2, 8), (8, 2), (3, 7), (7,3), (4, 6), (6, 4), (5, 5), (10, 10).故“x+y是10的倍数”的概率为£ =卷=0.1 •【点睛】本题考查等可能事件的概率，是一个关于数字的题目，数字问题是概率中经常出现的题目，一般可以列举出要求的事件，然后根据概率公式计算.19.(1) y=x - 2, a= - 1； (2) k=3.【解析】【分析】(1)根据平移的性质求出一次函数的解析式，根据无交点求出a的值，1y ——(2)解方程组.x 可求出A的坐标是(1, -1),由x轴平分AAOB的面积，可知B的纵坐标是1, j = x —2代入一次函数解析式可求出B的坐标是（3, 1）,即可求出答案.【详解】（1）直线y=x向右平移2个单位后的解析式是y=x - 2,即直线AB的解析式为y=x-2,得：x - 2=—,则x2 - 2x - a=0,x△=4+4a=0,解得：a= - 1,一1（2）由（1）可得方程组丿x ,y = x-2\ x — \解得：\ ,A的坐标是（1, - 1）,Tx轴平分AAOB的面积，.°.B的纵坐标是1,在y=x-2中，令y=l,解得：x=3,则B的坐标是（3, 1）, 代入y=±可得：k=3.x【点睛】本题考查了一次函数和反比例函数的交点问题，根的判别式，平移的性质，三角形的面积的应用，及待定系数法求反比例函数解析式，题目是一道比较好的题目，难度适中.20.3-3^6【解析】【分析】直接利用负指数幕的性质以及绝对值的性质和二次根式的性质分别化简得出答案.【详解】解：原式=9-2辰2血-（6-茜），=9-4A/6 -6 + A/6,=3-3A/6【点睛】此题主要考查了二次根式的混合运算，正确化简各数是解题关键.21.（1） 2-2A/3 : （2） l<x<3；（3） - 3.【解析】【分析】(1)根据实数的运算法则进行计算(2)根据不等式组的解法解答，注意去分母(3)先根据一元二次方程的根与系数之间的关系求未知数，再化简求值.【详解】解：(1) |2 —的|+(血+ 1)°—3tan30°+(—I)""* = 2-V3+l-3x —+ 1-23= 2-73+1-73+1-2=2-2 也2x—1 > 0—1 —X解不等式1 —x> ---------- ,得：x<3,2解不等式x-l>0,得：x>l, x<3 x-1 >0故不等式组的解集为l<x<3；(3)由根与系数的关系得：Xi+X2=3, X I X2= - 1,1 1 x. +则一+ —= ~ =-3 .【点睛】此题重点考察学生对实数的运算，不等式组的解，一元二次方程根与系数之间的关系的理解，掌握实数的运算法则，不等式组和一元二次方程的解法是解题的关键.22.(1) 36 - 35=2X35； (2) 3n+1 - 3n=2X3n.【解析】【分析】由®32- 31=2X31；②3彳-3J2X32；③34 - 33=2X33；④35 - 34=2X34-得出第⑤个等式,以及第n个等式的底数不变，指数依次分别是n+1、n、n.【详解】解：(1)由®32- 31=2X31；②3彳-32=2x32；③34-3S=2X33；④35 - 34=2X34…得出第⑤个等式36 - 35 =2X35；故答案为：36 - 35=2X36；(2)由©32-31=2X31；②33-32=2x32； (3)34 - 33=2X33；④35 - 34=2X34…得出第n 个等式的底数不变，指数依次分别是n+1、n、n,即3n+1 - 3n=2X3n.证明：左边=3说-3"=3X3°-3"=3°X (3-1) =2X3n=右边，所以结论得证.故答案为：3n+1-3n=2X3n.【点睛】此题考查数字的变化规律，找出数字之间的运算规律，得出规律，利用规律，解决问题.【解析】【分析】—1 —X(2) l-x> -------------- \2,(2) m的值为1或一1(1)把(0, 0)代入y=+—2(m+l)x+2m+l可求出m的值，可得二次函数解析式，配方即可得出C点坐标；(2)令y=0,可用m 表示出&和X2,即可表示出AB的距离，根据二次函数解析式可用含m的代数式表示顶点C的坐标，根据以A、B、C为顶点的三角形是直角三角形可得关于m的方程，解方程求出m的值即可.【详解】(1)解:Vy=x2—2(m+l)x+2m+l 的图像经过点(0, 0).•.2m+l=0,12当m=—丄时，y=x2—x= (x —丄)2——,2 2 4•••顶点C的坐标(丄，2 4(2)解：当y=0 时X2—2(m+l)x+2m+l=0.°.xi=2m+l, X2=l,•*.AB= |2m|,Vy=x2—2(m+l)x+2m+l= (x—m—l)2—m2,顶点C的坐标(m+1, —m2),•.•以A、B、C为顶点的三角形是直角三角形，/. 2m2 = |2m|,当2m2=2m 时，mi=0, m2=l,当21^=—2m 时，mi=0, m2= —1,当m=0 时，AB=0 (舍)答：m的值为1或一1.【点睛】本题考查二次函数的图象及二次函数与一元二次方程，根据二次函数的解析式表示出顶点C的坐标和AB 的长是解题关键.25. (1)画图见解析；(2)证明见解析.【解析】【分析】(1)根据题意作图即可；⑵由PM丄AB, PN丄AC, PA平分ZBAC,可得PM=PN,再求出ZDPM=ZEPN,证明△ PMD^APNE,即可求【详解】解：⑴线段PM, PN如图所示.・・・PM=PN・・・ZPMA=ZPNA=90° ,・・・ZMPN+ZMAN=180° ,V ZADP+ZAEP=180° ,A ZDAE+ZDPE=180° ,・•・ ZMPN=ZDPE,・•・ ZDPM=ZEPN,•••△PMD 竺△PNE(ASA),・・・PD=PE・【点睛】本题考查的是全等三角形，熟练掌握全等三角形的性质是解题的关键.2019-2020学年数学中考模拟试卷一、选择题1. 函数y = yj2-x+—^—中自变量x 的取值范围是（）x-1 A. x<2B ・C ・ xV2 且兀工1D ・2. 如图，点B 、C 、E 在同一条直线上，AABC 与ACDE 都是等边三角形，则下列结论不一定成立的是（）A. AACE^ABCD B ・△BGC^AAFC C ・△DCG9/\ECF D ・△ADB^ZkCEA 3.如图，将面积为S 的矩形ABCD 的四边BA 、CB 、DC 、AD 分别延长至E 、F 、G 、H,使得AE=CG, BF=BC, FB 2DH 二AD,连接EF, FG, GH, HE, AF, CH.若四边形EFGH 为菱形，——=—,则菱形EFGH 的面积是（）AB 3A. 2SB. -52 7C. 3S D ・一S24.若关于x 的方程3x 2 - 2x+m=0的一个根是- 1,则m 的值为（）26.如图，在反比例函数y=-—的图象上有一动点A,连结A0并延长交图象的另一支于点B,在第一象限兀内有一点C,满足AC=BC,当点A 运动时，点C 始终在函数y='的图象上运动，若tanZCAB=3,则kX的值为（）A. -5 B ・-1 C ・ 1D. 5如图，直线AD 〃BC,若Zl=40°,ZBAC=80° ,则Z2的度数为（C. 50°D. 40°5.2 A. -B ・ 6C ・ 8D ・ 1837. 函数y=2x'-4x ・4的顶点坐标是( )A. (1, -6)B ・(1, -4)C ・(・ 3, -6)D ・(-3,-4)8. 一个两位数，十位数字比个位数字的2倍大1,若将这个两位数减去36恰好等于个位数字与十位数字对调后所得的两位数，则这个两位数是( )10. 如图是某几何体的三视图，则该几何体的表面积为11. 在-3, -1, 1, 3四个数中，比-2小的数是( )二、填空题13. 如图，AB 是00的直径，点D 、E 是半圆的三等分点，AE 、BD 的延长线交于点C,若CE=2,则图中 阴」影部分的面积为_•A. 86 氏68 C. 97 D. 739. 在一个不透明的口袋中装有2个绿球和若干个红球, 摸出-个球，摸到绿球的概率为?则红球的个数是(这些球除颜色外无其它差别，从这个口袋中随机A.2B.4C.6D.8C. 24+6^3D. 16+6^3A. 1B. - 1C. -3D.12. 如图，这是健健同学的小测试卷, 判断题：每小题20分(D 2是分式 (2) (-2^ )3=-6/他应该得到的分数是(⑷ J9=±3(x )(5) 65啲补角是125。
2019中考数学规律探索题(中考找规律题目-有答案)
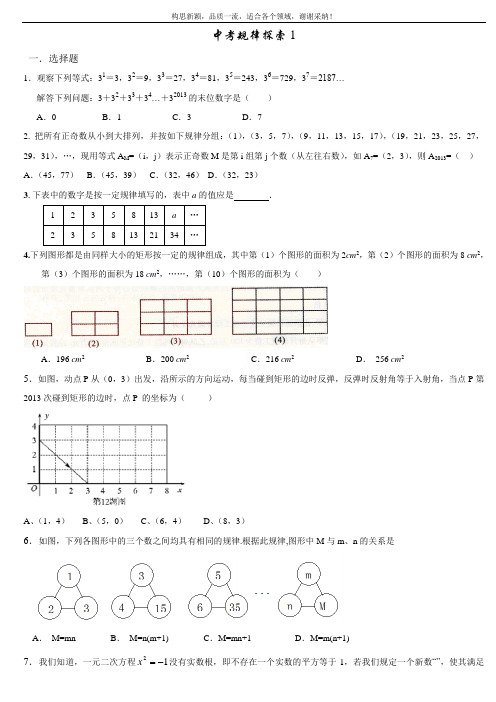
中考规律探索1一．选择题1．观察下列等式：31＝3，32＝9，33＝27，34＝81，35＝243，36＝729，37＝2187… 解答下列问题：3＋32＋33＋34…＋32013的末位数字是（ ） A ．0 B ．1 C ．3 D ．72. 把所有正奇数从小到大排列，并按如下规律分组：（1），（3，5，7），（9，11，13，15，17），（19，21，23，25，27，29，31），…，现用等式A M =（i ，j ）表示正奇数M 是第i 组第j 个数（从左往右数），如A 7=（2，3），则A 2013=（ ） A ．（45，77） B ．（45，39） C ．（32，46） D ．（32，23）3.下表中的数字是按一定规律填写的，表中a 的值应是 ．1 2 3 5 8 13 a (2)358132134…4.下列图形都是由同样大小的矩形按一定的规律组成，其中第（1）个图形的面积为2cm 2，第（2）个图形的面积为8 cm 2，第（3）个图形的面积为18 cm 2，……，第（10）个图形的面积为（ ）A ．196 cm 2B ．200 cm 2C ．216 cm 2D ． 256 cm 25．如图，动点P 从（0，3）出发，沿所示的方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P 第2013次碰到矩形的边时，点P 的坐标为（ ）A 、（1，4）B 、（5，0）C 、（6，4）D 、（8，3）6．如图，下列各图形中的三个数之间均具有相同的规律.根据此规律,图形中M 与m 、n 的关系是A ． M=mnB ． M=n(m+1)C ．M=mn+1D ．M=m(n+1)7．我们知道，一元二次方程12-=x 没有实数根，即不存在一个实数的平方等于-1，若我们规定一个新数“”，使其满足12-=i (即方程12-=x 有一个根为)，并且进一步规定: 一切实数可以与新数进行四则运算，且原有的运算律和运算法则仍然成立，于是有,1i i =12-=i ，,).1(23i i i i i -=-=⋅=.1)1()(2224=-==i i 从而对任意正整数n ，我们可得到,.)(.4414i i i i i i n n n ===+同理可得,1,,143424=-=-=++n n n i i i i 那么，20132012432i i i i i i +⋅⋅⋅++++的值为A ．0B ．1C ．-1D ．8．下列图形都是由同样大小的棋子按一定的规律组成，其中第①个图形有1颗棋子，第②个图形一共有6颗棋子，第③个图形一共有16颗棋子，…，则第⑥个图形中棋子的颗数为（ ）A ．51B ．70C ．76D ．81二．填空题1．观察下列图形中点的个数，若按其规律再画下去，可以得到第n 个图形中所有的个数为 （用含n 的代数式表示）．2．如图，在直角坐标系中，已知点A （﹣3，0）、B （0，4），对△OAB 连续作旋转变换，依次得到△1、△2、△3、△4…，则△2013的直角顶点的坐标为 ．3．如图，正方形ABCD 的边长为1，顺次连接正方形ABCD 四边的中点得到第一个正方形A 1B 1C 1D 1，由顺次连接正方形A 1B 1C 1D 1四边的中点得到第二个正方形A 2B 2C 2D 2…，以此类推，则第六个正方形A 6B 6C 6D 6周长是 ．图① 图② 图③···（第8题图）4．直线上有2013个点，我们进行如下操作：在每相邻两点间插入1个点，经过3次这样的操作后，直线上共有个点．5．如图，古希腊人常用小石子在沙滩上摆成各种形状来研究数．例如：称图中的数1，5，12，22…为五边形数，则第6个五边形数是．6 ．如图，是用火柴棒拼成的图形，则第n个图形需根火柴棒．7．观察规律：1=12；1+3=22；1+3+5=32；1+3+5+7=42；…，则1+3+5+…+2013的值是．8．如图12，一段抛物线：y＝－x(x－3)（0≤x≤3），记为C1，它与x轴交于点O，A1；将C1绕点A1旋转180°得C2，交x 轴于点A2；将C2绕点A2旋转180°得C3，交x 轴于点A3；……如此进行下去，直至得C13．若P（37，m）在第13段抛物线C13上，则m =_________．9.直线上有2013个点，我们进行如下操作：在每相邻两点间插入1个点，经过3次这样的操作后，直线上共有个点. 10．观察下列各式的计算过程：5×5=0×1×100+25，15×15=1×2×100+25，25×25=2×3×100+25，35×35=3×4×100+25，…………请猜测，第n个算式(n为正整数)应表示为____________________________．11．将连续的正整数按以下规律排列，则位于第7行、第7列的数x是__ __．12、如下图，每一幅图中均含有若干个正方形，第①幅图中含有1个正方形；第②幅图中含有5个正方形；……按这样的规律下去，则第（6）幅图中含有 个正方形；13．将一些半径相同的小圆按如图所示的规律摆放：第1个图形有6个小圆， 第2个图形有10个小圆， 第3个图形有16个小圆， 第4个图形有24个小圆， ……，依次规律，第6个图形有 个小圆．14.已知一组数2，4，8，16，32，…，按此规律，则第n 个数是 ． 15、我们知道，经过原点的抛物线的解析式可以是y ＝ax 2＋bx (a ≠0) （1）对于这样的抛物线：当顶点坐标为（1，1）时，a ＝__________；当顶点坐标为（m ，m ），m ≠0时，a 与m 之间的关系式是__________；（2）继续探究，如果b ≠0，且过原点的抛物线顶点在直线y ＝kx (k ≠0)上，请用含k 的代数式表示b ；（3）现有一组过原点的抛物线，顶点A 1，A 2，…，A n 在直线y ＝x 上，横坐标依次为1，2，…，n （为正整数，且n ≤12），分别过每个顶点作x 轴的垂线，垂足记为B 1，B 2，…，B n ，以线段A n B n 为边向右作正方形A n B n C n D n ，若这组抛物线中有一条经过D n ，求所有满足条件的正方形边长．16．如图，所有正三角形的一边平行于x 轴，一顶点在y 轴上，从内到外，它们的边长依次为2，4，6，8，…，顶点依次用1A 、2A 、3A 、4A 、…表示，其中12A A 与x 轴、底边12A A 与45A A 、45A A 与78A A 、…均相距一个单位，则顶点3A 的坐标是 ，22A 的坐标是 ．xy A 9A 6A 3A 8A 7A 5A 4A 2A 1O第16题图••••••①② ③17．如图，已知直线l ：y=33x ，过点A （0，1）作y 轴的垂线交直线l 于点B ，过点B 作直线l 的垂线交y 轴于点A 1；过点A 1作y 轴的垂线交直线l 于点B 1，过点B 1作直线l 的垂线交y 轴于点A 2；……按此作法继续下去，则点A 2013的坐标为 ．18、如图，在平面直角坐标系中，一动点从原点O 出发，按向上，向右，向下，向右的方向不断地移动，每移动一个单位，得到点A 1（0，1），A 2（1，1），A 3（1，0），A 4（2，0），…那么点A 4n ＋1（n 为自然数）的坐标为 （用n 表示）19．当白色小正方形个数n 等于1，2，3…时，由白色小正方形和和黑色小正方形组成的图形分别如图所示．则第n 个图形中白色小正方形和黑色小正方形的个数总和等于_____________．（用n 表示，n 是正整数）20. （2013•衢州4分）如图，在菱形ABCD 中，边长为10，∠A=60°．顺次连结菱形ABCD 各边中点，可得四边形A 1B 1C 1D 1；顺次连结四边形A 1B 1C 1D 1各边中点，可得四边形A 2B 2C 2D 2；顺次连结四边形A 2B 2C 2D 2各边中点，可得四边形A 3B 3C 3D 3；按此规律继续下去…．则四边形A 2B 2C 2D 2的周长是 ；四边形A 2013B 2013C 2013D 2013的周长是 ．21.一组按规律排列的式子：ａ２，43a ，65a ,87a ,….则第n 个式子是________ 22.观察下面的单项式：a ，﹣2a 2，4a 3，﹣8a 4，…根据你发现的规律，第8个式子是 ．23.如图，已知直线l：y=x，过点M（2，0）作x轴的垂线交直线l于点N，过点N作直线l的垂线交x轴于点M1；过点M1作x轴的垂线交直线l于N1，过点N1作直线l的垂线交x轴于点M2，…；按此作法继续下去，则点M10的坐标为．24.为庆祝“六•一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛．如图所示：按照上面的规律，摆第（n）图，需用火柴棒的根数为．答案：选择题：1、C 2、C 3、21 4、B 5、D 6、D 7、D 8、 C填空题：1、（n+1）2 2、（8052,0） 3、0.5 4、16097 5、51 6、2n+1 7、1014049 8、 2 9、16097 10、[10(n-1)+5]2=100n(n-1)+25 11、85 12、91 13、46 14、2n 15、（1）－1；a ＝－1m（或am ＋1＝0）； （2）解：∵a ≠0 ∴y ＝ax 2＋bx ＝a (x ＋2b a)2－24b a∴顶点坐标为（－2ba ，－24b a ）∵顶点在直线y ＝kx 上∴k (－2ba )＝－24b a∵b ≠0∴b ＝2k（3）解：∵顶点A n 在直线y ＝x 上 ∴可设A n 的坐标为（n ，n ），点D n 所在的抛物线顶点坐标为（t ，t ）由（1）（2）可得，点D n 所在的抛物线解析式为y ＝－1tx 2＋2x∵四边形A n B n C n D n 是正方形∴点D n 的坐标为（2n ，n ） ∴－1t(2n )2＋2×2n ＝n∴4n ＝3t∵t 、n 是正整数，且t ≤12，n ≤12∴n ＝3，6或9∴满足条件的正方形边长为3，6或916、（0，31-），（－8，－8）. 17、()()201340260,40,2或（注：以上两答案任选一个都对）18、（2n ，1） 19、n 2+4n 20、20；21、221na n （n 为正整数）22、-128a 8 23、（884736,0） 24、6n+2规律探索21、 我们平常用的数是十进制数，如2639=2×103+6×102+3×101+9×100，表示十进制的数要用10个数码（又叫数字）：0，1，2，3，4，5，6，7，8，9。
安徽省2019年中考数学二轮复习题型四：规律探索题(含答案)
题型四 规律探索题类型一 数式规律探索1. (2018霍邱县一模)如下数表是由1开始的连续自然数组成的，观察规律并完成各题的解答：(1)第9行的最后一个数是________；(2)第n 行的第一个数是________，第n 行共有________个数；第n 行各数之和为____________．2. (2018安庆二模)观察下列等式： (1)1－12＋11×2＝1；(2)12－14＋13×4＝13； (3)13－16＋15×6＝15； …根据上述规律解决下列问题：(1)写出第(4)个等式：(________)－(________)＋(________)＝(________)； (2)写出你猜想的第(n )个等式，并证明．3. 观察下列等式：①11＋12－12＝11；②13＋14－112＝12；③15＋16－130＝13；④17＋18－156＝14；…(1)请根据以上规律写出第5个等式：__________________________；(2)猜想并写出第n个等式，并验证其正确性．4. 观察下列由连续的正整数组成的宝塔形等式：第1层1＋2＝3；第2层4＋5＋6＝7＋8；第3层9＋10＋11＋12＝13＋14＋15；第4层16＋17＋18＋19＋20＝21＋22＋23＋24；…(1)填空：第6层等号右侧的第一个数是________，第n层等号右侧的第一个数是________(用含n的式子表示，n是正整数)，数字2017排在第几层？请简要说明理由；(2)求第99层右侧最后三个数字的和．5. (2018太和县模拟)观察下列等式：①1＋2＝3；②4＋5＋6＝7＋8；③9＋10＋11＋12＝13＋14＋15；④16＋17＋18＋19＋20＝21＋22＋23＋24；…(1)试写出第五个等式；(2)根据你的发现，试说明145是第几行的第几个数？6. 按如下方式排列正整数，第1行有1个数，第2行有3个数，第3，4行分别有7个、13个数．依此规律，解答下列问题：12 3 43 4 5 6 7 8 94 5 6 7 8 9 10…15 16…(1)第10行有________个数，第n行有________个数(结果用含n的式子表示)；(2)第2，3，4行都含有数4，其中第2行最先出现4，那么2019最先出现在第几行？7. 已知下列等式：①32－12＝8，②52－32＝16，③72－52＝24，…(1)请仔细观察，写出第4个式子；(2)根据以上式子的规律，写出第n个式子，并用所学知识说明第n个等式成立；(3)利用(2)中发现的规律计算：8＋16＋24＋…＋792＋800.8. 【问题提出】观察下列图形，回答问题：第8题图由此可以得出第1个图形中所有线段的长度的和是1，第2个图形中所有线段的长度的和是4，第3个图形中所有线段的长度的和是10，第4个图形中共有________条线段，所有线段的长度的和是________；【规律探索】在计算第1，2，3个图形中所有线段的长度的和的时候，得出了下列等式： 1×1＝1×2×36；1×2＋2×1＝2×3×46；1×3＋2×2＋3×1＝3×4×56；第4个等式为____________； …【问题解决】求第n 个图形中所有线段的长度的和．9. (2017安徽19题)我们知道，1＋2＋3＋…＋n ＝n （n ＋1）2，那么12＋22＋32＋…＋n 2结果等于多少呢？在图①所示三角形数阵中，第1行圆圈中的数为1，即12；第2行两个圆圈中数的和为2＋2，即22；……；第n 行n 个圆圈中数的和为n ＋n ＋…＋n ,\s \do 4(n 个n ))，即n 2.这样，该三角形数阵中共有n （n ＋1）2个圆圈，所有圆圈中数的和为12＋22＋33＋…＋n 2.第9题图①【规律探究】将三角形数阵经两次旋转可得如图②所示的三角形数阵，观察这三个三角形数阵各行同一位置圆圈中的数(如第n －1行的第一个圆圈中的数分别为n －1，2，n )，发现每个位置上三个圆圈中数的和均为________．由此可得，这三个三角形数阵所有圆圈中数的总和为：3(12＋22＋32＋…＋n 2)＝________，因此，12＋22＋32＋…＋n 2＝________．第9题图②【解决问题】根据以上发现，计算12＋22＋32＋…＋201721＋2＋3＋…＋2017的结果为________．类型二图形规律探索1. 下列各图形中的“”的个数和“△”的个数是按照一定规律摆放的：第1题图(1)观察图形，填写下表：(2)当n＝________时，“△”的个数是“”的个数的2倍．2. 用同样大小的“”按如图所示的规律摆放：第2题图(1)第5个图形有多少枚“”？(2)第几个图形有2018枚“”？请说明理由．3. 如图，图①中小黑点的个数记为a1＝4，图②中小黑点的个数记为a2＝8，图③中小黑点的个数记为a3＝13，…第3题图根据以上图中的规律完成下列问题：(1)图④中小黑点的个数记为a4，则a4＝________；(2)图n中小黑点的个数记为a n，则a n＝________(用含n的式子表示)；(3)第几个图形中的小黑点的个数为43个？4. (1)观察下列图与等式的关系，并填空：(2)一堆按“放置方式①”放置的圆圈，小明数得共有165个圆圈，请你计算最上面有几个圆圈？5. (2018安徽名校大联考)如图，下列每个图案均是由若干边长为1的小正方形按一定的规律堆叠而成，探究规律，解答问题．第5题图(1)请根据你的探究直接写出：第10个图案中共有______个小正方形，第n 个图案中共有______个小正方形；(2)是否存在有37个小正方形的图案？若存在，请求出是第几个图案；若不存在，请说明理由．6. 观察下面的点阵图和相应的等式，探究其中的规律：(1)认真观察图①，并填写出第4个点阵图相应的等式．第6题图①(2)结合(1)观察图②，并填写出第5个点阵图相应的等式．第6题图②(3)通过猜想，直接写出(2)中与第n个点阵图相对应的等式．7. (2018怀远县模拟)如图，正方形ABCD内部有若干个点，用这些点以及正方形ABCD 的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠)：第7题图(1)填写下表：(2)原正方形能否被分割成2008个三角形？若能，求此时正方形ABCD 内部有多少个点？若不能，请说明理由.8. (2018合肥包河区一模)如图，每个图形可以看成由上下左右4个等腰梯形组成或者是由外围大正方形减去正中间的正方形(阴影部分)所得，而每个等腰梯形又由若干个更小的全等正方形和全等等腰直角三角形组成，且等腰直角三角形的面积正好是小正方形面积的一半，设小正方形的面积为1，则第1个图形的面积为4×(2×1＋4×12)＝16，第2个图形的面积为4×(5×1＋5×12)＝30，第3个图形的面积为4×(9×1＋6×12)＝48，…根据上述规律，解答下列问题：(1)第4个图形的面积为：4×(____×1＋____×12)＝____，(2)第n 个图形的面积为：4×[____×1＋____×12](用含n 的式子填空)；(3)上面的图形还可看成一个大正方形再减去中间1个小正方形组成，这时，第1个图形的面积为(32)2－2，第2个图形的面积为(42)2－2，第3个图形的面积为(52)2－2，…再根据这个规律，完成下列问题：①按此规律，第n 个图形的面积为：[____]2－2(用含n 的式子填空)； ②比较两个猜想，写出你发现的结论并验证．第8题图9. (2016安徽)(1)观察下列图形与等式的关系，并填空：第9题图①(2)观察下图，根据(1)中结论，计算图中黑球的个数，用含有n的代数式填空：1＋3＋5＋…＋(2n－1)＋(________)＋(2n－1)＋…＋5＋3＋1＝________．第9题图②类型一 数式规律探索1. 解：(1)81；【解法提示】根据题意，观察发现：第1行的最后一个数为12＝1，第2行的最后一个数为22＝4，第3行的最后一个数为32＝9，第4行的最后一个数为42＝16，第5行的最后一个数为52＝25，第6行的最后一个数为62＝36，…，∴第n 行的最后一个数为n 2，∴第9行的最后一个数是81.(2)(n －1)2＋1，2n －1, (n 2－n ＋1)(2n －1)．【解法提示】观察发现：第1行的第一个数为(1－1)2＋1＝1，第2行的第一个数为(2－1)2＋1＝2，第3行的第一个数为(3－1)2＋1＝5，第4行的第一个数为(4－1)2＋1＝10，第5行的第一个数为(5－1)2＋1＝17，第6行的第一个数为(6－1)2＋1＝26，…，∴第n 行第一个数为(n －1)2＋1；观察发现：第1行共有1个数，第2行共3个数，第3行共5个数，第4行共7个数，第5行共9个数，第6行共11个数，…，∴第n 行共(2n －1)个数；由(1)知第n 行的最后一个数为n 2，∴第n 行的各数之和为（n －1）2＋1＋n 22·(2n －1)＝(n 2－n ＋1)(2n －1)．2. 解：(1)14，18，17×8，17；【解法提示】观察上述等式发现：第(1)个等式：1－12×1＋11×（1＋1）＝12×1－1＝1；第(2)个等式：12－12×2＋1（2×2－1）×（2×2）＝12×2－1＝13；第(3)个等式：13－12×3＋1（2×3－1）×（2×3）＝12×3－1＝15；∴第(4)个等式为：14－12×4＋1（2×4－1）×（2×4）＝12×4－1＝17.即14－18＋17×8＝17.(2)第(n )个等式为1n －12n ＋12n （2n －1）＝12n －1.证明：左边＝2（2n －1）－（2n －1）＋12n （2n －1）＝4n －2－2n ＋1＋12n （2n －1）＝12n －1＝右边．∴原式成立．3. 解：(1)19＋110－190＝15；【解法提示】观察发现：第①个等式：12×1－1＋12×1－1（2×1－1）（2×1）＝11；第②个等式：12×2－1＋12×2－1（2×2－1）（2×2）＝12；第③个等式：12×3－1＋12×3－参考答案1（2×3－1）（2×3）＝13；第④个等式：12×4－1＋12×4－1（2×4－1）（2×4）＝14；∴第⑤个等式：12×5－1＋12×5－1（2×5－1）（2×5）＝15，即19＋110－190＝15；(2)根据上述规律，得第n 个等式为12n －1＋12n －12n （2n －1）＝1n .证明：左边＝2n ＋2n －1－12n （2n －1）＝2（2n －1）2n （2n －1）＝1n ＝右边，∴等式成立．4. (1)43，n 2＋n ＋1；2017排在第44层，理由略；(2)第99层右侧最后三个数字的和为29994.5. 解：(1)根据题意可得，第五个等式为25＋26＋27＋28＋29＋30＝31＋32＋33＋34＋35；(2)根据已知等式得，第n 行的第1个数为n 2， ∵122＝144，∴145是第12行的第2个数. 6. 解：(1)91，n 2－n ＋1；【解法提示】根据题意可知，第2行最后一个数为4＝22，数字个数是22－1；第3行最后一个数为9＝32，数字个数是32－2；第4行最后一个数为16＝42，数字个数是42－3；…，∴第10行最后一个数为102＝100，数字个数是102－9＝91； 第n 行最后一个数为n 2，数字个数是n 2－(n －1)＝n 2－n ＋1. (2)∵第44行最后一个数是442＝1936，第45行第一个数字是45，而最后一个数字是452＝2025，45＜2019＜2025， ∴2019最先出现在第45行．7. 解：(1)∵第1个式子为：32－12＝(2×1＋1)2－(2×1－1)2＝8×1；第2个式子为：52－32＝(2×2＋1)2－(2×2－1)2＝8×2；第3个式子为：72－52＝(2×3＋1)2－(2×3－1)2＝8×3；∴第4个式子为：(2×4＋1)2－(2×4－1)2＝92－72＝8×4＝32； 即第4个式子为：92－72＝32； (2)由(1)的推理过程可得，第n 个式子为：(2n ＋1)2－(2n －1)2＝8n ；证明：∵左边＝4n 2＋4n ＋1－4n 2＋4n －1＝8n ＝右边，∴所写等式成立；(3)8＋16＋24＋…＋792＋800＝32－12＋52－32＋72－52＋…＋2012－1992＝2012－1＝40400.8. 解：【问题提出】10，20；【规律探索】1×4＋2×3＋3×2＋4×1＝4×5×66；【问题解决】n （n ＋1）（n ＋2）6.9. 解：【规律探究】2n ＋1，n （n ＋1）（2n ＋1）2，n （n ＋1）（2n ＋1）6；【解法提示】第n －1行的第一个圆圈中的数分别为n －1，2，n ，则n －1＋2＋n ＝2n ＋1；3(12＋22＋32＋…＋n 2)＝(1＋2＋3＋…＋n )(2n ＋1)＝n （n ＋1）（2n ＋1）2；12＋22＋32＋…＋n 2＝n （n ＋1）（2n ＋1）2·13＝n （n ＋1）（2n ＋1）6.【解决问题】1345. 【解法提示】 12＋22＋32＋…＋201721＋2＋3＋…＋2017＝2017×（2017＋1）（2×2017＋1）62017×（2017＋1）2＝2×2017＋13＝1345.类型二 图形规律探索1. 解：(1)完成表格如下：个数(2)11.【解法提示】根据题意知n （n ＋1）2＝2×3n ，解得n ＝0(舍去)或n ＝11, ∴当n ＝11时，“△”的个数是“”的个数的2倍． 2. 解：(1)图①有2枚“”，2＝2×12，图②有8枚“”，8＝2×22，图③有18枚“”，18＝2×32， …图⑤有2×52＝50，∴第五个图形有50枚“”；(2)由(1)可得第n 个图形有(2n 2)枚“”，令2n 2＝2018， 此方程无整数解， ∴没有哪个图形有2018枚“”．3. 解：(1)19；【解法提示】根据题意知a 4＝1＋2＋3＋4＋5＋4＝19.(2)12n 2＋52n ＋1； 【解法提示】a n ＝1＋2＋3＋…＋n ＋n ＋1＋n ＝n （n ＋1）2＋2n ＋1＝12n 2＋52n ＋1.(3)当12n 2＋52n ＋1＝43时，解得：n ＝7(负值舍去)，∴第7个图形中的小黑点的个数为43个. 4. 解：(1)12×52，30，2n ，3n （n ＋1）2；(2)由题意得，3n （n ＋1）2＝165，解得n 1＝10，n 2＝－11(舍去)，即最上面有10个圆圈．5. 解：(1)56，n （n ＋1）2＋1(或n 2＋n ＋22)；【解法提示】观察发现：第1个图案有1＋1＝2个小正方形；第2个图案有1＋2＋1＝4个小正方形； 第3个图案有1＋2＋3＋1＝7个小正方形； 第4个图案有1＋2＋3＋4＋1＝11个小正方形；…∴第10个图案有1＋2＋3＋4＋…＋10＋1＝56个小正方形； 第n 个图案有1＋2＋3＋4＋…＋n ＋1＝n （n ＋1）2＋1个小正方形.(2)存在．理由如下： 令n （n ＋1）2＋1＝37，解得n ＝－9(舍去)，或n ＝8，∴存在有37个小正方形的图案，是第8个图案． 6. 解：(1)1＋2＋3＋4＝（1＋4）×42＝10；(2)10＋15＝52； (3)由(1)(2)可知，n （n －1）2＋n （n ＋1）2＝n 2.【解法提示】可以将(2)中点阵图分为两部分，一部分与(1)的点阵图完全相同，剩余部分与(1)中前一部分的点阵图完全相同，因此可以得出(2)中第n 个点阵图等于(1)中第n 个点阵图和n －1个点阵图之和，∴n 2＝n （n －1）2＋n （n ＋1）2.7. 解：(1)填写下表：【解法提示】观察图形发现：有1个点时，内部分割成4个三角形；有2个点时，内部分割成4＋2＝6个三角形；有3个点时，内部分割成4＋2×2＝8个三角形；有4个点时，内部分割成4＋2×3＝10个三角形；…∴有n 个点时，内部分割成4＋2×(n －1)＝(2n ＋2)个三角形；(2)能．令2n ＋2＝2008，解得n ＝1003.即此时正方形ABCD 内部有1003个点．8. 解：(1)14，7，70；(2)(2＋3＋4＋…＋n ＋n ＋1)(形式不唯一)，n ＋3；(3)①(n ＋2)2；【解法提示】观察图形可知，第1个图形的面积为[(1＋2)2]2－2＝(32)2－2；第2个图形的面积为[(2＋2)2]2－2＝(42)2－2，第3个图形的面积为[(3＋2)2]2－2＝(52)2－2，…∴第n 个图形的面积为[(n ＋2)2]2－2.② 4[(2＋3＋4＋…＋n ＋n ＋1)×1＋12(n ＋3)]＝[(n ＋2)2]2－2.证明：右边＝2n 2＋8n ＋6； 左边＝4[n （n ＋3）2＋n ＋32]＝2(n ＋3)(n ＋1)＝2n 2＋8n ＋6，∴左边＝右边．即4[(2＋3＋4＋…＋n ＋n ＋1)×1＋12(n ＋3)]＝[(n ＋2)2]2－2.9. 解：(1)42；n 2；【解法提示】观察每一行图形变换，可以发现，当小球有4行时，小球的总个数＝4×4＝42(个)，∴第一个空填“42”；根据此规律可知，当小球有n 行时，小球的总数＝n ·n ＝n 2，∴第二个空填“n 2”． (2)2n ＋1；2n 2＋2n ＋1.【解法提示】在连续的奇数中，2n －1后边的数是2n ＋1，∴第一个空填“2n ＋1”；由第(1)小题的结论可知，在等式的左边的数中，“2n －1”前面的所有数之和等于n 2，后面的所有的数之和也等于n 2，∴总和＝n 2＋(2n ＋1)＋n 2＝2n 2＋2n ＋1，∴等式的右边填“2n 2＋2n ＋1”．。
中考一轮复习--专题五 规律探索题
(3)通过对简单、特殊情况的观察,再推广到一般情况.
2.规律探究的基本原则:
(1)遵循类推原则,项找项的规律,和找和的规律,差找差的规律,积
找积的规律.
(2)遵循有序原则,从特殊开始,从简单开始,先找3个,发现规律,再
验证运用规律.
类型一
类型二
类型三
类型一 数式的变化规律
例1(2019·安徽)观察以下等式:
∴S5= =-1-a,
4
∴S6=-S5-1=a.
1
1
∴S7= = =S1,
6
故此规律为 6 个一循环,
∵2 018÷6=336 余 2,
1+
∴S2 018=- .
1
2
3
4
5
6
7
4.(2018·黑龙江龙东区)如图,已知等边△ABC的边长是2,以BC边上
的高AB1为边作等边三角形,得到第一个等边△AB1C1;再以等边
(2)∵2 020÷3=673…1,∴需要小正方形674个,大正方形673个.
1
2
3
4
5
6
7
7.图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上
面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.
将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有
n(n + 1)
圆圈的个数为1+2+3+…+n= 2 .如果图3和图4中的圆圈各有13
为
.
类型一
类型二
类型三
分析:(1)观察图形,结合已知条件,得出将基本图每复制并平移一
次,特征点增加5个,由此得出图4中特征点的个数为17+5=22个,进
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2019安徽中考数学 规律探索题 专题训练
类型一 数式规律探索
1.观察下列等式，按照等式排列的规律填空：
①
121
1222=--， ②
221
2322=--， ③
32
1
3422=--， …
（1）根据上述规律，请写出第4个等式；
（2）写出第n 个等式（用含n 的代数式表示），并证明等式成立.
解：（1）由题中等式的变化规律可得，第4个等式为
421
4522=--； （2）第n 个等式是
n n n =--+2
1
)1(22. 证明：∵左边=21)1(22--+n n =21
1222--++n n n =n ，右边=n ，
∴第n 个等式是
n n n =--+2
1
)1(22成立. 2.观察下列等式：
第一个等式：2
212
21
2112213⨯-⨯=⨯⨯=
a ； 第二个等式：3
232231
2212324⨯-⨯=⨯⨯=a ； 第三个等式：4
343241
2312435⨯-
⨯=⨯⨯=a ； 第四个等式：5
454251
2412546⨯-
⨯=⨯⨯=a ； …
按上述规律，回答以下问题： （1）猜想并写出第n 个等式；
（2）证明你写出的等式的正确性.
解：（1）根据上述规律可得，第n 个等式：1
12)1(1
-212)1(2++•+•=•++=n n n n n n n n n a ；
（2）证明：∵右边=12)1(1-21+•+•n n n n =12)1(-1)2(+•++n n n n n =1
2
)1(2
+•++n n n n =左边， ∴等式成立.
类型二 图形规律探索
3.如图，用正三角形、正四边形和正六边形按如图所示的规律拼图案，即从第二个图案开始，每个图案中正三角形的个数都比上一个图案中正三角形的个数多4个.
第3题图 （1）求第四个图案中正三角形的个数；
（2）求第n 个图案中正三角形的个数（用含n 的代数式表示）. 解：（1）∵第一个图案中正三角形的个数为6=2+4×1； 第二个图案中正三角形的个数为10=2+2×4； 第三个图案中正三角形的个数为14=2+3×4； …
∴第四个图案中正三角形的个数为18=2+4×4；
（2）由（1）可得，第n 个图案中正三角形的个数为4n +2.
4.如图，是由m ×m （m 为奇数）个小正方形组成的图形，我们把图中所有的x ，y 相加得到的多项式称为“正方形多项式”.
第4题图
（1）观察以上图形并完成下表：
猜想：第n（n为正整数）个图形中的“正方形多项式”为；
（2）当x的个数为676个，y的个数为625个时，判断其是否在同一个“正方形多项式”中，并说明理由.
解：（1）36，25，36x+25y，(n+1)2x+n2y；
【解法提示】∵第1个图形中的“正方形多项式”为4x+y，第2个图形中的“正方形多项式”为9x+4y，第3个图形中的“正方形多项式”为16x+9y，第4个图形中的“正方形多项式”为25x+16y，∴第5个图形中的“正方形多项式”为36x+25y，∴第n（n为正整数）个图形中的“正方形多项式”为(n+1)2x+n2y.
（2）x、y在同一个“正方形多项式”中.理由如下：
当x的个数为676个时，(n+1)2=676，解得n=25，
当y的个数为625个时，n2=625，得n=25，
∴x、y在同一个“正方形多项式”中.。