章末检测 9
人教A版高中数学必修二第9章章末检测(含答案)

第九章章末检测(时间:120分钟,满分150分)一、选择题(本大题共8小题,每小题5分,共40分.)1.某防疫站对学生进行身体健康调查,欲采用分层随机抽样的方法抽取样本.某中学共有学生2 000名,从中抽取了一个样本量为200的样本,其中男生103名,则该中学共有女生为( )A .1 030名B .97名C .950名D .970名【答案】D 【解析】由题意,知该中学共有女生2 000×200-103200=970(名).故选D .2.(2020年北京期末)艺术体操比赛共有7位评委分别给出某选手的原始评分,评定该选手的成绩时,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分.5个有效评分与7个原始评分相比,不变的数字特征是( )A .中位数B .平均数C .方差D .极差【答案】A 【解析】根据题意,从7个原始评分中去掉1个最高分、1个最低分,得到5个有效评分,与7个原始评分相比,不变的中位数.故选A .3.(2020年河北月考)已知某校高一、高二年级学生人数均为600人,参加社团的高一和高二的人数比为2∶3,现从参加社团的同学中按分层抽样的方式抽取45人,则抽取的高二学生人数为( )A .9B .18C .27D .36【答案】C 【解析】由分层抽样的性质可得,抽取的高二学生人数为45×32+3=27.故选C .4.(2020年永州月考)在样本频率分布直方图中,共有5个小长方形,已知中间小长方形的面积是其余4个小长方形面积之和的13,且中间一组的频数为10,则这个样本量是( )A .20B .30C .40D .50【答案】C 【解析】所有长方形的面积和为1,因为中间小长方形的面积是其余4个小长方形面积之和的13,所以中间的面积为14,又中间一组的频数为10,所以样本容量为10÷14=40.故选C .5.(2019年惠州期末)某地区连续六天的最低气温(单位:℃)为:9,8,7,6,5,7,则该六天最低气温的平均数和方差分别为( )A .7和53B .8和83C .7和1D .8和23【答案】A 【解析】由题意,六天最低气温的平均数x =16×(9+8+7+6+5+7)=7,方差s 2=16×[(9-7)2+(8-7)2+(7-7)2+(6-7)2+(5-7)2+(7-7)2]=53.故选A .6.假设从高一年级全体同学(500人)中随机抽出60人参加一项活动,利用随机数法抽取样本时,先将500名同学按000,001,…,499进行编号,如果从随机数表第8行第11列的数开始,按三位数连续向右读取,最先抽出的4名同学的号码是(下面摘取了此随机数表第7行和第8行)( )84421 75331 57245 50688 77047 44767 21763 35025 63016 37859 16955 56719 98105 07175 12867 35807 A .455 068 047 447 B .169 105 071 286 C .050 358 074 439 D .447 176 335 025【答案】B 【解析】由随机数表法的随机抽样的过程可知最先抽出的4名同学的号码为169,105,071,286.7.(2020年阜阳期末)某单位去年的开支分布的折线图如图1所示,在这一年中的水、电、交通开支(单位:万元)如图2所示,则去年的水费开支占总开支的百分比为( )图1图2A .6.25%B .7.5%C .10.25%D .31.25%【答案】A 【解析】由拆线图知去年水、电、交通支出占总支出的百分比为20%,由条形图得去年水、电、交通支出合计为250+450+100=800(万元),其中水费支出250(万元),∴去年的水费开支占总开支的百分比为250800×20%=6.25%.故选A .8.在发生某公共卫生事件期间,有专业机构认为该事件在一段时间内没有发生大规模群体感染的标志为“连续10天,每天新增疑似病例不超过7人”.根据过去10天甲、乙、丙、丁四地新增疑似病例数据,一定符合该标志的是( )A .甲地:总体均值为3,中位数为4B .乙地:总体均值为1,总体方差大于0C .丙地:中位数为2,众数为3D .丁地:总体均值为2,总体方差为3【答案】D 【解析】A 中,中位数为4,可能存在大于7的数;同理,在C 中也有可能;B 中的总体方差大于0,叙述不明确,如果方差太大,也有可能存在大于7的数;D 中,因为平均数为2,根据方差公式,如果有大于7的数存在,那么方差不可能为3.故选D .二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,有选错的得0分,部分选对的得3分.9.下列叙述正确的是( )A .极差与方差都反映了数据的集中程度B .方差是没有单位的统计量C .标准差比较小时,数据比较分散D .只有两个数据时,极差是标准差的2倍【答案】AD 【解析】由极差与方差的定义可知A 正确;方差是有单位的,其单位是原始数据单位的平方,B 错误;标准差较小时,数据比较集中,C 错误;只有两个数据x 1,x 2时,极差等于|x 2-x 1|,平均数为x 1+x 22,所以方差s 2=12⎣⎢⎡⎦⎥⎤⎝ ⎛⎭⎪⎫x 1-x 1+x 222+⎝ ⎛⎭⎪⎫x 2-x 1+x 222=14(x 1-x 2)2,则标准差s 2=12|x 2-x 1|,D 正确.故选AD .10.某学校为了调查学生在一周生活方面的支出情况,抽出了一个样本量为n 的样本,其频率分布直方图如图所示,其中支出在[50,60)元的学生有60人,则下列说法正确的是( )A .样本中支出在[50,60)元的频率为0.03B .样本中支出不少于40元的人数有132C .n 的值为200D .若该校有2 000名学生,则一定有600人支出在[50,60)元【答案】BC 【解析】A 中,样本中支出在[50,60)元的频率为1-(0.01+0.024+0.036)×10=0.3,故A 错误;B 中,样本中支出不少于40元的人数有0.0360.03×60+60=132,故B 正确;C 中,n =600.3=200,故C 正确;D 中,若该校有2 000名学生,则可能有600人支出在[50,60)元,故D 错误.故选BC .11.某地某所高中2019年的高考考生人数是2016年高考考生人数的1.5倍,为了更好地对比该校考生的升学情况,统计了该校2016年和2019年的高考升学情况,得到如下柱状图:则下列结论正确的是()A.与2016年相比,2019年一本达线人数有所增加B.与2016年相比,2019年二本达线人数增加了0.5倍C.与2016年相比,2019年艺体达线人数相同D.与2016年相比,2019年不上线的人数有所增加【答案】AD【解析】依题意,设2016年高考考生人数为x,则2019年高考考生人数为1.5x,由24%·1.5x-28%·x=8%·x>0,故选项A正确;由(40%·1.5x-32%·x)÷32%·x =0.875,故选项B不正确;由8%·1.5x-8%·x=4%·x>0,故选项C不正确;由28%·1.5x -32%·x=10%·x>0,故选项D正确.故选AD.12.给出三幅统计图如图所示:A.从折线统计图能看出世界人口的变化情况B.2050年非洲人口将达到大约15亿C .2050年亚洲人口比其他各洲人口的总和还要多D .从1957年到2050年各洲中北美洲人口增长速度最慢【答案】AC 【解析】从折线统计图能看出世界人口的变化情况,故A 正确;从条形统计图中可知2050年非洲人口大约将大于15亿,故B 错误;从扇形统计图中可知2050年亚洲人口比其他各洲人口的总和还要多,故C 正确;由题中三幅统计图并不能得出从1957年到2050年中哪个洲人口增长速度最慢,故D 错误.故选AC .三、填空题(本大题共4小题,每小题5分,共20分,请把答案填写在题中横线上) 13.一支田径队有男运动员48人,女运动员36人,若用分层抽样的方法从该队的全体运动员中抽取一个样本量为21的样本,则抽取男运动员的人数为________.【答案】12 【解析】抽取的男运动员的人数为2148+36×48=12. 14.将样本量为100的某个样本数据拆分为10组,若前七组的频率之和为0.79,而剩下的三组的频率依次相差0.05,则剩下的三组中频率最高的一组的频率为________.【答案】0.12 【解析】设剩下的三组中频率最高的一组的频率为x ,则另两组的频率分别为x -0.05,x -0.1.因为频率总和为1,所以0.79+(x -0.05)+(x -0.1)+x =1,解得x =0.12.15.12,13,25,26,28,31,32,40的25%分位数为________.【答案】19 【解析】因为8×25%=2,8×80%=6.4,所以25%分位数为x 2+x 32=13+252=19.16.下图是根据某中学为地震灾区捐款的情况而制作的统计图,已知该校共有学生3 000人,由统计图可得该校共捐款为________元.【答案】37 770 【解析】由扇形统计图可知,该中学高一、高二、高三分别有学生960人、990人、1 050人.由条形统计图知,该中学高一、高二、高三人均捐款分别为15元、13元、10元,所以共捐款15×960+13×990+10×1 050=37 770(元).四、解答题(本大题共6小题,17题10分,其余小题为12分,共70分,解答应写出必要的文字说明、证明过程或演算步骤)17.为调查某班学生的平均身高,从50名学生中抽取110,应如何抽样?若知道男生、女生的身高显著不同(男生30人,女生20人),应如何抽样?解:从50名学生中抽取110,即抽取5人,采用简单随机抽样法(抽签法或随机数法).若知道男生、女生的身高显著不同,则采用分层抽样法,按照男生与女生的人数比为30∶20=3∶2进行抽样,则男生抽取3人,女生抽取2人.18.(2020年辽宁学业考试)某学校随机抽取部分新生调查其上学所需时间(单位:分钟),并将所得数据绘制成频率分布直方图(如图).已知上学所需时间的范围是[0,100],样本数据分组为[0,20),[20,40),[40,60),[60,80),[80,100].(1)求直方图中x的值;(2)如果上学所需时间在[60,100]的学生可申请在学校住宿,请估计该校800名新生中有多少名学生可以申请住宿.解:(1)由直方图可得到20x+0.025×20+0.006 5×20+0.003×2×20=1,解得x=0.012 5.(2)由直方图可知,新生上学所需时间在[60,100]的频率为0.003×2×20=0.12,所以800×0.12=96(名).所以800名新生中估计有96名学生可以申请住宿.19.某汽车制造厂分别从A,B两种轮胎中各随机抽取了8个进行测试,列出了每一个轮胎行驶的最远里程数(单位:1 000 km):轮胎A96112971081001038698轮胎B10810194105969397106(1)分别计算(2)分别计算A,B两种轮胎行驶的最远里程的极差、方差;(3)根据以上数据,你认为哪种型号轮胎的性能更加稳定?解:(1)A 轮胎行驶的最远里程的平均数为18×(96+112+97+108+100+103+86+98)=100,中位数为12×(100+98)=99.B 轮胎行驶的最远里程的平均数为18×(108+101+94+105+96+93+97+106)=100,中位数为12×(101+97)=99.(2)A 轮胎行驶的最远里程的极差为112-86=26,方差为18×[(-4)2+122+(-3)2+82+02+32+(-14)2+(-2)2]=55.25,B 轮胎行驶的最远里程的极差为108-93=15,方差为18×[82+12+(-6)2+52+(-4)2+(-7)2+(-3)2+62]=29.5,(3)根据以上数据,A 轮胎和B 轮胎的最远行驶里程的平均数相同,但B 轮胎行驶的最远里程的极差和方差相对于A 轮胎较小,所以B 轮胎性能更加稳定.20.某幼儿园根据部分同年龄段女童的身高数据绘制了频率分布直方图,其中身高的变化范围是[96,106](单位:厘米),样本数据分组为[96,98),[98,100),[100,102),[102,104),[104,106].(1)求出x 的值;(2)已知样本中身高小于100厘米的人数是36,求出总样本量N 的数值;(3)根据频率分布直方图提供的数据及(2)中的条件,求出样本中身高位于[98,104)的人数.解:(1)由题意(0.050+0.100+0.150+0.125+x )×2=1,解得x =0.075. (2)设样本中身高小于100厘米的频率为p 1,则p 1=(0.050+0.100)×2=0.300. 而p 1=36N ,∴N =36p 1=360.300=120.(3)样本中身高位于[98,104)的频率p 2=(0.100+0.150+0.125)×2=0.750,∴身高位于[98,104)的人数n =p 2N =0.750×120=90.21.为了让学生了解环保知识,增强环保意识,某中学举行了一次环保知识竞赛,共有900名学生参加了这次竞赛.为了了解本次竞赛的成绩情况,从中抽取了部分学生的成绩(得分取正整数,满分为100分)进行统计.请你根据下面尚未完成的频率分布表和频率分布直方图,解答下列问题:组号 分组 频数 频率 1 [50,60) 4 0.08 2 [60,70) 8 0.16 3 [70,80) 10 0.20 4 [80,90) 16 0.32 5 [90,100] 合计—(1)填充频率分布表中的空格;(2)如图,不具体计算频率组距,补全频率分布直方图;(3)估计这900名学生竞赛的平均成绩(结果保留整数,同一组中的数据用该组区间的中点值作代表).解:(1)40.08=50,即样本量为50.第5组的频数为50-4-8-10-16=12,从而第5组的频率为1250=0.24.又各小组频率之和为1,所以频率分布表中的四个空格应分别填12,0.24,50,1.(2)设第一个小长方形的高为h 1,第二个小长方形的高为h 2,第五个小长方形的高为h 5,则h 1h 2=48=12,h 1h 5=412=13. 补全的频率分布直方图如图所示.(3)50名学生竞赛的平均成绩为x =4×55+8×65+10×75+16×85+12×9550=79.8≈80(分).所以估计这900名学生竞赛的平均成绩约为80分.22.共享单车入驻泉州一周年以来,因其“绿色出行,低碳环保”的理念而备受人们的喜爱,值此周年之际,某机构为了了解共享单车使用者的年龄段、使用频率、满意度等三个方面的信息,在全市范围内发放5 000份调查问卷,回收到有效问卷3 125份,现从中随机抽取80份,分别对使用者的年龄段、26~35岁使用者的使用频率、26~35岁使用者的满意度进行汇总,得到如下三个表格:表(一)使用者年龄段25岁以下26岁~35岁36岁~45岁45岁以上人数2040 1010表(二)使用频率 0~6次/月7~14次/月15~22次/月23~31次/月人数510 205表(三)满意度 非常满意(9~10)满意(8~9)一般(7~8)不满意(6~7)人数1510105(1)依据上述表格完成下列三个统计图形:(2)某城区现有常住人口30万,请用样本估计总体的思想,试估计年龄在26岁~35岁之间,每月使用共享单车在7~14次的人数.解:(1)(2)由表(一)可知年龄在26岁~35岁之间的有40人,占总抽取人数的12,所以30万人口中年龄在26岁~35岁之间的约有30×12=15(万人).由表(二)可知,年龄在26岁~35岁之间每月使用共享单车在7~14次之间的有10人,占总抽取人数的14,所以年龄在26岁~35岁之间的15万人中,每月使用共享单车在7~14次之间的约有15×14=154(万人).。
高中化学选择性必修二 第一章章末检测练习下学期(解析版)

第一章章末检查一、选择题1.元素周期表长周期共有18个纵行,从左到右排为18列,即碱金属是第1列,稀有气体是第18列。
按这种规定,下列说法正确的是()A.第9列元素中没有非金属B.第15列元素的原子最外层的电子排布是n s2n p5C.最外层电子排布为n s2的元素一定在第2列D.第11、12列为d区的元素【答案】A【解析】第9列元素是过渡元素,没有非金属,A项正确;第15列元素的最外层电子排布是n s2n p3,B项错误;最外层电子排布为n s2的元素也可能是过渡元素或0族元素He,C项错误;11、12列为ds区元素,D项错误。
2.金属钛对人体的体液无毒且有惰性,能与肌肉和骨骼生长在一起,有“生物金属”之称。
下列有关Ti和Ti的说法中正确的是()A.Ti和Ti的质量数相同,互称为同位素B.Ti和的质子数相同,互称同位素C.Ti和Ti的质子数相同,是同一种核素D.Ti和Ti核外电子数相同,中子数不同,不能互称为同位素【答案】B【解析】同位素的质子数相等,中子数不相等。
Ti和Ti的质子数均为22,中子数分别为26和28。
3.自从1803年英国化学家、物理学家道尔顿提出原子假说以来,人类对原子结构的研究不断深入、不断发展,通过实验事实不断地丰富、完善原子结构理论。
请判断下列关于原子结构的说法正确的是()A.所有的原子都含有质子、中子和电子三种基本构成微粒B.所有的原子中的质子、中子和电子三种基本构成微粒的个数都是相等的C.原子核对电子的吸引作用的实质是原子核中的质子对核外电子的吸引D.原子中的质子、中子和电子三种基本构成微粒不可能再进一步分成更小的微粒【答案】C【解析】所有的原子都含有质子和电子,并且二者在数值上是相等的。
因为质子和电子带的电荷相等,而电性相反,故整个原子是电中性的。
需要注意的是,并不是所有的原子都是由质子、中子和电子组成的,如H中就只含有一个质子和一个电子,没有中子。
多数原子的中子数和质子数比较接近但没有必然的数量关系,A、B错误。
2020学年新教材高中数学第九章统计章末综合检测(九)新人教A版必修第二册(最新整理)

2019-2020学年新教材高中数学第九章统计章末综合检测(九)新人教A 版必修第二册编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019-2020学年新教材高中数学第九章统计章末综合检测(九)新人教A版必修第二册)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019-2020学年新教材高中数学第九章统计章末综合检测(九)新人教A版必修第二册的全部内容。
章末综合检测(九)(时间:120分钟,满分:150分)一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.某公司生产A,B,C三种不同型号的轿车,其产量之比为2∶3∶4,为检验该公司的产品质量,用分层随机抽样的方法抽取一个容量为n的样本,若样本中A种型号的轿车比B种型号的轿车少8辆,则n=()A.96 B.72C.48 D.36解析:选B。
由题意得错误!n-错误!n=8,所以n=72。
故选B.2.从某一总体中抽取一个个体数为200的样本,得到分组与频数如下:[10,15),6;[15,20),8;[20,25),13;[25,30),35;[30,35),46;[35,40),34;[40,45),28;[45,50),15;[50,55),10;[55,60],5。
则样本在[35,60]上的频率是( )A.0。
69 B.0.46C.1 D.不存在解析:选B.由题可知,样本在[35,60]上的频率应为(34+28+15+10+5)÷200=0。
46.3.2019年高考某题的得分情况如下:得分(分)01234百分率(%)37.08。
九年级 数学《第二十一章_一元二次方程_》章末检测 考试卷

5·3全练《第二十一章 一元二次方程 》章末检测1.(2019江苏盐城东台期中)下列关于x 的方程中,一定是元二次方程的为( )A. 222(3)x x -=+ B. 20ax bx c ++=C. 2350x x+-= D. 210x -=2.(2019天津宁河期中)x =2不是下列哪一个方程的解?( ) A. 3(2)0x -= B. 2232x x -= C. (2)(2)0x x -+= D. 220x x -+=3.(2020河南郑州金水月考)用配方法解方程224x x -=,下列配方正确的是( )A. 2(2)6x -=B. 2(2)2x += C. 2(2)2x -=- D. 2(2)2x -=4.(2020江西南昌进贤期中)不解方程,判断下列一元二次方程中,一定有实数根的是( ) A. 240x x -+= B. 220x x -+-= C. 2420190x x --= D. 220200x x -+=5.(2020广西来宾忻城期中)已知关于x 的方程22210x mx m --+=的一个根是2-,则m 的值是( )A.5或-1B.-5或-1C.5或1D.-5或16.(2019河南周口川汇期中)在设计人体雕像时,使雕像的上部与下部的高度比等于下部与全部的高度比可以增加视觉美感.如果雕像高度为2m ,设雕像下部高为x m ,则x 满足( )A. 22(2)x x =-B. 2(2)2x x -= C. 22(2)x x =+ D. 2(2)2x x +=7.(2020独家原创试题)若()22220a =,则2a 的值为( )A. 2+B. 2C. 2+或2-D. 2-8.(2019贵州遵义中考)一元二次方程2310x x -+=的两个根为12x x ,,则2121232x x x x ++-的值是( )A.10B.9C.8D.79.(2020独家原创试题)一个菱形两条对角线的长是方程214480x x -+=的两个根,则该菱形的面积为( )A.48B.24C.14或24D.24或4810.如图,要设计一幅宽为20cm ,长为30cm 的矩形图案,其中有两横两竖的彩条,横、竖彩条的宽度比为2:3,如果要使所有彩条所占面积为原矩形图案面积的三分之一,那么横彩条和竖彩条的宽度分别是( )A. 2cm 和3cmB.13和12cm C. 53cm 和52cm D. 25cm 和35cm二、填空题(每小题3分,共24分)11.(2020江苏苏州太仓期中)将一元二次方程1(2)53x x -=化为二次项系数为“1”的一般形式是_______.12.(2019吉林延边安图月考)若2x =-是关于x 的一元二次方程240ax -=的一个解,则这个方程的另一个解是_______.13.已知代数式2(1)x x +与代数式33x -的值互为相反数,则x 的值为_______.14.关于x 的方程23ax bx c ++=的解与(1)(4)0x x --=的解相同,则5a b +的值为______.15.(2019湖南邵阳中考)关于x 的一元二次方程220x x m --=有两个不相等的实数根,则m 的最小整数值是_______.16.(2018湖北潜江月考)一人患了流感,经过两轮传染后共有64人患了流感如果不及时控制,第三轮将又有_____人被传染.17.(2019湖南张家界中考)《田亩比类乘除捷法》是我国古代数学家杨辉的著作,其中有一个数学问题:“直田积八百六十四步,只云长阔共六十步,问长多阔几何?”意思是:一块矩形田地的面积为864平方步,只知道它的长与宽共60步,问它的长比宽多多少步?根据题意得,长比宽多_______步.18.(2019四川成都中考)已知12x x ,是关于x 的一元二次方程2210x x k ++-=的两个实数根,且22121213x x x x -+=,则k 的值为_______.三、解答题(共46分)19.(每小题4分,共8分)用适当的方法解下列方程:(1)22(31)(1)x x -=+;(2)21202x x +-=.20.(2019广西玉林中考)(8分)某养殖场为了响应党中央的扶贫政策,今年起采用“场内+农户”养殖模式,同时加强对蛋鸡的科学管理,蛋鸡的产蛋率不断提高,三月份和五月份的产蛋量分别是2.5万kg 与3.6万kg ,现假定该养殖场蛋鸡产蛋量的月增长率相同. (1)求该养殖场蛋鸡产蛋量的月增长率;(2)假定当月产的鸡蛋当月在各销售点全部销售出去,且每个销售点每月平均销售量最多为0.32万kg 如果要完成六月份的鸡蛋销售任务,那么该养殖场在五月份已有的销售点的基础上至少再增加多少个销售点?21.(2017四川南充中考)(10分)已知关于x 的一元二次方程2(3)0x m x m ---=.(1)求证:方程有两个不相等的实数根;(2)如果方程的两实根为12x x 、,且2122127x x x x -+=,求m 的值.22.(2020河南郑州中原月考)(10分)如下图,要利用面墙(墙长为55m ),用100m 的围栏建羊圈,基本结构为三个大小相同的矩形.(1)如果围成的总面积为400m 2,求羊圈的边AB ,BC 长各为多少? (2)保持羊圈的基本结构,羊圈总面积是否可以达到800m 2?请说明理由.23.(2019重庆汐坪坝月考)(10分)小飞文具店今年7月份购进一批笔记本,共2290本,每本进价为10元,该文具店决定从8月份开始进行销售,若每本售价为11元,则可全部售完;且每本售价每增长1元,销量就减少30本.(1)若该种笔记本在8月份的销售量不低于2200本,则8月份每本售价应不高于多少元?(2)由于生产商提高造纸工艺,该笔记本的进价提高了10%,文具店为增加笔记本的销量进行了销售调整,售价比8月份在(1)的条件下的最高售价减少了17%m,结果9月份的销量比8月份在(1)的条件下的最低销量增加了%m,9月份的销售利润达到6600元,求m的值.参考答案1.答案:D解析:选项A ,整理得6110x +=,所以不是一元二次方程;选项B ,20ax bx c ++=中未明确a 的取值情况,所以不一定是一元二次方程;选项C ,2350x x+-=不是整式方程,所以不是一元二次方程;选项D ,210x -=是一元二次方程.故选D. 2.答案:D解析:将x =2代入各方程左边,选项A ,左边=3(22)⨯-=0,右边=0,故x =2是3(2)x ⨯-的解;选项B ,左边=22232⨯-⨯=2,右边=2,故x =2是2232x x -=的解;选项C ,左边=(2-2)×(2+2)=0,右边=0,故x =2是(2)(2)0x x -+=的解;选项D ,左边=22-2+2=4,右边=0,故x =2不是220x x -+=的解.故选D.3.答案:A解析:移项得242x x -=,配方得24424x x -+=+,即2(2)6x -=.故选A.4.答案:C解析:选项A 中,∵2(1)414150∆=--⨯⨯=-<,∴方程没有实数根;选项B 中∵214(1)(2)70∆=-⨯-⨯-=-<,∴方程没有实数根;选项C ,2(4)41(2019)80920∆=--⨯⨯-=>,方程有两个不相等的实数根;选项D 中,∵2(1)41202080790∆=--⨯⨯=-<,∴方程没有实数根故选C. 5.答案:A解析:把x =-2代入方程22210x mx m --+=,得24410m m +-+=.解得m =5(经检验满足Δ≥0)或m =-1(经检验满足Δ≥0).故选A. 6.答案:A解析:因为雕像下部高为x m ,所以雕像上部高为(2)x - m ,根据题意得22x xx-=,即22(2)(0)x x x =-≠.故选A.7.答案:A解析:∵()22220a =,22a +=±22a =或22a =-,即2a 的值为2.故选A. 8.答案:D解析:由根与系数的关系得123x x +=,121x x = .∵1x 为一元二次方程2310x x -+=的根,∴211310x x -+=,21131x x =-,()21212121212123231323333x x x x x x x x x x x x ++-=-++-=++-=⨯137+-=.故选D.9.答案:B解析:因式分解,得(6)(8)0x x --=,1268x x ==,,即菱形两条对角线长为6和8,菱形的面积=168242=⨯⨯=.故选B. 10.答案:C解析:设横彩条的宽度为x c m ,则竖彩条的宽度为32x c m ,由题图可知一个横彩条的面积为(20)x ⨯ c m 2,一个竖彩条的面积为3302x ⎛⎫⨯ ⎪⎝⎭c m 2,有四个重叠的部分,重叠部分的面积为342x x ⎛⎫⨯⨯ ⎪⎝⎭c m 2,因为所有彩条所占面积为原矩形图案面积的三分之一,所以列方程为33122023042030223x x x x ⨯⨯+⨯⨯-⨯⨯=⨯⨯,解得125203x x ==,(不合题意,舍去),所以横彩条的宽度为53cm ,竖彩条的宽度为52cm.故选C.二、填空题11.答案:22150x x --=解析:方程两边都乘3得(2)15x x -=,化为一般形式是22150x x --=. 12.答案:2x =解析:把2x =-代入方程240ax -=得440a -=, 解得1a =(经检验满足题意),设另一个解为1x ,则124x -=-,所以12x =,故方程的另一个解是2x =.13.答案:12或-3解析:根据题意得2(1)330x x x ++-=,整理得22530x x +-=,其中253a b c ===-,,,所以224542(3)490b ac ∆=-=-⨯⨯-=>,所以5572224b x a -±-±-±===⨯,所以12132x x ==-,.故x 的值为12或-3.14.答案:0解析:因为(1)(4)0x x --=,所以10x -=或40x -=,所以1214x x ==, 把1x =代入方程23ax bx c ++=,得3a b c ++=,把4x =代入方程23ax bx c ++=,得1643a b c ++=,所以164a b c a b c ++=++,整理得50a b +=.15.答案:0解析:一元二次方程220x x m --=有两个不相等的实数根,∴440m ∆=+>,1m >-,又大于-1的最小整数是0,故答案为0. 16.答案:448解析:设一个患者一轮传染x 人, 根据题意得1(1)64x x x +++=, 整理得22630x x +-=,解得1279x x ==-,(不合题意,舍去), 第三轮将传染64⨯7=448(人). 17.答案:12解析:设长为x 步,则宽为(60)x -步,由题意得(60)x x -=864,解得123624x x ==,(舍去),当36x =时,6024x -=,长比宽多36-24=l2(步). 18.答案:-2解析:根据题意得121221x x x x k +=-=-,,∴()22212121212343(1)13x x x x x x x x k +-=+-=--=,2k =-(经检验满足题意).三、解答题19.解:(1)移项,得22(31)(1)0x x --+=.因式分解,得(311)(311)0x x x x -++---=, 即8(1)0x x -=.于是有80x =或10x -=, ∴1201x x ==,.(2)1212a b c ===-,,,2214142502b ac ⎛⎫-=-⨯⨯-=> ⎪⎝⎭,∴方程有两个不相等的实数根.∴x ===,∴121144x x ---== 20.解:(1)设该养殖场蛋鸡产蛋量的月增长率为x ,根据题意,得22.5(1)3.6x +=,解得120.220% 2.2x x ===-,(舍去). 答:该养殖场蛋鸡产蛋量的月增长率为20%. (2)设再增加y 个销售点,根据题意,得3.60.32 3.6(120%)y +≥⨯+,解得94y ≥,又y 取整数,∴3y ≥. 答:至少再增加3个销售点.2l.解:(1)证明:∵2(3)0x m x m ---=,∴222[(3)]41()29(1)80m m m m m ∆=---⨯⨯-=-+=-+>,∴方程有两个不相等的实数根.(2)∵方程2(3)0x m x m ---=的两实根为12x x 、,且2212127x x x x +-=,∴123x x m +=-,12x x m =-,()2121237x x x x +-=,∴2(3)3()7m m --⨯-=,解得1212m m ==,, 故m 的值是1或2.22.解:(1)设AB=x m ,则BC=(1004)x -m , ∵100455x -≤, ∴11.25x ≥.由题意知,(1004)400x x -=,即2251000x x -+=, 解得12205x x ==,(舍), ∴AB=20m ,BC=100-4×20=20m.答:羊圈的边AB 长为20m ,BC 长为20m. (2)不能.理由:设AB=y m 时,羊圈总面积可以达到800m 2, 由题意,得(1004)800y y -=,即2252000y y -+=,∵125200a b c ==-=,,, ∴224(25)412001750b ac -=--⨯⨯=-<,∴方程无实数根,∴羊圈总面积不可能达到800m 2. 23.解:(1)设8月份每本售价为x 元, 依题意得229030(11)2200x --≥, 解得14x ≤.初中数学精选习题3 / 3 答:8月份每本售价应不高于14元.(2)9月份每本的进价为10(110%)⨯+元,每本售价为1141%7m ⎛⎫⨯- ⎪⎝⎭元, 根据题意,得1141%10(110%)2200(1%)66007m m ⎡⎤⎛⎫--+⨯+= ⎪⎢⎥⎝⎭⎣⎦, 令%m t =,则原方程可化为(32)(1)3t t -+=,解得10t =(不合题意,舍去),20.5t =,则50m =.答:m 的值是50.。
高中数学必修二:各章章末检测(含解析)
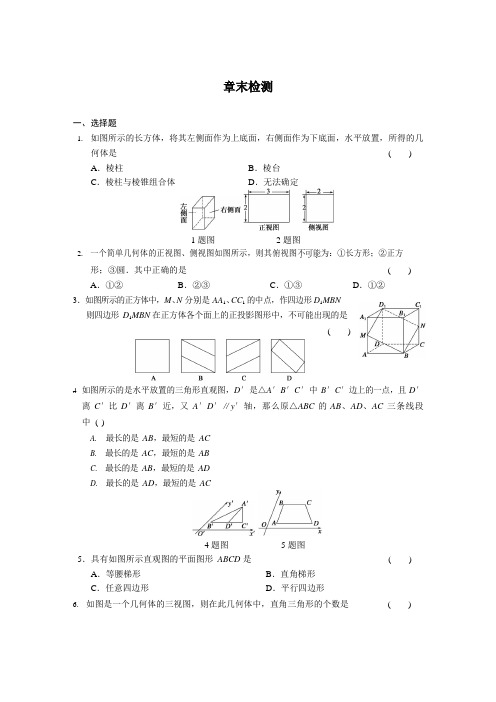
章末检测一、选择题1.如图所示的长方体,将其左侧面作为上底面,右侧面作为下底面,水平放置,所得的几何体是( ) A.棱柱B.棱台C.棱柱与棱锥组合体D.无法确定1 题图2 题图2.一个简单几何体的正视图、侧视图如图所示,则其俯视图不.可.能.为:①长方形;②正方形;③圆.其中正确的是( ) A.①②B.②③C.①③D.①②3.如图所示的正方体中,M、N分别是AA1、CC1的中点,作四边形D1MBN则四边形D1MBN 在正方体各个面上的正投影图形中,不可能出现的是( )4.如图所示的是水平放置的三角形直观图,D′是△A′B′C′中B′C′边上的一点,且D′离C′比D′离B′近,又A′D′∥y′轴,那么原△ABC 的AB、AD、AC 三条线段中( )A.最长的是AB,最短的是ACB.最长的是AC,最短的是ABC.最长的是AB,最短的是ADD.最长的是AD,最短的是AC4 题图5 题图5.具有如图所示直观图的平面图形ABCD 是( ) A.等腰梯形B.直角梯形C.任意四边形D.平行四边形6.如图是一个几何体的三视图,则在此几何体中,直角三角形的个数是( )A .1B .2C .3D .47. 如图,网格纸上小正方形的边长为 1,粗线画出的是某几何体的三视图,则此几何体的体积为()A .6B .9C .12D .188. 平面α截球 O 的球面所得圆的半径为 1,球心 O 到平面α的距离为 2,则此球的体积为() B .4 3πC .4 6πD .6 3π9. 如图所示,则这个几何体的体积等于()A .4B .6C .8D .1210. 将正三棱柱截去三个角(如图 1 所示,A ,B ,C 分别是△GHI 三边的中点)得到几何体如图 2,则该几何体按图 2 所示方向的侧视图为选项图中的()11. 圆锥的表面积是底面积的 3 倍,那么该圆锥的侧面展开图扇形的圆心角为( )A .120°B .150°C .180°D .240°12. 已知三棱锥 S -ABC 的所有顶点都在球 O 的球面上,△ABC 是边长为 1 的正三角形,SC 为球 O 的直径,且 SC =2,则此棱锥的体积为()A. 6πA.26二、填空题B.36 C.23 D.2213.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的(填入所有可能的几何体前的编号).①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱14.已知某三棱锥的三视图(单位:cm)如图所示,则该三棱锥的体积等于cm3.15.已知各顶点都在一个球面上的正四棱柱高为4,体积为16,则这个球的表面积是.16.一个水平放置的圆柱形储油桶(如图所示),桶内有油部分所在圆弧占底面圆周长的1,则油桶直立时,油的高度与桶的高度的比值是.4三、解答题17.某个几何体的三视图如图所示(单位:m),(1)求该几何体的表面积(结果保留π);(2)求该几何体的体积(结果保留π).18.如图是一个空间几何体的三视图,其中正视图和侧视图都是边长为2 的正三角形,俯视图如图.(1)在给定的直角坐标系中作出这个几何体的直观图(不写作法);(2)求这个几何体的体积.19.如图所示,在四边形ABCD 中,∠DAB=90°,∠ADC=135°,AB=5,CD=2 2,AD=2,求四边形ABCD 绕AD 旋转一周所成几何体的表面积及体积.20.如图所示,有一块扇形铁皮OAB,∠AOB=60°,OA=72 cm,要剪下来一个扇形环ABCD,作圆台形容器的侧面,并且余下的扇形OCD 内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面).试求:(1)AD 的长;(2)容器的容积.= 答案1.A 2.B 3.D 4.C 5.B 6.D 7.B 8.B 9.A 10.A 11.C 12.A 13.①②③⑤ 14.1 15.24π 16.1- 1 4 2π17.解 由三视图可知:该几何体的下半部分是棱长为 2 m 的正方体,上半部分是半径为 1 m 的半球.(1) 几何体的表面积为 S 1× 24π×12+6×22-π×12=24+π(m 2).(2)几何体的体积为 V =23+1×4×π×13=8+2π(m 3).2 3 318.解 (1)直观图如图.(2) 这个几何体是一个四棱锥. 它的底面边长为 2,高为 3,所以体积 V =1×22× 3=4 3.3 319.解 S 表面=S 圆台底面+S 圆台侧面+S 圆锥侧面=π×52+π×(2+5)×5+π×2×2 2=(4 2+60)π.V =V 圆台-V 圆锥 =1π(r 2+r r +r 2)h -12 ′1 12 2 3πr 1h3 =1π(25+10+4)×4-1π×4×2 3 3 148 π. 320.解 (1)设圆台上、下底面半径分别为 r 、R ,AD =x ,则 OD =72-x ,由题意得2πR =60·π×72 180 72-x =3R即 AD 应取 36 cm.R =12,∴ .x =36 (2)∵2πr =π·OD =π·36,3 3 ∴r =6 cm ,圆台的高 h = x 2-(R -r )2= 362-(12-6)2=6 35. ∴V =1 2+Rr +r 2)=1π·6 35·(122+12×6+62)=504 35π(cm 3).πh (R 3 3=章末检测一、选择题1.下列推理错误的是( ) A.A∈l,A∈α,B∈l,B∈α⇒l⊂αB.A∈α,A∈β,B∈α,B∈β⇒α∩β=ABC.l⊄α,A∈l⇒A∉α D.A∈l,l⊂α⇒A∈α2.长方体ABCD-A1B1C1D1 中,异面直线AB,A1D1 所成的角等于( ) A.30°B.45°C.60°D.90°3.下列命题正确的是( )A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行4.在空间四边形ABCD 的边AB,BC,CD,DA 上分别取E、F、G、H 四点,如果EF,GH 交于一点P,则( )A.P 一定在直线BD 上B.P 一定在直线AC 上C.P 一定在直线AC 或BD 上D.P 既不在直线AC 上,也不在直线BD 上5.给定下列四个命题:①若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行;②若一个平面经过另一个平面的垂线,那么这两个平面相互垂直;③垂直于同一直线的两条直线相互平行;④若两个平面垂直,那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直.其中,为真命题的是( )A.①和②B.②和③C.③和④D.② 和④ 6.已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,直线AB∥l,直线AC⊥l,直线m∥α,m∥β,则下列四种位置关系中,不一定成立的是( )A.AB∥m B.AC⊥m C.AB∥βD.AC⊥β7.如图(1)所示,在正方形SG1G2G3 中,E,F 分别是G1G2 及G2G3 的中点,D 是EF 的中点,现在沿SE,SF 及EF 把这个正方形折成一个四面体,使G1,G2,G3 三点重合,重合后的点记为G,如图(2)所示,那么,在四面体S-EFG 中必有( )A.SG⊥△EFG 所在平面B.SD⊥△EFG 所在平面C.GF⊥△SEF 所在平面D.GD⊥△SEF 所在平面8.如图所示,在正方体ABCD—A1B1C1D1 中,若E 是A1C1 的中点,则直线CE 垂直于( )A.AC B.BD C.A1D D.A1D18 题图9 题图9.如图所示,将等腰直角△ABC 沿斜边BC 上的高AD 折成一个二面角,此时∠B′AC=60°,那么这个二面角大小是( ) A.90°B.60°C.45°D.30°10.如图,ABCD-A1B1C1D1 为正方体,下面结论错误的是( )A.BD∥平面CB1D1B.AC1⊥BDC.AC1⊥平面CB1D1D.异面直线AD 与CB1 所成的角为60°10 题图11 题图11.如图所示,在长方体ABCD—A1B1C1D1 中,AB=BC=2,AA1=1,则BC1 与平面BB1D1D所成角的正弦值为( )A. 63B.2 65C. 155D. 10512.已知正四棱柱ABCD-A1B1C1D1 中,AB=2,CC1=2 2,E 为CC1 的中点,则直线AC1与平面BED 的距离为( )A.2二、填空题D.113.设平面α∥平面β,A、C∈α,B、D∈β,直线AB 与CD 交于点S,且点S 位于平面α,β之间,AS=8,BS=6,CS=12,则SD=.14.下列四个命题:①若a∥b,a∥α,则b∥α;②若a∥α,b⊂α,则a∥b;③若a∥α,则B. 3C. 2a 平行于α内所有的直线;④若a∥α,a∥b,b⊄α,则b∥α.其中正确命题的序号是.15.如图所示,在直四棱柱ABCD—A1B1C1D1 中,当底面四边形A1B1C1D1 满足条件时,有A1C⊥B1D1(注:填上你认为正确的一种情况即可,不必考虑所有可能的情况).15 题图16 题图16.如图所示,已知矩形ABCD 中,AB=3,BC=a,若PA⊥平面AC,在BC 边上取点E,使PE⊥DE,则满足条件的E 点有两个时,a 的取值范围是.三、解答题17.如图所示,长方体ABCD-A1B1C1D1 中,M、N 分别为AB、A1D1 的中点,判断MN 与平面A1BC1 的位置关系,为什么?18.ABCD 与ABEF 是两个全等正方形,AM=FN,其中M∈AC,N∈BF.求证:MN∥平面BCE.19.如图,在四棱锥P-ABCD 中,底面ABCD 是矩形,PA⊥底面ABCD,E 是PC 的中点.已知AB=2,AD=2 2,PA=2.求:(1)三角形PCD 的面积;(2)异面直线BC 与AE 所成的角的大小.20.如图所示,ABCD 是正方形,O 是正方形的中心,PO⊥底面ABCD,底面边长为a,E 是PC 的中点.(1)求证:PA∥面BDE;(2)求证:平面PAC⊥平面BDE;(3)若二面角E-BD-C 为30°,求四棱锥P-ABCD 的体积.21.如图,四棱锥P-ABCD 中,底面ABCD 为菱形,PA⊥底面ABCDAC=2 2,PA=2,E 是PC 上的一点,PE=2EC.(1)证明:PC⊥平面BED;(2)设二面角A-PB-C 为90°,求PD 与平面PBC 所成角的大小.答案1.C 2.D 3.C 4.B 5.D 6.D 7.A 8.B 9.A 10.D 11.D 12.D 13.914.④15.B1D1⊥A1C1(答案不唯一)16.a>617.解直线MN∥平面A1BC1,M 为AB 的中点,证明如下:∵MD/∈平面A1BC1,ND/∈平面A1BC1.∴MN⊄平面A1BC1.如图,取A1C1 的中点O1,连接NO1、BO1.∵NO1 綊1D1C1,MB 綊1D1C1,2 2∴NO1 綊MB.∴四边形NO1BM 为平行四边形.∴MN∥BO1.又∵BO1⊂平面A1BC1,∴MN∥平面A1BC1.18.证明如图所示,连接AN,延长交BE 的延长线于P,连接CP.∵BE∥AF,∴FN=AN,NB NP由AC=BF,AM=FN 得MC=NB.∴FN=AM. NB MC∴AM=AN,MC NP∴MN∥PC,又PC⊂平面BCE.AC ∴MN ∥平面 BCE .19. 解 (1)因为 PA ⊥底面 ABCD ,所以 PA ⊥CD .又 AD ⊥CD ,所以 CD ⊥平面 PAD ,从而 CD ⊥PD . 因 为 PD = 22+(2 2)2=2 3,CD =2,所以三角形 PCD 的面积为1×2×2 3=2 3.2(2)如图,取 PB 中点 F ,连接 EF 、AF ,则 EF ∥BC ,从而∠AEF (或其补角)是异面直线BC 与 AE 所成的角.在△AEF 中,由 EF = 2,AF = 2,AE =2 知△AEF 是等腰直角三角形, 所以∠AEF =45°.因此,异面直线 BC 与 AE 所成的角的大小是 45°. 20.(1)证明 连接 OE ,如图所示.∵O 、E 分别为 AC 、PC 的中点,∴OE ∥P A. ∵OE ⊂面 BDE ,PA ⊄面 BDE , ∴PA ∥面 BDE .(2) 证明 ∵PO ⊥面 ABCD ,∴PO ⊥BD .在正方形 ABCD 中,BD ⊥AC , 又∵PO ∩AC =O , ∴BD ⊥面 PAC . 又∵BD ⊂面 BDE , ∴面 PAC ⊥面 BDE .(3) 解 取 OC 中点 F ,连接 EF .∵E 为 PC 中点,∴EF 为△POC 的中位线,∴EF ∥PO . 又∵PO ⊥面 ABCD ,∴EF ⊥面 ABCD . ∵OF ⊥BD ,∴OE ⊥BD .∴∠EOF 为二面角 E -BD -C 的平面角,∴∠EOF =30°.在 Rt △OEF 中,OF =1OC =1 = 2a ,∴EF =OF ·tan 30°= 6a ,2 4 4 12 ∴OP =2EF = 6a .62 3 ∴V P1 6 6-ABCD= ×a × = . 361821.(1)证明 因为底面 ABCD 为菱形, 所以 BD ⊥AC .又 PA ⊥底面 ABCD ,所以 PC ⊥BD . 如图,设 AC ∩BD =F ,连接 EF .因为 AC =2 2,PA =2,PE =2EC ,故 PC =2 3,EC =2 3,FC = 2,3从而PC= 6,FC AC= 6. EC因为PC =AC,∠FCE =∠PCA ,FC EC所以△FCE ∽△PCA ,∠FEC =∠PAC =90°.由此知 PC ⊥EF . 因为 PC 与平面 BED 内两条相交直线 BD ,EF 都垂直, 所以 PC ⊥平面 BED .(2)解 在平面 PAB 内过点 A 作 AG ⊥PB ,G 为垂足. 因为二面角 A -PB -C 为 90°, 所以平面 PAB ⊥平面 PBC . 又平面 PAB ∩平面 PBC =PB , 故 AG ⊥平面 PBC ,AG ⊥BC .因为 BC 与平面 PAB 内两条相交直线 PA ,AG 都垂直, 故 BC ⊥平面 PAB ,于是 BC ⊥AB , 所以底面 ABCD 为正方形,AD =2, PD = PA 2+AD 2=2 2. 设 D 到平面 PBC 的距离为 d .因为 AD ∥BC ,且 AD ⊄平面 PBC ,BC ⊂平面 PBC ,故 AD ∥平面 PBC ,A 、D 两点到平面 PBC 的距离相等,即 d =AG = 2. 设 PD 与平面 PBC 所成的角为α,则 sin α= d =1.PD 2 所以 PD 与平面 PBC 所成的角为 30°.章末检测一、选择题1.若直线过点(1,2),(4,2+ 3),则此直线的倾斜角是()A .30°B .45°C .60°D .90°2.如果直线 ax +2y +2=0 与直线 3x -y -2=0 平行,则系数 a 为 ( )A .-3B .-6C .-3 2 3.若经过点(3,a )、(-2,0)的直线与经过点(3,-4) 1D.2 3 a 的值为( )且斜率为 的直线垂直,则 2A.5 2B.2 5 C .10 D .-104.过点(1,0)且与直线 x -2y -2=0 平行的直线方程是 ( )A .x -2y -1=0B .x -2y +1=0C .2x +y -2=0D .x +2y -1=05.实数 x ,y 满足方程 x +y -4=0,则 x 2+y 2 的最小值为 A .4 B .6 C .8 ()D .126.点 M (1,2)与直线 l :2x -4y +3=0 的位置关系是 () A .M ∈l B .M ∉l C .重合 D .不确定7.直线 mx +ny -1=0 同时过第一、三、四象限的条件是()A .mn >0B .mn <0C .m >0,n <0D .m <0,n <08. 若点 A (-2,-3),B (-3,-2),直线 l 过点 P (1,1)且与线段 AB 相交,则 l 的斜率 k 的取值范围是() A .k ≤3或 k ≥4B .k ≤-4或 k ≥-34 3 C.3≤k ≤4 3 4 D .-4≤k ≤-34 33 49.已知直线 l 1:ax +4y -2=0 与直线 l 2:2x -5y +b =0 互相垂直,垂足为(1,c ),则 a +b +c 的值为 ()A .-4B .20C .0D .2410.过点 P (0,1)且和 A (3,3),B (5,-1)距离相等的直线的方程是() A .y =1B .2x +y -1=0C .y =1 或 2x +y -1=0D .2x +y -1=0 或 2x +y +1=011. 直线 mx +ny +3=0 在 y 轴上的截距为-3,而且它的倾斜角是直线 3x -y =3 3倾斜角的 2 倍,则 ()A .m =- 3,n =1B .m =- 3,n =-3C .m = 3,n =-3D .m = 3,n =10,7 12. 过点A 3 与B (7,0)的直线 l 1 与过点(2,1),(3,k +1)的直线 l 2 和两坐标轴围成的四边 形内接于一个圆,则实数 k 等于 ()A .-3B .3C .-6D .6二、填空题13.若 O (0,0),A (4,-1)两点到直线 ax +a 2y +6=0 的距离相等,则实数 a =.14. 甲船在某港口的东 50 km ,北 30 km 处,乙船在同一港口的东 14 km ,南 18 km 处,那么甲、乙两船的距离是 .15. 已知直线 l 与直线 y =1,x -y -7=0 分别相交于 P 、Q 两点,线段 PQ 的中点坐标为(1, -1),那么直线 l 的斜率为.16. 已知实数 x ,y 满足 y =-2x +8,当 2≤x ≤3 时,则y的最大值为.x三、解答题17. 已知点 M 是直线 l : 3x -y +3=0 与 x 轴的交点,将直线 l 绕点 M 旋转 30°,求所得到的直线 l ′的方程.18. 求直线 l 1:2x +y -4=0 关于直线 l :3x +4y -1=0 对称的直线 l 2 的方程.19. 在△ABC 中,已知 A (5,-2)、B (7,3),且 AC 边的中点 M 在 y 轴上,BC 边的中点 N 在x 轴上,求:(1) 顶点 C 的坐标; (2) 直线 MN 的方程.20. 如图,已知△ABC 中 A (-8,2),AB 边上的中线 CE 所在直线的方程为x +2y -5=0,AC 边上的中线 BD 所在直线的方程为 2x -5y +8=0, 求直线 BC 的方程.21. 光线沿直线 l 1:x -2y +5=0 射入,遇直线 l :3x -2y +7=0 后反射,求反射光线所在的直线方程.22. 某房地产公司要在荒地 ABCDE (如图)上划出一块长方形地面(不改变方位)建一幢公寓,问如何设计才能使公寓占地面积最大?并求出最大面积(精确到 1 m 2).-5=0 答案1.A 2.B 3.D 4.A 5.C 6.B 7.C 8.C 9.A 10.C 11.D 12.B 13.-2 或 4 或 6 14.60 km15.-23 16.217.解 在 3x -y +3=0 中,令 y =0,得 x =- 3,即 M (- 3,0).∵直线 l 的斜率 k = 3,∴其倾斜角θ=60°.若直线 l 绕点 M 逆时针方向旋转 30°,则直线 l ′的倾斜角为 60°+30° =90°,此时斜率不存在,故其方程为 x =- 3.若直线 l 绕点 M 顺时针方向旋转 30°,则直线 l ′的倾斜角为 60°-30°=30°,此时斜率为 tan 30°= 3,故其方程为 y = 3(x + 3),3 3 即 x - 3y + 3=0.综上所述,所求直线方程为 x + 3=0 或 x - 3y + 3=0.18.解 设直线 l 2 上的动点 P (x ,y ),直线 l 1 上的点 Q (x 0,4-2x 0),且 P 、Q 两点关于直线 l :3x +4y -1=0 对称,则有|3x +4y -1| |3x 0+4(4-2x 0)-1|= , 5 5 y -(4-2x 0)=4.x -x 03 消去 x 0,得 2x +11y +16=0 或 2x +y -4=0(舍). ∴直线 l 2 的方程为 2x +11y +16=0.5+x 0,y 0-219.解 (1)设 C (x 0,y 0),则 AC 中点 M 2 2 ,7+x 0 y 0+3,BC 中点 N 2 2 .∵M 在 y 轴上,∴5+x 0=0,x 0=-5.2 ∵N 在 x 轴上,∴y 0+3=0,y 0=-3,即 C (-5,-3).2 (2)∵M 0,-52 ,N (1,0).∴直线 MN x y 的方程为 + 15=1. - 2 即 5x -2y -5=0.x 0-8y 0+2 ,20. 解 设 B (x 0,y 0),则 AB 中点 E 的坐标为 2 2 ,由条件可得:2x 0-5y 0+8=0x 0-8+2·y 0+2 , 2 2205y 0+8=0 得 , x 0+2y 0-14=0x 2 x 0=6 y 0=4,即 B (6,4),同理可求得 C 点的坐标为(5,0).故所求直线 BC 的方程为y -0=x -5,即 4x -y -20=0.4-0 6-521. 解 设直线 x -2y +5=0 上任意一点 P (x ,y )关于直线 l 的对称点为 P ′(x ,y ),则y 0-y=-2,30 0x +x 0,y +y 0x 0-x又 PP ′的中点 Q 2 2 在l 上, ∴3 x +x 0 y +y 0× -2× 2 2 +7=0,y 0-y =-2,x 0-x3 由 3×x +x 0-(y +y )+7=0.2 可得 P 点的坐标为x 0=-5x +12y -42,y 0=12x +5y +28,13 13代入方程 x -2y +5=0 中,化简得 29x -2y +33=0, ∴所求反射光线所在的直线方程为 29x -2y +33=0.22. 解 在线段 AB 上任取一点 P ,分别向 CD 、DE 作垂线划出一块长方形土地,以 BC ,EA的交点为原点,以 BC ,EA 所在的直线为 x 轴,y 轴,建立直角坐标系,则 AB 的方程为 x + y=1,30 20 x ,20-2x设 P 3 ,则长方形的面积20-2xS =(100-x ) 80- 3 (0≤x ≤30).化简得 S =-2x 2+20+6 000(0≤x ≤30).3 3 当 x =5,y 50= 时,S 最大,其最大值为 6 017 m .3章末检测一、选择题1.方程x2+y2+2ax+2by+a2+b2=0 表示的图形是( )A.以(a,b)为圆心的圆B.以(-a,-b)为圆心的圆C.点(a,b)D.点(-a,-b)2.点P(m,3)与圆(x-2)2+(y-1)2=2 的位置关系为( ) A.点在圆外B.点在圆内C.点在圆上D.与m 的值有关3.空间直角坐标系中,点A(-3,4,0)和B(x,-1,6)的距离为86,则x 的值为( )A.2 B.-8C.2 或-8 D.8 或-24.若直线x-y+1=0 与圆(x-a)2+y2=2 有公共点,则实数a 的取值范围是( )A.[-3,-1] B.[-1,3]C.[-3,1] D.(-∞,-3]∪[1,+∞)5.设A、B 是直线3x+4y+2=0 与圆x2+y2+4y=0 的两个交点,则线段AB 的垂直平分线的方程是( ) A.4x-3y-2=0 B.4x-3y-6=0C.3x+4y+6=0 D.3x+4y+8=06.圆x2+y2-4x=0 过点P(1,3)的切线方程为( ) A.x+3y-2=0 B.x+3y-4=0C.x-3y+4=0 D.x-3y+2=07.对任意的实数k,直线y=kx+1 与圆x2+y2=2 的位置关系一定是( )A.相离B.相切C.相交但直线不过圆心D.相交且直线过圆心8.已知圆O:x2+y2=5 和点A(1,2),则过A 且与圆O 相切的直线与两坐标轴围成的三角形的面积为( )A.5 B.10 C.252D.2549.将直线2x-y+λ=0 沿x 轴向左平移1 个单位,所得直线与圆x2+y2+2x-4y=0 相切,则实数λ的值为( )A.-3 或7 B.-2 或8 C.0 或10 D.1 或1110.已知圆C:x2+y2-4x=0,l 是过点P(3,0)的直线,则( ) A.l 与C 相交B.l 与C 相切C.l 与C 相离D.以上三个选项均有可能11.若直线mx+2ny-4=0(m、n∈R,n≠m)始终平分圆x2+y2-4x-2y-4=0 的周长,则mn 的取值范围是( )A.(0,1) B.(0,-1)C.(-∞,1) D.(-∞,-1)12.过点P(-2,4)作圆O:(x-2)2+(y-1)2=25 的切线l,直线m:ax-3y=0 与直线l 平行,则直线l 与m 的距离为( )A.4 B.2 C.85D.125二、填空题13.与直线2x+3y-6=0 关于点(1,-1)对称的直线方程为.14.过点P(-2,0)作直线l 交圆x2+y2=1 于A、B 两点,则|PA|·|PB|=.15.若垂直于直线2x+y=0,且与圆x2+y2=5 相切的切线方程为ax+2y+c=0,则ac 的值为.16.在平面直角坐标系xOy 中,圆C 的方程为x2+y2-8x+15=0,若直线y=kx-2 上至少存在一点,使得以该点为圆心,1为半径的圆与圆C有公共点,则k的最大值是.三、解答题17.自点A(-3,3)发出的光线l 射到x 轴上,被x 轴反射,其反射光线所在的直线与圆x2+y2-4x-4y+7=0 相切,求光线l 所在直线的方程.18.已知圆x2+y2+x-6y+m=0 与直线x+2y-3=0 相交于P,Q 两点,O 为原点,若OP⊥OQ,求实数m 的值.19.已知圆x2+y2-6mx-2(m-1)y+10m2-2m-24=0(m∈R).(1)求证:不论m 为何值,圆心在同一直线l 上;(2)与l 平行的直线中,哪些与圆相交、相切、相离;(3)求证:任何一条平行于l 且与圆相交的直线被各圆截得的弦长相等.20.如图,已知圆O:x2+y2=1 和定点A(2,1),由圆O 外一点P(a,b向圆O 引切线PQ,切点为Q,且有|PQ|=|PA|.(1)求a、b 间关系;(2)求|PQ|的最小值;(3)以P 为圆心作圆,使它与圆O 有公共点,试在其中求出半径最小的圆的方程.1+k 2答案章末检测1.D 2.A 3.C 4.C 5.B 6.D 7.C 8.D 9.A 10.A 11.C 12.A 13.2x +3y +8=0 14.3 15.±5 16.4 317. 解 如图所示,已知圆 C :x 2+y 2-4x -4y +7=0 关于 x 轴对称的圆为 C 1:(x -2)2+(y +2)2=1,其圆心 C 1 的坐标为(2,-2),半径为 1,由光的反射定律知,入射光线所在直线方程与圆 C 1 相切.设l 的方程为 y -3=k (x +3),即 kx -y +3+3k =0. 则|5k +5|=1,即 12k 2+25k +12=0.∴k 1=-4,k 2=-3.3 4则 l 的方程为 4x +3y +3=0 或 3x +4y -3=0.18. 解 设P ,Q 两点坐标为(x 1,y 1)和(x 2,y 2),由 OP ⊥OQ 可得 x 1x 2+y 1y 2=0, x 2+y 2+x -6y +m =0, 由x +2y -3=0, 可得 5y 2-20y +12+m =0.①所以 y 1y 2=12+m,y 1+y 2=4.5 又 x 1x 2=(3-2y 1)(3-2y 2)=9-6(y 1+y 2)+4y 1y 2=9-24+4(12+m ),5所以 x 1x 2+y 1y 2=9-24+4(12+m )+12+m =0,5 5 解得 m =3.将 m =3 代入方程①,可得Δ=202-4×5×15=100>0,可知 m =3 满足题意,即 3 为所求 m 的值.19.(1)证明 配方得:(x -3m )2+[y -(m -1)]2=25,设圆心为(x ,y ),x =3m 则 , y =m -1消去 m 得 x -3y -3=0,则圆心恒在直线 l :x -3y -3=0 上.10 22+12( (2) 解 设与 l 平行的直线是 l 1:x -3y +b =0,则圆心到直线 l 1 的距离为 d =|3m -3(m -1)+b | |3+b |∵圆的半径为 r =5,∴当 d <r ,即-5 10-3<b <5 10-3 时,直线与圆相交; 当 d =r ,即 b =±5 10-3 时,直线与圆相切;当 d >r ,即 b <-5 10-3 或 b >5 10-3 时,直线与圆相离.(3) 证明 对于任一条平行于 l 且与圆相交的直线 l 1:x -3y +b =0,由于圆心到直线 l 1 的距离 d |3+b |弦长=2 r 2-d 2且 r 和 d 均为常量.∴任何一条平行于 l 且与圆相交的直线被各圆截得的弦长相等. 20.解 (1)连接 OQ 、OP ,则△OQP 为直角三角形,又|PQ |=|PA |,所以|OP |2=|OQ |2+|PQ |2=1+|PA |2,所以 a 2+b 2=1+(a -2)2+(b -1)2,故 2a +b -3=0.(2)由|PQ |2=|OP |2-1=a 2+b 2-1=a 2+9-12a +4a 2-1=5a 2- 12a +8=5(a -1.2)2+0.8,得|PQ |min =2 5.5 (3)以 P 为圆心的圆与圆 O 有公共点,半径最小时为与圆 O 相切的情形,而这些半径的最小值为圆 O 到直线 l 的距离减去圆 O 的半径,圆心 P 为过原点且与 l 垂直的直线 l ′与 l 的交点 P 0,所以 r = 3 -1=3 5-1,5 又 l ′:x -2y =0,联立 l :2x +y -3=0 得 P 0(6,3).5 5 所以所求圆的方程为(x -6)2+(y -3)2= 3 5-1)2.5 5 510 10= .= ,。
高中生物【基因的表达】章末过关检测试题

高中生物【基因的表达】章末过关检测试题一、单项选择题:本题共15小题,每小题2分,共30分。
每小题只有一个选项符合题目要求。
1.下图为核苷酸的模式图,下列相关叙述正确的是()A.DNA与RNA在核苷酸上只有②不同B.如果要构成ATP,在①位置上加上两个磷酸即可C.人体内的③有5种,②有2种D.③在细胞核内共有4种解析:选C。
分析题图可知,①是磷酸,②是五碳糖,③是碱基。
DNA与RNA在核苷酸上的不同主要有两点,一是在DNA中②为脱氧核糖,在RNA中②为核糖;二是在DNA中③有A、T、C、G 4种,在RNA中③有A、U、C、G 4种,A错误。
如果要构成ATP,要在①位置上加上两个磷酸,②应为核糖,③应为腺嘌呤,B错误。
人体内既有RNA又有DNA,故人体内的③有5种,②有2种,C正确。
DNA和RNA 均可存在于细胞核内,故③在细胞核内共有5种,D错误。
2.下图中的a、b、c、d分别代表人体内的四种大分子化合物,下列有关叙述不正确的是()A.分子c的种类有61种,只含三个碱基B.b、c、d的合成离不开化合物a,这四种大分子化合物的主要合成场所相同C.b、c、d三种化合物能同时存在于同一个细胞器中D.a、b彻底水解后可得到四种不同的化合物和四种相同的化合物解析:选A。
分析题图可知,c为tRNA,由多个核糖核苷酸聚合形成,故tRNA 含有多个碱基,A错误;a代表DNA,b、c、d分别代表mRNA、tRNA、rRNA,这三种RNA都是由DNA转录而来,转录主要在细胞核中进行,DNA的合成也主要在细胞核中进行,B正确;线粒体和叶绿体中能进行转录和翻译,含有这三种RNA,C正确;a、b彻底水解后可得到四种不同的化合物——核糖、脱氧核糖、T、U,四种相同的化合物是A、C、G、磷酸,D正确。
3.关于转录和翻译的叙述,错误的是()A.转录时以核糖核苷酸为原料B.转录时RNA聚合酶能识别DNA中特定碱基序列C.mRNA在核糖体上移动翻译出蛋白质D.不同密码子编码同种氨基酸可增强密码的容错性解析:选C。
人教版高一生物必修二章末测试题全套带答案解析.doc

最新人教版高一生物必修二章末测试题全套带答案解析第一章章末过关检测(时间:60分钟满分:100分)一、选择题(共14小题,每小题4分,共56分)1.下列叙述中,错误的是()A.豌豆的高茎和矮茎是一对相对性状B.纯合子自交后代是纯合子,杂合子自交后代不一定是杂合子C.运用假说一演绎法验证的实验结果总与预期相符D.在杂种后代中,同时岀现显性性状和隐性性状的现象叫做性状分离答案C解析豌豆的高茎和矮茎属于同种生物同一性状的不同表现类型,因此是一对相对性状,A 项正确。
纯合子自交后代都是纯合子,但杂合子自交后代不一定是杂合子,如DdDD、Dd、dd, B项正确。
在观察和分析的基础上提出问题以后,通过推理和想象提出解释问题的假说, 根据假说进行演绎推理,再通过实验检验演绎推理的结论。
如果实验结果与预期结论相符,证明假说正确,反之,说明假说错误,C项错误。
在杂种后代中,同时出现显性性状和隐性性状的现彖叫做性状分离,D项正确。
2.下列问题可以通过自交解决的是()①鉴定一株高茎豌豆是否为纯合子②区别女娄菜披针型和狭披针型的显隐性关系③不断提高小麦抗病纯合子的比例A.①③B.②③C.①②D.①②③答案A解析高茎豌豆为显性个体,可以通过自交观察后代是否有性状分离判断是否为纯合子。
连续自交可以提高纯合子的比例。
3.已知某一动物种群中仅有Aabb和AAbb两种类型个体(aa的个体在胚胎期致死),两对基因遵循基因自由组合定律,Aabb : AAbb=l : 1,且该种群中雌雄个体比例为1 : 1,个体间可以自由交配,则该种群自由交配产生的成活子代屮能稳定遗传的个体所占比例是()A. B. C・D・答案B解析该种群中Aabb : AAbb=l : 1,且雌雄个体比例为1 : 1,自由交配时有早AabbX £ Aabb、早AAbbX$AAbb、早AabbX^AAbb、早A Abb X £ Aabb四乖中,成活子代中能稳定遗传的个体有=。
新人教版高中数学必修第一册第一章章末检测试卷

14.设集合S={x|x<-1或x>5},T={x|a<x<a+8},S∪T=R,则a的取 值范围是_{_a_|_-__3_<_a_<_-__1_}_.
借助数轴可知aa<+-8>15,, ∴-3<a<-1.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的
四个选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2
分,有选错的得0分)
9.设集合S={x|-2≤x≤8},T={x|0<x<4},若集合P⊆(∁RT)∩S,则P可 以是
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
四、解答题(本大题共6小题,共70分) 17.(10 分 ) 已 知 全 集 U = {1,2,3,4,5,6,7,8} , A = {x|x2 - 3x + 2 = 0} , B = {x∈Z|1≤x≤5},C={x∈Z|2<x<9}.求 (1)A∪(B∩C);
20.(12分)已知集合A={-4,2a-1,a2},B={a-5,1-a,9},分别求适 合下列条件的a的值. (1)9∈(A∩B);
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
∵9∈(A∩B), ∴2a-1=9或a2=9, ∴a=5或a=3或a=-3. 当a=5时,A={-4,9,25},B={0,-4,9}; 当a=3时,a-5=1-a=-2,不满足集合元素的互异性; 当a=-3时,A={-4,-7,9},B={-8,4,9}, 所以a=5或a=-3.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
章末检测9一、选择题(本题包括14小题,每小题4分,共56分。
每小题给出的四个选项中只有一个选项正确)1.下列关于有机物的说法正确是( )A.乙烯、氯乙烯都属于不饱和烃B.油脂、蛋白质都能发生水解反应C.乙酸、乙酸乙酯都不能与金属Na反应D.苯不与任何酸反应解析:氯乙烯属于卤代烃,卤代烃属于烃的衍生物,A项错误;乙酸含有羧基,可与金属钠发生置换反应,C项错误;在一定条件下,苯可与硝酸发生取代反应,生成硝基苯,D项错误。
答案:B2.下列有关叙述中错误的是( )A.纤维素分子是由葡萄糖单元构成的,可以表现出一些多元醇的性质B.蔗糖和淀粉的水解产物不同C.判断油脂皂化反应基本完成的现象是反应后静置,反应液不分层D.煤中含有苯和甲苯,可用先干馏后分馏的方法得到解析:煤中不含苯和甲苯,由煤制取苯和甲苯是煤在干馏时发生化学反应生成的,D项错误。
答案:D3.下列关于高分子化合物的叙述中正确的是( )A.我国禁止商家无偿提供塑料袋,目的是减少商家经济压力B.回收并合理处理聚乙烯塑料废物有利于环境保护C.石油产品都可用于聚合反应D.聚丙烯的结构简式为CH2CH2CH2解析:禁止商家无偿提供塑料袋的目的是减少白色污染,A项错;合理回收并利用塑料有利于原料的重新再利用,符合环保的要求,B项正确;石油通过分馏直接得到的汽油中主要由烷烃构成,不能发生聚合反应,C项错;根据加聚反应的原理可知聚丙烯的结构简式为,D项错。
答案:B4.(密码改编)下列关于取代反应的说法正确的是( )A.取代反应只能发生在有机物之间B.有机物分子中只有一个原子或原子团被另一个其他原子或原子团替代C.某一种有机物不可能既发生加成反应又能发生取代反应D.取代反应的生成物不可能是一种化合物解析:A项中,Cl2和CH4之间的取代反应就是无机物和有机物之间的取代;B 项中,CH4中的H原子可以被逐个取代,生成CH3Cl、CH2Cl2、CHCl3、CCl4;C 项中,当一种有机物含有多种性质的原子或原子团时,则既可发生取代反应也可发生加成反应;取代反应的实质是取而代之,所以其生成物不可能是一种化合物。
答案:D5.下列有机化合物既能使酸性高锰酸钾溶液退色,又能使溴水因反应而退色的是( )A.苯B.聚乙烯C.环己烷D.环己烯解析:苯分子中尽管含有碳碳不饱和键,但这种化学键不同于碳碳双键,不能被酸性高锰酸钾所氧化,也不能与溴水发生加成反应;聚乙烯、环己烷分子中的化学键是饱和的,不能与酸性高锰酸钾溶液或溴水反应;环己烯中含有碳碳不饱和键,可以使酸性高锰酸钾溶液退色,又能使溴水因加成反应而退色。
答案:D6.下列反应中,属于加成反应的是( )A.CH2Cl2+Cl2CHCl3+HClB.2CH3CH2OH+2Na2CH3CH2ONa+H2↑C.+HNO3+H2OD.CH3CH CH2+Br2解析:A项属于取代反应;B项属于置换反应;C项属于取代反应。
答案:D7.下列关于有机化合物的说法正确的是( )A.和是两种不同的物质B.由乙烯之间的相互加成可以得到聚乙烯C.丁烷有3种同分异构体D.1 mol乙酸与足量乙醇在浓硫酸催化下加热,可生成1 mol 乙酸乙酯解析:A项中两物质是同种物质;C项,丁烷有两种同分异构体;D项,因有机反应的不彻底性,生成的乙酸乙酯的量小于1 mol。
答案:B8.(密码原创)下列关于常见有机化合物的说法中正确的是( )A.乙烷和Cl2在光照条件下反应生成6种氯代产物B.乙烯和聚乙烯都能与溴的四氯化碳溶液发生加成反应C.乙醇、乙酸和乙酸乙酯都能发生氧化反应和取代反应D.糖类、油脂和蛋白质都是人体必需的营养物质,它们的组成元素相同解析:乙烷的二氯代物、三氯代物、四氯代物存在同分异构体,因此氯代产物超过6种,A项错误;乙烯含有双键,能与溴的四氯化碳溶液发生加成反应,但聚乙烯中结构单元为—CH2—CH2—,不能与溴的四氯化碳溶液发生加成反应,B项错误;糖类、油脂和蛋白质都是人体必需的营养物质,糖类、油脂的组成元素为C、H、O,但蛋白质的组成元素为C、H、O、N等,D项错误。
答案:C9.既不是同素异形体,又不是同分异构体、同系物或同位素的一组物质是( )A.HCOOC2H5、CH3CH2COOHB.O2、O3C.D.H、D、T解析:A项是同分异构体;B项是同素异形体;D项是同位素。
答案:C10.(2011·山东卷,11)下列与有机物结构、性质相关的叙述错误的是( )A.乙酸分子中含有羧基,可与NaHCO3溶液反应生成CO2B.蛋白质和油脂都属于高分子化合物,一定条件下都能水解C.甲烷和氯气反应生成一氯甲烷,与苯和硝酸反应生成硝基苯的反应类型相同D.苯不能使溴的四氯化碳溶液退色,说明苯分子中没有与乙烯分子中类似的碳碳双键解析:乙酸属于一元羧酸,酸性强于碳酸,所以可与NaHCO3溶液反应生成CO2,A项正确;油脂是高级脂肪酸的甘油酯,属于酯类,但不属于高分子化合物,B项不正确;甲烷和氯气反应生成一氯甲烷,以及苯和硝酸反应生成硝基苯的反应都属于取代反应,C项正确;只要分子中含有碳碳双键就可以与溴的四氯化碳溶液发生加成反应,从而使之退色,D项正确。
答案:B11.(密码原创)丙酸钠是常用的防腐剂之一,该物质可以由丙酸与烧碱反应制得。
下面关于丙酸和丙酸钠的理解错误的是( )A.丙酸有多种同分异构体B.丙酸与乙酸互为同系物C.检验一种添加剂是丙酸钠还是氯化钠可用pH试纸D.丙酸分子中三个碳原子和两个氧原子一定在同一个平面上解析:丙酸没有羧酸类的同分异构体,但有甲酸乙酯、乙酸甲酯等多种同分异构体,A项正确;丙酸、乙酸都只有一个羧基官能团,而且相差一个CH2,属于同系物,B项正确;丙酸钠水解显碱性,而氯化钠不水解,故可以用pH试纸检验丙酸钠、氯化钠水溶液的碱性来鉴别二者,C项正确;丙酸分子中羧基碳原子、两个氧原子及与羧基直接相连的碳原子在一个平面上,但甲基碳原子可能不在上述四原子构成的平面中,D项错误。
答案:D12.下列关于有机物的关系描述正确的是( )A.甲烷与氯气反应后生成的二氯甲烷,有邻二氯甲烷和对二氯甲烷两种同分异构体B.2甲基丙烯与1丁烯互为同系物C.根据苯的凯库勒式()可知邻二氯甲苯有两种同分异构体D.淀粉和纤维素的化学式都可用(C6H10O5)n表示,但两者不是同系物,也不互为同分异构体解析:A项中由于甲烷是一种正四面体结构的分子,其二氯代物不存在同分异构体;B项中两物质的分子式相同,互为同分异构体,而不是同系物;C项中苯的凯库勒式是苯的表示方式,但其结构不是单双键交替,所以邻二氯甲苯只有一种结构而不存在同分异构体;D项中淀粉和纤维素是高分子化合物,其分子中的n值不同,且结构不同,所以既不互为同分异构体也不是同系物。
答案:D13.(密码原创)下图所示结构简式所代表的物质是制备一种具有抗氧化性的药物的原料。
下列对该原料物质的叙述正确的是( )A.该物质的分子式是C18H18O4B.该物质能够发生加成反应、取代反应C.1 mol该物质跟氢气反应,最多消耗8 mol氢气D.1 mol该物质与足量氢氧化钠溶液反应,最多消耗氢氧化钠为1 mol解析:该物质的分子式为C18H16O4,A项错误;该物质结构中含有苯环和双键,能发生加成反应,含有苯环及羧基,能发生取代反应,B项正确;从结构简式中可以看出其中含有两个苯环、1个双键,等效于7个双键,因此1 mol该物质与H2反应,最多消耗7 mol H2,C项错;1 mol上述物质中含有1 mol羧基、1 mol酯基,因此与足量NaOH溶液反应,最多消耗2 mol NaOH,D项错误。
答案:B14.下图是一些常见有机物的转化关系,关于反应①~⑦的说法错误的是( )A.反应①是加成反应B.只有反应②是加聚反应C.只有反应⑦是取代反应D.反应④⑤⑥⑦是取代反应解析:①是加成反应,②是加聚反应,④⑥既是酯的水解反应又是取代反应,⑤⑦既是酯化反应又是取代反应。
答案:C二、非选择题(本题包括4小题,共44分)15.(10分)(密码原创)(1)若有甲酸(HCOOH)、乙酸(CH3COOH)、甲醇(CH3OH)和乙醇(CH3CH2OH)在一定条件下同一反应体系中发生酯化反应,理论上生成种酯,其中哪些是同分异构体?。
(2)写出由乙炔生产聚氯乙烯合成树脂所涉及的有机化学反应方程式。
①,反应类型为;②,反应类型为。
解析:(1)酯化反应是羧酸和醇生成酯与水,其实质是酸去羟基醇去氢,所以组合共有4种,分别为甲酸甲酯HCOOCH3,甲酸乙酯HCOOCH2CH3,乙酸甲酯CH3COOCH3,乙酸乙酯CH3COOCH2CH3;其中甲酸乙酯和乙酸甲酯分子式相同结构式不同,属于同分异构体。
(2)可以采用逆推法:聚氯乙烯←氯乙烯←乙炔。
答案:(1)4 甲酸乙酯和乙酸甲酯(2)①CH≡CH+HCl CH2CHCl 加成反应②加聚反应16.(12分)有机化合物A、B、C、D、E有下列关系:E且常温常压下,A、B为液体,C、D、E为固体,D易溶解于水,C难溶于冷水,在热水中可以部分形成溶液,且C遇到碘水变为蓝色。
B的蒸气质量是相同状况下相同体积的乙烷的2倍,D的相对分子质量是180。
A、B、D可以与新制取的Cu(OH)2反应,其中B生成蓝色溶液,A、D在加热的条件下生成砖红色沉淀,A、D能够和银氨溶液发生银镜反应。
(1)通过计算推断A、B、C、D的结构简式。
A:;B:;C:;D:。
(2)写出下列化学方程式。
①B+Cu(OH)2:;②D+Cu(OH)2:;③A+银氨溶液:;④C+在稀硫酸的作用下水解:。
解析:“C遇到碘水变为蓝色”说明C是淀粉,结合D的相对分子质量及C水解的条件可知D为葡萄糖,葡萄糖中含有羟基,能够发生酯化反应,故B中含有羧基,结合B的相对分子质量为60可知B为乙酸,A在加热的条件下与新制的氢氧化铜反应生成砖红色的氧化亚铜可知A为乙醛。
答案:(1)CH3CHO CH3COOH (C6H10O5)n(淀粉)CH2OH(CHOH)4CHO(2)①2CH3COOH+Cu(OH)2(CH3COO)2Cu+2H2O②CH2OH(CHOH)4CHO+2Cu(OH)2CH2OH(CHOH)4COOH+Cu2O↓+2H2O③CH3CHO+2Ag(NH3)2OH CH3COONH4+2Ag↓+3NH3+H2O④(C6H10O5)n(淀粉)+nH2O nC6H12O6(葡萄糖)17.(12分)(密码原创)已知信息如下:①CH3CH2Br+NaOH CH3CH2OH+NaBr。
②有机化合物A的球棍模型如下图所示:如下图所示,油脂水解和A在碱性水溶液中都能生成B。
油脂B A试回答下列问题:(1)B的结构简式为,其中含有的官能团是。
