第1章综合能力测试题
北师大版七年级数学上册第一章综合测试题
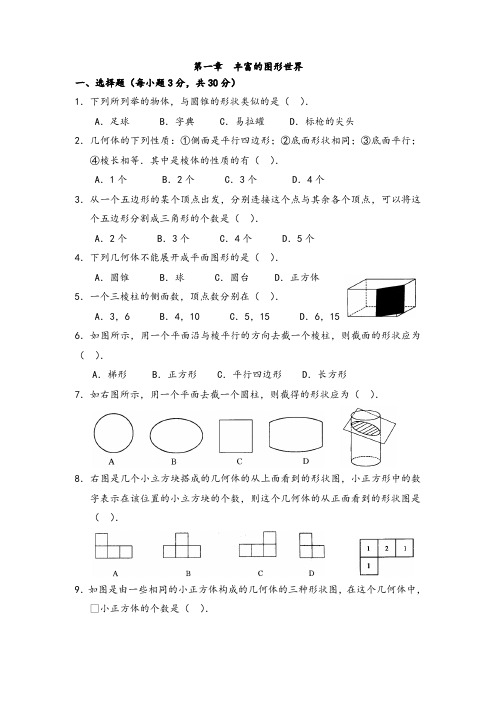
第一章丰富的图形世界一、选择题（每小题3分，共30分）1．下列所列举的物体，与圆锥的形状类似的是（）．A．足球 B．字典 C．易拉罐 D．标枪的尖头2．几何体的下列性质：①侧面是平行四边形；②底面形状相同；③底面平行；④棱长相等．其中是棱体的性质的有（）．A．1个 B．2个 C．3个 D．4个3．从一个五边形的某个顶点出发，分别连接这个点与其余各个顶点，可以将这个五边形分割成三角形的个数是（）．A．2个 B．3个 C．4个 D．5个4．下列几何体不能展开成平面图形的是（）．A．圆锥 B．球 C．圆台 D．正方体5．一个三棱柱的侧面数，顶点数分别在（）．A．3，6 B．4，10 C．5，15 D．6，156．如图所示，用一个平面沿与棱平行的方向去截一个棱柱，则截面的形状应为（）．A．梯形 B．正方形 C．平行四边形 D．长方形7．如右图所示，用一个平面去截一个圆柱，则截得的形状应为（）．8．右图是几个小立方块搭成的几何体的从上面看到的形状图，小正方形中的数字表示在该位置的小立方块的个数，则这个几何体的从正面看到的形状图是（）．9．如图是由一些相同的小正方体构成的几何体的三种形状图，在这个几何体中，•小正方体的个数是（）．从正面看从左面看从上面看A．6个 B．5个 C．7个 D．4个10．观察左图，左边的图形绕着给定的直线旋转一周后可能形成的几何体是（）．二、填空题（每小题3分，共18分）11．线与面相交成______，面与面相交成______．12．如图所示，电视台的摄像机1，2，3，4在不同位置拍摄了四幅画面，则A 图像是_____号摄像机所拍，B图像是_____号摄像机所拍，C图像是_____号摄像机所拍，D•图像是____号摄像机所拍．13．如图所示，将它按虚线位置翻折，将对连粘在一起，围成一个几何体，这个几何体是_______．14．一个圆锥是由一个平面和一个曲面所组成，它们相交成一个圆，•且这个锥体从正面看到的形状图为一个边长为3cm的等边三角形，求其从上面看到的形状图的的面积________．15．从每个顶点出发的所有棱长相等，所有面形状，•大小完全相同的正多边形的几何体称为正多面体．其面数+顶点数-棱数=______．16．如图所示，用一个平面去截一个三棱柱，所截得的图形是______．三、解答题（共52分）17．（6分）如图，桌面上放置了一些几何体，•请按每个图下面的要求画出这些物体的形状图．从正面看从上面看从右面看18．（6分）如图所示的正方体表面分别标上字母A～F，•问这个正方体各个面上的字母对面各是什么字母？19．19．（8分）如图是由几个小立方块所搭成几何体的从上面看到的形状图，•小正方形中的数字表示在该位置小立方块的个数，请画出这个几何体的从正面、从左面看到的形状图．20．（8分）如图是由16个棱长为2厘米的小正方体搭成的，求它的表面积．21．（10分）下图是由几个小立方块所搭成几何体的从上面、从正面看到的形状图．（1）这样搭建的几何体最少，最多各需要多少个小立方块？（2）请画出各种情况的从左面看到的形状图．从正面看从上面看答案:1．D 2．B 3．B 4．B 5．A 6．D 7．B 8．B9．B 10．D 11．点，线 12．2，3，4，1 13．四棱柱14．94cm2 15．2 16．三角形17．从正面看从上面看从右面看 18．A─E C─F B─D19．从正面看从左面看20．（9+7+9）×2×4=200（cm2）21．（1）最少11种最多17种（2）共19种，下面未完全画出．掌握的三个数学答题方法树枝答题法关注数学题的解题过程2014年上海市中考状元徐瑜卿认为,数学是一门思维学科,并不是平时做题多就一定会拿高分。
七年级数学上册第1章【名师选题】第一章综合能力检测卷(人教版)
第一章综合能力检测卷―、选择题(每题3分,共30分）1.下列有关“0”的叙述中,错误的是( ) A.0既不是正数,也不是负数B.O ℃是零上温度和零下温度的分界线C.海拔是0 m 表示没有海拔D.0是最小的自然数2.大米包装袋上(10±0.1)kg 的标识表示此袋大米重( ）A.(9.9~10.1)kgB.10.1kgC.9.9kgD.10kg 3.据媒体报道,我国最新研制的“察打一体”无人机的速度极快,经测试最高速度可达204000米/分,204000用科学记数法表示正确的是( ) 4.下列说法错误的是( )A.-2的相反数是2B.3的倒数是13C.(-3)-(-5)=2D.-11,0,4这三个数中最小的是0. 5.下列等式成立的是( )A.88-= B.()11--=-C.()1133÷-= D.236-⨯=6.若21a =,b 是2的相反数,则a b +的值为( )A.-3B.-1C.-1或-3D.1或-3 7.有理数,a b 在数轴上对应的点的位置如图所示,则必有( )A.0a b +>B.0a b -<C.0ab >D.0ab< 8.下列算式中,运算结果最大的是( ) A.()232--B.()()432-⨯-C.()()4334-÷- D.()23132⎛⎫-⨯- ⎪⎝⎭9.数学家发明了一个魔术盒,当任意有理数对(a,6)进入其中时,会得到一个新的有理数a 2+b-1.例如把(3,-2)放入其中,就会得到32+(-2)-1=6现将有理数对(-1,3)放入其中,得到有理数m,再将有理数对(m,l)放入其中,得到的有理数是( )A.3B.6C.9D.12 10.下列说法正确的是( )A.若a b ≠,则22a b ≠B.a b ≠,则a b >C.若a b =,则a=bD.若a b ≠,则a b > 二、填空题(每题3分,共18分） 11.计算：()231-+-=_______12.近似数8.06⨯106精确到______位,把347560000精确到百万位是______. 13.阅览室某一书架上原有图书20本,规定每天归还图书记为正,借出图书记为负,经过两天,借阅的情况如下(单位:本）：-3,+1,-1,+2,则该书架上现有图书______本14.若两个数的乘积等于-1,则称其中一个数是另一个数的负倒数,则213-的负倒数为______.15.宁宁同学设计了一个计算程序,如下表：根据表格中各个数据的对应关系,可得a 的值是______.16.请你只在“加、减、乘、除和括号”中选择使用,可以重复,将四个数-2,4,-6,8组成算式(四个数都用且每个数只能用一次）,使运算结果为24,你列出的算式是_______.(只写一种） 三、解答题(共52分）17.(6分)把下列各数分别填入相应的集合里：-4, 43--,0,119,-3.14,1024,-(+5). (1)正数集合：{ …} (2)负数集合：{ …} (3)整数集合：{ …} (4)分数集合：{ …} 18.(12分)计算下列各题：(1)21354834824⎛⎫--+⨯ ⎪⎝⎭;(2)()()()234134224⎡⎤-+-⨯-+--÷⎣⎦;(3) 222223418333⎛⎫⎛⎫⎛⎫-⨯--⨯--÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭(4) ()153********⎛⎫-⨯--+⨯ ⎪⎝⎭19.(8分)某书店举行图书促销,毎位促销人员以销售500本为基准,超过的记为正,不足的记为负,其中一组10名促销员的销售结果如下(单位:本）:4,2,3,-7,-3,-8,3,4,8,-1.这组促销人员的总销售量超过,还是不足总销售基准？相差多少？若每本图书的利润为2.7元,则这一组此次促销所得总利润为多少元？20.(8分)若,a b 互为相反数,,c d 互为倒数,m 的绝对值是l,n 是有理数且既不是正数也不是负数,求()()()2016122016a b m cd n a b c d -++-++++的值.21.(8分）已知有若干个数,第1个数记为1a ,第2个数记为2a ,第3个数记为3a ……第n 个数记为n a ,若113a =-,从第二个数起,每个数都等于1与前面那个数的差的倒数.(1)分别求出2a ,3a ,4a 的值; (2)计算1a +2a +3a +…+36a 的值.22.(10分）阅读理解题:如图,从左边第一个格子开始向右数,在每个格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.(1)根据上述条件,可知x =_______,●=_______,〇=_______. (2)试判断第2016个格子中的数是多少,并说明理由.(3)判断:前n 个格子中所填整数之和是否可能为2016?若能,求出n 的值,若不能,请说明理由.(4)若在前三个格子中任取两个数并用大数减去小数得到差值,然后将所有的差值累加起来称为累差值.例如前三项的累差值为11-+-+-●〇●〇,则前三项的累差值为_______;若取前10项,则前10项的累差值为多少？(请给出必要的计算过程）参考答案与解析第一章综合能力检测卷1.C2.A 【解析】(10±0.1)kg 的含义是此袋大米最少重9.9kg,最多重10.1kg.故选A.3.C4.D 【解析】-11,0,4这三个数中最小的是-11,所以D 错误.故选D.5.A 【解析】选项A,因为88-=,所以A 符合题意;选项B,因为()111--=≠-所以B 不符合题意;选项C,因为()111333÷-=-≠所以C 不符合题意;选项D,因为2366-⨯=-≠,所以D 不符合题意.故选A.6.C 【解析】因为21a =,b 是2的相反数,所以1,2a b =±=-.①当1a =,2b =-时,121a b +=-=-;②当1a =-,2b =-时,123a b +=--=-.综上,a b +的值为-1或-3.故选C.7.D 【解析】由题中数轴,可知0,0a b ><,且a b <,所以0a b +<,0a b ->,0ab <,0ab<,所以A,B,C 均错误,D 正确.故选D. 8.A 【解析】()()2232525--=-=,()()()43231648-⨯-=-⨯=-,()()()438134816464-÷-=÷-=-,()()231127327244⎛⎫-⨯-=-⨯=- ⎪⎝⎭,因为27814825464-<-<-<所以A 项的运算结果最大.故选A. 9.C 【解析】将有理数对(-1,3)放入其中,得()21313m =-+-=,再将有理数对(m ,l),即(3,1)放入其中,得到的有理数是32+1=9.故选C.10.B 【解析】当a b =-时, 22a b =,故A 错误;若a b ≠,则a b =或 a b =-故C 错误;当2,1a b =-=时, a b >,此时a b <故D 错误.故选B.11.4【解析】()231314-+-=+=. 12.万 3.48⨯10813.19【解析】由题意,得-3+(+1)+(-1)+(+2)=-1(本）,20+(-1)=19(本）,故该书架上现有图书19本.14.35-【解析】25133-=,因为53135-⨯=-所以213-的负倒数是35-.15.1011【解析】输出的数据分子分别为2,4,6,8,……,分母为从3开始的连续奇数,由此得出1011a =. 16.()()8642⨯-÷÷-⎡⎤⎣⎦.(答案不唯一)17.【解析】(1)正数集合：{119,1024,…};(2)负数集合：{-4, 43--,-3.14,-(+5),…};(3)整数集合：{-4,0,1024,-(+5),…}; (4)分数集合：{43--,119,-3.14,…}. 18.【解析】(1)213548348242135=48484848348243212181012⎛⎫--+⨯ ⎪⎝⎭⨯-⨯-⨯+⨯=--+= (2)()()()()()()2341342241316284154253⎡⎤-+-⨯-+--÷⎣⎦=-+-⨯+--÷=--+=-(3) 22222341833342934189344418332203⎛⎫⎛⎫⎛⎫-⨯--⨯--÷ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎛⎫=-⨯-⨯--⨯⎪⎝⎭=---=- (4)()()()()()()1538156121015381561210153120612101531201201206121020503634⎛⎫-⨯--+⨯ ⎪⎝⎭⎛⎫=-⨯⨯--+ ⎪⎝⎭⎛⎫=-⨯--+ ⎪⎝⎭⎛⎫⎛⎫⎛⎫=-⨯-+-⨯-+-⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=+-=19.【解析】因为4+2+3-7-3-8+3+4+8-1=5(本）, 所以这组促销人员的总销售量超过总销售基准,超过5本. 500⨯lO+5=505(本）,505⨯2.7=1363.5(元）. 所以这一组此次促销所得总利润为1363.5元.20.【解析】因为,a b 互为相反数, ,c d 互为倒数,m 的绝对值是1,n 是有理数且既不是正数也不是负数,所以0,1,1,0,a b cd m n +===±=所以()()()201612201620161102016a b m cd n a b c d -++-++++=+-+=.21.【解析】(1)234114111,4,41131431343a a a =======--⎛⎫-- ⎪⎝⎭.(2)由(1)可知题中给出的是1313,,4,,,4,3434--…排成的一组数,3个数为一组,从1a 到36a 共有12组这样的数,故1a +2a +3a +…+36134125334a ⎛⎫=-++⨯= ⎪⎝⎭.22.【解析】(1)1 7 -3 根据题意,得x =l,●=7,〇=-3.(2)第2016个格子中的数是-3.理由如下： 由题意可知格子中的数依次是1,7,-3,1,7,-3,…, 因为2016÷3=672,所以第2016个格子中的数为-3. ⑶能.因为1+7+(-3)=5,而2016=5⨯403+1,所以n =403⨯3+1=1210. (4)20因为前10个数中1出现了4次,7与-3各出现了3次, 所以前10项的累差值为()7333210--⨯⨯=.。
第1章习题及参考答案《畜禽解剖生理》
第1章综合测试题一、名词解释1．细胞:2．新陈代谢：3．感应性：4．细胞的分化：5．器官：6．系统：7．有机体：8．神经调节：9．体液调节：10．矢状面：11．额面(水平面)：12．横切面(冠状面)：二、填空题1．细胞的基本结构包括（）、（）和（）。
2．神经元胞体包括（）、（）和（）三部分。
3．生物膜由两层（）和嵌入其中的（）组成。
4．（）是位于细胞膜与细胞核之间，生活状态下呈半透明的胶状物质。
5．神经元由（）和（）两部分构成。
6．动物细胞中已发现的细胞器有“一网、五体、三微”，即（）、（）、（）、（）、（）、（）、（）、（）和（）。
7．细胞核由（）、（）和（）构成。
8．细胞繁殖通过细胞分裂的方式进行，主要有（）、（）和（）三种类型。
9．畜禽体的基本组织可分为（）、（）、（）和（）四大类。
10．根据上皮组织的功能和形态结构的特点，将其分为（）、（）、（）和（）四类。
11．神经元的突起从胞体伸出，分为两种:一种是树枝状的短突，有多个，称（）；另一种是细而长的单突，称（）。
12．根据结缔组织的形态结构和功能的不同，将其分为（）、（）、（）、（）、（）、（）、（）。
13．结缔组织的功能主要有（）、（）、（）、（）、（）、（）和（）等作用。
14．肌细胞一般呈纤维状，故又叫（）。
15．根据肌细胞的形态结构、分布和功能特点，肌组织可分为（）、（）和（）三种。
三、选择题1．（）是动物体内分布最广、形态结构最多样化的一类组织。
A. 神经组织B. 肌肉组织C. 结缔组织D. 上皮组织2．与地面平行，将畜禽体分为背、腹两个不对称部分的切面称为（）。
A.额面B. 失状面C.横切面D.以上都不是3．持续时间较长，作用范围较广的功能调节方式是（）A.神经调节B. 体液调节C.自身调节D.以上都不是4．（）由基质、细胞器和内含物组成。
A.细胞膜B. 细胞质C.细胞核D.以上都不是四、判断题1．消化系统由口腔、咽、食管、胃、肠、肛门及消化腺等器官构成。
第1章综合测试题
第一章综合测试题本卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，考试时间90分钟，满分100分第Ⅰ卷(选择题共45分)一、单项选择题(每小题1.5分，共45分)经过20多年的改革开放，我国区域合作与开发已取得很大成绩，尤其是在一些经济基础较好、开发较早的沿海、沿江地区，区域内经济体之间的联系和合作日趋紧密，出现了以上海为中心的长江三角洲地区；以广州、深圳、珠海为中心的珠江三角洲地区；以北京、天津、大连、沈阳为中心的环渤海经济圈。
读下图并结合材料，完成1～3题。
1．有关B地区在经济建设中出现的主要问题的叙述，不正确的是() A．国有大中型企业缺乏活力B．能源、水源不足C．港口建设的区位条件不好D．产业结构转型困难【答案】 C【解析】根据经纬度可判断B地区是环渤海地区，该区大中型企业多，且问题较多；由于重工业较多、人口密集，导致水源、能源不足；由于沿海地势低平、临着内海渤海，而利于修筑港口和船舶停岸，又由于经济较发达、有广阔的经济腹地而使该区港口区位较好。
2．A地区与90°W同纬度地区农业发展的共同的有利条件是() A．同处于温带季风气候区，雨热同期B．都有大河三角洲，地势平坦，土壤肥沃C．同处在本国最大的工业区D．都是生产规模大，机械化水平高【答案】 B【解析】A是长江三角洲地区，90°W同纬度地区是美国南部农业带，在密西西比河河口地带；美国没有温带季风气候，美国南部也不是其最大工业区，其最大工业区应在五大湖沿岸的东北工业区；长江三角洲的农业主要是水稻种植业，由于人多、经济较落后而机械化程度低。
但二者都是大河三角洲地区。
3．如下图所示，2000年与1985年相比，C地区的产业结构发生了深刻变化，这种变化说明影响工业区位的某些因素在减弱，具体地说主要是下列因素中的()A．廉价劳动力B．科技水平C．交通条件D．信息【答案】 A【解析】两个时间段对比可知，2000年该地高科技产业比重大大上升，廉价劳动力型的工业产值比重下降，这说明廉价劳动力这一因素在减弱。
北师大版2020八年级数学上册第一章勾股定理自主学习单元综合能力达标测试题1(附答案详解)
北师大版2020八年级数学上册第一章勾股定理自主学习单元综合能力达标测试题1（附答案详解）1．在△ABC中，∠C=90°，AC=6cm，BC=8cm，则AB等于（）A．2cm B．8cm C．10cm D．100cm2．等腰三角形底长为24，底边上的高为5，则这个三角形的周长为( )A．37 B．60 C．34 D．533．古埃及人曾经用如图所示的方法画直角：把一根长绳打上等距离的13个结，然后以3个结间距、4个结间距、5个结间距的长度为边长，用木桩钉成一个三角形，其中一个角便是直角，这样做的道理是（）A．直角三角形两个锐角互补B．三角形内角和等于180°C．如果三角形两条边长的平方和等于第三边长的平方D．如果三角形两条边长的平方和等于第三边长的平方，那么这个三角形是直角三角形4．如图，等腰三角形ABC底边上的高AD为4 cm，周长为16 cm，则△ABC的面积是（）A．14 cm2B．13 cm2C．12 cm2D．8 cm25．如图，在波平如镜的湖面上，有一朵盛开的美丽的红莲，它高出水面3尺．突然一阵大风吹过，红莲被吹至一边，花朵刚好齐及水面，如果知道红莲移动的水平距离为6尺，则水是（）尺．A．3.5 B．4 C．4.5 D．56．如图，Rt△ABC中，∠ACB=90°，AC=3，BC=4，将边AC沿CE翻折，使点A落在AB上的点D处；再将边BC沿CF翻折，使点B落在CD的延长线上的点B′处，两条折痕与斜边AB分别交于点E、F，则线段B′F的长为（）A．35B．45C．23D．327．如图，小亮将升旗的绳子拉到旗杆底端，绳子末端刚好接触到地面，然后将绳子末端拉到距离旗杆8 m处，发现此时绳子末端距离地面2 m，则旗杆的高度(滑轮上方的部分忽略不计)为( )A．12 m B．13 m C．16 m D．17 m8．如图，数轴上点A，B表示的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB 长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M表示的数是( )A．3B．5C．6D．79．以下各组数为边长，不能组成直角三角形的是（）．A．1.5，2，2.5 B．40，50，60 C．7，25，24 D．54，1，3410．有一个面积为1的正方形，经过一次“生长”后，在他的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了右图，如果继续“生长”下去，它将变得“枝繁叶茂”，请你算出“生长”了2018次后形成的图形中所有的正方形的面积和是（）A．2017 B．2018 C．2019 D．111．在ABC ∆中，90,ACB CD ∠=︒是高，若,,BC a AC b ==,,AB c CD h ==,AD k BD p ==，且3,4a b ==，则____,____,____,____c p k h ====．12．如图，一架云梯长10米，斜靠在一面墙上，梯子顶端离地面6米，要使梯子顶端离地面8米，则梯子的底部在水平面方向要向左滑动______米．13．已知，如图，△OBC 中是直角三角形，OB 与x 轴正半轴重合，∠OBC=90°，且OB=1，BC=3，将△OBC 绕原点O 逆时针旋转60°再将其各边扩大为原来的2倍，使OB 1=OC ，得到△OB 1C 1，将△OB 1C 1绕原点O 逆时针旋转60°再将其各边扩大为原来的2倍，使OB 2=OC 1，得到△OB 2C 2，…，如此继续下去，得到△OB 2015C 2015，则点C 2015的坐标是_____．14．如图ABC 与ADE 都是以A 为直角顶点的等腰直角三角形，DE 交AC 于点F ，若5AB =，32=AD ，当CEF △是直角三角形时，则BD 的长为__________．15．如图，在四边形ABCD 中，AD BC ∥，DE BC ⊥，垂足为点E ，连接AC 交DE 于点F ，点G 为AF 的中点，2ACD ACB ∠=∠．若4DG =，1EC =，则DE 的长为__________．16．如图，在ABC 中，AB 32=，BC 1=，ABC 45∠=，以AB 为边作等腰直角ABD ，使ABD 90∠=，连接CD ，则线段CD 的长为________．17．如图，△OPQ 是边长为2的等边三角形，若正比例函数的图象过点P ，则它的表达式是y ＝_____18．如图，正方形网格中，每个小正方形的边长为1，则网格上的ABC △是__________三角形．19．三角形中两条较短的边为a ＋b ，a-b(a>b),则当第三条边为_______时，此三角形为直角三角形．20．如图，在直角三角形纸片ABC 中，∠ACB ＝90°，AC ＝2，BC ＝4，点D 在边AB 上，以CD 为折痕将△CBD 折叠得到△CPD ，CP 与边AB 交于点E ，若△DEP 为直角三角形，则BD 的长是_____21．如图，在等边△ABC 中，D 为BC 上一点，∠BAD =3∠CAD, BC=2．（1）求△ABC 的面积；（2）求CD 的值．22．（1）在右面的方格纸中，以线段AB为一边，画一个正方形；（2）如果图中小方格的面积为1平方厘米，你知道（1）中画出的正方形的面积是多大吗？解释你的计算方法.23．如图，直角坐标系中的网格由单位正方形构成.△ABC中，A点坐标为（2，3）、B （-2，0）、C（0，-1）.（1）AB的长为_____，∠ACB的度数为______；（2）若以A、B、C及点D为顶点的四边形为平行四边形，请写出D点的坐标___________，并在图中画出平行四边形.24．如图是一个三级台阶,它的每一级的长、宽和高分别等于5 cm,3 cm和1 cm,A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物.请你想一想,这只蚂蚁从A点出发,沿着台阶面爬到B点,最短线路是多少?25．小明剪了两张直角三角形纸片，进行了如下的操作：操作一：如图1，将Rt△ABC沿某条直线折叠，使斜边的两个端点A与B重合，折痕为DE．（1）如果AC＝6cm，BC＝8cm，则△ACD的周长为cm；（2）如果∠B0，则∠CAD= 度；35操作二：如图2，小明拿出另一张Rt△ABC纸片，将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，若AC＝9cm，BC＝12cm，请求出CD的长．26．如图1所示，等边△ABC 中，AD 是BC 边上的中线，根据等腰三角形的“三线合一”特性，AD 平分∠BAC ，且AD ⊥BC ，则有∠BAD=30°，BD=CD=12AB ．于是可得出结论“直角三角形中， 30°角所对的直角边等于斜边的一半”．请根据从上面材料中所得到的信息解答下列问题：（1）如图2所示，在△ABC 中，∠ACB=90°，BC 的垂直平分线交AB 于点D ，垂足为E ，当BD=5cm ，∠B=30°时，△ACD 的周长= ．（2）如图3所示，在△ABC 中，AB=AC ，∠A=120°，D 是BC 的中点，DE ⊥AB ，垂足为E ，那么BE ：EA= ．（3）如图4所示，在等边△ABC 中，D 、E 分别是BC 、AC 上的点，且AE=DC ，AD 、BE 交于点P ，作BQ ⊥AD 于Q ，若BP=2，求BQ 的长．27．已知四边形ABCD 中，10AB =，8BC =，26CD =，45DAC ∠=︒，15DCA =︒∠．（1）求ADC 的面积．（2）若E 为AB 中点，求线段CE 的长．28．在Rt△ABC 中，∠C=90°，BC=3，AC=4．现在要将交ABC 扩充成等腰三角形，且扩充的部分是以AC为直角边的直角三角形，求扩充后等腰三角形的周长．赵佳同学是这样操作的：如图 1 所示，延长BC 到点 D，使CD=BC，连接AD．所以，△ADB 为符合条件的三角形．则此时△ADB的周长为____________．请你在图2、图3中再设计两种扩充方案，并直接写出扩充后等腰三角形的周长．图2的周长：______________；图3的周长：______________.29．如图（1），Rt△AOB中，∠A=90°，∠AOB=60°，OB=23，∠AOB的平分线OC交AB于C，过O点做与OB垂直的直线ON．动点P从点B出发沿折线BC﹣CO 以每秒1个单位长度的速度向终点O运动，运动时间为t秒，同时动点Q从点C出发沿折线CO﹣ON以相同的速度运动，当点P到达点O时P、Q同时停止运动．（1）求OC、BC的长；（2）设△CPQ的面积为S，求S与t的函数关系式；（3）当P在OC上Q在ON上运动时，如图（2），设PQ与OA交于点M，当t为何值时，△OPM为等腰三角形？求出所有满足条件的t值．30．如图,长方体的长BE=15cm,宽AB=10cm,高AD=20cm,点M在CH上,且CM=5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点M,需要爬行的最短距离是多少?参考答案1．C【解析】【分析】已知直角三角形两直角边，可以直接利用勾股定理来求斜边.【详解】解：∵在△ABC中，∠C=90°，AC=6cm，BC=8cm，∴斜边22AB=+=.6810故选C.【点睛】运用勾股定理：a，b，c是直角三角形的三条边，c为斜边，则满足c2=a2+b2是解题的关键. 2．B【解析】【分析】根据等腰三角形的性质和勾股定理可求得等腰三角形的腰，据此即可得解．【详解】解：如图：BC=24cm，AD=5cm，△ABC中，AB=AC，AD⊥BC；则BD=DC=BC=6cm；Rt△ABD中，AD=5cm，BD=12cm；由勾股定理，得：AB===13cm,∴△ABC的周长是13+13+24=60cm，故选：B．【点睛】本题主要考查了等腰三角形的性质以及勾股定理的应用．3．D【解析】分析：根据勾股定理的逆定理即可判断．详解：设相邻两个结点的距离为m，则此三角形三边的长分别为3m、4m、5m，∵（3m）2+（4m）2=（5m）2，∴以3m、4m、5m为边长的三角形是直角三角形．（如果三角形的两条边的平方和等于第三边的平方，那么这个三角形是直角三角形）故选D．点睛：此题考查了勾股定理的证明，属于基础题，注意仔细阅读题目所给内容，得到解题需要的信息，比较简单．4．C【解析】【分析】设BD=xcm，由题意表示出AB的长度，根据勾股定理列方程求出x，进而求出△ABC的面积．【详解】设BD=xcm，∵等腰△ABC，∴AB=AC，∵AD⊥BC，∴BD=CD=xcm，∴AB=12（16﹣2x），由勾股定理可得：[12（16﹣2x）]2=x2+42，解得x=3，∴BC=2BD=6cm，∴S△ABC=12×6×4=12cm2．故选C．【点睛】本题关键在于设未知数，根据勾股定理列方程求解．5．C【解析】试题分析：如图，设水深h尺，在Rt△ABC中，AB＝h，AC＝h＋3，BC＝6，由勾股定理得，AC 2＝AB 2＋BC 2，即（h+3）2＝h 2＋62，∴h 2＋6h ＋9=h 2＋36，6h ＝27，解得h=4．5．故答案选C ．考点：勾股定理．6．B 【解析】【分析】首先根据折叠可得CD=AC=3，BC=4，∠ACE=∠DCE ，∠BCF=∠B /CF ，CE ⊥AB ，然后求得△BCF 是等腰直角三角形，进而求得∠B /GD=90°，CE-EF=125，ED=AE=95，从而求得B /D=1，DF=35，在Rt △B /DF 中，由勾股定理即可求得B /F 的长． 【详解】解：根据首先根据折叠可得CD=AC=3，B /C=B4，∠ACE=∠DCE ，∠BCF=∠B /CF ，CE ⊥AB ，∴BD=4-3=1，∠DCE+∠B /CF=∠ACE+∠BCF ，∴∠ACB=90°，∴∠ECF=45°，∴△ECF 是等腰直角三角形，∴EF=CE ，∠EFC=45°，∴∠BFC=∠B /FC=135°，∴∠B /FD=90°，∵S △ABC =12AC×BC=12AB×CE ， ∴AC×BC=AB×CE ，∵根据勾股定理求得AB=5，∴CE=125，∴EF=125，22AC CE -=95∴DE=EF-ED=35， ∴B /22B D DF '-=45 故选：B ．【点睛】此题主要考查了翻折变换，等腰三角形的判定和性质，勾股定理的应用等，根据折叠的性质求得相等的角是解本题的关键．7．D【解析】【分析】根据题意画出示意图，设旗杆高度为x，可得AC=AD=x，AB=（x﹣2）m，BC=8m，在Rt△ABC中利用勾股定理可求出x．【详解】设旗杆高度为x，则AC=AD=x，AB=（x﹣2）m，BC=8m，在Rt△ABC中，AB2+BC2=AC2，即（x﹣2）2+82=x2，解得：x=17，即旗杆的高度为17米．故选D．【点睛】考查了勾股定理的应用，解答本题的关键是构造直角三角形，构造直角三角形的一般方法就是作垂线．8．B【解析】【分析】先依据勾股定理可求得OC的长，从而得到OM的长，于是可得到点M对应的数．【详解】解：由题意得可知：OB=2，BC=1，依据勾股定理可知：∴故选：B．【点睛】本题考查勾股定理、实数与数轴，熟练掌握相关知识是解题的关键．9．B【解析】分析：判断是否可以作为直角三角形的三边长，则判断两小边的平方和是否等于最长边的平方即可．详解：A. ()()2221.52 2.5+=，是直角三角形，故此选项错误；B. 222405060，+≠不是直角三角形，故此选项正确；C. 22272425，+=是直角三角形，故此选项错误；D. 22235144⎛⎫⎛⎫+= ⎪ ⎪⎝⎭⎝⎭，是直角三角形，故此选项错误. 故选B.点睛：考查勾股定理的逆定理：如果三角形两条边的平方和等于第三条边的平方，那么这个三角形是直角三角形.10．C【解析】【分析】根据勾股定理和正方形的面积公式，知“生长”1次后，以直角三角形两条直角边为边长的正方形的面积和等于以斜边为边长的正方形的面积，即所有正方形的面积和是2×1=2；“生长”2次后，所有的正方形的面积和是3×1=3，推而广之即可求解． 【详解】设直角三角形的是三条边分别是a ，b ，c ．根据勾股定理，得a 2+b 2=c 2，即正方形A 的面积+正方形B 的面积=正方形C 的面积=1．推而广之，“生长”了2019次后形成的图形中所有的正方形的面积和是2019×1=2019． 故选：C ．【点睛】此题主要是能够根据勾股定理发现每一次得到的新的正方形的面积和与原正方形的面积之间的关系．11．5，91612,,555【解析】【分析】运用勾股定理可求解c，由三角形面积公式可求解h，再利用勾股定理可分别求解出k和p. 【详解】由勾股定理得：c2=a2+b2=9+16=25，则c=5；由三角形面积公式可得：ab=ch，则3×4=5×h，则h=125；由勾股定理得：b2=k2+h2，则16= k2+(125)2，则k=165，a2=p2+h2，则9= p2+(125)2，则p=95.【点睛】本题考查了勾股定理和三角形面积公式的应用.12．2【解析】【分析】如图，先利用勾股定理求出BC的长，再利用勾股定理求出CE的长，根据BE=BC-CE即可得答案.【详解】如图，AB=DE=10，AC=6，DC=8，∠C =90°，∴BC=2222106AB AC-=-=8，CE=2222108DE DC-=-=6，∴BE=BC-CE=2（米），故答案为2.【点睛】本题考查了勾股定理的应用，熟练掌握勾股定理是解题的关键.13．（22016，0）【解析】∵∠OBC=90°，OB=1，BC=，∵将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍，使OB1=OC，∴OC1=2OC=2×2=4=22，OC2=2OC1=2×4=8=23，OC3=2OC2=2×8=16=24，…，OC n=2n+1，∴OC2015=22016，∵2015÷6=335…5，∴点C2015与点C5在同一射线上，在x轴正半轴，坐标为（22016，0）．点睛：根据直角三角形得出∠BOC=60°，然后求出OC1、OC2、OC3、…、OC n的长度，再根据周角等于360°，每6个为一个循环组，求出点C2015是第几个循环组的第几个点，再根据变化规律写出点的坐标即可．14．113【解析】∵△ABC、△ADE都是以A为直角顶点的等腰直角三角形，∴AB=AC，AD=AE，∠BAC=∠DAE=90°，∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，∴在△ABD和△ACE中：AB ACBAD CAEAD AE=⎧⎪∠=∠⎨⎪=⎩，∴△ABD≌△ACE，∴BD=CE.①如图1，当∠CFE=90°时，AF⊥DE，∴AF=EF=22AE=23232=，∴CF=AC-AF=5-3=2，∴在Rt△CEF中，223213+=∴13②如图2：当∠CEF=90°时，∠AEC=90°+45°=135°，∵△ABD ≌△ACE ，∴∠ADB=∠AEC=135°，∴∠ADB+∠ADE=135°+45°=180°，∴点B 、D 、F 三点共线，过点A 作AG ⊥DE 于点G ，则AG=DG=22AD=2323⨯=， ∴在Rt △ABG 中，BG=22534-=，∴BD=BG-DG=4-3=1.综上所述，131.1515【解析】∵AD BC ∥，DE BC ⊥．∴DAC ACB ∠=∠，90ADE DEC ∠=∠=︒．∵G 为AF 的中点．∴AG GD GF ==．∴ADG DAG ACB ∠=∠=∠．∴2DGC ADG DAG ACB ∠=∠+∠=∠．∵DG DC =．∵4DG =，1EC =．∴4DC =，∵90DEC ∠=︒． ∴222241DE DC EC =-=-15=．点睛：本题考查了勾股定理，直角三角形斜边上中线性质的应用，解此题的关键是求出DG=DC 后利用勾股定理求DE 的长．16．13【解析】【分析】延长BC 交AD 于点E ，根据等腰直角三角形的性质求出AD ，再求出BE=DE=12AD 并得到BE ⊥AD ，然后求出CE ，在Rt △CDE 中，利用勾股定理列式计算即可得CD 的长．【详解】延长BC 交AD 于点E ，∵∠ABD=90°,∠ABC=45°，∴∠DBC=45°，∵AB=BD ，∴BE=DE=12AD ，BE ⊥AD ， ∵2，∴AD=6，∴DE=BE=3，∵BC=1，∴CE=2，∴CD2=DE2+CE2∴【点睛】本题考查的是等腰三角形和勾股定理，熟练掌握这两点是解题的关键.17．【解析】分析：过点P作PD⊥x轴于点D，由等边三角形的性质可知OD=12OQ=1，再根据勾股定理求出PD的长，故可得出P点坐标，再利用待定系数法求出直线OP的解析式即可．详解：解：过点P作PD⊥x轴于点D，∵△OPQ是边长为2的等边三角形，∴OD=12OQ=12×2=1，在Rt△OPD中，∵OP=2，OD=1，∴PD=∴P（1，设直线OP的解析式为y=kx（k≠0），k，∴直线OP的解析式为y．．点睛：本题考查的是用待定系数法求正比例函数的解析式，先根据题意得出点P 的坐标是解答此题的关键．18．直角三角形【解析】∵2223213AB =+=，2224652BC =+=，2221865AC =+=，∴222AB BC AC +=,∴ABC △为直角三角形．点睛：本题考查了勾股定理逆定理的应用，如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形.192222a b +【解析】 22a b a b ++-（）（）2222a b +. 2222a b +204552． 【解析】【分析】分两种情形：①如图1中，当∠EDF =90°时，作CH ⊥AB 于H ．只要证明CH =DH ，即可解决问题；②如图2中，当∠DEF =90°时，设DE =x ，则EF =2x ，DF =BD 5，构建方程即可解决问题．【详解】解：如图1中，当∠EDF =90°时，作CH ⊥AB 于H ．在Rt△ACB中，∵AC=2，BC=4，∴AB=2224+=25，∴CH=AC BCAB⋅=455．∵∠ACB=∠AHC=90°，∴∠ACH+∠BCH=90°，∠BCH+∠B=90°，∴∠ACH=∠B=∠F．∵CH∥DF，∴∠F=∠HCE，∴∠ACH=∠HCE，∠DCE=∠DCB，∴∠HCD=45°，∴HC=HD=45．∵AH=22AC CH-=255，∴BD=AB﹣AH﹣DH=25﹣655=455．如图2中，当∠DEF=90°时，设DE=x，则EF=2x，DF=BD=5x．∵AE+DE+BD=25，∴255+x+5x=25，∴x=2﹣255，∴BD=5x=25﹣2．综上所述：BD的长为455或25﹣2．故答案为455或52．【点睛】本题考查了翻折变换、勾股定理、等腰直角三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造直角三角形解决问题，学会用分类讨论的首先思考问题，属于中考填空题中的压轴题．21．（1）S△ABC32）3【解析】【分析】（1）过点A作AM⊥BC于M，根据已知可得BM=CM=12BC=1，然后根据勾股定理求得AM的长，再利用三角形的面积公式进行求解即可；（2）过点D作DN⊥AC于N，根据已知则可得到△ADM≌△AND，从而得DM=DN，AN=AM=3，继而得CN=AC-AB=2-3，设DM=DN=x，则CD=CM-DM=1-x，在Rt△CDN中，利用勾股定理求得x即可得.【详解】(1) 过点A作AM⊥BC于M，∵△ABC是等边三角形，∴BM=CM=12BC=1，∠BAM=∠CAM=30°，在Rt△CAM中，AM2+CM2=AC2，∴AM 2+12=22 ，∴AM=3，∴S△ABC=12BC·AM =12×2×3=3；（2）∵∠BAD=3∠CAD，∠BAD+∠CAD=∠BAC=60°，∴∠CAD=14∠BAC=15°，∠MAD=∠MAC-∠DAC=15°，∴AD平分∠MAC ，过点D作DN⊥AC于N，则△ADM≌△AND，∴DM=DN，3∴3，设DM=DN=x，则CD=CM-DM=1-x，在Rt△CDN中，DN2+CN2=CD2，x232=(1-x)2 ，解得：3-3，∴3【点睛】本题考查了等边三角形的性质，勾股定理、全等三角形的判定与性质等，添加辅助构造直角三角形进行解题是关键.22．（1）作图见解析；（2）正方形的面积是53，解释见解析.【解析】试题分析：（1）在网格中分别过点A作AD⊥AB于点A，过点B作BC⊥AB于点B，并使AD=AB=BC，再连接CD即可得到所求正方形；（2）如图，由勾股定理易得AB=22+=，再由正方形的面积公式即可计算出正2753方形ABCD的面积了.试题解析：（1）如图，过A、B分别作AD⊥AB，BC⊥AB，并且使得AD=BC=AB，连接CD，则图中所得四边形ABCD为所求正方形；（2）如图，∵图中小方格为的面积为1cm2，∴小方格的边长为1cm，∴AB=222753+=,=AB2=53.∴S正方形ABCD23．（1）5 90°（2）（0，4）或（4，2）或（-4，-4），平行四边形如图.【解析】分析：（1）由勾股定理即可求得AB，BC，AC的值，然后由勾股定理逆定理，可判定△ABC是直角三角形； （2）首先根据题意画出图形，然后根据图可求得平行四边形中D 点的坐标．详解：（1）根据点A 和点B 的坐标可知：AB =()22223++=5；同理可得BC =()22111++=5，AC =2224+=5， 所以有(5)2+(25)2=52，即222BC AC AB +=，故△ABC 是直角三角形，且∠ACB =90°. （2）点D 的坐标为（0，4）或（4，2）或（-4，-4），所作平行四边形如图所示.点睛：考查平行四边形的性质, 坐标与图形性质，注意数形结合思想在解题中的应用. 24．蚂蚁爬行的最短线路为13 cm .【解析】试题分析：根据题意，先将图形平面展开（如图所示），根据“两点之间，线段最短”可得蚂蚁爬行的最短距离为线段AB 的长，再用勾股定理求得AB 的长即可.试题解析：如图所示,将台阶展开.∵AC=3×3+1×3=12,BC=5,∴AB 2=AC 2+BC 2=132,∴AB=13(cm).∴蚂蚁爬行的最短线路为13 cm .点睛：本题考查了平面展开-最短路径问题，解决这类问题的基本思路是化曲面问题为平面问题，再用所学的知识解决．25．操作一：（1）14 cm ；（2）∠CAD =20度；操作二：CD=4.5cm【解析】【分析】操作一：（1）依据DE 垂直平分AB ，可得AD=BD ，依据△ACD 的周长=AD+CD+AC=BD+CD+AC=BC+AC 进行计算即可；（2）依据DE 垂直平分AB ，可得AD=BD ，即可得出∠B=∠BAD=35°，再根据Rt △ABC中，∠BAC=90°-35°=55°，即可得到∠CAD=55°-35°=20°；操作二：设CD=DE=x ，则BD=12-x ，Rt △ABC 中，15AB ==,BE=15-9=6，依据Rt △BDE 中，DE 2+BE 2=BD 2，可得方程x 2+62=（12-x ）2，即可得CD=4.5cm ．【详解】操作一：(1)由折叠可得，DE 垂直平分AB ，∴AD =BD ，∴△ACD 的周长为AD +CD +AC =BD +CD +AC =BC +AC =8+6=14(cm )故答案为14；(2)由折叠可得，DE 垂直平分AB ，∴AD =BD ，∴35B BAD ∠=∠=，又∵Rt △ABC 中,903555BAC ∠=-=，∴553520CAD ∠=-=，故答案为20；操作二：∵AC=9cm ，BC=12cm ，∴15AB ==（cm ），根据折叠性质可得AC=AE=9cm ，∴BE=AB ﹣AE=6cm ，设CD=x ，则BD=12﹣x ，DE=x ，在Rt △BDE 中，由题意可得方程x 2+62=（12﹣x ）2，解之得x=4.5，∴CD=4.5cm ．【点睛】考查线段的垂直平分线的性质，三角形的内角和以及勾股定理，掌握勾股定理是解题的关键.26．（1）15cm ；（2）3：1；（3）【解析】整体分析：(1)由“直角三角形中，30°角所对的直角边等于斜边的一半”求AC 的长；(2)连接AD ，由“三线合一”得∠BAD=60°，利用直角三角形中的30°角所对的直角边的性质，分别把BE ，EA 用BD 表示；(3)证明△BAE≌△ACD，得∠BPQ=60°，结合勾股定理求解.解：(1)∵DE 是线段BC 的垂直平分线，∠ACB=90°，∴CD=BD，AD=BD ．又∵在△ABC 中，∠ACB=90°，∠B=30°， ∴AC=12AB ， ∴△ACD 的周长=AC+AB=3BD=15cm ．故答案为15cm ；(2)连接AD ，如图所示．∵在△ABC 中，AB=AC ，∠A=120°，D 是BC 的中点，∴∠BAD=60°．又∵DE⊥AB，，EA=12AD ，AD ，∴EA=1212AD ， ∴BE:AE=3:1．故答案为3:1．(3)∵△ABC 为等边三角形．∴AB=AC，∠BAC=∠ACB=60°，在△BAE 和△ACD 中，AE=CD ，∠BAC=∠ACB，AB=AC ，∴△BAE≌△ACD(SAS)，∴∠ABE=∠CAD．∵∠BPQ 为△ABP 外角，∴∠BPQ=∠ABE+∠BAD．∴∠BPQ=∠CAD+∠BAD=∠BAC=60°，∵BQ⊥AD，∴∠PBQ=30°，∴BP=2PQ=2，∴PQ=1，2BP PQ -2221-3．27．（1）933-（2）5【解析】试题分析：（1）如图，过点C 作CF ⊥AD 于点F ，由此可得∠CFA=90°，由已知条件可得∠CDF=60°，从而可得∠DCF=30°，即可由CD 的长度求得DF 、CF 及AF 的长度，从而可得AD 的长度，就可计算出△ADC 的面积了；（2）在Rt △ACF 中由CF 32CAF=45°可求得AC 的长，结合已知的AB=10、BC=8可的AC 2+BC 2=AB 2，从而可证得∠ACB=90°，结合点E 是AB 的中点，即可得到CE=12AB=5. 试题解析：（1）过点C 作CF AD ⊥，交AD 延长线于点F ，∵45DAC ∠=︒，15DCA ∠=︒，∴CDF DAC DCA ∠=∠+∠ 451560=︒+︒=︒，在Rt CFD 中，26CD =，∴ 162DF CD ==， ()()222226632CF CD DF =-=-=，∴ 326AD AF DF =-=-，∴ 12ADC S AD CF =⨯ ()1236322=⨯-⨯ 933=-．（2）在Rt AFC 中，∵ 45DAC ∠=︒，32CF =∴ 22326AC CF ===，在ABC 中，∵ 2222268AC BC AB +=+=∴ △ABC 是直角三角形，又∵ E 为AB 中点，∴ 1110522CE AB ==⨯=． 28．16 5 403 【解析】试题分析：利用勾股定理可求出AB 的长进而得出△ADB 的周长；再根据题目要求扩充成AC 为直角边的直角三角形，利用AB=BD ，AD=BD ，分别得出答案．试题解析：∵在Rt △ABC 中，∠C=90°，BC=3，AC=4，CD=BC ，∴5=，则AD=AB=5，故此时△ADB 的周长为：5+5+6=16；如图2所示：AD=BD 时，设DC=x ，则AD=x+3，在Rt △ADC 中，（x+3）2=x 2+42，解得：x=76， 故AD=3+76=256 ， 则此时△ADB 的周长为：256+256+5=403 ； 如图3所示：AB=BD 时，在Rt △ADC 中，=则此时△ADB的周长为：故答案为（1）16；（2）403． 【点睛】本题主要考查对勾股定理，等腰三角形的性质等知识点的理解和掌握，能通过分类求出等腰三角形的所有情况是解此题的关键．29．（1）OC=2，BC=2；（2）S 与t 的函数关系式是：S=22(02)4)t t ⎧<≤⎪⎪-+<≤；（3）当t 为83时，△OPM 是等腰三角形． 【解析】整体分析：（1）先求出OA ，判断OC=CB ，再在Rt △AOC 中用勾股定理列方程求解；（2）分点P 在BC 上，与点C 重合，在CO 上，与点O 重合四种情况分类讨论，注意画出相应的图形，利用三角形的面积公式和三角形面积的和差关系求解；（3）因为等腰三角形的腰不确定，所以需要分三种情况讨论，利用等腰三角形的性质列方程求解.（1）解：∵∠A=90°，∠AOB=60°，∴∠B=30°，∴OA=12由勾股定理得：AB=3，∵OC平分∠AOB，∴∠AOC=∠BOC=30°=∠B，∴OC=BC，在△AOC中，AO2+AC2=CO2，∴(3)²+（3﹣OC）2=OC2，∴OC=2=BC，答：OC=2，BC=2．（2）解：①当P在BC上，Q在OC上时，0＜t＜2，则CP=2﹣t，CQ=t，过P作PH⊥OC于H，∴∠HCP=60°，∠HPC=30°，∴CH=12CP=12（2﹣t），HP=32（2﹣t），∴S△CPQ=12CQ×PH=12×t×3（2﹣t），即S=﹣3t2+3t；②当t=2时，P在C点，Q在O点，此时，△CPQ不存在，∴S=0，③当P在OC上，Q在ON上时2＜t＜4，过P作PG⊥ON于G，过C作CZ⊥ON于Z，∵CO=2，∠NOC=60°，∴3CP=t﹣2，OQ=t﹣2，∠NOC=60°，∴∠GPO=30°，∴OG=12OP=12（4﹣t），34﹣t），∴S△CPQ=S△COQ﹣S△OPQ=12×（t﹣2）×3﹣12×（t﹣2）×34﹣t），即3233．④当t=4时，P 在O 点，Q 在ON 上，如图（3）过C 作CM ⊥OB 于M ，CK ⊥ON 于K ，∵∠B=30°，由（1）知BC=2，∴CM=12BC=1， 有勾股定理得：3∵3，∴333，∴S=12PQ×CK=12×2×33 综合上述：S 与t 的函数关系式是：S=2233(02)333(24)t t t ⎧+<≤⎪⎪⎨⎪+<≤⎪； （3）解：如图（2），∵ON ⊥OB ，∴∠NOB=90°，∵∠B=30°，∠A=90°，∴∠AOB=60°， ∵OC 平分∠AOB ，∴∠AOC=∠BOC=30°，∴∠NOC=90°﹣30°=60°， ①OM=PM 时，∠MOP=∠MPO=30°， ∴∠PQO=180°﹣∠QOP ﹣∠MPO=90°， ∴OP=2OQ ，∴2（t ﹣2）=4﹣t ，解得：t=83， ②PM=OP 时，∠PMO=∠MOP=30°， ∴∠MPO=120°，∵∠QOP=60°，∴此时不存在； ③OM=OP 时，过P 作PG ⊥ON 于G ，OP=4﹣t ，∠QOP=60°， ∴∠OPG=30°，∴GO=12（4﹣t ），34﹣t ）， ∵∠AOC=30°，OM=OP ，∴∠OPM=∠OMP=75°， ∴∠PQO=180°﹣∠QOP ﹣∠QPO=45°，∴34﹣t ），∵OG+QG=OQ，∴12（4﹣t）+3（4﹣t）=t﹣2，解得：t=623+综合上述：当t为83或6233+时，△OPM是等腰三角形．30．25cm【解析】分析: 将立体图形展开成平面图形,然后根据两点之间线段距离最短,利用根据勾股定理进行求解,根据立体展开成平面图形情况分类讨论进行进行比较.详解:将长方体沿CH,HE,BE剪开翻折,使面ABCD和面BEHC在同一个平面内,连接AM,如图1,由题意可得:MD=MC+CD=5+10=15cm,AD=20cm,在Rt△ADM中,根据勾股定理得:AM=25cm,将长方体沿CH、GD、GH剪开翻折,使面ABCD和面D CH G在同一个平面内,连接AM，如图2,由题意得:BM=BC+MC=20+5=25（cm）,AB=10cm,在Rt△ABM中,根据勾股定理得:AM29cm,将长方体沿CD、CH、GH剪开翻折,连接AM,如图3,由题意得:AC=AB+BC=10+20=30（cm）,MC=5cm,在Rt△ACM中,根据勾股定理得:AM37cm,∵25＜29＜37则需要爬行的最短距离是25cm.点睛:本题考查了勾股定理的拓展应用,“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.。
人教版高中地理必修第二册第一章综合测试试卷含答-案答案在前1
第一章综合测试答案解析一、1.【答案】D【解析】我国人口密度东西差异原因，应该从自然环境因素和社会经济因素等方面去综合考虑。
2.【答案】B【解析】要想缩小地区间的人口密度差异，无论是提高人口出生率还是进行移民都不能从根本上解决问题，应该从西部地区生态环境的改善和地区经济发展上进行努力。
3.【答案】B【解析】根据轮廓可判断A 处是欧洲，B 处是南亚，C 处是东亚和东南亚。
南亚成为人类大陆，即说明其人口分布稠密，这与其自然条件优越、农业发达有关。
4.【答案】C【解析】从位置上看，D 处位于亚欧大陆中部，成为人口孤岛，说明其周围地区人口稀少，而在此区域内人口稠密。
5.【答案】B【解析】自然环境因素是影响人口分布的最基本的因素，但随着生产力水平的提高，自然环境因素的影响逐渐减小；在社会经济因素中，生产力发展水平对人口分布的影响最显著。
另外，历史、宗教、习俗等因素也对人口分布产生影响。
6.【答案】C【解析】海拔越高，人口密度越小；湿润地区人口密度大。
两图的纵坐标都为人口密度。
左图中的横坐标为海拔，右图中的横坐标为年降水量。
所以本题选择C 选项。
【考点】地理图表的判读能力7.【答案】B【解析】图中A 点海拔接近4 000 米，可能为青藏高原地区；E 点降水量小，应位于西北地区，可能为塔克拉玛干沙漠；C 点海拔低，应位于东部沿海地区；D 点降水量大，人口密度高，应位于南方沿海地区。
所以本题选择B 选项。
8.【答案】C【解析】从图中信息看，箭头B 代表了国际人口迁移，选项中只有我国明清时期人口移居东南亚和来我国工作的外籍工人属于国际人口迁移。
9.【答案】A【解析】箭头A 代表的是国内人口迁移，目前我国国内的人口迁移的主要流向是由中、西部地区向东部地区迁移。
10.【答案】A【解析】读图分析可知，外出农民工增量变化曲线在2010～2011 年斜率最陡，由此可判断该时段我国外出农民工增量变化最显著。
11.【答案】B【解析】人口出生率对外出农民工增量变化无明显影响；外出农民工户籍转变成城市居民户籍极少，不是影响外出农民工增量变化的主要原因；由于近年来国家鼓励农民工返乡创业，导致跨省外出农民工数量减少；东部沿海地区产业转型升级，对农民工劳动技能要求提高，农民工因劳动技能低，外出就业困难，使外出农民工增量减小。
(人教版)初中生物八年级上册 第五单元第一章综合测试(含答案)01
第五单元第一章综合测试一、选择题（40分）1.涡虫和水螅都有口无肛门，但它们却分别属于不同的无脊椎动物类群。
这两种动物的主要区别是（）A.身体呈两侧对称还是辐射对称B.是单细胞还是多细胞C.身体有无分节D.体表有无外骨骼2.昆虫是地球上种类和数量最多的一类动物。
下列有关昆虫的说法，正确的是（）A.昆虫体表覆盖着外骨骼，属于甲壳动物B.昆虫的身体分为头、胸、腹、躯干四部分C.昆虫的发育过程是完全变态发育D.昆虫一般有两对翅，适于飞行3.俗话说“蛙满塘，谷满仓”，青蛙是“田园卫士”。
青蛙既能在水中生活，又能在陆地生活的主要原因是（）A.青蛙体表无覆盖物，失水较快B.青蛙的呼吸依赖肺和皮肤两种器官C.在水中或陆地都没有足够的食物D.身体散热差，不能长时间留在水中4.鸟类区别于其他各种动物的最显著特征是（）①体表有羽毛；②前肢变为翼；③用肺呼吸并用气囊辅助呼吸；④心脏四腔；⑤体温恒定；⑥卵生、体内受精。
A.①②③B.④⑤⑥C.①③⑤D.②④⑥5.为了适应空中飞行生活，家鸽在其内部构造上出现了一些变化，你认为下列不属于家鸽适应飞行生活的特点是（）A.食量大，消化能力强B.直肠很短，不存粪便C.无膀胱，不存尿液D.体温恒定，适应能力强6.根据体内有无脊椎骨，下列动物和蚯蚓不属于同一类的是（）A.蛔虫B.菜青虫C.蜈蚣D.蛇7.海马用鳍辅助运动，用鳃呼吸，有由脊椎骨构成的脊柱，而且终身生活在水中。
据此，你判断海马属于（）A.节肢动物B.爬行动物C.哺乳动物D.鱼类8.下列对各种动物特征及其功能的描述错误的一项是（）A.家鸽体内有气囊，可辅助呼吸B.蚯蚓身体分节，适于躯体灵活运动C.鲤鱼身体呈流线型，被有鳞片，适于游泳D.家兔盲肠发达，适于消化肉类食物9.小明在某山区进行野外考察时找到了一种动物，经观察其具有如下特点：身体呈蠕虫状，细长而柔软，分成许多体节。
则他发现该动物的环境最可能是（）A.海水中B.河流中C.潮湿、有机物丰富的土壤中D.可能在B处，也可能在C处10.有位同学捉到一只青蛙，他将它放在有较多水的鱼缸中，准备精心饲养，观察蛙的活动，可是第二天蛙就死掉了，其死亡的原因是（）A.无法呼吸到充足的氧气B.饥饿C.受到惊吓D.水质有问题11.下列四种动物特征的描述正确的是（）A.涡虫——背腹扁平，体表有角质层，有口无肛门B.蛔虫——身体由相似的体节组成，有口有肛门C.河蚌——身体表面有外套膜，用气管呼吸D.蚯蚓——身体呈圆筒形，体壁湿润能进行气体交换12.“授人以鱼，不如授人以渔”，下面属于鱼类的是（）A.娃娃鱼B.鱿鱼C.鳄鱼D.草鱼13.鸟类和哺乳类都是恒温动物，下列哪项特点与维持体温的恒定没有直接的关系（）A.心脏四腔，血液输送氧气的能力强B.口中无齿或牙齿有分化，消化系统发达C.神经系统发达，具有调节体温的作用D.体表被毛或被覆羽毛，有保温作用14.下列哪项不是节肢动物共同特点（）A.体表有外骨骼B.身体和附肢都分节C.足和触角分节D.都会飞行15.抹香鲸生活在海洋中，但它却属于哺乳动物，主要原因是（）A.用肺呼吸B.心脏有四腔C.体温恒定D.胎生、哺乳16.爬行动物比两栖动物更适应陆地生活的原因是（）①体表覆盖角质鳞片或甲；②完全用肺呼吸；③生殖和发育离开了水；④卵表面有坚韧的卵壳；⑤皮肤裸露。
必修一第一二章综合测试题
必修一第一、二章综合测试题2014.10第Ⅰ卷（选择题共60分）1．用一般光学显微镜观察生物的细胞与组织，下列叙述不正确的是（）A．用10倍物镜观察水绵玻片时，玻片与物镜的距离为0.5 cm，若改用30倍物镜观察时，则玻片与物镜的距离应调整在1.5 cm左右B．若载玻片上有d字母，则视野下呈现p字母C．观察向日葵叶片的保卫细胞时，若将玻片标本向右方移动，则视野下保卫细胞向左方移动D．视野下观察到眼虫游向右上方，则应将玻片向右上方移动以便追踪2.下列关于HIV、幽门螺杆菌、人体肿瘤细胞的叙述，正确的是( )A．都含有DNA B．都具有增殖能力 C．都属于原核生物 D．都含有核糖体3.下列四组生物中，都属于真核生物的是( )A．噬菌体和根霉B．细菌和草履虫 C．蓝藻和酵母菌 D．衣藻和变形虫4．下列关于原核细胞的叙述，不正确的是 ( )A．没有细胞器，但有细胞壁B．无成形细胞核，也没有染色体C．具有与真核细胞相似的细胞膜和细胞质D．虽无成形的细胞核，但有一环状DNA分子5．对下列生物特征的叙述，正确的是( )①酵母菌②乳酸菌③硝化细菌④衣藻⑤金鱼藻⑥烟草花叶病毒A．①②⑥都是原核生物，且都能发生突变B．①②③都不含叶绿素，且都是分解者C．①③都是异养生物，且都能进行有氧呼吸D．③④⑤都具有细胞结构，且都有细胞壁6．右图表示人体细胞中四种主要元素占细胞鲜重的百分比，其中表示碳元素的是( )A．甲 B．乙 C．丙 D．丁7．下图是由4个圆所构成的元素概念的关系图，其中4为最大圆，3、2、1依次减小。
试判断符合这种关系的是（）A.1.大量元素、2.主要元素、3.基本元素、4.最基本元素B.1.基本元素、2.最基本元素、3.大量元素、 4.主要元素C.1.最基本元素、2.基本元素、3.主要元素、4.大量元素D.1.主要元素、2.大量元素、3.最基本元素、4.基本元素8．淀粉酶、纤维素和DNA都含有的元素是 ( )A．C H O B．C H O N S P C．C H O N D．C H N P9.下列不能与斐林试剂反应生成砖红色沉淀的是（）①葡萄糖②淀粉③蔗糖④麦芽糖⑤果糖⑥纤维素A．①④⑤B．②③⑥C．①⑤⑥D．①②④10.一般说来，每100克蛋白质平均含氮为16克，这些氮主要存在于蛋白质的A．—CO—NH—B．游离的氨基 C．游离的羧基 D．R基11．对下表中所列待测物质的检测，所选用的试剂及预期结果都正确的是（ ）A.①③B.②③C.①④D.②④12.若一个氨基酸分子有两个羧基，其中一个羧基在R 基上，则另一个羧基 A ．与氨基端相连 B ．与连有氨基的碳原子相连 C ．与氢相连 D ．与羧基端相连13．某蛋白质由3条多肽链、N 个氨基酸组成，下列关于该蛋白质说法正确的是 A.形成该蛋白质时产生了N 个水分子 B.该蛋白质中至少含有N 个肽键C.该蛋白质中至少含有3个游离的羧基D.合成该蛋白质至少需要20种氨基酸 14．下列有关蛋白质的叙述正确的是 ( ) A ．DNA 的复制与蛋白质无关B ．蛋白质具有多样性，是由于氨基酸的种类、数目、排列顺序和空间结构不同C ．同一生物体不同组织细胞核内的DNA 不同，蛋白质也不相同D ．某蛋白质分子由4条肽链组成，含有m 个氨基酸，每个氨基酸的平均相对分子质量为a ，则该蛋白质的相对分子质量为ma －18m ＋7215.已知某种氨基酸的R 基是-CH 2-CH 2-NH 2。
八年级物理上册(人教版)：第一章综合能力测试题
第一章综合能力测试题时间：90分钟满分：100分题号一二三四五总分得分一、选择题(每小题3分，共30分)1．下列现象属于机械运动的是(D)A．秋虫鸣叫B．星光闪闪C．滴水成冰D．雨滴下落2．我国宇航员在太空中走出“神舟十号”载人飞船站在舱口，举起了五星红旗．某同学说他是静止的，他选择的参照物是(D)A．太阳B．地球C．月亮D．“神舟十号”飞船3．如图是小明用刻度尺测量一条形金属片长度的情形，该刻度尺的分度值和金属片的长度分别是(D)A．1cm 5.50cm B．1cm8.30cmC．1mm8.30cm D．1mm 2.80cm第3题图第4题图4．从图中的两幅组成的画中，请你观察并判断两车的运动情况是(A)A．卡车运动，轿车静止B．卡车静止，轿车运动C．两车都运动D．两车都静止5．(2014，荆州)为了践行“绿色环保”的生活理念，小张、小王、小李从同一地点A 沿同一道路同时出发，最终都到达地点B，小张驾驶电瓶车以30km/h的速度匀速前进，小王以5m/s的速度跑步匀速前进，小李以每分钟通过0.6km的速度骑自行车匀速前进，则(C)A．小张先到达B地B．小王先到达B地C．小李先到达B地D．三人同时到达B地6．卧龙大桥是襄阳首座斜拉桥，全长4343.5米，桥面宽31.5米，双向六车道．如果一辆大车通过该桥的速度是60千米/小时，则所用的时间是(保留整数位)(A) A．4min B．6minC．8min D．10min7．甲、乙两位同学进行百米赛跑，假如把他们的运动近似看作匀速直线运动处理，他们同时从起跑线起跑，经过一段时间后他们的位置如图所示，在图中分别作出在这段时间内两人运动路程s、速度v与时间t的关系图象，正确的是(B)8．用同一张底片对着小球运动的路径每隔0.1s拍一次照，得到的照片如图所示，则小球运动的平均速度是(C)A．0.25m/s B．0.2m/sC．0.17m/s D．无法确定9．小明骑自行车去上学，他在前一半路程的速度是4m/s，他感觉要迟到了，便以6m/s 的速度走完了后一半路程，那么他在整个过程中的平均速度是(B)A．4m/s B．4.8m/s C．5m/s D．6m/s10．某学习小组对一辆在平直公路上做直线运动的小车进行观测研究．他们记录了小车在某段时间内通过的路程与所用的时间，并根据记录的数据绘制了路程与时间的关系图象，如图所示．根据图象可以判断(C)A．2～5s内，小车做匀速直线运动B．5～8s内，小车做加速运动C．0～5s内，小车的平均速度是0.4m/sD．小车在0～2s内比在5～8s内运动得快二、填空题(每空1分，共23分)11．在下列横线上填上合适的单位或数字：某人身高约165__cm__，步行的速度约为5__km/h__；一辆小轿车在高速公路上行驶时的速度为85__km/h__，按照这个速度走完255km的路程需要的时间为__3__h.12．如图所示，用A、B两刻度尺测同一木块的边长，就分度值而言，__A__尺精密些，就使用方法而言，__A__尺正确．第12题图第14题图第15题图13．小明骑着自行车上学，以小明背着的书包为参照物，小明是__静止__(选填“运动”或“静止”)的．小明骑自行车的平均速度为4m/s，其物理意义是__每秒通过的路程为4米__，小明从家到学校骑车用了10min，则小明家到学校的距离约__2400__m.14．如图所示是竖直向上抛出的小球上升过程中每隔相等的时间曝光一次所得的照片．从图中可以判断：小球在a、b位置间的平均速度__大于__(选填“大于”“小于”或“等于”)在c、d位置间的平均速度．15．甲、乙两辆小车在平直的路面上向东运动，测出它们运动的路程和时间，并依据数据做出了相应的路程—时间关系图象，如图所示．由图知小车甲做__匀速直线__运动，速度大小为__15__m/s.若以甲为参照物，乙车向__西__运动．16．两个做匀速直线运动的物体甲和乙，它们通过的路程之比为3∶4，所用时间之比为2∶3，则甲、乙两物体速度之比为__9∶8__；若他们通过相同的路程，则它们所用时间之比为__8∶9__．17．甲、乙、丙三辆小车同时、同地向同一方向运动，它们运动的图象如图(a)、(b)所示，由图象可知：若以甲车为参照物，则__乙__(选填“乙”或“丙”)车静止；甲车的运动时间如图(c)所示，则秒表记录的时间为__175__s，甲车通过的路程为__700__m.18．中国310渔政执法船，最大航速达40.7km/h，某日上午，它驶离广州渔政码头，开赴南海某海域执法．以310渔政船为参照物，渔政码头是__运动__(选填“运动”或“静止”)的，若310渔政船以最大航速到达离广州1100km的南海某处，需要__27__h(保留整数)．19．如图所示，是某汽车启动和到达的时间以及对应的里程表(盘面指示为千米数)的示数．由图可知，汽车行驶的里程数为__120__km，平均速度为__11.1__m/s(小数点后保留一位数字)．20．宁波市14个路段启用“绿波带”设置，设置“绿波带”能使按绿波速度行驶的车辆一路绿灯通过．曾有记者在早高峰时段驾车通过世纪大道，在实施绿波的12km路段用时10min，比实施前减少了5min，该车平均速度提高了__24__km/h.三、简答题(8分)21．小华同学买了一盒自动铅笔用的铅芯，但包装盒上注明的笔芯直径看不清楚了，小华想用实验方法测出笔芯的直径，他只有最小分度值是1mm的三角板一块，小华能否测量出笔芯的直径？请写出实验步骤．解：把几根铅笔芯紧密排列在一起，用三角板测出宽度a，则铅笔芯直径d＝an.四、实验探究题(共22分)22．(12分)如图所示：(1)在测物体的长度时，两种使用方法中正确的是__甲__图，铅笔的长度应为__3.25__cm.(2)用刻度尺测某课本的长度需要多次测量，多次测量的目的是__减小误差__．若用毫米刻度尺测量，四次读数分别是25.98cm、26.00cm、26.02cm、26.42cm.其中错误的数据是__26.42cm__，该课本的长度应为__26.00cm__．(3)若有一把刻度尺是用金属材料制成的，且这种金属材料受温度变化很明显，那么在严冬季节用它测量物体的长度时，其测量结果将__偏大__(选填“偏大”“偏小”或“不变”)．23．(10分)某物理兴趣小组利用带有刻度尺的斜面、小车和数值钟“测量小车的平均速度”，如图所示，图中显示的是他们测量过程中的小车在甲、乙、丙三个位置及其对应时间的情形，显示时间的格式是“时：分：秒”．(1)请你根据图示完成下表．小车由甲至乙小车由乙至丙小车由甲至丙路程s/cm 26 64 90时间t/s 2 4 6平均速度v/cm·s－113 1615(2)分析表中的数据，小车全程是做匀速运动吗？为什么？解：(2)不是．因为小车前段路程运动慢，后段路程运动快，小车全程做的不是匀速运动．五、计算题(共17分)24．(7分)十一期间，小明一家开车外出旅游，途中看到如图所示的限速牌．小明用了10min 的时间通过了这段10km 长的限速路段，请你通过计算说明他超速了吗？解：小明开车的速度为v ＝s t ＝10km16h ＝60km/h ＞40km/h ，所以超速．25．(10分)如表是福州至厦门D6201次列车沿途部分站点的到站、发车时刻表．车站 里程/km到站、发车时刻福州 0 7：12 莆田 105 7：54 7：56 泉州 174 8：17 8：19厦门2769：02(1)列车从福州到莆田的平均速度为多少km/h? (2)列车在7：55的速度多大？解：(1)由列车时刻表可知，列车从福州到莆田行驶的路程s ＝105km ，列车从福州到莆田行驶的时间t ＝7：54－7：12＝42min ＝0.7h ，则平均速度v ＝s t ＝105km0.7h＝150km/h.(2)由表可得在7：55时列车处于静止状态，故瞬时速度为零．。
九年级数学上一二章综合测试卷
一、选择题：
1、若一元二次方程(m－2)x2+3(m2+15)x+m2－4=0的常数项是0，则m为（）
A、2B、±2C、－2D、－10
2、下列关于 的一元二次方程中，有两个不相等的实数根的方程是（ ）
Ａ． Ｂ． Ｃ． Ｄ．
3、用配方法解下列方程时，配方错误的是（）
A、三边中线的交点B、三条角平分线的交点
C、三边上高的交点D、三边垂直平分线的交点
13、△ABC中，∠A∶∠B∶∠C=1∶2∶3，若BC=2，则AB等于（）
A.1 B. 2 C.4 D.
14、△ABC的周长为12cm，面积为6cm2、则其内角平分线的交点O到AB的距离为
A、1cm B、2cm C、3cm D、4cm
（7）（8）（9）
10、△ABC的∠B、∠C的平分线相交于T，且∠BTC＝130°，则∠A＝。
三、解答题
1、解下列方程：（每小题3分，共12分）
①4x2–32x+4=0（配方法）②2 （公式法）
③ （分解因式法）④ （分解因式法）
2、已知 、 、 均为实数且 ，求方程 的根；
3、菱形ABCD的边长是5，两条对角线交于O点，且AO、BO的长分别是关于 的方程 的根，求 的值。
8、如图8所示，P是等边三角形ABC内一点，将△ABP绕点B顺时针方向旋转60°，得到△CBP′，若PB=3，则PP′=。
9、如图9所示，某小区规划在一个长为40 m、宽为26 m的矩形场地ABCD上修建三条同样宽的甬路，使其中两条与AB平行，另一条与AD平行，其余部分种草.若使每一块草坪的面积为144 m2，求甬路的宽度.若设甬路的宽度为xm，则x满足的方程为.
苏教版初中生物七年级上册第一章综合测试试卷-含答案01
第一章综合测试第Ⅰ部分 选择题60分一、选择题（共30小题，每小题2分，共计60分）1.古诗文中有提到“橘生淮南则为橘，生于淮北则为枳”，说的是橘树生长在淮河以南的地方就是橘树，生长在准河以北的地方就是枳树，比喻环境变了，事物的性质也变了，这体现了（）A.生物适应环境B.环境适应生物C.生物影响环境D.环境影响生物2.下列不是生物的是（）A.病毒B.生石花C.克隆牛D.珊瑚3.下列哪项不是生物的活动影响生存环境的实例（）A.温带地区的阔叶树在秋天落叶B.大面积植树造林可净化空气、缓解温室效应，调节局部地区的气候C.甲烷菌分解植物茎叶和人畜粪便中的有机物，可用来生产沼气和污水净化D.屎壳郎能清除地面上的动物粪便，有利于草等植物的生长4.《齐民要术》是我国古代的农业百科全书，对世界农业科学史产生了重要的影响。
其中对菜地的管理有“有草锄之”的论述。
种菜要锄草，因为杂草与蔬菜之间的关系是（）A.竞争B.合作C.寄生D.共生5.以下成语中的生物具有系统的是（）A.绿草如茵B.百花齐放C.岁寒松柏D.狡兔三窟6.谷文昌同志带领东山人民战飞沙、抓绿化，把荒岛打造成了宝岛。
这事例说明（）A.生物影响环境B.生物适应环境C.环境影响生物D.环境适应生物7.自然选择学说合理解释了生物进化的原因，是生物进化理论的核心。
提出自然选择学说的科学家是（）A.米勒B.林奈C.达尔文D.巴斯德8.四位同学在校园周边调查几种植物之后，依次发表了各自不同的见解，如图示。
你认为不正确的是（）A.B.C.D.9.生物命名法——双名法的提出者是（）A.林奈B.巴斯德C.达尔文D.列文·虎克10.武汉为应对疫情推出的移动医疗空间的名字是（）A.胶囊医院B.太空舱医院C.方舱医院D.露天医院11.生物必须适应环境才能生存，这种适应表现在生物的形态、结构和生理等各方面，否则会被自然界淘汰。
如蝗虫有外骨骼适应陆地干旱的环境，鸟骨骼中空适应飞行生活。
第1章有理数(综合能力拔高卷)(考试版)
【高效培优】2022—2023学年七年级数学上册必考重难点突破必刷卷（沪科版）【单元测试】第1章有理数（综合能力拔高卷）学校:___________姓名：___________班级：___________考号：___________ 一、选择题（本大题共10个小题，每小题3分，共30分；在每小题给出的四个选项中，只有一项是符合题目要求的）1．在实数113，03.14159264.21，3π中，有理数的个数为（）A．3B．4C．5D．6 2．－2022的倒数的绝对值是（）A．2022B．12022-C．－2022D．120223．对于|m－1|，下列结论正确的是（）A．|m－1|≥|m|B．|m－1|≤|m|C．|m－1|≥|m|－1D．|m－1|≤|m|－14．如图的数轴被墨迹盖住一部分，被盖住的整数点有（）个．A．9B．10C．11D．125．下面有理数比较大小，正确的是（）A．0＜2-B．4-＜3C．2-＜3-D．1＜4-6．近年来，我国的自然天气受到厄尔尼诺现象的影响，因此2020年的冬天是一个温暖的冬季，并不是特别寒冷．在十一月份的某一天，黑河市某地最高气温4°C，最低气温是7°C，这一天最高气温与最低气温的温差是（）A．3C B．11C C．3C-D．11C-7．下列运算正确的是（）A．﹣2+（﹣5）＝﹣（5﹣2）＝﹣3B．（+3）+（﹣8）＝﹣（8﹣3）＝﹣5C．（﹣9）﹣（﹣2）＝﹣（9+2）＝﹣11D．（+6）+（﹣4）＝+（6+4）＝+108．已知一天有86400秒，一年按365天计算共有31536000秒，“中国飞人”苏炳添经过5年（约157680000秒），从里约到东京，以9秒83创亚洲纪录的成绩成为首位闯进奥运会男子百米决赛的中国人，将数据157680000用科学记数法表示为（）A．81.576810⨯B．815.76810⨯C．71.576810⨯D．715.76810⨯9．下列由四舍五入法得到的近似数，对其描述正确的是（）A．1.20精确到十分位B．1.20万精确到百分位C．1.20万精确到万位D．51.2010⨯精确到千位10．某原料供应商对购买其原料的顾客实行如下优惠办法：（1）一次购买金额不超过1万元，不予优惠；（2）一次购买金额超过1万元，但不超过3万元，九折优惠；（3）一次购买超过3万元的，其中3万元九折优惠，超过3万元的部分八折优惠．某公司分两次在该供应商处购买原料，分别付款7800元和25200元．如果该公司把两次购买的原料改为一次购买的话，那么该公司一共可少付款（）A．3360 元B．2780 元C．1460 元D．1360元二、填空题（本大题共6个小题，每题3分，共18分）11．比较大小：8_____|﹣8|，﹣56_____﹣67，|﹣3.2|_____﹣（+3.2）（用“＝”，“＜”，“＞”填空）12．315-的相反数是______，倒数是______，绝对值是______．13．用四舍五入法取近似数：3.6782≈_______．（精确到0.01）14．如图的数轴上有两处不小心被墨水淹没了，所标注的数据是墨水部分边界与数轴相交点的数据；则被淹没的整数点有_____个，负整数点有_____个，被淹没的最小的负整数点所表示的数是_____．15．天宫二号是中国首个具备补加功能的载人航天科学实验空间实验室，天宫二号的轨道高度约为393000m，393000m用科学记数法表示为_____m．16．气象台记录了某地本周七天的气温变化情况（如下表），其中正号表示的数据是比前一天上升的温度，负号表示的数据是比前一天降低的温度，已知上周日气温为3℃，根据表中数据，请你判断该地本周最低气温是________℃．三、解答题（本大题共8个小题，共72分；第1718每小题6分，第1921每小题8分，第22小题10分，第23小题12分，第24小题14分）17．计算（1）4+（﹣2）2×2﹣（﹣36）÷4；（2）16÷（﹣2）3﹣（18-）×（﹣4）．（3）42112(3)(7)6⎡⎤--⨯--÷-⎣⎦ （4）315711(1)()8()2812242-+÷--⨯-18．把下列各数分别填入相应的集合内．12-，3，7.8，0.01-，227，2021，15-，0，—143，—45%． (1)正数集：{ }⋯； (2)负分数集：{ }⋯； (3)非正整数集：{ }⋯； (4)有理数集：{ }⋯． 19．有理数a 、b 、c 在数轴上的位置如图．(1)用“＞”或“＜”填空：b ﹣c 0，a +b +3 0b c + 0． (2)3b c a b a c +-++--． 20．将下列各数在数轴上表示出来，并用“<”连接：3-， 1， 0， 3.5， 2.5， 112比较大小：________<________<________<________<_________<_________21．现有20箱苹果，以每箱30千克为标准，超过或不足的千克数分别用正数，负数来表示，记录如下：(1)从20箱中任选两箱，它们的千克数的差最大为kg ； (2)与标准质量相比，20箱苹果是超过或不足多少千克？(3)若这批苹果进价为6元/千克，售价为8元/千克，这批苹果全部卖完（不计损坏）共赚了多少元？22．某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km ）： （1）接送完第5批客人后，该驾驶员在公司的什么方向，距离公司多少千米？ （2）若该出租车每千米耗油0.1升，那么在这过程中共耗油多少升？（3）若该出租车的计价标准为：行驶路程不超过3km 收费10元，超过3km 的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？23．阅读材料：2018年3月5日上午9时，十三届全国人大一次会议在人民大会堂开幕，听取国务院总理李克强作政府工作报告，李克强总结回顾过去五年工作指出：第十二届全国人民代表大会第一次会议以来的五年，是我国发展进程中极不平凡的五年，……五年来，经济实力跃上新台阶，国内生产总值从54万亿元增加到82.7万亿元，年均增长7.1%，占世界经济比重从11.4%提高到15%左右，对世界经济增长贡献率超过30%财政收入从11.7万亿元增加到17.3万亿元居民消费价格年均上涨1.9%，保持较低水平城镇新增就业6600万人以上，13亿多人口的大国实现了比较充分就业解决问题：（1）请你把数据“6600万”用科学记数法表示出来； （2）数据“82.7万亿”精确到哪一位？24．数轴体现了数形结合的数学思想，若数轴上点A ，B 表示的数分别为a ，b ，则A 、B两点之间的距离表示为ABa b ．如：点A 表示的数为2，点B 表示的数为3，则231AB =-=．问题提出：(1)填空：如图，数轴上点A 表示的数为−2，点B 表示的数为13，A 、B 两点之间的距离AB =______，线段AB 的中点表示的数为______．(2)拓展探究：若点P 从点A 出发，以每秒3个单位长度的速度沿数轴向右运动，同时点Q 从点B 出发．以每秒2个单位长度的速度向左运动．设运动时间为t 秒（t >0）℃用含t 的式子表示：t 秒后，点Р表示的数为______；点Q 表示的数为______； ℃求当t 为何值时，P 、Q 两点相遇，并写出相遇点所表示的数．(3)类比延伸：在（2）的条件下，如果P 、Q 两点相遇后按照原来的速度继续运动，当各自到达线段AB 的端点后立即改变运动方向，并以原来的速度在线段AB 上做往复运动，那么再经过多长时间P 、Q 两点第二次相遇．请直接写出所需要的时间和此时相遇点所表示的数．。
小学五年级语文(上册)一单元综合能力测试卷及答案
小学五年级语文(上册)一单元综合能力测试卷及答案班级：姓名：满分：100分考试时间：90分钟题序一二三四五六七八九十总分得分一、看拼音，写词语，注意书写整洁美观。
bái hèdiǎn lǐyóu yǒng fán zhíshòu ruòhuāng tang lǎn duòhuī huáng二、用“\” 划去句子中加点字不正确的读音。
1．远处传来一片哗．笑（huāhuá）和告别的声音。
2．如今，当我来到金字塔下，望着这人间的奇迹，更禁．（jīn jìn）不住思绪激荡。
3．沉睡的牲畜．（chùxù），无声的低地，漆黑的夜晚，只有远处的几座灯塔在闪烁着微弱的光芒。
4．你看，天上地下，黄澄澄，金灿灿，一片耀眼的色调，着．（zhuózháo）实是一副开阔而雄浑的画卷。
三、形近字组词诣（______）阅（______）犹（______）豫（______）裕（______）指（______）阐（______）扰（______）像（______）浴（______）四、把下列词语补充完整，并按要求写词语。
字里（____）间①半（____）半（____）派头十（____）②平平（____）（____）天衣无（____）闭目养（____）③（____）来（____）去④全神（____）注一（____）一样1.仿照①写ABAC式词语：________________2.仿照②写AABB式词语：_________________3.仿照③写含有一对反义词的词语：__________________4.写出④的近义词___________，④的反义词_________。
五、我会选词填空。
一……就……虽然……但是……因为……所以……不是……而是……1.（___）人生短暂如白驹过隙，（___）我们要珍惜生命，充分利用时间来完成自己的理想。
高中数学 第一章 统计综合能力测试(含解析)北师大版必修3-北师大版高一必修3数学试题
【成才之路】2015-2016学年高中数学第一章统计综合能力测试北师大版必修3本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分．时间120分钟，满分150分．第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的)1．2015年的世界无烟日(5月31日)之前，小华学习小组为了了解本地区大约有多少成年人吸烟，随机调查了100个成年人，结果其中有15个成年人吸烟．对于这个关于数据收集与处理的问题，下列说法正确的是( )A．调查的方式是普查B．本地区约有15%的成年人吸烟C．样本是15个吸烟的成年人D．本地区只有85个成年人不吸烟[答案] B[解析]调查方式显然是抽样调查，∴A错误．样本是这100个成年人．∴C也错误，显然D不正确．故选B.2．某班的78名同学已编号1,2,3，…，78，为了解该班同学的作业情况，老师收取了学号能被5整除的15名同学的作业本，这里运用的抽样方法是( )A．简单随机抽样法 B.系统抽样法C．分层抽样法 D.抽签法[答案] B[解析]所抽出的编号都间隔5，故是系统抽样．3．下列问题，最适合用简单随机抽样的是( )A．某电影院有32排座位，每排有40个座位，座位号为1～40.有一次报告会坐满了听众，报告会结束后为听取意见，要留下32名听众进行座谈B．从10台冰箱中抽出3台进行质量检查C．某学校在编人员160人．其中行政人员16人，教师112人，后勤人员32人．教育部门为了解学校机构改革意见，要从中抽取一个容量为20的样本D．某乡农田有：山地8 000亩，丘陵12 000亩，平地24 000亩，洼地4 000亩. 现抽取农田480亩估计全乡农田某种作物的平均亩产量[答案] B[解析]A项的总体容量较大，用简单随机抽样法比较麻烦；B项的总体容量较小，用简单随机抽样法比较方便；C项由于学校各类人员对这一问题的看法可能差异较大，不宜采用简单随机抽样法；D 项的总体容量较大，且各类田地的产量差别很大，也不宜采用简单随机抽样法．4．一个容量为50的样本数据，分组后，组距与频数如下：[12.5,15.5)，2；[15.5,18.5)，8；[18.5,21.5)，9；[21.5，24.5)，11；[24.5,27.5)，10；[27.5,30.5)，6；[30.5,33.5)，4.根据分组情况估计小于30.5的数据占( )A ．18% B.30% C ．60% D.92%[答案] D[解析] (2＋8＋9＋11＋10＋6)÷50＝92%.5．如图所示的是2006年至2015年某省城镇居民百户家庭人口数的茎叶图，图中左边的数字从左到右分别表示城镇居民百户家庭人口数的百位数字和十位数字，右边的数字表示城镇居民百户家庭人口数的个位数字，从图中可以得到2006年至2015年此省城镇居民百户家庭人口数的平均数为( )2 9 1 1 5 83 0 2 6 31247[答案] B[解析] 由茎叶图得到2006年至2015年城镇居民百户家庭人口数为：291,291,295,298,302,306,310,312,314,317，所以平均数为291＋291＋295＋298＋302＋306＋310＋312＋314＋31710＝3 03610＝303.6.6．某地区共有10万户居民，该地区城市住户与农村住户之比为4∶6，根据分层抽样方法，调查了该地区1 000户居民冰箱拥有情况，调查结果如下表所示，那么可以估计该地区农村住户中无冰箱的总户数约为( )万户 C ．1.76万户 D.0.24万户[答案] A[解析] 由于城市住户与农村住户之比为4∶6，城市住户有4万户，农村住户有6万户，调查的1 000户居民中共400户城市住户，有600户农村住户，其中农村住户中无冰箱的有160户，所以可估计该地区农村住户中无冰箱的总户数约为10×1601 000＝1.6(万户)．7．对某商店一个月内每天的顾客人数进行了统计，得到样本的茎叶图(如图所示)，则该样本的中位数、众数、极差分别是( )1 2 520 2 3 33 1 24 4 8 94 5 5 5 7 7 8 8 950 0 1 1 4 7 96 17 8A.46,45,56B.46,45,53C．47,45,56 D.45,47,53[答案] A[解析]本题考查了茎叶图的应用及其样本的中位数、众数、极差等数字特征，由茎叶图可知，中位数为46，众数为45，极差为68－12＝56.在求一组数据的中位数时，一定不要忘记先将这些数据排序再判断．8．有一个容量为200的样本，其频率分布直方图如图所示．根据样本的频率分布直方图估计，样本数据落在区间[10,12)内的频数为( )A．18 B.36C．54 D.72[答案] B[解析]频率分布直方图中所有小矩形的面积之和为1，每个小矩形的面积表示样本数据落在该区间内的频率，故样本数据落在区间[10,12)内的频率为1－2×(0.02＋0.05＋0.15＋0.19)＝0.18，故样本数据落在区间[10,12)内的频数为0.18×200＝36.9.已知两个变量x，y之间具有线性相关关系，测得(x，y)的四组值分别为(1,2)，(2,4)，(3,5)，(4,7)，则y与x之间的回归直线方程为( )A．y＝0.8x＋3 B.y＝－1.2x＋7.5C．y＝1.6x＋0.5 D.y＝1.3x＋1.2[答案] C[解析] 利用排除法． ∵x ＝14(1＋2＋3＋4)＝ 2.5，y ＝14(2＋4＋5＋7)＝4.5，由于回归直线方程y ＝bx ＋a 必过定点(2.5,4.5)，故排除A 、D.又由四组数值知y 随x 的增大而增大，知b >0，排除B.10．某路段检查站监控录像显示，在某时段内，有 1 000辆汽车通过该站，现在随机抽取其中的200辆汽车进行车速分析，分析的结果表示为如下图的频率分布直方图，则估计在这一时段内通过该站的汽车中速度不小于90 km/h 的约有( )A ．100辆 B.200辆 C ．300辆 D.400辆[答案] C[解析] 由题图可知汽车中车速在[60,90)的频率为10×(0.01＋0.02＋0.04)＝0.7， ∴在[90,110]的频率为(1－0.7)＝0.3.∴车速不小于90 km/h 的汽车数量约为0.3×1 000＝300辆．11.某人5次上班途中所花的时间(单位：分钟)分别为x ，y,10,11,9，已知这组数据的平均数为10，方差为2，则|x －y |的值为( )A ．1 B.2 C ．3 D.4[答案] D[解析] 依题意，可得 ⎩⎪⎨⎪⎧10＝x ＋y ＋10＋11＋95，2＝15[x －102＋y －102＋10－102＋11－102＋9－102]，⇒⎩⎪⎨⎪⎧x ＋y ＝20，x －102＋y －102＝8，⇒⎩⎪⎨⎪⎧x ＝12y ＝8，或⎩⎪⎨⎪⎧x ＝8y ＝12，所以|x－y|＝4.12．甲，乙，丙三名运动员在某次测试中各射击20次，三人测试成绩的频率分布条形图分别如图1，图2和图3，若s甲，s乙，s丙分别表示他们测试成绩的标准差，则( )A．s甲<s乙<s丙 B.s甲<s丙<s乙C．s乙<s甲<s丙 D.s丙<s甲<s乙[答案] D[解析]由频率分布条形图可得甲，乙，丙三名运动员的平均成绩分别为x－甲＝0.25×(7＋8＋9＋10)＝8.5；x－乙＝0.3×7＋8×0.2＋9×0.2＋10×0.3＝8.5；x－丙＝0.2×7＋8×0.3＋9×0.3＋10×0.2＝8.5，s2甲＝0.25×(1.52＋0.52＋0.52＋1.52)＝1.25；s2乙＝0.3×1.52＋0.52×0.2＋0.52×0.2＋1.52×0.3＝1.45；s2丙＝0.2×1.52＋0.52×0.3＋0.52×0.3＋1.52×0.2＝1.05，∴s丙<s甲<s乙．第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题，每小题5分，共20分，将正确答案填在题中横线上)13．一个容量为40的样本，共分成6组，第1～4组的频数分别为10,5,7,6，第5组的频率是0.10，则第6组的频率是________．[答案]0.20[解析]第5组的频数为40×0.10＝4，第6组的频数为40－(10＋5＋7＋6＋4)＝8，则频率为840＝0.20.14．(2015·某某文，12)已知样本数据x1，x2，…，x n的均值x＝5，则样本数据2x1＋1,2x2＋1，…，2x n＋1的均值为________．[答案]11[解析]因为样本数据x1，x2，…，x n的均值x＝5，所以样本数据2x1＋1,2x2＋1，…，2x n＋1的均值为2x＋1＝2×5＋1＝11.15．(2014·某某，6)设抽测的树木的底部周长均在区间[80,130]上，其频率分布直方图如图所示，则在抽测的60株树木中，有________株树木的底部周长小于100cm.[答案] 24[解析] 本题考查频率分布直方图．由题意在抽测的60株树木中，底部周长小于100cm 的株数为(0.015＋0.025)×10×60＝24.频率分布直方图中的纵坐标为频率组距，此处经常误认为纵坐标是频率．16．下图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为________.0 8 9 10 3 5(注：方差s 2＝1n[(x 1－x －)2＋(x 2－x －)2＋…＋(x n －x －)2]，其中x －为x 1，x 2，…，x n 的平均数)[答案] 6.8[解析] 本题考查茎叶图、方差的概念． 由茎叶图知x －＝8＋9＋10＋13＋155＝11，∴s 2＝15[(8－11)2＋(9－11)2＋(10－11)2＋(13－11)2＋(15－11)2]＝6.8.三、解答题(本大题共6个小题，共70分，解答应写出文字说明、证明过程或演算步骤) 17．(本小题满分10分)在同等条件下，对30辆同一型号的汽车进行耗油1升所行走路程的试验，得到如下数据(单位：km)：14．1 12.3 13.7 14.0 12.8 12.9 13.1 13．6 14.4 13.8 12.6 13.8 12.6 13.2 13．3 14.2 13.9 12.7 13.0 13.2 13.5 13．6 13.4 13.6 12.1 12.5 13.1 13.5 13．2 13.4以前两位数为茎画出上面数据的茎叶图(只有单侧有数据)，并找出中位数．[解析]茎叶图如图所示.1213566789130112223445566 6 788914012 4中位数为13.35.18．(本小题满分12分)某高级中学共有学生3 000名，各年级男、女人数如下表：高一年级高二年级高三年级女生523x y男生487490z已知在全校学生中随机抽取1名，抽到高二年级女生的概率是0.17.(1)问高二年级有多少名女生？(2)现对各年级用分层抽样的方法在全校抽取300名学生，问应在高三年级抽取多少名学生？[解析](1)由题设可知x3000＝0.17，所以x＝510.(2)高三年级人数为y＋z＝3000－(523＋487＋490＋510)＝990，现用分层抽样的方法在全校抽取300名学生，应在高三年级抽取的人数为：3003000×990＝99名．答：(1)高二年级有510名女生；(2)在高三年级抽取99名学生．19．(本小题满分12分)为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量(单位：千克)，并将所得数据分组，画出频率分布直方图(如图所示)．分组频率[1.00,1.05)(1)(2)估计数据落在[1.15，1.30)中的概率为多少；(3)将上面捕捞的100条鱼分别作一记号后再放回水库，几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条，请根据这一情况来估计该水库中鱼的总条数．[解析] (1)根据频率分布直方图可知，频率＝组距×频率组距故可得下表：(2)0.30＋0.15＋0.02＝中的概率约为0.47. (3)120×1006＝2000.所以水库中鱼的总条数约为2000条．20．(本小题满分12分)某农场为了从三种不同的西红柿品种中选出高产稳定的西红柿品种，分别在5块试验田上试种，每块试验田均为0.5公顷，产量情况如下表：问哪一种西红柿既高产又稳定？[解析] 因为x 甲＝15(21.5＋20.4＋22.0＋21.2＋19.9)＝21.0(kg)，x 乙＝15(21.3＋18.9＋18.9＋21.4＋19.8)＝20.06(kg)， x 丙＝15(17.8＋23.3＋21.4＋19.9＋20.9)＝20.66(kg)，所以s 甲＝15[21.5－21.02＋…＋19.9－21.02]≈0.756(kg)；s 乙＝15[21.3－21.062＋…＋19.8－21.062]≈1.104(kg)；s 丙＝15[17.8－20.662＋…＋20.9－20.662]≈1.807(kg)．由于x 甲>x 丙>x 乙，s 甲<s 乙<s 丙，所以甲种西红柿既高产又稳定．21．(本小题满分12分)某某统计局就某地居民的月收入调查了10 000人，并根据所得数据画出了样本的频率分布直方图(每个分组包括左端点，不包括右端点，如第一组表示收入在[1 000,1 500))．(1)求居民月收入在[3 000,3 500)的频率； (2)根据频率分布直方图算出样本数据的中位数；(3)为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10 000人中用分层抽样的方法抽出100人作进一步分析，则月收入在[2 500,3 000)的这段应抽多少人？[解析] (1)月收入在[3 000,3 500)的频率为0.000 3×(3 500－3 000)＝0.15. (2)∵0.000 2×(1 500－1 000)＝0.1， 0．000 4×(2 000－1 500)＝0.2， 0．000 5×(2 500－2 000)＝0.25，0．1＋0.2＋0.25＝0.55>0.5.∴样本数据的中位数为2 000＋0.5－0.1＋0.20.000 5＝2 000＋400＝2 400(元)．(3)居民月收入在[2 500,3 000)的频率为0.000 5×(3 000－2 500)＝0.25， 所以10 000人中月收入在[2 500,3 000)的人数为0.25×10 000＝2 500(人)， 再从10 000人中分层抽样方法抽出100人，则月收入在[2 500,3 000)的这段应抽取100×2 50010 000＝25(人)．22.(本小题满分12分)(2015·新课标Ⅰ理，19)某公司为确定下一年度投入某种产品的宣传费，需了解年宣传费x (单位：千元)对年销售量y (单位：t)和年利润z (单位：千元)的影响．对近8年的年宣传费x i 和年销售量y i (i ＝1，2，…，8)数据作了初步处理，得到下面的散点图及一些统计量的值．表中w i ＝x i ，w ＝，(1)根据散点图判断，y ＝a ＋bx 与y ＝c ＋d x 哪一个适宜作为年销售量y 关于年宣传费x 的回归方程类型？(给出判断即可，不必说明理由)(2)根据(1)的判断结果及表中数据，建立y 关于x 的回归方程；(3)已知这种产品的年利润z 与x ，y 的关系为z ＝0.2y －x .根据(2)的结果回答下列问题：(①年宣传费x ＝49时，年销售量及年利润的预报值是多少？ ②年宣传费x 为何值时，年利润的预报值最大？附：对于一组数据(u 1，v 1)，(u 2，v 2)，…，(u n ，v n )，其回归直线v ＝α＋βu 的斜率和截距的最小二乘估计分别为word 11 / 11 β^＝，α^＝v －β^u .[解析] (1)由散点图可以判断，y ＝c ＋d x 适合作为年销售量y 关于年宣传费x 的回归方程类型．(2)令w ＝x ，先建立y 关于w 的线性回归方程，由于d ^＝∑i ＝18w i －wy i －y ∑i ＝18 w i －w2＝108.81.6＝68， c ^＝y －d ^w ＝563－68×6.8＝100.6.∴y 关于w 的线性回归方程为y ^＝100.6＋68w ，∴y 关于x 的回归方程为y ^＝100.6＋68x .(3)①由(2)知，当x ＝49时，年销售量y 的预报值y ^＝100.6＋6849＝576.6，年利润z 的预报值z ^＝576.6×0.2－49＝66.32.②根据(2)的结果知，年利润z 的预报值z ^＝0.2(100.6＋68x )－x＝－x ＋13.6x ＋20.12，∴当x ＝13.62＝6.8，即x ＝46.24时，z ^取得最大值． 故年宣传费为46.24千元时，年利润的预报值最大．。
北师大版生物七年级上册：第1章综合测试(含答案)
第1章综合测试一、选择题1.企鹅能生活在南极，这体现了生物与环境之间的关系是（）A.生物能适应环境B.生物能影响环境C.环境能影响生物D.环境能适应生物2.生活在纬度越低、气候越炎热地区的企鹅，个体越小，越有利于身体散热。
这一事实可作什么特征的具体实例：（）①适应性②应激性③遗传性和变异性④竞争性A.①②B.③④C.①③D.②④3.袁隆平院士利用野生水稻与栽培水稻杂交获得新品种，是利用了（）A.生物的多样性B.基因的多样性C.生态系统的多样性D.生物的生长特性4.葱的地上部分和地下部分颜色不同，造成这种差异的主要环境因素是（）A.水分B.空气C.温度D.阳光5.有“鸽子树”和“植物界中的熊猫”之称的中国特有的珍稀植物依次是（）A.珙桐，银杉B.珙桐、银杏C.珙桐、水杉D.银杉、银杏6.下列属于生物的是（）A.雪人B.机器人C.真菌D.铁锈7.下列属于生态系统的是（）A.清澈的河水B.罗平的油菜花C.滇池湿地公园D.挺拔的迎客松8.蚂蚁、蜜蜂往往成千上百只生活在一起，组成一个大家庭，这是一种什么关系（）A.竞争B.合作C.捕食D.寄生9.含羞草的部分小叶受到震动后会合拢下垂，这是（）A.生物进行呼吸B.生物的发育C.生物对外界刺激做出反应D.生物的生长10.下列选项中属于生物的是（）A.珊瑚虫B.蛇毒C.橡胶D.钟乳石11.下列关于生物基本特征的叙述，不正确的是（）A.生物的生活需要营养B.生物都能进行呼吸C.生物能排出代谢废物D.所有的生物都会动12.下列生物中属于植物的是（）A.丹顶鹤B.感冒病毒C.鼠疫杆菌D.玉米13.不同生物生存环境的范围是不同的。
下列生物中，在地球上生存范围最窄的是（）A.老鼠B.苍蝇C.麻雀D.北极熊14.下列属于最大的生态系统的是（）A.海洋生态系统B.生物圈C.草原生态系统D.森林生态系统15.在探究“植物对空气温度和湿度的影响”实验中，如果将草地上早、中、晚的湿度平均值做成曲线，就可以了解（）A.草地、裸地、灌木丛的温度差异B.无对照，不能说明任何问题C.草地一天内的湿度变化D.草地、裸地、灌木丛一天中湿度变化的异同16.生物多样性不包括（）A.生物种类的多样性B.生物数量的多样性C.生态系统的多样性D.基因的多样性17.寒冷的冬天，法国梧桐纷纷落叶，松树却依然郁郁葱葱，这表明了（）A.它们都适应寒冷的环境B.法国梧桐不适应寒冷的环境C.松树与法国梧桐进行生存斗争D.松树比法国梧桐更适应寒冷的环境18.下列各项中，不能称为生态系统的是（）A.一块农田中的所有生物B.一个养有金鱼和水草的小鱼缸C.一条河流D.一个植物园19.下面可以看作一个生态系统的是（）A.一片森林里所有的树木和所有的动物B.一个鱼缸中的所有金鱼、水草和鱼虫C.一个烧杯中取自池塘的水、泥土和浮游生物D.一个池塘中的所有水蚤、分解者和水草二、综合题20.阅读下述材料，回答问题：欧洲航海者的日记显示，在15世纪以前，毛里求斯岛上的渡渡鸟随处可见。
2019—2020学年度苏科版八年级物理上册 第一章 声现象 单元综合能力提升测试卷
第一章声现象单元综合能力提升测试卷时间：90分钟满分：100分一、选择题（每小题只有一个选项符合题意，每小题3分，共45分）1．如图所示，在探究“声音是由物体振动产生的”实验中，将正在发声的音叉紧靠悬线下的轻质小球，发现小球被多次弹开．这样做是为了A．使音叉的振动尽快停下来B．把声音的振动时间延迟C．把音叉的微小振动放大，便于观察D．使声波被多次反射形成回声2．如图所示为北京天坛公园里堪称声学建筑奇观之一的圜丘．当游客站在圜丘顶层的天心石上说话时，会感到声音特别洪亮．下列关于声音变得特别洪亮的解释中正确的是A．声音变成了超声波B．圜丘上装有扩音器C．建筑师利用了声音的折射原理D．回声与原声混在一起，声音得到了加强3．如图所示，用一张硬卡片先后快拨和慢拨木梳的齿，可用来研究声音的A．响度B．音调C．音色D．声速4．如图所示，蝴蝶飞行时翅膀振动的频率为5～6 Hz，蜜蜂飞行时翅膀振动的频率为300～500 Hz.当它们从你的身后飞过时，你A．只能听到蝴蝶的声音B．只能听到蜜蜂的声音C．蝴蝶和蜜蜂的声音都能听到D．蝴蝶和蜜蜂的声音都听不到5．如图所示，将一把钢尺紧按在桌面上，一端伸出桌边，拨动钢尺，听它振动发出的声音。
改变钢尺伸出桌边的长度，再次用力拨动，使钢尺两次振动的幅度大致相同，听它发出声音的变化。
这个实验用来探究A．声音能否在固体中传播B．响度与物体振幅的关系C．音调与物体振动频率的关系D．音色与发声体的哪些因素有关6．地下自来水管爆裂，检漏工人常用木棍或金属棒“听漏”(如图所示)，用木棍或金属棒的目的是A．增大声源振动的频率B．使声音沿固体传播改变音色C．让声音沿固体传播，听到的声音更响D．使发声体振动的振幅增大，增大响度7．据报道，世界“吼王”杰米·温德拉曾“吼”出超过100分贝的声音，如图是他“吼”出声音将玻璃杯震碎的情景。
下列有关他“吼”出的声音的说法正确的是A．声音传递了能量B．声音只在玻璃杯中传播C．声音是玻璃杯振动产主的D．声音的分贝数越高其频率越大8．如图所示是蚊子和老牛的一段对话，下列对这段对话的描述正确的是A．蚊子飞行时发出的声音响度小，牛的叫声音调高B．蚊子飞行时发出的声音音调低，牛的叫声响度小C．蚊子飞行时发出的声音音调高，牛的叫声响度大D．蚊子飞行时发出的声音响度大，牛的叫声音调低9．如图所示，在两个完全相同的高脚玻璃杯内装有相同深度的水，当用筷子轻轻敲击杯子时，两个杯子就会发出相同的声音。
2019—2020学年度苏科版八年级物理上册 第一章 声现象 单元综合能力提升测试卷
第一章声现象单元综合能力提升测试卷时间：90分钟满分：100分一、选择题（每小题只有一个选项符合题意，每小题3分，共45分）1．如图所示，在探究“声音是由物体振动产生的”实验中，将正在发声的音叉紧靠悬线下的轻质小球，发现小球被多次弹开．这样做是为了A．使音叉的振动尽快停下来B．把声音的振动时间延迟C．把音叉的微小振动放大，便于观察D．使声波被多次反射形成回声2．如图所示为北京天坛公园里堪称声学建筑奇观之一的圜丘．当游客站在圜丘顶层的天心石上说话时，会感到声音特别洪亮．下列关于声音变得特别洪亮的解释中正确的是A．声音变成了超声波B．圜丘上装有扩音器C．建筑师利用了声音的折射原理D．回声与原声混在一起，声音得到了加强3．如图所示，用一张硬卡片先后快拨和慢拨木梳的齿，可用来研究声音的A．响度B．音调C．音色D．声速4．如图所示，蝴蝶飞行时翅膀振动的频率为5～6 Hz，蜜蜂飞行时翅膀振动的频率为300～500 Hz.当它们从你的身后飞过时，你A．只能听到蝴蝶的声音B．只能听到蜜蜂的声音C．蝴蝶和蜜蜂的声音都能听到D．蝴蝶和蜜蜂的声音都听不到5．如图所示，将一把钢尺紧按在桌面上，一端伸出桌边，拨动钢尺，听它振动发出的声音。
改变钢尺伸出桌边的长度，再次用力拨动，使钢尺两次振动的幅度大致相同，听它发出声音的变化。
这个实验用来探究A．声音能否在固体中传播B．响度与物体振幅的关系C．音调与物体振动频率的关系D．音色与发声体的哪些因素有关6．地下自来水管爆裂，检漏工人常用木棍或金属棒“听漏”(如图所示)，用木棍或金属棒的目的是A．增大声源振动的频率B．使声音沿固体传播改变音色C．让声音沿固体传播，听到的声音更响D．使发声体振动的振幅增大，增大响度7．据报道，世界“吼王”杰米·温德拉曾“吼”出超过100分贝的声音，如图是他“吼”出声音将玻璃杯震碎的情景。
下列有关他“吼”出的声音的说法正确的是A．声音传递了能量B．声音只在玻璃杯中传播C．声音是玻璃杯振动产主的D．声音的分贝数越高其频率越大8．如图所示是蚊子和老牛的一段对话，下列对这段对话的描述正确的是A．蚊子飞行时发出的声音响度小，牛的叫声音调高B．蚊子飞行时发出的声音音调低，牛的叫声响度小C．蚊子飞行时发出的声音音调高，牛的叫声响度大D．蚊子飞行时发出的声音响度大，牛的叫声音调低9．如图所示，在两个完全相同的高脚玻璃杯内装有相同深度的水，当用筷子轻轻敲击杯子时，两个杯子就会发出相同的声音。
人教版(五四学制)六年级上册第一单元综合能力测试题含答案
部编人教版五四制六年级上册第一单元综合能力测试题一、积累与运用（20分）1·下列句子中的字音和字形完全正确的一项是（）（2分）A·那些小丘的线条是那么柔美，就像只用绿色渲（xuān）染，不用墨线勾勒（lèi）的中国画那样，到处翠色欲流，轻轻流入云际。
B·在细雨迷朦中，着了水滴的丁香格外妩（fǔ）媚。
花墙边两株紫色的，如同印象派的画，线条模（mú）糊了，直向窗前的莹白渗过来。
C·每到春来，伏案时抬头便看见檐（yán）前积雪。
雪色映进窗来，香气直透豪端。
人也似乎轻灵的多，不那么混浊笨拙（zhuō）了。
D·我在原野上摇拽，使原野风光更加旖（qǐ）旎；我在清风中呼吸，使清风芬芳馥（fù）郁。
2·下列词语运用恰当的一项是（）（2分）A·忽然，像被一阵风吹来似的，远处的小丘上出现了一群马，马上的男女老少穿着各色的衣裳，群马疾驰，襟飘带舞，像一条彩虹向我们飞过来。
B·我们要虚心向老师请教，做到不耻下问。
C·我本来就对那里的情况不熟悉，你却硬要派我去，这不是差强人意吗？D·桂林的山水、黄山的松，真是巧夺天工。
3·下列句子中没有语病的一项是（）（2分）A·这种蝴蝶和候鸟一样，冬天都飞往南方，夏天又飞向北方，每天平均飞行大约四十多公里。
B·学习成绩的提高，主要取决于学生自身是否努力。
C·中考复习中，不少学生存在着复习重点不突出，时间安排不合理的现象，有的甚至记住了前面的知识，又忘记了后面的知识。
D·最近全国各地加大了对醉酒驾车的惩处力度，为的是避免那些骇人听闻的交通事故不再发生。
4·下面句子中标点使用恰当的一项是（）（2分）A·我微睡时，黑夜星空的千万颗亮晶晶的眼睛对我察看；我醒来时，白昼的那只硕大的独眼向我凝视。
鲁教版2020八年级数学上册第一章因式分解自主学习单元综合能力达标测试题1(附答案详解)
鲁教版2020八年级数学上册第一章因式分解自主学习单元综合能力达标测试题1（附答案详解）1．小强是一位密码编译爱好者，在他的密码手册中，有这样一条信息：a ﹣b ，x ﹣y ，x +y ，a +b ，x 2﹣y 2，a 2﹣b 2分别对应下列六个字；益、爱、我、广、游、美．现将（x 2﹣y 2）a 2﹣（x 2﹣y 2）b 2因式分解，结果呈现的密码信息可能是（ ）A ．我爱美B ．广益游C ．爱我广益D ．美我广益 2．将代数式245x x +-因式分解的结果为（ ）A ．(x+5)(x －1)B ．(x －5)(x+1)C ．(x+5)(x+1)D ．(x －5)(x －1) 3．下列因式分解错误的是( )A ．22()()x y x y x y －＝+－B ．2269(3)x x x ++＝+C ．2()x xy x x y +＝+D ．222()x y x y +＝+4．下列各式从左到右的变形，是因式分解的是（ ）A ．296(3)(3)6x x x x -+=+-+xB ．2(5)(2)310x x x x +-=+-C ．22816(4)x x x -+=-D ．221(2)1x x x x ++=++5．下列各等式中，从左到右的变形是因式分解的是（ ）A ．()2x x y x xy ⋅-=-B ．()23131x x x x +-=+- C ．()22()2x y y x x y --=- D ．222x x x x ⎛⎫-=- ⎪⎝⎭6．下列分解因式正确的是（ ）A ．11331m n n x x x x ++⎛⎫-=- ⎪⎝⎭B ．()2214412m m m +-=-C ．()()22541221x x x x -=--=+-- 27．下列各多项式在有理数范围内，可用平方差公式分解因式的是（ ）A ．a 2+4B ．a 2-2C ．-a 2+4D ．-a 2-48．下列各式能用完全平方公式分解的是（ ）A ．229m n -B ．2224p pq q -+C ．2244x xy y --+D ．()()2961m n m n +-++ 9．实数m ＝20183－2018，下列各数中不能整除m 的是（ ）A ．2020B ．2019C ．2018D ．201710．下列各式中，不能完全用平方公式分解的个数为（ ）①x 2﹣10x +25；②4a 2+4a ﹣1；③x 2﹣2x ﹣1；④m 2﹣m +14；⑤4x 4﹣x 2+14． A ．1个 B ．2个 C ．3个 D ．4个11．因式分解：x 2-2xy+y 2-1=___________.12．已知：210a a ++=，则20102009200821a a a a a ++⋅⋅⋅+++的值是________. 13．如果多项式26x mx +-在整数范围内可以因式分解，那么m 可以的取值是________（写出一个即可）14．若()2242x ax x ++=-，则a =_____．15．因式分解：2222m m n n --+=____________16．分解因式22am an -=______．17．已知1x y -=，那么22111636x xy y -+=______. 18．若ab+bc+ca ＝﹣3，且a+b+c ＝0，则a 4+b 4+c 4＝_____．19．分解因式：32226ax a x +=______.20．给出三个多项式：，，，请选择你最喜欢的两个多项式进行加法运算，再把结果因式分解．21．因式分解：a 4-18a 2+8122．把下列各式因式分解：（1）a 3﹣4a 2+4a（2）a 2（x ﹣y ）+b 2（y ﹣x ）23．（1）已知25x x +=-，求5432242112x x x x x +++-+的值.（2）已知353x x -=-，求7654322496132913x x x x x x x +---++-的值.24．计算:()2(2)2(2)x y z x y z x y z +--+-++25．因式分解：（1）4x 2﹣64（2）81a 4﹣72a 2b 2+16b 426．因式分解：(1)x 2-x-6； (2)ax 2-2axy+ay 227．()22(2)+221x xy y x y -+-++；参考答案1．C【解析】【分析】将原式进行因式分解即可求出答案．【详解】解：原式＝（x2﹣y2）（a2﹣b2）＝（x﹣y）（x+y）（a﹣b）（a+b）且x﹣y，x+y，a+b，a﹣b四个代数式分别对应爱、我，广，益，∴结果呈现的密码信息可能是：“爱我广益”，故选：C．【点睛】本题考查了公式法的因式分解运用，熟练掌握因式分解的方法是解本题的关键2．A【解析】【分析】利用十字相乘法进行因式分解即可.【详解】245+-=(x+5)(x－1)x x故选A.【点睛】此题主要考查因式分解的方法，解题的关键是熟知因式分解的方法.3．D【解析】【分析】根据公式特点判断，然后利用排除法求解．【详解】A、是平方差公式，故A选项正确；B、是完全平方公式，故B选项正确；C、是提公因式法，故C选项正确；D、（x＋y）2＝x2＋2xy＋y2，故D选项错误；【点睛】本题主要考查了对于学习过的两种分解因式的方法的记忆与理解，需熟练掌握． 4．C【解析】【分析】根据因式分解的定义对各选项进行逐一分析即可．【详解】解：A 、(x +3)(x -3)+6x 不是几个因式积的形式，故不是因式分解，故本选项错误； B 、x 2+3x -10不是几个因式积的形式，故不是因式分解，故本选项错误；C 、方程右边是几个因式积的形式，故是因式分解，故本选项正确；D 、x （x+2）+1不是几个因式积的形式，故不是因式分解，故本选项错误．故选C ．【点睛】本题考查的是分解因式的定义，即把一个多项式化为几个整式的积的形式，这种变形叫做把这个多项式因式分解，也叫做分解因式．5．C【解析】【分析】根据因式分解是把一个多项式化为几个整式的积的形式，进而判断即可．【详解】解：A. ()2x x y x xy ⋅-=-，不是几个整式的积的形式，不属于因式分解，故本选项不符合题意；B. ()23131x x x x +-=+-，不是几个整式的积的形式，不属于因式分解，故本选项不符合题意；C. ()22()2x y y x x y --=-，是几个整式的积的形式，属于因式分解，故本选项符合题意； D.222x x x x ⎛⎫-=- ⎪⎝⎭式子右边不是几个整式的积的形式，所以不属于因式分解，故本选项不符合题意；【点睛】本题考查了因式分解的定义，能熟记因式分解的定义的内容是解此题的关键，注意：把一个多项式化成几个整式的积的形式，叫因式分解．6．B【解析】【分析】根据因式分解的定义及方法逐项分析即可.【详解】 A. 11331m n n x x x x ++⎛⎫-=- ⎪⎝⎭的右边中的分母含字母，故不正确； B. ()22144=12m m m +--，正确；C. ()()22541221x x x x -=--=+--的右边不是积的形式，故不正确； D. ()223231a ab a a a b -+=-+，故不正确. 故选B.【点睛】本题考查了因式分解，把一个多项式化成几个整式的乘积的形式，叫做因式分解. 7．C【解析】【分析】平方差公式为22()()a b a b a b -=-+，则被分解的因式需要符合两个数的平方再作差的形式，即为22a b -的形式.而题干给出的是在有理数的范围内，则公式中,a b 要为有理数.【详解】A.不符合22a b -的形式，排除B.原式可化为22a -，符合22a b -的形式，但出现了无理数，排除C. 原式可化为2224(2)a a -=-(2)(2)a a =-+，符合D. 不能化为22a b -的形式，排除【点睛】本题考察了运用平方差公式法因式分解，对于平方差公式22()()a b a b a b -=-+务必牢记. 8．D【解析】【分析】能用完全平方公式分解因式的多项式的特点为：①有两个平方项，且符号相同，②还有一项是两平方项底数积的2倍，据此即可求得答案．【详解】解：A 、含有两项，不符合完全平方式的特点，不能用完全平方公式分解；B 、两平方项底数乘积的2倍为4pq ，此式不符合完全平方式的特点，不能用完全平方公式分解；C 、两平方项的符号不同，不符合完全平方式的特点，不能用完全平方公式分解；D 、符合完全平方式的特点，能用完全平方公式分解．故选D ．【点睛】此题考查了完全平方公式分解因式的知识．注意掌握能用完全平方公式分解因式的多项式的特点为：①有两个平方项，且符号相同，②还有一项是两平方项底数积的2倍． 9．A【解析】【分析】根据因式分解即可求解．【详解】解：20183−2018＝2018（20182−1）＝2018×（2018＋1）（2018−1）＝2018×2019×20172018×2019×2017能被2017、2018、2019整除，不能被2020整除．故选：A ．【点睛】本题考查了因式分解的应用，解决本题的关键是提公因式法与公式法分解因式． 10．C【解析】【分析】直接利用完全平方公式分解因式进而得出答案．【详解】①x 2﹣10x +25＝（x ﹣5）2，不合题意；②4a 2+4a ﹣1无法用平方公式分解，符合题意；③x 2﹣2x ﹣1无法用平方公式分解，符合题意；④m 2﹣m +14＝（m ﹣12）2，不合题意； ⑤4x 4﹣x 2+14无法用平方公式分解，符合题意； 故选：C ．【点睛】本题考查了利用完全平方公式分解因式，熟练掌握完全平方公式:a 2±2ab +b 2(a ±b )2是解答本题的关键．11．（x+y+1）（x-y-1）【解析】【分析】前三项先利用完全平方公式分解因式，然后再利用平方差公式进行分解.【详解】解：2221x xy y -+-=2()1x y --=(1)(1)x y x y -+--；故答案为：(1)(1)x y x y -+--.【点睛】此题主要考查了公式法分解因式，熟练运用公式法进行分解因式是解题的关键． 12．1【解析】【分析】将所求分组进行提公因式，然后将210a a ++=整体代入即可解答．【详解】20102009200821a a a a a ++⋅⋅⋅+++＝()200822)11(1+a a a a a a ++⋅⋅⋅+++ =0+..+0+1=1故答案为：1．【点睛】本题考查了因式分解的应用，合理分组、整体代入即可轻松解答． 13．5【解析】【分析】把-6分成6和-1，进而得出即原式分解为（x+6）（x-1），即可得到答案．【详解】当26x mx +-=(x+6)(x−1)时，m=6+(−1)=5，故答案为5.【点睛】此题考查因式分解-十字相乘法，解题关键在于把-6分成6和-1.14．-4【解析】【分析】直接利用完全平方公式得出a 的值．【详解】解：∵()2242x ax x ++=-，∴4a =-故答案为：4-【点睛】此题主要考查了公式法分解因式，正确应用公式是解题关键．15．()(2)m n m n -+-【解析】【分析】原式两两分组，分别用平方差和提公因式分解后再提公因式（m -n ）即可.【详解】解：原式=2222m n m n ---（）（）=（m -n ）（m +n ）-2（m -n ）=(m -n )(m +n -2)故答案为：(m -n )(m +n -2).【点睛】此题考查了因式分解-分组分解法，难点是采用两两分组还是三一分组．16．()()a m n m n +-【解析】【分析】原式提取a ，再利用平方差公式分解即可．【详解】原式()()()22a m n a m n m n =-=+-，故答案为：()()a m n m n +-【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键．因式分解常用的方法有：①提公因式法；②公式法；③十字相乘法；④分组分解法. 因式分解必须分解到每个因式都不能再分解为止.17．16【解析】【分析】 先把22111636x xy y -+分解因式，在把1x y -=，代入计算，即可.【详解】 ∵22111636x xy y -+=2222)11((66)x xy y x y -+=-， ∴当1x y -=时，原式=2116⨯=16. 【点睛】本题主要考查因式分解和代数式的值，把多项式分解因式后，再整体代入求值，是解题的关键.18．18【解析】【分析】由a +b +c ＝0，利用平方公式结合ab +bc +ca ＝﹣3可得出a 2+b 2+c 2＝6，由ab +bc +ca ＝﹣3，利用平方公式结合a +b +c ＝0可得出a 2b 2+b 2c 2+c 2a 2＝9，再由a 2+b 2+c 2＝6，利用平方公式结合a 2b 2+b 2c 2+c 2a 2＝9即可求出a 4+b 4+c 4＝18，此题得解．【详解】解：a+b+c ＝0，两边平方得：a 2+b 2+c 2+2ab+2bc+2ca ＝0，∵ab+bc+ca＝﹣3，∴a 2+b 2+c 2+2×（﹣3）＝0，∴a 2+b 2+c 2＝6．ab+bc+ca ＝﹣3，两边平方得：a 2b 2+b 2c 2+c 2a 2+2ab 2c+2abc 2+2a 2bc ＝9，即a 2b 2+b 2c 2+c 2a 2+2abc （a+b+c ）＝9，∴a 2b 2+b 2c 2+c 2a 2＝9．a 2+b 2+c 2＝6，两边平方得：a 4+b 4+c 4+2a 2b 2+2b 2c 2+2c 2a 2＝36，∴a 4+b 4+c 4＝36﹣2（a 2b 2+b 2c 2+c 2a 2）＝18．故答案为：18．【点睛】本题考查因式分解的应用以及完全平方公式，重复利用完全平方公式求出a 4+b 4+c 4的值是解题关键．19．()223ax x a +【解析】【分析】观察原式2ax 3＋6a 2x 2，找到公因式2ax 2，提出即可得出答案．【详解】32226ax a x +=()223ax x a +；故答案为：()223axx a +．【点睛】 此题考查了提公因式法的直接应用，考查了对一个多项式因式分解的能力．一般地，因式分解有两种方法，提公因式法，公式法，能提公因式先提公因式，然后再考虑公式法．要求灵活运用各种方法进行因式分解．该题是直接提公因式法的运用．20．+＝x 2（x +6）；或+＝x （x +1）（x ﹣1）；或+＝x （x +1）2． 【解析】【分析】本题考查整式的加法运算，找出同类项，然后只要合并同类项就可以了．【详解】∵＝x 3＋6x 2＝x 2（x ＋6）； 或＝x 3﹣x ＝x （x 2﹣1）＝x （x ＋1）（x ﹣1）； 或＝x 3＋2x 2＋x ＝x （x 2＋2x ＋1）＝x （x ＋1）2．【点睛】本题考查了提公因式法，公式法分解因式，解题关键是熟记公式结构．21．22(a+3)(a-3)【解析】【分析】利用完全平方公式、平方差公式进行因式分解【详解】解：原式=22222a -=[(a+3)(a-3)](a+3)(a-3)=（9） 【点睛】本题主要考查因式分解中的公式法，掌握平方差公式是关键22．（1）a （a ﹣2）2；（2）（x ﹣y ）（a +b ）（a ﹣b ）．【解析】【分析】（1）原式提取公因式后，利用完全平方公式分解即可；（2）原式提取公因式后，利用平方差公式分解即可．【详解】（1）a 3﹣4a 2+4a＝a （a 2﹣4a +4）＝a （a ﹣2）2；（2）a 2（x ﹣y ）+b 2（y ﹣x ）＝（x ﹣y ）（a 2﹣b 2）＝（x ﹣y ）（a +b ）（a ﹣b ）．【点睛】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键． 23．(1)7；(2)8.【解析】【分析】（1）拆项，分组可得原式32222()552(5)()x x x x x x x x x =+++++-++2(5)7x x -+++；（2）运用分组分解法进行变形得：原式3432(53)(227)8x x x x x x =-+++--+.【详解】(1)543232222242112552(5)()()x x x x x x x x x x x x x x +++-+=+++++-++2(5)77x x -+++=．(2)由已知得3530x x -+=，原式3432(53)(227)8x x x x x x =-+++--+，故原式8=．【点睛】考核知识点：运用因式分解求值.掌握分组分解法是关键.24．-8y 2-2z 2-4xy-2xz【解析】【分析】根据平方差公式和完全平方公式计算即可.【详解】原式=2222(2)[(2)2(2)]x y z x y z x y z ---++++=22222244(4442)x y yz z x y z yz xy xz -+--+++++=228242y z xy xz ----【点睛】本题主要考查完全平方式和平方差公式的应用，注意细心计算.25．(1) 4(x-4)(x+4) (2)(3a+2b)2(3a-2b)2【解析】【分析】（1）先提取公因式再用公式法进行因式分解；（2）先用完全平方公式进行因式分解，再用平方差公式进行因式分解即可.【详解】（1）4x 2﹣64=4(x 2-16)=4(x-4)(x+4)（2）81a 4﹣72a 2b 2+16b 4=(9a 2-4b 2)2=[(3a+2b)(3a-2b)]2=(3a+2b)2(3a-2b)2【点睛】此题主要考查因式分解，解题的关键是灵活运用提取公因式法与公式法进行因式分解. 26．(1) (x+2)(x-3)； (2)a(x-y)2.【解析】【分析】（1）直接利用十字相乘法分解因式得出即可；（2）直接提取公因式a ，进而再用完全平方公式得出答案；【详解】(1)x2-x-6=(x+2)(x-3)；(2)ax2-2axy+ay2=a(x2-2xy+y2)=a(x-y)2.【点睛】此题主要考查了提取公因式法以及公式法分解因式，熟练应用乘法公式是解题关键．27．(x−y−1)2.【解析】【分析】直接利用完全平方公式分解因式得出即可．【详解】()22-+-++=(x−y)2−2(x−y)+1=(x−y−1)2.(2)+221x xy y x y【点睛】此题考查因式分解-运用公式法，解题关键在于掌握运算公式.。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第一章综合能力测试题(时间：90分钟满分：100分)一、选择题(每小题3分，共36分)1．PM2.5是指空气中直径很小的颗粒，其直径还不到人的头发丝粗细的二十分之一. PM2.5中的“2.5”是表示颗粒直径的数值，它的单位是(D)A．米B．分米C．厘米D．微米2．历史上把如图示意的长度定为1 英寸，1 英寸约为(D)A．2.5 km B．2.5 m C．2.5 dm D．2.5 cm错误!错误!,第3题图) 3．如图是小明用刻度尺测量一条形金属片长度的情形，该刻度尺的分度值和金属片的长度分别是(D)A．1 cm 5.50 cm B．1 cm8.30 cmC．1 mm8.30 cm D．1 mm 2.80 cm4．关于机械运动，下列说法正确的是(C)A．机械运动就是物质的一切运动B．机械运动与参照物的选择无关C．机械运动是指一个物体相对于另一个物体的位置变化D．机械运动就是一切机械的运动，空气的流动不属于机械运动5．小明爸爸的车因红灯在路口等待时，坐在车内的小明突然感觉自家的小车在后退，其实车子并没有动，小明有这种感觉是因为他选择的参照物是(A)A．旁边车道先行的公交车B．小明爸爸C．地面D．自家小车6．短跑运动员5 s跑了50 m，羚羊奔跑的速度是20 m/s，汽车的行驶速度是54 km/h，三者速度从小到大的排列顺序是(C)A．汽车、羚羊、运动员B．羚羊、汽车、运动员C．运动员、汽车、羚羊D．运动员、羚羊、汽车7．图甲是某物体运动的图象，则图乙中与之相对应的图象是(B)8．“频闪摄影”是研究物体运动时常用的一种实验方法，摄影在暗室中进行，闪光灯每隔一定的时间闪光一次，底片就记录下这时物体的位置，如图是甲、乙两个网球从左向右运动时的频闪照片，则下列说法正确的是(B)A．甲球运动的时间比乙球短B．甲球运动速度基本保持不变C．乙球做匀速圆周运动D．乙球的运动速度越来越小9．甲、乙两物体先后从同地沿同方向做匀速直线运动，甲比乙先运动2秒，甲运动6秒时通过的路程为6米，此时甲、乙间的距离为2米，在如图所示的a、b、c三条图线中，乙的s－t图象(D)A．一定是图线a B．一定是图线bC．可能是图线b D．可能是图线c,第9题图),第10题图) 10．龟和兔在路程为s0的一段平直赛道上进行赛跑竞技比赛，它们赛跑的路程－时间图象如图所示. 下列说法正确的是(D)A．在完成s0赛段的比赛中，龟和兔都做匀速直线运动B．在完成s0赛段的比赛中，龟比兔先到达比赛的终点C．在完成s0赛段的比赛中，兔总是比龟跑得快D．在完成s0赛段的比赛中，兔比龟的平均速度大11．若采用发光二极管，则通电后亮起的时间会比采用灯丝的白炽灯大约快0.5 s，故有助于后车驾驶员提前作出反应，假设后车以50 km/h的车速匀速前进，则在0.5 s的时间内，后车前行的距离大约为(B)A．3 m B．7 m C．12 m D．25 m12．一辆汽车在平直的公路上行驶了120 km的路程，前半段路程的平均速度为60 km/h，后半段路程的平均速度为40 km/h. 则汽车行驶这120 km(C)A．所用时间为2.4 h B．所用时间为2.6 hC．平均速度为48 km/h D．平均速度为50 km/h二、填空题(每空1分，共23分)13．亲爱的同学，请你应用所学物理知识解答下列问题：如图所示的刻度尺，其分度值为__1__mm，小红用该刻度尺对实际长度为70.0 cm的课桌进行测量，所测得的数据约为66.7 cm，经过分析，导致该测量结果错误的原因可能是__把刻度尺的总长度看成它的量程__，改正错误后，为了减小实验误差，还要进行__多次测量求平均值__.14．在下列横线上填上合适的单位或数字：某人身高约165__cm__，步行的速度约为5__km/h__；一辆小轿车在高速公路上行驶时的速度为85__km/h__，按照这个速度走完255 km的路程需要的时间为__3__h.15．2015年8月11日，来自挪威的翼装飞行运动员艾斯朋从天门山顶跳下，另一位极限运动员比约恩借助飞机低空跳伞，二位选手各自飞行一段时间后，低空跳伞者准确地落在翼装飞行者身上并短暂停留. 若以艾斯明为参照物，比约恩是__静止__的，此时若以地面为参照物，则比约恩是__运动__的.16．小明骑着自行车上学，以小明背着的书包为参照物，小明是__静止__(选填“运动”或“静止”)的. 小明骑自行车的平均速度为4 m/s，其物理意义是__每秒通过的路程为4米__，小明从家到学校骑车用10 min，则小明家到学校的距离约__2400__m.17．甲、乙两个物体同时从同一地点向西做直线运动，速度与时间关系如图所示. 以甲为参照物，乙向__东__做直线运动，经过6 s，甲、乙两物体相距__30__m.,第17题图),第18题图)18．甲、乙两辆小车在平直的路面上向东运动，测出它们的路程和时间，并依据数据作出了两车路程－时间关系图象，如图所示. 由图可知小车甲做__匀速直线__运动，速度大小为__15__m/s. 若以甲为参照物，乙车向__西__运动.19．如图所示，一木块在水平面上运动时在相等时间内连续拍摄4次“频闪”照片，频闪的时间间隔为0.02 s. 从频闪照片可判断，该木块做__匀速__(选填“匀速”或“变速”)直线运动. 木块从1位置运动到2位置的距离是__1.80__cm. 木块从1位置到4位置运动的速度为__0.9__m/s.20．甲、乙、丙三辆小车同时、同地向同一方向运动，它们运动的图象如图(a)、(b)所示，由图象可知：若以甲车为参照物，则__乙__(选填“乙”或“丙”)车静止；甲车的运动时间如图(c)所示，则秒表记录的时间为__175__s，甲车通过的路程为__700__m.三、简答题(4分)21．小华同学买了一盒自动铅笔用的笔芯，但包装盒上注明的笔芯直径看不清楚了，小华想用实验方法测出笔芯的直径，他只有最小分度值是1 mm的三角板一块，小华能否测量出笔芯的直径？请写出实验步骤.解：把几根铅笔芯紧密排列在一起，用三角板测出宽度a，则铅笔芯直径d＝an四、实验探究题(共21分)22．(6分)如图所示：(1)在测量物体的长度时，两种使用方法中正确的是__甲__图，铅笔的长度应为__3.30__cm.(2)用刻度尺测某课本的长度需要多次测量，多次测量的目的是__减小误差__. 若用毫米刻度尺测量，四次读数分别是25.98 cm 、26.00 cm 、26.02 cm 、26.42 cm. 其中错误的数据是__26.42_cm __，该课本的长度应为__26.00_cm __.(3)若有一把刻度尺是用金属材料制成的，且这种金属材料受温度影响变化很明显，那么在严冬季节用它测量物体的长度时，其测量结果__偏大__(选填“偏大”“偏小”或“不变”).23．(10分)为了探究小车沿斜面下滑的速度是否变化，如何变化，小明按图完成了如下实验.路段 距离/cm 运动时间/s平均速度/(m·s －1)AB 40.0 2 __0.2__ BC__40.0____1____0.4__AC 80.0 3 __0.27__的速度__越来越大__(选填“越来越大”或“越来越小”).(2)该实验的原理是__v ＝st__.(3)斜面底部用金属片挡住，其设置的目的是__便于测量时间__.(4)斜面选择的坡度不能过大，以免__坡度太大，小车运动时间太短，不好测量__，也不能过小，以免__坡度太缓，小车可能静止不动__.24．(5分)下表是卡车沿直线平稳行驶和电车、机车启动过程中各个不同时刻的速度(从启动一段时间后开始计时)，请你比较和分析表中数据，回答下列问题.t /s 对象v /(m·s －1) 0 5 10 15 20 卡车 20 20 20 20 20 电车57.51012.515机车 12 14.5 17 19.5 22__匀速直线__(2)电车的速度与时间的定性关系是__速度随时间的增加而增大__. (3)电车的速度v 与时间t 的定量关系是v ＝__(5＋0.5t )m/s __.(4)通过分析电车和机车的速度随时间变化的规律，发现它们__在相等时间内，速度的增加量__是相同的.五、计算题(共16分)25．(6分)一列200 m 长的轻轨列车，以15 m/s 的速度通过2.8 km 的立交轿，则列车从上轿至完全通过大桥所用的时间为多少？解：时间t＝s/v＝(2800 m＋200 m)/(15 m/s)＝200 s26．(10分)轨道交通具有便捷、运载量大、污染小、安全性高等优点，有利于减缓城市交通拥堵、减少汽车尾气排放等. 宁波市轨道交通工程1号线部分信息如下表所示.1号线起止点车站(座)线路长度(km)总长地下地上投资(亿元)速度(km/h)建设期(年)一期高桥西——东外环19 21.3 14.4 6.9 99.8 332009～2014二期东外环——北仑17 23.3 0 23.3 45.0 422012～2015__高__((2)目前宁波市城区公交车的平均行驶速度约为25 km/h，随着私家车数量的增加，这一数值可能将更低. 1号线一期(线路接近直线)建成前后，市民乘坐公共交通工具，从高桥西到东外环至少可节省多少小时？(3)若1号线全线建成，预计全程的平均速度可达多少千米/时？解：(2)公交车从高桥西到东外环的时间t1＝s1/v1＝21.3 km25 km/h＝0.852 h，地铁从高桥西到东外环的时间t2＝s1/v2＝21.3 km33 km/h≈0.645 h，可节省的时间t＝t1－t2＝0.852 h－0.645 h＝0.207 h(3)地铁由东外环到北仑所用的时间t3＝s2/v3＝23.3 km42 km/h≈0.555 h，全程的平均速度v＝s总/t总＝(21.3 km＋23.3 km)/(0.645 h＋0.555 h)≈37.2 km/h.。