关于柔性航天器动力学模型降阶问题(1)
飞翼式柔性飞机纵向动力学建模与稳定性分析

飞翼式柔性飞机纵向动力学建模与稳定性分析沈华勋;徐亮;陆宇平;何真【摘要】柔性飞行器在飞行过程中容易发生大变形,这种变形将导致机翼甚至整个飞行器的气动弹性和飞行动力学特性发生变化,特别是对稳定性的影响.本文采用三段式刚体假设,以变上反角的方式来描述机翼的展向弯曲变形,对一类飞翼式柔性飞行器进行了纵向动力学建模,并进一步分析了操纵面、推力和迎角与上反角的关系,以及变上反角对飞行稳定性的影响.结果表明,在保持速度和高度不变的情况下,稳定性受上反角的影响比较明显,如果变形过大,飞行器将变为动不稳定,且短周期模态不能保持.因此,为了保持飞机的纵向稳定性,必须要控制飞机的变形.【期刊名称】《动力学与控制学报》【年(卷),期】2016(014)003【总页数】6页(P241-246)【关键词】柔性飞行器;上反角;动力学建模;稳定性【作者】沈华勋;徐亮;陆宇平;何真【作者单位】南京航空航天大学自动化学院,南京211106;南京航空航天大学自动化学院,南京211106;南京航空航天大学自动化学院,南京211106;南京航空航天大学自动化学院,南京211106【正文语种】中文引言第一次关于柔性飞行器的研究来自于NASA的Daedalus项目,目的是设计一款高空长航时飞行器[1].在此基础上,NASA又提出飞机环境研究和传感器技术计划,从而研制出以Helios为代表的一类飞翼式飞行器[2].与常规飞行器相比,这类飞行器最显著的特点是飞行高度高,续航时间长,机翼轻且展弦比大.然而大量的研究表明[3-14]:这样的结构使得飞机在飞行过程中机翼容易发生大幅度的变形,这种变形会改变机翼的质量分布和气动载荷分布,从而导致机翼甚至整个飞行器的气动弹性和飞行动力学特性发生变化.且其气动弹性与变形过程动力学特性具有时变、非线性、多自由度和多状态变量的特征,使其动力学特性分析变得相当复杂.因此,针对这类飞行器,由基于线性、小变形假设推导的传统模型得到的结果不一定可靠.例如,2003年6月26日,NASA的Helios无人机在飞行试验时坠毁,这与机翼的弹性效应不无关联.NASA调查后指出,这次事故的根本原因在于缺乏对柔性特性的认识以及设计、分析柔性飞行器的相关工具[2].此外,还指出:“建立一个多学科(结构、空气动力学、控制等)模型,用来描述这种飞行器变形时的非线性动态特性是必要的[2]”.近年来,国内外学者对各种柔性飞行器的飞行动力学特性以及气动弹性问题进行了大量的研究.Patil和Hodges[3-4]首先将几何非线性引入到飞机气动弹性和结构当中,他们采用有限元法对飞翼式飞机的飞行动力学稳定性进行了分析以及非线性仿真.在单独机翼研究的基础上,Cesnik和Su[5-8]的研究团队进一步采用组合梁模型对全机几何非线性气动弹性和飞行动力学稳定性问题进行了广泛的研究.张健等人[9-11]采用Hodges几何精确完全本征梁模型和ONERA气动失速模型对梁式飞机模型进行了较为深入的研究.谢长川和杨超[12-14]的研究团队基于MSC/NASTRAN对大柔性飞机气动弹性问题进行了深入的研究,并提出了可同时考虑结构几何非线性效应与曲面气动力效应的大柔性飞机静气动弹性配平和载荷分析方法.然而,以上研究者虽然对柔性飞机进行了大量且深入的研究,且研究成果能够真实的反应出机翼变形对飞行动力学特性的影响,但模型过于复杂,不利于控制研究.本文以Helios飞行器为研究对象,在考虑多个螺旋桨发动机以及多个操纵面的基础上,以变上反角方式来描述机翼的展向弯曲变形,建立一类面向控制的飞翼式柔性飞机的纵向非线性动力学模型,并研究操纵面、迎角以及螺旋桨推力与上反角的关系,以及上反角对飞行器纵向稳定性的影响.1.1 几何模型描述及简化在航天领域中,对具有弹性结构的附件进行建模时,主要分为两种[15]:一种是将其简化为多个刚体,并用含有弹簧和阻尼的接点相联;另一种是将其等效为柔性梁/板,再用有限元思想和分析力学相关理论进行推导建模.本文采用第一种方法对Helios进行建模.从图1可以看出Helios飞行器结构比较复杂,为了便于研究,将该飞行器平分为3段,2为内翼,1、3为外翼;其中,每段翼又由一个螺旋桨推力发动机、带有副翼的主翼和配有升降舵的尾翼3部分组成.外翼与内翼通过含有阻尼的扭簧联接,外翼可以通过绕扭簧转动来改变上反角,且左右两上反角变化是同步的.模型建立时,忽略扭簧的尺寸,以相对邻接刚体固定的几何点表示各扭簧.将该飞行器的模型视为3块刚体翼联结成的刚体系,组成一个系统.简化模型如图2所示,a、b、c为各个刚体翼的质心,d为机体重心,j为扭簧中心.1.2 运动学分析从图2和图3可分别得到刚体翼2、3坐标系之间的转换矩阵Rx(η)和气流坐标系Sa与机体坐标系Sb之间的转换矩阵(α,β)设飞行器重心处的速度在气流坐标系下为V,迎角为α,侧滑角β,三者与机体坐标系的速度分量之间的关系如下:在上反角η=0时,b、d重合,当上反角改变,机体重心的位置也会随之改变,因此,3块刚体翼的速度、迎角及侧滑角也各不相同.根据刚体之间的几何运动关系,依次得出第i(i=1,2,3)块刚体翼的速度在体轴系中的分量如下式中q是俯仰角速度,s是主翼展长.由(1)(2)(3)(4)(5)式分别可得各刚体的速度Vi、迎角αi及侧滑角βi.2.1 飞行器的线运动和角运动刚体动力学方程的使用条件是惯性坐标系,忽略地球曲率和转速,重力加速度不随飞行高度变化.根据牛顿第二定律可以建立飞行器在合外力F作用的线运动和合力矩M作用下的角运动方程.线运动方程角运动方程I是飞行器的转动惯量张量,表达式为I=∑[m†(〈li,d,li,d〉E-li,d⊗li,d)]+Rx(η)I†+I†+Rx(-η)I†式中m†是单块刚体翼的质量(m=3m†),I†为刚体相对自身固连惯性主轴的惯性张量,E是3×3单位矩阵,li,d是点i到点d的空间向量(i=a,b,c).根据1.1节,改变上反角时,需要克服内外翼之间的扭簧力矩,力矩为2.2 含参量的纵向运动非线性模型飞行器所受总的空气动力为P,总空气动力沿气流坐标系各轴的分量分别为Xa,Ya 和Za,又通常用D和L分别表示阻力和升力,于是D=-X,L=-Z根据气流坐标系与机体坐标系之间的转换关系,有其中.气流坐标系下每块刚体翼的主翼和尾翼所受的空气动力:由(1)(2)(11)式分别可得主翼和尾翼在机体坐标系下的空气动力:由于上反角的变化会引起机体重心的变化,从而使得重心与机体轴系不重合,同时也导致各刚体翼间的气动力不同,故需在传统模型的基础上对飞机的角运动进行修正,得飞行器所受的总力矩:式中lw,i,lt,i分别表示主翼1/4弦线和尾翼1/4弦线到机体质心的空间向量,cw是主翼弦长.内外翼间的扭簧力矩沿x方向的分量如下最终可以得到气流坐标系下飞行器纵向动力学方程:其中h是高度,航迹倾斜角μ=θ-α,并且式中是每块刚体翼上螺旋桨推力,κc为扭簧阻尼系数,κk为扭簧弹性常数.飞翼式柔性飞机几何模型如图2所示,飞机其他参数如表1.在飞行高度为12192m 飞行速度为9.1m/s的条件下,对飞机在不同上反角情况下进行配平,由平衡原理可知,升力与重力、螺旋桨发动机推力与阻力合力为零,俯仰力矩以及飞机内部力矩都为零.其中δao=δa,i,δac=δa,2,δeo=δe,i,δec=δe,2,i=1,3,配平结果如图4、5所示.外翼的操作面舵偏角随上反角的变化很小,因此可以忽略其对飞行器的影响.内翼操作面舵偏角受上反角的影响比较大:升降舵随上反角的增大而减小,副翼先减小后增大.此外,推力随上反角变化也比较明显.当机翼发生大变形时,外翼有效迎角变小,从而导致升力减小,使得飞机高度下降,因此,为了保持飞行器速度和高度的不变,需要在加大推力时,同时上偏升降舵和副翼,以产生抬头力矩,增大迎角弥补升力损失以及辅助爬升,这也与图5反应的迎角变化相符.飞行器的非线性模型一般可以描述为=Ax+Bu,其中(x0,u0).Andrés分析了3种由系统非线性模型转换为线性模型的方法:雅克比线性化(Jacobian linearization)、状态变换(State transformation)、方程替换(Function substitution),其中第1种是最常用的[16].考虑到Jacobian线性化本身也是传统飞行器分析的基本方法,本文采用该方法对非线性动力学方程线性化处理,其基本思路是将柔性飞行器不同η下的非线性模型在各自的平衡点处线性化,得到一组小扰动线性模型,对这组模型进行插值运算就得到一个独立的包含η的线性模型,基于该线性模型,可以分析系统的运动模态.注意到Jacobian线性化方法依赖于平衡点的选取,在前文已经得到了模型在不同上反角下的平衡点.根据上述思路,最终可以得出柔性飞行器纵向运动的线性化模型: 式中,控制变量u=[ΔδacΔδaoΔδecΔδeoΔδT]T;状态变量.柔性飞行器的长、短周期运动模态随η变化如图6所示.随着η的增加,长周期模态的频率先减小后增大,阻尼逐渐变小,且阻尼线穿过虚轴,在η=20°时,由动稳定变为动不稳定.因此,系统在不加控制的情况下,为了保持飞行器仍能稳定飞行,上反角不易大于20°.长周期模态随η变化的根轨迹曲线如图6(a)所示.短周期模态的根轨迹如图6(b)所示.从图中可以看出,短周期模态特征根随η的改变有很大的变化,并且在η=35°时,由共轭根变为一对实数根;上反角η的增大,导致俯仰转动惯量Iy增大,相应的频率也就变小,因此,短周期模态并不能很好的反应出柔性飞行器的变形状态.这一变化趋势与NATASHA[3]和UM/NAST[7]的基本一致,但本文研究的是以变上反角方式描述机翼的展向弯曲变形对飞机纵向动稳定性的影响,且所得根轨迹的频率变化较大,而文献[3]、[7]研究的是中心挂载对飞机纵向动稳定性的影响,故存在差异.表2和表3分别给出了本文和文献[3]、[7]的长短周期模态特征值结果.本文在考虑多推进系统、多操纵面的基础上,以变上反角的方式来描述机翼的展向弯曲变形,采用三段式刚体假设和传统刚体飞机六自由度方程相结合的方法,建立了飞翼式柔性飞行器的纵向动力学模型,并对飞行器在1g的飞行条件进行了稳定性分析,得出如下结论:(1)上反角增加,则螺旋桨推力增大,迎角增大,内翼升降舵舵偏角减小,副翼偏角先减小后增大,外翼的操纵面舵偏角随着上反角的增大而变小,但变化幅度很小.(2)上反角的变化对飞行器的稳定性有较大的影响.当η较小时,长周期模态仍能保持稳定;当η=20°时长周期变为不稳定.短周期模态的变化很明显,由共轭根变为实数根.*The project supported by the National Natural Science Foundation of China (91016017), Natural Science Foundation of Jiangsu Province, China (BK20130806) and Funding of Graduate Innovation Center inNUAA(kfjj20150322), the Foundamental Research Funds for the Central Universites† Corresponding author E-mail:**************.cn【相关文献】1 Langford J. The daedalus project: a aummary of lessons learned. In:Aircraft Design Systems and Operations Conference. Seattle: AIAA,1989~20482 Noll T E, Brown J M, Perez-Davis M E, et al. Investigation of the helios prototype aircraft mishap volume I:mishap report. NASA,20043 Patil M, Hodges D H. Flight dynamic of highly flexible flying wings. Journal of Aircraft,2006,43(6):1790~17984 Patil M. Nonlinear gust response of highly flexible aircraft. In:48thAIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Honolulu, Hawaii: AIAA 2007~21035 Cesnik, C E S, Su W H. Nonlinear aeroelastic modeling and analysis of fully flexible aircraft. In:46th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Austin, Texas: AIAA, 2005~21696 Shearer C M, Cesnik C E S. Nonlinear flight dynamics of very flexible aircraft. Journal of Aircraft, 2007,44(5):1528~15457 Su W H. Coupled nonlinear aeroelasticity and flight dynamics of fully flexibleaircraft[PhD Thesis]. USA: University of Michigan, 20088 Palacios R, Cesnik C E S. Structural models for flight dynamic analysis of very flexible aircraft. In:50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference. Palm Springs, California: AIAA 2009~24039 张健,向锦武. 侧向随动力作用下大展弦比柔性机翼的稳定性. 航空学报, 2010,31(11):2115~2123 (Zhang J, Xiang J W. Stability of high-aspect-ratio flexible wings loaded by a lateralfollower force. Acta Aeronautica et Astronautica Sinica, 2010,31(11):2115~2123 (in Chiniese))10 张健,向锦武. 柔性飞机非线性气动弹性与飞行动力学耦合静、动态特性. 航空学报,2011,32(9):1569~1582 ( Zhang J, Xiang J W. Static and dynamic characteristics of coupled nonlinear aeroelasticity and flight dynamics of flexible aircraft. Acta Aeronautica et Astronautica Sinica, 2011,32(9):1569~1582 (in Chiniese))11 Zhang J, Xiang J W. Preliminary validation of a coupled model of nonlinear aeroelasticity and flight dynamic for HALE aircraft. In:3rd International Symposium on Systems and Control in Aeronautics and Astronautics, 201012 谢长川,吴志刚,杨超. 大展弦比柔性机翼的气动弹性分析. 北京航空航天大学学报,2003,29(12):1087~1090 ( Xie C C, Wu Z G, Yang C. Aeroelastic analysis of flexible large aspect ratio wing. Journal of Beijing University of Aeronautics and Astronautics,2003,29(12):1087~1090 (in Chiniese))13 Xie C C, Yang C. Linearization method of nonlinear aeroelastic stability for complete aircraft with high-aspect-ratio wings. Science China Technological Sciences,2011,54(2):403~41114 Yang C, Wang L B, Xie C C, et al. Aeroelastic trim and flight loads analysis of flexible aircraft with large deformations. Science China Technological Sciences,2012,55(10):2700~271115 李东旭. 挠性航天器结构动力学. 北京: 科学出版社, 2010 (Li D X. Flexible spacecraft structure dynamics. Beijing: Science China Press, 2010 (in Chiniese))16 殷明,陆宇平,何真. 变体飞行器LPV建模与鲁棒增益调度控制. 南京航空航天大学学报, 2013,45(2):201~208 (Yin M, Lu Y P, He Z. LPV Modeling and robust gain scheduling control of morphing aircraft. Journal of Nanjing University of Aeronautics and Astronautics, 2013,45(2):201~208 (in Chiniese))。
可变构型复合柔性结构航天器动力学建模研究

Fi 2 On ob tc n g r t n o e t e sngs tli g. ri o i f u ai fr moe sn i aelt o e
这类 复合柔 性结 构航 天器 因其 动力学特 性是 时
刚体类 航天 器 中 , 些 柔 性 附 件 已发 展 成 复 合柔 性 有
史 纪 鑫 等 : 变 构 型 复 合柔 性结 构航 天器 动力 学建 模 研 究 可
11 3
复杂 的多 , 必须 在混 合 坐 标 和 正则 模 态 建 模 方法 的 基础上 进行 发展 , 以满 足 控 制 系统 对 全 星 级 和 附件
式 中 , 为星体 质 心相对 标称 位 置 的摄 动量 ;
的太 阳电池阵 类某些 遥感 卫 星 系统 ( 2 。这 些 复 图 ) 合柔性 结构 类航 天 器 的 显 著特 征 表 现 在 : 是 作 为 一 附件 级控 制对 象 的大 型柔 性 附 件 ( 物 面 天线 或 太 抛 阳电池 阵) 其驱 动 机 构 不 直接 同 中心 刚体 连 接 , , 而 是通过 长 的柔性 摇 臂 支 架 同星 体 固接 , 而形 成 复 从 合柔性 结构 系统 ; 是 作 为 系 统级 控 制 对象 的整 星 二 系统 , 由于 驱动 机构 相 对 柔 性 支架 的随 动控 制 或 指 向控 制 , 其 附件 结 构 和 全 星 构 型均 呈 现 为典 型 的 使 变结 构变构 型 系统 。
=
c + c c + + u + u 。
() 2
及其 各类耦 合 系数 表 达式 , 并通 过 算 例 对 其 正确 性
进行 了校 验 。
其 中
=
c +
+
c+ :
c :
多充液可机动柔性航天器模块化建模和耦合动力学分析

第35卷第1期2024年3月广西科技大学学报JOURNAL OF GUANGXI UNIVERSITY OF SCIENCE AND TECHNOLOGY Vol.35No.1 Mar.2024多充液可机动柔性航天器模块化建模和耦合动力学分析罗厚麟,吴文军*,王佐(广西科技大学机械与汽车工程学院,广西柳州545616)摘要:针对现代航天器因携带多类型充液贮箱及可机动柔性附件而导致的动力学建模困难,文中基于参数辨识理论和有限元方法实现了该类复杂航天器的模块化建模。
首先,考虑航天器运行时贮箱内液体的小幅晃动问题,利用球形贮箱小幅晃动的参数化模型推导出球形充液贮箱小幅晃动的动力学方程;其次,根据薄板小幅振动理论,运用有限单元法建立柔性附件四边形板单元动力学模型,将附件相对航天器变化的姿态角代入坐标转换矩阵,构造柔性附件作大范围机动时的时变坐标转换矩阵。
再次,基于凯恩方程推导航天器整体系统的动力学状态方程,利用MATLAB软件编制出相应的模块化建模程序。
最后,通过数值算例分析,研究典型构型航天器中柔性附件以不同方式机动的系统整体耦合动力学性能,验证了该建模方法的通用性、适用性和准确性。
关键词:充液柔性航天器;参数化模型;有限单元法;凯恩方程;模块化建模中图分类号:V412.4;V448.2DOI:10.16375/45-1395/t.2024.01.0010引言现代航天器不断向多任务、模块化和长寿命方向发展,携带诸多设备和大尺寸柔性附件的航天器是复杂的刚-液-柔耦合系统,准确建立系统动力学模型不仅能描述航天器系统的耦合动力学特性,也能为系统控制律的设计提供理论依据和前期研究基础。
航天器的典型构型通常为中心刚体携带多个充液贮箱,外侧连接太阳能帆板。
太阳能电池板因具有较大长宽尺度和极小厚度的几何尺寸特征,根据具体长宽比可简化为Euler-Bernoulli梁模型[1-3]或Kirchhoff-Love薄板模型[4]。
中心刚体-柔性梁刚柔耦合动力学模型降阶研究

中心刚体-柔性梁刚柔耦合动力学模型降阶研究李莉;刘铸永;洪嘉振【摘要】The finite element method is widely used to describe the elastic deformations of flexible bodies,which leads to a large number of elastic coordinates and large computational burden.In order to reduce the degree-of-freedom of flexible bodies,a modal method and a Krylov method were used to reduce the degree-of-freedom of the flexible hub-beam system.Then the finite element model,and the reduced models based on modal method and Krylov method were used to do simulation respectively.The numerical simulations show that using the Krylov method shows faster convergence than using the modal method.It means that Krylov method is an efficient meth-od to implement model reduction of flexible multibody system.%有限单元法被广泛的采用来描述柔性体的弹性变形,然而有限元节点坐标数目庞大,将会给动力学方程求解带来巨大的计算负担。
如何降低柔性体的自由度,是当前柔性多体系统动力学研究的一个重要命题。
大范围运动柔性航天器的递推有限段法分析

对 柔性部 件进行 离散 ,将 系统构 造成 为 带关 节柔 性 的 多刚体 系统 ,然后 采 用 空间算 子 代数 理 论建 立递推 动力 学方 程 ,保证 了分 段 引入 大量 广 义 坐标 的 情 况 下计 算 量 仅 呈 线性 增 长 ,
很 好地 克服 了分段后 系统 运算 量急剧 增 长的 问题 。最后 给 出双 柔 性杆 机械 臂 系统 的仿 真 算 例 ,分 别采 用空 间算子代 数算 法 ( OA) 与牛 顿欧拉 法 ( S NE)建模 ,数值 仿真 结果表 明采 用S oA 法 与 NE法 建模所 得计 算 结果 完全一 致 。对 比 两种 方 法计 算 时 间表 明 ,S OA 法 计
中央 高 校 基 本科 研 业 务 费 专 项 资 金 ( YWF 1—20 1 一00 9 )资 助 项 目 收 稿 日期 :2 1 62 。 收修 改 稿 日期 :2 1 01 0 10 —2 0 11 —8
,
王 旦旦一 一 生 旦 窒 型 兰 垫 查 z 为 固定 在 B 上 以 0 ( 为段 的左端 )为 原点 的直 角坐 标系 三轴 , ,yk 0 选 z 和 各 轴分 别与 B
吒
o [
Z
图 1 柔 性 梁 离散 模 型
Fi Se m e t o 1 f lxi e g.1 g n m de o fe bl be m a
Hale Waihona Puke 图 2 段 问几 何 关 系描 述
Fi 2 Rea ie g. ltv po iin s to be we n e t e s gm e t ns
在 B( 愚一1 ,… , )体上 任取 一段 B ( ,2 ; 一1 ,… ,n ),其受 力情 况如 图 3 示 。 ,2 所 图 3中下 标 1 、2分别 表示左 端 和右 端 。对于 各 向 同性 等截 面 梁 ,若分 段 时 采用 等 值 分段 的 方
柔性板的模态价值降阶及其主动控制研究
是需要由控制系统抑 制
r
X12 … Xn 1 Xn 2 ] T ,
(2 )
( )
的输出量 , C �d ∈R 2 和 C �r ∈ R 2 分别为位移观 测 矩阵和速率观测矩阵 .
×n
× n
= C ri , C i
T
ωi = Cd i /
[2]
(6) : (7)
则第 i阶模态的模态价值为 式中 ,
- 自由梁的模态函数 , 详见文献 [ 1 ]. 假 定截 取板 的前阶模态作为结构的真实响应 , 则可得出柔性板 的动力学方程为 :
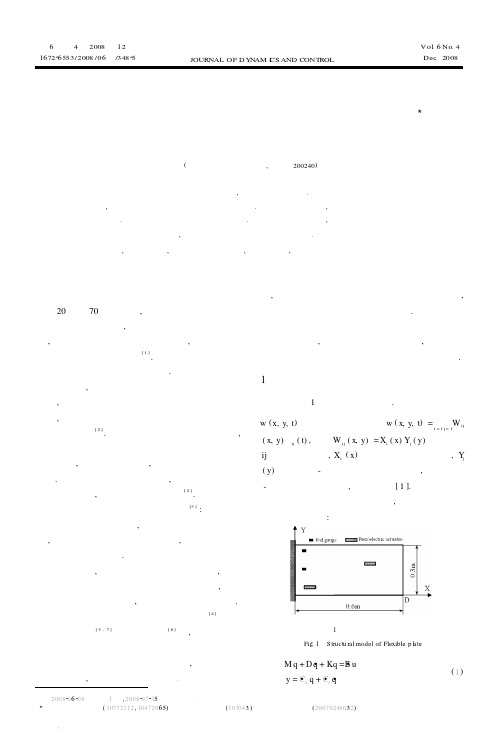
图 1 柔性板结构示意图
Fig . 1 S tructu ral model of Flexible p late
Mq ¨ +Dq �+ Kq = B �u y=C �d q + C �r q �
(1)
2008 2 06 2 09 收到第 1 稿 , 2008 2 07 215 收到修改稿. 3 国家自然科学基金 ( 10772112 , 104720 65) 、 教育部重点项目 ( 10704 3 ) 和高校博士点基金 ( 200702480 32 ) 资助项目
'
第 4期
章敏等 : 柔性板的模态价值降阶及其主动控制研究
47e25列给出了模态价值结果其中为采用公式4所得出的精确解为采用近似公式7的结果mqi为各阶模态价值占总价值的百分比计算时因为方程中的观测点为板右下角点因此公式q为标量取值为因为本文考虑的柔性板为弱阻尼和频率足够分开因此柔性板的模态价值降阶及其主动控制研究v1的结果和v2的基本相同这也验证了模态价值近似解在弱阻尼频率足够分开的情况下是适用同时可以看到对于自由响应模态分析前两阶模态价值之和已经达到总价值的99
大柔性飞行器的低阶建模方法及仿真分析
大柔性飞行器的低阶建模方法及仿真分析赵子绮;徐亮;陆宇平【摘要】大柔性飞行器模型采用有限元思路建模往往造成阶次较高,模型复杂等问题,不利于进行系统研究以及飞行控制一体化设计。
文章基于常规刚柔解耦思路,建立了面向控制的大柔性飞行器低阶简化模型,用以对飞行控制进行研究,探索刚柔特性对飞行稳定性和控制设计的影响。
通过仿真软件Matlab对建立的非线性大柔性飞行器模型运动特性进行分析。
最终,得出了不同刚度条件下的仿真曲线,从而验证了模型正确性和可行性,为后续控制设计提供了实现基础。
%The VFA model was usually produced by finite element, which lead to the problemof high order and complexity, it was harmful for doing research on the system and brought difficulty to integrated design for flight control. In this paper, a new modeling method was proposed for flight control, using conventional decoupling for rigid coupling, which could be used to research the flight stability caused by rigid characteristics. Then, the simulation software (Matlab) was applied to analysis the kinematics of the non-linear VFA model, whichcorrectness and feasibility was verified, and in order to realize the control design further, the simulation to analyze the flight performance was also done in the condition of different value of stiffness.【期刊名称】《电子设计工程》【年(卷),期】2016(024)016【总页数】4页(P5-8)【关键词】大柔性飞行器;建模;仿真;模型配平【作者】赵子绮;徐亮;陆宇平【作者单位】南京航空航天大学江苏南京 211100;南京航空航天大学江苏南京211100;南京航空航天大学江苏南京 211100【正文语种】中文【中图分类】TN96大柔性无人机(VFA)近年来成为特殊航空器研究热点,它能够在高空完成较大范围的长时间飞行[1],然而质轻的特点使其在飞行中会产生明显的机翼结构变形,从而改变气动结构[2-3]。
大角速度柔性航天器动力学模型修正
第 3 O卷 2 0 1 3年 第 6期
文章编号: 1 0 0 6 — 1 6 3 0 ( 2 0 1 3 ) 0 6 0 0 3 2 — 0 3
大 角速 度柔 性 航 天 器 动力 学 模 型 修正
罗 婧, 陈士 明, 董 云 峰
wi t h r e l a t i ve l y l a r ge a ngu l a r v e l o c i t y wa s de r i v e d i n t hi s p ap e r . Ai m t o t he s pa c e c r a f t s wi t h l a r g e a ngu l a r ve l oc i t y,
0 引 言
现代航 天 器常有 太 阳帆板 、 机械臂 、 大 型天线 等 大 型柔性 附加 , 柔性 航 天 器 在空 间应 用及 空 问科 学 研究 中的作 用 日益 突显口 ] 。研究 发现柔 性振 动不 仅 是 姿态控 制 的干扰 , 而且 是受控 对象 的一部 分 , 柔 性
学模 型 ( 如 文献 [ 3 、 6 、 7 ] 采 用 的动 力 学模 型 ) 仅适 于 姿态 稳定 即角速 度 较小 的情 况 , 对 有较 大 角 速 度 的 航 天器不 再适 用 。为此 , 本文 对 中心 刚体 加 柔 性 附
mo d i f i e d d y n a mi c mo d e 1 wa s v a l i d f o r s p a c e c r a f t s wi t h r e l a t i v e l y b i g a n g u l a r v e l o c i t y .
柔性机构的动态建模及模型降阶策略研究
r a t e l l l i c r o — d i s p l a c e n mn t b y t h e s i mp l e s h a p e o f l f e x i b l e c h a i n,b u t p r e c i s e c o n t r o l o f t h e a mo u n t o f t h e c u r r e n t f l e x i b l e me c h a n i s m h a s
在 自由端 的剪 切力 , ,并 似 没梁 的材 料 均质 ,仪 产
生 线 性 弹性 变 形 干 ¨ 小位移 。
2 g
、
‘
’
2 单 一 柔性铰链 的』 L f , , S 定 义
,
・
,
._
、
单 一 莱性 铰 链 住 不 发 生较 大 转 动 时 产 牛 线 性 弹 性
一
’’
所构 建的柔性机构常 常应用 于进给单元形成微位移运
收 稿 日期 :2 0 1 6 — 0 5 一 1 0
基 金 项 目 :国 家 f j 然科 学 基 金 资 助项 目 ( 5 1 3 0 5 2 9 9 ) 作者简 介 :杨 磊 ( 1 9 8 0 一) ,男,硕士 ,讲 师,研究方 向为机械设计及应用力学。E — ma i l
/ r 、 /
1 . 2 柔性机 构 装配
标志 f ) ( 域 模 方 法 可 以 川 1 j - 表 示 一 个 柔 机 构 ,
如 图 4所爪 ,首先要将柔 r t : - f ; L 构J } _ } j 订限元方法 , J 出 米 ,然后拙取 出标志 区域模 ,然后 计算每 ・ 个刚体
柔性机器人动力学建模与运动控制
柔性机器人动力学建模与运动控制柔性机器人是一种特殊类型的机器人,其关节以柔性器件取代了传统的刚性结构,且机器人身体呈现出类人型的结构。
由于其扭曲和弯曲能力,柔性机器人拥有传统机器人无法比拟的灵活性以及使用场景的扩展性,特别是在高度重复的工作领域和狭小空间中准确操作的优势非常明显。
但是,由于柔性机器人的惯性和非线性行为的存在,其动力学建模和运动控制也比传统机器人更为复杂。
因此,柔性机器人的动力学建模以及运动控制成为了该领域的重要研究方向之一。
柔性机器人的动力学建模首先需要对柔性结构进行建模。
根据构造方式和柔性部分的几何形状,可以将柔性结构模型分为连续杆 (Beam) 模型、连续壳(Shell)模型和连续弦(String)模型。
其中,连续杆模型是目前使用最为广泛的一种柔性结构模型,其用作建立柔性机器人的动力学模型也得到了重视。
连续杆模型假设柔性结构为非直线形态,其动力学方程首先考虑连续杆模型受到的内部剪力和弯矩的作用,然后加载特定的动力学模型和控制器进行运动控制。
柔性机器人的非线性行为包括但不限于惯性效应、柔性振动、接触和撞击等。
在柔性机器人的动力学分析中,这些非线性效应必须被纳入考虑。
其中,柔性振动是最常见的非线性效应之一。
柔性杆的自然频率取决于杆的几何形状、杆的固有物理特性和外部载荷等因素。
为避免柔性结构的自然频率在运动过程中和控制频率匹配,需要对运动轨迹进行优化处理,以降低杆的振幅和振荡频率。
柔性机器人的运动控制是针对其柔性结构特性而设计的。
从控制方法上,柔性机器人的运动控制可以分为基于模型的控制、自适应控制和视觉反馈控制等。
基于模型的控制需要建立柔性机器人的动力学模型,并为柔性机器人提供理论指导。
自适应控制采用柔性机器人测量结果和控制输入之间的反馈循环,可以实时调整控制策略,从而使柔性机器人达到较好的控制效果。
视觉反馈控制基于传感器获取的视觉信息,实现对柔性机器人的位移、速度和姿态状态的实时掌控。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Gi2p ( s ) , Gi2p ( s ) =
( c 1 i + c 2 is) d i 2 s + 2∀ i# is + #i
2
内平衡降阶并不是在通常的模态空间内降阶 , 而是在经过线性变换后的内平衡空间内进行降阶 , 从而解决当模态密集时存在的降阶困难。为进行内 平衡降阶, 采用对角化动力学方程 ( 1) , 并设保留 p 阶模态, 将方程写成状态方程形式为: % = A % + Bu, y = C% , 式中 : %= [ A=
附件组成: 中心体可 为刚体、柔性体或 两者的组 合; 附件铰接于中心体, 相对于中心体可作缓慢转 动。为了将航天器的整体运动 ( 刚体运动) 与变形 运动区分开, 使它们明确反映在所建立的动力学模 型中 , 采用了通常的混合坐标法的处理方法 , 引入 固连于中心体局部的中心体固连坐标系。此坐标系
[ 收稿日期 ] [ 作者简介 ] 2001- 04- 16; 修回日期 2001- 06- 20
3
保留模态的选取
为了进一步降低动力学模型的阶数, 应在模型
中去掉一些模态, 剩下的模态称为保留模态。已有 一系列选取保留模态的准则。除了频率准则、惯性 完备性准则和传递函数准则外, 对大型柔性航天器 常采用以下两条准则。 3 1 模态价值分析[ 4] 模态价 值分 析 ( MCA ) 通过 计算 模态 价 值, 提供了一 种选择保留模态的方 法。与其他方 法相 比, 模态价值分析直接将模态选择与控制目标联系 起来 , 因而更加合理。设对角化动力学方程为 : + 2 ! + ! 2 = Du, y = C 1 + C2 , 式中 ( 1)
C- B 模态集由部件的固定界面正则模态和对 于界面坐标的约束模态组成。解特征值问题可得固 定界面保留正则模态阵, 它的各列由若干个保留的 正则模态组成。 对于界面坐标的约束模态是被约束的界面自由 度释放时形成的静模态, 其定义为当界面自由度依 次为单位位移 , 而 其他界面自 由度位移 强制为零 时, 由此产生的一系列静态位移。 采用 Craig - Bampt on 模态集, 由通常的动力 学综合步骤可导出航天器动力学方程。显然 , 方程 中除包含弹性正则模态坐标外 , 还包含界面约束模 态坐标。由于在结构变形中引入对于界面坐标的约 束模态以计及高阶弹性模态的影响 , 因而可采用较 少的弹性模态, 且提高了建模精度。但由于在动力 学方程中出现约束模态坐标, 因而动力学方程的阶 数较高。 2 3 MacNeal Rubin ( M- R) 模态集[ 2, 3] M - R 模态集由自由界面正则模态和剩余模态 组成。自由界面正则模态阵的各列由保留的若干个 正则模态组成。 剩余模态是用来弥补略去的高阶模态的。它定 义为依次作用单位力于部件的界面自由度上得到的 相应于被略去的高阶弹性模态的一系列静位移。 采用自由界面模态综合法 , 可导出航天器的动 力学方程。应注意这时由于要满足部件间界面协调 条件 , 剩余模态坐标和弹性正则模态坐标是不相独 立的 , 因而方程中表示变形的坐标只有弹性正则模 态坐标。与采用 Craig - Bampt on 模 态集相比 , 采 用 MacNeal- Rubin 模态集时, 系统方程中只需用 部件的保留弹性正则模态坐标描述结构变形 , 因而 得到的动力学方程的阶数较低。同时, 采用 Mac Neal- Rubin 模态集进行模态展开具有很好的收敛 性, 使所导出的动力学方程较好地反映了航天器的 动力学特性。 2 4 系统结构弹性变形模态集 采用航天器相对于中心体固定坐标系的系统结 构弹性变形模态 , 也可建立其动力学模型。与采用
[ 6]
G 2p ( j #) - G k ( j #)
2p
∀
∃ 2
i= k+ 1
∃i , k < 2 p
式中 G ( s) = C [ sI - A] B 为全阶模型的传 递矩阵, Gk ( s) 为 截断后的 k 阶 模型的传 递矩 阵。传递矩阵可写成各弹性模态部分之和 :
∀
- 1
G2p ( s ) =
ui =
i
i
式中 c 和 i 分别为相应于中心体变形和附件变 形的模态矩阵 ( 模态集 ) , c 和 i 为相应的模态 坐标。模态集的选取就是要选择合适的 c 和 i, 以便用较少的项表示变形。常用的模态集有四种。 2 1 部件弹性正则模态集 选用中心体和附件弹性变形的正则模态表示它
2
常用模态集
柔性航天器可典型地看成由中心体和若干柔性
为模态坐标, ∀ 为阻尼对角阵 , ! 为模态
频率对角阵, u 和 y 分别为输入和输出变量。考虑 开环的情况, 这时控制目标函数为: V = E
!y
0
∀
T
Qy d t ,
式中 E 为期望算子 , Q 为反映 y 各分 量重要性的 一个矩阵。 考虑 N 个模态, 有 C1 = [ c11 #c 1 N ] , C2 = [ c21 #c 2 N ] , 业已证明 [ 5 ] , 在弱阻尼的条件下, 有
62
中国工程科学
2p
第3卷
可以按模态价值的大小对模态进行排列 , 保留 那些价值高的模态, 略去那些价值很小的模态。一 般讲 , 模态价值并不按频率大小排列。若模态价值 分析要求保留的模态数太多, 则应修改控制目标 , 保留合理的模态数。一般讲, 保留模态的选择是个 反复的过程。 3 2 内平衡降阶
们的变形 , 这可看成是对通常混合坐标法的推广。 应注意所采用的正则模态是相应于有关连体坐标系 的。经过适当的 步骤, 可得 到航天 器的动力 学方 程。由于中心体和附件变形均是相对于相应的附体 系而言的 , 因而动力学方程中所用的中心体弹性模 态为其自由界面正则模态, 而附件弹性模态为固定
缪炳祺 ( 1940- ) , 男 , 江苏无锡市人 , 浙江工业大学机电学院教授
i T 2 T b ibT i ( c 1 ic 1 i + #i c 2 ic 2 i ) 2 4∀ i #i
( 4)
% ∃ i , i = 1, #, p
]
0 - !
2
I - 2 ∀!
, B=
0 D
, C = [ C1
C2 ]
按平衡降阶思想, 具有小 ∃i 的模态较不受作 用力的影响, 并对输出的贡献较小。由于 ∃ i 表示 模态的影响程度, 因而可称为模态影响系数。 模态频率的分离程度可按以下准则判断: max ( ∀ i, ∀ j ) max ( # i, # j) ! 1, i & j | #i - #j |
上面方程中已除去了刚体模态 , 因而矩阵 A 的所有特征值均具有负实部。 所谓 内平衡 模型是 指其 能控和 能观 Gramian 阵 W 和 V 相等, 且已对角化: W = V = & = diag{ ∃ i , i = 1, #, 2 p } 。 这里能控和能观 Gram ian 阵的定义为 : W=
( 5)
若满足式 ( 5) , 则说频率 #i , #j 足够分 开, 但大部分空间结构呈现频率密集成团的状况, 上述 准则将不被满足。这时一般的经验是不管上述准则 方程 , 仍按 Gregory 提供的近似表达式计算各模态 的∃ i 并按其大小进行模态选取; 或者可以将不满 足准则方程的那些模态集结成组 , 对每个密集模态 组进行分析以确定是否需保留具有小模态影响系数 的模态 [ 8] 。在 这种情况下 , 将保留所有具有 大的 ∃i 的模态和一些具有小的 ∃i 的模态。可采用前面 的误差边界方程来确定应保留多少模态。
N
( 2)
V =
i= 1
Vi,
2 T 2
式中 V i 表示第 i 个模态的模态价值 , 且有 ( c 1 i Qc 1 i + #i c 2 iQc 2 i ) ∃i Vi = , 3 4∀ i #i
T
( 3)
式中 # 和 ∀ i 分别为第 i 个模态频率和模态阻尼比, 为 ∃2 i 第 i 个模态广义力的强度 ( 当考虑受白噪声 激励时) , 或第 i 个模态坐标的初始速率的均方值 ( 当考虑初始速度扰动时 ) 。由式 ( 3 ) 可知, 刚体 模态的模态价值为无穷大, 显然应该保留。
[ 摘要 ]
针对柔性航天器动力学模型的降阶问题 , 综述了 动力学建 模中几种常 用的模态 集 , 介绍了用 于选择
系统 保留模态的有关准则。通常的模态价值分析和内平 衡理论是 用于航 天器系 统模态 的选取 , 而 不是直 接用于 动力学建模时 的部件模态或系统结构弹 性变形 模态 的选取 , 因而存 在如 何应用 上述 准则 于动力 学建 模的问 题。 为此 , 提出了一个动力学建模时的降阶策略 ; 还提供了 一个数值 例子 , 以 对采用 不同的模 态集建 模时的 结果进 行比较 , 并表明如何采用上述准则于航天器的动力学建模。
2001 年 11 月 第 3 卷第 11 期 研究报告
中国工程科学 Engineering Science
Nov. 2001 Vol 3 No 11
关于柔性航天器动力学模型降阶问题
缪炳祺1 , 曲广吉2 , 夏邃勤1 , 程道生2
( 1. 浙江工业大学机电学院, 杭州 310014; 2. 北京空间飞行器总体设计部 , 北京 100086)
第 11 期
缪炳祺等: 关于柔性航天器动力学模型降阶问题
61
界面正则模态。为了保证所得到的动力学模型足以 反映航天器的动力学特性 , 所取的弹性正则模态应 足够多。对于中心体 柔性较大、附件较 大的航天 器, 单纯采用部件弹性正则模态集有时不能很好地 表示变形。 2 2 Craig Bampton ( C- B) 模态集
T T T
式中 ∀ , ! 的第 i 个元素, di i, # i 分别是对角阵 ∀ 是 D 的第 i 行 , c 1 i , c 2 i 分别是 C 1 , C 2 的第 i 列。 Gregory 证明 [ 7] , 具有分离频率的小阻尼结构 的模态模型近似为平衡的, 此外 , 他还得到了计算 标量 ∃ i 的近似表达式为: ∃i % ∃ p+
