图乘法
合集下载
结构力学课件 第6章 图乘法
三、注意事项： 注意事项：
1.若 Aω与 1.若 取负值
yc
在杆件的同侧，取正值；反之， 在杆件的同侧，取正值；反之，
2.当图乘法的适用条件不满足时的处理方法： 当图乘法的适用条件不满足时的处理方法： 当图乘法的适用条件不满足时的处理方法 a）曲杆或EI=EI（x）时，只能用积分法求位移； ）曲杆或 只能用积分法求位移； （ ） b）当EI分段为常数或单位弯矩图、荷载弯矩图均非 ） 分段为常数或单位弯矩图、 分段为常数或单位弯矩图 直线时， 直线时，应分段图乘再叠加 3.yc应取自直线图中。若两图均为直线图形，也可 应取自直线图中。若两图均为直线图形， 图的面积乘其形心所对应的M 用 M 图的面积乘其形心所对应的 P 图的竖标来计 算。
2
yc = h
1 2 ql 2 = × × ×l×h ∆ CD = ∑ EI EI 3 8 qhl 3 = (→ ← ) 12 EI
ω yc
为常数，求刚架A点的竖向位 例 3. 已知 EI 为常数，求刚架 点的竖向位 并绘出刚架的变形曲线。 移 ∆ Ay ，并绘出刚架的变形曲线。
F
解：作荷载内力图和单位荷载内力图
M=1
M P图
∆ CV
300 × 6 2 = × ×6× 2 2 3 1 2 − × 6 × 45 × 3 = 6660 3
6
M A图
Fp=1
M C图
为常数， 例 5. 已知 EI 为常数，求 ∆Cy 。 q
A
l 2
C
B
l 2
解：作荷载内力图和单位荷载内力图
ql 2 2
A
ql 2 8
C
l 2
1
B A
二、图乘法原理
MM P 图乘法求位移的一般 ds 表达式为 ∫ EI 1 ∆=∑ Aω yC 1 = ∫ MM P ds EI EI
结构力学图乘法
W12 W21
二、 位移互等定理
在任一线性变形体系中，由荷载FP1引起的 与荷载FP2相应的位移影响系数δ21等于由荷载 FP2引起的与荷载FP1相应的位移影响系数δ12。
即
δ12= δ21
FP1
12
FP 2
12
11
21
状态I
12
22
状态II
由功的互等定理可得： FP112 FP221
1 81 2
4
21
20
y2
( 4 3
12) 3
3
y3
1 2
(1 1 /
2)
3 4
B
1 EI
(1 y1
2 y2
3 y3 )
1 EI
(64 1 2
4
20 3
32 3 ) 34
1 (32 80 8) 13.33 ( )
Ma2 16EI
21
21
/
F
a2 16EI
12
12
/M
a2 16EI
12 21
例2 验证位移互等定理。
FP1=5kN.m 1
EI 4m
2
1
Δ21
1m
FP2=3kN
Δ12
2
EI
4m
1m
3 5
11
1
解：
11
1 10
21
EI
2
5
4
1 3
3EI
12
1 EI
和量纲 (W FP1FP2 ) 上仍然保持相等。
二、 位移互等定理
在任一线性变形体系中，由荷载FP1引起的 与荷载FP2相应的位移影响系数δ21等于由荷载 FP2引起的与荷载FP1相应的位移影响系数δ12。
即
δ12= δ21
FP1
12
FP 2
12
11
21
状态I
12
22
状态II
由功的互等定理可得： FP112 FP221
1 81 2
4
21
20
y2
( 4 3
12) 3
3
y3
1 2
(1 1 /
2)
3 4
B
1 EI
(1 y1
2 y2
3 y3 )
1 EI
(64 1 2
4
20 3
32 3 ) 34
1 (32 80 8) 13.33 ( )
Ma2 16EI
21
21
/
F
a2 16EI
12
12
/M
a2 16EI
12 21
例2 验证位移互等定理。
FP1=5kN.m 1
EI 4m
2
1
Δ21
1m
FP2=3kN
Δ12
2
EI
4m
1m
3 5
11
1
解：
11
1 10
21
EI
2
5
4
1 3
3EI
12
1 EI
和量纲 (W FP1FP2 ) 上仍然保持相等。
图乘法
§4.5 图乘法
(Graphic Multiplication Method)
刚架与梁的位移计算公式为： 刚架与梁的位移计算公式为：
∆ iP = ∑ ∫ MM P ds EI
在杆件数量多的情况下,不方便 下面介绍 在杆件数量多的情况下 不方便. 不方便 计算位移的图乘法. 计算位移的图乘法
一、图乘法 MM P ds ∫ EI 1 对于等 = ∫ M M P ds (对于等 截面杆) 截面杆 EI
ωyc
五、应用举例
图示梁EI 为常数， 点竖向位移。 例 3(a). 图示梁 为常数，求C点竖向位移。 点竖向位移
ql 2 / 2
MP
q ql 2 / 8
A
∆c = ∑
ωyc
l/2 C
1
C
l/2
B
1 1 ql 2 1 l = ⋅l ⋅ ⋅ ⋅ EI EI 3 2 2 2
l/2
Mi
1 ql 3 = ⋅ (↓) 24 EI
EI
试求图示结构B点竖向位移 点竖向位移. 例. 试求图示结构 点竖向位移
Pl EI l EI
MP
P B
l
Mi
=1
l
解: ∆ By = ∑
=∑
MM P ∫ EI ds
ωy c
EI 1 1 2 ( ⋅ Pl ⋅ l ⋅ l + Pl ⋅ l ⋅ l ) = EI 2 3 4 Pl 3 = ⋅ (↓) 3 EI
=1 1/ 2
1 1 Pl 1 Pl 2 ϕB = − ( ⋅ l ⋅ ⋅ ) = − ( EI 2 4 2 16EI
)
取 yc的图形必 须是直线,不能是曲 须是直线 不能是曲 线或折线. 线或折线
(Graphic Multiplication Method)
刚架与梁的位移计算公式为： 刚架与梁的位移计算公式为：
∆ iP = ∑ ∫ MM P ds EI
在杆件数量多的情况下,不方便 下面介绍 在杆件数量多的情况下 不方便. 不方便 计算位移的图乘法. 计算位移的图乘法
一、图乘法 MM P ds ∫ EI 1 对于等 = ∫ M M P ds (对于等 截面杆) 截面杆 EI
ωyc
五、应用举例
图示梁EI 为常数， 点竖向位移。 例 3(a). 图示梁 为常数，求C点竖向位移。 点竖向位移
ql 2 / 2
MP
q ql 2 / 8
A
∆c = ∑
ωyc
l/2 C
1
C
l/2
B
1 1 ql 2 1 l = ⋅l ⋅ ⋅ ⋅ EI EI 3 2 2 2
l/2
Mi
1 ql 3 = ⋅ (↓) 24 EI
EI
试求图示结构B点竖向位移 点竖向位移. 例. 试求图示结构 点竖向位移
Pl EI l EI
MP
P B
l
Mi
=1
l
解: ∆ By = ∑
=∑
MM P ∫ EI ds
ωy c
EI 1 1 2 ( ⋅ Pl ⋅ l ⋅ l + Pl ⋅ l ⋅ l ) = EI 2 3 4 Pl 3 = ⋅ (↓) 3 EI
=1 1/ 2
1 1 Pl 1 Pl 2 ϕB = − ( ⋅ l ⋅ ⋅ ) = − ( EI 2 4 2 16EI
)
取 yc的图形必 须是直线,不能是曲 须是直线 不能是曲 线或折线. 线或折线
结构力学(第三章)-图乘法
( M x tan ) 1 x tan M P dx EI tan
xM P dx
图乘法求位移公式为:
图乘法的 适用条件是 什么?
EI tan 1 xc yc EI EI
ip
yc
EI
例. 试求图示梁B端转角.
A
P
B B
MP
A
M 1 B 1
B
c
y c
ql 2 / 2
ql 2 / 8
例 4. 图示梁 EI 为常数，求C点竖向位移 。 q ql 2 / 8 ql 2 / 2
MP
A
l/2 C
1
q q
l/2
B
l/2
Mi
c
y c
C ql / 2 ql 2 / 8
ql 2 / 8 ql 2 / 4 ql 2 / 8
ql / 2
§3.4 图乘法及其应用
(Graphic Multiplication Method and its Applications)
刚架与梁的位移计算公式为：
iP MM P ds EI
在杆件数量多的情况下,不方便. 下面介绍 计算位移的图乘法.
一、图乘法
MM P ds EI 1 图乘法是Vereshagin于 M M P ds (对于等 截面杆) EI 1925年提出的，他当时 1 为莫斯科铁路运输学院 MM P dx (对于直杆) EI 的学生。
1 1
B
Mi
l
ql / 4
2
l
ql 2 / 4
1/ l
0 解：作荷载弯矩图和单位荷载弯矩图
q
MP
5结构力学图乘法.
（1）常见图形面积和形心：
矩 形
a
l
A al
xc 1 l 2 xc 1 3l
xc 1 4l
3 xc 8 l
三角形
a
l
A 1 2 al A 1 3 al A 2 3 al
l
a
l
标准二次 抛物线
a
l
a
A 2 3 al
xc 1 l 2
（2） 梯形相乘
A1
A2
M M
i
K
dx A1 y1 A2 y 2
1 M M P dx EI
(M x tanα)
yc
xc x
M
x
图乘法是Vereshagin于1925年 提出的，他当时为莫斯科铁路 运输学院的学生。
4、 注意事项
KP AP yc EI
还记得 吗？
（1）必须符合图乘法的适用条件； （2） 必须取自直线图形； （3）同侧弯矩图相乘为正，反之为负； （4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解； （5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
如果将AC段的 M P图如下图那样分块，就比 16 较麻烦。 4kN 4 2kN/m 8 M P图 4 A C C A 2m 4kN.m 例2 求 B, EI等于常数。 12kN.m 4kN C 4m
2kN/m
4kN.m 4m B 7kN
A
5kN
解： 作 M 图 M P 图，如下页图所示。
12
c
y2
d
M图
（3）一般形式的二次抛物线图形相乘 （4）曲线图形与折线图形相乘
M M
i
K
矩 形
a
l
A al
xc 1 l 2 xc 1 3l
xc 1 4l
3 xc 8 l
三角形
a
l
A 1 2 al A 1 3 al A 2 3 al
l
a
l
标准二次 抛物线
a
l
a
A 2 3 al
xc 1 l 2
（2） 梯形相乘
A1
A2
M M
i
K
dx A1 y1 A2 y 2
1 M M P dx EI
(M x tanα)
yc
xc x
M
x
图乘法是Vereshagin于1925年 提出的，他当时为莫斯科铁路 运输学院的学生。
4、 注意事项
KP AP yc EI
还记得 吗？
（1）必须符合图乘法的适用条件； （2） 必须取自直线图形； （3）同侧弯矩图相乘为正，反之为负； （4）拱、曲杆结构和连续变截面的结构只能通过积 分的方式求解； （5）应用图乘法首先熟练掌握常用图形面积及形心 位置。
如果将AC段的 M P图如下图那样分块，就比 16 较麻烦。 4kN 4 2kN/m 8 M P图 4 A C C A 2m 4kN.m 例2 求 B, EI等于常数。 12kN.m 4kN C 4m
2kN/m
4kN.m 4m B 7kN
A
5kN
解： 作 M 图 M P 图，如下页图所示。
12
c
y2
d
M图
（3）一般形式的二次抛物线图形相乘 （4）曲线图形与折线图形相乘
M M
i
K
第五节图乘法
4m C 4m
MP图(kN·m)
须注意两点：一是对于斜杆CD， 解：求解本题∆DV时，须注意两点：一是对于斜杆 ，应以杆 轴为基线计算；二是对于阶形住AC，应按EI不同分段图乘 不同分段图乘。 轴为基线计算；二是对于阶形住 ，应按 不同分段图乘。 (1)作MP图 作
A1 = 2 × 12.65 × 45 = 379.5 3
§6-5 图乘法
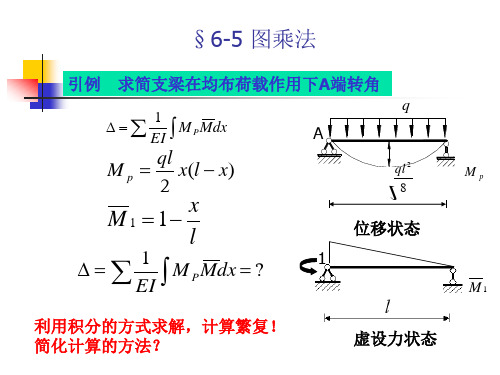
求简支梁在均布荷载作用下A端转角 引例 求简支梁在均布荷载作用下 端转角
1 ∆=∑ ∫ M P Mdx EI
q
A
ql 2 8
ql M p = x(l − x) 2
Mp
x M 1 = 1− l
1 ∆=∑ ∫ M P Mdx = ? EI
利用积分的方式求解，计算繁复！ 利用积分的方式求解，计算繁复！ 简化计算的方法？ 简化计算的方法？ 1
2.5kN/m D 2EI (12.65m) 3EI B 8m 4EI A 12m
20kN 100 A2 C A3 20 B A4 A A5
(45)
A1
D
4m C 4m
140
MP图(kN·m)
1 A2 = × 12.65 × 100 = 632.5 2
A4 =
A5 =
1 × 8 × 20 = 80 2
A q B l/2 l
ql 2 ( ) 32
ql
C l/2
并按A 作MP图，并按 1、A2、A3、A4四部 分划分，如图6-22b所示 分划分，如图 所示
∆CV 1 = ( A1 y01 + A2 y02 + A3 y03 − A4 y04 ) EI 1 = EI 1 l ql 2 l l ql 2 3 )× + ( × )× l ( × × 3 2 2 4 2 2 2
图乘法
均布荷载作用区段的弯矩图与直线 段图乘。
几种常见图形的面积和形心的位置：
a
b
h
h l/2 顶点 l/2
(a+l)/3 (b+l)/3
l
A=hl/2
二次抛物线A=2hl/3 顶点
h
h
顶点
3l/4
l/4
二次抛物线A=hl/3
5l/8
3l/8
二次抛物线A=2hl/3
h
h
顶点
4l/5
l/5
三次抛物线A=hl/4
DCH
=
2 EI
1 4m 4m 2
(1 80KN • m 2 160KN • m)
3
3
1067KN • m3
=
()
EI
例4-8：试求图示伸臂梁A端 的角位移φA及C端的竖向位移 ΔCV。 EI = 5104 KN • m2 解：做出MP图和 M 图分别如 图b、c、d所示。
将图b与图c相乘则得
Mi yC yC=x0tgα x
②图乘法的应用条件：a）EI=常数；b）直杆；c）两个弯矩图
至少有一个是直线。
③竖标yC取在直线图形中，对应另一图形的形心处。 ④面积AP与竖标yC在杆的同侧， AP yC 取正号，否则取负号。
⑤几种常见图形的情况：
单位荷载弯矩图由若干直线段组成 时，就应该分段图乘。
至少有一个是直线。
③竖标yC 取在直线图形中，对应另一图形的形心处。 ④面积AP与竖标yC在杆的同侧， AP yC 取正号，否则取负号。
⑤几种常见图形的面积和形心的位置：
h
顶点
3l/4
l/4
h l/2 顶点 l/2
二次抛物线ω=hl/3
结构力学-图乘法
1
NP
N
1
结构力学电子教案
第七章
静定结构位移计算
第23页
DP
M M P ds EI
F N FNP l EA
1 1 4 1 2 2 ( 2 2 8 ) 3 ( 2 2 2 ) 3 ( 3 2 0 . 5 ) 1 EI 4 1 2 2 1 ( 4 8 ) ( 4 8 ) ( 4 2 ) 1 2 EI 2 3 2 3 3 1 1 EA
Δ Cy
结构力学电子教案
第七章
静定结构位移计算
第17页
解 绘出实际状态及虚拟状态的 M P 、M 图。
72
2 16 8 4 2 16 8
20
4
MP图
y5 y 4 y 3
y1 y2
结构力学电子教案
第七章
静定结构位移计算
第18页
Cy
yc
EI
[( 4 20 )( 4 ) ( 4 4 )( 4 )] EI 2 3 3 2
B
xd
A
xc
B
A
M M P ds EI
tg EI
xc
yc
EI
结构力学电子教案
第七章
静定结构位移计算
第4页
B
A
M M P ds EI
tg EI
xc
yc
EI
由此可见，上述积分式等于一个弯矩图的面积 乘以其形 心处所对应的另一个直线弯矩图上的纵距 y c ，再除以EI。 这就是图形相乘法的计算公式，简称为图乘法。
NP
N
1
结构力学电子教案
第七章
静定结构位移计算
第23页
DP
M M P ds EI
F N FNP l EA
1 1 4 1 2 2 ( 2 2 8 ) 3 ( 2 2 2 ) 3 ( 3 2 0 . 5 ) 1 EI 4 1 2 2 1 ( 4 8 ) ( 4 8 ) ( 4 2 ) 1 2 EI 2 3 2 3 3 1 1 EA
Δ Cy
结构力学电子教案
第七章
静定结构位移计算
第17页
解 绘出实际状态及虚拟状态的 M P 、M 图。
72
2 16 8 4 2 16 8
20
4
MP图
y5 y 4 y 3
y1 y2
结构力学电子教案
第七章
静定结构位移计算
第18页
Cy
yc
EI
[( 4 20 )( 4 ) ( 4 4 )( 4 )] EI 2 3 3 2
B
xd
A
xc
B
A
M M P ds EI
tg EI
xc
yc
EI
结构力学电子教案
第七章
静定结构位移计算
第4页
B
A
M M P ds EI
tg EI
xc
yc
EI
由此可见，上述积分式等于一个弯矩图的面积 乘以其形 心处所对应的另一个直线弯矩图上的纵距 y c ，再除以EI。 这就是图形相乘法的计算公式，简称为图乘法。
图乘法
1.2.3图乘法图乘法是关于的简化计算方法。
在一定的应用条件下，图乘法可给出该积分的数值解，而且是精确解。
适用条件（1）杆件为直杆；（2）EI为常数（等截面）；（3）和图中至少应有一个直线图形。
对于等截面直杆所构成的梁和刚架，都能同时满足以上三个条件，因而均可采用弯矩图图乘的方法，简称图乘法。
算位移的公式（1-15）式中为、图中某一图形的面积；为与该截面形心对应的另一个图形的竖标。
这样，就将较为复杂的积分运算问题简化为求图形的面积、形心和标距等几何运算问题。
三）几种常见图形的面积的形心位置在图1-15中，给出了位移计算中几种常见图形的面积公式和形心位置。
图1-15【注意】在所示的各次抛物线图形中，抛物线“顶点”处的切线都是与基线平行的。
这种图形可称为抛物线标准图形。
应用图中有关公式时，应注意这个特点。
（四）图乘法计算位移必须注意的几个问题（1）必须取自直线图形。
（2）与若在杆件同侧时，其乘积取正号；反之，取负号。
（3）如果两个图形都是直线图形，则可取自其中任何一个图形。
（4）如果图是曲线图形，图是折线图形，则应分段互乘，最后叠加。
（5）如果图形比较复杂（由不同类型的多个荷载作用绘出），其面积和形心位置不便确定时，则可利用“区段叠加法”的逆运算，将其分解为几个简单的标准图形，并将它们分别与另一个图形图乘，最后叠加。
（6）如果杆件EI分段变化时，可分段图乘，最后叠加。
（7）如果EI沿杆长连续变化或是曲杆和拱结构，则必须用积分计算位移。
（1）绘实际荷载作用下的图；（2）根据所求位移，加相应单位力，绘图；（3）代入式（1-15）求位移：【注意】根据计算结果的正负号，判定位移的实际方向，并在计算值之后所加的圆括号中，标明其实际方向。
图乘法
移； （2）当EI分段为常数；或单位弯矩图、荷载弯矩
图均为非直线。
此时的处理方法：应分段图乘再叠加。
二．图形分解和图乘的分段叠加
10
在实际计算中，当弯矩图的形心位置或面积不便于确定
时，常将该图形分解为几个易于确定形心位置和面积的部分， 并将它们分别与另一图形相乘，然后再将所得结果相加。下面 分几种情况讨论。
yD
x xD
∫C M M Pds
D EI
EI=常数 直杆 ds=dx
D 1
∫ =
1 EI
C D
M M Pdx
tanα=常数
∫ ∫ =
tanα EI
D C
xM Pdx
=
tanα EI
C D
xdω
dω = M Pdx
为
MP
图中有阴影线的微面积；=
tanα EI
ω⋅
xD
xdω 为微面积对 D点的面积矩。
C
=
23Ph2 72 EI
3h/4
Mk
2/3
例 求铰C左、右两侧截面相对转角33
EI = 常数
q
C a
a
a
qa 2 qa2
34
11 2
qa2 /8
2
1
qa 2
M P 图 （kN·m）
2 M 图 (m)
ΔφC
=
1 EI
[2 3
⋅a⋅
qa 2 8
×
1 2
+ 2 ⋅ a ⋅ qa2 × ( 1 +1) 3 82
−A3ql 3 4
(
2 3
2l
+
1 3
l)
l
− −
图均为非直线。
此时的处理方法：应分段图乘再叠加。
二．图形分解和图乘的分段叠加
10
在实际计算中，当弯矩图的形心位置或面积不便于确定
时，常将该图形分解为几个易于确定形心位置和面积的部分， 并将它们分别与另一图形相乘，然后再将所得结果相加。下面 分几种情况讨论。
yD
x xD
∫C M M Pds
D EI
EI=常数 直杆 ds=dx
D 1
∫ =
1 EI
C D
M M Pdx
tanα=常数
∫ ∫ =
tanα EI
D C
xM Pdx
=
tanα EI
C D
xdω
dω = M Pdx
为
MP
图中有阴影线的微面积；=
tanα EI
ω⋅
xD
xdω 为微面积对 D点的面积矩。
C
=
23Ph2 72 EI
3h/4
Mk
2/3
例 求铰C左、右两侧截面相对转角33
EI = 常数
q
C a
a
a
qa 2 qa2
34
11 2
qa2 /8
2
1
qa 2
M P 图 （kN·m）
2 M 图 (m)
ΔφC
=
1 EI
[2 3
⋅a⋅
qa 2 8
×
1 2
+ 2 ⋅ a ⋅ qa2 × ( 1 +1) 3 82
−A3ql 3 4
(
2 3
2l
+
1 3
l)
l
− −
结构力学图乘法
FN FPb M FQ 状态II FPa
M ds ds EI FN ds ds EA
ds 0
kFQ GA
ds
令状态I的平衡力系在状态II的位移上做虚功，得到：
0 ds FN ds W12 FP M ds FQ FQ kFQ FN FN M M ds ds ds EI GA EA
yc
几中常见图形的面积和形心的计算公式
a b 顶点
C
lb 3
C
5l 8
la 3
3l 8
l
l
三角形
l h AP 2
二次抛物线
2 Ap h l 3
顶点
c
顶点
( n 1) l n2
c
l n2
3l/4 l
l/4
l
二次抛物线
l h Ap 3
N 次抛物线
lh n1
3. 图形相乘的几种情况
1
作业：
4-3 (a)；(c)
§4-5 互等定理
互等定理适用于线性变形体系，即体系产生的 是小变形，且杆件材料服从虎克定律。
一、 功的互等定理
功的互等本质上是虚功互等。
下图给出状态I和状态II。
FP1 2 FP
FPa
FPb
A
1 2 a b
a
b
B
A
1 2 B a 1 b 2
所以
即
F F
P P
11 FP 2 FP 2 FPa a FPb b
在任一线性变形体系中，第一状态的外力 在第二状态的位移上所做的虚功W12等于第二状 态的外力在第一状态的位移上所做的虚功W21。
结构力学-图乘法
实例分析：圆轴扭转内力计算
第一段
M1 = (T1 + T2) × L/2
第二段
M2 = (T2 + T1) × L/2
实例分析：圆轴扭转内力计算
01
4. 比较M1和M2的大小，取较大 者作为圆轴内的最大扭矩。
02
5. 根据扭矩的正负号，绘制扭矩 图。
Part
04
组合变形图乘法
组合变形基本概念及分类
者联系起来，从而求解结构位移。
图乘法适用条件及限制
适用条件Βιβλιοθήκη 01载荷作用下，结构的变形是线性的，即变 形量与载荷成正比。
03
02
结构变形符合小变形假设，即变形量与结构 尺寸相比很小。
04 限制
图乘法只适用于线性弹性问题，对于非线 性问题或塑性变形问题不适用。
05
06
在应用图乘法时，需要保证图形函数的准 确性，否则会影响计算结果的精度。
Part
02
弯曲内力图乘法
弯曲内力基本概念
01
02
03
弯曲内力
指构件在受到外力作用时， 其内部产生的抵抗弯曲变 形的力。
剪力
作用于构件横截面上的内 力，其方向与构件轴线垂 直。
弯矩
作用于构件横截面上的内 力偶矩，其大小等于该截 面左侧或右侧所有外力对 截面形心的力矩之和。
弯曲内力图乘法求解步骤
图乘法优点总结
直观性
图乘法通过图形表示结构 中的力学元素和它们之间 的关系，使得分析结果更 直观，易于理解和解释。
高效性
相较于数值分析方法，图 乘法能够更快地给出结构 分析的近似解，适用于初 步设计和快速评估。
适用性广
图乘法可应用于各种不同 类型的结构，包括静定结 构和超静定结构，具有较 广泛的适用性。
5.5 图乘法
P=1
a/2
a/2 M 3a/4
例：求图示梁C点的挠度。
？ D = 1 Pl 2 l = Pl 3 C EI 2 6 12 EI
C
Ay0 EI
1l l
××
222
×5 Pl 6
5 Pl 3 48 EI
P
l/2
Pl
5Pl/6
C
l/2
MP
P=1
l/2
C l/6
5
M
⑦非标准图形乘直线形
2）假设：温度沿截面高度为线性分布。
t0 (h1t2 h2t1) / h (t1 t2 ) / 2 t1
t t2 t1
3）微段的变形
t0
at0
t2
d / ds [a (t2 t1)ds / h] / ds
h h1 h2 ds
at1ds dθ
at0ds at2ds
二、位移互等定理
P1
①
P112 P221 12 P2 21 P1
△21
P2
②
△12
d ij ij Pj 称为位移影响系数，等于Pj=1所引起的与Pi相应的位移。 d12 d 21
位移互等定理：在任一线性变形体系中，由荷载P1所引起的与荷载P2相
应的位移影响系数δ21 等于由荷载P2所引起的与荷载P1相应的位移影响系数 δ12 。或者说,由单位荷载P1=1所引起的与荷载P2相应的位移δ21等于由单位荷 载P2=1所引起的与荷载P1相应的位移δ12 。
二次抛物线A=2hl/3 顶点
h
顶点
3l/4
l/4
二次抛物线A=hl/3
5l/8
3l/8
结构力学图乘法
2、图乘法原理 y
d A =MPdx
A MP
A 面积
形心 C MP图 B
dx
O
x
M xtgα
yC
yC=xCtg
B
A
xC
x
由此可知，计算位移的积分就等于一 个弯矩图的面积A乘以其形心所对应的 另一个直线弯矩图上的竖标yC，再除以 EI，于是积分运算转化为数值乘除运 算，此法即称图乘法。
剪力与轴力项能用图乘法？
3、图乘法求位移的一般表达式
注意：
yc [1].
应取自直线图中。 [2].若 A 与 yc 在杆件的同侧, 取正值;反之,取负值（不是MP与M 图位于杆件同侧或异侧）。 [3]. 如图形较复杂，可分解为几个简 单图形。
二、图乘法步骤 (1) 画出结构在实际荷载作用下的弯 矩图（荷载弯矩图）MP； (2) 根据所求位移选定相应的虚拟力 状态，画出单位弯矩图M(注：M图不标 单位）； (3) 分段计算一个弯矩图形的面积A 及其形心所对应的另一个弯矩图形的竖 标yC； (4) 将A、yC代入图乘法公式计算所 求位移。
【预习】：静定结构的位计算习题课
解：1、求φA ① 实际荷载作用 下的弯矩图MP如图(b) 所示。 ② 在A端加单位力 偶m=1，其单位弯矩图M 如图(c)所示。
③ MP图面积及其形心 对应M图竖标分别为：
A=2/3*l*1/8*ql2=ql3/12 yC=1/2 ④ 计算φA φA=1/EI*A*yC =1/EI*ql3/12*1/2=ql3/24 EI
（3）异侧组合
（4）非规则抛物线图形
由区段叠加法作的弯矩图 ，其弯矩 图可以看成一个直线弯矩图和一个规 则抛物线图形的叠加 。
MB
结构力学第三章图乘法
l ql 2 1 l ) 2 8 22
17 ql 4 () 384 EI
ql2 / 8
ql2 / 8
练习
图示结构 EI 为常数，求AB两点(1)相对竖向位
移,(2)相对水平位移,(3)相对转角 。
Pl
l
PP
AB
ABY
对称yc 结构的对称弯矩图与
其E反I 对称弯矩图图乘,结果
yc
1 1 3q2l l (
3l
l
q2l l )
EI EI3 8 2 4 2 2 8 4
5q3l () 12E8I
三、应用举例
例 4. 图示梁 EI 为常数，求C点竖向位移 。
ql 2 / 2
q ql2 / 8
MP A l/2C l/2 B
l/2
1
c
yc
EI
1 ( 2 l ql2 1 l 1 l ql2 2 l EI 3 2 32 2 2 2 2 2 3 2
Mi
ql 2 / 2
C q
1 l ql2 1 l ) 22 8 32
ql 2 / 8 17 ql 4
()
384 EI
ql2 / 32
MP 1 (1 为l P零l. 2 l 4 l Pl l 2)
l
ll
11
反对称弯矩图EI 2
3
10 Pl3 ()
3 EI
M i
ABX
yc 0
EI
AB
yc 0
EI
11
对称弯矩图
11
1
Mi
Mi
l
l
1
图乘法
1.2.3图乘法图乘法是关于的简化计算方法。
在一定的应用条件下，图乘法可给出该积分的数值解，而且是精确解。
（一）图乘法的适用条件（1）杆件为直杆；（2）E I为常数（等截面）；（3）和图中至少应有一个直线图形。
对于等截面直杆所构成的梁和刚架，都能同时满足以上三个条件，因而均可采用弯矩图图乘的方法，简称图乘法。
（二）图乘法计算位移的公式（1-15）式中为、图中某一图形的面积；为与该截面形心对应的另一个图形的竖标。
这样，就将较为复杂的积分运算问题简化为求图形的面积、形心和标距等几何运算问题。
（三）几种常见图形的面积的形心位置在图1-15中，给出了位移计算中几种常见图形的面积公式和形心位置。
图1-15【注意】在所示的各次抛物线图形中，抛物线“顶点”处的切线都是与基线平行的。
这种图形可称为抛物线标准图形。
应用图中有关公式时，应注意这个特点。
（四）图乘法计算位移必须注意的几个问题（1）必须取自直线图形。
（2）与若在杆件同侧时，其乘积取正号；反之，取负号。
（3）如果两个图形都是直线图形，则可取自其中任何一个图形。
（4）如果图是曲线图形，图是折线图形，则应分段互乘，最后叠加。
（5）如果图形比较复杂（由不同类型的多个荷载作用绘出），其面积和形心位置不便确定时，则可利用“区段叠加法”的逆运算，将其分解为几个简单的标准图形，并将它们分别与另一个图形图乘，最后叠加。
（6）如果杆件E I分段变化时，可分段图乘，最后叠加。
（7）如果E I沿杆长连续变化或是曲杆和拱结构，则必须用积分计算位移。
（五）图乘法的计算步骤（1）绘实际荷载作用下的图；（2）根据所求位移，加相应单位力，绘图；（3）代入式（1-15）求位移：【注意】根据计算结果的正负号，判定位移的实际方向，并在计算值之后所加的圆括号中，标明其实际方向。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
= 3.5325103 m
3.5103 m = 3.5mm()
=
=
+
+
均布荷载按简支梁进行叠加 ， 按第22页图3-2方法。
集中荷载、均布荷载分别做 弯矩图，然后进行叠加 。
作业： 第77页 4-3（a）、（b）、4-4 （b）
休息一下
作业情况
一、桁架的内力标注在图上。 二、取隔离体：如3-20（a) 图
由Ⅰ-Ⅰ左边隔离体算出FNB后，取下 面四个结点A、B、C、D分别计算？
三、抄作业。 CD是二力杆，有
这样画隔离体的？
这是什么 隔离体？
返回
§4—4 图乘法
MiMk
ds
直杆
MiMk
dx
EI =C
1
EI
EI
EI
MiMk dx
D
=
1 EI
P
aa 2
2 3
a 2
2
a
2
3a 2
4
a 2
2
Pa
23Pa3 =
24EI 例：求图示梁C点的挠度。
？ D = 1 Pl 2 l = Pl 3 C EI 2 6 12 EI
DC
=
wy0
EI
=
1l l
××
222
×5 Pl 6
= 5 Pl 3 48 EI
P
P
MP
Pa
Pa
a
a
a
P=1
a/2
a/2 M 3a/4
P
l/2
Pl
5Pl/6
C
l/2
MP
P=1
l/2
C l/6
M
图乘法 位移计算举例
D
=
MM EI
P
dx
=
AP yC
EI
①∑表示对各杆和各杆段分别图乘而后相加。
②图乘法的应用条件：a）EI=常数；b）直杆；c）两个弯矩图
至少有一个是直线。
③竖标yC 取在直线图形中，对应另一图形的形心处。 ④面积AP与竖标yC在杆的同侧， AP yC 取正号，否则取负号。
（1）M 图的BC段没有弯矩，只需 在AB段进行图乘。
（2）两图均为直线， M 图上取面 积，MP图上取相应竖标，较为简便。
DCH
=
2 EI
1 4m 4m 2
(1 80KN • m 2 160KN • m)
3
3
1067KN • m3
=
()
EI
例4-8：试求图示伸臂梁A端 的角位移φA及C端的竖向位移 ΔCV。 EI = 5104 KN • m2 解：做出MP图和 M 图分别如 图b、c、d所示。
至少有一个是直线。
③竖标yC取在直线图形中，对应另一图形的形心处。 ④面积AP与竖标yC在杆的同侧， AP yC 取正号，否则取负号。
⑤几种常见图形的情况：
单位荷载弯矩图由若干直线段组成 时，就应该分段图乘。
MMP
EI
dx
=
1 EI
( AP1 y1
AP2 y2
AP3 y3 )
两个梯形相乘时，不必找出梯形的
⑤几种常见图形的面积和形心的位置：
h
顶点
3l/4
l/4
h l/2 顶点 l/2
二次抛物线ω=hl/3
二次抛物线ω=2hl/3
⑥当图乘法的适用条件不满足时的处理 方法：
a）曲杆或 EI=EI（x）时，只能用积 分法求位移；
b）当 EI 分段为常数或 M、MP 均非直线时，应分段图乘再叠加。
⑦非标准图形乘直线形
（1）
S = 9/6×（2×6×2 +2 ×4×3
6
4
+6 ×3+4×2） =111
2
3
9
S=9/6×（2×6×2－2×4×3+6×3－4×2）=15
（2）
2
（3）
3
4
4
6
6
3 2
9
9
S = 9/6×（2×6×2+2×4×3－6×3－4×2）= 33
（4）
2
6
3 S = 9/6×（－2×6×2+2×0×3 +6×3－0×2） = －9
将图b与图c相乘则得
A
=
1 5104
1 2
48
6
1 3
1
= 9.6104 rad ( )
结果中的负号表示φA 的 实际方向与Ｍ＝１的方向 相反，即逆时针方向。
将图b与图d相乘则得
BC 段 在 均 布 荷 载 和 集 中荷载作用下，其弯矩图 不是标准的抛物线图形。
= 2.88103 0.6525103
l
A=hl/2
二次抛物线A=2hl/3 顶点
h
h
顶点
3l/4
l/4
二次抛物线A=hl/3
5l/8
3l/8
二次抛物线A=2hl/3
h
h
顶点
4l/5
l/5
三次抛物线A=hl/4
顶点
(n+1)l/(n+2) l/(n+2)
n次抛物线A=hl/(n+1)
例：求图示梁中点的挠度。
？ D= 1 1 3a 3aPa EI 2 4
Mi是直线
1
EI
B
A Mk xtgadx
=
1 tga
EI
B
A xMk dx
Mk
AP
x
dx
=
1 EI
tga×AP
xC =
1 EI
APyC
y
xC
D = MM P dx = AP yC
注：
EI
EI
α Mi=xtgα
①∑表示对各杆和各杆段分别图乘再相加。
Mi yC yC=x0tgα x
②图乘法的应用条件：a）EI=常数；b）直杆；c）两个弯矩图
MMP dx = 1 (
EI
EI
M M P'dx
M M P"dx)
MMP
EI
dx
=
1 EI
( al 2
ya
bl 2
yb )
ya
=
2c1d 33
yb
= 1c 3
2d 3
均布荷载作用区段的弯矩图与直线 段图乘。
几种常见图形的面积和形心的位置：
a
b
h
h l/2 顶点 l/2
(a+l)/3 (b+l)/3
形心，而将一个梯形分解为两个三角 形，然后分别与另一梯形图乘。
MMP dx = 1 (
EI
EI
M M P'dx
M M P"dx)
MMP
EI
dx
=
1 EI
( al 2
ya
bl 2
yb )
ya
=
2c1d 33
yb
=
1c 3
2d 3
两个图形都呈直线变化，但均含有
不同符号的两部分，图乘时也将其中 一图形分解为三角形。
(2 3
l
ql 2 8
)
1 2
=
ql 3 24EI
(
)
将图b与图d相乘则得
DCV
=
1 EI
( AP1 y1 AP2 y2 )
2 2 l ql 2 5
5ql 4
= ( ) l =
()
EI 3 2 8 32 384EI
例4-7：试求图示刚架C点的水平位 移 NhomakorabeaCH。EI为常数。
解：做出MP图和 M 图分别如图b、c 所示。
a）直线形乘直线形
M M dx =AP1 y AP2 y
ik
1
2
a
AP1
Mi
AP2
b
l/3
l/3
l/3
= al 2c d bl c 2d
2 3 3 23 3
c
y1
Mk
y2
d
= l (2ac2bd ad bc)
6
各种直线形乘直线形，都可以用该公式处理。如竖标在基线
同侧乘积取正，否则取负。
9
b)非标准抛物线成直线形
a h
b ＝a
+
举例
b h
c l
d
S
=
l
6 (2ac 2bd
ad
bc ) 2hl
3
cd 2
例4-6：试求图示简支梁A
端的角位移 A 和中点C的竖
向位移 DCV 。EI为常数。
解：荷载作用下的弯矩图和两个单 位弯矩图分别如图b、c、d所示。
将图b与图c相乘则得
A
=
1 EI
3.5103 m = 3.5mm()
=
=
+
+
均布荷载按简支梁进行叠加 ， 按第22页图3-2方法。
集中荷载、均布荷载分别做 弯矩图，然后进行叠加 。
作业： 第77页 4-3（a）、（b）、4-4 （b）
休息一下
作业情况
一、桁架的内力标注在图上。 二、取隔离体：如3-20（a) 图
由Ⅰ-Ⅰ左边隔离体算出FNB后，取下 面四个结点A、B、C、D分别计算？
三、抄作业。 CD是二力杆，有
这样画隔离体的？
这是什么 隔离体？
返回
§4—4 图乘法
MiMk
ds
直杆
MiMk
dx
EI =C
1
EI
EI
EI
MiMk dx
D
=
1 EI
P
aa 2
2 3
a 2
2
a
2
3a 2
4
a 2
2
Pa
23Pa3 =
24EI 例：求图示梁C点的挠度。
？ D = 1 Pl 2 l = Pl 3 C EI 2 6 12 EI
DC
=
wy0
EI
=
1l l
××
222
×5 Pl 6
= 5 Pl 3 48 EI
P
P
MP
Pa
Pa
a
a
a
P=1
a/2
a/2 M 3a/4
P
l/2
Pl
5Pl/6
C
l/2
MP
P=1
l/2
C l/6
M
图乘法 位移计算举例
D
=
MM EI
P
dx
=
AP yC
EI
①∑表示对各杆和各杆段分别图乘而后相加。
②图乘法的应用条件：a）EI=常数；b）直杆；c）两个弯矩图
至少有一个是直线。
③竖标yC 取在直线图形中，对应另一图形的形心处。 ④面积AP与竖标yC在杆的同侧， AP yC 取正号，否则取负号。
（1）M 图的BC段没有弯矩，只需 在AB段进行图乘。
（2）两图均为直线， M 图上取面 积，MP图上取相应竖标，较为简便。
DCH
=
2 EI
1 4m 4m 2
(1 80KN • m 2 160KN • m)
3
3
1067KN • m3
=
()
EI
例4-8：试求图示伸臂梁A端 的角位移φA及C端的竖向位移 ΔCV。 EI = 5104 KN • m2 解：做出MP图和 M 图分别如 图b、c、d所示。
至少有一个是直线。
③竖标yC取在直线图形中，对应另一图形的形心处。 ④面积AP与竖标yC在杆的同侧， AP yC 取正号，否则取负号。
⑤几种常见图形的情况：
单位荷载弯矩图由若干直线段组成 时，就应该分段图乘。
MMP
EI
dx
=
1 EI
( AP1 y1
AP2 y2
AP3 y3 )
两个梯形相乘时，不必找出梯形的
⑤几种常见图形的面积和形心的位置：
h
顶点
3l/4
l/4
h l/2 顶点 l/2
二次抛物线ω=hl/3
二次抛物线ω=2hl/3
⑥当图乘法的适用条件不满足时的处理 方法：
a）曲杆或 EI=EI（x）时，只能用积 分法求位移；
b）当 EI 分段为常数或 M、MP 均非直线时，应分段图乘再叠加。
⑦非标准图形乘直线形
（1）
S = 9/6×（2×6×2 +2 ×4×3
6
4
+6 ×3+4×2） =111
2
3
9
S=9/6×（2×6×2－2×4×3+6×3－4×2）=15
（2）
2
（3）
3
4
4
6
6
3 2
9
9
S = 9/6×（2×6×2+2×4×3－6×3－4×2）= 33
（4）
2
6
3 S = 9/6×（－2×6×2+2×0×3 +6×3－0×2） = －9
将图b与图c相乘则得
A
=
1 5104
1 2
48
6
1 3
1
= 9.6104 rad ( )
结果中的负号表示φA 的 实际方向与Ｍ＝１的方向 相反，即逆时针方向。
将图b与图d相乘则得
BC 段 在 均 布 荷 载 和 集 中荷载作用下，其弯矩图 不是标准的抛物线图形。
= 2.88103 0.6525103
l
A=hl/2
二次抛物线A=2hl/3 顶点
h
h
顶点
3l/4
l/4
二次抛物线A=hl/3
5l/8
3l/8
二次抛物线A=2hl/3
h
h
顶点
4l/5
l/5
三次抛物线A=hl/4
顶点
(n+1)l/(n+2) l/(n+2)
n次抛物线A=hl/(n+1)
例：求图示梁中点的挠度。
？ D= 1 1 3a 3aPa EI 2 4
Mi是直线
1
EI
B
A Mk xtgadx
=
1 tga
EI
B
A xMk dx
Mk
AP
x
dx
=
1 EI
tga×AP
xC =
1 EI
APyC
y
xC
D = MM P dx = AP yC
注：
EI
EI
α Mi=xtgα
①∑表示对各杆和各杆段分别图乘再相加。
Mi yC yC=x0tgα x
②图乘法的应用条件：a）EI=常数；b）直杆；c）两个弯矩图
MMP dx = 1 (
EI
EI
M M P'dx
M M P"dx)
MMP
EI
dx
=
1 EI
( al 2
ya
bl 2
yb )
ya
=
2c1d 33
yb
= 1c 3
2d 3
均布荷载作用区段的弯矩图与直线 段图乘。
几种常见图形的面积和形心的位置：
a
b
h
h l/2 顶点 l/2
(a+l)/3 (b+l)/3
形心，而将一个梯形分解为两个三角 形，然后分别与另一梯形图乘。
MMP dx = 1 (
EI
EI
M M P'dx
M M P"dx)
MMP
EI
dx
=
1 EI
( al 2
ya
bl 2
yb )
ya
=
2c1d 33
yb
=
1c 3
2d 3
两个图形都呈直线变化，但均含有
不同符号的两部分，图乘时也将其中 一图形分解为三角形。
(2 3
l
ql 2 8
)
1 2
=
ql 3 24EI
(
)
将图b与图d相乘则得
DCV
=
1 EI
( AP1 y1 AP2 y2 )
2 2 l ql 2 5
5ql 4
= ( ) l =
()
EI 3 2 8 32 384EI
例4-7：试求图示刚架C点的水平位 移 NhomakorabeaCH。EI为常数。
解：做出MP图和 M 图分别如图b、c 所示。
a）直线形乘直线形
M M dx =AP1 y AP2 y
ik
1
2
a
AP1
Mi
AP2
b
l/3
l/3
l/3
= al 2c d bl c 2d
2 3 3 23 3
c
y1
Mk
y2
d
= l (2ac2bd ad bc)
6
各种直线形乘直线形，都可以用该公式处理。如竖标在基线
同侧乘积取正，否则取负。
9
b)非标准抛物线成直线形
a h
b ＝a
+
举例
b h
c l
d
S
=
l
6 (2ac 2bd
ad
bc ) 2hl
3
cd 2
例4-6：试求图示简支梁A
端的角位移 A 和中点C的竖
向位移 DCV 。EI为常数。
解：荷载作用下的弯矩图和两个单 位弯矩图分别如图b、c、d所示。
将图b与图c相乘则得
A
=
1 EI